GRONINGEN

While still a physics student in the Netherlands in 1972 I came upon a book entitled Inadvertent Climate Modification (Matthews Reference Matthews, Kellogg and Robinson1971). A crucial part of the book was the first decade of Dave Keeling’s CO₂ record at Mauna Loa, which showed a clear increase every single year (still true today, 50 years later!). That book convinced me that CO₂ emissions could become a serious global problem, and I decided to change my future career from physics to earth sciences!

Keeling started the modern atmospheric CO₂ record in 1957 in several places: Antarctica, near the summit of the Mauna Loa volcano on Hawai’i, on the Scripps Pier in La Jolla, California, and on ships (https://keelingcurve.ucsd.edu/). He chose an infrared absorption method, thoroughly supported by very careful calibrations. With the wet chemical methods used before Keeling the measurement noise was so large that any interpretation of changes in the global CO₂ content was hazardous. Before air bubbles trapped in ice cores became the method of choice, isotopic ratios in tree rings presented a possible alternative way to extend the modern CO₂ record back in time, or to at least learn something about the carbon cycle. Wim Mook, the director of “Isotopenfysica”, the environmental isotope section in the physics lab of the University of Groningen, took me on as a PhD candidate in 1973 to measure and interpret isotopic ratios in tree rings. We scoured the Netherlands for old trees, but there were not many. Ship building in previous centuries had taken care of that. We could get slabs of four trees, felled by a wind storm, going back to the middle of the 19th century. Wim asked me to build a proportional counter with capacity for large samples, so that our ¹⁴C measurements could be very precise. After some experimentation I built a system of 7 identical proportional counters, about 1 m long and 4 cm diameter each, with 6 closely packed around the central one. Purified CO₂ sample gas filled the counters at 6 bar of pressure. Each sample required a substantial bag of wood chips cut from one ring, to produce a counting rate of 240 ¹⁴C counts per minute, and relative precision of 1.3 permil in 2 days of counting (Tans and Mook Reference Tans and Mook1979). We counted a few samples for 3 days, just so that we could reach 1.0 permil. The Suess effect stood out beautifully in our tree ring data up to 1950, and we also saw a hint of the 11-year solar cycle in the oldest samples. We used the ¹⁴C bomb spike in 1963 to confirm that there was no transport of carbon between adjacent rings after different chemical pre-treatments of the wood before combustion to CO₂.

At the same time I was measuring ¹³C/¹²C and ¹⁸O/¹⁶O in the same tree rings to document the ¹³C/¹²C signature of the Suess effect. The isotope ratios turned out to be difficult to interpret. We found enormous variability between the years and between trees. There appeared to be a decrease of ¹³C/¹²C from 1850 to 1900, but in the 20th century the trend went in the “wrong” direction. Since we had large slabs of the four trees we could sample the entire circumference of each ring. Within-ring variations were up to ∼4.5‰, but correlated strongly between adjacent rings. Alas, our chosen (free-standing) trees had not evolved with our application in mind; there were clearly other and larger influences on the ¹³C/¹²C signature than the Suess Effect, at least up to 1970. In early 1978, a few months before my thesis defense, Wim Mook and I attended a climate conference in Vienna, at which H. Freyer showed results obtained from a few dozen trees (Freyer and Wiesberg Reference Freyer and Wiesberg1973; Freyer Reference Freyer1979). His average ¹³C/¹²C ratio declined by about 1‰ from 1900 to 1970. This decline was 2/3 of what he could expect when he took the estimated CO₂ increase from 1900 to 1970, assigned the fossil fuel isotopic signature to it, and then diluted that in the atmosphere with an estimated pre-industrial isotopic signature.

I knew by then that the measured decrease shown by Freyer had to be too large as a global number. I was convinced of that because during the writing of my thesis I had developed a simple and intuitive way to deal with isotopic ratios and exchanges between reservoirs (Tans et al. Reference Tans, Berry and Keeling1993). In the following ¹²C_a, ¹³C_a, and C_a denote atmospheric abundances. Here we only consider exchange with the oceans in some detail, but other carbon reservoirs such as terrestrial plants and soils can be treated similarly. When writing abundance ratios not as R_a = ¹³C_a/¹²C_a but as the ratio of ¹³C_a to total carbon, R_a = ¹³C_a/(¹²C_a+¹³C_a) = ¹³C_a/C_a, one gets ¹³C_a = R_a C_a. The change in time of ¹³C_a can then be split into two components,

$${\rm{d}}{(^{{\rm{13}}}}{{\rm{C}}_{\rm{a}}})/{\rm{dt}} = {\rm{d}}({{\rm{R}}_{\rm{a}}}{{\rm{C}}_{\rm{a}}})/{\rm{dt}} = {{\rm{C}}_{\rm{a}}}{\rm{d}}{{\rm{R}}_{\rm{a}}}/{\rm{dt}} + {{\rm{R}}_{\rm{a}}}{\rm{d}}{{\rm{C}}_{\rm{a}}}/{\rm{dt}}.$$

For air-sea gas exchange we have

$$\matrix{ {{\rm{d}}{{\rm{C}}_{\rm{a}}}/{\rm{dt}} = {{\rm{F}}_{{\rm{fos}}}} + {{\rm{F}}_{{\rm{oa}}}} - {{\rm{F}}_{{\rm{ao}}}}{\mkern 1mu} {\rm{and}}} \cr {{\rm{d}}{(^{{\rm{13}}}}{{\rm{C}}_{\rm{a}}})/{\rm{dt}} = {{\rm{R}}_{{\rm{fos}}}}{{\rm{F}}_{{\rm{fos}}}} + {\alpha _{{\rm{oa}}}}{{\rm{R}}_{\rm{o}}}{{\rm{F}}_{{\rm{oa}}}} - {\alpha _{{\rm{ao}}}}{{\rm{R}}_{\rm{a}}}{{\rm{F}}_{{\rm{ao}}}}.} \cr } $$

The symbol “F” stands for fluxes, with the subscript “ao” meaning “from atmosphere to oceans”, etc. F_ao is governed by the partial pressure of CO₂ at the air-water interface which closely follows C_a. R_o is the isotopic ratio of surface ocean carbon, and the alphas are kinetic isotopic fractionation factors, slightly different from 1, for air-sea gas exchange in both directions. The previous three expressions lead to

$${{\rm{C}}_{\rm{a}}}\ {\rm{d}}{{\rm{R}}_{\rm{a}}}/{\rm{dt}} = {{\rm{F}}_{{\rm{fos}}}}({{\rm{R}}_{{\rm{fos}}}}-{{\rm{R}}_{\rm{a}}})-{{\rm{F}}_{{\rm{ao}}}}({\alpha _{{\rm{ao}}}} - {\rm{1}})\,{{\rm{R}}_{\rm{a}}} + {{\rm{F}}_{{\rm{oa}}}}({\alpha _{{\rm{oa}}}}{{\rm{R}}_{\rm{o}}}-{{\rm{R}}_{\rm{a}}})$$

If the oceans are (on average) in equilibrium with the atmosphere we have both F_oa = F_ao and α_oaR_o = α_aoR_a. We can define R_a ^eq as the isotopic ratio the atmosphere would have if it were completely determined by equilibrium with the surface oceans, R_a ^eq = (α_oa/α_ao)R_o. The factor α_oa/α_ao is the temperature dependent isotopic equilibrium ratio between the atmosphere and total dissolved inorganic carbon (DIC) in the surface oceans. Because we are talking here about the global average flux we need an average that is weighted by the product of area, dissolved CO₂ (see below), and rate of air-sea gas exchange. The latter is correlated with wind speed for which we can take climatological averages. The factor R_o is very nearly the same almost everywhere in the surface oceans. We will come back to this later. Using R_a ^eq we can separate the effect of total carbon fluxes (F_ao – F_oa) and the pure isotopic fluxes in the last term of Equation (1):

(1) $$\matrix{ {{{\rm{C}}_{\rm{a}}}{\rm{d}}{{\rm{R}}_{\rm{a}}}/{\rm{dt}} = {{\rm{F}}_{{\rm{fos}}}}\left( {{{\rm{R}}_{{\rm{fos}}}} - {{\rm{R}}_{\rm{a}}}} \right) - {{\rm{F}}_{{\rm{ao}}}}\left( {{\alpha _{{\rm{ao}}}} - {\rm{1}}} \right){\mkern 1mu} {{\rm{R}}_{\rm{a}}} + {{\rm{F}}_{{\rm{oa}}}}\left( {{\alpha _{{\rm{ao}}}}{{\rm{R}}_{\rm{a}}}^{{\rm{eq}}} - {{\rm{R}}_{\rm{a}}}} \right),{\mkern 1mu} {\rm{and}}{\mkern 1mu} {\rm{after}}{\mkern 1mu} {\rm{some}}{\mkern 1mu} {\rm{regrouping}}} \hfill \cr {{{\rm{C}}_{\rm{a}}}{\rm{d}}{{\rm{R}}_{\rm{a}}}/{\rm{dt}} = {{\rm{F}}_{{\rm{fos}}}}({{\rm{R}}_{{\rm{fos}}}} - {{\rm{R}}_{\rm{a}}}) - ({{\rm{F}}_{{\rm{ao}}}} - {{\rm{F}}_{{\rm{oa}}}}){\mkern 1mu} ({\alpha _{{\rm{ao}}}} - {\rm{1}}){\mkern 1mu} {{\rm{R}}_{\rm{a}}} + {{\rm{F}}_{{\rm{oa}}}}{\alpha _{{\rm{ao}}}}({{\rm{R}}_{\rm{a}}}^{{\rm{eq}}} - {{\rm{R}}_{\rm{a}}})} \hfill \cr } $$

If desired, Equation (1) can be easily recast in terms of the customary delta notation by dividing every R by R_std, where the standard is PDB and it has also been redefined as the ratio of ¹³C_std to total carbon C_std. Then R_x/R_std = 1+δ_x. In this way the redefined numerical value of δ changes by a factor of 1-R_std, which is very close to (1-0.011). The middle term of Equation (1) is the effect on the atmospheric isotopic ratio of a net total CO₂ flux (F_ao –F_oa) into the oceans, and α_ao is ∼0.998, very close to 1, so that this contribution is close to zero. The case of exchange between the atmosphere and terrestrial ecosystems is different. Isotopic fractionation during photosynthesis is much larger, with α = ∼0.98, so then the middle term is important. The last term in Equation (1) describes pure isotopic equilibration that always takes place regardless of what the net total flux is.

Net exchange of total CO₂ on the water side is controlled by fast equilibrium reactions between dissolved CO₂ and HCO₃ ⁻ and CO₃ ⁻² ions, collectively called dissolved inorganic carbon (DIC). If the relative increase of atmospheric CO₂ is 10%, chemical equilibrium between the atmosphere and oceans is restored when the relative increase of DIC is only about 1% and the pH is lowered. This difference of a factor of ∼10 is called the Revelle factor (Broecker et al. Reference Broecker, Takahashi, Simpson and Peng1979). Therefore the upper ocean mixed layer is equilibrated relatively quickly, and needs to be replaced by deeper waters to restart CO₂ uptake. The Revelle factor does not apply to isotopic equilibration because a ¹²CO₂ molecule is replaced by a ¹³CO₂ or vice versa. As a result, an isotopic anomaly disappears from the atmosphere more quickly than a total CO₂ anomaly. The last term of Equation (1) is proportional to the global one-way flux F_ao (or F_oa, they are almost the same) which in 1970 was estimated to be about 80 billion metric ton carbon (GtonC) per year, and today about 100 GtonC/yr because of higher atmospheric CO₂ and dissolved CO₂ in surface waters.

Because Freyer’s observed decrease of ¹³C/¹²C in tree rings appeared to be too large, as explained in the previous paragraphs, I questioned him, and it turned out that he had selected a subset of the trees that were sampled. All trees had been selected for location, not in a forest, but in places with good access to “clean” air, such as facing the ocean in the prevailing winds. However, when the measurement results of a tree showed features that appeared to contradict his expectations, he found reasons to not consider those results. I thought that was embarrassing. Minze Stuiver and colleagues, in a paper discussing many of the potential problems with the reconstruction of atmospheric CO₂ from tree rings, also found it hard to reconcile Freyer’s record with atmospheric history going back a few centuries (Stuiver Reference Stuiver, Burk and Quay1984).

Today, many years later, we have obtained a good record of recent pre-industrial ¹³C/¹²C and CO₂ from ice cores, especially the high-resolution record from Law Dome in coastal Antarctica (Francey et al. Reference Francey, Ellison, Etheridge, Trudinger, Enting, Leuenberger, Langenfelds and Steele1999). The ice core data show that δ¹³C decreased from –6.7 to –6.9‰ between 1900 and 1950. After 1950 the rate of decrease accelerated, in 1970 δ¹³C was –7.2‰, and in 2019 –8.5‰ (Figure 1). The Law Dome record matches well with NOAA/Global Monitoring Laboratory (GML)’s Global Greenhouse Gas Reference Network (GGGRN) for many gases and isotopic ratios (https://gml.noaa.gov/ccgg/trends/).

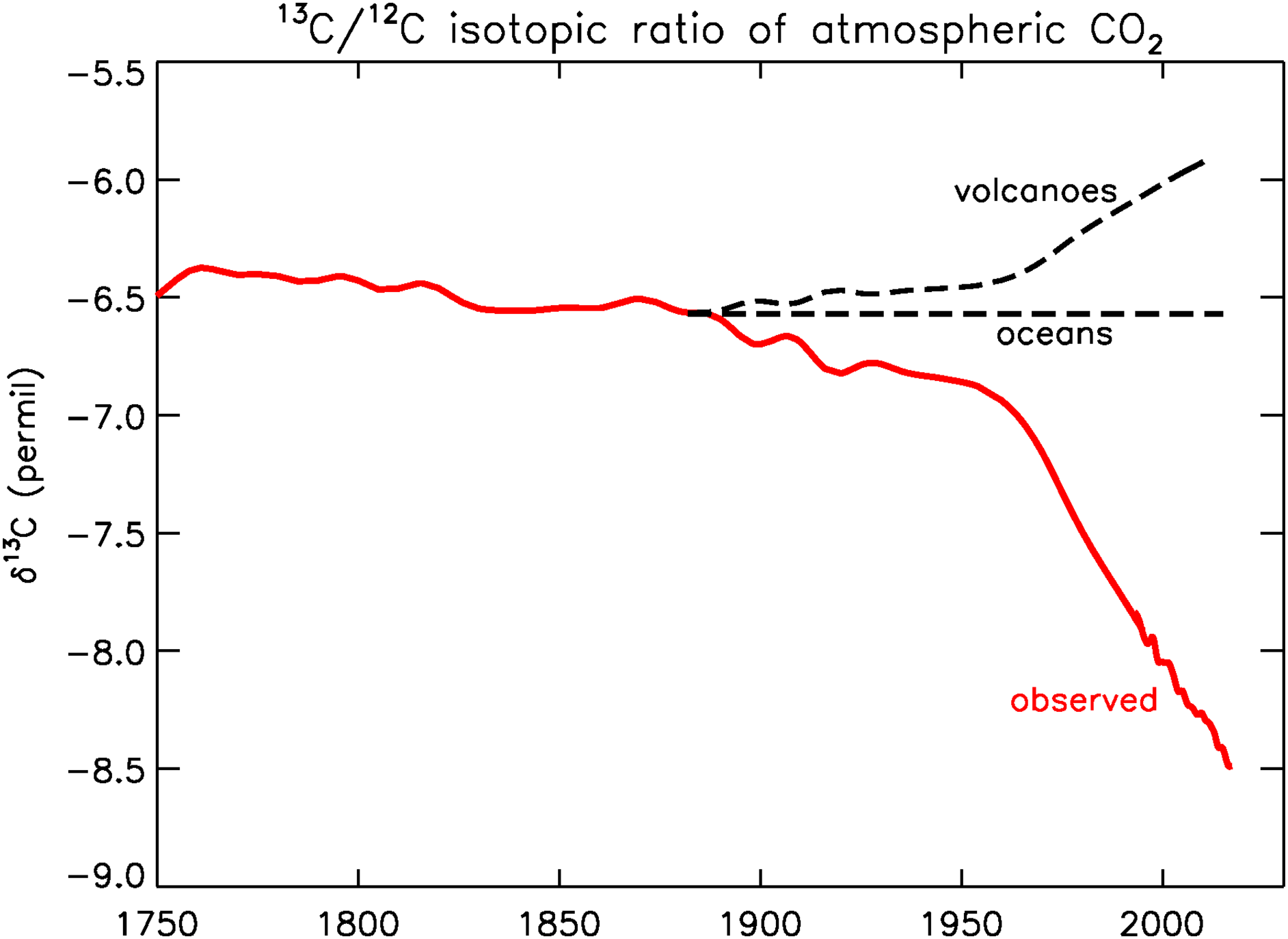
Figure 1 Observed ¹³C/¹²C ratio of atmospheric CO₂ (red). After 1992, data from Inst. Arctic and Alpine Research (INSTAAR), U. of Colorado; Before 1992, Francey et al. (Reference Francey, Ellison, Etheridge, Trudinger, Enting, Leuenberger, Langenfelds and Steele1999). Dashed black lines, hypothetical atmospheric histories if the CO₂ enhancement had been produced by volcanism or by ocean outgassing. (Please see electronic version for color figures.)

NOAA

After my PhD defense in Groningen in 1978 our family moved to the Scripps Institution of Oceanography for my postdoc with Dave Keeling. After Scripps I did a six-year stint with the astrophysics group in Lawrence Berkeley Lab in Berkeley, CA, where I worked on measurements of ¹⁴C with the 88” cyclotron, and on trying to develop extremely precise measurements of the O₂/N₂ ratio of atmospheric air, using Raman scattering. Neither project was successful. The O₂/N₂ project was done with NOAA funding, which led to my move to NOAA in 1985 at the invitation of Lester Machta, who was then director of NOAA’s Air Resources Laboratory.

We now come back to the globally weighted average R_a ^eq which exerts a major influence on the isotopic ratio of atmospheric CO₂. We participated in the research cruise GasEx98, in the early summer of 1998, in the mid North Atlantic on the NOAA ship Ron Brown. The aim was to better quantify the process of air-sea gas exchange so that the atmosphere would tell us more about the oceans and vice versa. Two groups made independent atmospheric measurements using both eddy covariance and vertical gradients. One was a collaboration of Rik Wanninkhof and Wade McGillis (Reference Wanninkhof and McGillis1999), and the second group consisted of Jim Smith, Michael Hahn and myself of GGGRN. The measurements were very hard because average vertical gradients from the top of a mast near the bow to 1–2 m above the water were only a small fraction of 1 ppm. There were also many potential artifacts to avoid, caused by ship motion, flow distortion around the ship, salt and moisture in the air intake lines, and more. Eddy covariance relies on tiny differences in mole fraction between up- and down-going eddies. Jim thought he had a correlation signal until he shut down the flow through the analyzer—the signal remained! When the air in the analyzer cell does not change at all there should be no correlation with vertical wind velocity variations (which had already been corrected for ship motion). When he turned the orientation of the analyzer 90 degrees, the signal changed in magnitude but did not go away. He traced it to torques exerted by the ship motion on the optical beam chopper wheel which changed the on-off timing by small amounts. The other group also had an optical chopper, but they believed their data to be good enough to give them evidence to conclude that the air-sea gas transfer velocity depends on the third power of wind speed (Wanninkhof and McGillis Reference Wanninkhof and McGillis1999). I argued—in vain—that a cubic would upset the global R_a ^eq value by giving more weight to cold waters at southern high latitudes and less weight to warm waters at low latitudes. δ_a ^eq (as in R_a ^eq = 1+δ_a ^eq) increases with temperature by 0.114‰/K. δ_a ^eq over 0^oC waters is –9.8‰, over 26^oC waters −6.8‰. The cubic relationship would have pushed pre-industrial global δ¹³C to become lower, well outside the observed range of –6.5 to –6.3‰ (Francey et al. Reference Francey, Ellison, Etheridge, Trudinger, Enting, Leuenberger, Langenfelds and Steele1999) assuming that other factors remain equal. As far as I can tell, the cubic has quietly disappeared by now. This story also illustrates how difficult it can be to get reliable observational data for the very small differences that drive carbon exchange on large spatial scales.

FOSSIL FUELS AND THE GLOBAL CARBON BUDGET

The observed atmospheric history of ¹³C/¹²C tells us in a qualitative way that the sources of the CO₂ enhancement must be of an organic nature, either modern or old, as shown in Figure 1. Photosynthesis depletes ¹³C/C by about 20‰ relative to its atmospheric source, and the observed atmospheric history reflects that. It has been argued by fossil fuel apologists that the CO₂ explosion observed in the atmosphere is not caused by the burning of coal, oil, and natural gas. No, they say that it comes from the oceans, or from volcanoes. If a sustained ocean “burp” is the cause, the ¹³C_a/C_a ratio would not have changed, as is sketched in Figure 1, because the atmospheric ratio has been (nearly) in equilibrium with the ocean surface over geologic times. In fact, the total amount of carbon in DIC was ∼60 times larger than in the atmosphere during the Holocene, so the oceans “dictate” the ¹³C_a/C_a ratio in the long term. If the cause is volcanic, the recent atmospheric ratio would have become more enriched because volcanic CO₂ has a ¹³C/C ratio close to that of the standard PDB, which is a limestone, or ∼0 ‰. It has been sketched in Figure 1 as a scaled mirror image (w.r.t. the constant level labeled “oceans”) of the red curve.

Also in the case of ¹⁴C the Revelle factor does not apply, but the nuclear bomb ¹⁴C peak’s observed decay in the atmosphere has nevertheless caused much confusion for the climate debate. It has been used to argue, especially in circles receiving money from the coal and oil/gas industry (Oreskes and Conway Reference Oreskes and Conway2010), that the CO₂ increase from fossil fuel burning cannot be a problem because the ¹⁴C history shows that the residence time of CO₂ in the atmosphere is only a few years (e.g., Starr Reference Starr1993; Essenhigh Reference Essenhigh2009). They typically are not aware of the Revelle factor and/or have CO₂ effectively disappear as if a chemical lifetime applies as with CH₄ or N₂O. Also, they typically have to postulate sources other than fossil fuels to match observations, and that’s exactly what they are looking for.

In the last two decades atmospheric ¹⁴CO₂ has become diluted enough by ¹⁴C-free fossil CO₂ for its ¹⁴C_a/C_a ratio to drop below ¹⁴C_o/C_o in the subtropical ocean gyres (e.g., Guilderson Reference Guilderson, Schrag and Cane2004; and for the atmosphere, Lee Reference Lee, Dlugokencky, Turnbull, Lee, Lehman, Miller, Petron, Lim, Lee, Lee and Park2020), so that the atmosphere is pulling back out of the gyres some of the excess bomb ¹⁴C that entered in earlier decades. Again, it’s the isotopic ratio disequilibrium term (R_a ^eq – R_a) in Equation (1), but in this case R_a ^eq is regional, limited to the gyres. Although the equivalent of Equation (1) for ¹⁴C looks different because of corrections for isotopic fractionation and nuclear decay, the isotopic disequilibrium term works the same. Since total carbon in the oceans, C_o, is so much larger than C_a, globally averaged isotopic equilibrium between the two reservoirs (¹⁴C_o/C_o = ¹⁴C_a/C_a), forces almost all bomb ¹⁴C to eventually end up in the oceans. That split is very different for the total carbon anomaly (see below). Incidentally, a situation where ocean surface waters have higher ¹⁴C_o/C_o than ¹⁴C_a/C_a has probably not existed for hundreds of millions of years, except perhaps when geomagnetic reversals could have caused large cosmic ray anomalies. It does show, qualitatively, that the emissions creating today’s CO₂ excursion must come from very old carbon.

CLIMATE POLICIES AND SCIENCE

We cannot assume that people who think that CO₂ emissions just disappear, in a few years or more slowly in a century or so, constitute a small minority. We should remember that in the early days of Integrated Assessment Models (combining physical and socio-economic models) CO₂ was often given a residence time as if it simply disappeared. No wonder that the optimal economic strategy to deal with climate change often came out as “Wait, it will be cheaper to tackle it later when we are so much wealthier and technology has advanced further” (e.g., Nordhaus Reference Nordhaus1992; for a critique, Dietz Reference Dietz and Stern2015). Economists do not know whether we will indeed be wealthier in the future, even by their own definition of wealth. It is an assumption, coded into the models as a “future discount factor” that is ultimately based on a belief that exponential growth can continue indefinitely which appears quite common in mainstream economics. Estimates of desirable growth rates tended to come down in recent decades, from ∼5% to ∼2% per year. Two percent is still absurd, it corresponds to a doubling time of 35 years. Any sustained exponential growth on our finite earth turns into a guaranteed disaster, which we can now clearly see the onset of, and not only in the realm of climate change.

Furthermore, we actually know that CO₂ does not disappear at all. The emissions anomaly is shared with the oceans and terrestrial ecosystems. When equilibrium with the full oceans is restored in a thousand years or so after the fossil CO₂ pulse, about 17% of the excess CO₂ remains in the atmosphere “forever”, and 83% in the oceans when we only consider chemistry, implicitly assuming that ocean circulation and marine biology remain unchanged. Here we have also ignored carbon stored in terrestrial ecosystems, which lost carbon from land use change in the 19th and early 20th centuries, but regained it after 1950 when widespread fertilizer use took off and when higher CO₂ may have also fertilized terrestrial ecosystems. Any lifetime choice I have seen for the CO₂ anomaly ignored the “permanent” airborne fraction of ∼17%. It could be larger, or less, depending on ocean circulation and marine biology but those are hard to predict at this point. “Permanent” is in quotation marks because on a time scale of 3–7 thousand years the dissolved CO₂ (CO₂ + H₂O ⇔ H₂CO_3, Arrhenius Reference Arrhenius1896) will be neutralized (H₂CO₃ + CaCO₃ ⇒ Ca²⁺ + 2HCO₃ ⁻) by the dissolution of CaCO₃ sediments and coral reefs (Archer et al. Reference Archer, Eby, Brovkin, Ridgwell, Cao, Mikolajewicz, Caldeira, Matsumoto, Munhoven, Montenegro and Tokos2009). Even then the CO₂ would still be there, in the oceans, but at least not in the atmosphere any more.

The mistaken residence time or lifetime of CO₂ emissions is still with us to this day. To assist policy makers the Intergovernmental Panel on Climate Change (IPCC) introduced a measure, Global Warming Potential (GWP) in their Second Assessment Report (IPCC Reference Schimel1996), to compare the climate impact of emissions of different gases with each other. What matters are the strength and location of optical absorption/emission lines and the amount of time each gas remains in the atmosphere. These comparisons work well for gases that are photochemically destroyed and a lifetime can be defined. CO₂ was picked as the reference, so that the climate impact of each gas is expressed as CO₂ equivalents, often denoted as CO₂e or CO₂eq. But which lifetime do we assign to CO₂? It simply does not apply. The chosen solution was to implement a “time horizon”, let’s call it H, and only estimate the cumulative heat retained in the atmosphere from the time of emissions until H years later. IPCC (Reference Schimel1996) chose three values of H, 20, 100, and 500 years of which 100 was widely adopted by governments for reporting emissions, but 20 has also been used, while 500 did not get any traction. Obviously, H=100 and even more so H=20 understate the real impact of longer lived gases. It worked as an invitation to create a bias toward short-term policies, effectively ignoring the long-term effects, notwithstanding the known fact that our global climate (and ocean acidification) problem is very long-lived (Tans Reference Tans1997). It is effectively irreversible by natural processes on time scales of human civilizations. It is essentially a moral issue; our generation refusing to take responsibility for our own actions. Later IPCC assessments tried to remedy the misperception by adding a discussion of CO₂’s very long tail, but it was too late. At the time of this writing I have requests from three different journals to review papers claiming to define improved lifetimes for CO₂. One of those papers I have seen already three times, submitted to one journal after another.

The CO₂ Seasonal Cycle and Annual Variations

When CO₂ and its δ¹³C ratio are studied together we can immediately see that the seasonal cycle in the Northern Hemisphere is almost entirely caused by terrestrial ecosystems (Figure 2). We use low-pass smoothing (in the frequency domain) filters to remove high frequency variability (Thoning et al. Reference Thoning, Tans and Komhyr1989). The seasonal cycles of δ¹³C very nearly mirror those of total CO₂, including the little pause in January–February, and they show that on average the isotopic signature of the seasonal source/sink is −18.8‰ relative to the atmospheric reservoir over 2010–2015. The pause in January–February occurs because respiration from soils and vegetation is at a minimum at the lowest temperatures in winter. The signature of −18.8‰ is close to the measured isotopic discrimination during photosynthesis in C3 plants. The addition or removal of 1 ppm of CO₂ depleted by 18.8‰ is mixed into 394 ppm, making a change of the atmospheric isotopic ratio of −0.0477‰/ppm. The amplitude of the seasonal cycle in the Southern Hemisphere is much smaller, is out of phase with the Northern Hemisphere, and lacks the tight correlation shown in Figure 2.

Figure 2 Five years of CO₂ and δ¹³C measurements in the same air samples at the Mauna Loa Observatory at 3.4 km altitude, near the summit of the volcano. The long-term trend has been removed from both records, leaving the seasonal cycle. Black diamond symbols, individual flask air samples; red smooth curves are drawn using a low-pass filter removing high frequency variability.

To extract the long-term trend from the data we set the low-pass cutoff low enough that we effectively have a smoother with a full width at half maximum (FWHM) of 1.00 year, which strongly suppresses the seasonal cycle. We call this the (de-seasonalized) long-term trend, or “trend” for short. It has been subtracted from the data to produce the (de-trended) seasonal cycles in Figure 2. Next, we make similar plots for the growth rate (time derivative) of the trends of CO₂ and δ¹³C, but over a longer time span (Figure 3). Dave Keeling’s collaborator Bob Bacastow (Reference Bacastow1976) discovered a correlation between these interannual variations of the CO₂ growth rate and the El Niño Southern Oscillation (ENSO). They are primarily caused by seasonal and annual anomalies of precipitation, temperature, insolation, etc. affecting the terrestrial biosphere. The center points of El Niño and La Niña episodes are indicated by arrows.

Figure 3 Time derivative of the long-term trends of CO₂ and δ¹³C at the Mauna Loa Observatory. Upward arrows are at the center points of major El Niño episodes, and downward dashed arrows indicate the center points of major La Niña episodes.

There is now a large body of literature on the subject, but I want to draw attention to the average growth rate of CO₂ at Mauna Loa. Over 1995–2015 it is 2.00 ppm/year, and −0.026‰/year for δ¹³C. If we (mistakenly) were to dilute 2.0 ppm/year at −19‰ (a rough average for the depletion of fossil fuels and cement relative to the atmosphere) into a reservoir of 381 ppm (an approximate atmospheric average during 1995−2015), we would predict a rate of decrease for δ¹³C of −0.100‰/year, four times larger than we observed. Isotopic exchange is large enough sometimes to have the d(δ¹³C)/dt growth rate go in the “wrong” direction, whereas the dC_a/dt growth rate is always positive. The figure suggests that terrestrial variations are the largest component of the observed annual variability but that the oceans also contribute.