Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Fukunaga, Takuro
Halldórsson, Magnús M.
and
Nagamochi, Hiroshi
2007.
FSTTCS 2007: Foundations of Software Technology and Theoretical Computer Science.
Vol. 4855,
Issue. ,
p.
84.
Cardinal, Jean
Fiorini, Samuel
and
Joret, Gwenaël
2009.
Mathematical Theory and Computational Practice.
Vol. 5635,
Issue. ,
p.
79.
Flammini, Michele
Monaco, Gianpiero
Moscardelli, Luca
Shachnai, Hadas
Shalom, Mordechai
Tamir, Tami
and
Zaks, Shmuel
2009.
Minimizing total busy time in parallel scheduling with application to optical networks.
p.
1.
NONNER, TIM
and
SOUZA, ALEXANDER
2009.
APPROXIMATING THE JOINT REPLENISHMENT PROBLEM WITH DEADLINES.
Discrete Mathematics, Algorithms and Applications,
Vol. 01,
Issue. 02,
p.
153.
Nonner, Tim
and
Souza, Alexander
2009.
Algorithmic Aspects in Information and Management.
Vol. 5564,
Issue. ,
p.
279.
Flammini, Michele
Monaco, Gianpiero
Moscardelli, Luca
Shachnai, Hadas
Shalom, Mordechai
Tamir, Tami
and
Zaks, Shmuel
2010.
Minimizing total busy time in parallel scheduling with application to optical networks.
Theoretical Computer Science,
Vol. 411,
Issue. 40-42,
p.
3553.
Nonner, Tim
2010.
Algorithm Theory - SWAT 2010.
Vol. 6139,
Issue. ,
p.
176.
Kaiqian Ou
Yinlong Xu
and
Shengli Fu
2012.
Rate selection for wireless networks with intraand inter-session network coding.
p.
4707.
Abdallah, Yara
Zheng, Zizhan
Shroff, Ness B.
and
El Gamal, Hesham
2012.
On the efficiency-vs-security tradeoff in the smart grid.
p.
1954.
Pirwani, Imran A.
and
Salavatipour, Mohammad R.
2012.
A Weakly Robust PTAS for Minimum Clique Partition in Unit Disk Graphs.
Algorithmica,
Vol. 62,
Issue. 3-4,
p.
1050.
Catanzaro, Daniele
Labbé, Martine
and
Halldórsson, Bjarni V.
2012.
Bioinformatics Research and Applications.
Vol. 7292,
Issue. ,
p.
24.
Cardinal, Jean
Fiorini, Samuel
and
Joret, Gwenaël
2012.
Minimum Entropy Combinatorial Optimization Problems.
Theory of Computing Systems,
Vol. 51,
Issue. 1,
p.
4.
Catanzaro, Daniele
Labbe, Martine
and
Halldorsson, Bjarni V.
2013.
An Integer Programming Formulation of the Parsimonious Loss of Heterozygosity Problem.
IEEE/ACM Transactions on Computational Biology and Bioinformatics,
Vol. 10,
Issue. 6,
p.
1391.
Correa, José R.
and
Megow, Nicole
2015.
Clique partitioning with value-monotone submodular cost.
Discrete Optimization,
Vol. 15,
Issue. ,
p.
26.
Nonner, Tim
2016.
Capacitated Max-Batching with interval graph compatibilities.
Theoretical Computer Science,
Vol. 613,
Issue. ,
p.
79.
Catanzaro, Daniele
Chaplick, Steven
Felsner, Stefan
Halldórsson, Bjarni V.
Halldórsson, Magnús M.
Hixon, Thomas
and
Stacho, Juraj
2017.
Max point-tolerance graphs.
Discrete Applied Mathematics,
Vol. 216,
Issue. ,
p.
84.
Abdallah, Yara
Zheng, Zizhan
Shroff, Ness B.
El Gamal, Hesham
and
El-Fouly, Tarek M.
2017.
The Impact of Stealthy Attacks on Smart Grid Performance: Tradeoffs and Implications.
IEEE Transactions on Control of Network Systems,
Vol. 4,
Issue. 4,
p.
886.
Boysen, Nils
Briskorn, Dirk
and
Schwerdfeger, Stefan
2018.
The identical-path truck platooning problem.
Transportation Research Part B: Methodological,
Vol. 109,
Issue. ,
p.
26.
Porretta, Luciano
Catanzaro, Daniele
Halldórsson, Bjarni V.
and
Fortz, Bernard
2019.
A Branch & Price algorithm for the minimum cost clique cover problem in max-point tolerance graphs.
4OR,
Vol. 17,
Issue. 1,
p.
75.
Levin, M. Sh.
2022.
On the Clique Partitioning of a Graph.
Journal of Communications Technology and Electronics,
Vol. 67,
Issue. S2,
p.
S267.
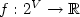 (provided by an oracle), the problem [PCliqW] consists in finding a partition into cliques of V(G) of minimum cost. Here, the cost of a partition is the sum of the costs of the cliques in the partition.We provide a polynomial time dynamic program for the case where G is an interval graph and f belongs to a subclass of submodular set functions, which we call “value-polymatroidal”.This provides a common solution for various generalizations of the coloringproblem in co-interval graphs such as max-coloring,“Greene-Kleitman's dual”, probabilist coloring and chromatic entropy. In the last two cases, this is the first polytime algorithm for co-interval graphs. In contrast, NP-hardness of related problems is discussed. We also describe an ILP formulation for [PCliqW] which gives a common polyhedral framework to express min-max relations such as ${\overline{\chi}}=\alpha$
(provided by an oracle), the problem [PCliqW] consists in finding a partition into cliques of V(G) of minimum cost. Here, the cost of a partition is the sum of the costs of the cliques in the partition.We provide a polynomial time dynamic program for the case where G is an interval graph and f belongs to a subclass of submodular set functions, which we call “value-polymatroidal”.This provides a common solution for various generalizations of the coloringproblem in co-interval graphs such as max-coloring,“Greene-Kleitman's dual”, probabilist coloring and chromatic entropy. In the last two cases, this is the first polytime algorithm for co-interval graphs. In contrast, NP-hardness of related problems is discussed. We also describe an ILP formulation for [PCliqW] which gives a common polyhedral framework to express min-max relations such as ${\overline{\chi}}=\alpha$ 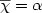 for perfect graphs and the polymatroid intersection theorem. This approach allows to provide a min-max formula for [PCliqW] if G is the line-graph of a bipartite graph and f is submodular.However, this approach fails to provide a min-max relation for [PCliqW] if G is an interval graphs and f is value-polymatroidal.
for perfect graphs and the polymatroid intersection theorem. This approach allows to provide a min-max formula for [PCliqW] if G is the line-graph of a bipartite graph and f is submodular.However, this approach fails to provide a min-max relation for [PCliqW] if G is an interval graphs and f is value-polymatroidal.
