(1) Shepherdson proved that a discrete unitary commutative semi-ring A+ satisfies IE0 (induction scheme restricted to quantifier free formulas) iff A is integral part of a real closed field; and Berarducci asked about extensions of this criterion when exponentiation is added to the language of rings. Let T range over axiom systems for ordered fields with exponentiation; for three values of T we provide a theory $_{\llcorner} T _{\lrcorner}$ 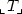in the language of rings plus exponentiation such that the models (A, expA) of $_{\llcorner} T _{\lrcorner}$ 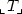are all integral parts A of models M of T with A+ closed under expM and expA = expM | A+. Namely T = EXP, the basic theory of real exponential fields; T = EXP+ the Rolle and the intermediate value properties for all 2x-polynomials; and T = Texp, the complete theory of the field of reals with exponentiation. (2)$_{\llcorner}$Texp$_{\lrcorner}$ is recursively axiomatizable iff Texp is decidable. $_{\llcorner}$Texp$_{\lrcorner}$ implies LE0(xy) (least element principle for open formulas in the language <,+,x,-1,xy) but the reciprocal is an open question. $_{\llcorner}$Texp$_{\lrcorner}$ satisfies “provable polytime witnessing”: if $_{\llcorner} $Texp$_{\lrcorner}$ proves ∀x∃y : |y| < |x|k)R(x,y) (where $|y|:=_{\llcorner}$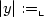log(y)$_{\lrcorner}$, k < ω and R is an NP relation), then it proves ∀x R(x,ƒ(x)) for some polynomial time function f. (3) We introduce “blunt” axioms for Arithmetics: axioms which do as if every real number was a fraction (or even a dyadic number). The falsity of such a contention in the standard model of the integers does not mean inconsistency; and bluntness has both a heuristic interest and a simplifying effect on many questions – in particular we prove that the blunt version of $_{\llcorner} $Texp$_{\lrcorner}$ is a conservative extension of $_{\llcorner} $Texp$_{\lrcorner}$ for sentences in ∀Δ0(xy) (universal quantifications of bounded formulas in the language of rings plus xy). Blunt Arithmetics – which can be extended to a much richer language – could become a useful tool in the non standard approach to discrete geometry, to modelization and to approximate computation with reals.