Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T13:52:49.718Z Has data issue: false hasContentIssue false
  • English
  • Français

Study of irreducible balanced pairs for substitutive languages

Published online by Cambridge University Press:  15 January 2008

Julien Bernat
Julien Bernat*
Affiliation:
IML CNRS UMR 6206 Campus de Luminy, Case 907 13288 Marseille, Cedex 9, France; bernat@iml.univ-mrs.fr
Get access

Abstract

Let $\mathcal{L}$ 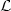be a language. A balanced pair (u,v) consists of two words u and v in $\mathcal{L}$ 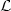which have the same number of occurrences of each letter. It is irreducible if the pairs of strict prefixes of u and v of the same length do not form balanced pairs. In this article, we are interested in computing the set of irreducible balanced pairs on several cases of languages. We make connections with the balanced pairs algorithm and discrete geometrical constructions related to substitutive languages. We characterize substitutive languages which have infinitely many irreducible balanced pairs of a given form.

Keywords

Substitutive languagesbalanced pairsalgorithm on words.
Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 42 , Issue 4: Fibonacci words , October 2008 , pp. 663 - 678
Copyright
© EDP Sciences, 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adamczewski, B., Balances for fixed points of primitive substitutions. Theoret. Comput. Sci. 307 (2003) 47–75. CrossRef
Ambrož, P., Masáková, Z., Pelantová, E. and Frougny, C., Palindromic complexity of infinite words associated with simple Parry numbers. Ann. Inst. Fourier (Grenoble) 56 (2006) 2131–2160. CrossRef
Arnoux, P. and Ito, S., Pisot substitutions and Rauzy fractals. Bull. Belg. Math. Soc. Simon Stevin 8 (2001) 181–207.
Arnoux, P. and Rauzy, G., Représentation géométrique de suites de complexité 2n + 1. Bull. Soc. Math. France 119 (1991) 199–215. CrossRef
P. Arnoux, V. Berthé, H. Ei and S. Ito, Tilings, quasicrystals, discrete planes, generalized substitutions, and multidimensional continued fractions, in Discrete models: combinatorics, computation, and geometry (Paris, 2001). Discrete Math. Theor. Comput. Sci. Proc., AA, pp. 059–078 (electronic). Maison Inform. Math. Discrèt. (MIMD), Paris (2001).
Arnoux, P., Berthé, V. and Ito, S., Discrete planes, $\mathbb Z\sp 2$ -actions, Jacobi-Perron algorithm and substitutions. Ann. Inst. Fourier (Grenoble) 52 (2002) 305–349. CrossRef
Barge, M. and Diamond, B., Proximality in Pisot Tiling Spaces. Fund. Math. 194 (2007) 191–238. CrossRef
Barge, M. and Kwapisz, J., Geometric theory of unimodular Pisot substitutions. Amer. J. Math. 128 (2006) 1219–1282. CrossRef
J. Bernat, Symmetrized β-integers (2006) Submitted.
J. Bernat, V. Berthé and H. Rao, On super-coincidence condition of substitutions (2006) Preprint.
J. Berstel, Fibonacci words – a survey, in The Book of L, pp. 13–27. Springer-Verlag (1986).
Berthé, V. and Tijdeman, R., Lattices and multi-dimensional words. Theoret. Comput. Sci. 319 (2004) 177–202. CrossRef
Canterini, V. and Siegel, A., Geometric representation of substitutions of Pisot type. Trans. Amer. Math. Soc. 353 (2001) 5121–5144. CrossRef
Cassaigne, J., Ferenczi, S. and Zamboni, L.Q., Imbalances in Arnoux-Rauzy sequences. Ann. Inst. Fourier (Grenoble) 50 (2000) 1265–1276. CrossRef
de Luca, A., A combinatorial property of the Fibonacci words. Inform. Process. Lett. 12 (1981) 193–195. CrossRef
Droubay, X., Palindromes in the Fibonacci word. Inform. Process. Lett. 55 (1995) 217–221. CrossRef
Droubay, X., Justin, J. and Pirillo, G., Epi-Sturmian words and some constructions of de Luca and Rauzy. Theoret. Comput. Sci. 255 (2001) 539–553. CrossRef
Durand, F., A characterization of substitutive sequences using return words. Discrete Math. 179 (1998) 89–101. CrossRef
Durand, F., Host, B. and Skau, C., Substitutional dynamical systems, Bratteli diagrams and dimension groups. Ergod. Theor. Dyn. Syst. 19 (1999) 953–993. CrossRef
Fabre, S., Dépendance de systèmes de numération associés à des puissances d'un nombre de Pisot. Theoret. Comput. Sci. 158 (1996) 65–79. CrossRef
Frougny, C., Confluent linear numeration systems. Theoret. Comput. Sci. 106 (1992) 183–219. CrossRef
Host, B., Valeurs propres des systèmes dynamiques définis par des substitutions de longueur variable. Ergod. Theor. Dyn. Syst. 6 (1986) 529–540. CrossRef
Ito, S. and Rao, H., Atomic surfaces, tilings and coincidences I. Irreducible case. Israel J. Math. 153 (2006) 129–155. CrossRef
Justin, J. and Pirillo, G., On a characteristic property of Arnoux-Rauzy sequences. RAIRO-Theor. Inf. Appl. 36 (2002) 385–388. CrossRef
Livshits, A.N., Some examples of adic transformations and automorphisms of substitutions. Selecta Math. Soviet. 11 (1992) 83–104. Selected translations.
M. Lothaire, Algebraic Combinatorics On Words. Cambridge University Press (2002).
Martensen, B.F., Generalized balanced pair algorithm. Topology Proc. 28 (2004) 163–178.
Parry, W., On the β-expansions of real numbers. Acta Math. Acad. Sci. Hungar. 11 (1960) 401–416. CrossRef
N. Pytheas Fogg, Substitutions in Dynamics, Arithmetics and Combinatoric, edited by V. Berthé, S. Ferenczi, C. Mauduit and A. Siegel. Lecture Notes in Mathematics 1794 (2002).
M. Queffélec, Substitution dynamical systems–spectral analysis. Lecture Notes in Mathematics 1294 (1987).
Risley, R.N. and Zamboni, L.Q., A generalization of Sturmian sequences: combinatorial structure and transcendence. Acta Arith. 95 (2000) 167–184.
Rényi, A., Representations for real numbers and their ergodic properties. Acta Math. Acad. Sci. Hungar. 8 (1957) 477–493. CrossRef
Rosema, S. and Tijdeman, R., The Tribonacci substitution. INTEGERS Electronic Journal of Combinatorial Number Theory 3 (2005) 1553–1732.
Sirvent, V.F. and Solomyak, B., Pure discrete spectrum for one-dimensional substitution systems of Pisot type. Canad. Math. Bull. 45 (2002) 697–710. CrossRef
Sirvent, V.F. and Wang, Y., Self-affine tiling via substitution dynamical systems and Rauzy fractals. Pacific J. Math. 206 (2002) 465–485. CrossRef
W.P. Thurston, Groups, tilings and finite state automata. Summer 1989 AMS Colloquium Lectures (1989).
Vuillon, L., Balanced words. Bull. Belg. Math. Soc. Simon Stevin 10 (2003) S787–S805.