Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T10:56:03.950Z Has data issue: false hasContentIssue false
  • English
  • Français

EFFECTIVE INSEPARABILITY, LATTICES, AND PREORDERING RELATIONS

Part of: Computability and recursion theory

Published online by Cambridge University Press:  12 July 2019

URI ANDREWS  and
ANDREA SORBI
URI ANDREWS
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF WISCONSINMADISON, WI53706-1388, USAE-mail: andrews@math.wisc.eduURL: http://www.math.wisc.edu/andrews/
ANDREA SORBI
Affiliation:
DIPARTIMENTO DI INGEGNERIA DELL’INFORMAZIONE E SCIENZE MATEMATICHE UNIVERSITÀ DI SIENASIENA, I-53100, ITALYE-mail: andrea.sorbi@unisi.itURL: http://www3.diism.unisi.it/sorbi/
Get access Rights & Permissions [Opens in a new window]

Abstract

We study effectively inseparable (abbreviated as e.i.) prelattices (i.e., structures of the form 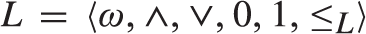$L = \langle \omega , \wedge , \vee ,0,1,{ \le _L}\rangle$ where ω denotes the set of natural numbers and the following four conditions hold: (1) 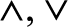$\wedge , \vee$ are binary computable operations; (2) 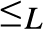${ \le _L}$ is a computably enumerable preordering relation, with 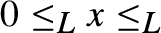$0{ \le _L}x{ \le _L}1$ for every x; (3) the equivalence relation 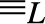${ \equiv _L}$ originated by 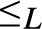${ \le _L}$ is a congruence on L such that the corresponding quotient structure is a nontrivial bounded lattice; (4) the 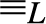${ \equiv _L}$ -equivalence classes of 0 and 1 form an effectively inseparable pair of sets). Solving a problem in (Montagna & Sorbi, 1985) we show (Theorem 4.2), that if L is an e.i. prelattice then 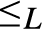${ \le _L}$ is universal with respect to all c.e. preordering relations, i.e., for every c.e. preordering relation R there exists a computable function f reducing R to 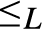${ \le _L}$ , i.e., 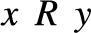$xRy$ if and only if 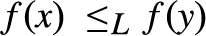$f\left( x \right){ \le _L}f\left( y \right)$ , for all 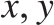$x,y$ . In fact (Corollary 5.3) ${ \le _L}$ is locally universal, i.e., for every pair 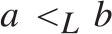$a{ < _L}b$ and every c.e. preordering relation R one can find a reducing function f from R to ${ \le _L}$ such that the range of f is contained in the interval 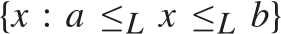$\left\{ {x:a{ \le _L}x{ \le _L}b} \right\}$ . Also (Theorem 5.7) 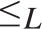${ \le _L}$ is uniformly dense, i.e., there exists a computable function f such that for every 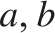$a,b$ if 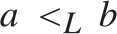$a{ < _L}b$ then 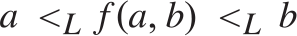$a{ < _L}f\left( {a,b} \right){ < _L}b$ , and if 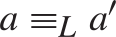$a{ \equiv _L}a\prime$ and 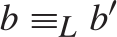$b{ \equiv _L}b\prime$ then 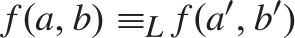$f\left( {a,b} \right){ \equiv _L}f\left( {a\prime ,b\prime } \right)$ . Some consequences and applications of these results are discussed: in particular (Corollary 7.2) for 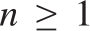$n \ge 1$ the c.e. preordering relation on 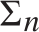${{\rm{\Sigma }}_n}$ sentences yielded by the relation of provable implication of any c.e. consistent extension of Robinson’s system R or Q is locally universal and uniformly dense; and (Corollary 7.3) the c.e. preordering relation yielded by provable implication of any c.e. consistent extension of Heyting Arithmetic is locally universal and uniformly dense.

Keywords

computable reducibility on preorderseffective inseparabilityuniform finite precompletenessuniform density

MSC classification

Primary: 03D30: Other degrees and reducibilities
Secondary: 03D45: Theory of numerations, effectively presented structures
Type
Research Article
Information
The Review of Symbolic Logic , Volume 14 , Issue 4 , December 2021 , pp. 838 - 865
Check for updates
Copyright
© Association for Symbolic Logic 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Andrews, U., Badaev, S., & Sorbi, A. (2017). A survey on universal computably enumerable equivalence relations. In Day, A., Fellows, M., Greenberg, N., Khoussainov, B., Melnikov, A. and Rosamond, F., editors. Computability and Complexity. Essays Dedicated to Rodney G. Downey on the Occasion of His 60th Birthday. Cham: Springer, pp. 418–451.CrossRefGoogle Scholar
Andrews, U., Lempp, S., Miller, J. S., Ng, K. M., San Mauro, L., & Sorbi, A. (2014). Universal computably enumerable equivalence relations. Journal of Symbolic Logic, 79(1), 60–88.CrossRefGoogle Scholar
Avigad, J. & Feferman, S. (1998). Gödels’ functional (“Dialectica”) interpretation. In Buss, S. R., editor. Handbook Proof Theory. Amsterdam: Elsevier, pp. 2–69.Google Scholar
Balbes, R. & Dwinger, P. (1974). Distributive Lattices. Columbia, Missouri: University of Missouri Press.Google Scholar
Bernardi, C. & Montagna, F. (1984). Equivalence relations induced by extensional formulae: Classifications by means of a new fixed point property. Fundamenta Mathematicae, 124, 221–232.CrossRefGoogle Scholar
Case, J. (1974). Periodicity in generations of automata. Journal of Mathematical System Theory, 8(1), 15–32.CrossRefGoogle Scholar
de Jongh, D. & Visser, A. (1996). Embeddings of Heyting algebras. In Hodges, W., Hyland, M., Steinhorn, C., and Truss, J., editors. Logic: From Foundations to Applications, European Logic Colloqium. Oxford and New York: Clarendon Press and Oxford University Press, pp. 187–213.Google Scholar
Fokina, E., Friedman, S., Harizanov, V., Knight, J., McCoy, C., & Montalbán, A. (2012). Isomorphism relations on computable structures. Journal of Symbolic Logic, 77(1), 122–132.CrossRefGoogle Scholar
Fokina, E., Khoussainov, B., Semukhin, P., & Turetsky, D. (2016). Linear orders realized by c.e. equivalence relations. Journal of Symbolic Logic, 81(2), 463–482.CrossRefGoogle Scholar
Galvin, F. & Jónsson, B. (1961). Distributive sublattices of a free lattice. Canadian Journal of Mathematics, 13, 265–272.CrossRefGoogle Scholar
Gavryushkin, A., Jain, S., Khoussainov, B., & Stephan, F. (2014). Graphs realised by r.e. equivalence relations. Annals of Pure and Applied Logic, 165(7–8), 1263–1290.CrossRefGoogle Scholar
Gavryushkin, A., Khoussainov, A., & Stephan, F. (2016). Reducibilities among equivalence relations induced by recursively enumerable structures. Theoretical Computer Science, 612(25), 137–152.CrossRefGoogle Scholar
Hajek, P. & Pudlak, P. (1998). Metamathematics of First-Order Arithmetic. Perspectives in Mathematical Logic. Berlin: Springer-Verlag.Google Scholar
Ianovski, E., Miller, R., Nies, A., & Ng, K. M. (2014). Complexity of equivalence relations and preorders from computability theory. Journal of Symbolic Logic, 79(3), 859–881.CrossRefGoogle Scholar
Lachlan, A. H. (1987). A note on positive equivalence relations. Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, 33, 43–46.CrossRefGoogle Scholar
Montagna, F. (1982). Relative precomplete numerations and arithmetic. Journal of Philosophical Logic, 11, 419–430.CrossRefGoogle Scholar
Montagna, F. & Sorbi, A. (1985). Universal recursion theoretic properties of r.e. preordered structures. Journal of Symbolic Logic, 50(2), 397–406.CrossRefGoogle Scholar
Nerode, A. & Remmel, J. B. (1985). A survey of lattices of recursively enumerable substructures. In Nerode, A. and Shore, R. A., editors. Recursion Theory (Ithaca, N.Y., 1982), Proceedings of Symposia in Pure Mathematics, Vol. 42. Providence, RI: American Mathematical Society, pp. 323–375.CrossRefGoogle Scholar
Nies, A. (2000). Effectively dense Boolean algebras and their applications. Transactions of the American Mathematical Society, 352, 4989–5012.CrossRefGoogle Scholar
Odifreddi, P. (1999). Classical Recursion Theory (Volume II). Studies in Logic and the Foundations of Mathematics, Vol. 143. Amsterdam: North-Holland.Google Scholar
Pour-El, M. B. & Kripke, S. (1967). Deduction preserving “Recursive Isomorphisms” between theories. Fundamenta Mathematicae, 61, 141–163.CrossRefGoogle Scholar
Rogers, H. Jr. (1967). Theory of Recursive Functions and Effective Computability. New York: McGraw-Hill.Google Scholar
Selivanov, V. (2003). Positive structures. In Cooper, S. B. and Goncharov, S. S., editors. Computability and Models. New York: Springer, pp. 321–350.CrossRefGoogle Scholar
Shavrukov, V. Y. (1993). Subalgebras of diagonalizable algebras of theories containing arithmetic. Dissertationes Mathematicae, 323, 82pp.Google Scholar
Shavrukov, V. Y. (1996). Remarks on uniformly finitely precomplete positive equivalences. Mathematical Logic Quarterly, 42, 67–82.CrossRefGoogle Scholar
Shavrukov, V. Y. (2010). Effectively inseparable Boolean algebras in lattices of sentences. Archive for Mathematical Logic, 49(1), 69–89.CrossRefGoogle Scholar
Shavrukov, V. Y. & Visser, A. (2014). Uniform density in Lindenbaum algebras. Notre Dame Journal of Formal Logic, 55(4), 569–582.CrossRefGoogle Scholar
Smoryński, C. (1991). Logical Number Theory I: An Introduction. Berlin, Heidelberg: Springer-Verlag.CrossRefGoogle Scholar
Soare, R. I. (1987). Recursively Enumerable Sets and Degrees. Perspectives in Mathematical Logic, Omega Series. Heidelberg: Springer Verlag.CrossRefGoogle Scholar
Visser, A. (1980). Numerations, λ-calculus & arithmetic. In Seldin, J. P. and Hindley, J. R., editors. To H. B. Curry: Essays on Combinatory Logic, Lambda Calculus and Formalism. London: Academic Press, pp. 259–284.Google Scholar
Visser, A. (1982). On the completeness principle. Annals of Mathematical Logic, 22, 263–295.CrossRefGoogle Scholar
Visser, A. (1985). Evaluation, provably deductive equivalence in Heyting Arithmetic of substitution instances of propositional formulas. Logic Group Preprint Series 4, University of Utrecht, Utrecht.Google Scholar
Zambella, D. (1993). Shavrukov’s theorem on the subalgebras of diagonalizable algebras of theories containing $I{{\rm{\Delta }}_0} + {\rm{Exp}}$ . Notre Dame Journal of Formal Logic, 34(3), 147–157.Google Scholar