The fission hypothesis suggests that close binary stars form due to global nonaxisymmetric instabilities in rotating, quasistatically contracting stars. We study this hypothesis by using an explicit, donor cell, finite difference 3-D hydrodynamic code with self-gravitation to follow dynamic two-armed instabilities in rapidly rotating polytropes. Typical grids are 32 × 16 × 16 in cylindrical coordinates 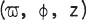and assume reflection symmetry about the equator plane and rotation axis. Initial conditions are obtained by applying density perturbations δρ = aρ cos 2ϕ with a = 0.10 or 0.33 to axisymmetric equilibrium models with the same angular momentum distribution but with various values of polytropic index n and of β = T/|W| where T = total rotational kinetic energy and W = total gravitational energy. We find dynamic growth of perturbations when β ≳ 0.30 for both n = ½ and 3/2. To within the limitations of our methods, this agrees well with the classical dynamic stability limit of β ≈ 0.274 for the bar modes of the Maclaurin spheroids. An unstable case with n = 3/2 and β = 0.33 is evolved for about ten initial central rotation periods. The part of the star inside corotation develops into a stable bone-shaped or dumbbell-shaped structure after about three pattern rotations. At about the same time, material outside corotation is ejected in the form of two trailing spiral arms. These arms wrap due to differential rotation, merge into a detached disk, and eventually narrow into a radially expanding ring with slight cos 2ϕ density enhancements. The ring contains 16% of the mass but more than half the angular momentum. The central bone-shaped object is an analog of the Riemann S-type ellipsoids. Fluid circulates dynamically and stably from one knob of the bone to the other. In this sense, the object is probably better described as a triaxial star than as a contact binary. Similar behavior is exhibited by an extensive n = ½ and β = 0.33 evolution. This work was supported by U.S. National Science Foundation Grant AST-7821449.