Article contents
Estimation of local error by a neural model in an inverse scattering problem
Published online by Cambridge University Press: 21 June 2005
Abstract
Characterization of optical gratings by resolution of inverse scattering problem has become a widely used tool. Indeed, it is known as a non-destructive, rapid and non-invasive method in opposition with microscopic characterizations. Use of a neural model is generally implemented and has shown better results by comparison with other regression methods. The neural network learns the relationship between the optical signature and the corresponding profile shape. The performance of such a non-linear regression method is usually estimated by the root mean square error calculated on a data set not involved in the training process. However, this error estimation is not very significant and tends to flatten the error in the different areas of variable space. We introduce, in this paper, the calculation of local error for each geometrical parameter representing the profile shape. For this purpose a second neural network is implemented to learn the variance of results obtained by the first one. A comparison with the root mean square error confirms a gain of local precision. Finally, the method is applied in the optical characterization of a semi-conductor grating with a 1 $\mu $ 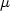 m period.
m period.
Information
- Type
- Research Article
- Information
- Copyright
- © EDP Sciences, 2005
References
- 3
- Cited by

