1 Introduction
Catamorphisms are functions that compute abstractions over algebraic data types (ADTs), such as lists or trees. The definition of a catamorphism is based on a simple recursion scheme, called a fold in the context of functional programming (Meijer et al., Reference Meijer, Fokkinga and Paterson1991). Examples of catamorphisms on lists of integers include functions that compute the orderedness of a list, the length of a list, and the sum of its elements. Similarly, examples of catamorphisms on trees are functions that compute the size of a tree, the height of a tree, and the minimum integer value at its nodes.
Through catamorphisms we can specify many useful program properties such as, for instance, the property that the list computed by a program for sorting lists is indeed sorted, or the property that the output list has the same length of the input list. For this reason, program analysis tools based on abstract interpretation (Cousot and Cousot, Reference Cousot and Cousot1977; Hermenegildo et al., Reference Hermenegildo, Puebla, Bueno and López-García2005) and program verifiers (Suter et al., 2011) have implemented special purpose techniques that handle catamorphisms.
In recent years, it has been shown that verification problems that use catamorphisms can be reduced to satisfiability problems for constrained Horn clauses (CHCs) by following a general approach that is very well suited for automatic proofs (Bjørner et al., 2015; De Angelis et al., Reference De Angelis, Fioravanti, Gallagher, Hermenegildo, Pettorossi and Proietti2022; Gurfinkel, Reference Gurfinkel2022). A practical advantage of CHC-based verification is that it is supported by several CHC solvers which can be used as back-end tools (Blicha et al., Reference Blicha, Fedyukovich, Hyvärinen and Sharygina2022; De Angelis and Govind V. K., 2022; Komuravelli et al., Reference Komuravelli, Gurfinkel and Chaki2016; Hojjat and Rümmer, Reference Hojjat and Rümmer2018).
Unfortunately, the direct translation of catamorphism-based verification problems into CHCs is not always helpful, because CHC solvers often lack mechanisms for computing solutions by performing induction over ADTs. To overcome this difficulty, some CHC solvers have been extended with special purpose satisfiability algorithms that handle (some classes of) catamorphisms (Govind et al., 2022; Hojjat and Rümmer, Reference Hojjat and Rümmer2018; Kostyukov et al., Reference Kostyukov, Mordvinov and Fedyukovich2021; Gurfinkel, Reference Gurfinkel2022). For instance, the module of Eldarica for solving CHCs has been extended by allowing constraints that use the built-in size function counting the number of function symbols in the ADTs (Hojjat and Rümmer, Reference Hojjat and Rümmer2018).
In this paper, we consider a class of catamorphisms that is strictly larger than the ones handled by the above mentioned satisfiability algorithms, and we follow an approach based on the transformation of CHCs (De Angelis et al., Reference De Angelis, Fioravanti, Gallagher, Hermenegildo, Pettorossi and Proietti2022, Reference De Angelis, Fioravanti, Pettorossi and Proietti2023). In particular, given a set
![]() $P$
of CHCs that uses catamorphisms and includes one or more queries encoding the properties of interest, we transform
$P$
of CHCs that uses catamorphisms and includes one or more queries encoding the properties of interest, we transform
![]() $P$
into a new set
$P$
into a new set
![]() $P'$
such that: (i)
$P'$
such that: (i)
![]() $P$
is satisfiable if and only if
$P$
is satisfiable if and only if
![]() $P'$
is satisfiable, and (ii) no catamorphism is present in
$P'$
is satisfiable, and (ii) no catamorphism is present in
![]() $P'$
. Thus, the satisfiability of
$P'$
. Thus, the satisfiability of
![]() $P'$
can be verified by a CHC solver that is not extended for handling catamorphisms.
$P'$
can be verified by a CHC solver that is not extended for handling catamorphisms.
The main difference between the technique we present in this paper and the above cited works (De Angelis et al., Reference De Angelis, Fioravanti, Gallagher, Hermenegildo, Pettorossi and Proietti2022, Reference De Angelis, Fioravanti, Pettorossi and Proietti2023) is that the algorithm we present here does not require that we specify suitable properties of how the catamorphisms relate to every predicate occurring in the given set
![]() $P$
of CHCs. For instance, if we want to verify that the output list
$P$
of CHCs. For instance, if we want to verify that the output list
![]() $S$
of the set of CHCs defining
$S$
of the set of CHCs defining
![]() ${\textit{quicksort}}(L,S)$
has the same length of the input list
${\textit{quicksort}}(L,S)$
has the same length of the input list
![]() $L$
, we need not specify that, for the auxiliary predicate
$L$
, we need not specify that, for the auxiliary predicate
![]() ${\textit{partition}}(X,\textit{Xs},\textit{Ys},\textit{Zs})$
that divides the list
${\textit{partition}}(X,\textit{Xs},\textit{Ys},\textit{Zs})$
that divides the list
![]() $\textit{Xs}$
into the two lists
$\textit{Xs}$
into the two lists
![]() $\textit{Ys}$
and
$\textit{Ys}$
and
![]() $\textit{Zs}$
, it is the case that the length of
$\textit{Zs}$
, it is the case that the length of
![]() $\textit{Xs}$
is the sum of the lengths of
$\textit{Xs}$
is the sum of the lengths of
![]() $\textit{Ys}$
and
$\textit{Ys}$
and
![]() $\textit{Zs}$
. This property can automatically be derived by the CHC solver when it looks for a model of the set of CHCs obtained by transformation. In this sense, our technique may allow the discovery of some lemmas needed for the proof of the property of interest.
$\textit{Zs}$
. This property can automatically be derived by the CHC solver when it looks for a model of the set of CHCs obtained by transformation. In this sense, our technique may allow the discovery of some lemmas needed for the proof of the property of interest.
We will show through a benchmark set of list and tree processing algorithms expressed as sets of CHCs, that our transformation technique is indeed effective and is able to drastically increase the performance of state-of-the-art CHC solvers such as Eldarica (Hojjat and Rümmer, Reference Hojjat and Rümmer2018) (with the built-in catamorphism size) and Z3 with the SPACER engine (de Moura and Bjørner, Reference de Moura and Bjørner2008; Komuravelli et al., Reference Komuravelli, Gurfinkel and Chaki2016).
The rest of the paper is organized as follows. In Section 2, we recall some preliminary notions on CHCs and catamorphisms. In Section 3 we show an introductory example to motivate our technique. In Section 4 we present our transformation algorithm and prove that it guarantees the equisatisfiability of the initial sets of CHCs and the transformed sets of CHCs. In Section 5 we present the implementation of our technique in the VeriCaT
![]() $_{\!\mathit{abs}}$
tool, and through an experimental evaluation, we show the beneficial effect of the transformation on both Eldarica and Z3 CHC solvers. We will consider several abstractions based on catamorphisms relative to lists and trees, such as size, minimum element, orderedness, element membership, element multiplicity, and combinations thereof. Finally, in Section 6, we discuss related work and we outline future research directions.
$_{\!\mathit{abs}}$
tool, and through an experimental evaluation, we show the beneficial effect of the transformation on both Eldarica and Z3 CHC solvers. We will consider several abstractions based on catamorphisms relative to lists and trees, such as size, minimum element, orderedness, element membership, element multiplicity, and combinations thereof. Finally, in Section 6, we discuss related work and we outline future research directions.
2 Basic notions
The programs and the properties we consider in this paper are expressed as sets of constrained Horn clauses written in a many-sorted first-order language
![]() $\mathcal{L}$
with equality (=). Constraints are expressions of the linear integer arithmetic (LIA) and the boolean algebra (Bool). The theories of LIA and Bool will be collectively denoted by
$\mathcal{L}$
with equality (=). Constraints are expressions of the linear integer arithmetic (LIA) and the boolean algebra (Bool). The theories of LIA and Bool will be collectively denoted by
![]() $\mathit{LIA\cup Bool}$
. The equality symbol = will be used both for integers and booleans. In particular, a constraint is a quantifier-free formula
$\mathit{LIA\cup Bool}$
. The equality symbol = will be used both for integers and booleans. In particular, a constraint is a quantifier-free formula
![]() $c$
, where LIA constraints may occur as subexpressions of boolean constraints, according to the SMT approach (Barrett et al., Reference Barrett, Sebastiani, Seshia and Tinelli2009). The syntaxes of a constraint
$c$
, where LIA constraints may occur as subexpressions of boolean constraints, according to the SMT approach (Barrett et al., Reference Barrett, Sebastiani, Seshia and Tinelli2009). The syntaxes of a constraint
![]() $c$
and an elementary LIA constraint
$c$
and an elementary LIA constraint
![]() $d$
are as follows:
$d$
are as follows:
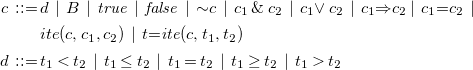 \begin{align*}c\,::=\,&d\,\,|\,\,{B}\,\,|\,\,\mathit{true}\,\,|\,\,\mathit{false}\,\,|\,\sim \!c\,\,|\,\,c_1 \,{\&}\,c_2\,\,|\,\,c_1{\vee }\, c_2\,\,|\,\,c_1\!\Rightarrow \!c_2\,|\,\,c_1\!=\!c_2\,\,|\\ &{ite}(c, c_1, c_2)\,\,|\,\,t\!=\!\mathit{ite}(c, t_1, t_2)\\d\,::=\,&t_1 < t_2\,\,|\,\,t_1 \leq t_2\,\,|\,\,t_1 = t_2\,\,|\,\,t_1 \geq t_2\,\,|\,\,t_1 \gt t_2 \end{align*}
\begin{align*}c\,::=\,&d\,\,|\,\,{B}\,\,|\,\,\mathit{true}\,\,|\,\,\mathit{false}\,\,|\,\sim \!c\,\,|\,\,c_1 \,{\&}\,c_2\,\,|\,\,c_1{\vee }\, c_2\,\,|\,\,c_1\!\Rightarrow \!c_2\,|\,\,c_1\!=\!c_2\,\,|\\ &{ite}(c, c_1, c_2)\,\,|\,\,t\!=\!\mathit{ite}(c, t_1, t_2)\\d\,::=\,&t_1 < t_2\,\,|\,\,t_1 \leq t_2\,\,|\,\,t_1 = t_2\,\,|\,\,t_1 \geq t_2\,\,|\,\,t_1 \gt t_2 \end{align*}
where:(i)
![]() $B$
is a boolean variable, (ii)
$B$
is a boolean variable, (ii)
![]() $\sim$
, &,
$\sim$
, &,
![]() $\vee$
, and
$\vee$
, and
![]() $\Rightarrow$
denote negation, conjunction, disjunction, and implication, respectively, (iii) the ternary function ite denotes the if-then-else operator (i.e.
$\Rightarrow$
denote negation, conjunction, disjunction, and implication, respectively, (iii) the ternary function ite denotes the if-then-else operator (i.e.
![]() $\mathit{ite}(c, c_1, c_2)$
has the following semantics: if
$\mathit{ite}(c, c_1, c_2)$
has the following semantics: if
![]() $c$
then
$c$
then
![]() $c_{1}$
else
$c_{1}$
else
![]() $c_{2}$
), and (iv)
$c_{2}$
), and (iv)
![]() $t$
, possibly with subscripts,
$t$
, possibly with subscripts,
![]() $t$
,
$t$
,
![]() $t_{1}$
and
$t_{1}$
and
![]() $t_{2}$
is a LIA term of the form
$t_{2}$
is a LIA term of the form
![]() $a_0+a_1X_1+\ldots +a_nX_n$
with integer coefficients
$a_0+a_1X_1+\ldots +a_nX_n$
with integer coefficients
![]() $a_0,\dots, a_n$
and integer variables
$a_0,\dots, a_n$
and integer variables
![]() $X_1,\ldots, X_n$
.
$X_1,\ldots, X_n$
.
The integer and boolean sorts are said to be basic sorts. A recursively defined sort (such as the sort of lists and trees) is said to be an algebraic data type (ADT, for short).
An atom is a formula of the form
![]() $p(t_{1},\ldots, t_{m})$
, where
$p(t_{1},\ldots, t_{m})$
, where
![]() $p$
is a predicate symbol not occurring in
$p$
is a predicate symbol not occurring in
![]() $\textit{LIA}\cup \textit{Bool}$
, and
$\textit{LIA}\cup \textit{Bool}$
, and
![]() $t_{1},\ldots, t_{m}$
are first-order terms in
$t_{1},\ldots, t_{m}$
are first-order terms in
![]() $\mathcal{L}$
. A constrained Horn clause (CHC), or simply, a clause, is an implication of the form
$\mathcal{L}$
. A constrained Horn clause (CHC), or simply, a clause, is an implication of the form
![]() $H\leftarrow c, G$
. The conclusion
$H\leftarrow c, G$
. The conclusion
![]() $H$
, called the head, is either an atom or false, and the premise, called the body, is the conjunction of a constraint
$H$
, called the head, is either an atom or false, and the premise, called the body, is the conjunction of a constraint
![]() $c$
and a conjunction
$c$
and a conjunction
![]() $G$
of zero or more atoms.
$G$
of zero or more atoms.
![]() $G$
is said to be a goal. A clause is said to be a query if its head is false, and a definite clause, otherwise. Without loss of generality, at the expense of introducing suitable equalities, we assume that every atom of the body of a clause has distinct variables (of any sort) as arguments. Given an expression
$G$
is said to be a goal. A clause is said to be a query if its head is false, and a definite clause, otherwise. Without loss of generality, at the expense of introducing suitable equalities, we assume that every atom of the body of a clause has distinct variables (of any sort) as arguments. Given an expression
![]() $e$
, by
$e$
, by
![]() $\textit{vars}(e)$
we denote the set of all variables occurring in
$\textit{vars}(e)$
we denote the set of all variables occurring in
![]() $e$
. By
$e$
. By
![]() $\mathit{bvars(e)}$
(or
$\mathit{bvars(e)}$
(or
![]() $\mathit{adt}$
-
$\mathit{adt}$
-
![]() $\mathit{vars}(e)$
) we denote the set of variables in
$\mathit{vars}(e)$
) we denote the set of variables in
![]() $e$
whose sort is a basic sort (or an ADT sort, respectively). The universal closure of a formula
$e$
whose sort is a basic sort (or an ADT sort, respectively). The universal closure of a formula
![]() $\varphi$
is denoted by
$\varphi$
is denoted by
![]() $\forall (\varphi )$
.
$\forall (\varphi )$
.
A
![]() $\mathbb{D}$
-interpretation for a set
$\mathbb{D}$
-interpretation for a set
![]() $S$
of CHCs is an interpretation where the symbols of
$S$
of CHCs is an interpretation where the symbols of
![]() $\textit{LIA}\cup \textit{Bool}$
are interpreted as usual. A
$\textit{LIA}\cup \textit{Bool}$
are interpreted as usual. A
![]() $\mathbb{D}$
-interpretation
$\mathbb{D}$
-interpretation
![]() $I$
is said to be a
$I$
is said to be a
![]() $\mathbb{D}$
-model of
$\mathbb{D}$
-model of
![]() $S$
if all clauses of
$S$
if all clauses of
![]() $S$
are true in
$S$
are true in
![]() $I$
. A set
$I$
. A set
![]() $S$
of CHCs is said to be
$S$
of CHCs is said to be
![]() $\mathbb{D}$
-satisfiable (or satisfiable, for short) if it has a
$\mathbb{D}$
-satisfiable (or satisfiable, for short) if it has a
![]() $\mathbb{D}$
-model, and it is said to be
$\mathbb{D}$
-model, and it is said to be
![]() $\mathbb{D}$
-unsatisfiable (or unsatisfiable, for short), otherwise.
$\mathbb{D}$
-unsatisfiable (or unsatisfiable, for short), otherwise.
Given a set
![]() $P$
of definite clauses, there exists a least
$P$
of definite clauses, there exists a least
![]() $\mathbb{D}$
-model of
$\mathbb{D}$
-model of
![]() $P$
, denoted
$P$
, denoted
![]() $M(P)$
(Jaffar and Maher, Reference Jaffar and Maher1994). Let
$M(P)$
(Jaffar and Maher, Reference Jaffar and Maher1994). Let
![]() $P$
be a set of definite clauses and for
$P$
be a set of definite clauses and for
![]() $i=1,\ldots, n$
,
$i=1,\ldots, n$
,
![]() $Q_i$
be a query. Then
$Q_i$
be a query. Then
![]() $P \cup \{Q_1,\ldots, Q_n\}$
is satisfiable if and only if, for
$P \cup \{Q_1,\ldots, Q_n\}$
is satisfiable if and only if, for
![]() $i=1,\dots, n$
,
$i=1,\dots, n$
,
![]() $M(P)\models Q_i$
.
$M(P)\models Q_i$
.
The catamorphisms we consider in this paper are defined by first-order, relational recursive schemata as we now indicate. Similar definitions are introduced also in (higher-order) functional programming (Meijer et al., Reference Meijer, Fokkinga and Paterson1991; Hinze et al., Reference Hinze, Wu and Gibbons2013).
Let
![]() $f$
be a predicate symbol with
$f$
be a predicate symbol with
![]() $m + n$
arguments (for
$m + n$
arguments (for
![]() $m\!\geq \! 0$
and
$m\!\geq \! 0$
and
![]() $n\!\geq \! 0$
) with sorts
$n\!\geq \! 0$
) with sorts
![]() $\alpha _1,\ldots, \alpha _m,$
$\alpha _1,\ldots, \alpha _m,$
![]() $\beta _1,\ldots, \beta _n$
, respectively. We say that
$\beta _1,\ldots, \beta _n$
, respectively. We say that
![]() $f$
is a functional predicate from sort
$f$
is a functional predicate from sort
![]() $\alpha _1\!\times \!\ldots \!\times \!\alpha _m$
to sort
$\alpha _1\!\times \!\ldots \!\times \!\alpha _m$
to sort
![]() $\beta _1\!\times \!\ldots \!\times \!\beta _n$
, with respect to a given set
$\beta _1\!\times \!\ldots \!\times \!\beta _n$
, with respect to a given set
![]() $P$
of definite clauses that define
$P$
of definite clauses that define
![]() $f$
, if
$f$
, if
![]() $M(P)\! \models \! \forall X,\!Y,\! Z.\ f(X,\!Y) \wedge f(X,\!Z) \rightarrow Y\!=\!Z$
, where
$M(P)\! \models \! \forall X,\!Y,\! Z.\ f(X,\!Y) \wedge f(X,\!Z) \rightarrow Y\!=\!Z$
, where
![]() $X$
is an
$X$
is an
![]() $m$
-tuple of distinct variables, and
$m$
-tuple of distinct variables, and
![]() $Y$
and
$Y$
and
![]() $Z$
are
$Z$
are
![]() $n$
-tuples of distinct variables. In this case, when we write the atom
$n$
-tuples of distinct variables. In this case, when we write the atom
![]() $f(X,Y)$
, we mean that
$f(X,Y)$
, we mean that
![]() $X$
and
$X$
and
![]() $Y$
are the tuples of the input and output variables of
$Y$
are the tuples of the input and output variables of
![]() $f$
, respectively. We say that
$f$
, respectively. We say that
![]() $f$
is a total predicate if
$f$
is a total predicate if
![]() $M(P) \models \forall X \exists Y.\ f(X,Y)$
. In what follows, a ‘total, functional predicate’
$M(P) \models \forall X \exists Y.\ f(X,Y)$
. In what follows, a ‘total, functional predicate’
![]() $f$
from a tuple
$f$
from a tuple
![]() $\alpha$
of sorts to a tuple
$\alpha$
of sorts to a tuple
![]() $\beta$
of sorts is said to be a ‘total function’ in
$\beta$
of sorts is said to be a ‘total function’ in
![]() $\mbox{[}\alpha \rightarrow \beta \mbox{]}$
, and it is denoted by
$\mbox{[}\alpha \rightarrow \beta \mbox{]}$
, and it is denoted by
![]() $f \in \mbox{[}\alpha \rightarrow \beta \mbox{]}$
.
$f \in \mbox{[}\alpha \rightarrow \beta \mbox{]}$
.
Now we introduce the notions of a list catamorphism and a binary tree catamorphism. We leave to the reader the task of introducing, the definitions of similar catamorphisms for recursively defined algebraic data types that may be needed for expressing the properties of interest. Let
![]() $\alpha$
,
$\alpha$
,
![]() $\beta$
,
$\beta$
,
![]() $\gamma$
, and
$\gamma$
, and
![]() $\delta$
be (products of) basic sorts. Let
$\delta$
be (products of) basic sorts. Let
![]() $\mathit{list}(\beta )$
be the sort of lists with elements of sort
$\mathit{list}(\beta )$
be the sort of lists with elements of sort
![]() $\beta$
, and
$\beta$
, and
![]() $\mathit{btree}(\beta )$
be the sort of binary trees with values of sort
$\mathit{btree}(\beta )$
be the sort of binary trees with values of sort
![]() $\beta$
.
$\beta$
.
Definition 1 (List and Binary Tree Catamorphisms). A list catamorphism
![]() $\ell$
is a total function in
$\ell$
is a total function in
![]() $[\alpha \!\times \!\mathit{list}(\beta ) \rightarrow \gamma ]$
defined as follows:
$[\alpha \!\times \!\mathit{list}(\beta ) \rightarrow \gamma ]$
defined as follows:
-
L1.
 $\ell (X,[\,],Y) \leftarrow \mathit{\ell \, us basis}(X,Y)$
$\ell (X,[\,],Y) \leftarrow \mathit{\ell \, us basis}(X,Y)$
-
L2.
 $\ell (X,[H|T],Y) \leftarrow f(X,T,\mathit{Rf}),\ \ell (X,T,R),\ \mathit{\ell \, us combine}(X,H,R,\mathit{Rf},Y)$
$\ell (X,[H|T],Y) \leftarrow f(X,T,\mathit{Rf}),\ \ell (X,T,R),\ \mathit{\ell \, us combine}(X,H,R,\mathit{Rf},Y)$
where
![]() $\,$
:
$\,$
:
![]() $({\textrm{i}})\,\mathit{\ell \, us basis}$
$({\textrm{i}})\,\mathit{\ell \, us basis}$
![]() $\in$
$\in$
![]() $[\alpha \!\rightarrow \!\gamma ]$
,
$[\alpha \!\rightarrow \!\gamma ]$
,
![]() $({\textrm{ii}})\,\mathit{\ell \, us combine}$
$({\textrm{ii}})\,\mathit{\ell \, us combine}$
![]() $\in$
$\in$
![]() $[\alpha \!\times \!\beta \!\times \!\gamma \!\times \!\delta \rightarrow \gamma ]$
, and
$[\alpha \!\times \!\beta \!\times \!\gamma \!\times \!\delta \rightarrow \gamma ]$
, and
![]() $({\textrm{iii}})\,f$
is itself a list catamorphism in
$({\textrm{iii}})\,f$
is itself a list catamorphism in
![]() $[\alpha \!\times \!\mathit{list}(\beta ) \rightarrow \delta ]$
.
$[\alpha \!\times \!\mathit{list}(\beta ) \rightarrow \delta ]$
.
A binary tree catamorphism
![]() $\mathit{bt}$
is a total function in
$\mathit{bt}$
is a total function in
![]() $[\alpha \!\times \!\mathit{btree}(\beta ) \rightarrow \gamma ]$
defined as follows:
$[\alpha \!\times \!\mathit{btree}(\beta ) \rightarrow \gamma ]$
defined as follows:
-
BT1.
 $\mathit{bt}(X,\mathit{leaf},Y) \leftarrow \mathit{bt\, us basis}(X,Y)$
$\mathit{bt}(X,\mathit{leaf},Y) \leftarrow \mathit{bt\, us basis}(X,Y)$
-
BT2.
 $\mathit{bt}(X,\mathit{node}(L,N,R),Y) \leftarrow g(X,L,\mathit{RLg}),\ g(X,R,\mathit{RRg}),$
$\mathit{bt}(X,\mathit{node}(L,N,R),Y) \leftarrow g(X,L,\mathit{RLg}),\ g(X,R,\mathit{RRg}),$
 $\mathit{bt}(X,L,\mathit{RL}),\ \mathit{bt}(X,R,\mathit{RR}),\ \mathit{bt\, us combine}(X,N,\mathit{RL,RR,RLg,RRg},Y)$
$\mathit{bt}(X,L,\mathit{RL}),\ \mathit{bt}(X,R,\mathit{RR}),\ \mathit{bt\, us combine}(X,N,\mathit{RL,RR,RLg,RRg},Y)$
where
![]() $\,$
:
$\,$
:
![]() $({\textrm{i}})\,\mathit{bt\, us basis}$
$({\textrm{i}})\,\mathit{bt\, us basis}$
![]() $\in$
$\in$
![]() $[\alpha \rightarrow \gamma ]$
,
$[\alpha \rightarrow \gamma ]$
,
![]() $({\textrm{ii}})$
$({\textrm{ii}})$
![]() $\mathit{bt\, us combine}$
$\mathit{bt\, us combine}$
![]() $\in$
$\in$
![]() $[\alpha \!\times \!\beta \!\times \!\gamma \!\times \!\gamma \!\times \!\delta \!\times \!\delta \rightarrow \gamma ]$
, and
$[\alpha \!\times \!\beta \!\times \!\gamma \!\times \!\gamma \!\times \!\delta \!\times \!\delta \rightarrow \gamma ]$
, and
![]() $({\textrm{iii}})\,g$
is itself a binary tree catamorphism in
$({\textrm{iii}})\,g$
is itself a binary tree catamorphism in
![]() $[\alpha \!\times \!\mathit{btree}(\beta ) \rightarrow \delta ]$
.
$[\alpha \!\times \!\mathit{btree}(\beta ) \rightarrow \delta ]$
.
Instances of the schemas of the list catamorphisms and the binary tree catamorphisms (see Definition1 above) may lack some components, such as the parameter
![]() $X$
of basic sort
$X$
of basic sort
![]() $\alpha$
, or the catamorphisms
$\alpha$
, or the catamorphisms
![]() $f$
or
$f$
or
![]() $g$
. The possible presence of these components makes the class of catamorphisms considered in this paper strictly larger than the ones used by other CHC-based approaches (Govind V. K. et al., 2022; Hojjat and Rümmer, Reference Hojjat and Rümmer2018; Kostyukov et al., Reference Kostyukov, Mordvinov and Fedyukovich2021; Gurfinkel, Reference Gurfinkel2022).
$g$
. The possible presence of these components makes the class of catamorphisms considered in this paper strictly larger than the ones used by other CHC-based approaches (Govind V. K. et al., 2022; Hojjat and Rümmer, Reference Hojjat and Rümmer2018; Kostyukov et al., Reference Kostyukov, Mordvinov and Fedyukovich2021; Gurfinkel, Reference Gurfinkel2022).
3 An introductory example
Let us consider a set of CHCs for doubling lists of integers (see clauses 1–4 in Figure 1). We have that: (i)
![]() $\mathit{double}(\mathit{Xs},\mathit{Zs})$
holds if and only if list Zs is the concatenation of two copies of the same list Xs of integers, (ii)
$\mathit{double}(\mathit{Xs},\mathit{Zs})$
holds if and only if list Zs is the concatenation of two copies of the same list Xs of integers, (ii)
![]() $\mathit{eq(Xs,\!Ys)}$
holds if and only if list
$\mathit{eq(Xs,\!Ys)}$
holds if and only if list
![]() $\mathit{Xs}$
is equal to list
$\mathit{Xs}$
is equal to list
![]() $\mathit{Ys}$
, and (iii)
$\mathit{Ys}$
, and (iii)
![]() $\mathit{append(Xs,Ys,Zs)}$
holds if and only if list Zs is the result of concatenating list Ys to the right of list Xs.
$\mathit{append(Xs,Ys,Zs)}$
holds if and only if list Zs is the result of concatenating list Ys to the right of list Xs.
Let us assume that we want to verify the following Even property: if
![]() $\mathit{double}(\mathit{Xs},\mathit{Zs})$
holds, then for any integer
$\mathit{double}(\mathit{Xs},\mathit{Zs})$
holds, then for any integer
![]() $X$
, the number of occurrences of
$X$
, the number of occurrences of
![]() $X$
in Zs is an even number. In order to do so, we use the list catamorphism
$X$
in Zs is an even number. In order to do so, we use the list catamorphism
![]() $\mathit{listcount(X,Zs,M)}$
(see clauses 5–6 in Figure 1) that holds if and only if
$\mathit{listcount(X,Zs,M)}$
(see clauses 5–6 in Figure 1) that holds if and only if
![]() $M$
is the number of occurrences of
$M$
is the number of occurrences of
![]() $X$
in list
$X$
in list
![]() $\mathit{Zs}$
. Note that
$\mathit{Zs}$
. Note that
![]() $\mathit{listcount(X,Zs,M)}$
is indeed a list catamorphism because clauses 5–6 are instances of clauses
$\mathit{listcount(X,Zs,M)}$
is indeed a list catamorphism because clauses 5–6 are instances of clauses
![]() $L1$
–
$L1$
–
![]() $L2$
in Definition1, when: (i)
$L2$
in Definition1, when: (i)
![]() $\ell$
is listcount, (ii)
$\ell$
is listcount, (ii)
![]() $Y$
is
$Y$
is
![]() $N$
, (iii)
$N$
, (iii)
![]() $\mathit{\ell \, us basis}(X,Y)$
is the LIA constraint
$\mathit{\ell \, us basis}(X,Y)$
is the LIA constraint
![]() $N\!=\!0$
, (iv)
$N\!=\!0$
, (iv)
![]() $f(X,T,\mathit{Rf})$
is absent, and (v)
$f(X,T,\mathit{Rf})$
is absent, and (v)
![]() $\mathit{\ell \, us combine}(X,H,R,\mathit{Rf},Y)$
is the LIA constraint
$\mathit{\ell \, us combine}(X,H,R,\mathit{Rf},Y)$
is the LIA constraint
![]() $N\!=\mathit{ite}(X\!=\!H, \mathit{NT}\!+\!\textrm{1},\mathit{NT})$
.
$N\!=\mathit{ite}(X\!=\!H, \mathit{NT}\!+\!\textrm{1},\mathit{NT})$
.
Our verification task can be expressed as query 7 in Figure 1, whereby we derive
![]() $\mathit{false}$
if the number
$\mathit{false}$
if the number
![]() $M$
of occurrences of
$M$
of occurrences of
![]() $X$
in
$X$
in
![]() $\mathit{Zs}$
is odd (recall that we assume that
$\mathit{Zs}$
is odd (recall that we assume that
![]() $M \!=\! 2\,N\!+\!1$
is a
$M \!=\! 2\,N\!+\!1$
is a
![]() $\mathit{LIA}$
constraint).
$\mathit{LIA}$
constraint).

Fig. 1. The initial set of CHCs (clauses 1–6) and query 7 that specifies that the number of occurrences of an element
![]() $X$
in the list
$X$
in the list
![]() $\mathit{Zs}$
is even.
$\mathit{Zs}$
is even.
Now, neither the CHC solver Eldarica nor Z3 is able to prove the satisfiability of clauses 1–7 and thus, those solvers are not able to show the Even property. By the transformation technique we will propose in this paper, we get a new set of clauses whose satisfiability can be shown by Z3 and thus, the Even property is proved.
To perform this transformation, we use the information that the property to be verified is expressed through the catamorphism
![]() $\mathit{listcount}$
. However, in contrast to previous approaches (De Angelis et al., Reference De Angelis, Fioravanti, Gallagher, Hermenegildo, Pettorossi and Proietti2022, Reference De Angelis, Fioravanti, Pettorossi and Proietti2023), we need not specify any property of the catamorphism
$\mathit{listcount}$
. However, in contrast to previous approaches (De Angelis et al., Reference De Angelis, Fioravanti, Gallagher, Hermenegildo, Pettorossi and Proietti2022, Reference De Angelis, Fioravanti, Pettorossi and Proietti2023), we need not specify any property of the catamorphism
![]() $\mathit{listcount}$
when it acts upon the predicates
$\mathit{listcount}$
when it acts upon the predicates
![]() $\mathit{double}$
,
$\mathit{double}$
,
![]() $\mathit{eq}$
, and
$\mathit{eq}$
, and
![]() $\mathit{append}$
. For instance, we need not specify that if Zs is the concatenation of Xs and Ys, then for any
$\mathit{append}$
. For instance, we need not specify that if Zs is the concatenation of Xs and Ys, then for any
![]() $X$
, the number of occurrences of
$X$
, the number of occurrences of
![]() $X$
in Zs is the sum of the numbers of occurrences of
$X$
in Zs is the sum of the numbers of occurrences of
![]() $X$
in
$X$
in
![]() $\mathit{Xs}$
and
$\mathit{Xs}$
and
![]() $\mathit{Ys}$
. Indeed, in the approach we propose in this paper, we have only to specify the association of every ADT sort with a suitable catamorphism or, in general, a conjunction of catamorphisms. In particular, in our double example, we associate the sort of integer lists, denoted
$\mathit{Ys}$
. Indeed, in the approach we propose in this paper, we have only to specify the association of every ADT sort with a suitable catamorphism or, in general, a conjunction of catamorphisms. In particular, in our double example, we associate the sort of integer lists, denoted
![]() $\mathit{list(int)}$
, with the catamorphism
$\mathit{list(int)}$
, with the catamorphism
![]() $\mathit{listcount}$
. Then, we rely on the CHC solver for the discovery, after the transformation described in the following sections, of suitable relations between the variables that represent the output of the listcount catamorphism atoms. Thus, by applying the technique proposed in this paper, much less ingenuity is required on the part of the programmer for verifying program correctness with respect to the previously proposed approaches.
$\mathit{listcount}$
. Then, we rely on the CHC solver for the discovery, after the transformation described in the following sections, of suitable relations between the variables that represent the output of the listcount catamorphism atoms. Thus, by applying the technique proposed in this paper, much less ingenuity is required on the part of the programmer for verifying program correctness with respect to the previously proposed approaches.
Our transformation technique introduces, for each predicate
![]() $p$
occurring in the initial set of CHCs, a new predicate
$p$
occurring in the initial set of CHCs, a new predicate
![]() $\textit{newp}$
defined by the conjunction of a
$\textit{newp}$
defined by the conjunction of a
![]() $p$
atom and, for each argument of
$p$
atom and, for each argument of
![]() $p$
with ADT sort
$p$
with ADT sort
![]() $\tau$
, the catamorphism atom(s) with which
$\tau$
, the catamorphism atom(s) with which
![]() $\tau$
has been associated. In particular, in the case of our double example, for the predicate
$\tau$
has been associated. In particular, in the case of our double example, for the predicate
![]() $\mathit{double}$
we introduce the new predicate
$\mathit{double}$
we introduce the new predicate
![]() $\mathit{new}1$
(for simplicity, we call it
$\mathit{new}1$
(for simplicity, we call it
![]() $\mathit{new}1$
, instead of
$\mathit{new}1$
, instead of
![]() $\mathit{newdouble}$
) whose definition is clause
$\mathit{newdouble}$
) whose definition is clause
![]() $D1$
in Figure 2. The body of that clause is the conjunction of the atom
$D1$
in Figure 2. The body of that clause is the conjunction of the atom
![]() $\mathit{double}(B,E)$
and two listcount catamorphism atoms, one for each of the integer lists
$\mathit{double}(B,E)$
and two listcount catamorphism atoms, one for each of the integer lists
![]() $B$
and
$B$
and
![]() $E$
, as listcount is the catamorphism with which the sort of integer lists has been associated. Similarly, for the predicates
$E$
, as listcount is the catamorphism with which the sort of integer lists has been associated. Similarly, for the predicates
![]() $\mathit{append}$
and
$\mathit{append}$
and
![]() $\mathit{eq}$
whose definitions are respectively clauses
$\mathit{eq}$
whose definitions are respectively clauses
![]() $D2$
and
$D2$
and
![]() $D3$
listed in Figure 2.
$D3$
listed in Figure 2.

Fig. 2. Clauses
![]() $D1$
–
$D1$
–
![]() $D4$
are the predicate definitions introduced during transformation. Clauses 11–23 are the clauses derived after transformation from clauses 1–6 and query 7 of Figure 1.
$D4$
are the predicate definitions introduced during transformation. Clauses 11–23 are the clauses derived after transformation from clauses 1–6 and query 7 of Figure 1.
Thus, we derive a new version of the initial CHCs where each predicate
![]() $p$
has been replaced by the corresponding newp. Then, by applying variants of the fold/unfold transformation rules, we derive a final, transformed set of CHCs. When the CHC solver looks for a model of this final set of CHCs, it is guided by the fact that suitable constraints, inferred from the query, must hold among the arguments of the newly introduced predicates, such as newp, and thus, the solver can often be more effective.
$p$
has been replaced by the corresponding newp. Then, by applying variants of the fold/unfold transformation rules, we derive a final, transformed set of CHCs. When the CHC solver looks for a model of this final set of CHCs, it is guided by the fact that suitable constraints, inferred from the query, must hold among the arguments of the newly introduced predicates, such as newp, and thus, the solver can often be more effective.
In our transformation we also introduce, for each predicate newp, a predicate called
![]() $\mathit{newp\, us woADTs}$
whose definition is obtained by removing the ADT arguments from the definition of newp. For the CHC solvers, it is often easier to find a model for
$\mathit{newp\, us woADTs}$
whose definition is obtained by removing the ADT arguments from the definition of newp. For the CHC solvers, it is often easier to find a model for
![]() $\mathit{newp\, us woADTs}$
, rather than for
$\mathit{newp\, us woADTs}$
, rather than for
![]() $\textit{newp}$
, because the solvers need not handle ADTs at all. However, since each
$\textit{newp}$
, because the solvers need not handle ADTs at all. However, since each
![]() $\mathit{newp\, us woADTs}$
is an overapproximation of
$\mathit{newp\, us woADTs}$
is an overapproximation of
![]() $\textit{newp}$
, by using the clauses with the ADTs removed, one could wrongly infer unsatisfiability in cases when, on the contrary, the initial set of CHCs is satisfiable.
$\textit{newp}$
, by using the clauses with the ADTs removed, one could wrongly infer unsatisfiability in cases when, on the contrary, the initial set of CHCs is satisfiable.
Now, in order to make it easier for the solvers to show satisfiability of sets of CHCs and, at the same time, to guarantee the equisatisfiability of the derived set of clauses with respect to the initial set, we add to every atom in the body of every derived clause for
![]() $\mathit{newp}$
the corresponding atom without ADT arguments (see Theorem1 for the correctness of these atom additions). By performing these transformation steps starting from clauses 1–6 and query 7 (listed in Figure 1) together with the specification that every variable of sort
$\mathit{newp}$
the corresponding atom without ADT arguments (see Theorem1 for the correctness of these atom additions). By performing these transformation steps starting from clauses 1–6 and query 7 (listed in Figure 1) together with the specification that every variable of sort
![]() $\mathit{list}(\mathit{int})$
should be associated with a listcount atom, we derive using our transformation algorithm
$\mathit{list}(\mathit{int})$
should be associated with a listcount atom, we derive using our transformation algorithm
![]() ${\mathcal{T}}_{\mathit{abs}}$
(see Section 4) clauses 11–23 listed in Figure 2. These derived clauses are indeed shown to be satisfiable by the Z3 solver, and thus the Even property is proved.
${\mathcal{T}}_{\mathit{abs}}$
(see Section 4) clauses 11–23 listed in Figure 2. These derived clauses are indeed shown to be satisfiable by the Z3 solver, and thus the Even property is proved.
4 CHC transformation via catamorphic abstractions
In this section we present our transformation algorithm, called
![]() ${\mathcal{T}}_{\mathit{abs}}$
, whose input is: (i) a set
${\mathcal{T}}_{\mathit{abs}}$
, whose input is: (i) a set
![]() $P$
of definite clauses, (ii) a query
$P$
of definite clauses, (ii) a query
![]() $Q$
expressing the property to be verified, and (iii) for each ADT sort, a conjunction of catamorphisms whose definitions are included in
$Q$
expressing the property to be verified, and (iii) for each ADT sort, a conjunction of catamorphisms whose definitions are included in
![]() $P$
. Algorithm
$P$
. Algorithm
![]() ${\mathcal{T}}_{\mathit{abs}}$
introduces a set of new predicates, which incorporate as extra arguments some information coming from the catamorphisms, and transforms
${\mathcal{T}}_{\mathit{abs}}$
introduces a set of new predicates, which incorporate as extra arguments some information coming from the catamorphisms, and transforms
![]() $P\cup \{Q\}$
into a new set
$P\cup \{Q\}$
into a new set
![]() $P'\cup \{Q'\}$
such that
$P'\cup \{Q'\}$
such that
![]() $P\cup \{Q\}$
is satisfiable if and only if so is
$P\cup \{Q\}$
is satisfiable if and only if so is
![]() $P'\cup \{Q'\}$
.
$P'\cup \{Q'\}$
.
The transformation is effective when the catamorphisms used in the new predicate definitions establish relations that are useful to solve the query. In particular, it is often helpful to use in the new definitions catamorphisms that include the ones occurring in the query, such as the catamorphism
![]() $\mathit{listcount}$
of our introductory
$\mathit{listcount}$
of our introductory
![]() $\mathit{double}$
example. However, as we will see later, there are cases in which it is important to consider catamorphisms not present in the query (see Example2). The choice of the suitable catamorphisms to be used in the transformation rests upon the programmer’s ingenuity and on her/his understanding of the program behavior. The problem of chosing the most suitable catamorphisms in a fully automatic way is left for future research.
$\mathit{double}$
example. However, as we will see later, there are cases in which it is important to consider catamorphisms not present in the query (see Example2). The choice of the suitable catamorphisms to be used in the transformation rests upon the programmer’s ingenuity and on her/his understanding of the program behavior. The problem of chosing the most suitable catamorphisms in a fully automatic way is left for future research.
4.1 Catamorphic abstraction specifications
The predicates in
![]() $P$
different from catamorphisms are called program predicates. An atom whose predicate is a program predicate is called a program atom and an atom whose predicate is a catamorphism predicate is called a catamorphism atom. Without loss of generality, we assume that no clause in
$P$
different from catamorphisms are called program predicates. An atom whose predicate is a program predicate is called a program atom and an atom whose predicate is a catamorphism predicate is called a catamorphism atom. Without loss of generality, we assume that no clause in
![]() $P$
has occurrences of both program atoms and catamorphism atoms. The query
$P$
has occurrences of both program atoms and catamorphism atoms. The query
![]() $Q$
given in input to
$Q$
given in input to
![]() ${\mathcal{T}}_{\mathit{abs}}$
is of the form:
${\mathcal{T}}_{\mathit{abs}}$
is of the form:
![]() $\mathit{false} \ \leftarrow c, \mathit{cata}_1(X,T_1,Y_1), \ldots, \mathit{cata}_n(X,T_n,Y_n), \mathit{p}(Z)$
$\mathit{false} \ \leftarrow c, \mathit{cata}_1(X,T_1,Y_1), \ldots, \mathit{cata}_n(X,T_n,Y_n), \mathit{p}(Z)$
where: (i)
![]() $\mathit{p}(Z)$
is a program atom and
$\mathit{p}(Z)$
is a program atom and
![]() $\mathit{Z}$
is a tuple of distinct variables; (ii)
$\mathit{Z}$
is a tuple of distinct variables; (ii)
![]() $\mathit{cata}_1,$
$\mathit{cata}_1,$
![]() $\ldots, \mathit{cata}_n$
are catamorphism predicates; (iii)
$\ldots, \mathit{cata}_n$
are catamorphism predicates; (iii)
![]() $c$
is a constraint; (iv)
$c$
is a constraint; (iv)
![]() $X$
is a tuple of distinct variables of basic sort; (v)
$X$
is a tuple of distinct variables of basic sort; (v)
![]() ${T_1},\ldots, {T_n}$
are ADT variables occurring in
${T_1},\ldots, {T_n}$
are ADT variables occurring in
![]() $Z$
; and (vi)
$Z$
; and (vi)
![]() $Y_1,\ldots, Y_n$
are pairwise disjoint tuples of distinct variables of basic sort not occurring in
$Y_1,\ldots, Y_n$
are pairwise disjoint tuples of distinct variables of basic sort not occurring in
![]() $\mathit{vars}(\{X,Z\})$
. Without loss of generality, we assume that the
$\mathit{vars}(\{X,Z\})$
. Without loss of generality, we assume that the
![]() $\mathit{cata}_{i}$
’s over the same ADT variable are all distinct (this assumption is trivially satisfied by query 7 of Figure 1). For each ADT sort
$\mathit{cata}_{i}$
’s over the same ADT variable are all distinct (this assumption is trivially satisfied by query 7 of Figure 1). For each ADT sort
![]() $\tau$
, a catamorphic abstraction for
$\tau$
, a catamorphic abstraction for
![]() $\tau$
is a conjunction of catamorphisms defined as follows:
$\tau$
is a conjunction of catamorphisms defined as follows:
![]() $\mathit{cata}_\tau (X,T,Y_{1},\ldots, Y_{n}) =_{\mathit{def}} \mathit{cata}_1(X,T,Y_1), \ldots, \mathit{cata}_n(X,T,Y_n)$
$\mathit{cata}_\tau (X,T,Y_{1},\ldots, Y_{n}) =_{\mathit{def}} \mathit{cata}_1(X,T,Y_1), \ldots, \mathit{cata}_n(X,T,Y_n)$
where: (i)
![]() $T$
is a variable of ADT sort
$T$
is a variable of ADT sort
![]() $\tau$
, (ii)
$\tau$
, (ii)
![]() $X,Y_{1},\ldots, Y_{n}$
are tuples of variables of basic sort, (iii) the variables in
$X,Y_{1},\ldots, Y_{n}$
are tuples of variables of basic sort, (iii) the variables in
![]() $\{X,Y_{1},\ldots, Y_{n}\}$
are all distinct, and (iv) the
$\{X,Y_{1},\ldots, Y_{n}\}$
are all distinct, and (iv) the
![]() $\mathit{cata_{i}}$
predicates are all distinct.
$\mathit{cata_{i}}$
predicates are all distinct.
Given catamorphic abstractions for the ADT sorts
![]() $\tau _{1},\ldots, \tau _{k}$
, a catamorphic abstraction specification for the set
$\tau _{1},\ldots, \tau _{k}$
, a catamorphic abstraction specification for the set
![]() $P$
of CHCs is a set of expressions, one expression for each program predicate
$P$
of CHCs is a set of expressions, one expression for each program predicate
![]() $p$
in
$p$
in
![]() $P$
that has at least one argument of ADT sort. The expression for the predicate
$P$
that has at least one argument of ADT sort. The expression for the predicate
![]() $p$
is called the catamorphic abstraction specification for
$p$
is called the catamorphic abstraction specification for
![]() $p$
and it is of the form:
$p$
and it is of the form:
![]() $p(Z) \Longrightarrow \mathit{cata}_{\tau _1}(X,T_1,V_1), \ldots, \mathit{cata}_{\tau _k}(X,T_k,V_k)$
$p(Z) \Longrightarrow \mathit{cata}_{\tau _1}(X,T_1,V_1), \ldots, \mathit{cata}_{\tau _k}(X,T_k,V_k)$
where: (i)
![]() $Z$
is a tuple of distinct variables, (ii)
$Z$
is a tuple of distinct variables, (ii)
![]() $T_1,\ldots, T_k$
are the distinct variables in
$T_1,\ldots, T_k$
are the distinct variables in
![]() $Z$
of (not necessarily distinct) ADT sorts
$Z$
of (not necessarily distinct) ADT sorts
![]() $\tau _1,\ldots, \tau _k$
, respectively, (iii)
$\tau _1,\ldots, \tau _k$
, respectively, (iii)
![]() $V_1,\ldots, V_k$
are pairwise disjoint tuples of distinct variables of basic sort not occurring in
$V_1,\ldots, V_k$
are pairwise disjoint tuples of distinct variables of basic sort not occurring in
![]() $\mathit{vars}(\{X,Z\})$
; and (iv)
$\mathit{vars}(\{X,Z\})$
; and (iv)
![]() $\textit{vars}(X) \cap \textit{vars}(Z)\!=\!\emptyset$
.
$\textit{vars}(X) \cap \textit{vars}(Z)\!=\!\emptyset$
.
Example 1. Let us consider our introductory double example (see Figure 1) and the catamorphic abstraction for the sort
![]() $\mathit{list(int)}$
:
$\mathit{list(int)}$
:
![]() $\mathit{cata}_{\mathit{list(int)}}(X,L,N) =_{\mathit{def}} \mathit{listcount}(X,L,N)$
$\mathit{cata}_{\mathit{list(int)}}(X,L,N) =_{\mathit{def}} \mathit{listcount}(X,L,N)$
This abstraction determines the following catamorphic abstraction specifications for the predicates
![]() $\mathit{double}$
,
$\mathit{double}$
,
![]() $\mathit{eq}$
, and
$\mathit{eq}$
, and
![]() $\mathit{append}$
(and thus, for the set
$\mathit{append}$
(and thus, for the set
![]() $\{1,\ldots, 6\}$
of clauses):
$\{1,\ldots, 6\}$
of clauses):
![]() $\mathit{double}(\mathit{Xs},\mathit{Zs}) \Longrightarrow \mathit{listcount}(X,\mathit{Xs},N1),\ \mathit{listcount}(X,\mathit{Zs},N2)$
$\mathit{double}(\mathit{Xs},\mathit{Zs}) \Longrightarrow \mathit{listcount}(X,\mathit{Xs},N1),\ \mathit{listcount}(X,\mathit{Zs},N2)$
![]() $\mathit{eq}(\mathit{Xs},\mathit{Zs}) \Longrightarrow \mathit{listcount}(X,\mathit{Xs},N1),\ \mathit{listcount}(X,\mathit{Zs},N2)$
$\mathit{eq}(\mathit{Xs},\mathit{Zs}) \Longrightarrow \mathit{listcount}(X,\mathit{Xs},N1),\ \mathit{listcount}(X,\mathit{Zs},N2)$
![]() $\mathit{append}(\mathit{Xs},\!\!\mathit{Ys},\!\mathit{Zs}) \Longrightarrow \mathit{listcount}(X,\!\mathit{Xs},\!N1), \mathit{listcount}(X,\!\!\mathit{Ys},\!N2), \mathit{listcount}(X,\!\mathit{Zs},\!N3)$
$\mathit{append}(\mathit{Xs},\!\!\mathit{Ys},\!\mathit{Zs}) \Longrightarrow \mathit{listcount}(X,\!\mathit{Xs},\!N1), \mathit{listcount}(X,\!\!\mathit{Ys},\!N2), \mathit{listcount}(X,\!\mathit{Zs},\!N3)$
Note that no relationships among the variables
![]() $N1$
,
$N1$
,
![]() $N2$
, and
$N2$
, and
![]() $N3$
are stated by the specifications. Those relationships will be discovered by the solver after transformation.
$N3$
are stated by the specifications. Those relationships will be discovered by the solver after transformation.
Example 2. Let us consider: (i) a set
![]() $\mathit{Quicksort}$
of clauses where predicate
$\mathit{Quicksort}$
of clauses where predicate
![]() $\mathit{quicksort}(L,S)$
holds if
$\mathit{quicksort}(L,S)$
holds if
![]() $S$
is obtained from list
$S$
is obtained from list
![]() $L$
by the quicksort algorithm and (ii) the following query:
$L$
by the quicksort algorithm and (ii) the following query:
![]() $\mathit{false} \ \leftarrow \ \mathit{BS}\!=\!\mathit{false},\ \mathit{is\, us asorted(S,\!BS)},\ \mathit{quicksort}(L,S)$
(Ord)
$\mathit{false} \ \leftarrow \ \mathit{BS}\!=\!\mathit{false},\ \mathit{is\, us asorted(S,\!BS)},\ \mathit{quicksort}(L,S)$
(Ord)
where
![]() $\mathit{is}\, us\mathit{asorted(S,\!BS)}$
returns
$\mathit{is}\, us\mathit{asorted(S,\!BS)}$
returns
![]() $\mathit{BS}\!=\!\mathit{true}$
if the elements of
$\mathit{BS}\!=\!\mathit{true}$
if the elements of
![]() $S$
are ordered in weakly ascending order, and
$S$
are ordered in weakly ascending order, and
![]() $\mathit{BS}\!=\!\mathit{false}$
, otherwise. The catamorphism
$\mathit{BS}\!=\!\mathit{false}$
, otherwise. The catamorphism
![]() $\mathit{is\, us asorted}$
is defined in term of the catamorphism
$\mathit{is\, us asorted}$
is defined in term of the catamorphism
![]() $\mathit{hd}$
, as follows:
$\mathit{hd}$
, as follows:
![]() $\mathit{is\, us asorted}([\,],\mathit{B}) \leftarrow \mathit{B}\!=\!\mathit{true}$
$\mathit{is\, us asorted}([\,],\mathit{B}) \leftarrow \mathit{B}\!=\!\mathit{true}$
![]() $\mathit{is\, us asorted}([H | T],\mathit{B}) \leftarrow \mathit{B}\!=\!(\mathit{IsDef \Rightarrow (H\! \leq \! HdT\ \&\ BT))}$
,
$\mathit{is\, us asorted}([H | T],\mathit{B}) \leftarrow \mathit{B}\!=\!(\mathit{IsDef \Rightarrow (H\! \leq \! HdT\ \&\ BT))}$
,
![]() $\mathit{hd}(T,\mathit{IsDef},\mathit{HdT}),\ \mathit{is\, us asorted}(T,\mathit{BT})$
$\mathit{hd}(T,\mathit{IsDef},\mathit{HdT}),\ \mathit{is\, us asorted}(T,\mathit{BT})$
![]() $\mathit{hd}([\,],\mathit{IsDef},\mathit{Hd}) \leftarrow \ \mathit{IsDef} \!=\! \mathit{false}, \ \mathit{Hd}\!=\!0$
$\mathit{hd}([\,],\mathit{IsDef},\mathit{Hd}) \leftarrow \ \mathit{IsDef} \!=\! \mathit{false}, \ \mathit{Hd}\!=\!0$
![]() $\mathit{hd}([H|T],\mathit{IsDef},\mathit{Hd}) \leftarrow \mathit{IsDef}\!=\!\mathit{true},\ \mathit{Hd\!=\!H}.$
$\mathit{hd}([H|T],\mathit{IsDef},\mathit{Hd}) \leftarrow \mathit{IsDef}\!=\!\mathit{true},\ \mathit{Hd\!=\!H}.$
![]() $\mathit{hd}(L,\mathit{IsDef},\mathit{Hd})$
holds if either
$\mathit{hd}(L,\mathit{IsDef},\mathit{Hd})$
holds if either
![]() $L$
is the empty list (
$L$
is the empty list (
![]() $\mathit{IsDef}\!=\!\textit{false}$
) and
$\mathit{IsDef}\!=\!\textit{false}$
) and
![]() $\textit{Hd}$
is
$\textit{Hd}$
is
![]() $0$
or
$0$
or
![]() $L$
is a nonempty list (
$L$
is a nonempty list (
![]() $\mathit{IsDef}\!=\!\textit{true}$
) and
$\mathit{IsDef}\!=\!\textit{true}$
) and
![]() $\textit{Hd}$
is its head. Thus,
$\textit{Hd}$
is its head. Thus,
![]() $\mathit{hd}$
is a total function. Note that the arbitrary value
$\mathit{hd}$
is a total function. Note that the arbitrary value
![]() $0$
is not used in the clauses for
$0$
is not used in the clauses for
![]() $\mathit{is\, us asorted}$
.
$\mathit{is\, us asorted}$
.
Let us consider a catamorphic abstraction
![]() $\mathit{cata_{\mathit{list(int)}}}$
for the sort
$\mathit{cata_{\mathit{list(int)}}}$
for the sort
![]() $\mathit{list(int)}$
, which is the sort of the variables
$\mathit{list(int)}$
, which is the sort of the variables
![]() $L$
and
$L$
and
![]() $S$
in
$S$
in
![]() $\mathit{quicksort}(L,S)$
. That abstraction, consisting of the conjunction of three list catamorphisms
$\mathit{quicksort}(L,S)$
. That abstraction, consisting of the conjunction of three list catamorphisms
![]() $\mathit{listmin}$
,
$\mathit{listmin}$
,
![]() $\mathit{listmax}$
, and
$\mathit{listmax}$
, and
![]() $\mathit{is\, us asorted}$
, is defined as follows:
$\mathit{is\, us asorted}$
, is defined as follows:
![]() $\mathit{cata_{\mathit{list(int)}}(L,BMinL,MinL,BMaxL,MaxL,BL)}=_{\mathit{def}}$
$\mathit{cata_{\mathit{list(int)}}(L,BMinL,MinL,BMaxL,MaxL,BL)}=_{\mathit{def}}$
![]() $\mathit{listmin(L,BMinL,MinL),\ listmax(L,BMaxL,MaxL),\ is\, us asorted(L,BL)}$
$\mathit{listmin(L,BMinL,MinL),\ listmax(L,BMaxL,MaxL),\ is\, us asorted(L,BL)}$
where: (i) if
![]() $L$
is not empty,
$L$
is not empty,
![]() $\mathit{listmin(L,BMinL,MinL)}$
holds if
$\mathit{listmin(L,BMinL,MinL)}$
holds if
![]() $\mathit{BMinL}\!=\!\mathit{true}$
and
$\mathit{BMinL}\!=\!\mathit{true}$
and
![]() $\mathit{MinL}$
is the minimum integer in
$\mathit{MinL}$
is the minimum integer in
![]() $L$
, and (ii) otherwise, if
$L$
, and (ii) otherwise, if
![]() $L$
is empty,
$L$
is empty,
![]() $\mathit{listmin(L,BMinL,MinL)}$
holds if
$\mathit{listmin(L,BMinL,MinL)}$
holds if
![]() $\mathit{BMinL}\!=\!\mathit{false}$
and
$\mathit{BMinL}\!=\!\mathit{false}$
and
![]() $\textit{MinL}\!=\!0$
. If
$\textit{MinL}\!=\!0$
. If
![]() $\mathit{BMinL}\!=\!\mathit{false}$
, then
$\mathit{BMinL}\!=\!\mathit{false}$
, then
![]() $\mathit{MinL}$
should not be used elsewhere in the clause where
$\mathit{MinL}$
should not be used elsewhere in the clause where
![]() $\mathit{listmin(L,BMinL,MinL)}$
occurs. Analogously for
$\mathit{listmin(L,BMinL,MinL)}$
occurs. Analogously for
![]() $\mathit{listmax}$
, instead of
$\mathit{listmax}$
, instead of
![]() $\mathit{listmin}$
. Then, the catamorphic abstraction specification for
$\mathit{listmin}$
. Then, the catamorphic abstraction specification for
![]() $\mathit{quicksort}$
is as follows:
$\mathit{quicksort}$
is as follows:
![]() $\mathit{quicksort(L,S) \Longrightarrow }$
$\mathit{quicksort(L,S) \Longrightarrow }$
![]() $\mathit{listmin(L,\!BMinL,\!MinL),\ listmax(L,\!BMaxL,\!MaxL),\ is\, us asorted(L,\!BL)},$
$\mathit{listmin(L,\!BMinL,\!MinL),\ listmax(L,\!BMaxL,\!MaxL),\ is\, us asorted(L,\!BL)},$
![]() $\mathit{listmin(S,\!BMinS,\!MinS),\ listmax(S,\!BMaxS,\!MaxS),\ is\, us asorted(S,\!BS)}$
$\mathit{listmin(S,\!BMinS,\!MinS),\ listmax(S,\!BMaxS,\!MaxS),\ is\, us asorted(S,\!BS)}$
Now, let us assume that in the set of clauses defining
![]() $\mathit{quicksort}(L,S)$
, we have the atom
$\mathit{quicksort}(L,S)$
, we have the atom
![]() $\mathit{partition(\!V\!,\!L,\!A,\!B)}$
that, given the integer
$\mathit{partition(\!V\!,\!L,\!A,\!B)}$
that, given the integer
![]() $V$
and the list
$V$
and the list
![]() $L$
, holds if
$L$
, holds if
![]() $\mathit{A}$
is the list made out of the elements of
$\mathit{A}$
is the list made out of the elements of
![]() $L$
not larger than
$L$
not larger than
![]() $V$
, and
$V$
, and
![]() $B$
is the list made out of the remaining elements of
$B$
is the list made out of the remaining elements of
![]() $L$
larger than
$L$
larger than
![]() $V$
. We have that the catamorphic abstraction specification for
$V$
. We have that the catamorphic abstraction specification for
![]() $\mathit{partition}$
which has the list arguments
$\mathit{partition}$
which has the list arguments
![]() $L$
,
$L$
,
![]() $A$
, and
$A$
, and
![]() $B$
, is as follows:
$B$
, is as follows:
![]() $\mathit{partition(V\!\!,\!L,\!A,\!B) \Longrightarrow }$
$\mathit{partition(V\!\!,\!L,\!A,\!B) \Longrightarrow }$
![]() $\mathit{listmin(L,\!BMinL,\!MinL),\ listmax(L,\!BMaxL,\!MaxL),\ is\, us asorted(L,\!BL)},$
$\mathit{listmin(L,\!BMinL,\!MinL),\ listmax(L,\!BMaxL,\!MaxL),\ is\, us asorted(L,\!BL)},$
![]() $\mathit{listmin(A,\!BMinA,\!MinA),\ listmax(A,\!BMaxA,\!MaxA),\ is\, us asorted(A,\!BA),}$
$\mathit{listmin(A,\!BMinA,\!MinA),\ listmax(A,\!BMaxA,\!MaxA),\ is\, us asorted(A,\!BA),}$
![]() $\mathit{listmin(B,\!BMinB,\!MinB),\ listmax(B,\!BMaxB,\!MaxB),\ is\, us asorted(B,\!BB)}$
$\mathit{listmin(B,\!BMinB,\!MinB),\ listmax(B,\!BMaxB,\!MaxB),\ is\, us asorted(B,\!BB)}$
Note that the catamorphisms listmin and listmax are not present in the query Ord. However, they are needed for stating the property that, if
![]() $\textit{partition}(V\!,\!L,\!A,\!B)$
holds, then the maximum element of the list
$\textit{partition}(V\!,\!L,\!A,\!B)$
holds, then the maximum element of the list
![]() $A$
is less than or equal to the minimum element of the list
$A$
is less than or equal to the minimum element of the list
![]() $B$
. This is a key property useful for proving the orderedness of the list
$B$
. This is a key property useful for proving the orderedness of the list
![]() $S$
constructed by
$S$
constructed by
![]() $\mathit{quicksort}(L,S)$
. The fact that the catamorphisms listmin and listmax are helpful in the proof of the orderedness of
$\mathit{quicksort}(L,S)$
. The fact that the catamorphisms listmin and listmax are helpful in the proof of the orderedness of
![]() $S$
rests upon programmer’s intuition. However, in our approach the programmer need not explicitly state all the properties of listmin and listmax which are needed for the proof. Indeed, the relationships among the output variables of listmin and listmax are automatically inferred by the CHC solver.
$S$
rests upon programmer’s intuition. However, in our approach the programmer need not explicitly state all the properties of listmin and listmax which are needed for the proof. Indeed, the relationships among the output variables of listmin and listmax are automatically inferred by the CHC solver.
4.2 Transformation rules
The rules for transforming CHCs that use catamorphisms are variants of the usual fold/unfold rules for CHCs (De Angelis et al., Reference De Angelis, Fioravanti, Gallagher, Hermenegildo, Pettorossi and Proietti2022).
A transformation sequence from an initial set
![]() $S_{0}$
of CHCs to a final set
$S_{0}$
of CHCs to a final set
![]() $S_{n}$
of CHCs is a sequence
$S_{n}$
of CHCs is a sequence ![]() of sets of CHCs such that, for
of sets of CHCs such that, for
![]() $i\!=\!0,\ldots, n\!-\!1,$
$i\!=\!0,\ldots, n\!-\!1,$
![]() $S_{i+1}$
is derived from
$S_{i+1}$
is derived from
![]() $S_i$
, denoted
$S_i$
, denoted ![]() , by performing a transformation step consisting in applying one of the following transformation Rules R1–R5.
, by performing a transformation step consisting in applying one of the following transformation Rules R1–R5.
The objective of a transformation sequence constructed by algorithm
![]() ${\mathcal{T}}_{\mathit{abs}}$
is to derive from a given set
${\mathcal{T}}_{\mathit{abs}}$
is to derive from a given set
![]() $S_{0}$
a new, equisatisfiable set
$S_{0}$
a new, equisatisfiable set
![]() $S_{n}$
in which for each program predicate
$S_{n}$
in which for each program predicate
![]() $p$
in
$p$
in
![]() $S_{0}$
, there is a new predicate newp whose definition is given by the conjunction of an atom for
$S_{0}$
, there is a new predicate newp whose definition is given by the conjunction of an atom for
![]() $p$
with some catamorphism atoms. With respect to p, the predicate newp has extra arguments that hold the values of the catamorphisms for the arguments of
$p$
with some catamorphism atoms. With respect to p, the predicate newp has extra arguments that hold the values of the catamorphisms for the arguments of
![]() $p$
with ADT sort.
$p$
with ADT sort.
(R1) Definition Rule. Let
![]() $D$
be a clause of the form
$D$
be a clause of the form
![]() $\mathit{newp}(X_1,\ldots, X_k)\leftarrow \textit{Catas}, A$
, where: (1) newp is a predicate symbol not occurring in the sequence
$\mathit{newp}(X_1,\ldots, X_k)\leftarrow \textit{Catas}, A$
, where: (1) newp is a predicate symbol not occurring in the sequence ![]() constructed so far, (2)
constructed so far, (2)
![]() $\{X_1,\ldots, X_k\} = \mathit{vars}(\{\textit{Catas},A\})$
, (3) Catas is a conjunction of catamorphism atoms, with
$\{X_1,\ldots, X_k\} = \mathit{vars}(\{\textit{Catas},A\})$
, (3) Catas is a conjunction of catamorphism atoms, with
![]() $\textit{adt-vars}(\textit{Catas})\subseteq \textit{adt-vars}(A)$
, and (4)
$\textit{adt-vars}(\textit{Catas})\subseteq \textit{adt-vars}(A)$
, and (4)
![]() $A$
is a program atom. By the definition introduction rule we add
$A$
is a program atom. By the definition introduction rule we add
![]() $D$
to
$D$
to
![]() $S_i$
and we get the new set
$S_i$
and we get the new set
![]() $S_{i+1}= S_i\cup \{D\}$
.
$S_{i+1}= S_i\cup \{D\}$
.
We will say that
![]() $D$
is a definition for
$D$
is a definition for
![]() $A$
.
$A$
.
For any
![]() $i\!\geq \!0$
, by
$i\!\geq \!0$
, by
![]() $\mathit{Defs}_i$
we denote the set of clauses, called definitions, introduced by Rule R1 during the construction of the sequence
$\mathit{Defs}_i$
we denote the set of clauses, called definitions, introduced by Rule R1 during the construction of the sequence ![]() .
.
Example 3. In our double example, by applying the definition rule we may introduce the following clause, whose variables of sort
![]() $\mathit{list(int)}$
are
$\mathit{list(int)}$
are
![]() $B$
and
$B$
and
![]() $E$
(the underlining of the list variables
$E$
(the underlining of the list variables
![]() $B$
and
$B$
and
![]() $E$
has been omitted here):
$E$
has been omitted here):
![]() $D1$
.
$D1$
.
![]() $\mathit{new}1(A,\!B,\!C,\!E,\!F) \leftarrow \mathit{listcount}(A,\!B,\!C),\ \mathit{listcount}(A,\!E,\!F),\ \mathit{double}(B,\!E)$
$\mathit{new}1(A,\!B,\!C,\!E,\!F) \leftarrow \mathit{listcount}(A,\!B,\!C),\ \mathit{listcount}(A,\!E,\!F),\ \mathit{double}(B,\!E)$
Thus,
![]() $S_1 = S_0 \cup \{D1\}$
, where
$S_1 = S_0 \cup \{D1\}$
, where
![]() $S_0$
consists of clauses 1–7 of Figure 1.
$S_0$
consists of clauses 1–7 of Figure 1.
By making use of the
![]() $\mathit{Unf}$
function (see Definition2), we introduce the unfolding rule (see Rule R2), which consists of some unfolding steps followed by the application of the functionality property, which was presented in previous work (De Angelis et al., Reference De Angelis, Fioravanti, Gallagher, Hermenegildo, Pettorossi and Proietti2022). Recall that list and binary tree catamorphisms and, in general, all catamorphisms are assumed to be total functions (see Definition1).
$\mathit{Unf}$
function (see Definition2), we introduce the unfolding rule (see Rule R2), which consists of some unfolding steps followed by the application of the functionality property, which was presented in previous work (De Angelis et al., Reference De Angelis, Fioravanti, Gallagher, Hermenegildo, Pettorossi and Proietti2022). Recall that list and binary tree catamorphisms and, in general, all catamorphisms are assumed to be total functions (see Definition1).
Definition 2 (One-step Unfolding). Let
![]() $D$
:
$D$
:
![]() $H\leftarrow c,L,A,R$
be a clause, where
$H\leftarrow c,L,A,R$
be a clause, where
![]() $A$
is an atom, and let
$A$
is an atom, and let
![]() $P$
be a set of definite clauses with
$P$
be a set of definite clauses with
![]() $\mathit{vars}(D)\cap \mathit{vars}(P)=\emptyset$
. Let
$\mathit{vars}(D)\cap \mathit{vars}(P)=\emptyset$
. Let
![]() $K_{1}\leftarrow c_{1}, B_{1},\,\ldots, \,K_{m}\leftarrow c_{m}, B_{m}$
, with
$K_{1}\leftarrow c_{1}, B_{1},\,\ldots, \,K_{m}\leftarrow c_{m}, B_{m}$
, with
![]() $m\!\geq \!0$
, be the clauses in
$m\!\geq \!0$
, be the clauses in
![]() $P$
, such that, for
$P$
, such that, for
![]() $j=1,\ldots, m$
:
$j=1,\ldots, m$
:
![]() $(\textrm{i})$
there exists a most general unifier
$(\textrm{i})$
there exists a most general unifier
![]() $\vartheta _j$
of
$\vartheta _j$
of
![]() $A$
and
$A$
and
![]() $K_j$
, and
$K_j$
, and
![]() $(\textrm{ii})$
the conjunction of constraints
$(\textrm{ii})$
the conjunction of constraints
![]() $(c, c_{j})\vartheta _j$
is satisfiable.
$(c, c_{j})\vartheta _j$
is satisfiable.
One-step unfolding produces the following set of CHCs:
![]() $\mathit{Unf}(D,A,P)=\{(H\leftarrow c,{c}_j,L, B_j, R) \vartheta _j \mid j=1, \ldots, m\}$
.
$\mathit{Unf}(D,A,P)=\{(H\leftarrow c,{c}_j,L, B_j, R) \vartheta _j \mid j=1, \ldots, m\}$
.
In the sequel, Catas denotes a conjunction of catamorphism atoms.
(R2) Unfolding Rule. Let
![]() $D$
:
$D$
:
![]() $\mathit{newp}(U) \leftarrow \mathit{Catas}, A$
be a definition in
$\mathit{newp}(U) \leftarrow \mathit{Catas}, A$
be a definition in
![]() $S_i \cap \textit{Defs}_i$
, where
$S_i \cap \textit{Defs}_i$
, where
![]() $A$
is a program atom, and
$A$
is a program atom, and
![]() $P$
be the set of definite clauses in
$P$
be the set of definite clauses in
![]() $S_i$
. We derive a new set UnfD of clauses by the following three steps.
$S_i$
. We derive a new set UnfD of clauses by the following three steps.
Step 1. (One-step unfolding of program atom)
![]() $\mathit{UnfD}:=\mathit{Unf}(D,A,P)$
;
$\mathit{UnfD}:=\mathit{Unf}(D,A,P)$
;
Step 2. (Unfolding of the catamorphism atoms)
-
while there exists a clause
 $E$
:
$E$
:
 $H\! \leftarrow d,{L}, C,{R}$
in
$H\! \leftarrow d,{L}, C,{R}$
in
 $\mathit{UnfD}$
, for some conjunctions
$\mathit{UnfD}$
, for some conjunctions
 $L$
and
$L$
and
 $R$
of atoms, such that
$R$
of atoms, such that
 $C$
is a catamorphism atom whose argument of ADT sort is not a variable do
$C$
is a catamorphism atom whose argument of ADT sort is not a variable do
![]() $\mathit{UnfD}:=(\mathit{UnfD}\setminus \{E\}) \cup \mathit{Unf(E,C,P)}$
;
$\mathit{UnfD}:=(\mathit{UnfD}\setminus \{E\}) \cup \mathit{Unf(E,C,P)}$
;
Step 3. (Applying Functionality on catamorphism atoms)
-
while there exists a clause
 $E$
:
$E$
:
 $H \leftarrow d,{L}, \mathit{cata}(X,T,Y1), \mathit{cata}(X,T,Y2),{R}$
in
$H \leftarrow d,{L}, \mathit{cata}(X,T,Y1), \mathit{cata}(X,T,Y2),{R}$
in
 $\mathit{UnfD}$
, for some catamorphism
$\mathit{UnfD}$
, for some catamorphism
 $\mathit{cata}$
do
$\mathit{cata}$
do
![]() $\mathit{UnfD}:=(\mathit{UnfD}-\{E\}) \cup \{H \leftarrow d, Y1\!=\!Y2,{L}, \mathit{cata}(X,T,Y1),{R}\}$
.
$\mathit{UnfD}:=(\mathit{UnfD}-\{E\}) \cup \{H \leftarrow d, Y1\!=\!Y2,{L}, \mathit{cata}(X,T,Y1),{R}\}$
.
Then, by unfolding clause
![]() $D$
, we get the new set of clauses
$D$
, we get the new set of clauses
![]() $S_{i+1}= (S_i \setminus \{D\}) \cup \textit{UnfD}$
.
$S_{i+1}= (S_i \setminus \{D\}) \cup \textit{UnfD}$
.
Example 4. For instance, in our double example, by unfolding clause
![]() $D1$
we get:
$D1$
we get:
![]() $E1$
.
$E1$
.
![]() $\mathit{new}1(A,\!B,\!C,\!E,\!F)\! \leftarrow \! \mathit{listcount}(A,\!B,\!C),\ \mathit{listcount}(A,\!E,\!F),\ \mathit{eq}(B,\!G),\ \mathit{append}(B,\!G,\!E)$
$\mathit{new}1(A,\!B,\!C,\!E,\!F)\! \leftarrow \! \mathit{listcount}(A,\!B,\!C),\ \mathit{listcount}(A,\!E,\!F),\ \mathit{eq}(B,\!G),\ \mathit{append}(B,\!G,\!E)$
Thus,
![]() $S_{2}=S_0 \cup \{E1\}$
.
$S_{2}=S_0 \cup \{E1\}$
.
By the following catamorphism addition rule, we use the catamorphic abstraction specifications for adding catamorphism atoms to the bodies of clauses. Here and in what follows, for any two conjunctions
![]() $G_1$
and
$G_1$
and
![]() $G_2$
of atoms, we say that
$G_2$
of atoms, we say that
![]() $G_1$
is a subconjunction of
$G_1$
is a subconjunction of
![]() $G_2$
if every atom of
$G_2$
if every atom of
![]() $G_1$
is an atom of
$G_1$
is an atom of
![]() $G_2$
.
$G_2$
.
(R3) Catamorphism Addition Rule. Let
![]() $C$
:
$C$
:
![]() $H\leftarrow c, \textit{Catas}, A_1,\ldots, A_m$
be a clause in
$H\leftarrow c, \textit{Catas}, A_1,\ldots, A_m$
be a clause in
![]() $S_i$
, where
$S_i$
, where
![]() $H$
is either false or a program atom, and
$H$
is either false or a program atom, and
![]() $A_1,\ldots, A_m$
are program atoms. Let
$A_1,\ldots, A_m$
are program atoms. Let
![]() $E$
be the clause derived from
$E$
be the clause derived from
![]() $C$
as follows:
$C$
as follows:
for
![]() $k=1,\ldots, m$
do
$k=1,\ldots, m$
do
-
- let
 $\mathit{Catas}_{k}$
be the conjunction of every catamorphism atom
$\mathit{Catas}_{k}$
be the conjunction of every catamorphism atom
 $F$
in
$F$
in
 $\textit{Catas}$
such that
$\textit{Catas}$
such that
 $\mathit{adt\mbox{-}vars}(A_k) \cap \mathit{adt\mbox{-}vars}(F) \neq \emptyset$
;
$\mathit{adt\mbox{-}vars}(A_k) \cap \mathit{adt\mbox{-}vars}(F) \neq \emptyset$
; -
- let
 $A_k \Longrightarrow \mathit{cata}_1(X,T_1,Y_1),\ldots, \mathit{cata}_n(X,T_n,Y_n)$
be a catamorphic abstraction specification for the predicate of
$A_k \Longrightarrow \mathit{cata}_1(X,T_1,Y_1),\ldots, \mathit{cata}_n(X,T_n,Y_n)$
be a catamorphic abstraction specification for the predicate of
 $A_k$
, where the variables in
$A_k$
, where the variables in
 $Y_1,\ldots, Y_n$
do not occur in
$Y_1,\ldots, Y_n$
do not occur in
 $C$
, and the conjunction
$C$
, and the conjunction
 $\mathit{cata}_1(X,T_1,Y_1),\ldots, $
$\mathit{cata}_1(X,T_1,Y_1),\ldots, $
 $\mathit{cata}_n(X,T_n,Y_n)$
can be split into two subconjunctions
$\mathit{cata}_n(X,T_n,Y_n)$
can be split into two subconjunctions
 $B_1$
and
$B_1$
and
 $B_2$
such that:
$B_2$
such that:
-
(i) a variant
 $B_1\vartheta$
of
$B_1\vartheta$
of
 $B_1$
, for a substitution
$B_1$
, for a substitution
 $\vartheta$
acting on
$\vartheta$
acting on
 $\mathit{vars}(B_{1})$
, is a subconjunction of
$\mathit{vars}(B_{1})$
, is a subconjunction of
 $\mathit{Catas}_{k}$
, and
$\mathit{Catas}_{k}$
, and -
(ii) for every catamorphism atom
 $\mathit{cata}_j(X,T_j,Y_j)$
in
$\mathit{cata}_j(X,T_j,Y_j)$
in
 $B_2\vartheta$
, there is no catamorphism atom in
$B_2\vartheta$
, there is no catamorphism atom in
 $\mathit{Catas}_k$
of the form
$\mathit{Catas}_k$
of the form
 $\mathit{cata}_j(V,T_j,W)$
(i.e., there is no catamorphism atom with the same predicate acting on the same ADT variable
$\mathit{cata}_j(V,T_j,W)$
(i.e., there is no catamorphism atom with the same predicate acting on the same ADT variable
 $T_{j}$
);
$T_{j}$
);
-
- add the conjunction
 $B_2\vartheta$
to the body of
$B_2\vartheta$
to the body of
 $C$
.
$C$
.
Then, by the catamorphism addition rule, we get the new set
![]() $S_{i+1}= (S_i \setminus \{C\}) \cup \{E\}$
.
$S_{i+1}= (S_i \setminus \{C\}) \cup \{E\}$
.
Example 5. In our double example, by applying the catamorphism addition rule to clause
![]() $E1$
, we add the catamorphism
$E1$
, we add the catamorphism
![]() $\mathit{listcount}(A,\!H,\!I)$
, and we get:
$\mathit{listcount}(A,\!H,\!I)$
, and we get:
![]() $E2$
.
$E2$
.
![]() $\mathit{new}1(A,\!B,\!C,\!E,\!F) \leftarrow \mathit{listcount}(A,\!B,\!C),\ \mathit{listcount}(A,\!E,\!F),\ \mathit{listcount}(A,\!H,\!I),$
$\mathit{new}1(A,\!B,\!C,\!E,\!F) \leftarrow \mathit{listcount}(A,\!B,\!C),\ \mathit{listcount}(A,\!E,\!F),\ \mathit{listcount}(A,\!H,\!I),$
![]() $\mathit{eq}(B,\!H),\ \mathit{append}(B,\!H,\!E)$
$\mathit{eq}(B,\!H),\ \mathit{append}(B,\!H,\!E)$
Thus, we get the new set of clauses
![]() $S_{3}=S_0 \cup \{E2\}$
.
$S_{3}=S_0 \cup \{E2\}$
.
The following folding rule allows us to replace conjunctions of catamorphism atoms and program atoms by new program atoms whose predicates has been introduced in previous applications of the definition rule.
(R4) Folding Rule. Let
![]() $C$
:
$C$
:
![]() $H\leftarrow c, \textit{Catas}^{C}, A_1,\ldots, A_m$
be a clause in
$H\leftarrow c, \textit{Catas}^{C}, A_1,\ldots, A_m$
be a clause in
![]() $S_i$
, where either
$S_i$
, where either
![]() $H$
is false or
$H$
is false or
![]() $C$
has been obtained by the unfolding rule, possibly followed by the application of the catamorphism addition rule.
$C$
has been obtained by the unfolding rule, possibly followed by the application of the catamorphism addition rule.
![]() $\textit{Catas}^{C}$
is a conjunction of catamorphisms and
$\textit{Catas}^{C}$
is a conjunction of catamorphisms and
![]() $A_1,\ldots, A_m$
are program atoms. For
$A_1,\ldots, A_m$
are program atoms. For
![]() $k=1,\ldots, m,$
$k=1,\ldots, m,$
-
- let
 $\mathit{Catas}_{k}^{C}$
be the conjunction of every catamorphism atom
$\mathit{Catas}_{k}^{C}$
be the conjunction of every catamorphism atom
 $F$
in
$F$
in
 $\textit{Catas}^{C}$
such that
$\textit{Catas}^{C}$
such that
 $\mathit{adt\mbox{-}vars}(A_k) \cap \mathit{adt\mbox{-}vars}(F) \neq \emptyset$
;
$\mathit{adt\mbox{-}vars}(A_k) \cap \mathit{adt\mbox{-}vars}(F) \neq \emptyset$
; -
- let
 $D_k$
:
$D_k$
:
 $H_k \leftarrow \mathit{Catas}^{D}_{k}, A_k$
be a clause in
$H_k \leftarrow \mathit{Catas}^{D}_{k}, A_k$
be a clause in
 $\mathit{Defs}_i$
(modulo variable renaming) such that
$\mathit{Defs}_i$
(modulo variable renaming) such that
 $\mathit{Catas}^{C}_{k}$
is a subconjunction of
$\mathit{Catas}^{C}_{k}$
is a subconjunction of
 $\mathit{Catas}^D_{k}$
.
$\mathit{Catas}^D_{k}$
.
Then, by folding
![]() $ C$
using
$ C$
using
![]() $ D_1,\ldots, D_m$
, we derive clause
$ D_1,\ldots, D_m$
, we derive clause
![]() $E$
:
$E$
:
![]() $ H\leftarrow c, H_1,\ldots, H_m$
, and we get the new set of clauses
$ H\leftarrow c, H_1,\ldots, H_m$
, and we get the new set of clauses
![]() $ S_{i+1}= (S_{i}\setminus \{C\})\cup \{E \}$
.
$ S_{i+1}= (S_{i}\setminus \{C\})\cup \{E \}$
.
Example 6. In order to fold clause
![]() $E2$
(see Example 5) according to the folding rule R4, we introduce for the program atoms
$E2$
(see Example 5) according to the folding rule R4, we introduce for the program atoms
![]() $\mathit{append}(B,H,E)$
and
$\mathit{append}(B,H,E)$
and
![]() $\mathit{eq}(B,H)$
that occur in the body of
$\mathit{eq}(B,H)$
that occur in the body of
![]() $E2$
, the new definitions
$E2$
, the new definitions
![]() $D2$
and
$D2$
and
![]() $D3$
, respectively. Those new definitions are shown in Figure 2. Then, by folding clause
$D3$
, respectively. Those new definitions are shown in Figure 2. Then, by folding clause
![]() $E2$
using
$E2$
using
![]() $D2$
and
$D2$
and
![]() $D3$
, we get:
$D3$
, we get:
![]() $E3$
.
$E3$
.
![]() $\mathit{new}1(A,\!B,\!C,\!E,\!F) \leftarrow \mathit{new}2(A,\!M,\!K,\!E,\!F,\!B,\!C),\ \mathit{new}3(A,\!M,\!K,\!B,\!C)$
.
$\mathit{new}1(A,\!B,\!C,\!E,\!F) \leftarrow \mathit{new}2(A,\!M,\!K,\!E,\!F,\!B,\!C),\ \mathit{new}3(A,\!M,\!K,\!B,\!C)$
.
Also, query
![]() $7$
(see Figure 1) can be folded using definition
$7$
(see Figure 1) can be folded using definition
![]() $D1$
, and we get:
$D1$
, and we get:
![]() $E4$
.
$E4$
.
![]() $\mathit{false} \leftarrow C\!=\!2\,D\!+\!1,\ \mathit{new}1(A,\!E,\!F,\!G,\!C)$
$\mathit{false} \leftarrow C\!=\!2\,D\!+\!1,\ \mathit{new}1(A,\!E,\!F,\!G,\!C)$
Thus,
![]() $S_{4}=(S_0 \setminus \{7\}) \cup \{E3,E4,D2,D3\}$
. Then, we will continue by transforming the newly introduced definitions
$S_{4}=(S_0 \setminus \{7\}) \cup \{E3,E4,D2,D3\}$
. Then, we will continue by transforming the newly introduced definitions
![]() $D2$
and
$D2$
and
![]() $D3$
.
$D3$
.
The following Rule R5 is a new transformation rule that allows us: (i) to introduce new predicates by erasing ADT arguments from existing predicates, and (ii) to add atoms with these new predicates to the body of a clause.
(R5) Erasure Addition Rule. Let
![]() $A$
be the atom
$A$
be the atom
![]() $p(t_1,\ldots, t_k,u_1,\ldots, u_m)$
, where
$p(t_1,\ldots, t_k,u_1,\ldots, u_m)$
, where
![]() $t_1,\ldots, t_k$
have (possibly distinct) basic sorts and
$t_1,\ldots, t_k$
have (possibly distinct) basic sorts and
![]() $u_1,\ldots, u_m$
have (possibly distinct) ADT sorts. We define the ADT-erasure of
$u_1,\ldots, u_m$
have (possibly distinct) ADT sorts. We define the ADT-erasure of
![]() $A$
, denoted
$A$
, denoted
![]() $\chi _{\!\mathit{wo}}(A)$
, to be the atom
$\chi _{\!\mathit{wo}}(A)$
, to be the atom
![]() $p\_{\mathit{woADTs}}(t_1,\ldots, t_k)$
, where
$p\_{\mathit{woADTs}}(t_1,\ldots, t_k)$
, where
![]() $p\_{\mathit{woADTs}}$
is a new predicate symbol. Let
$p\_{\mathit{woADTs}}$
is a new predicate symbol. Let
![]() $C$
:
$C$
:
![]() $H\leftarrow c, A_1,\ldots, A_n$
be a clause in
$H\leftarrow c, A_1,\ldots, A_n$
be a clause in
![]() $S_i$
.
$S_i$
.
Then, by the erasure addition rule, from
![]() $C$
we derive the two new clauses:
$C$
we derive the two new clauses:
![]() $\chi _{\!\mathit{wo}}(H)\!\leftarrow \! c, \chi _{\!\mathit{wo}}(\!A_1\!),\ldots, \chi _{\!\mathit{wo}}(\!A_n\!)$
, denoted
$\chi _{\!\mathit{wo}}(H)\!\leftarrow \! c, \chi _{\!\mathit{wo}}(\!A_1\!),\ldots, \chi _{\!\mathit{wo}}(\!A_n\!)$
, denoted
![]() $\chi _{\!\mathit{wo}}(C)$
, and
$\chi _{\!\mathit{wo}}(C)$
, and
![]() $H\!\leftarrow \! c, A_1,\chi _{\!\mathit{wo}}(\!A_1\!),\ldots, A_n, \chi _{\!\mathit{wo}}(\!A_n\!)$
, denoted
$H\!\leftarrow \! c, A_1,\chi _{\!\mathit{wo}}(\!A_1\!),\ldots, A_n, \chi _{\!\mathit{wo}}(\!A_n\!)$
, denoted
![]() $\chi _{\!\mathit{w\&wo}}(C)$
,
$\chi _{\!\mathit{w\&wo}}(C)$
,
and we get the new set of clauses
![]() $S_{i+1}= \{\chi _{\!\mathit{w\&wo}}(C) \mid C\in S_i\}\ \cup \ \{\chi _{\!\mathit{wo}}(C) \mid C$
is a clause in
$S_{i+1}= \{\chi _{\!\mathit{w\&wo}}(C) \mid C\in S_i\}\ \cup \ \{\chi _{\!\mathit{wo}}(C) \mid C$
is a clause in
![]() $S_i$
whose head is not false}.
$S_i$
whose head is not false}.
Example 7. Let us consider clause
![]() $E3$
of Example 6. We have that:
$E3$
of Example 6. We have that:
![]() $\chi _{\!\mathit{wo}}(\mathit{new}1(A,B,C,E,F))$
$\chi _{\!\mathit{wo}}(\mathit{new}1(A,B,C,E,F))$
![]() $=$
$=$
![]() $\mathit{new}1\, us \mathit{woADTs}(A,C,F)$
,
$\mathit{new}1\, us \mathit{woADTs}(A,C,F)$
,
![]() $\chi _{\!\mathit{wo}}(\mathit{new}2(A,M,K,E,F,B,C))$
$\chi _{\!\mathit{wo}}(\mathit{new}2(A,M,K,E,F,B,C))$
![]() $=$
$=$
![]() $\mathit{new}2\, us \mathit{woADTs}(A,K,F,C)$
,
$\mathit{new}2\, us \mathit{woADTs}(A,K,F,C)$
,
![]() $\chi _{\!\mathit{wo}}(\mathit{new}3(A,M,K,B,C))$
$\chi _{\!\mathit{wo}}(\mathit{new}3(A,M,K,B,C))$
![]() $=$
$=$
![]() $\mathit{new}3\, us \mathit{woADTs}(A,K,C)$
.
$\mathit{new}3\, us \mathit{woADTs}(A,K,C)$
.
Thus, from clause
![]() $E3$
, by erasure addition we get clauses 12 and 18 of Figure 2.
$E3$
, by erasure addition we get clauses 12 and 18 of Figure 2.
The following theorem is a consequence of well-known results for CHC transformations (see, for instance, the papers cited in a recent survey (De Angelis et al., Reference De Angelis, Fioravanti, Gallagher, Hermenegildo, Pettorossi and Proietti2022)).
Theorem 1 (Correctness of the Rules). Let ![]() be a transformation sequence using Rules R1–R5. Then,
be a transformation sequence using Rules R1–R5. Then,
![]() $S_0$
is satisfiable if and only if
$S_0$
is satisfiable if and only if
![]() $S_n$
is satisfiable.
$S_n$
is satisfiable.
Proof. The proof consists in showing that Rules R1–R5 presented earlier in this section can be derived from the transformation rules considered in previous work (De Angelis et al., Reference De Angelis, Fioravanti, Gallagher, Hermenegildo, Pettorossi and Proietti2022) and proved correct based on results by Tamaki and Sato (Tamaki and Sato, Reference Tamaki and Sato1986) for logic programs and Etalle and Gabbrielli (Etalle and Gabbrielli, Reference Etalle and Gabbrielli1996) for constraint logic programs. Below we will recall these transformation rules.
Let us first introduce the notion of stratification for a set of clauses (Lloyd, Reference Lloyd1987). Let
![]() $\mathbb{N}$
be the set of the natural numbers and Pred be the set of the predicate names. A level mapping is a function
$\mathbb{N}$
be the set of the natural numbers and Pred be the set of the predicate names. A level mapping is a function
![]() $\lambda \!:\mathit{Pred}\!\rightarrow \!\mathbb{N}$
. For every predicate
$\lambda \!:\mathit{Pred}\!\rightarrow \!\mathbb{N}$
. For every predicate
![]() $p$
, the natural number
$p$
, the natural number
![]() $\lambda (p)$
is said to be the level of
$\lambda (p)$
is said to be the level of
![]() $p$
. Level mappings are extended to atoms by stating that the level
$p$
. Level mappings are extended to atoms by stating that the level
![]() $\lambda (A)$
of an atom
$\lambda (A)$
of an atom
![]() $A$
is the level of its predicate symbol. A clause
$A$
is the level of its predicate symbol. A clause
![]() $ H\leftarrow c, A_{1}, \ldots, A_{n}$
is stratified with respect to
$ H\leftarrow c, A_{1}, \ldots, A_{n}$
is stratified with respect to
![]() $\lambda$
if either
$\lambda$
if either
![]() $H$
is false or, for
$H$
is false or, for
![]() $ i\!=\!1,\ldots, n$
,
$ i\!=\!1,\ldots, n$
,
![]() $\lambda (H)\geq \lambda (A_i)$
. A set
$\lambda (H)\geq \lambda (A_i)$
. A set
![]() $P$
of CHCs is stratified with respect to
$P$
of CHCs is stratified with respect to
![]() $\lambda$
if all clauses of
$\lambda$
if all clauses of
![]() $P$
are stratified with respect to
$P$
are stratified with respect to
![]() $\lambda$
.
$\lambda$
.
A DUFR-transformation sequence from
![]() $S_{0}$
to
$S_{0}$
to
![]() $S_{n}$
is a sequence
$S_{n}$
is a sequence ![]() of sets of CHCs such that, for
of sets of CHCs such that, for
![]() $i\!=\!0,\ldots, n\!-\!1,$
$i\!=\!0,\ldots, n\!-\!1,$
![]() $S_{i+1}$
is derived from
$S_{i+1}$
is derived from
![]() $S_i$
, denoted
$S_i$
, denoted ![]() , by applying one of the following rules: (i) Rule D, (ii) Rule U, (iii) Rule F, and (iv) Rule G. (To avoid confusion with Rules R1–R5 presented earlier in this section, in this proof we use the letters D, U, F, and G to identify the rules presented in previous work (De Angelis et al., Reference De Angelis, Fioravanti, Gallagher, Hermenegildo, Pettorossi and Proietti2022).) We assume that the initial set
, by applying one of the following rules: (i) Rule D, (ii) Rule U, (iii) Rule F, and (iv) Rule G. (To avoid confusion with Rules R1–R5 presented earlier in this section, in this proof we use the letters D, U, F, and G to identify the rules presented in previous work (De Angelis et al., Reference De Angelis, Fioravanti, Gallagher, Hermenegildo, Pettorossi and Proietti2022).) We assume that the initial set
![]() $S_0$
is stratified with respect to a given level mapping
$S_0$
is stratified with respect to a given level mapping
![]() $\lambda$
.
$\lambda$
.
(Rule D) Let
![]() $D$
be the clause
$D$
be the clause
![]() $\textit{newp}(X_1,\ldots, X_k)\leftarrow c,A_1,\ldots, A_m$
, where: (1) newp is a predicate symbol not occurring in the sequence
$\textit{newp}(X_1,\ldots, X_k)\leftarrow c,A_1,\ldots, A_m$
, where: (1) newp is a predicate symbol not occurring in the sequence ![]() constructed so far, (2)
constructed so far, (2)
![]() $c$
is a constraint, (3) the predicate symbols of
$c$
is a constraint, (3) the predicate symbols of
![]() $A_1,\ldots, A_m$
occur in
$A_1,\ldots, A_m$
occur in
![]() $S_0$
, and (4)
$S_0$
, and (4)
![]() $\{X_1,\ldots, X_k\}\subseteq \mathit{vars}(\{c,A_1,\ldots, A_m\})$
. Then, by Rule D, we get
$\{X_1,\ldots, X_k\}\subseteq \mathit{vars}(\{c,A_1,\ldots, A_m\})$
. Then, by Rule D, we get
![]() $S_{i+1}= S_i\cup \{D\}$
. We define the level mapping
$S_{i+1}= S_i\cup \{D\}$
. We define the level mapping
![]() $\lambda$
of newp to be equal to
$\lambda$
of newp to be equal to
![]() $\textit{max}\,\{\lambda (A_i) \mid i=1,\ldots, m\}$
.
$\textit{max}\,\{\lambda (A_i) \mid i=1,\ldots, m\}$
.
For any
![]() $i\geq 0$
, we denote by
$i\geq 0$
, we denote by
![]() $\textit{Defs}_i$
the set of clauses introduced by Rule D during the construction of
$\textit{Defs}_i$
the set of clauses introduced by Rule D during the construction of ![]() .
.
Rule U consists in an application of the one-step unfolding of Definition2.
(Rule U) Let
![]() $C$
:
$C$
:
![]() $H\leftarrow c,G_L,A,G_R$
be a clause in
$H\leftarrow c,G_L,A,G_R$
be a clause in
![]() $S_i$
, where
$S_i$
, where
![]() $A$
is an atom. Then, by applying Rule U to
$A$
is an atom. Then, by applying Rule U to
![]() $C$
with respect to
$C$
with respect to
![]() $A$
, we get
$A$
, we get
![]() $S_{i+1}= (S_i\setminus \{C\}) \cup \mathit{Unf}(C,A,S_0)$
.
$S_{i+1}= (S_i\setminus \{C\}) \cup \mathit{Unf}(C,A,S_0)$
.
(Rule F) Let
![]() $C$
:
$C$
:
![]() $H\leftarrow c, G_L,Q,G_R$
be a clause in
$H\leftarrow c, G_L,Q,G_R$
be a clause in
![]() $S_i$
, and let
$S_i$
, and let
![]() $D$
:
$D$
:
![]() $K \leftarrow d, B$
be a variant of a clause in
$K \leftarrow d, B$
be a variant of a clause in
![]() $\textit{Defs}_i$
. Suppose that: (1) either
$\textit{Defs}_i$
. Suppose that: (1) either
![]() $H$
is
$H$
is
![]() $\mathit{false}$
or
$\mathit{false}$
or
![]() $\lambda (H) \geq \lambda (K)$
, and (2) there exists a substitution
$\lambda (H) \geq \lambda (K)$
, and (2) there exists a substitution
![]() $\vartheta$
such that
$\vartheta$
such that
![]() $Q\!=\! B\vartheta$
and
$Q\!=\! B\vartheta$
and
![]() $\mathbb{D}\models \forall (c \rightarrow d\vartheta )$
. Then, by applying Rule F to
$\mathbb{D}\models \forall (c \rightarrow d\vartheta )$
. Then, by applying Rule F to
![]() $C$
using
$C$
using
![]() $D$
, we derive clause
$D$
, we derive clause
![]() $E$
:
$E$
:
![]() $ H\leftarrow c, G_{\!L}, K\vartheta, G_{\!R}$
, and we get
$ H\leftarrow c, G_{\!L}, K\vartheta, G_{\!R}$
, and we get
![]() $ S_{i+1}= (S_{i}\setminus \{C\})\cup \{E \}$
.
$ S_{i+1}= (S_{i}\setminus \{C\})\cup \{E \}$
.
In the next Rule R, called goal replacement, and in the rest of the proof, by
![]() $\textit{Definite}(S_0)$
we denote the set of definite clauses belonging to
$\textit{Definite}(S_0)$
we denote the set of definite clauses belonging to
![]() $S_0$
.
$S_0$
.
(Rule R) Let
![]() $C$
:
$C$
:
![]() ${H}\leftarrow c, c_{1},{G}_{L},{G}_{1},{G}_{R}$
be a clause in
${H}\leftarrow c, c_{1},{G}_{L},{G}_{1},{G}_{R}$
be a clause in
![]() ${S}_{i}$
. Suppose that the following two conditions hold:
${S}_{i}$
. Suppose that the following two conditions hold:
(R.1)
![]() $M(\textit{Definite}(S_0)\cup \mathit{Defs}_i) \models \forall \,( (\exists T_1.\, c_{1}\! \wedge \!{G}_{1}) \leftrightarrow (\exists T_2.\, c_{2}\! \wedge \!{G}_{2}))$
, and
$M(\textit{Definite}(S_0)\cup \mathit{Defs}_i) \models \forall \,( (\exists T_1.\, c_{1}\! \wedge \!{G}_{1}) \leftrightarrow (\exists T_2.\, c_{2}\! \wedge \!{G}_{2}))$
, and
(R.2) either
![]() $H$
is
$H$
is
![]() $\mathit{false}$
or, for every atom
$\mathit{false}$
or, for every atom
![]() $A$
occurring in
$A$
occurring in
![]() $G_2$
and not in
$G_2$
and not in
![]() $G_1$
,
$G_1$
,
![]() $\lambda (H)\!\gt \!\lambda (\mathit{A})$
$\lambda (H)\!\gt \!\lambda (\mathit{A})$
where:
![]() $T_1 = \mathit{vars}(\{c_{1},{G}_{1}\}) \setminus \mathit{vars}(\{{H}, c,{G}_{L},{G}_{R}\})$
, and
$T_1 = \mathit{vars}(\{c_{1},{G}_{1}\}) \setminus \mathit{vars}(\{{H}, c,{G}_{L},{G}_{R}\})$
, and
![]() $T_2 = \mathit{vars}(\{c_{2},{G}_{2}\}) \setminus \mathit{vars}(\{{H}, c,{G}_{L},{G}_{R}\})$
.
$T_2 = \mathit{vars}(\{c_{2},{G}_{2}\}) \setminus \mathit{vars}(\{{H}, c,{G}_{L},{G}_{R}\})$
.
Then, by Rule R, in clause
![]() $C$
we replace
$C$
we replace
![]() $c_1,G_1$
by
$c_1,G_1$
by
![]() $c_2,G_2$
, and we derive clause
$c_2,G_2$
, and we derive clause
![]() $D$
:
$D$
:
![]() ${H}\leftarrow c, c_{2},{G}_{L},{G}_{2},{G}_{R}$
. We get
${H}\leftarrow c, c_{2},{G}_{L},{G}_{2},{G}_{R}$
. We get
![]() $S_{i+1} = (S_{i}\setminus \{C\})\cup \{D\}$
.
$S_{i+1} = (S_{i}\setminus \{C\})\cup \{D\}$
.
The following result guarantees that, for any DUFR-transformation sequence ![]() satisfying Condition (C),
satisfying Condition (C),
![]() $S_0$
and
$S_0$
and
![]() $S_n$
are equisatisfiable (Tamaki and Sato, Reference Tamaki and Sato1986; Etalle and Gabbrielli, Reference Etalle and Gabbrielli1996; De Angelis et al., Reference De Angelis, Fioravanti, Gallagher, Hermenegildo, Pettorossi and Proietti2022).
$S_n$
are equisatisfiable (Tamaki and Sato, Reference Tamaki and Sato1986; Etalle and Gabbrielli, Reference Etalle and Gabbrielli1996; De Angelis et al., Reference De Angelis, Fioravanti, Gallagher, Hermenegildo, Pettorossi and Proietti2022).
Theorem 2 (Correctness of the DUFR-Transformation Rules). Let ![]() be a DUFR-transformation sequence. Suppose that the following condition holds:
be a DUFR-transformation sequence. Suppose that the following condition holds:
-
(C) for
 $i \!=\! 1,\ldots, n\!-\!1$
, if
$i \!=\! 1,\ldots, n\!-\!1$
, if  by folding a clause in
by folding a clause in
 $S_i$
using a definition
$S_i$
using a definition
 $D\!:$
$D\!:$
 $H \leftarrow c,B$
in
$H \leftarrow c,B$
in
 $\mathit{Defs}_i$
, then, for some
$\mathit{Defs}_i$
, then, for some
 $j\! \in \!\{1,\ldots, i\!-\!1,i\!+\!1,\ldots, n\!-\!1\}$
,
$j\! \in \!\{1,\ldots, i\!-\!1,i\!+\!1,\ldots, n\!-\!1\}$
,  by unfolding
by unfolding
 $D$
with respect to an atom
$D$
with respect to an atom
 $A$
such that
$A$
such that
 $\lambda (H)=\lambda (A)$
.
$\lambda (H)=\lambda (A)$
.
Then,
(1) for
![]() $i=1,\ldots, n,$
$i=1,\ldots, n,$
![]() $M(\mathit{Definite}(S_0)\cup \mathit{Defs}_i) = M(\mathit{Definite}(S_i)),$
and
$M(\mathit{Definite}(S_0)\cup \mathit{Defs}_i) = M(\mathit{Definite}(S_i)),$
and
(2)
![]() $S_0$
is satisfiable if and only if
$S_0$
is satisfiable if and only if
![]() $S_n$
is satisfiable.
$S_n$
is satisfiable.
Now, we will show that each application of Rules R1–R5 can be obtained by one or more applications of Rules D, U, F, R. Furthermore, for any transformation sequence ![]() constructed using Rules R1–R5, there exists a DUFR-transformation sequence
constructed using Rules R1–R5, there exists a DUFR-transformation sequence ![]() satisfying Condition (C) of Theorem2.
satisfying Condition (C) of Theorem2.
In order to recast Rules R1–R5 in terms of Rules D, U, F, and R, we first introduce a suitable level mapping
![]() $\lambda$
defined as follows: for any predicate
$\lambda$
defined as follows: for any predicate
![]() $q$
, (i)
$q$
, (i)
![]() $\lambda (q)\!= \!2$
, if
$\lambda (q)\!= \!2$
, if
![]() $q$
is a program predicate of the initial set of clauses or a new program predicate introduced by Rule R1, and (ii)
$q$
is a program predicate of the initial set of clauses or a new program predicate introduced by Rule R1, and (ii)
![]() $\lambda (q)\!= \!1$
, if
$\lambda (q)\!= \!1$
, if
![]() $q$
is a catamorphism predicate, and (iii)
$q$
is a catamorphism predicate, and (iii)
![]() $\lambda (q)\!= \!0$
, if
$\lambda (q)\!= \!0$
, if
![]() $q$
is a new predicate symbol introduced by Rule R5. We have that the initial set
$q$
is a new predicate symbol introduced by Rule R5. We have that the initial set
![]() $S_0$
of CHCs is stratified with respect to
$S_0$
of CHCs is stratified with respect to
![]() $\lambda$
. Let us first consider the four Rules R1–R4.
$\lambda$
. Let us first consider the four Rules R1–R4.
-
• Rule R1 is a particular case of Rule D, where in the body of clause
 $D$
, (i) the constraint
$D$
, (i) the constraint
 $c$
is absent, (ii) exactly one atom among
$c$
is absent, (ii) exactly one atom among
 $A_1,\ldots, A_m$
is a program atom, (iii) all other atoms are catamorphism atoms, and (iv)
$A_1,\ldots, A_m$
is a program atom, (iii) all other atoms are catamorphism atoms, and (iv)
 $\{X_1,\ldots, X_k\}= \mathit{vars}(\{A_1,\ldots, A_m\})$
. By our definition of the level mapping,
$\{X_1,\ldots, X_k\}= \mathit{vars}(\{A_1,\ldots, A_m\})$
. By our definition of the level mapping,
 $\lambda (\mathit{newp})=2$
, as one of the
$\lambda (\mathit{newp})=2$
, as one of the
 $A_i$
’s is a program atom.
$A_i$
’s is a program atom. -
• Rule R2 consists of applications of Rules U and R. Indeed, in R2, (i) Steps 1 and 2 are applications of Rule U where
 $P$
is
$P$
is
 $S_0$
, and (ii) Step 3 is an application of Rule R. To see Point (ii), note that every catamorphism
$S_0$
, and (ii) Step 3 is an application of Rule R. To see Point (ii), note that every catamorphism
 $\mathit{cata}$
is, by definition, a functional predicate (see Section 2), and hence
$\mathit{cata}$
is, by definition, a functional predicate (see Section 2), and hence
 $M(\mathit{Definite}(S_0))\models \forall (\mathit{cata}(X,T,Y1) \wedge \mathit{cata}(X,T,Y2) \rightarrow Y1\!=\!Y2)$
. Thus, for any
$M(\mathit{Definite}(S_0))\models \forall (\mathit{cata}(X,T,Y1) \wedge \mathit{cata}(X,T,Y2) \rightarrow Y1\!=\!Y2)$
. Thus, for any
 $i\geq 0$
,
$i\geq 0$
, $M(\mathit{Definite}(S_0) \cup \mathit{Defs}_i)\models \forall (\mathit{cata}(X,T,Y1) \wedge \mathit{cata}(X,T,Y2) \leftrightarrow $
$M(\mathit{Definite}(S_0) \cup \mathit{Defs}_i)\models \forall (\mathit{cata}(X,T,Y1) \wedge \mathit{cata}(X,T,Y2) \leftrightarrow $
 $ Y1\!=\!Y2 \wedge \mathit{cata}(X,T,Y1))$
$ Y1\!=\!Y2 \wedge \mathit{cata}(X,T,Y1))$
that is, Condition (R.1) of Rule R holds. Also Condition (R.2) holds, as the head
 $H$
of the clause has a predicate
$H$
of the clause has a predicate
 $\mathit{newp}$
introduced by definition, and hence
$\mathit{newp}$
introduced by definition, and hence
 $\lambda (\mathit{newp})=2$
, while we have stipulated that
$\lambda (\mathit{newp})=2$
, while we have stipulated that
 $\lambda (\mathit{cata})=1$
.
$\lambda (\mathit{cata})=1$
. -
• Rule R3 consists of applications of Rule R. Indeed, R3 adds to the body of a clause
 $C$
(zero or more) catamorphism atoms
$C$
(zero or more) catamorphism atoms
 $\mathit{cata}_j(X,T_j,Y_j)$
such that no variable in the tuple
$\mathit{cata}_j(X,T_j,Y_j)$
such that no variable in the tuple
 $Y_j$
occurs in
$Y_j$
occurs in
 $C$
. The assumption that catamorphisms are total functions enforces that
$C$
. The assumption that catamorphisms are total functions enforces that
 $M(\mathit{Definite}(S_0)) \models \forall X, T_j\ \exists Y_j.\ \mathit{cata}_j(X,T_j,Y_j)$
, and hence
$M(\mathit{Definite}(S_0)) \models \forall X, T_j\ \exists Y_j.\ \mathit{cata}_j(X,T_j,Y_j)$
, and hence $M(\mathit{Definite}(S_0) \cup \mathit{Defs}_i)\models \forall ( true \leftrightarrow \exists Y_j.\ \mathit{cata}_j(X,T_j,Y_j))$
$M(\mathit{Definite}(S_0) \cup \mathit{Defs}_i)\models \forall ( true \leftrightarrow \exists Y_j.\ \mathit{cata}_j(X,T_j,Y_j))$
that is, Condition (R.1) of Rule R holds. Also Condition (R.2) holds, as the head
 $H$
of clause
$H$
of clause
 $C$
is either
$C$
is either
 $\mathit{false}$
or a program atom. In the latter case
$\mathit{false}$
or a program atom. In the latter case
 $\lambda (H)=2$
, while we have stipulated that
$\lambda (H)=2$
, while we have stipulated that
 $\lambda (\mathit{cata}_j)=1$
.
$\lambda (\mathit{cata}_j)=1$
. -
• Rule R4 consists of applications of Rules R and F. Indeed, an application of Rule R3 is equivalent to the following for-loop of applications of Rules R and F: for
 $k\!=\!1,\ldots, m$
, first, (i) the addition of the catamorphism atoms occurring (modulo variable renaming) in
$k\!=\!1,\ldots, m$
, first, (i) the addition of the catamorphism atoms occurring (modulo variable renaming) in
 $\mathit{Catas}^{D}_{k}$
and not in its subconjunction
$\mathit{Catas}^{D}_{k}$
and not in its subconjunction
 $\mathit{Catas}^{C}_{k}$
(as mentioned above, this catamorphism addition is an instance of Rule R), and then, (ii) the application of Rule F, thereby replacing the conjunction
$\mathit{Catas}^{C}_{k}$
(as mentioned above, this catamorphism addition is an instance of Rule R), and then, (ii) the application of Rule F, thereby replacing the conjunction
 $(\mathit{Catas}^{D}_{k}, A_k)$
by
$(\mathit{Catas}^{D}_{k}, A_k)$
by
 $H_k$
.
$H_k$
.
Therefore, for any transformation sequence ![]() constructed using Rules R1–R4, there exists a DUFR-transformation sequence
constructed using Rules R1–R4, there exists a DUFR-transformation sequence ![]() . When applying Rule R4 to a clause
. When applying Rule R4 to a clause
![]() $C$
during the construction of
$C$
during the construction of ![]() , either the head of
, either the head of
![]() $C$
is false or
$C$
is false or
![]() $C$
has been obtained by the unfolding rule (possibly followed by catamorphism addition). This implies that in
$C$
has been obtained by the unfolding rule (possibly followed by catamorphism addition). This implies that in ![]() we have that Condition (C) of Theorem2 holds. Thus, by Theorem2 we get:
we have that Condition (C) of Theorem2 holds. Thus, by Theorem2 we get:
![]() $M(\mathit{Definite}(S_0)\cup \mathit{Defs}_i) = M(\mathit{Definite}(S_i))$
.
$M(\mathit{Definite}(S_0)\cup \mathit{Defs}_i) = M(\mathit{Definite}(S_i))$
.
Now, suppose that we apply Rule R5 to the set
![]() $S_i$
of clauses. We have that, for every predicate
$S_i$
of clauses. We have that, for every predicate
![]() $p$
occurring in
$p$
occurring in
![]() $S_i,$
$S_i,$
![]() $M(\!\mathit{Definite}(S_i) \cup \chi _{\!\mathit{wo}}(S_i))\models \forall (p(X_1,\ldots, \!X_k,\!Y_{\!1},\ldots, \!Y_m) \rightarrow p\_{\mathit{woADTs}}(X_1,\ldots, \!X_k))$
(
$M(\!\mathit{Definite}(S_i) \cup \chi _{\!\mathit{wo}}(S_i))\models \forall (p(X_1,\ldots, \!X_k,\!Y_{\!1},\ldots, \!Y_m) \rightarrow p\_{\mathit{woADTs}}(X_1,\ldots, \!X_k))$
(
![]() $\dagger$
)
$\dagger$
)
where
![]() $\chi _{\!\mathit{wo}}(S_i) = \{\chi _{\!\mathit{wo}}(C) \mid C$
is a clause in
$\chi _{\!\mathit{wo}}(S_i) = \{\chi _{\!\mathit{wo}}(C) \mid C$
is a clause in
![]() $S_i$
whose head is not false
$S_i$
whose head is not false
![]() $\}$
. Now, it is the case that an application of Rule R5 is realized by a sequence of applications of Rule R. Indeed, for each addition of an atom
$\}$
. Now, it is the case that an application of Rule R5 is realized by a sequence of applications of Rule R. Indeed, for each addition of an atom
![]() $p\_{\mathit{woADTs}}(t_1,\ldots, t_k)$
to the body of a clause
$p\_{\mathit{woADTs}}(t_1,\ldots, t_k)$
to the body of a clause
![]() $C$
by R5, Condition (R.1) holds, as the above relation
$C$
by R5, Condition (R.1) holds, as the above relation
![]() $(\dagger )$
is equivalent to:
$(\dagger )$
is equivalent to:
![]() $M(\mathit{Definite}(S_i) \cup \chi _{\!\mathit{wo}}(S_i))\models$
$M(\mathit{Definite}(S_i) \cup \chi _{\!\mathit{wo}}(S_i))\models$
![]() $\forall (p(X_1,\ldots \!,X_k,Y_1,\ldots \!,\!Y_m) \leftrightarrow (p(X_1,\ldots \!,X_k,Y_1,\ldots \!,\!Y_m) \wedge p\_{\mathit{woADTs}}(X_1,\ldots, X_k)))$
$\forall (p(X_1,\ldots \!,X_k,Y_1,\ldots \!,\!Y_m) \leftrightarrow (p(X_1,\ldots \!,X_k,Y_1,\ldots \!,\!Y_m) \wedge p\_{\mathit{woADTs}}(X_1,\ldots, X_k)))$
and
![]() $M(\mathit{Definite}(S_i)\cup \chi _{\!\mathit{wo}}(S_i)) = M(\mathit{Definite}(S_0\cup \chi _{\!\mathit{wo}}(S_i)) \cup \mathit{Defs}_i)$
, because the predicates in
$M(\mathit{Definite}(S_i)\cup \chi _{\!\mathit{wo}}(S_i)) = M(\mathit{Definite}(S_0\cup \chi _{\!\mathit{wo}}(S_i)) \cup \mathit{Defs}_i)$
, because the predicates in
![]() $\chi _{\!\mathit{wo}}(S_i)$
do not occur in
$\chi _{\!\mathit{wo}}(S_i)$
do not occur in
![]() $S_0,\ldots, S_i$
. Also Condition (R.2) holds, because the head
$S_0,\ldots, S_i$
. Also Condition (R.2) holds, because the head
![]() $H$
of
$H$
of
![]() $C$
is either false or
$C$
is either false or
![]() $\lambda (H)\!\geq \! 1$
and
$\lambda (H)\!\geq \! 1$
and
![]() $\lambda (p\_{\mathit{woADTs}})\!=\!0$
.
$\lambda (p\_{\mathit{woADTs}})\!=\!0$
.
Therefore, for any transformation sequence ![]() constructed using Rules R1–R5, there exists a DUFR-transformation sequence
constructed using Rules R1–R5, there exists a DUFR-transformation sequence ![]() . Then, by Theorem2, we get that
. Then, by Theorem2, we get that
![]() $S_0$
is satisfiable if and only if
$S_0$
is satisfiable if and only if
![]() $S_n$
is satisfiable.
$S_n$
is satisfiable.
4.3 The transformation algorithm
 ${\mathcal{T}}_{abs}$
${\mathcal{T}}_{abs}$
The set of the new predicate definitions needed during the execution of the transformation algorithm
![]() ${\mathcal{T}}_{\mathit{abs}}$
is not given in advance. In general, that set depends on: (i) the initial set
${\mathcal{T}}_{\mathit{abs}}$
is not given in advance. In general, that set depends on: (i) the initial set
![]() $P$
of CHC clauses, (ii) the given query
$P$
of CHC clauses, (ii) the given query
![]() $Q$
specifying the property of interest to be proved, and (iii) the given catamorphic abstraction specification
$Q$
specifying the property of interest to be proved, and (iii) the given catamorphic abstraction specification
![]() $\alpha$
for
$\alpha$
for
![]() $P$
. As we will see, we may compute that set of new definitions as the least fixpoint of an operator, called
$P$
. As we will see, we may compute that set of new definitions as the least fixpoint of an operator, called
![]() $\tau _{P\cup \{Q\},\alpha }$
, which transforms a given set
$\tau _{P\cup \{Q\},\alpha }$
, which transforms a given set
![]() $\Delta$
of predicate definitions into a new set
$\Delta$
of predicate definitions into a new set
![]() $\Delta '$
of predicate definitions. First, we need the following notions.
$\Delta '$
of predicate definitions. First, we need the following notions.
Two definitions
![]() $D_1$
and
$D_1$
and
![]() $D_2$
are said to be equivalent, denoted
$D_2$
are said to be equivalent, denoted
![]() $D_1\equiv D_2,$
if they can be made identical by performing the following transformations: (i) renaming of the head predicate, (ii) renaming of the variables, (iii) reordering of the variables in the head, and (iv) reordering of the atoms in the body. We leave it to the reader to check that the results presented in this section are indeed independent of the choice of a specific definition in its equivalence class.
$D_1\equiv D_2,$
if they can be made identical by performing the following transformations: (i) renaming of the head predicate, (ii) renaming of the variables, (iii) reordering of the variables in the head, and (iv) reordering of the atoms in the body. We leave it to the reader to check that the results presented in this section are indeed independent of the choice of a specific definition in its equivalence class.
A set
![]() $\Delta$
of definitions is said to be monovariant if, for each program predicate
$\Delta$
of definitions is said to be monovariant if, for each program predicate
![]() $p$
, in
$p$
, in
![]() $\Delta$
there is at most one definition having an occurrence of
$\Delta$
there is at most one definition having an occurrence of
![]() $p$
in its body. The transformation algorithm
$p$
in its body. The transformation algorithm
![]() ${\mathcal{T}}_{\mathit{abs}}$
and the operator
${\mathcal{T}}_{\mathit{abs}}$
and the operator
![]() $\tau _{P\cup \{Q\},\alpha }$
work on monovariant sets of definitions and are defined by means of the
$\tau _{P\cup \{Q\},\alpha }$
work on monovariant sets of definitions and are defined by means of the
![]() $\mathit{Define}$
,
$\mathit{Define}$
,
![]() $\mathit{Unfold}$
,
$\mathit{Unfold}$
,
![]() $\mathit{AddCata}$
,
$\mathit{AddCata}$
,
![]() $\mathit{Fold}$
, and
$\mathit{Fold}$
, and
![]() $\mathit{AddErasure}$
functions defined in Figure 3.
$\mathit{AddErasure}$
functions defined in Figure 3.
In the definition of the Define function we assume that, for each clause
![]() $C$
in Cls and each catamorphism atom
$C$
in Cls and each catamorphism atom
![]() $\textit{Cata}$
in the body of
$\textit{Cata}$
in the body of
![]() $C$
, there is a program atom
$C$
, there is a program atom
![]() $A$
in the body of
$A$
in the body of
![]() $C$
such that
$C$
such that
![]() $\mathit{adt\mbox{-}vars}(\textit{Cata}) \subseteq \mathit{adt\mbox{-}vars}(A)$
. If
$\mathit{adt\mbox{-}vars}(\textit{Cata}) \subseteq \mathit{adt\mbox{-}vars}(A)$
. If
![]() $A$
is absent for a catamorphism atom having the ADT variable
$A$
is absent for a catamorphism atom having the ADT variable
![]() $X$
of sort
$X$
of sort
![]() $\tau$
, in order to comply with our assumption, we add to the body of
$\tau$
, in order to comply with our assumption, we add to the body of
![]() $C$
a program atom
$C$
a program atom
![]() $\textit{true}_\tau (X)$
that is defined on the (possibly recursive) structure of sort
$\textit{true}_\tau (X)$
that is defined on the (possibly recursive) structure of sort
![]() $\tau$
and holds for every
$\tau$
and holds for every
![]() $X$
of sort
$X$
of sort
![]() $\tau$
. For instance, for the sort
$\tau$
. For instance, for the sort
![]() $\mathit{list(int)}$
, the program atom
$\mathit{list(int)}$
, the program atom
![]() $\textit{true}_{\mathit{list(int)}}(X)$
will be defined by the two clauses
$\textit{true}_{\mathit{list(int)}}(X)$
will be defined by the two clauses
![]() $\textit{true}_{\mathit{list(int)}}([\,])$
and
$\textit{true}_{\mathit{list(int)}}([\,])$
and
![]() $\textit{true}_{\mathit{list(int)}}([H|T]) \leftarrow \textit{true}_{\mathit{list(int)}}(T)$
, where
$\textit{true}_{\mathit{list(int)}}([H|T]) \leftarrow \textit{true}_{\mathit{list(int)}}(T)$
, where
![]() $H$
is an integer variable. Note that, by adding to clause
$H$
is an integer variable. Note that, by adding to clause
![]() $C$
the atom
$C$
the atom
![]() $\textit{true}_\tau (X)$
, we get a clause equivalent to
$\textit{true}_\tau (X)$
, we get a clause equivalent to
![]() $C$
.
$C$
.

Fig. 3. The
![]() $\mathit{Define}$
,
$\mathit{Define}$
,
![]() $\mathit{Unfold}$
,
$\mathit{Unfold}$
,
![]() $\mathit{AddCata}$
,
$\mathit{AddCata}$
,
![]() $\mathit{Fold}$
, and
$\mathit{Fold}$
, and
![]() $\mathit{AddErasure}$
functions.
$\mathit{AddErasure}$
functions.
Definition 3 (Domain of Definitions). We denote by
![]() $\mathcal D$
a maximal set of definitions such that
$\mathcal D$
a maximal set of definitions such that
-
(D1) for every definition
 $\mathit{newp}(X_1,\ldots, X_k)\leftarrow{Catas}, A$
in
$\mathit{newp}(X_1,\ldots, X_k)\leftarrow{Catas}, A$
in
 $\mathcal D$
, for every ADT variable
$\mathcal D$
, for every ADT variable
 $X_i$
occurring in the program atom
$X_i$
occurring in the program atom
 $A$
, for each catamorphism predicate cata in the conjunction Catas of catamorphism atoms, at most one catamorphism atom of the form
$A$
, for each catamorphism predicate cata in the conjunction Catas of catamorphism atoms, at most one catamorphism atom of the form
 $\mathit{cata}(\ldots, X_i,\dots )$
occurs in Catas, and
$\mathit{cata}(\ldots, X_i,\dots )$
occurs in Catas, and -
(D2)
 $\mathcal D$
does not contain equivalent definitions.
$\mathcal D$
does not contain equivalent definitions.It follows directly from our assumptions that
 $\mathcal D$
is a finite set.
$\mathcal D$
is a finite set.
Now we define a partial order (
![]() $\sqsubseteq$
), a join operation (
$\sqsubseteq$
), a join operation (
![]() $\sqcup$
) and a meet operation (
$\sqcup$
) and a meet operation (
![]() $\sqcap$
) for definitions and also for monovariant subsets of definitions in
$\sqcap$
) for definitions and also for monovariant subsets of definitions in
![]() $\mathcal D$
.
$\mathcal D$
.
Definition 4. Let
![]() $D_1$
:
$D_1$
:
![]() $\mathit{newp}1(U_1) \leftarrow \mathit{Catas}_1, \mathit{Catas}, A$
and
$\mathit{newp}1(U_1) \leftarrow \mathit{Catas}_1, \mathit{Catas}, A$
and
![]() $D_2$
:
$D_2$
:
![]() $\mathit{newp}2(U_2) \leftarrow \mathit{Catas}_2, \mathit{Catas}, A$
be two definitions in
$\mathit{newp}2(U_2) \leftarrow \mathit{Catas}_2, \mathit{Catas}, A$
be two definitions in
![]() $\mathcal D$
for the same program atom
$\mathcal D$
for the same program atom
![]() $A$
, where
$A$
, where
![]() $\mathit{Catas}, \mathit{Catas}_1$
, and
$\mathit{Catas}, \mathit{Catas}_1$
, and
![]() $\mathit{Catas}_2$
are conjunctions of catamorphism atoms. We assume that the variables in
$\mathit{Catas}_2$
are conjunctions of catamorphism atoms. We assume that the variables in
![]() $D_1$
and
$D_1$
and
![]() $D_2$
have been renamed and the atoms in their bodies have been reordered so that
$D_2$
have been renamed and the atoms in their bodies have been reordered so that
![]() $(\mathit{Catas}, A)$
is the maximal common subconjunction of atoms in their bodies, that is, there exists no atom
$(\mathit{Catas}, A)$
is the maximal common subconjunction of atoms in their bodies, that is, there exists no atom
![]() $\mathit{Cata}$
in
$\mathit{Cata}$
in
![]() $\mathit{Catas}_1$
and no variant of
$\mathit{Catas}_1$
and no variant of
![]() $D_2$
of the form
$D_2$
of the form
![]() $\mathit{newp}2(U^{\prime}_2) \leftarrow \mathit{Catas}^{\prime}_2, \mathit{Catas}, A$
, such that
$\mathit{newp}2(U^{\prime}_2) \leftarrow \mathit{Catas}^{\prime}_2, \mathit{Catas}, A$
, such that
![]() $\mathit{Cata}$
is an atom in
$\mathit{Cata}$
is an atom in
![]() $\mathit{Catas}^{\prime}_2$
.
$\mathit{Catas}^{\prime}_2$
.
-
(i)
 $D_2$
is an extension of
$D_2$
is an extension of
 $D_1$
, written
$D_1$
, written
 $D_1\sqsubseteq D_2$
, if
$D_1\sqsubseteq D_2$
, if
 $\mathit{Catas}_1$
is the empty conjunction;
$\mathit{Catas}_1$
is the empty conjunction; -
(ii) By
 $D_1 \sqcup D_2$
we denote the definition
$D_1 \sqcup D_2$
we denote the definition
 $D_3$
:
$D_3$
:
 $\mathit{newp}3(U_3) \leftarrow \mathit{Catas}_1, \mathit{Catas}_2, \mathit{Catas}, A$
, where
$\mathit{newp}3(U_3) \leftarrow \mathit{Catas}_1, \mathit{Catas}_2, \mathit{Catas}, A$
, where
 $U_3$
is a tuple consisting of the distinct variables occurring in
$U_3$
is a tuple consisting of the distinct variables occurring in
 $(U_1,U_2)$
;
$(U_1,U_2)$
; -
(iii) By
 $D_1 \sqcap D_2$
we denote the definition
$D_1 \sqcap D_2$
we denote the definition
 $D_3$
:
$D_3$
:
 $\mathit{newp}3(U_3) \leftarrow \mathit{Catas}, A$
, where
$\mathit{newp}3(U_3) \leftarrow \mathit{Catas}, A$
, where
 $U_3$
is a tuple consisting of the variables occurring in both
$U_3$
is a tuple consisting of the variables occurring in both
 $U_1$
and
$U_1$
and
 $U_2.$
$U_2.$
Let
![]() $\Delta _1$
and
$\Delta _1$
and
![]() $\Delta _2$
be two monovariant subsets of
$\Delta _2$
be two monovariant subsets of
![]() $\mathcal D$
.
$\mathcal D$
.
-
(iv)
 $\Delta _2$
is an extension of
$\Delta _2$
is an extension of
 $\Delta _1$
, written
$\Delta _1$
, written
 $\Delta _1\sqsubseteq \Delta _2$
, if for each
$\Delta _1\sqsubseteq \Delta _2$
, if for each
 $D_1$
in
$D_1$
in
 $\Delta _1$
there exists
$\Delta _1$
there exists
 $D_2$
in
$D_2$
in
 $\Delta _2$
such that
$\Delta _2$
such that
 $D_1\sqsubseteq D_2$
;
$D_1\sqsubseteq D_2$
; -
(v)
 $\Delta _1 \sqcup \Delta _2 = \{D \mid D$
is the only definition in
$\Delta _1 \sqcup \Delta _2 = \{D \mid D$
is the only definition in
 $\Delta _1\cup \Delta _2$
for some program atom in
$\Delta _1\cup \Delta _2$
for some program atom in $\Delta _1\cup \Delta _2 \}\ \cup$
$\Delta _1\cup \Delta _2 \}\ \cup$
 $\{D_1\sqcup D_2 \mid D_1$
and
$\{D_1\sqcup D_2 \mid D_1$
and
 $D_2$
are definitions for the same program atom in
$D_2$
are definitions for the same program atom in $\Delta _1$
and
$\Delta _1$
and
 $\Delta _2$
, respectively
$\Delta _2$
, respectively
 $\}$
;
$\}$
; -
(vi)
 $\Delta _1 \sqcap \Delta _2 = \{D_1 \sqcap D_2 \mid D_1$
and
$\Delta _1 \sqcap \Delta _2 = \{D_1 \sqcap D_2 \mid D_1$
and
 $D_2$
are the definitions for the same program atom in
$D_2$
are the definitions for the same program atom in $\Delta _1$
and
$\Delta _1$
and
 $\Delta _2$
, respectively
$\Delta _2$
, respectively
 $\}.$
$\}.$
Let
![]() $\mathcal P_m(\mathcal D)$
denote the set of monovariant subsets of
$\mathcal P_m(\mathcal D)$
denote the set of monovariant subsets of
![]() $\mathcal D$
. We have that
$\mathcal D$
. We have that
![]() $(\mathcal P_m(\mathcal D), \sqsubseteq, \sqcup, \sqcap )$
is a lattice and, since
$(\mathcal P_m(\mathcal D), \sqsubseteq, \sqcup, \sqcap )$
is a lattice and, since
![]() $\mathcal D$
is a finite set, it is also a complete lattice. We define the operator
$\mathcal D$
is a finite set, it is also a complete lattice. We define the operator
![]() $\tau _{P\cup \{Q\},\alpha }\!: \mathcal P_m (\mathcal D) \rightarrow \mathcal P_m (\mathcal D)$
as follows:
$\tau _{P\cup \{Q\},\alpha }\!: \mathcal P_m (\mathcal D) \rightarrow \mathcal P_m (\mathcal D)$
as follows:
![]() $\tau _{P\cup \{Q\},\alpha }(\Delta ) =_{\mathit{def}} \mathit{Define}\big (\mathit{AddCata}\big (\mathit{Unfold}(\Delta, P) \cup \{Q\},\alpha \big ),\Delta \big )$
$\tau _{P\cup \{Q\},\alpha }(\Delta ) =_{\mathit{def}} \mathit{Define}\big (\mathit{AddCata}\big (\mathit{Unfold}(\Delta, P) \cup \{Q\},\alpha \big ),\Delta \big )$
Now, we show that the operator
![]() $\tau _{P\cup \{Q\},\alpha }$
is a well defined function from
$\tau _{P\cup \{Q\},\alpha }$
is a well defined function from
![]() $\mathcal P_m (\mathcal D)$
to itself, that is, for any
$\mathcal P_m (\mathcal D)$
to itself, that is, for any
![]() $\Delta \in \mathcal P_m (\mathcal D)$
, the set
$\Delta \in \mathcal P_m (\mathcal D)$
, the set
![]() $\Delta ' = \tau _{P\cup \{Q\},\alpha }(\Delta )$
is an element of
$\Delta ' = \tau _{P\cup \{Q\},\alpha }(\Delta )$
is an element of
![]() $\mathcal P_m (\mathcal D)$
.
$\mathcal P_m (\mathcal D)$
.
First, note that: (i) the Define function introduces (see the (Add) case) a new definition for a program predicate only if no definition for that predicate already belongs to
![]() $\Delta$
, and (ii) Define replaces (see the (Extend) case) a definition for a program predicate by a new definition for the same predicate. Thus, if
$\Delta$
, and (ii) Define replaces (see the (Extend) case) a definition for a program predicate by a new definition for the same predicate. Thus, if
![]() $\Delta$
is monovariant, so is
$\Delta$
is monovariant, so is
![]() $\Delta '$
. Moreover, no two equivalent clauses will belong to
$\Delta '$
. Moreover, no two equivalent clauses will belong to
![]() $\Delta '$
(see Point (D2) of Definition3).
$\Delta '$
(see Point (D2) of Definition3).
Note also that, due to the definition of function AddCata (see, in particular, Point (ii) of Rule R3 applied by that function), Point (D1) of Definition3 holds, and in particular, for every ADT variable
![]() $X_i$
in the body of any new definition in
$X_i$
in the body of any new definition in
![]() $\Delta '$
, and for every catamorphism predicate
$\Delta '$
, and for every catamorphism predicate
![]() $cata$
, there is at most one catamorphism atom of the form
$cata$
, there is at most one catamorphism atom of the form
![]() $\mathit{cata}(\ldots, X_i,\ldots )$
.
$\mathit{cata}(\ldots, X_i,\ldots )$
.
Lemma 1 (Existence and Uniqueness of the Fixpoint of
![]() $\tau _{P\cup \{Q\},\alpha }$
). The operator
$\tau _{P\cup \{Q\},\alpha }$
). The operator
![]() $\tau _{P\cup \{Q\},\alpha }$
is monotonic on the finite lattice
$\tau _{P\cup \{Q\},\alpha }$
is monotonic on the finite lattice
![]() $\mathcal P_m(\mathcal D)$
. Thus, it has a least fixpoint
$\mathcal P_m(\mathcal D)$
. Thus, it has a least fixpoint
![]() $\textit{lfp}(\tau _{P\cup \{Q\},\alpha })$
, also denoted
$\textit{lfp}(\tau _{P\cup \{Q\},\alpha })$
, also denoted
![]() $\tau _{\mathit{fix}}$
, which is equal to
$\tau _{\mathit{fix}}$
, which is equal to
![]() $\tau _{P\cup \{Q\},\alpha }^n(\emptyset )$
, for some natural number
$\tau _{P\cup \{Q\},\alpha }^n(\emptyset )$
, for some natural number
![]() $n$
.
$n$
.
Proof.
In order to prove the monotonicity of
![]() $\tau _{P\cup \{Q\},\alpha }$
, let us assume that
$\tau _{P\cup \{Q\},\alpha }$
, let us assume that
![]() $\Delta _1$
and
$\Delta _1$
and
![]() $\Delta _2$
are two sets of monovariant definitions in
$\Delta _2$
are two sets of monovariant definitions in
![]() $\mathcal P_m (\mathcal D)$
, with
$\mathcal P_m (\mathcal D)$
, with
![]() $\Delta _1 \sqsubseteq \Delta _2$
. Let
$\Delta _1 \sqsubseteq \Delta _2$
. Let
![]() $D_1\in \tau _{P\cup \{Q\},\alpha }(\Delta _1)$
be a definition for program atom
$D_1\in \tau _{P\cup \{Q\},\alpha }(\Delta _1)$
be a definition for program atom
![]() $A$
. We consider two cases.
$A$
. We consider two cases.
(Case 1) There is no definition for
![]() $A$
in
$A$
in
![]() $\Delta _1$
. Then, by construction, according to the Define function (see Figure 3),
$\Delta _1$
. Then, by construction, according to the Define function (see Figure 3),
![]() $D_1$
can be viewed as the result of a sequence of join operations of the form:
$D_1$
can be viewed as the result of a sequence of join operations of the form:
![]() $E_0\sqcup E_1 \sqcup \ldots \sqcup E_n$
, with
$E_0\sqcup E_1 \sqcup \ldots \sqcup E_n$
, with
![]() $n\!\geq \!0$
, where: (1) clause
$n\!\geq \!0$
, where: (1) clause
![]() $E_0$
has been obtained by the (Add) case of Define, and (2) for
$E_0$
has been obtained by the (Add) case of Define, and (2) for
![]() $i\!=\!1,\ldots, n$
, clause
$i\!=\!1,\ldots, n$
, clause
![]() $E_0\sqcup \ldots \sqcup E_{i}$
is a clause obtained by the (Extend) case of Define from clause
$E_0\sqcup \ldots \sqcup E_{i}$
is a clause obtained by the (Extend) case of Define from clause
![]() $E_0\sqcup \ldots \sqcup E_{i-1}$
. In particular, for all
$E_0\sqcup \ldots \sqcup E_{i-1}$
. In particular, for all
![]() $i\!=\!0,\ldots, n$
, clause
$i\!=\!0,\ldots, n$
, clause
![]() $E_i$
is a clause of the form
$E_i$
is a clause of the form
![]() $\mathit{newp}_i(V_i) \leftarrow \mathit{Catas_i}, A$
obtained from a clause
$\mathit{newp}_i(V_i) \leftarrow \mathit{Catas_i}, A$
obtained from a clause
![]() $H\leftarrow c, G$
(here and below in this proof
$H\leftarrow c, G$
(here and below in this proof
![]() $H$
may be false) in
$H$
may be false) in
![]() $\mathit{AddCata}(\mathit{Unfold}(\Delta _1,P) \cup \{Q\},\alpha )$
such that
$\mathit{AddCata}(\mathit{Unfold}(\Delta _1,P) \cup \{Q\},\alpha )$
such that
![]() $A$
is a program atom in
$A$
is a program atom in
![]() $G$
and
$G$
and
![]() $\mathit{Catas_i}$
is the conjunction of all catamorphism atoms
$\mathit{Catas_i}$
is the conjunction of all catamorphism atoms
![]() $F$
in
$F$
in
![]() $G$
with
$G$
with
![]() $\mathit{adt\mbox{-}vars}(F)\subseteq \mathit{adt\mbox{-}vars}(A)$
.
$\mathit{adt\mbox{-}vars}(F)\subseteq \mathit{adt\mbox{-}vars}(A)$
.
(Case 2) There is a definition
![]() $E_0$
for
$E_0$
for
![]() $A$
in
$A$
in
![]() $\Delta _1$
. Then, similarly to Case 1, by construction,
$\Delta _1$
. Then, similarly to Case 1, by construction,
![]() $D_1 = E_0\sqcup \ldots \sqcup E_n$
, where, for
$D_1 = E_0\sqcup \ldots \sqcup E_n$
, where, for
![]() $i\!=\!1,\ldots, n$
, with
$i\!=\!1,\ldots, n$
, with
![]() $n\!\geq \!0$
,
$n\!\geq \!0$
,
![]() $E_0\sqcup \ldots \sqcup E_i$
is a clause obtained by the (Extend) case of Define.
$E_0\sqcup \ldots \sqcup E_i$
is a clause obtained by the (Extend) case of Define.
Now, since
![]() $\Delta _1 \sqsubseteq \Delta _2$
, for each clause
$\Delta _1 \sqsubseteq \Delta _2$
, for each clause
![]() $H\leftarrow c, G$
in
$H\leftarrow c, G$
in
![]() $\mathit{AddCata}(\mathit{Unfold}(\Delta _1,P)\cup \{Q\},\alpha )$
, there exists a clause
$\mathit{AddCata}(\mathit{Unfold}(\Delta _1,P)\cup \{Q\},\alpha )$
, there exists a clause
![]() $H\leftarrow c, C, G$
in the set of clauses
$H\leftarrow c, C, G$
in the set of clauses
![]() $\mathit{AddCata}(\mathit{Unfold}(\Delta _2,P) \cup \{Q\},\alpha )$
, where
$\mathit{AddCata}(\mathit{Unfold}(\Delta _2,P) \cup \{Q\},\alpha )$
, where
![]() $C$
is a conjunction of catamorphism atoms, and then, by construction,
$C$
is a conjunction of catamorphism atoms, and then, by construction,
![]() $\textit{Define} (\mathit{AddCata}(\mathit{Unfold}(\Delta _2,P)\cup \{Q\},\alpha ),\Delta _2)$
contains, for
$\textit{Define} (\mathit{AddCata}(\mathit{Unfold}(\Delta _2,P)\cup \{Q\},\alpha ),\Delta _2)$
contains, for
![]() $i\!=\!1,\ldots, n$
, a clause
$i\!=\!1,\ldots, n$
, a clause
![]() $E^{\prime}_i$
, with
$E^{\prime}_i$
, with
![]() $E_i\sqsubseteq E^{\prime}_i$
. Then, there exists
$E_i\sqsubseteq E^{\prime}_i$
. Then, there exists
![]() $D_2 \in \tau _{P\cup \{Q\},\alpha }(\Delta _2)$
such that
$D_2 \in \tau _{P\cup \{Q\},\alpha }(\Delta _2)$
such that
![]() $D_1\! =\! (E_0\sqcup \ldots \sqcup E_n) \sqsubseteq (E^{\prime}_0\sqcup \ldots \sqcup E^{\prime}_n) \sqsubseteq (E^{\prime}_0\sqcup \ldots \sqcup E^{\prime}_n \sqcup F_{1}\sqcup \ldots \sqcup F_r) = D_2$
, with
$D_1\! =\! (E_0\sqcup \ldots \sqcup E_n) \sqsubseteq (E^{\prime}_0\sqcup \ldots \sqcup E^{\prime}_n) \sqsubseteq (E^{\prime}_0\sqcup \ldots \sqcup E^{\prime}_n \sqcup F_{1}\sqcup \ldots \sqcup F_r) = D_2$
, with
![]() $r\geq 0$
. (Note that, since
$r\geq 0$
. (Note that, since
![]() $\Delta _1\sqsubseteq \Delta _2$
, in
$\Delta _1\sqsubseteq \Delta _2$
, in
![]() $\mathit{AddCata}(\mathit{Unfold}(\Delta _2,P) \cup \{Q\},\alpha )$
there may be clauses that are derived from definitions in
$\mathit{AddCata}(\mathit{Unfold}(\Delta _2,P) \cup \{Q\},\alpha )$
there may be clauses that are derived from definitions in
![]() $\Delta _2$
that are not extensions of definitions in
$\Delta _2$
that are not extensions of definitions in
![]() $\Delta _1$
. In the bodies of those clauses there may be some variants of
$\Delta _1$
. In the bodies of those clauses there may be some variants of
![]() $A$
that determine
$A$
that determine
![]() $r$
extra applications of the (Extend) case of Define.) Therefore, by Definition4,
$r$
extra applications of the (Extend) case of Define.) Therefore, by Definition4,
![]() $\tau _{P\cup \{Q\},\alpha }(\Delta _1) \sqsubseteq \tau _{P\cup \{Q\},\alpha }(\Delta _2)$
.
$\tau _{P\cup \{Q\},\alpha }(\Delta _1) \sqsubseteq \tau _{P\cup \{Q\},\alpha }(\Delta _2)$
.
Thus,
![]() $\tau _{P\cup \{Q\},\alpha }$
is monotonic with respect to
$\tau _{P\cup \{Q\},\alpha }$
is monotonic with respect to
![]() $\sqsubseteq$
. Since
$\sqsubseteq$
. Since
![]() $\mathcal P_m(\mathcal D)$
is a finite, hence complete, lattice,
$\mathcal P_m(\mathcal D)$
is a finite, hence complete, lattice,
![]() $\tau _{P\cup \{Q\},\alpha }$
has a least fixpoint
$\tau _{P\cup \{Q\},\alpha }$
has a least fixpoint
![]() $\textit{lfp}(\tau _{P\cup \{Q\},\alpha })$
, which can be computed as
$\textit{lfp}(\tau _{P\cup \{Q\},\alpha })$
, which can be computed as
![]() $\tau _{P\cup \{Q\},\alpha }^n(\emptyset )$
, for some natural number
$\tau _{P\cup \{Q\},\alpha }^n(\emptyset )$
, for some natural number
![]() $n$
.
$n$
.
Now, we define our transformation algorithm
![]() ${\mathcal{T}}_{\mathit{abs}}$
as follows:
${\mathcal{T}}_{\mathit{abs}}$
as follows:
![]() ${\mathcal{T}}_{\mathit{abs}}$
${\mathcal{T}}_{\mathit{abs}}$
![]() $(P\cup \{Q\},\alpha ) = \mathit{AddErasure}\big (\mathit{Fold}\big (\mathit{AddCata}\big (\mathit{Unfold}(\tau _{\mathit{fix}},P) \cup \{Q\},\,\alpha \big ),\tau _{\mathit{fix}}\big ) \big )$
$(P\cup \{Q\},\alpha ) = \mathit{AddErasure}\big (\mathit{Fold}\big (\mathit{AddCata}\big (\mathit{Unfold}(\tau _{\mathit{fix}},P) \cup \{Q\},\,\alpha \big ),\tau _{\mathit{fix}}\big ) \big )$
The termination of
![]() ${\mathcal{T}}_{\mathit{abs}}$
follows immediately from the fact that the functions Unfold, AddCata, Fold, and AddErasure terminate and the least fixpoint
${\mathcal{T}}_{\mathit{abs}}$
follows immediately from the fact that the functions Unfold, AddCata, Fold, and AddErasure terminate and the least fixpoint
![]() $\tau _{\mathit{fix}}$
is computed in a finite number of steps (see Lemma1). Thus, by the correctness of the transformation rules (see Theorem1), we get the following result.
$\tau _{\mathit{fix}}$
is computed in a finite number of steps (see Lemma1). Thus, by the correctness of the transformation rules (see Theorem1), we get the following result.
Theorem 3 (Total Correctness of Algorithm
![]() ${\mathcal{T}}_{\mathit{abs}}$
).
${\mathcal{T}}_{\mathit{abs}}$
).
![]() ${\mathcal{T}}_{\mathit{abs}}$
terminates for any set
${\mathcal{T}}_{\mathit{abs}}$
terminates for any set
![]() $\mathit{P}$
of definite clauses, query
$\mathit{P}$
of definite clauses, query
![]() $Q$
, and catamorphic abstraction specification
$Q$
, and catamorphic abstraction specification
![]() $\alpha$
. Also,
$\alpha$
. Also,
![]() $P \cup \{Q\}$
is satisfiable if and only if
$P \cup \{Q\}$
is satisfiable if and only if
![]() ${\mathcal{T}}_{\mathit{abs}}$
${\mathcal{T}}_{\mathit{abs}}$
![]() $(P\cup \{Q\},\alpha )$
is satisfiable.
$(P\cup \{Q\},\alpha )$
is satisfiable.
Finally, we would like to comment on the fact that our transformation algorithm
![]() ${\mathcal{T}}_{\mathit{abs}}$
introduces a monovariant set of definitions. Other definition introduction policies could have been considered. In particular, one could introduce more than one definition for each program predicate, thus producing a polyvariant set of definitions. The choice between monovariant and polyvariant sets of definitions has been subject to ample discussion in the literature (De Angelis et al., Reference De Angelis, Fioravanti, Gallagher, Hermenegildo, Pettorossi and Proietti2022) and both have advantages and disadvantages. We will show in the next section that our technique performs quite well in our benchmark. However, we leave a more accurate experimental evaluation to future work.
${\mathcal{T}}_{\mathit{abs}}$
introduces a monovariant set of definitions. Other definition introduction policies could have been considered. In particular, one could introduce more than one definition for each program predicate, thus producing a polyvariant set of definitions. The choice between monovariant and polyvariant sets of definitions has been subject to ample discussion in the literature (De Angelis et al., Reference De Angelis, Fioravanti, Gallagher, Hermenegildo, Pettorossi and Proietti2022) and both have advantages and disadvantages. We will show in the next section that our technique performs quite well in our benchmark. However, we leave a more accurate experimental evaluation to future work.
5 Implementation and experimental evaluation
In this section we provide some details on the implementation of algorithm
![]() ${\mathcal{T}}_{\mathit{abs}}$
, and on its experimental evaluation.
${\mathcal{T}}_{\mathit{abs}}$
, and on its experimental evaluation.
Implementation. We have implemented algorithm
![]() ${\mathcal{T}}_{\mathit{abs}}$
in a tool, called VeriCaT
${\mathcal{T}}_{\mathit{abs}}$
in a tool, called VeriCaT
![]() $_{\!\mathit{abs}}$
, based on VeriMAP (De Angelis et al., Reference De Angelis, Fioravanti, Pettorossi and Proietti2014), which is a system for transforming CHCs. In order to check satisfiability of sets of CHCs (before and after their transformation) we have used the following two solvers: (i) Eldarica (v. 2.0.9) (Hojjat and Rümmer, Reference Hojjat and Rümmer2018), and (ii) Z3 (v. 4.12.2) (de Moura and Bjørner, Reference de Moura and Bjørner2008) with the SPACER engine (Komuravelli et al., Reference Komuravelli, Gurfinkel and Chaki2016) and the global guidance option (Krishnan et al., Reference Krishnan, Chen, Shoham and Gurfinkel2020).
$_{\!\mathit{abs}}$
, based on VeriMAP (De Angelis et al., Reference De Angelis, Fioravanti, Pettorossi and Proietti2014), which is a system for transforming CHCs. In order to check satisfiability of sets of CHCs (before and after their transformation) we have used the following two solvers: (i) Eldarica (v. 2.0.9) (Hojjat and Rümmer, Reference Hojjat and Rümmer2018), and (ii) Z3 (v. 4.12.2) (de Moura and Bjørner, Reference de Moura and Bjørner2008) with the SPACER engine (Komuravelli et al., Reference Komuravelli, Gurfinkel and Chaki2016) and the global guidance option (Krishnan et al., Reference Krishnan, Chen, Shoham and Gurfinkel2020).
The tool VeriCaT
![]() $_{\!\mathit{abs}}$
manipulates clauses as indicated in the following three phases.
$_{\!\mathit{abs}}$
manipulates clauses as indicated in the following three phases.
(Phase 1) A pre-processing phase. In this phase VeriCaT
![]() $_{\!\mathit{abs}}$
produces a catamorphic abstraction specification
$_{\!\mathit{abs}}$
produces a catamorphic abstraction specification
![]() $\alpha$
starting from: (i) a given set
$\alpha$
starting from: (i) a given set
![]() $P$
of CHCs, and (ii) the catamorphic abstractions for the ADTs occurring in
$P$
of CHCs, and (ii) the catamorphic abstractions for the ADTs occurring in
![]() $P$
. For instance, in the case of our introductory example double (see Figure 1), Phase 1 produces the catamorphic abstraction specifications for
$P$
. For instance, in the case of our introductory example double (see Figure 1), Phase 1 produces the catamorphic abstraction specifications for
![]() $\mathit{double}$
,
$\mathit{double}$
,
![]() $\mathit{eq}$
, and
$\mathit{eq}$
, and
![]() $\mathit{append}$
we have listed in Example1, starting from clauses 1–6 and the catamorphic abstraction
$\mathit{append}$
we have listed in Example1, starting from clauses 1–6 and the catamorphic abstraction
![]() $\mathit{cata}_{\mathit{list}(\mathit{int})} =_{\mathit{def}}{\mathit{listcount}(X,L,N)}$
,
$\mathit{cata}_{\mathit{list}(\mathit{int})} =_{\mathit{def}}{\mathit{listcount}(X,L,N)}$
,
In the following example, referring to a treesort algorithm, we present the VeriCaT
![]() $_{\!\mathit{abs}}$
syntax for representing: (i) the catamorphic abstractions given in input, using the directive cata_abs, and (ii) the catamorphic abstraction specifications produced in output, after Phase 1, using the directive spec.
$_{\!\mathit{abs}}$
syntax for representing: (i) the catamorphic abstractions given in input, using the directive cata_abs, and (ii) the catamorphic abstraction specifications produced in output, after Phase 1, using the directive spec.
Example 8. Let treesort(L,S) and visit(T,L) be two atoms included in a CHC encoding of the treesort algorithm. The atom treesort(L,S) holds if and only if S is the list of integers obtained by applying the treesort algorithm to the list L of integers. The auxiliary atom visit(T,L) holds if and only if L is the list of integers obtained by a depth first visit of the tree T with integers at its nodes. The catamorphic abstractions for the ADT sorts
![]() $\mathit{list(int)}$
and
$\mathit{list(int)}$
and
![]() $\mathit{tree(int)}$
used by our tool VeriCaT
$\mathit{tree(int)}$
used by our tool VeriCaT
![]() $_{\!\mathit{abs}}$
during Phase 1, are as follows:
$_{\!\mathit{abs}}$
during Phase 1, are as follows:
:- cata_abs list(int)
![]() $\texttt{==}\gt$
listcount(X,L,C).
$\texttt{==}\gt$
listcount(X,L,C).
:- cata_abs tree(int)
![]() $\texttt{==}\gt$
treecount(X,T,C).
$\texttt{==}\gt$
treecount(X,T,C).
The catamorphisms listcount(X,L,B) and treecount(X,T,A) count the occurrences of the integer X in the list L and in the tree T, respectively. In general, the directive cata_abs for a sort
![]() $\tau$
is as follows:
$\tau$
is as follows:
:- cata_abs
![]() $\tau$
$\tau$
![]() $\texttt{==}\gt$
catamorphisms acting on
$\texttt{==}\gt$
catamorphisms acting on
![]() $\tau$
.
$\tau$
.
For the program predicates treesort and visit, the catamorphic abstraction specifications produced by VeriCaT
![]() $_{\!\mathit{abs}}$
after Phase 1, are as follows:
$_{\!\mathit{abs}}$
after Phase 1, are as follows:
:- spec treesort(L,S)
![]() $\texttt{==}\gt$
X
$\texttt{==}\gt$
X
![]() $\texttt{=}$
Y, listcount(X,S,A), listcount(Y,L,B).
$\texttt{=}$
Y, listcount(X,S,A), listcount(Y,L,B).
:- spec visit(T,L)
![]() $\texttt{==}\gt$
X
$\texttt{==}\gt$
X
![]() $\texttt{=}$
Y, treecount(X,T,A), listcount(Y,L,B).
$\texttt{=}$
Y, treecount(X,T,A), listcount(Y,L,B).
Note that both the tree catamorphism treecount(X,T,A) and the list catamorphism listcount(Y,L,B) occur in the catamorphic specification for visit(T,L).
(Phase 2) A fold/unfold transformation phase. In this phase VeriCaT
![]() $_{\!\mathit{abs}}$
computes the fixpoint
$_{\!\mathit{abs}}$
computes the fixpoint
![]() $\tau _{\mathit{fix}}$
and the set
$\tau _{\mathit{fix}}$
and the set
![]() $T_w$
of clauses, which is
$T_w$
of clauses, which is
![]() $\mathit{Fold}\big (\!\mathit{AddCata}\big (\!\mathit{Unfold}(\tau _{\mathit{fix}},P)\! \cup\! \{Q\},\,\alpha \big ),\tau _{\mathit{fix}})$
. For the double introductory example (see Figure 1), we have that
$\mathit{Fold}\big (\!\mathit{AddCata}\big (\!\mathit{Unfold}(\tau _{\mathit{fix}},P)\! \cup\! \{Q\},\,\alpha \big ),\tau _{\mathit{fix}})$
. For the double introductory example (see Figure 1), we have that
![]() $P$
is the set
$P$
is the set
![]() $\{1,\ldots, 6\}$
of clauses, query
$\{1,\ldots, 6\}$
of clauses, query
![]() $Q$
is clause 7, and
$Q$
is clause 7, and
![]() $\alpha$
is the set of catamorphic abstraction specifications produced at Phase 1 (see Example1). Now,
$\alpha$
is the set of catamorphic abstraction specifications produced at Phase 1 (see Example1). Now,
![]() $\tau _{\mathit{fix}}$
is the set
$\tau _{\mathit{fix}}$
is the set
![]() $\{D1,D2,D3,D4\}$
of definitions listed in Figure 2 and the set
$\{D1,D2,D3,D4\}$
of definitions listed in Figure 2 and the set
![]() $T_w$
is as follows:
$T_w$
is as follows:
![]() $\mathit{false} \leftarrow C\!=\!2D+1,\ \mathit{new}1(A,E,F,G,C)$
$\mathit{false} \leftarrow C\!=\!2D+1,\ \mathit{new}1(A,E,F,G,C)$
![]() $\mathit{new}1(A,B,C,E,F) \leftarrow \mathit{new}2(A,M,K,E,F,B,C),\ \mathit{new}3(A,M,K,B,C)$
$\mathit{new}1(A,B,C,E,F) \leftarrow \mathit{new}2(A,M,K,E,F,B,C),\ \mathit{new}3(A,M,K,B,C)$
![]() $\mathit{new}2(A,B,C,B,C,[\,],G) \leftarrow G\!=\!0,\ \mathit{new}4(A,B,C)$
$\mathit{new}2(A,B,C,B,C,[\,],G) \leftarrow G\!=\!0,\ \mathit{new}4(A,B,C)$
![]() $\mathit{new}2(A,B,C,[E|F],G,[E|J],K) \leftarrow G\!=\!\mathit{ite}(A\!=\!E,N\!+\!1,N),\ K\!=\!\mathit{ite}(A\!=\!E,P\!+\!1,P),$
$\mathit{new}2(A,B,C,[E|F],G,[E|J],K) \leftarrow G\!=\!\mathit{ite}(A\!=\!E,N\!+\!1,N),\ K\!=\!\mathit{ite}(A\!=\!E,P\!+\!1,P),$
![]() $\mathit{new}2(A,B,C,F,N,J,P)$
$\mathit{new}2(A,B,C,F,N,J,P)$
![]() $\mathit{new}3(A,B,C,B,C) \leftarrow \mathit{new}4(A,B,C)$
$\mathit{new}3(A,B,C,B,C) \leftarrow \mathit{new}4(A,B,C)$
![]() $\mathit{new}4(A,[\,],B) \leftarrow B\!=\!0$
$\mathit{new}4(A,[\,],B) \leftarrow B\!=\!0$
![]() $\mathit{new}4(A,[B|C],D) \leftarrow D\!=\!\mathit{ite}(A\!=\!B,F\!+\!1,F),\ \mathit{new}4(A,C,F)$
$\mathit{new}4(A,[B|C],D) \leftarrow D\!=\!\mathit{ite}(A\!=\!B,F\!+\!1,F),\ \mathit{new}4(A,C,F)$
(Phase 3) A post-processing phase. In this phase, VeriCaT
![]() $_{\!\mathit{abs}}$
produces the following two additional sets of clauses by applying the
$_{\!\mathit{abs}}$
produces the following two additional sets of clauses by applying the
![]() $\mathit{AddErasure}$
function to
$\mathit{AddErasure}$
function to
![]() $T_w$
:
$T_w$
:
-
(i)
 $T_{\mathit{wo}}=\{\chi _{\mathit{wo}}(C) \mid C$
is a clause in
$T_{\mathit{wo}}=\{\chi _{\mathit{wo}}(C) \mid C$
is a clause in
 $T_w\}$
, that is,
$T_w\}$
, that is,
 $T_{\mathit{wo}}$
is made out of the clauses in
$T_{\mathit{wo}}$
is made out of the clauses in
 $T_w$
where every atom with ADT arguments has been replaced by its corresponding atom without ADT arguments, and
$T_w$
where every atom with ADT arguments has been replaced by its corresponding atom without ADT arguments, and -
(ii)
 $T_{\mathit{w\&wo}}=\{\chi _{\mathit{w\&wo}}(C) \mid C$
is a clause in
$T_{\mathit{w\&wo}}=\{\chi _{\mathit{w\&wo}}(C) \mid C$
is a clause in
 $T_w\} \cup \overline{T}_{\mathit{wo}}$
, that is,
$T_w\} \cup \overline{T}_{\mathit{wo}}$
, that is,
 $T_{\mathit{w\&wo}}$
is made out of the clauses in either (ii.1)
$T_{\mathit{w\&wo}}$
is made out of the clauses in either (ii.1)
 $T_w$
, where every atom in the body with ADT arguments is paired with its corresponding atom without ADT arguments, or (ii.2)
$T_w$
, where every atom in the body with ADT arguments is paired with its corresponding atom without ADT arguments, or (ii.2)
 $\overline{T}_{\!\mathit{wo}} = \{\chi _{\mathit{wo}}(C) \mid C$
is a clause in
$\overline{T}_{\!\mathit{wo}} = \{\chi _{\mathit{wo}}(C) \mid C$
is a clause in
 $T_{\mathit{w}}$
whose head is not false}.
$T_{\mathit{w}}$
whose head is not false}.
![]() $T_{\mathit{w\&wo}}$
is, indeed, the set of clauses computed by our transformation algorithm
$T_{\mathit{w\&wo}}$
is, indeed, the set of clauses computed by our transformation algorithm
![]() ${\mathcal{T}}_{\mathit{abs}}$
. The other two sets
${\mathcal{T}}_{\mathit{abs}}$
. The other two sets
![]() $T_{\mathit{w}}$
and
$T_{\mathit{w}}$
and
![]() $T_{\mathit{wo}}$
, produced by VeriCaT
$T_{\mathit{wo}}$
, produced by VeriCaT
![]() $_{\!\mathit{abs}}$
, will be used for comparing and analyzing the features of
$_{\!\mathit{abs}}$
, will be used for comparing and analyzing the features of
![]() $T_{\mathit{w\&wo}}$
, as we do in the experimental evaluation below.
$T_{\mathit{w\&wo}}$
, as we do in the experimental evaluation below.
For our introductory example double (see Figure 1), at the end of Phase 3, VeriCaT
![]() $_{\!\mathit{abs}}$
produces the following two sets of clauses (clause numbers refer to Figure 2):
$_{\!\mathit{abs}}$
produces the following two sets of clauses (clause numbers refer to Figure 2):
![]() ${T}_{\mathit{wo}}\!=\! \{\mathit{false} \leftarrow C\!=\!2D\!+\!1,{\mathit{new}1\, us \mathit{woADTs}}(A,\!F,\!C)\}$
${T}_{\mathit{wo}}\!=\! \{\mathit{false} \leftarrow C\!=\!2D\!+\!1,{\mathit{new}1\, us \mathit{woADTs}}(A,\!F,\!C)\}$
![]() $ \cup \ \{18,\ldots, 23\}$
, and
$ \cup \ \{18,\ldots, 23\}$
, and
![]() $T_{\mathit{w\&wo}} = \{11,\ldots, 23\}$
.
$T_{\mathit{w\&wo}} = \{11,\ldots, 23\}$
.
The set
![]() $\{18,\ldots, 23\}$
of clauses is
$\{18,\ldots, 23\}$
of clauses is
![]() $\overline{{T}}_{\mathit{wo}}$
of Point (ii.2) above.
$\overline{{T}}_{\mathit{wo}}$
of Point (ii.2) above.
Experimental evaluation. Our benchmark consists of 228 sets of CHCs that encode properties of various sorting algorithms (such as bubblesort, heapsort, insertionsort, mergesort, quicksort, selectionsort, and treesort), and simple list and tree manipulation algorithms (such as appending and reversing lists, constructing permutations, deleting copies of elements, manipulating binary search trees). Properties of those algorithms are expressed via catamorphisms. Here is a non-exhaustive list of the catamorphisms we used: (i)
![]() $\mathit{size(L,S)}$
, (ii)
$\mathit{size(L,S)}$
, (ii)
![]() $\mathit{listmin(L,Min)}$
, (iii)
$\mathit{listmin(L,Min)}$
, (iii)
![]() $\mathit{listmax(L,Max)}$
, and (iv)
$\mathit{listmax(L,Max)}$
, and (iv)
![]() $\mathit{sum(L,Sum)}$
computing, respectively, the size
$\mathit{sum(L,Sum)}$
computing, respectively, the size
![]() $S$
of list
$S$
of list
![]() $L$
, the minimum Min, the maximum Max, and the sum Sum of the elements of list
$L$
, the minimum Min, the maximum Max, and the sum Sum of the elements of list
![]() $L$
, (v)
$L$
, (v)
![]() $\mathit{is\, us asorted}(L,\mathit{BL})$
, which holds with
$\mathit{is\, us asorted}(L,\mathit{BL})$
, which holds with
![]() $\mathit{BL\!=\!true}$
if and only if list
$\mathit{BL\!=\!true}$
if and only if list
![]() $L$
is ordered in weakly ascending order, (vi) allpos
$L$
is ordered in weakly ascending order, (vi) allpos
![]() $(L,B)$
, which holds with
$(L,B)$
, which holds with
![]() $\mathit{B\!=\!true}$
if and only if list
$\mathit{B\!=\!true}$
if and only if list
![]() $L$
is made out of all positive elements, (vii)
$L$
is made out of all positive elements, (vii)
![]() $\mathit{member}(X,L,B)$
, which holds with
$\mathit{member}(X,L,B)$
, which holds with
![]() $\mathit{B\!=\!true}$
if and only if
$\mathit{B\!=\!true}$
if and only if
![]() $X$
is an element of the list
$X$
is an element of the list
![]() $L$
, and (viii)
$L$
, and (viii)
![]() $\mathit{listcount}(X,L,N)$
, which holds if and only if
$\mathit{listcount}(X,L,N)$
, which holds if and only if
![]() $N$
is the number
$N$
is the number
![]() $(\geq \!0)$
of occurrences of
$(\geq \!0)$
of occurrences of
![]() $X$
in the list
$X$
in the list
![]() $L$
. For some properties, we have used more than one catamorphism at a time and, in particular, for lists of integers, we have used the conjunction of
$L$
. For some properties, we have used more than one catamorphism at a time and, in particular, for lists of integers, we have used the conjunction of
![]() $\mathit{member}$
and
$\mathit{member}$
and
![]() $\mathit{listcount}$
, and for different properties, we have also used the conjunction of
$\mathit{listcount}$
, and for different properties, we have also used the conjunction of
![]() $\mathit{listmin, listmax}$
, and
$\mathit{listmin, listmax}$
, and
![]() $\mathit{\textit{is\, us asorted}}$
, as already indicated in the paper.
$\mathit{\textit{is\, us asorted}}$
, as already indicated in the paper.
A property holds if and only if its CHC encoding via a query
![]() $Q$
is satisfiable, and a verification task consists in using a CHC solver to check the satisfiability of
$Q$
is satisfiable, and a verification task consists in using a CHC solver to check the satisfiability of
![]() $Q$
. When the given property holds for a set
$Q$
. When the given property holds for a set
![]() $P$
of clauses, the solver should return sat and the property is said to be a sat property. Analogously, when a property does not hold, the solver should return unsat and the property is said to be an unsat property. In our benchmark, for each verification task of a sat property, we have considered a companion verification task whose CHCs have been modified so that the associated property is unsat. In particular, we have 114 sat properties and 114 unsat properties.
$P$
of clauses, the solver should return sat and the property is said to be a sat property. Analogously, when a property does not hold, the solver should return unsat and the property is said to be an unsat property. In our benchmark, for each verification task of a sat property, we have considered a companion verification task whose CHCs have been modified so that the associated property is unsat. In particular, we have 114 sat properties and 114 unsat properties.
We have performed our experiments on an Intel(R) Xeon(R) Gold 6238R CPU 2.20 GHz with 221 GB RAM under CentOS with a timeout of 600s per verification task. The results of our experiments are reported in Table 1. The VeriCaT
![]() $_{\!\mathit{abs}}$
tool and the benchmarks are available at https://fmlab.unich.it/vericatabs.
$_{\!\mathit{abs}}$
tool and the benchmarks are available at https://fmlab.unich.it/vericatabs.
Table 1. Properties proved by the solvers Eldarica and Z3 before and after the transformation performed by algorithm
![]() ${\mathcal{T}}_{\mathit{abs}}$
. In the before case, the input to the solver is the source set of clauses (src-columns), and in the after case, the input is
${\mathcal{T}}_{\mathit{abs}}$
. In the before case, the input to the solver is the source set of clauses (src-columns), and in the after case, the input is
![]() $T_{\mathit{w\&wo}}$
(
$T_{\mathit{w\&wo}}$
(
![]() $T_{\mathit{w{\&} wo}}$
-columns). The columns occur in pairs referring to the sat properties (
$T_{\mathit{w{\&} wo}}$
-columns). The columns occur in pairs referring to the sat properties (
![]() $s$
-columns) and the unsat properties (
$s$
-columns) and the unsat properties (
![]() $u$
-columns), respectively. The two
$u$
-columns), respectively. The two
![]() $T_w$
-columns and the two
$T_w$
-columns and the two
![]() $T_{\mathit{wo}}$
-columns refer to the input
$T_{\mathit{wo}}$
-columns refer to the input
![]() $T_{\mathit{w}}$
and
$T_{\mathit{w}}$
and
![]() $T_{\mathit{wo}}$
, respectively. The last column shows the time (in seconds) taken by
$T_{\mathit{wo}}$
, respectively. The last column shows the time (in seconds) taken by
![]() ${\mathcal{T}}_{\mathit{abs}}$
as implemented by VeriCaT
${\mathcal{T}}_{\mathit{abs}}$
as implemented by VeriCaT
![]() $_{\!\mathit{abs}}$
.
$_{\!\mathit{abs}}$
.
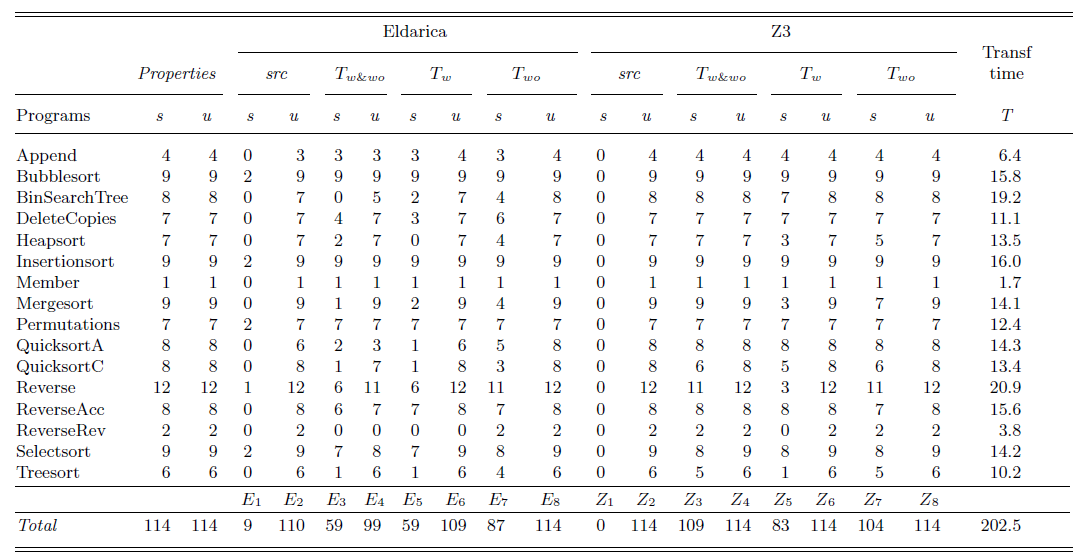
Table 1 shows that, for each verification task, the transformation of the CHCs allows a very significant improvement of the performance of the Z3 solver and also an overall improvement of the Eldarica solver (notably for sat properties).
In particular, before CHC transformation, Z3 did not prove any of the 114 sat properties of our benchmark. After CHC transformation, Z3 proved 109 of them to be sat (see columns
![]() $Z_{1}$
and
$Z_{1}$
and
![]() $Z_{3}$
of Table 1). The time cost of this improvement is very small. Indeed, most CHC transformations take well below 1.5s and only one of them takes a little more than 2s (for details, see column
$Z_{3}$
of Table 1). The time cost of this improvement is very small. Indeed, most CHC transformations take well below 1.5s and only one of them takes a little more than 2s (for details, see column
![]() $T$
, where each entry is the sum of the times taken for the individual transformation tasks of each row). The times taken by the solvers after transformation (not shown in Table 1) are usually quite small. In particular, for the 109 properties proved sat by Z3, the verification time was almost always below 1s. Only for 13 of them, it was between 1s and 4s. For the remaining five sat properties, Z3 exceeded the timeout limit.
$T$
, where each entry is the sum of the times taken for the individual transformation tasks of each row). The times taken by the solvers after transformation (not shown in Table 1) are usually quite small. In particular, for the 109 properties proved sat by Z3, the verification time was almost always below 1s. Only for 13 of them, it was between 1s and 4s. For the remaining five sat properties, Z3 exceeded the timeout limit.
Out of the 114 sat properties, Eldarica proved 9 sat properties (all relative to list size) before transformation and 59 sat properties (relative also to catamorphisms different from list size) after transformation (see columns
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{3}$
). However, one property that was proved sat before transformation, was not proved sat after transformation. This is the only example where the built-in size function of Eldarica has been more effective than our transformation-based approach.
$E_{3}$
). However, one property that was proved sat before transformation, was not proved sat after transformation. This is the only example where the built-in size function of Eldarica has been more effective than our transformation-based approach.
Given the 114 unsat properties, Z3 proved all of them to be unsat before transformation and also after transformation (see columns
![]() $Z_{2}$
and
$Z_{2}$
and
![]() $Z_{4}$
). The proofs before transformation took well-below 1s in almost all examples, and after transformation took an equal or shorter time for more than half of the cases.
$Z_{4}$
). The proofs before transformation took well-below 1s in almost all examples, and after transformation took an equal or shorter time for more than half of the cases.
Given the 114 unsat properties, Eldarica proved 110 of them to be unsat before transformation, and only 99 of them after transformation (see columns
![]() $E_{2}$
and
$E_{2}$
and
![]() $E_{4}$
). This is the only case where we experienced a degradation of performance after transformation. This degradation may be related to the facts that: (i) the number of clauses in the transformed set
$E_{4}$
). This is the only case where we experienced a degradation of performance after transformation. This degradation may be related to the facts that: (i) the number of clauses in the transformed set
![]() $T_{\mathit{w\&wo}}$
is larger than the number of clauses in the source set, and (ii) the clauses in
$T_{\mathit{w\&wo}}$
is larger than the number of clauses in the source set, and (ii) the clauses in
![]() $T_{\mathit{w\&wo}}$
have often more atoms in their bodies with respect to the source clauses.
$T_{\mathit{w\&wo}}$
have often more atoms in their bodies with respect to the source clauses.
If we consider the set
![]() $T_{\mathit{w}}$
, instead of
$T_{\mathit{w}}$
, instead of
![]() $T_{\mathit{w\&wo}}$
, we have a significant decrease in the number of clauses and the number of atoms in the bodies of clauses. In this case, Z3 proved 83 properties to be sat (less than for
$T_{\mathit{w\&wo}}$
, we have a significant decrease in the number of clauses and the number of atoms in the bodies of clauses. In this case, Z3 proved 83 properties to be sat (less than for
![]() $T_{\mathit{w\&wo}}$
, see columns
$T_{\mathit{w\&wo}}$
, see columns
![]() $Z_3$
and
$Z_3$
and
![]() $Z_5$
) and all 114 properties to be unsat (as for all other input sets of clauses, see columns
$Z_5$
) and all 114 properties to be unsat (as for all other input sets of clauses, see columns
![]() $Z_2$
,
$Z_2$
,
![]() $Z_4$
, and
$Z_4$
, and
![]() $Z_6$
). Eldarica proved 59 properties to be sat (the same as for
$Z_6$
). Eldarica proved 59 properties to be sat (the same as for
![]() $T_{\mathit{w\&wo}}$
, see columns
$T_{\mathit{w\&wo}}$
, see columns
![]() $E_3$
and
$E_3$
and
![]() $E_5$
) and 109 properties to be unsat (almost the same as for the source clauses, see columns
$E_5$
) and 109 properties to be unsat (almost the same as for the source clauses, see columns
![]() $E_2$
and
$E_2$
and
![]() $E_6$
).
$E_6$
).
Finally, we have considered the set
![]() $T_{\mathit{wo}}$
, instead of
$T_{\mathit{wo}}$
, instead of
![]() $T_{\mathit{w\& wo}}$
. For the 114 sat properties, Eldarica proved 87 of them (see column
$T_{\mathit{w\& wo}}$
. For the 114 sat properties, Eldarica proved 87 of them (see column
![]() $E_7$
), while Z3 proved 104 of them (see column
$E_7$
), while Z3 proved 104 of them (see column
![]() $Z_7$
). For the unsat properties both Eldarica and Z3 proved all of them (see columns
$Z_7$
). For the unsat properties both Eldarica and Z3 proved all of them (see columns
![]() $E_8$
and
$E_8$
and
![]() $Z_8$
). However, since
$Z_8$
). However, since
![]() $T_{\mathit{wo}}$
computes an overapproximation with respect to
$T_{\mathit{wo}}$
computes an overapproximation with respect to
![]() $T_{\mathit{w\& wo}}$
(and also with respect to
$T_{\mathit{w\& wo}}$
(and also with respect to
![]() $T_{\mathit{w}}$
), when the solver returns the answer unsat, one cannot conclude that the property at hand is indeed unsat. Both solvers, in fact, wrongly classified 10 sat properties as unsat.
$T_{\mathit{w}}$
), when the solver returns the answer unsat, one cannot conclude that the property at hand is indeed unsat. Both solvers, in fact, wrongly classified 10 sat properties as unsat.
In summary, our experimental evaluation shows that VeriCaT
![]() $_{\!\mathit{abs}}$
with Z3 as back-end solver outperforms the other CHC solving tools we have considered. Indeed, our tool shows much higher effectiveness than the others when verifying sat properties, while it retains the excellent performance of Z3 for unsat properties.
$_{\!\mathit{abs}}$
with Z3 as back-end solver outperforms the other CHC solving tools we have considered. Indeed, our tool shows much higher effectiveness than the others when verifying sat properties, while it retains the excellent performance of Z3 for unsat properties.
6 Conclusions and related work
It is well known that the proof of many program properties can be reduced to a proof of satisfiability of sets of CHCs (Bjørner et al., 2015; De Angelis et al., Reference De Angelis, Fioravanti, Gallagher, Hermenegildo, Pettorossi and Proietti2022; Gurfinkel, Reference Gurfinkel2022). In order to make it easier to automatically prove satisfiability, whenever a program is made out of many functions, possibly recursively defined and depending on each other, it is commonly suggested to provide properties also for the auxiliary functions that may occur in the program. Those extra properties basically play the role of lemmas, which often make the proof of a property of interest much easier.
We have focused our study on the automatic proof of properties of programs that compute over ADTs, when these properties can be defined using catamorphisms. In a previous paper (De Angelis et al., Reference De Angelis, Fioravanti, Pettorossi and Proietti2023), we have proposed an algorithm for dealing with a multiplicity of properties of the various program functions to be proved at the same time. In this paper, we have investigated an approach, whereby the auxiliary properties need not be explicitly defined, but it is enough to indicate the catamorphisms involved in their specifications. This leaves to the CHC solver the burden of discovering the suitable auxiliary properties needed for the proof of the property of interest. Thus, this much simpler requirement we make avoids the task of providing all the properties of the auxiliary functions occurring in the program. However, in principle, the proofs of the properties may become harder for the CHC solver. Our experimental evaluation shows that this is not the case if we follow a transformation-based approach. Indeed, the results presented in this paper support the following two-step approach: (1) use algorithm
![]() ${\mathcal{T}}_{\mathit{abs}}$
proposed here to derive a new, transformed set of CHCs from the given initial set of CHCs that translate the program together with its property of interest, and then, (2) use the Z3 solver with global guidance (Krishnan et al., Reference Krishnan, Chen, Shoham and Gurfinkel2020) on the derived set.
${\mathcal{T}}_{\mathit{abs}}$
proposed here to derive a new, transformed set of CHCs from the given initial set of CHCs that translate the program together with its property of interest, and then, (2) use the Z3 solver with global guidance (Krishnan et al., Reference Krishnan, Chen, Shoham and Gurfinkel2020) on the derived set.
We have shown that our approach is a valid alternative to the development of algorithms for extending CHC solvers with special purpose mechanisms that handle ADTs. In fact, recently proposed approaches extend CHC solvers to the case of CHCs over ADTs through the use of various mechanisms such as: (i) the combination with inductive theorem proving (Unno et al., Reference Unno, Torii and Sakamoto2017), (ii) the lemma generation based on syntax-guided synthesis from user-specified templates (Yang et al., Reference Yang, Fedyukovich and Gupta2019), (iii) the invariant discovery based on finite tree automata (Kostyukov et al., Reference Kostyukov, Mordvinov and Fedyukovich2021), and (iv) the use of suitable abstractions on CHCs with recursively defined function symbols (Govind V. K., Shoham, and Gurfinkel, Reference Gurfinkel2022).
One key feature of our algorithm
![]() ${\mathcal{T}}_{\mathit{abs}}$
is that it is sound and complete with respect to satisfiability, that is, the transformed set of CHCs is satisfiable if and only if so is the initial one. In this respect, our results here improve over previous work (De Angelis et al., Reference De Angelis, Fioravanti, Gallagher, Hermenegildo, Pettorossi and Proietti2022), where algorithm
${\mathcal{T}}_{\mathit{abs}}$
is that it is sound and complete with respect to satisfiability, that is, the transformed set of CHCs is satisfiable if and only if so is the initial one. In this respect, our results here improve over previous work (De Angelis et al., Reference De Angelis, Fioravanti, Gallagher, Hermenegildo, Pettorossi and Proietti2022), where algorithm
![]() ${\mathcal{T}}_{\mathit{cata}}$
only preserves soundness, that is, if the transformed set of CHCs is satisfiable, then so is the initial one, while if the transformed set is unsatisfiable, nothing can be inferred for the given set.
${\mathcal{T}}_{\mathit{cata}}$
only preserves soundness, that is, if the transformed set of CHCs is satisfiable, then so is the initial one, while if the transformed set is unsatisfiable, nothing can be inferred for the given set.
In our experiments, we have also realized the usefulness of having more catamorphisms acting together when verifying a specific property. For instance, in the case of the quicksort program, when using the catamorphism
![]() $\mathit{\textit{is \, us asorted}}$
alone, Z3 is unable to show (within the timeout of 600s) sortedness of the output list, while when using also the catamorphisms listmin and listmax, after transformation Z3 proved sortedness in less than 2s. We leave it for future work to automatically derive the catamorphisms that are useful for showing the property of interest, even if they are not strictly necessary for specifying that property.
$\mathit{\textit{is \, us asorted}}$
alone, Z3 is unable to show (within the timeout of 600s) sortedness of the output list, while when using also the catamorphisms listmin and listmax, after transformation Z3 proved sortedness in less than 2s. We leave it for future work to automatically derive the catamorphisms that are useful for showing the property of interest, even if they are not strictly necessary for specifying that property.
Our approach is very much related to abstract interpretation (Cousot and Cousot, Reference Cousot and Cousot1977), which is a methodology for checking properties by interpreting the program as computing over a given abstract domain. Catamorphisms can be seen as specific abstraction functions. Abstract interpretation techniques have been studied also in the field of logic programming. In particular, the CiaoPP preprocessor (Hermenegildo et al., Reference Hermenegildo, Puebla, Bueno and López-García2005) implements abstract interpretation techniques that use type-based norms, which are a special kind of integer-valued catamorphisms. These techniques have important applications in termination analysis (Bruynooghe et al., Reference Bruynooghe, Codish, Gallagher, Genaim and Vanhoof2007) and resource analysis (Albert et al., Reference Albert, Genaim, Gutiérrez and Martin-Martin2020).
Usually, abstract interpretation is the basis for sound analysis techniques by computing an (over-)approximation of the concrete semantics of a program, and hence these techniques may find counterexamples to the properties of interest that hold in the abstract semantics, but that are not feasible in the concrete semantics. As already mentioned, our transformation guarantees the equisatisfiability of the initial and the transformed CHCs, and hence all counterexamples found are feasible in the initial CHCs.
Among the various abstract interpretation techniques, the one which is most related to our verification approach, is the so-called model-based abstract interpretation (Gallagher et al., Reference Gallagher, Boulanger and Saglam1995). This abstract interpretation technique is based on the idea of defining a pre-interpretation, that is, an interpretation of the function symbols of a logic program over a specified domain of interest. That pre-interpretation is used for generating, via abstract compilation (De Angelis et al., Reference De Angelis, Fioravanti, Gallagher, Hermenegildo, Pettorossi and Proietti2022, Sec. 4.3), a domain program whose least model is an abstraction of the least model of the original program. Then, program properties can be inferred from the model of the domain program. One similarity is that pre-interpretations of ADT constructors can be seen as catamorphisms. Actually, our definition of a catamorphism is more general than the one of a pre-interpretation, in that: (i) we admit non-ADT additional parameters as, for instance, in the listcount predicate of our introductory example, and (ii) we allow mutually dependent predicates in the definitions of catamorphisms. Another similarity is that the abstract compilation used by model-based abstract interpretation can be seen as a program transformation and, indeed, it can be implemented by partial evaluation. However, as already mentioned for other abstract interpretation techniques, that transformation does not guarantee equisatisfiability and by using it, one can prove the satisfiability of the original set of clauses, but not its unsatisfiability.
Our transformation-based approach is, to a large extent, parametric with respect to the theory of constraints used in the CHCs. Thus, it can easily be extended to theories different from LIA and Bool used in this paper, and in particular, to other theories such as linear real/rational arithmetic or bit-vectors, as far as they are supported by the CHC solver. This is a potential advantage with respect to those abstract interpretation techniques that require the design of an ad-hoc abstract domain for each specific program analysis.
Acknowledgments
We thank Arie Gurfinkel for helpful suggestions on the use of the Z3 (SPACER) solver. We also thank John Gallagher and the anonymous referees of LOPSTR 2023 for helpful comments on previous versions of the paper. Finally, we express our gratitude to Robert Glück and Bishoksan Kafle for inviting us to write this improved, extended version of our LOPSTR 2023 paper. The authors are members of the INdAM Research Group GNCS.
Competing interests
The authors declare none.


























