I. INTRODUCTION
Wireless power transfer (WPT) is a major trend of the on-going research in electrical, electronics, and telecommunications sciences. Potential applications cover a wide range of fields, including automotive, energy generation, energy harvesting, bio-medical and industrial [Reference Wang, Stielau and Covic1–Reference Hirai, Kim and Kawamura6]. The motivations that bear such a broad set of applications are also many and various. In the automotive industry, for example, electric vehicles have a key impact in the next future. Moreover, in many industrial plants the need for contactless delivery of energy to moving loads is currently being almost mandatory since it allows overcoming limitations in terms of performance, reliability, and machinery maintenance due to the presence of sliding contacts or movable power cords. Solutions designed to replace such hardwired joints with contactless energy transfer (CET) links are widely envisaged in literature and stimulated the interest of many industrial activities, as well as numerous research and academic institutions [Reference Esser and Skudelny7–Reference Sample, Waters, Wisdom and Smith9].
Fortunately, most advances in WPT research can be shared among research groups that work on different topics, thus maximizing the payback of their efforts. Some features, however, require special attentions, and demand for dedicated optimization procedures. Let us consider again the case of industrial applications. Safety, reliability, and electro-magnetic compatibility (EMC) concerns on manufactured assemblies, for instance, dominate over efficiency and miniaturization issues. Nevertheless, on large-scale production, the feasibility and, more important, the cost of assembled products have a foremost impact. In particular, power applications must seriously take into account absolute maximum ratings of components, such as voltages, currents, and operating temperatures. Furthermore, large safety margins should be considered during the development of a brand-new design. Obviously, these considerations also apply to WPT systems. One of the most common technologies employed in WPT is the inductive power transfer (IPT), which relies on the mutual inductance between coils to deliver electrical power without any physical connection. IPT technology well suits a wide range of applications, which rate from a few milliwatts to several of kilowatts [Reference Budhia, Covic and Boys10–Reference Weinberger12]. For high-power systems, the considerations explained above introduce significant differences in the design of a high-power IPT unit. These include ferromagnetic cores, simplified compensation schemes, lower operating frequencies, and stranded wires, just to cite some examples [Reference Papastergiou, Macpherson and Fisher13, Reference Moradewicz and Kazmierkowski14]. As a result, some properties of the IPT device, such as efficiency, geometries, and versatility, are affected. For all these reasons, and in order to account for the different design approaches adopted in power systems, these ones are sometimes named differently, and referred to as CET systems [Reference Moradewicz and Kazmierkowski14–Reference Sibue, Kwimang, Ferrieux and Meunier20]. Cited works emphasize the key aspects of the CET system design, including evaluation of magnetic losses, predicted temperatures, and analysis of the external power supply. In fact, a CET application design includes wider aspects than the sole WPT unit modeling. In particular, the power converter behavior is strongly related to the electrical description of its load (the WPT device, in this case), and the choice of the optimal topology is not a simple task [Reference Papastergiou and Macpherson21]. For that reason, the power supply design must be considered as a constituent element of the entire CET system.
This paper is dedicated to the review of state-of-the art CET systems from the point of view of both theoretical and technological aspects. First, we address the main design roles that differentiate low-power IPT systems from high-power CET systems. Then we will discuss some popular emerging CET applications, their main subsystem-building blocks and their performance compared to the state-of-the-art CET solutions available in the literature.
The remaining of the paper is structured as follows. Section II first introduces the basics of the IPT technology, describes compensation schemes and its figures of merit; in Section III, the CET technology is presented and the differences with IPT emphasized; considerations on efficiency, compensation, and losses are also discussed in Section III. Section IV is dedicated to the critical evaluation of recent available CET systems, by analyzing their building blocks separately; in the last section we summarize the key points and envisage some future research on the discussed topic.
II. INDUCTIVE POWER TRANSFER
The IPT technology for WPT exploits the variation of the magnetic field flux shared among two or more physically decoupled coils to transfer electric power to one, two, or more loads [Reference Covic and Boys11]. Electric transformers are based on inductive coupling too, although are usually designed to transform the voltage, or ensure galvanic separation between circuits, instead of establishing a wireless link for energy transfer.
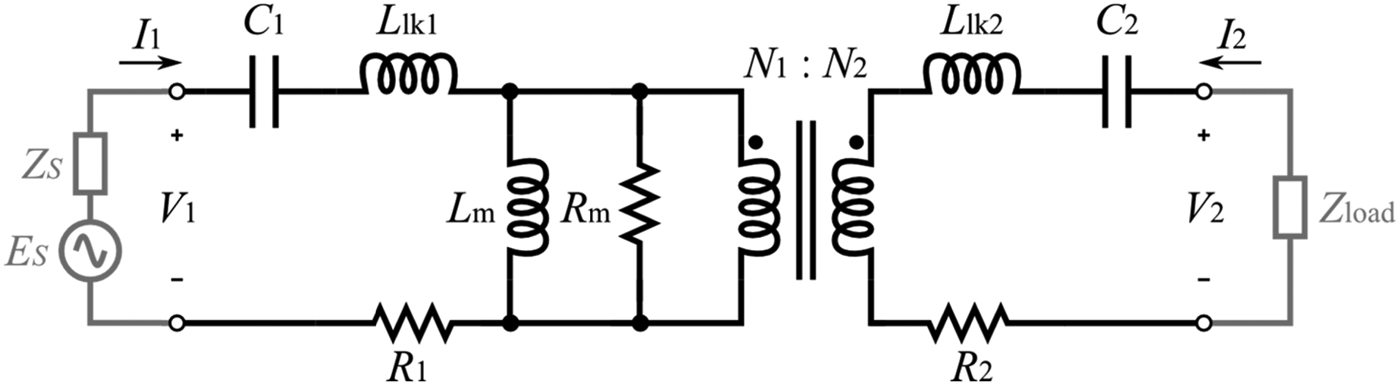
The widely used equivalent representation of an IPT device is based on coupled inductors, and usually also includes compensating (or resonant) capacitances and winding resistances, as show in Fig. 1.

Fig. 1. Power dissipated on the load and IPT device efficiency versus winding inductance (E S = 100 V; Z S = 0 Ω; Q 1, Q 2 = 100; R 1,2∈ [30·10−6, 350]Ω; C 1, C 2 resonant; R load = 50 Ω; k = 0.9; M∈ [9·10−9,9·10−4] H).
IPT systems are sometimes referred to as loosely coupled inductive power transfer (LCIPT) systems, in order to emphasize the fact that the coupling k,
between windings is way far from optimal [Reference Yang, Wang, Zhang and Li22]. As we will show shortly, in these cases the IPT system requires two compensating capacitances (C 1, C 2 in Fig. 1) designed to resonate with the coil inductances L 1, L 2. Coil resistances R 1, R 2 define the Q-factors as follows:
where ω is the radian frequency.
A) Compensation
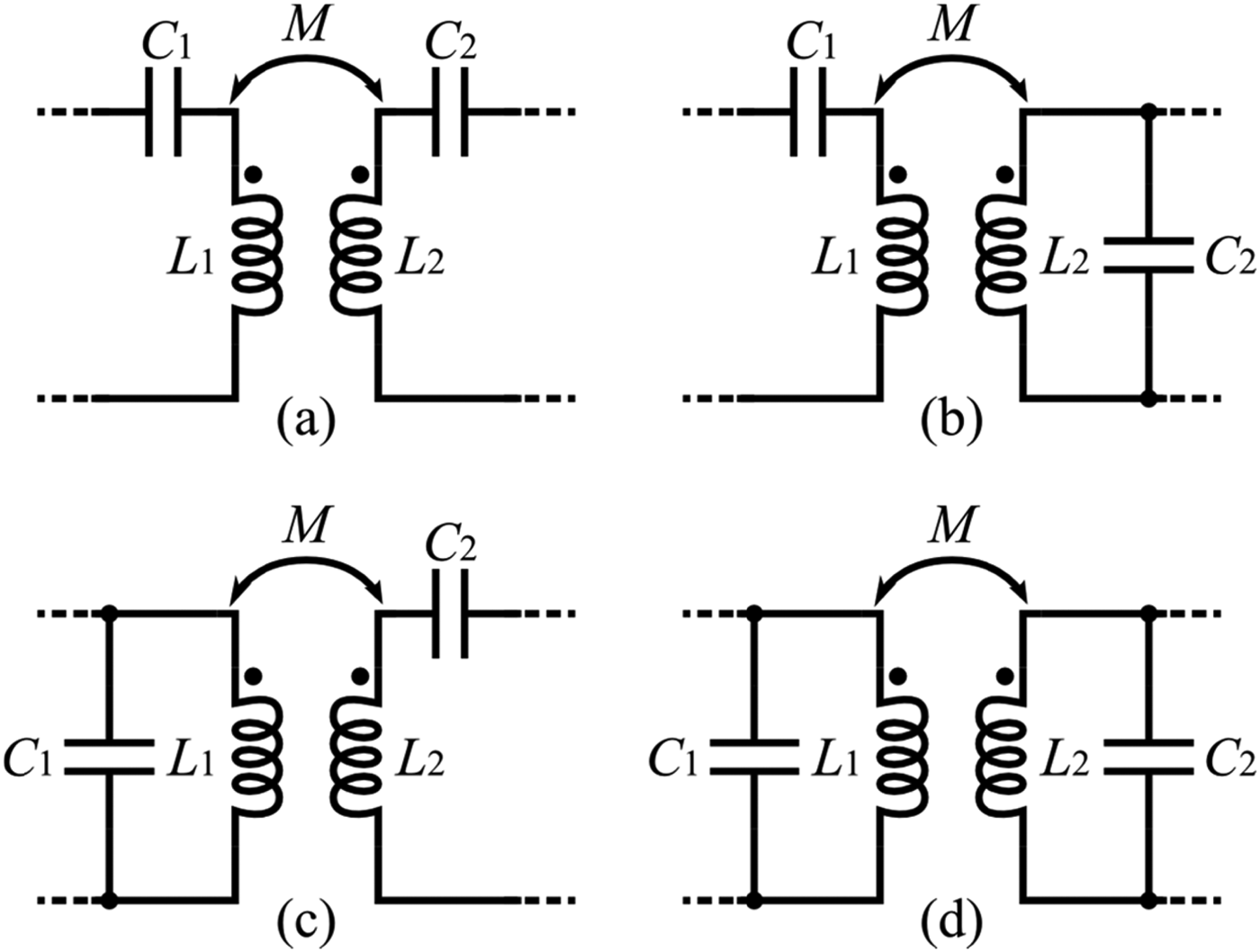
The main goals in the design of an IPT device are its efficiency and its power transfer capability. As described later in this section, in order to reduce losses in the system and maximize the transferred power, the inductance of the coils needs to be compensated [Reference Chen, Chu, Lin and Jou23]. An optimal compensation can be obtained by adding series or parallel capacitances that resonate with the coil inductances. Depending on the characteristics of the selected IPT devices and the constraints on load and source impedances, the optimal configuration of the compensating network (C 1, C 2 in Fig. 1) may vary. In Fig. 2, four possible compensation arrangements are shown. Primary and secondary compensating capacitors (C 1, C 2) are placed either in series (S) or in parallel (P) with the respective self-inductance (L 1, L 2).

Fig. 2. Efficiency versus magnetising inductance for different coupling coefficients in resonant and non-resonant conditions (E S = 100 V; Z S = 0 Ω; N 1 = N 2; Q 1, Q 2 = 100; R 1,2∈ [30·10−6, 350] Ω; R load = 50 Ω; f = 50 kHz, R m → ∞).
Literature provides several guidelines for choosing the best compensating topology, according to the system constraints, in order to maximize the IPT device efficiency or its power transfer capability, providing reliable values for the electrical quantities. As general rules, we can summarize the following considerations:
• If the load is variable, the system requires series primary compensation, since C 1 in SS or SP does not depend on R load [Reference Wang, Covic and Stielau24].
• If the magnetic coupling is variable, the system also requires series secondary compensation, since C 1 and C 2 in SS do not depend on M [Reference Moradewicz and Kazmierkowski14].
• If load and coupling are fixed, the best secondary compensating topology can be chosen according to load value and secondary inductance [Reference Yang, Wang, Zhang and Li22, Reference Kiani and Ghovanloo25].
• If the parasitic parallel capacitance of the windings is not negligible, the system requires parallel compensation, since the parallel resonator can also account for the parasitic capacitance of the coil [Reference Pinuela, Yates, Lucyszyn and Mitcheson26].
• If the real part of the equivalent impedance at the input port of the IPT device is dominated by coil resistances (e.g. dominating winding losses), the system requires parallel compensation, since a parallel capacitance can affect the real part of the equivalent impedance [Reference Low, Chinga, Tseng and Lin27].
Although even more complex compensation networks have been studied, such as adaptive matching [Reference Sample, Waters, Wisdom and Smith9, Reference Waters, Sample and Smith28], and additional self-resonant coils [Reference Chen, Chu, Lin and Jou23, Reference Ahn and Hong29], the SS compensation still represents a widely adopted solution, mainly because of its insensitivity to other parameters such as load and mutual inductance variations [Reference Kazmierkowski and Moradewicz18].
B) Efficiency
According to the previous paragraph, the expression of the efficiency of an IPT device is not unique, but depends on the adopted compensating network configuration. As said, SS compensation, although sub-optimal for certain cases, represents a robust topology, since capacitances only depend on the windings self-inductances L 1, L 2. Thus, let us consider the IPT device of Fig. 1. Its power efficiency η can be expressed as follows:
 $$\eqalign{&\eta=\displaystyle{{P_{load} } \over {P_1 }}=- \displaystyle{{{\mathop{\rm Re}\nolimits} \left[{{\bf V}_2 {\bf I}_2^ \ast } \right]} \over {{\mathop{\rm Re}\nolimits} \left[{{\bf V}_1 {\bf I}_1^ \ast } \right]}} \cr & \quad =\displaystyle{{R_{load} } \over {R_1 \displaystyle{{\left({X_2+X_{load} } \right)^2+\left({R_2+R_{load} } \right)^2 } \over {\omega ^2 M^2 }}+\left({R_2+R_{load} } \right)}}\comma \; }$$
$$\eqalign{&\eta=\displaystyle{{P_{load} } \over {P_1 }}=- \displaystyle{{{\mathop{\rm Re}\nolimits} \left[{{\bf V}_2 {\bf I}_2^ \ast } \right]} \over {{\mathop{\rm Re}\nolimits} \left[{{\bf V}_1 {\bf I}_1^ \ast } \right]}} \cr & \quad =\displaystyle{{R_{load} } \over {R_1 \displaystyle{{\left({X_2+X_{load} } \right)^2+\left({R_2+R_{load} } \right)^2 } \over {\omega ^2 M^2 }}+\left({R_2+R_{load} } \right)}}\comma \; }$$where X 2 = ωL 2–1/(ωC 2), and Z load = R load + jX load. Equation (3) shows that the relationship between efficiency and coupling (expressed by M) as well as between efficiency and resistance of windings (L 1, L 2) is not straightforward. Nevertheless, we can infer that primary resonance (or compensation) does not affect the efficiency, whereas secondary resonance (or compensation) and strong coupling improve the efficiency by “compressing” R 1.
C) Power transfer capability
In a realistic case, the generator introduces a series impedance (Z S ≠ 0 Ω, in Fig. 1), which accounts for additional losses. If the source impedance Z S is given, we may be interested into knowing the maximum available power at the output port of the IPT device. In other words, the power transfer capability should be optimized.
As for the SS topology, the maximum output power on the load is expressed by:
 $$\eqalign{ P_{load}&=- \displaystyle{1 \over 2}{\mathop{\rm Re}\nolimits} \left[{{\bf V}_2 {\bf I}_2^ \ast } \right]\cr &= \displaystyle{{R_{load} } \over 2}\displaystyle{{\left\vert {E_S } \right\vert ^2 } \over {\left\vert {\displaystyle{{\left({Z_S+Z_1 } \right)\left({Z_2+Z_{load} } \right)} \over {\omega M}}+\omega M} \right\vert ^2 }}.}$$
$$\eqalign{ P_{load}&=- \displaystyle{1 \over 2}{\mathop{\rm Re}\nolimits} \left[{{\bf V}_2 {\bf I}_2^ \ast } \right]\cr &= \displaystyle{{R_{load} } \over 2}\displaystyle{{\left\vert {E_S } \right\vert ^2 } \over {\left\vert {\displaystyle{{\left({Z_S+Z_1 } \right)\left({Z_2+Z_{load} } \right)} \over {\omega M}}+\omega M} \right\vert ^2 }}.}$$
In this case, primary and secondary compensations provide a direct advantage in terms of maximum available power at the output port. If we consider purely resistive load and source impedance (i.e. X load = X S = 0 Ω), and the coils are resonant (i.e. ![]() $\omega=\omega _0={1 / {\sqrt {L_1 C_1 } }}={1 / {\sqrt {L_2 C_2 } }}$), equation (4) turns into:
$\omega=\omega _0={1 / {\sqrt {L_1 C_1 } }}={1 / {\sqrt {L_2 C_2 } }}$), equation (4) turns into:
 $$P_{load}=\displaystyle{{R_{load} } \over 2}\displaystyle{{\left\vert {E_S } \right\vert ^2 } \over {\left\vert {\displaystyle{{R_S R_{load} } \over {\omega _0 M}}+\omega _0 M} \right\vert ^2 }}\comma \;$$
$$P_{load}=\displaystyle{{R_{load} } \over 2}\displaystyle{{\left\vert {E_S } \right\vert ^2 } \over {\left\vert {\displaystyle{{R_S R_{load} } \over {\omega _0 M}}+\omega _0 M} \right\vert ^2 }}\comma \;$$
and the power transfer capability is maximized. Further improvements can be achieved if the final load is a design parameter and is not given, by differentiating the second term of equation (5) with respect to ![]() $R_{load} $, as explained in [Reference Chen, Chu, Lin and Jou23].
$R_{load} $, as explained in [Reference Chen, Chu, Lin and Jou23].
III. CONTACTLESS ENERGY TRANSFER
The collection of possible IPT applications covers a wide range of power ratings, from a few milliwatts to several of kilowatts [Reference Budhia, Covic and Boys10–Reference Weinberger12]. As the requirement on the transferred power increases, the system-operating frequency is limited by the switching speed of the power converter [Reference Pedder, Brown and Skinner15]. Figure 3 shows the variations of the output power and of the efficiency with respect to the winding inductances for three configurations of resonant coils at 50, 500, and 5 MHz, respectively. The Q-factor of each coil is held constant (equal to 10), as can be obtained by piecewise optimization of coil and wire geometries, and the winding resistance of each ith-coil computed as

Fig. 3. Power dissipated on the load and IPT device efficiency versus winding inductance (E S = 100 V; Z S = 0 Ω; Q 1, Q 2 = 100 (R 1,2 ∈ [30 μ, 350Ω]); C 1, C 2 resonant; R load = 50 Ω; k = 0.9 (M ∈ [9 × 10−9, 9 × 10−4](H)).
according to equation (2).
As expected, as the frequency decreases, the best efficiency is obtained at higher values of inductance. In these cases, air coils may not be sufficient to achieve the required inductance, and ferromagnetic cores become necessary to limit the dimension of the IPT unit and contain winding losses by increasing the Q-factor.
In the literature, the distinction between IPT and CET is vague. Some works (e.g. [Reference Esser and Nagel30, Reference Theodoridis31]) refer to CET systems to aggregate different WPT technologies in the same device, such as inductive and capacitive power transfer or simply consider WPT systems based on non-inductive devices. However, the CET term should be adopted in place of the IPT one, to indicate systems characterized by strong magnetic coupling (equal to or greater than 0.8, often including magnetic cores) and low operating frequency (from 10 to 500 kHz); this allows high WPT efficiency (usually greater than 70%), and relatively high-power ratings (e.g. more than a kilowatt) [Reference Pedder, Brown and Skinner15, Reference Papastergiou and Macpherson16, Reference Lastowiecki and Staszewski32, Reference Smeets, Krop, Jansen and Lomonova33]. In these cases, the necessity of a contactless transfer of electrical power usually comes from the need of supplying moving parts, such as rotating disks or sliding loads.
The strong coupling and the high Q-values of CET systems are mandatory at high powers not only for preserving the system efficiency but, more important, for ensuring protection from the EMI point of view. This can be obtained by combining two technological realizations:
1. Air gap between coils negligible with respect to their dimensions (e.g. less than a tenth of the coil radius);
2. Coils wound on ferromagnetic cores.
The combination of the two features into the same CET device results into the design of an IPT unit that can be also considered as an electrical transformer [Reference Esser and Skudelny7]. Coils, however, can be differently shaped, in order to feature a proper magnetic circuit for the specific application. Although most systems adopt circular coils, rectangular windings are not uncommon [Reference Smeets, Overboom, Jansen and Lomonova19, Reference Gerrits, Krop, Encica and Lomonova34]. The latters have comparable performance, since at the CET operating frequencies, which lie in the kilohertz range, the conductor edges do not contribute significantly to the overall power losses. The coils shape also defines the geometry of the magnetic core: for circular coils, pot cores are generally employed, whereas for rectangular windings of sliding tracks the core shape can be more arbitrarily chosen. In these cases, E-shaped cores or rectangular blocks of ferromagnetic material can be used to enclose the magnetic flux.
A) Electrical equivalent representation
Because of the similarity between a CET unit and a transformer, the adopted equivalent electrical representation of the device is usually different from the diagram of Fig. 1, and the T-parameter representation visible in Fig. 4 is considered. The leakage inductances L lk1, L lk2 and the magnetizing inductance L m are shown instead of the self-inductances L 1, L 2. In addition, the number of turns of coils N 1, N 2, and the resistance R m, which accounts for losses in the magnetic core, are shown, whereas the other parameters remain unchanged.

Fig. 4. Electrical equivalent representation of the transformer used to model a CET unit.
A quick conversion between the CET representation and the IPT representation of a WPT unit is always possible by using equivalences summarized in Table 1, with the exception of the core resistance R m. In some cases, indeed, as for resonance analysis, the IPT diagram is more convenient.
Table 1. Conversion expressions between CET and IPT representations.

B) Efficiency
Especially when the power rating of the system becomes considerable, the CET design should maximize the efficiency of the IPT unit, rather than its power transfer capability, in order to contain power losses that contribute to the system self-heating. In literature, analytical expressions of the power transfer capability of a CET unit are quite uncommon indeed, whereas efficiency expressions may assume different forms. Forms based on the Q-factors of the coils have the advantage to characterize the system by geometrical and material properties only, although do not implement the dependence on the core resistance R m [Reference Kurschner, Rathge and Jumar35]. Conversely, forms based on the R- and L- parameters of Fig. 4 can include core losses as well [Reference Lastowiecki and Staszewski32, Reference Mecke and Rathge36, Reference Trevisan and Costanzo37]. By adopting the compensation topology of Fig. 4, the CET unit efficiency, as defined in equation (3), can be rewritten as
 $$\eta=\displaystyle{{R_{load} n^2 } \over {{\mathop{\rm Re}\nolimits} \left[{Z_{in} } \right]\, \left\vert {\displaystyle{{\left({R_{load}+Z_2 } \right)n^2 } \over {Z_m }}+1} \right\vert ^2 }}\comma \;$$
$$\eta=\displaystyle{{R_{load} n^2 } \over {{\mathop{\rm Re}\nolimits} \left[{Z_{in} } \right]\, \left\vert {\displaystyle{{\left({R_{load}+Z_2 } \right)n^2 } \over {Z_m }}+1} \right\vert ^2 }}\comma \;$$where
 $$\matrix{ {n=\displaystyle{{N_1 } \over {N_2 }}\comma \; } & {Z_i=j\omega L_{lki}+\displaystyle{1 \over {j\omega C_{lki} }}+R_i\comma \; \quad i=1\comma \; 2\comma \; ...\comma \; } \cr {Z_m=\displaystyle{{j\omega L_m R_m } \over {j\omega L_m+R_m }}\comma \; } & {Z_{in}=Z_1+\displaystyle{{n^2 \left({Z_2+R_{load} } \right)Z_m } \over {n^2 \left({Z_2+R_{load} } \right)+Z_m }}.}}$$
$$\matrix{ {n=\displaystyle{{N_1 } \over {N_2 }}\comma \; } & {Z_i=j\omega L_{lki}+\displaystyle{1 \over {j\omega C_{lki} }}+R_i\comma \; \quad i=1\comma \; 2\comma \; ...\comma \; } \cr {Z_m=\displaystyle{{j\omega L_m R_m } \over {j\omega L_m+R_m }}\comma \; } & {Z_{in}=Z_1+\displaystyle{{n^2 \left({Z_2+R_{load} } \right)Z_m } \over {n^2 \left({Z_2+R_{load} } \right)+Z_m }}.}}$$At resonance frequency ω0, equation (7) can be strongly simplified if we suppose R load ≫ R 2 and neglect core losses. In this particular case, the expression of efficiency turns into
Although core losses should not be neglected in a CET unit, equation (9) confirms that strong coupling, combined with the appropriate compensating network, improves the efficiency, as expected.
C) Compensation
CET systems usually implement capacitive resonance. A high coupling coefficient, however, can partially alleviate the absence of compensation. For example, works presented in [Reference Papastergiou, Macpherson and Fisher13, Reference Sibue, Kwimang, Ferrieux and Meunier20] do not explicitly implement capacitive compensation, thus do not operate at resonance. Figure 5 shows the plots of the efficiency versus the magnetizing inductance for different coupling coefficients in resonant and non-resonant conditions. In these plots, the coils Q factor is held constant; hence, as the inductance increases, the coil resistance increases as well, and the system efficiency begins to decrease after a certain point with a non-symmetrical behavior.

Fig. 5. Efficiency versus magnetizing inductance for different coupling coefficients in resonant and non-resonant conditions (E S = 100 V; Z S = 0 Ω; N 1 = N 2; Q 1, Q 2 = 100 (R 1,2 ∈ [30 μ, 350 Ω]); R load = 50 Ω; f = 50 kHz, R m → ∞).
As can be noted, as the mutual coupling increases, the difference in terms of efficiency between the resonant (compensated) and non-resonant (not compensated) cases becomes smaller. Therefore, a non-resonant design should be considered. In fact, for certain values of inductance and current ratings, the voltage levels across the corresponding resonant capacitor terminals may result prohibitive. To quantify this, we can compute the voltage magnitudes V C across capacitor C 1, under resonance conditions and N 1 = N 2, as:
The corresponding behavior is plotted in Fig. 6, versus the magnetizing inductance, for different source voltages (100, 200, and 300 V) and fixed windings resistance. Fixed resistances can be easily obtained by increasing the conductors effective section. In this case, a symmetrical behavior is observed, since the Q factor varies with the inductance.

Fig. 6. Voltage magnitude across capacitor C 1 versus magnetizing inductance for different source voltages (Z S = 0 Ω; N 1 = N 2; k = 0.9; R 1, R 2 = 0.5 Ω; R load = 50 Ω; f = 50 kHz, R m → ∞).
At 50 kHz, the resonant capacitance for a magnetizing inductance equal to 20 µH is approximately 500 nF. Commercial capacitors of such values can difficultly rate more than a few hundred volts, whereas the computed voltage is well above 1500 V. For this reason, as far as the power factor of the CET unit is not a concern, is not unusual to design high-power IPT systems way far from their resonant frequencies.
D) Losses
Power losses in CET systems cannot be neglected. Although efficiencies of CET units are often above 90%, a few tens of dissipated watts are enough to increase the device temperature to warning levels and put the whole system reliability in jeopardy. Three main factors are responsible for power losses in a CET unit: skin effect and proximity effect in windings, and eddy currents in the core.
1) WINDING LOSSES
The first parasitic element considered is the well-known skin effect, which results in an increase in the wire resistance when ac currents at higher frequencies circulate through them. The skin depth δ is defined as the depth below the surface of the conductor at which the current density J has fallen to 1/e of the current density at the surface J S. In round conductors, it is well approximated as:
 $$\delta=\sqrt {\displaystyle{{2\rho } \over {\omega \mu }}}\comma \;$$
$$\delta=\sqrt {\displaystyle{{2\rho } \over {\omega \mu }}}\comma \;$$where ρ is the resistivity of the conductor, ω is the angular frequency of current, and μ is the absolute magnetic permeability of the conductor.
Wires stacked in layers, the ones above the others, also suffer from the proximity effect that contributes to reduce the effective wire current cross-section due to the induced magnetic field from adjacent conductors [Reference Lotfi and Lee38]. Many works estimate the equivalent ac resistance of windings in magnetic components, when skin effect and proximity effect losses are considerable, such as [Reference Dowell39, Reference Ferreira40]. Generally, a strong reduction of these effects is obtained by adopting stranded wire, also called litz wire. Sullivan in [Reference Sullivan41] proposes a method to optimize the number of strands in a litz wire, by considering wire's thickness as well as core's geometries. Given the dc resistance of the winding, R dc, its dc + ac resistance can be estimated as follows:
 $$R_{ac+dc}=R_{dc} \left({1+\displaystyle{{\pi ^2 \omega ^2 \mu _0^2 N^2 n^2 d_c^6 \gamma } \over {768\rho _c^2 b_c^2 }}} \right).$$
$$R_{ac+dc}=R_{dc} \left({1+\displaystyle{{\pi ^2 \omega ^2 \mu _0^2 N^2 n^2 d_c^6 \gamma } \over {768\rho _c^2 b_c^2 }}} \right).$$In equation (12), the current is supposed sinusoidal and ω is the radian frequency, n the number of strands, N the number of turns, d c the diameter of the copper in each strand, ρ c the resistivity of the copper, b c the breadth of the window area of the core, and γ a factor accounting for non-uniform field distribution in windings, usually equal to one.
Hence, electrical losses of windings, P loss,e, can be computed as follows:
2) CORE LOSSES
Core losses represent a considerable portion of the total losses of a CET unit. The choice of the material employed as ferromagnetic core is essential to prevent an excessive self-heating and ensure high efficiency. The frequency range of CET systems (usually 20–200 kHz) demands for high-resistivity ferromagnetic materials, in order to prevent the circulating of strong eddy currents within the core. Soft ferrites are commonly employed in the frequency range of interest because, despite the lower point of magnetic saturation compared to steel, their high resistivity significantly reduces those parasitic currents. Eddy currents and magnetic hysteresis, both proportional to the B-field (or magnetic flux density), are responsible for magnetic core losses P loss,m within the core. An approximate computation of P loss,m, which includes eddy currents and magnetic hysteresis contributes, is possible thanks to the Steinmetz's equation [Reference Smeets, Krop, Jansen, Hendrix and Lomonova42]:
where V e is the effective volume of the core, ![]() $\hat B$ the peak flux density of a sine wave at frequency f, C m, x, y material constants, and C(T) a temperature correction factor. Such parameters can be derived from materials data sheets or retrieved from available surveys [Reference Steinmetz43, Reference van Horck44]. The peak flux density can be calculated by estimating the magnetizing current i m, or computing the current i m iteratively, due to the dependence of R m on P loss,m. The relation between B and i m is not immediate. However, as explained in [Reference Trevisan and Costanzo45], it can be expressed and approximated (if L lk1 is sufficiently small) as:
$\hat B$ the peak flux density of a sine wave at frequency f, C m, x, y material constants, and C(T) a temperature correction factor. Such parameters can be derived from materials data sheets or retrieved from available surveys [Reference Steinmetz43, Reference van Horck44]. The peak flux density can be calculated by estimating the magnetizing current i m, or computing the current i m iteratively, due to the dependence of R m on P loss,m. The relation between B and i m is not immediate. However, as explained in [Reference Trevisan and Costanzo45], it can be expressed and approximated (if L lk1 is sufficiently small) as:
where ![]() $\hat \iota _m $ is the magnetizing current peak and A e the effective area of the core. Computed P loss,m, the core resistance R m can be approximated by neglecting the leakage inductance L lk1 as:
$\hat \iota _m $ is the magnetizing current peak and A e the effective area of the core. Computed P loss,m, the core resistance R m can be approximated by neglecting the leakage inductance L lk1 as:
From equations (13) and (14) we can straightforwardly evaluate the loss ratio as:
In Fig. 7, these quantities are plotted versus number of turns for a constant output power (900 W) at two different frequencies, 50 and 100 kHz. The ferrite core considered in the analysis is a ®Ferroxcube 3C81 P66 pot core [46].

Fig. 7. Comparison between core and winding loss ratios versus number of turns at different frequencies for a constant output power (V 2 = 300 V; C1, C2 resonant; R load = 50 Ω; k = 0.9; coil radius = 18.5 mm; coil resistance per unit of length = 9.7 mΩ/m; strands number = 50; strand diameter = 0.1 mm; core window breadth = 10.6 mm; core reluctance = 9.8 × 10−5 turns2/H; ferrite = ®Ferroxcube 3C91; effective area = 717 mm2; effective volume = 88 200 mm3).
From the picture it is evident how the computation of the optimal trade-off among several design parameters, such as number of turns, frequency, and core type, is not immediate ad may require to be evaluated iteratively.
IV. CET SYSTEMS
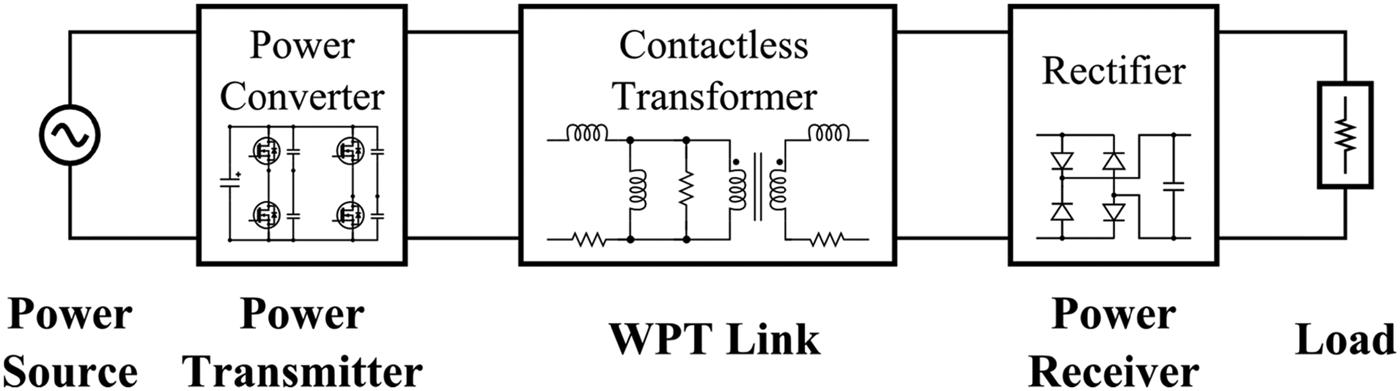
Figure 8 shows an overview of a CET system, represented by several building blocks.

Fig. 8. Overview of a CET system.
In a CET system, the primary source of energy is usually the mains. A switching-mode power supply is used to convert the mains frequency up to tens of kHz and acts as power transmitter for the WPT link. The inductive CET unit (i.e. a contactless transformer, in this case) constitutes the WPT link and the power receiver is often represented by an ac/dc power converter, or rectifying stage. Sometimes, the ac/dc conversion is unnecessary, and the final load is directly connected to the WPT link and represents the power receiver itself.
A) Power transmitter
In order to contain the size of the magnetic core, thus preventing its saturation, the mains 50-(or 60-) Hz voltage should be switched at a higher frequency. The direct generation of a pure sine wave is almost impossible at power ratings of CET systems. In these cases, the widely employed solution is represented by switching mode power supplies (SMPS). The state-of-the-art SMPS adopt soft-switching techniques in order to alleviate turn-on and turn-off losses of the switching network, theoretically extending the devices lifetime and avoiding possible electromagnetic interference (EMI) [Reference Lu, Cheng and Lee47, Reference Jovanovic and Jang48]. Soft-switching techniques rely on inductive loads to achieve zero-voltage or zero-current commutation of the switches [Reference Mohan, Undeland and Robbins49, Reference Erickson and Maksimovic50]. For high-power and high-frequency operation, zero-voltage switching (ZVS) converters are preferred over zero-current switching (ZCS) ones, because the parasitic elements of switching components facilitate the soft-switching mechanism [Reference Patterson and Divan51].
The presence of an inductive element (i.e. WPT link) suggests that the contactless transformer itself can be used to store the energy controlled by the converter. Authors of [Reference Papastergiou and Macpherson21], for example, propose a phase-shift ZVS full-bridge converter that exploits the inductive equivalent input impedance of the transformer and four parallel capacitances to achieve soft switching of active elements. Differently, the work presented in [Reference Valtchev, Borges, Brandisky and Klaassens17] introduces primary compensation and exploits this capacitance to realize a resonant tank that eases the resonant process of the converter.
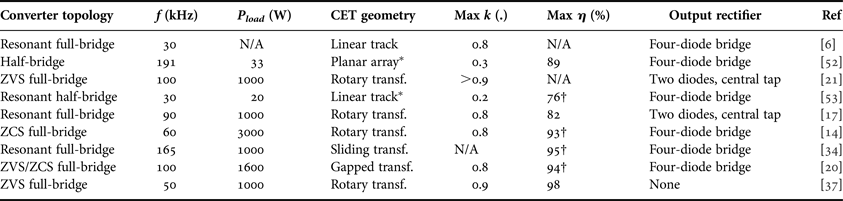
Table 2 shows comparisons of some state-of-the-art CET systems considered in this review. The adopted power converter topologies are shown, as well as system ratings, geometry of magnetic circuits (discussed next), and specifications of power receivers.
Table 2. CET systems comparison.

*Not a proper CET system (as intended in this work) due to the weak coupling.
†Includes power electronics efficiency.
B) WPT link
The WPT link represents the core of the system. In previous paragraphs, we described the theory of operation of a CET unit. In the following, instead, we present two different implementations of the IPT device widely discussed in CET-related literature: the sliding transformer and the rotary transformer.
1) LINEAR TRANSFORMER
The description of a CET system based on a linear transformer is formally introduced in [Reference Lastowiecki and Staszewski32], though studied in numerous other works, such as [Reference Hirai, Kim and Kawamura6, Reference Lin, Lin, Chang, Li and Chen53, Reference van der Pijl, Castilla and Bauer54]. A linear transformer, is composed by a linear track that constitutes a long magnetic primary circuit, or a long primary winding loop, and one or more secondary winding wound about a “magnetic pickup” free to move on the linear track, as shown in Fig. 9(a).

Fig. 9. Three-dimensional (3D) representations of (a) a linear transformer as in [32]; and (b) a sliding transformer as in [34].
As described in [Reference Gerrits, Krop, Encica and Lomonova34, Reference Smeets, Overboom, Jansen and Lomonova55], for example, the sliding transformer can also be intended differently. Authors of cited works propose a sliding transformer in which the primary track is segmented into several primary coils wound about several core blocks, and some secondary pickups that face primary coils along a secondary parallel track, as depicted in Fig. 9(b). This way, magnetic leakage and ohmic losses can be reduced, and the efficiency improved.
Finally, planar array geometry can be derived from the sliding transformer, as proposed in [Reference de Boeij, Lomonova and Vandenput56]. Similarly to a segmented primary linear track, several primary coils are distributed over a 2D surface, and a secondary pickup is free to move along two axes.
Typical applications of linear transformers are represented by electrical delivery systems for planar moving platforms. Some examples are drive belts, linearly moving motors, and power rails.
2) ROTARY TRANSFORMER
A rotary (or rotatable) transformer design represents one of the first implementation of a CET system [Reference Esser and Skudelny7, Reference Weinberger12]. Rotatable transformers are usually based on pot-core ferrite cores. A pot-core transformer is composed by two separate half cores, as shown in Fig. 10.

Fig. 10. (a) Three-dimensional (3D) representation of two half pot cores and their magnetic flux lines as in [37]; (b) prototyped version of a pot-core transformer with air gap as in [45].
In a standard application, a pot-core transformer encloses two windings wrapped about its central leg and a through-hole screw, or an external spring, tightens the half cores together. Conversely, pot cores for CET applications exploit the physical separation of the halves to allow the rotation of the one with respect to the other. Physical separation is obtained by ensuring an air gap between the halves.
In order to allow relative rotation, the windings must be detached as well. Two different winding topologies are possible, either adjacent windings or coaxial windings [Reference Papastergiou and Macpherson57]. In the former topology each winding is placed in its own half core, whereas in the latter windings are concentric. Many works compare the two different topologies, e.g. [Reference Smeets, Encica and Lomonova58]. Depending upon the final application, the one might be more favorable than the other. On the one hand, for example, the adjacent topology exploits the available room for windings in the window area of the core more efficiently, resulting in a lower magnetizing current and, in turn, lower losses. On the other hand, coaxial windings share the whole magnetic flux path of the transformer, resulting in lower leakage inductances and therefore higher coupling coefficient.
Typical applications of rotatable transformers are meant to replace rotary electrical joints, also known as slip rings. Such joints have wide use in both industrial and military areas, for example in robot arms, rotary working tools (as drilling machines, or sealers), and radars. For instance in [Reference Trevisan and Costanzo37, Reference Trevisan and Costanzo45], a CET system has been prototyped for power supplying rotatable parts of automatic machineries, namely sealing rollers. The system performance is reported and compared in Table 2. The design of the CET unit is optimized in terms of (i) wires geometries, in this implementation litz wires are adopted to minimize losses; (ii) number of turns; (iii) ferrite type. This way, the optimal trade-off between core and winding losses is realized by adopting analytical analyses presented in Section III.D and numerical simulations. At the stationary side, a power board implements soft-switching techniques, as specified in Table 2, which contributes to further reducing the overall system losses.
C) Power receiver
The power receiver usually implements a rectifying stage. The ac/dc conversion is necessary when the system load operates in the dc regime, such as batteries, logics, or dc drives. In these cases, the rectifier is constituted by a four-diode bridge or, alternatively, a two-diode bridge if the CET unit provides for a central tap. Authors of [Reference Madawala and Thrimawithana59] propose a “reversible rectifier,” instead, to allow bidirectional energy flow. Differently, when the system load is resistive, (a heater or a sealer, for example, as in [Reference Trevisan and Costanzo37]), the ac/dc conversion may be unnecessary if the resulting parasitic load reactance is negligible at the operating frequency.
V. CONCLUSION
In this paper, we have provided a deep discussion on the actual performances and challenges of the CET system design. Starting from an equivalent electrical representation of a WPT unit, we have first defined the main figures of merit, in terms of end-to-end efficiency and maximum power that can be transferred. Then we have considered possible combinations of compensating capacitive networks and critically discussed them with respect to the power levels involved. We have shown that the resonant condition of the wireless link is not always the best solution, but the transmitter and receiver mutual coupling needs to be included in such design considerations. We have proposed a formal definition of CET systems, in order to differentiate it from IPT in the context of WPT. In fact, applications that rate more than a kilowatt usually lay in the scope of CET, rather than IPT, because of the stronger coupling and higher inductance values required for reducing power losses and contain the dimensions of the WPT unit. We explained that capacitive compensation may be difficult to be implemented, due to high-voltage levels on capacitors. Thus, because of the tiny disadvantage in terms of efficiency for highly coupled systems, a non-resonant design of the CET device can be considered. On the contrary, power losses represent a major issue on CET units, because of the resulting increase in the device temperature. Seeking optimal trade-off between winding losses and core losses is essential in order to ensure best CET performance and reliability over time. This, however, requires a fine-tuning of several design parameters, such as core geometries, wire choice, frequency, and number of turns.
Finally, we reviewed and compared some state-of-the-art CET systems presented in recent literature. The system key parts, which are power transmitter, WPT link, and power receiver were analyzed separately. In particular, two main WPT link topologies can be found in literature: linear transformer (used with sliding loads) and rotary transformer (used with rotatable loads). Further sub-topologies make the CET system design even more challenging and should be deeply evaluated before prototyping.
Scientific and industrial interest on CET systems is growing, because this technology enables to overcome the severe limitations imposed by sliding or rotatable electrical joints at high-power levels. The scope of CET systems, however, is not limited to power transfer applications. In many cases, one or more feedback signals are required to be sent back from the moving load to the controlling/supplying unit. Therefore, a combined wireless power and information transfer problem arise. Some works already address this issue by combining multiple coils (e.g. power and information windings) in the same core, such as [Reference Bieler, Perrottet, Nguyen and Perriard60]. Other works, as [Reference Hirai, Kim and Kawamura6, Reference Kawamura, Ishioka and Hirai61], propose to modulate the data over the power signal. In either case, the research on CET systems is still far from conclusion, and further challenges are about to arise in the next years.
ACKNOWLEDGEMENTS
This work was partly supported by the R&D department of IMA Industries Srl, Bologna, Italy.