1 Introduction
Generalized quadrangles are point–line incidence geometries introduced by Tits [Reference Tits25] in an attempt to find geometric models for simple groups of Lie type. The classical generalized quadrangles arise in this way [Reference Payne and Thas21, Section 3]. Each admits one of the simple classical groups
![]() $T=\text{PSp}(4,q)\cong \unicode[STIX]{x1D6FA}_{5}(q)$
,
$T=\text{PSp}(4,q)\cong \unicode[STIX]{x1D6FA}_{5}(q)$
,
![]() $\text{PSU}(4,q)\cong \text{P}\unicode[STIX]{x1D6FA}_{6}^{-}(q)$
or
$\text{PSU}(4,q)\cong \text{P}\unicode[STIX]{x1D6FA}_{6}^{-}(q)$
or
![]() $\text{PSU}(5,q)$
acting transitively on flags (incident point–line pairs). Moreover, the point and line stabilizers are certain maximal subgroups of
$\text{PSU}(5,q)$
acting transitively on flags (incident point–line pairs). Moreover, the point and line stabilizers are certain maximal subgroups of
![]() $T$
, so
$T$
, so
![]() $T$
acts primitively on both points and lines. The classification of flag-transitive generalized quadrangles is a long-standing open problem. In addition to the classical families, only two other flag-transitive examples are known, up to point–line duality, with each admitting an affine group acting point-primitively but line-imprimitively. Hence, all of the known flag-transitive generalized quadrangles are also point-primitive (up to duality), and so it is natural to seek a classification of the point-primitive examples. Indeed, this is arguably a more difficult problem, because one begins with essentially no information about the action of the collineation group on lines, nor any notion of what “incidence” means, whereas in a flag-transitive point–line geometry, points and lines correspond to cosets of certain subgroups of the collineation group, and incidence is determined by nonempty intersection of these cosets.
$T$
acts primitively on both points and lines. The classification of flag-transitive generalized quadrangles is a long-standing open problem. In addition to the classical families, only two other flag-transitive examples are known, up to point–line duality, with each admitting an affine group acting point-primitively but line-imprimitively. Hence, all of the known flag-transitive generalized quadrangles are also point-primitive (up to duality), and so it is natural to seek a classification of the point-primitive examples. Indeed, this is arguably a more difficult problem, because one begins with essentially no information about the action of the collineation group on lines, nor any notion of what “incidence” means, whereas in a flag-transitive point–line geometry, points and lines correspond to cosets of certain subgroups of the collineation group, and incidence is determined by nonempty intersection of these cosets.
Here we prove the following theorem. The abbreviations HS (holomorph simple), HC (holomorph compound), SD (simple diagonal), CD (compound diagonal), PA (product action), AS (almost simple) and TW (twisted wreath) refer to the possible types of nonaffine primitive permutation group actions, in the sense of the O’Nan–Scott theorem as stated in [Reference Praeger, Li, Niemeyer, Hahn and Sabidussi22, Section 6]. In the second column of Table 1,
![]() $\text{soc}(G)$
denotes the socle of the group
$\text{soc}(G)$
denotes the socle of the group
![]() $G$
, namely the subgroup generated by its minimal normal subgroups. By
$G$
, namely the subgroup generated by its minimal normal subgroups. By
![]() $\text{fix}_{\unicode[STIX]{x1D6FA}}(h)$
we mean the number of elements fixed by a permutation
$\text{fix}_{\unicode[STIX]{x1D6FA}}(h)$
we mean the number of elements fixed by a permutation
![]() $h$
of the set
$h$
of the set
![]() $\unicode[STIX]{x1D6FA}$
, and
$\unicode[STIX]{x1D6FA}$
, and
![]() $\mathsf{Q}^{-}(5,2)$
denotes the unique generalized quadrangle of order
$\mathsf{Q}^{-}(5,2)$
denotes the unique generalized quadrangle of order
![]() $(2,4)$
. Note also that, in the notation for finite simple groups of Lie type used in Table 1 (and throughout the paper),
$(2,4)$
. Note also that, in the notation for finite simple groups of Lie type used in Table 1 (and throughout the paper),
![]() $\unicode[STIX]{x1D700}=\pm$
and
$\unicode[STIX]{x1D700}=\pm$
and
![]() $\text{A}_{n}^{+}=\text{A}_{n}$
,
$\text{A}_{n}^{+}=\text{A}_{n}$
,
![]() $\text{A}_{n}^{-}=^{2}\text{A}_{n}$
,
$\text{A}_{n}^{-}=^{2}\text{A}_{n}$
,
![]() $\text{D}_{n}^{+}=\text{D}_{n}$
,
$\text{D}_{n}^{+}=\text{D}_{n}$
,
![]() $\text{D}_{n}^{-}=^{2}\text{D}_{n}$
,
$\text{D}_{n}^{-}=^{2}\text{D}_{n}$
,
![]() $\text{E}_{6}^{+}=\text{E}_{6}$
,
$\text{E}_{6}^{+}=\text{E}_{6}$
,
![]() $\text{E}_{6}^{-}=^{2}\text{E}_{6}$
.
$\text{E}_{6}^{-}=^{2}\text{E}_{6}$
.
Theorem 1.1. If
![]() ${\mathcal{Q}}$
is a thick finite generalized quadrangle with a nonaffine collineation group
${\mathcal{Q}}$
is a thick finite generalized quadrangle with a nonaffine collineation group
![]() $G$
that acts primitively on the point set
$G$
that acts primitively on the point set
![]() ${\mathcal{P}}$
of
${\mathcal{P}}$
of
![]() ${\mathcal{Q}}$
, then the action of
${\mathcal{Q}}$
, then the action of
![]() $G$
on
$G$
on
![]() ${\mathcal{P}}$
does not have O’Nan–Scott type HC, and the conditions in Table 1 hold for the remaining O’Nan–Scott types.
${\mathcal{P}}$
does not have O’Nan–Scott type HC, and the conditions in Table 1 hold for the remaining O’Nan–Scott types.
Table 1. Conditions for Theorem 1.1. Here
![]() $T$
is a nonabelian finite simple group,
$T$
is a nonabelian finite simple group,
![]() $k\geqslant 2$
and
$k\geqslant 2$
and
![]() $r\geqslant 2$
. If
$r\geqslant 2$
. If
![]() $G$
acts primitively of type CD (resp. PA) on
$G$
acts primitively of type CD (resp. PA) on
![]() ${\mathcal{P}}$
, then
${\mathcal{P}}$
, then
![]() $G\leqslant H\wr \text{Sym}_{r}$
for some primitive group
$G\leqslant H\wr \text{Sym}_{r}$
for some primitive group
![]() $H\leqslant \text{Sym}(\unicode[STIX]{x1D6FA})$
of type SD (resp. AS) with socle
$H\leqslant \text{Sym}(\unicode[STIX]{x1D6FA})$
of type SD (resp. AS) with socle
![]() $T^{k}$
(resp.
$T^{k}$
(resp.
![]() $T$
).
$T$
).

Before we proceed, a remark is in order about the assumption in Theorem 1.1 that
![]() $G$
not be an affine group. If
$G$
not be an affine group. If
![]() $G$
is affine, then the generalized quadrangle
$G$
is affine, then the generalized quadrangle
![]() ${\mathcal{Q}}$
necessarily arises from a so-called pseudo-hyperoval in a projective space
${\mathcal{Q}}$
necessarily arises from a so-called pseudo-hyperoval in a projective space
![]() $\text{PG}(3n-1,q)$
with
$\text{PG}(3n-1,q)$
with
![]() $q$
even [Reference De Winter and Thas12]. In joint work with Glasby [Reference Bamberg, Glasby, Popiel and Praeger6], we were able to classify the generalized quadrangles admitting an affine group that acts primitively on points and transitively on lines: they are precisely the two flag-transitive, point-primitive, line-imprimitive generalized quadrangles mentioned above. However, without the extra assumption of transitivity on lines, the problem is equivalent to the classification of the pseudo-hyperovals that have an irreducible stabilizer. As explained in [Reference Bamberg, Glasby, Popiel and Praeger6, Remark 1.3], this latter problem would appear to be extremely difficult, and possibly intractable. It also has a rather different flavor to the cases treated in the present paper, and so we do not consider it further here.
$q$
even [Reference De Winter and Thas12]. In joint work with Glasby [Reference Bamberg, Glasby, Popiel and Praeger6], we were able to classify the generalized quadrangles admitting an affine group that acts primitively on points and transitively on lines: they are precisely the two flag-transitive, point-primitive, line-imprimitive generalized quadrangles mentioned above. However, without the extra assumption of transitivity on lines, the problem is equivalent to the classification of the pseudo-hyperovals that have an irreducible stabilizer. As explained in [Reference Bamberg, Glasby, Popiel and Praeger6, Remark 1.3], this latter problem would appear to be extremely difficult, and possibly intractable. It also has a rather different flavor to the cases treated in the present paper, and so we do not consider it further here.
Let us now establish some definitions and notation, before discussing further. By a point–line incidence geometry we mean a triple
![]() $\unicode[STIX]{x1D6E4}=({\mathcal{P}},{\mathcal{L}},\text{I})$
, where
$\unicode[STIX]{x1D6E4}=({\mathcal{P}},{\mathcal{L}},\text{I})$
, where
![]() ${\mathcal{P}}$
and
${\mathcal{P}}$
and
![]() ${\mathcal{L}}$
are sets whose elements are called points and lines, respectively, and
${\mathcal{L}}$
are sets whose elements are called points and lines, respectively, and
![]() $\text{I}\subseteq {\mathcal{P}}\times {\mathcal{L}}$
is a symmetric binary relation called incidence. We sometimes write
$\text{I}\subseteq {\mathcal{P}}\times {\mathcal{L}}$
is a symmetric binary relation called incidence. We sometimes write
![]() $\unicode[STIX]{x1D6E4}=({\mathcal{P}},{\mathcal{L}})$
instead of
$\unicode[STIX]{x1D6E4}=({\mathcal{P}},{\mathcal{L}})$
instead of
![]() $({\mathcal{P}},{\mathcal{L}},\text{I})$
, when we do not need to refer to the incidence relation explicitly. Two points (resp. lines) of
$({\mathcal{P}},{\mathcal{L}},\text{I})$
, when we do not need to refer to the incidence relation explicitly. Two points (resp. lines) of
![]() $\unicode[STIX]{x1D6E4}$
are said to be collinear (resp. concurrent) if they are incident with a common line (resp. point). A collineation of
$\unicode[STIX]{x1D6E4}$
are said to be collinear (resp. concurrent) if they are incident with a common line (resp. point). A collineation of
![]() $\unicode[STIX]{x1D6E4}$
is a permutation of
$\unicode[STIX]{x1D6E4}$
is a permutation of
![]() ${\mathcal{P}}\cup {\mathcal{L}}$
that preserves
${\mathcal{P}}\cup {\mathcal{L}}$
that preserves
![]() ${\mathcal{P}}$
and
${\mathcal{P}}$
and
![]() ${\mathcal{L}}$
setwise and preserves the incidence relation. By a collineation group of
${\mathcal{L}}$
setwise and preserves the incidence relation. By a collineation group of
![]() $\unicode[STIX]{x1D6E4}$
we mean a subgroup of the group of all collineations of
$\unicode[STIX]{x1D6E4}$
we mean a subgroup of the group of all collineations of
![]() $\unicode[STIX]{x1D6E4}$
, which is called the full collineation group.
$\unicode[STIX]{x1D6E4}$
, which is called the full collineation group.
A generalized quadrangle is a point–line incidence geometry
![]() ${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}})$
that satisfies the following two axioms: (i) two distinct points are incident with at most one common line, and (ii) given a point
${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}})$
that satisfies the following two axioms: (i) two distinct points are incident with at most one common line, and (ii) given a point
![]() $P$
and a line
$P$
and a line
![]() $\ell$
not incident with
$\ell$
not incident with
![]() $P$
, there exists a unique point incident with
$P$
, there exists a unique point incident with
![]() $\ell$
that is collinear with
$\ell$
that is collinear with
![]() $P$
. The second axiom implies that every pair in
$P$
. The second axiom implies that every pair in
![]() ${\mathcal{P}}\cup {\mathcal{L}}$
is contained in an ordinary quadrangle, and that
${\mathcal{P}}\cup {\mathcal{L}}$
is contained in an ordinary quadrangle, and that
![]() ${\mathcal{Q}}$
contains no triangles. All generalized quadrangles considered in this paper are assumed to be finite, in the sense that
${\mathcal{Q}}$
contains no triangles. All generalized quadrangles considered in this paper are assumed to be finite, in the sense that
![]() ${\mathcal{P}}$
and
${\mathcal{P}}$
and
![]() ${\mathcal{L}}$
are finite sets. If every point is incident with at least three lines, and every line is incident with at least three points, then
${\mathcal{L}}$
are finite sets. If every point is incident with at least three lines, and every line is incident with at least three points, then
![]() ${\mathcal{Q}}$
is said to be thick. In this case, there exist constants
${\mathcal{Q}}$
is said to be thick. In this case, there exist constants
![]() $s\geqslant 2$
and
$s\geqslant 2$
and
![]() $t\geqslant 2$
such that every point is incident with exactly
$t\geqslant 2$
such that every point is incident with exactly
![]() $t+1$
lines and every line is incident with exactly
$t+1$
lines and every line is incident with exactly
![]() $s+1$
points [Reference Van Maldeghem26, Corollary 1.5.3]. The pair
$s+1$
points [Reference Van Maldeghem26, Corollary 1.5.3]. The pair
![]() $(s,t)$
is called the order of
$(s,t)$
is called the order of
![]() ${\mathcal{Q}}$
. Observe also that there is a natural concept of point–line duality for generalized quadrangles: if
${\mathcal{Q}}$
. Observe also that there is a natural concept of point–line duality for generalized quadrangles: if
![]() $({\mathcal{P}},{\mathcal{L}})$
is a generalized quadrangle, then so is
$({\mathcal{P}},{\mathcal{L}})$
is a generalized quadrangle, then so is
![]() $({\mathcal{L}},{\mathcal{P}})$
; and if
$({\mathcal{L}},{\mathcal{P}})$
; and if
![]() $({\mathcal{P}},{\mathcal{L}})$
has order
$({\mathcal{P}},{\mathcal{L}})$
has order
![]() $(s,t)$
, then
$(s,t)$
, then
![]() $({\mathcal{L}},{\mathcal{P}})$
has order
$({\mathcal{L}},{\mathcal{P}})$
has order
![]() $(t,s)$
.
$(t,s)$
.
Let us now discuss Theorem 1.1 further. The primitive permutation groups on a finite set
![]() $\unicode[STIX]{x1D6E5}$
are classified into eight types according to the O’Nan–Scott Theorem as presented in [Reference Praeger, Li, Niemeyer, Hahn and Sabidussi22, Section 6]. In 2012, Bamberg et al. [Reference Bamberg, Giudici, Morris, Royle and Spiga5] showed that if a thick finite generalized quadrangle admits a collineation group
$\unicode[STIX]{x1D6E5}$
are classified into eight types according to the O’Nan–Scott Theorem as presented in [Reference Praeger, Li, Niemeyer, Hahn and Sabidussi22, Section 6]. In 2012, Bamberg et al. [Reference Bamberg, Giudici, Morris, Royle and Spiga5] showed that if a thick finite generalized quadrangle admits a collineation group
![]() $G$
that acts primitively on both points and lines, then
$G$
that acts primitively on both points and lines, then
![]() $G$
must be an almost simple (AS type) group. That is,
$G$
must be an almost simple (AS type) group. That is,
![]() $G$
must satisfy
$G$
must satisfy
![]() $T\leqslant G\leqslant \operatorname{Aut}(T)$
for some nonabelian finite simple group
$T\leqslant G\leqslant \operatorname{Aut}(T)$
for some nonabelian finite simple group
![]() $T$
. Given that there exist point-primitive generalized quadrangles that are line-transitive but line-imprimitive, our initial aim was to extend the result of [Reference Bamberg, Giudici, Morris, Royle and Spiga5] by relaxing the line-primitivity assumption to line-transitivity. In addition to handling the affine (HA type) case with Glasby [Reference Bamberg, Glasby, Popiel and Praeger6], we were also able to show that no such examples arise if the point action has type HS or HC [Reference Bamberg, Popiel and Praeger8].
$T$
. Given that there exist point-primitive generalized quadrangles that are line-transitive but line-imprimitive, our initial aim was to extend the result of [Reference Bamberg, Giudici, Morris, Royle and Spiga5] by relaxing the line-primitivity assumption to line-transitivity. In addition to handling the affine (HA type) case with Glasby [Reference Bamberg, Glasby, Popiel and Praeger6], we were also able to show that no such examples arise if the point action has type HS or HC [Reference Bamberg, Popiel and Praeger8].
Theorem 1.1 significantly strengthens and expands upon the results of [Reference Bamberg, Giudici, Morris, Royle and Spiga5], [Reference Bamberg, Popiel and Praeger8]. The idea behind its proof begins with the following observations. A primitive group
![]() $G\leqslant \text{Sym}(\unicode[STIX]{x1D6E5})$
of O’Nan–Scott type HC, CD, PA or TW preserves a Cartesian product decomposition
$G\leqslant \text{Sym}(\unicode[STIX]{x1D6E5})$
of O’Nan–Scott type HC, CD, PA or TW preserves a Cartesian product decomposition
![]() $\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6FA}^{r}$
, for some set
$\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6FA}^{r}$
, for some set
![]() $\unicode[STIX]{x1D6FA}$
and some
$\unicode[STIX]{x1D6FA}$
and some
![]() $r\geqslant 2$
. Therefore, in studying point-primitive generalized quadrangles, we are led in particular to consider generalized quadrangles with collineation groups that preserve a Cartesian product decomposition of the point set. The following theorem shows that the number of factors of such a decomposition becomes severely restricted under a fairly generic assumption on the group. Here a semiregular permutation group action is one in which only the identity element fixes a point, and if
$r\geqslant 2$
. Therefore, in studying point-primitive generalized quadrangles, we are led in particular to consider generalized quadrangles with collineation groups that preserve a Cartesian product decomposition of the point set. The following theorem shows that the number of factors of such a decomposition becomes severely restricted under a fairly generic assumption on the group. Here a semiregular permutation group action is one in which only the identity element fixes a point, and if
![]() $H_{1},\ldots ,H_{r}$
are permutation groups on sets
$H_{1},\ldots ,H_{r}$
are permutation groups on sets
![]() $\unicode[STIX]{x1D6FA}_{1},\ldots ,\unicode[STIX]{x1D6FA}_{r}$
, respectively, then the product action of the direct product
$\unicode[STIX]{x1D6FA}_{1},\ldots ,\unicode[STIX]{x1D6FA}_{r}$
, respectively, then the product action of the direct product
![]() $\prod _{i=1}^{r}H_{i}$
on the Cartesian product
$\prod _{i=1}^{r}H_{i}$
on the Cartesian product
![]() $\prod _{i=1}^{r}\unicode[STIX]{x1D6FA}_{i}$
is the action
$\prod _{i=1}^{r}\unicode[STIX]{x1D6FA}_{i}$
is the action
![]() $(\unicode[STIX]{x1D714}_{1},\ldots ,\unicode[STIX]{x1D714}_{r})^{(h_{1},\ldots ,h_{r})}=(\unicode[STIX]{x1D714}_{1}^{h_{1}},\ldots ,\unicode[STIX]{x1D714}_{r}^{h_{r}})$
. We also recall that a permutation group is said to act regularly if it acts transitively and semiregularly.
$(\unicode[STIX]{x1D714}_{1},\ldots ,\unicode[STIX]{x1D714}_{r})^{(h_{1},\ldots ,h_{r})}=(\unicode[STIX]{x1D714}_{1}^{h_{1}},\ldots ,\unicode[STIX]{x1D714}_{r}^{h_{r}})$
. We also recall that a permutation group is said to act regularly if it acts transitively and semiregularly.
Theorem 1.2. Let
![]() $\unicode[STIX]{x1D6FA}_{1},\ldots ,\unicode[STIX]{x1D6FA}_{r}$
be finite sets with
$\unicode[STIX]{x1D6FA}_{1},\ldots ,\unicode[STIX]{x1D6FA}_{r}$
be finite sets with
![]() $2\leqslant |\unicode[STIX]{x1D6FA}_{1}|\leqslant \cdots \leqslant |\unicode[STIX]{x1D6FA}_{r}|$
, where
$2\leqslant |\unicode[STIX]{x1D6FA}_{1}|\leqslant \cdots \leqslant |\unicode[STIX]{x1D6FA}_{r}|$
, where
![]() $r\geqslant 1$
, and let
$r\geqslant 1$
, and let
![]() $H_{i}\leqslant \text{Sym}(\unicode[STIX]{x1D6FA}_{i})$
for each
$H_{i}\leqslant \text{Sym}(\unicode[STIX]{x1D6FA}_{i})$
for each
![]() $i\in \{1,\ldots ,r\}$
. Assume further that
$i\in \{1,\ldots ,r\}$
. Assume further that
![]() $H_{1}$
is nontrivial and that its action on
$H_{1}$
is nontrivial and that its action on
![]() $\unicode[STIX]{x1D6FA}_{1}$
is not semiregular. Suppose that
$\unicode[STIX]{x1D6FA}_{1}$
is not semiregular. Suppose that
![]() $N=\prod _{i=1}^{r}H_{i}$
is a collineation group of a thick finite generalized quadrangle
$N=\prod _{i=1}^{r}H_{i}$
is a collineation group of a thick finite generalized quadrangle
![]() ${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}})$
of order not equal to
${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}})$
of order not equal to
![]() $(2,4)$
, such that
$(2,4)$
, such that
![]() ${\mathcal{P}}=\prod _{i=1}^{r}\unicode[STIX]{x1D6FA}_{i}$
and
${\mathcal{P}}=\prod _{i=1}^{r}\unicode[STIX]{x1D6FA}_{i}$
and
![]() $N$
has the product action on
$N$
has the product action on
![]() ${\mathcal{P}}$
. Then
${\mathcal{P}}$
. Then
![]() $r\leqslant 4$
, and every nonidentity element of
$r\leqslant 4$
, and every nonidentity element of
![]() $H_{1}$
fixes less than
$H_{1}$
fixes less than
![]() $|\unicode[STIX]{x1D6FA}_{1}|^{1-r/5}$
points of
$|\unicode[STIX]{x1D6FA}_{1}|^{1-r/5}$
points of
![]() $\unicode[STIX]{x1D6FA}_{1}$
.
$\unicode[STIX]{x1D6FA}_{1}$
.
The proof of Theorem 1.2 relies on the existence of a nonidentity element
![]() $h_{1}$
of
$h_{1}$
of
![]() $H_{1}$
that fixes at least one point of
$H_{1}$
that fixes at least one point of
![]() $\unicode[STIX]{x1D6FA}_{1}$
. If
$\unicode[STIX]{x1D6FA}_{1}$
. If
![]() $r\geqslant 2$
, one can then construct a collineation
$r\geqslant 2$
, one can then construct a collineation
![]() $(h_{1},1,\ldots ,1)\in N$
of
$(h_{1},1,\ldots ,1)\in N$
of
![]() ${\mathcal{Q}}$
that fixes at least
${\mathcal{Q}}$
that fixes at least
![]() $\prod _{i=2}^{r}|\unicode[STIX]{x1D6FA}_{i}|$
points of the Cartesian product
$\prod _{i=2}^{r}|\unicode[STIX]{x1D6FA}_{i}|$
points of the Cartesian product
![]() ${\mathcal{P}}=\prod _{i=1}^{r}\unicode[STIX]{x1D6FA}_{i}$
. Theorem 1.2 is then deduced from the following result, which bounds the number of points fixed by a nonidentity collineation of an arbitrary thick finite generalized quadrangle. The proofs of both theorems are given in Section 2.
${\mathcal{P}}=\prod _{i=1}^{r}\unicode[STIX]{x1D6FA}_{i}$
. Theorem 1.2 is then deduced from the following result, which bounds the number of points fixed by a nonidentity collineation of an arbitrary thick finite generalized quadrangle. The proofs of both theorems are given in Section 2.
Theorem 1.3. Let
![]() $\unicode[STIX]{x1D703}$
be a nonidentity collineation of a thick finite generalized quadrangle
$\unicode[STIX]{x1D703}$
be a nonidentity collineation of a thick finite generalized quadrangle
![]() ${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}})$
. Then either
${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}})$
. Then either
![]() $\unicode[STIX]{x1D703}$
fixes less than
$\unicode[STIX]{x1D703}$
fixes less than
![]() $|{\mathcal{P}}|^{4/5}$
points of
$|{\mathcal{P}}|^{4/5}$
points of
![]() ${\mathcal{Q}}$
, or
${\mathcal{Q}}$
, or
![]() ${\mathcal{Q}}$
is the unique generalized quadrangle
${\mathcal{Q}}$
is the unique generalized quadrangle
![]() $\mathsf{Q}^{-}(5,2)$
of order
$\mathsf{Q}^{-}(5,2)$
of order
![]() $(2,4)$
and
$(2,4)$
and
![]() $\unicode[STIX]{x1D703}$
fixes exactly
$\unicode[STIX]{x1D703}$
fixes exactly
![]() $15$
of the
$15$
of the
![]() $27$
points of
$27$
points of
![]() ${\mathcal{Q}}$
.
${\mathcal{Q}}$
.
Remark 1.4. Theorem 1.3 improves a particular case of a recent result of Babai on automorphism groups of strongly regular graphs [Reference Babai1, Theorem 1.7]. If
![]() ${\mathcal{Q}}$
has order
${\mathcal{Q}}$
has order
![]() $(s,t)$
then its collinearity graph, namely the graph with vertex set
$(s,t)$
then its collinearity graph, namely the graph with vertex set
![]() ${\mathcal{P}}$
and two vertices adjacent if and only if they are collinear in
${\mathcal{P}}$
and two vertices adjacent if and only if they are collinear in
![]() ${\mathcal{Q}}$
, is a strongly regular graph with parameters
${\mathcal{Q}}$
, is a strongly regular graph with parameters
![]() $v=|{\mathcal{P}}|=(s+1)(st+1)$
,
$v=|{\mathcal{P}}|=(s+1)(st+1)$
,
![]() $k=s(t+1)$
,
$k=s(t+1)$
,
![]() $\unicode[STIX]{x1D706}=s-1$
and
$\unicode[STIX]{x1D706}=s-1$
and
![]() $\unicode[STIX]{x1D707}=t+1$
. Roughly speaking, we have
$\unicode[STIX]{x1D707}=t+1$
. Roughly speaking, we have
![]() $v\approx s^{2}t$
and
$v\approx s^{2}t$
and
![]() $k\approx st$
, so the condition
$k\approx st$
, so the condition
![]() $k\leqslant n^{3/4}$
in assertion (b) of [Reference Babai1, Theorem 1.7] becomes
$k\leqslant n^{3/4}$
in assertion (b) of [Reference Babai1, Theorem 1.7] becomes
![]() $t\leqslant s^{2}$
, which is just Higman’s inequality for generalized quadrangles (see Lemma 2.1(ii)). Babai’s result, which applies far more generally to strongly regular graphs that are nontrivial, nongraphic and nongeometric, therefore implies that a nonidentity collineation
$t\leqslant s^{2}$
, which is just Higman’s inequality for generalized quadrangles (see Lemma 2.1(ii)). Babai’s result, which applies far more generally to strongly regular graphs that are nontrivial, nongraphic and nongeometric, therefore implies that a nonidentity collineation
![]() $\unicode[STIX]{x1D703}$
of
$\unicode[STIX]{x1D703}$
of
![]() ${\mathcal{Q}}$
can fix at most
${\mathcal{Q}}$
can fix at most
![]() $O(|{\mathcal{P}}|^{7/8})$
points. Theorem 1.3 sharpens the
$O(|{\mathcal{P}}|^{7/8})$
points. Theorem 1.3 sharpens the
![]() $7/8$
exponent in this bound to
$7/8$
exponent in this bound to
![]() $4/5$
in the case of collinearity graphs of generalized quadrangles (and replaces the “
$4/5$
in the case of collinearity graphs of generalized quadrangles (and replaces the “
![]() $O$
” by an explicit constant). (Note also that assertion (a) of [Reference Babai1, Theorem 1.7] sharpens the
$O$
” by an explicit constant). (Note also that assertion (a) of [Reference Babai1, Theorem 1.7] sharpens the
![]() $7/8$
exponent to
$7/8$
exponent to
![]() $5/6$
when, roughly,
$5/6$
when, roughly,
![]() $t\geqslant s$
: the condition
$t\geqslant s$
: the condition
![]() $k\geqslant n^{2/3}$
roughly translates to
$k\geqslant n^{2/3}$
roughly translates to
![]() $t\geqslant s$
, and the corresponding bound is
$t\geqslant s$
, and the corresponding bound is
![]() $O(\sqrt{kn})$
, with
$O(\sqrt{kn})$
, with
![]() $\sqrt{kn}\approx s^{3/2}t\geqslant (s^{2}t)^{5/6}\approx |{\mathcal{P}}|^{5/6}$
when
$\sqrt{kn}\approx s^{3/2}t\geqslant (s^{2}t)^{5/6}\approx |{\mathcal{P}}|^{5/6}$
when
![]() $t\geqslant s$
.)
$t\geqslant s$
.)
To aid our discussion, let us now state the following immediate corollary of Theorem 1.2.
Corollary 1.5. Let
![]() $\unicode[STIX]{x1D6FA}$
be a finite set with
$\unicode[STIX]{x1D6FA}$
be a finite set with
![]() $|\unicode[STIX]{x1D6FA}|\geqslant 2$
, and suppose that
$|\unicode[STIX]{x1D6FA}|\geqslant 2$
, and suppose that
![]() $H\leqslant \text{Sym}(\unicode[STIX]{x1D6FA})$
is nontrivial and not semiregular. Suppose that
$H\leqslant \text{Sym}(\unicode[STIX]{x1D6FA})$
is nontrivial and not semiregular. Suppose that
![]() $N=H^{r}$
,
$N=H^{r}$
,
![]() $r\geqslant 1$
, is a collineation group of a thick finite generalized quadrangle
$r\geqslant 1$
, is a collineation group of a thick finite generalized quadrangle
![]() ${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}})$
of order not equal to
${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}})$
of order not equal to
![]() $(2,4)$
, such that
$(2,4)$
, such that
![]() ${\mathcal{P}}=\unicode[STIX]{x1D6FA}^{r}$
and
${\mathcal{P}}=\unicode[STIX]{x1D6FA}^{r}$
and
![]() $N$
has the product action on
$N$
has the product action on
![]() ${\mathcal{P}}$
. Then
${\mathcal{P}}$
. Then
![]() $r\leqslant 4$
, and every nonidentity element of
$r\leqslant 4$
, and every nonidentity element of
![]() $H$
fixes less than
$H$
fixes less than
![]() $|\unicode[STIX]{x1D6FA}|^{1-r/5}$
points of
$|\unicode[STIX]{x1D6FA}|^{1-r/5}$
points of
![]() $\unicode[STIX]{x1D6FA}$
.
$\unicode[STIX]{x1D6FA}$
.
We apply Corollary 1.5 to groups
![]() $N$
that arise as subgroups of certain types of primitive groups. This in turn motivates certain questions about nonabelian finite simple groups. As illustration, consider the case where
$N$
that arise as subgroups of certain types of primitive groups. This in turn motivates certain questions about nonabelian finite simple groups. As illustration, consider the case where
![]() $\unicode[STIX]{x1D6FA}=T$
for some nonabelian finite simple group
$\unicode[STIX]{x1D6FA}=T$
for some nonabelian finite simple group
![]() $T$
, with
$T$
, with
![]() $H=T\times T$
acting on
$H=T\times T$
acting on
![]() $\unicode[STIX]{x1D6FA}$
via
$\unicode[STIX]{x1D6FA}$
via
![]() $\unicode[STIX]{x1D714}^{(x,x^{\prime })}=x^{-1}\unicode[STIX]{x1D714}x^{\prime }$
. This situation arises when
$\unicode[STIX]{x1D714}^{(x,x^{\prime })}=x^{-1}\unicode[STIX]{x1D714}x^{\prime }$
. This situation arises when
![]() $N$
is the socle (the subgroup generated by the minimal normal subgroups) of a primitive group of type HS (
$N$
is the socle (the subgroup generated by the minimal normal subgroups) of a primitive group of type HS (
![]() $r=1$
) or HC (
$r=1$
) or HC (
![]() $r\geqslant 2$
). If
$r\geqslant 2$
). If
![]() $x^{\prime }=x$
then the element
$x^{\prime }=x$
then the element
![]() $(x,x^{\prime })=(x,x)\in H$
fixes precisely
$(x,x^{\prime })=(x,x)\in H$
fixes precisely
![]() $|C_{T}(x)|$
points of
$|C_{T}(x)|$
points of
![]() $\unicode[STIX]{x1D6FA}$
, where
$\unicode[STIX]{x1D6FA}$
, where
![]() $C_{T}(x)$
is the centralizer of
$C_{T}(x)$
is the centralizer of
![]() $x$
in
$x$
in
![]() $T$
. Corollary 1.5 therefore implies that
$T$
. Corollary 1.5 therefore implies that
![]() $r\leqslant 4$
, and that
$r\leqslant 4$
, and that
![]() $|C_{T}(x)|<|T|^{1-r/5}$
for all
$|C_{T}(x)|<|T|^{1-r/5}$
for all
![]() $x\in T\setminus \{1\}$
. We therefore ask which nonabelian finite simple groups
$x\in T\setminus \{1\}$
. We therefore ask which nonabelian finite simple groups
![]() $T$
satisfy this condition. If
$T$
satisfy this condition. If
![]() $r=4$
then we require that
$r=4$
then we require that
![]() $|C_{T}(x)|<|T|^{1/5}$
for all
$|C_{T}(x)|<|T|^{1/5}$
for all
![]() $x\in T\setminus \{1\}$
, which is false for every nonabelian finite simple group
$x\in T\setminus \{1\}$
, which is false for every nonabelian finite simple group
![]() $T$
. Indeed, it is well known that every nonabelian finite simple group
$T$
. Indeed, it is well known that every nonabelian finite simple group
![]() $T$
contains an involution
$T$
contains an involution
![]() $x$
with
$x$
with
![]() $|C_{T}(x)|>|T|^{1/3}$
(in fact, every involution in
$|C_{T}(x)|>|T|^{1/3}$
(in fact, every involution in
![]() $T$
has this property [Reference Liebeck and Shalev19, Proposition 2.4]). For
$T$
has this property [Reference Liebeck and Shalev19, Proposition 2.4]). For
![]() $r\in \{1,2,3\}$
, we verify the following result in Section 3. Although this result follows from routine calculations, we include it here in case it proves to be a convenient reference.
$r\in \{1,2,3\}$
, we verify the following result in Section 3. Although this result follows from routine calculations, we include it here in case it proves to be a convenient reference.
Table 2. Possibilities for a nonabelian finite simple group
![]() $T$
with the property that
$T$
with the property that
![]() $|C_{T}(x)|<|T|^{1-r/5}$
for all
$|C_{T}(x)|<|T|^{1-r/5}$
for all
![]() $x\in T\setminus \{1\}$
, where
$x\in T\setminus \{1\}$
, where
![]() $r\in \{1,2,3\}$
.
$r\in \{1,2,3\}$
.
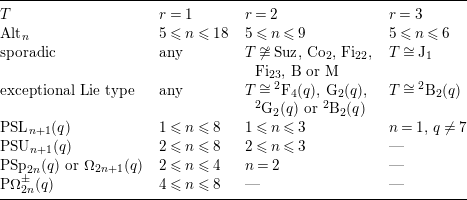
Proposition 1.6. Let
![]() $r\in \{1,2,3\}$
and let
$r\in \{1,2,3\}$
and let
![]() $T$
be a nonabelian finite simple group. Then either
$T$
be a nonabelian finite simple group. Then either
![]() $|C_{T}(x)|\geqslant |T|^{1-r/5}$
for some
$|C_{T}(x)|\geqslant |T|^{1-r/5}$
for some
![]() $x\in T\setminus \{1\}$
, or
$x\in T\setminus \{1\}$
, or
![]() $T$
is one of the groups listed in Table 2.
$T$
is one of the groups listed in Table 2.
Our new results about generalized quadrangles with point-primitive collineation groups are proved in Sections 4–6. Corollary 1.5 is applied not only to actions of type HS or HC as illustrated above, but also to types SD, CD and PA. In particular, the proof of Theorem 1.1 does not depend on the Classification of Finite Simple Groups (CFSG) to the extent that, for
![]() $G$
of type HC, CD or PA with socle
$G$
of type HC, CD or PA with socle
![]() $T^{r}\times T^{r}$
,
$T^{r}\times T^{r}$
,
![]() $T^{(k-1)r}$
or
$T^{(k-1)r}$
or
![]() $T^{r}$
, respectively, the proof that
$T^{r}$
, respectively, the proof that
![]() $r\leqslant 4$
depends only on Corollary 1.5. The CFSG is, however, needed to prove Proposition 1.6 and some of the results in Section 5. For type PA, the group
$r\leqslant 4$
depends only on Corollary 1.5. The CFSG is, however, needed to prove Proposition 1.6 and some of the results in Section 5. For type PA, the group
![]() $H$
in Corollary 1.5 is an almost simple primitive group, so we are led to consider lower bounds on the fixity of such a group, namely the maximum number of points that can be fixed by a nonidentity element. In Section 6, we discuss how refinements of a recent result of Liebeck and Shalev [Reference Liebeck and Shalev19, Theorem 4] on this problem, currently being carried out by Elisa Covato at the University of Bristol as part of her PhD research [Reference Covato11], can be adapted to further improve the bound
$H$
in Corollary 1.5 is an almost simple primitive group, so we are led to consider lower bounds on the fixity of such a group, namely the maximum number of points that can be fixed by a nonidentity element. In Section 6, we discuss how refinements of a recent result of Liebeck and Shalev [Reference Liebeck and Shalev19, Theorem 4] on this problem, currently being carried out by Elisa Covato at the University of Bristol as part of her PhD research [Reference Covato11], can be adapted to further improve the bound
![]() $r\leqslant 4$
in this case. In particular, for
$r\leqslant 4$
in this case. In particular, for
![]() $r\in \{3,4\}$
we are able to show that
$r\in \{3,4\}$
we are able to show that
![]() $T$
cannot be a sporadic simple group, and to rule out the case
$T$
cannot be a sporadic simple group, and to rule out the case
![]() $T\cong \text{Alt}_{n}$
except in one specific action when
$T\cong \text{Alt}_{n}$
except in one specific action when
![]() $n$
is a prime congruent to
$n$
is a prime congruent to
![]() $3$
modulo
$3$
modulo
![]() $4$
(see Table 1). The proof of Theorem 1.1 is presented in Section 7.
$4$
(see Table 1). The proof of Theorem 1.1 is presented in Section 7.
Section 8 concludes the paper with a discussion and some open problems. In light of the growing body of work toward a classification of point-primitive generalized quadrangles, and the possible avenues outlined in Remarks 5.11, 6.4 and Section 8 for attacking the cases left open by Theorem 1.1, we feel that the following conjecture can be made with a reasonable amount of confidence.
Conjecture 1.7. If a thick finite generalized quadrangle
![]() ${\mathcal{Q}}$
admits a collineation group
${\mathcal{Q}}$
admits a collineation group
![]() $G$
that acts primitively on the point set of
$G$
that acts primitively on the point set of
![]() ${\mathcal{Q}}$
, then
${\mathcal{Q}}$
, then
![]() $G$
is either affine or almost simple.
$G$
is either affine or almost simple.
2 Bounding the number of points fixed by a collineation
The facts summarized in the following lemma are well known. (The existence of an order is proved in [Reference Van Maldeghem26, Corollary 1.5.3], and proofs of assertions (i)–(iii) may be found in [Reference Payne and Thas21, Section 1.2].)
Lemma 2.1. Let
![]() ${\mathcal{Q}}$
be a thick finite generalized quadrangle. Then
${\mathcal{Q}}$
be a thick finite generalized quadrangle. Then
![]() ${\mathcal{Q}}$
has an order
${\mathcal{Q}}$
has an order
![]() $(s,t)$
, and the following properties hold:
$(s,t)$
, and the following properties hold:
(i)
 ${\mathcal{Q}}$
has
${\mathcal{Q}}$
has
 $(s+1)(st+1)$
points and
$(s+1)(st+1)$
points and
 $(t+1)(st+1)$
lines;
$(t+1)(st+1)$
lines;(ii)
 $s^{1/2}\leqslant t\leqslant s^{2}\leqslant t^{4}$
(Higman’s inequality);
$s^{1/2}\leqslant t\leqslant s^{2}\leqslant t^{4}$
(Higman’s inequality);(iii)
 $s+t$
divides
$s+t$
divides
 $st(st+1)$
.
$st(st+1)$
.
A point–line incidence geometry
![]() ${\mathcal{S}}=({\mathcal{P}},{\mathcal{L}},\text{I})$
is called a grid if there exist positive integers
${\mathcal{S}}=({\mathcal{P}},{\mathcal{L}},\text{I})$
is called a grid if there exist positive integers
![]() $s_{1}$
and
$s_{1}$
and
![]() $s_{2}$
such that the point set
$s_{2}$
such that the point set
![]() ${\mathcal{P}}$
can be written in the form
${\mathcal{P}}$
can be written in the form
![]() $\{P_{ij}\mid 0\leqslant i\leqslant s_{1},0\leqslant j\leqslant s_{2}\}$
, the line set
$\{P_{ij}\mid 0\leqslant i\leqslant s_{1},0\leqslant j\leqslant s_{2}\}$
, the line set
![]() ${\mathcal{L}}$
can be written in the form
${\mathcal{L}}$
can be written in the form
![]() $\{\ell _{k}\mid 0\leqslant k\leqslant s_{1}\}\cup \{\ell _{k}^{\prime }\mid 0\leqslant k\leqslant s_{2}\}$
, and we have
$\{\ell _{k}\mid 0\leqslant k\leqslant s_{1}\}\cup \{\ell _{k}^{\prime }\mid 0\leqslant k\leqslant s_{2}\}$
, and we have
![]() $P_{ij}\text{I}\ell _{k}$
if and only if
$P_{ij}\text{I}\ell _{k}$
if and only if
![]() $i=k$
, and
$i=k$
, and
![]() $P_{ij}\text{I}\ell _{k}^{\prime }$
if and only if
$P_{ij}\text{I}\ell _{k}^{\prime }$
if and only if
![]() $j=k$
. Each point of
$j=k$
. Each point of
![]() ${\mathcal{S}}$
is then incident with exactly two lines, and
${\mathcal{S}}$
is then incident with exactly two lines, and
![]() $|{\mathcal{P}}|=(s_{1}+1)(s_{2}+1)$
. Let us say that such a grid has parameters
$|{\mathcal{P}}|=(s_{1}+1)(s_{2}+1)$
. Let us say that such a grid has parameters
![]() $s_{1}$
and
$s_{1}$
and
![]() $s_{2}$
. Note that a grid with parameters
$s_{2}$
. Note that a grid with parameters
![]() $s_{1}=s_{2}$
is a generalized quadrangle of order
$s_{1}=s_{2}$
is a generalized quadrangle of order
![]() $(s_{1},1)$
. A dual grid is defined analogously, by swapping the roles of points and lines. That is, there exist positive integers
$(s_{1},1)$
. A dual grid is defined analogously, by swapping the roles of points and lines. That is, there exist positive integers
![]() $t_{1}$
and
$t_{1}$
and
![]() $t_{2}$
such that
$t_{2}$
such that
![]() ${\mathcal{L}}$
can be written in the form
${\mathcal{L}}$
can be written in the form
![]() $\{\ell _{ij}\mid 0\leqslant i\leqslant t_{1},0\leqslant j\leqslant t_{2}\}$
,
$\{\ell _{ij}\mid 0\leqslant i\leqslant t_{1},0\leqslant j\leqslant t_{2}\}$
,
![]() ${\mathcal{P}}$
can be written in the form
${\mathcal{P}}$
can be written in the form
![]() $\{P_{i}\mid 0\leqslant i\leqslant t_{1}\}\cup \{P_{j}^{\prime }\mid 0\leqslant j\leqslant t_{2}\}$
,
$\{P_{i}\mid 0\leqslant i\leqslant t_{1}\}\cup \{P_{j}^{\prime }\mid 0\leqslant j\leqslant t_{2}\}$
,
![]() $P_{k}\text{I}\ell _{ij}$
if and only if
$P_{k}\text{I}\ell _{ij}$
if and only if
![]() $i=k$
, and
$i=k$
, and
![]() $P_{k}^{\prime }\text{I}\ell _{ij}$
if and only if
$P_{k}^{\prime }\text{I}\ell _{ij}$
if and only if
![]() $j=k$
. In this case, each line is incident with exactly two points, and
$j=k$
. In this case, each line is incident with exactly two points, and
![]() $|{\mathcal{P}}|=(t_{1}+1)+(t_{2}+1)$
. Let us say that such a dual grid has parameters
$|{\mathcal{P}}|=(t_{1}+1)+(t_{2}+1)$
. Let us say that such a dual grid has parameters
![]() $t_{1}$
and
$t_{1}$
and
![]() $t_{2}$
.
$t_{2}$
.
If
![]() $\unicode[STIX]{x1D703}$
is a collineation of a generalized quadrangle
$\unicode[STIX]{x1D703}$
is a collineation of a generalized quadrangle
![]() ${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}})$
, then it makes sense to consider the point–line incidence geometry
${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}})$
, then it makes sense to consider the point–line incidence geometry
![]() ${\mathcal{Q}}_{\unicode[STIX]{x1D703}}=({\mathcal{P}}_{\unicode[STIX]{x1D703}},{\mathcal{L}}_{\unicode[STIX]{x1D703}})$
with
${\mathcal{Q}}_{\unicode[STIX]{x1D703}}=({\mathcal{P}}_{\unicode[STIX]{x1D703}},{\mathcal{L}}_{\unicode[STIX]{x1D703}})$
with
![]() ${\mathcal{P}}_{\unicode[STIX]{x1D703}}=\{P\in {\mathcal{P}}\mid P^{\unicode[STIX]{x1D703}}=P\}$
,
${\mathcal{P}}_{\unicode[STIX]{x1D703}}=\{P\in {\mathcal{P}}\mid P^{\unicode[STIX]{x1D703}}=P\}$
,
![]() ${\mathcal{L}}_{\unicode[STIX]{x1D703}}=\{\ell \in {\mathcal{L}}\mid \ell ^{\unicode[STIX]{x1D703}}=\ell \}$
, and incidence inherited from
${\mathcal{L}}_{\unicode[STIX]{x1D703}}=\{\ell \in {\mathcal{L}}\mid \ell ^{\unicode[STIX]{x1D703}}=\ell \}$
, and incidence inherited from
![]() ${\mathcal{Q}}$
. Here we call
${\mathcal{Q}}$
. Here we call
![]() ${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
the substructure of
${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
the substructure of
![]() ${\mathcal{Q}}$
fixed by
${\mathcal{Q}}$
fixed by
![]() $\unicode[STIX]{x1D703}$
. It may happen that
$\unicode[STIX]{x1D703}$
. It may happen that
![]() ${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
is a grid or a dual grid, or a generalized quadrangle. More specifically, we have the following result, based on the description of the possible structures of
${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
is a grid or a dual grid, or a generalized quadrangle. More specifically, we have the following result, based on the description of the possible structures of
![]() ${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
given by Payne and Thas [Reference Payne and Thas21, 2.4.1].
${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
given by Payne and Thas [Reference Payne and Thas21, 2.4.1].
Lemma 2.2. Let
![]() ${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}})$
be a thick finite generalized quadrangle of order
${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}})$
be a thick finite generalized quadrangle of order
![]() $(s,t)$
. Let
$(s,t)$
. Let
![]() $\unicode[STIX]{x1D703}$
be a nonidentity collineation of
$\unicode[STIX]{x1D703}$
be a nonidentity collineation of
![]() ${\mathcal{Q}}$
, and let
${\mathcal{Q}}$
, and let
![]() ${\mathcal{Q}}_{\unicode[STIX]{x1D703}}=({\mathcal{P}}_{\unicode[STIX]{x1D703}},{\mathcal{L}}_{\unicode[STIX]{x1D703}})$
be the substructure of
${\mathcal{Q}}_{\unicode[STIX]{x1D703}}=({\mathcal{P}}_{\unicode[STIX]{x1D703}},{\mathcal{L}}_{\unicode[STIX]{x1D703}})$
be the substructure of
![]() ${\mathcal{Q}}$
fixed by
${\mathcal{Q}}$
fixed by
![]() $\unicode[STIX]{x1D703}$
. Then at least one of the following conditions holds.
$\unicode[STIX]{x1D703}$
. Then at least one of the following conditions holds.
(i)
 ${\mathcal{P}}_{\unicode[STIX]{x1D703}}$
is empty.
${\mathcal{P}}_{\unicode[STIX]{x1D703}}$
is empty.(ii)
 ${\mathcal{L}}_{\unicode[STIX]{x1D703}}$
is empty and
${\mathcal{L}}_{\unicode[STIX]{x1D703}}$
is empty and
 ${\mathcal{P}}_{\unicode[STIX]{x1D703}}$
is a set of pairwise noncollinear points. In particular,
${\mathcal{P}}_{\unicode[STIX]{x1D703}}$
is a set of pairwise noncollinear points. In particular,
 $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant st+1$
.
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant st+1$
.(iii) All points of
 ${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
are incident with a common line, and
${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
are incident with a common line, and
 $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant s+1$
.
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant s+1$
.(iv) All points of
 ${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
are collinear with a common point, and
${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
are collinear with a common point, and  $$\begin{eqnarray}|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant s(t+1)+1.\end{eqnarray}$$
$$\begin{eqnarray}|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant s(t+1)+1.\end{eqnarray}$$
(v)
 ${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
is a grid. In this case, either
${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
is a grid. In this case, either
 $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|=(s+1)^{2}$
and
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|=(s+1)^{2}$
and
 $s\leqslant t$
, or
$s\leqslant t$
, or
 $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<s^{2}$
.
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<s^{2}$
.(vi)
 ${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
is a dual grid, and
${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
is a dual grid, and
 $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant 2(t+1)$
.
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant 2(t+1)$
.(vii)
 ${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
is a thick generalized quadrangle, and
${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
is a thick generalized quadrangle, and
 $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant (s+1)(t+1)$
.
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant (s+1)(t+1)$
.
In particular, either
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant (s+1)(t+1)$
; or
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant (s+1)(t+1)$
; or
![]() $s\geqslant t+3$
,
$s\geqslant t+3$
,
![]() ${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
is a grid and
${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
is a grid and
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<s^{2}$
.
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<s^{2}$
.
Proof. The possible structures (i)–(vii) of
![]() ${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
are given by [Reference Payne and Thas21, 2.4.1]. We verify the claimed upper bounds for
${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
are given by [Reference Payne and Thas21, 2.4.1]. We verify the claimed upper bounds for
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|$
. The bounds in cases (iii) and (iv) are immediate, because every line of
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|$
. The bounds in cases (iii) and (iv) are immediate, because every line of
![]() ${\mathcal{Q}}$
is incident with exactly
${\mathcal{Q}}$
is incident with exactly
![]() $s+1$
points, and every point of
$s+1$
points, and every point of
![]() ${\mathcal{Q}}$
is incident with exactly
${\mathcal{Q}}$
is incident with exactly
![]() $t+1$
lines. For case (ii), note [Reference Payne and Thas21, Section 2.7] that the maximum size of a set of pairwise noncollinear points in
$t+1$
lines. For case (ii), note [Reference Payne and Thas21, Section 2.7] that the maximum size of a set of pairwise noncollinear points in
![]() ${\mathcal{Q}}$
is
${\mathcal{Q}}$
is
![]() $st+1$
. For (v), if
$st+1$
. For (v), if
![]() ${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
is a dual grid with parameters
${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
is a dual grid with parameters
![]() $t_{1}$
and
$t_{1}$
and
![]() $t_{2}$
, then
$t_{2}$
, then
![]() $t_{1}\leqslant t$
and
$t_{1}\leqslant t$
and
![]() $t_{2}\leqslant t$
, and hence
$t_{2}\leqslant t$
, and hence
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant 2(t+1)$
.
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant 2(t+1)$
.
Now suppose that
![]() ${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
is a grid with parameters
${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
is a grid with parameters
![]() $s_{1}$
and
$s_{1}$
and
![]() $s_{2}$
, noting that
$s_{2}$
, noting that
![]() $s_{1}\leqslant s$
and
$s_{1}\leqslant s$
and
![]() $s_{2}\leqslant s$
, and assuming (without loss of generality) that
$s_{2}\leqslant s$
, and assuming (without loss of generality) that
![]() $s_{1}\geqslant s_{2}$
. If
$s_{1}\geqslant s_{2}$
. If
![]() $s_{1}=s_{2}=s$
then
$s_{1}=s_{2}=s$
then
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|=(s+1)^{2}$
, and
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|=(s+1)^{2}$
, and
![]() ${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
is a generalized quadrangle of order
${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
is a generalized quadrangle of order
![]() $(s,1)$
, so [Reference Payne and Thas21, 2.2.2(i)] implies that
$(s,1)$
, so [Reference Payne and Thas21, 2.2.2(i)] implies that
![]() $s\leqslant t$
. The case
$s\leqslant t$
. The case
![]() $s_{2}=s-1$
cannot occur, because if
$s_{2}=s-1$
cannot occur, because if
![]() $\unicode[STIX]{x1D703}$
fixes
$\unicode[STIX]{x1D703}$
fixes
![]() $s$
points incident with a line then it must also fix the final point; and if
$s$
points incident with a line then it must also fix the final point; and if
![]() $s_{2}\leqslant s-2$
then
$s_{2}\leqslant s-2$
then
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant (s+1)(s-1)<s^{2}$
. Finally, suppose that
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant (s+1)(s-1)<s^{2}$
. Finally, suppose that
![]() ${\mathcal{Q}}$
is a thick finite generalized quadrangle, and let
${\mathcal{Q}}$
is a thick finite generalized quadrangle, and let
![]() $(s^{\prime },t^{\prime })$
denote its order. Then
$(s^{\prime },t^{\prime })$
denote its order. Then
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|=(s^{\prime }+1)(s^{\prime }t^{\prime }+1)$
by Lemma 2.1(i). If
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|=(s^{\prime }+1)(s^{\prime }t^{\prime }+1)$
by Lemma 2.1(i). If
![]() $t^{\prime }=t$
then
$t^{\prime }=t$
then
![]() $s^{\prime }<s$
because
$s^{\prime }<s$
because
![]() $\unicode[STIX]{x1D703}\neq 1$
, so [Reference Payne and Thas21, 2.2.1] implies that
$\unicode[STIX]{x1D703}\neq 1$
, so [Reference Payne and Thas21, 2.2.1] implies that
![]() $s^{\prime }t=s^{\prime }t^{\prime }\leqslant s$
, and hence
$s^{\prime }t=s^{\prime }t^{\prime }\leqslant s$
, and hence
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant (s/t+1)(s+1)\leqslant (t^{2}/t+1)(s+1)=(s+1)(t+1)$
, where for the second inequality we use Lemma 2.1(ii). If
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant (s/t+1)(s+1)\leqslant (t^{2}/t+1)(s+1)=(s+1)(t+1)$
, where for the second inequality we use Lemma 2.1(ii). If
![]() $t^{\prime }<t$
then the dual statement of [Reference Payne and Thas21, 2.2.1] yields
$t^{\prime }<t$
then the dual statement of [Reference Payne and Thas21, 2.2.1] yields
![]() $s^{\prime }t^{\prime }\leqslant t$
, so
$s^{\prime }t^{\prime }\leqslant t$
, so
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|=(s^{\prime }+1)(s^{\prime }t^{\prime }+1)\leqslant (s+1)(t+1)$
.
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|=(s^{\prime }+1)(s^{\prime }t^{\prime }+1)\leqslant (s+1)(t+1)$
.
The final assertion is deduced by comparing the upper bounds on
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|$
established in each case. We observe that
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|$
established in each case. We observe that
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant (s+1)(t+1)$
except possibly in the second case of (v), where our bound is
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant (s+1)(t+1)$
except possibly in the second case of (v), where our bound is
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<s^{2}$
. However, if
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<s^{2}$
. However, if
![]() $s\leqslant t+2$
then in this case we have
$s\leqslant t+2$
then in this case we have
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<s^{2}<(s+1)(t+1)$
.◻
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<s^{2}<(s+1)(t+1)$
.◻
Remark 2.3. We mention a paper of Frohardt and Magaard [Reference Frohardt and Magaard14, Section 1.3], in which results analogous to Lemma 2.2 are obtained for generalized
![]() $d$
-gons with
$d$
-gons with
![]() $d\in \{6,8\}$
, namely generalized hexagons and generalized octagons. The known examples of such geometries admit point- and line-primitive actions of almost simple groups with socle
$d\in \{6,8\}$
, namely generalized hexagons and generalized octagons. The known examples of such geometries admit point- and line-primitive actions of almost simple groups with socle
![]() $^{3}\text{D}_{4}(q)$
or
$^{3}\text{D}_{4}(q)$
or
![]() $\text{G}_{2}(q)$
(for
$\text{G}_{2}(q)$
(for
![]() $d=6$
) and
$d=6$
) and
![]() $^{2}\text{F}_{4}(q)$
(for
$^{2}\text{F}_{4}(q)$
(for
![]() $d=8$
). Frohardt and Magaard use the aforementioned results to determine upper bounds for fixities of primitive actions of groups
$d=8$
). Frohardt and Magaard use the aforementioned results to determine upper bounds for fixities of primitive actions of groups
![]() $G$
with generalized Fitting subgroup
$G$
with generalized Fitting subgroup
![]() $^{3}\text{D}_{4}(q)$
,
$^{3}\text{D}_{4}(q)$
,
![]() $\text{G}_{2}(q)$
or
$\text{G}_{2}(q)$
or
![]() $^{2}\text{F}_{4}(q)$
(and they also treat the other exceptional Lie type groups of Lie rank
$^{2}\text{F}_{4}(q)$
(and they also treat the other exceptional Lie type groups of Lie rank
![]() $1$
or
$1$
or
![]() $2$
). By comparison, we instead apply Lemma 2.2 to determine which groups might act primitively on the points of a generalized
$2$
). By comparison, we instead apply Lemma 2.2 to determine which groups might act primitively on the points of a generalized
![]() $d$
-gon (with
$d$
-gon (with
![]() $d=4$
in our case). (We remark that we have also investigated point-primitive generalized hexagons and octagons, although via different methods than in the present paper [Reference Bamberg, Glasby, Popiel, Praeger and Schneider7], [Reference Morgan and Popiel20].)
$d=4$
in our case). (We remark that we have also investigated point-primitive generalized hexagons and octagons, although via different methods than in the present paper [Reference Bamberg, Glasby, Popiel, Praeger and Schneider7], [Reference Morgan and Popiel20].)
We now use Lemma 2.2 to prove Theorem 1.3, from which we deduce Theorem 1.2.
Proof of Theorem 1.3.
Let
![]() $(s,t)$
be the order of
$(s,t)$
be the order of
![]() ${\mathcal{Q}}$
, and let
${\mathcal{Q}}$
, and let
![]() ${\mathcal{Q}}_{\unicode[STIX]{x1D703}}=({\mathcal{P}}_{\unicode[STIX]{x1D703}},{\mathcal{L}}_{\unicode[STIX]{x1D703}})$
be the substructure of
${\mathcal{Q}}_{\unicode[STIX]{x1D703}}=({\mathcal{P}}_{\unicode[STIX]{x1D703}},{\mathcal{L}}_{\unicode[STIX]{x1D703}})$
be the substructure of
![]() ${\mathcal{Q}}$
fixed by
${\mathcal{Q}}$
fixed by
![]() $\unicode[STIX]{x1D703}$
. We must show that either
$\unicode[STIX]{x1D703}$
. We must show that either
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<|{\mathcal{P}}|^{4/5}$
, or
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<|{\mathcal{P}}|^{4/5}$
, or
![]() $(s,t)=(2,4)$
and
$(s,t)=(2,4)$
and
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|=15$
for
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|=15$
for
![]() ${\mathcal{Q}}=\mathsf{Q}^{-}(5,2)$
.
${\mathcal{Q}}=\mathsf{Q}^{-}(5,2)$
.
First suppose that
![]() $s\neq 2$
. By Lemma 2.2, we have either
$s\neq 2$
. By Lemma 2.2, we have either
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<s^{2}$
or
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<s^{2}$
or
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant (s+1)(t+1)$
. If
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant (s+1)(t+1)$
. If
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<s^{2}$
then
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<s^{2}$
then
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<|{\mathcal{P}}|^{4/5}$
since
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<|{\mathcal{P}}|^{4/5}$
since
![]() $|{\mathcal{P}}|=(s+1)(st+1)>s^{2}t\geqslant s^{5/2}$
by Lemma 2.1. If
$|{\mathcal{P}}|=(s+1)(st+1)>s^{2}t\geqslant s^{5/2}$
by Lemma 2.1. If
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant (s+1)(t+1)$
then it suffices to show that the function
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant (s+1)(t+1)$
then it suffices to show that the function
![]() $f(s,t)=((s+1)(st+1))^{4/5}-(s+1)(t+1)$
is positive for all
$f(s,t)=((s+1)(st+1))^{4/5}-(s+1)(t+1)$
is positive for all
![]() $s\geqslant 3$
, for all
$s\geqslant 3$
, for all
![]() $s^{1/2}\leqslant t\leqslant s^{2}$
. This is readily checked when
$s^{1/2}\leqslant t\leqslant s^{2}$
. This is readily checked when
![]() $s\in \{3,4\}$
, so assume that
$s\in \{3,4\}$
, so assume that
![]() $s\geqslant 5$
. Regarding
$s\geqslant 5$
. Regarding
![]() $s$
and
$s$
and
![]() $t$
as real variables, we have
$t$
as real variables, we have
As
![]() $s,t$
are positive, this derivative is positive if and only if
$s,t$
are positive, this derivative is positive if and only if
![]() $4s-h(s,t)>0$
. Since
$4s-h(s,t)>0$
. Since
![]() $s\geqslant 5$
and
$s\geqslant 5$
and
![]() $2\leqslant t\leqslant s^{2}$
, we have
$2\leqslant t\leqslant s^{2}$
, we have
![]() $h(s,t)\leqslant 5({\textstyle \frac{6}{5}}s)^{1/5}({\textstyle \frac{11}{10}}st)^{1/5}\leqslant 5({\textstyle \frac{33}{25}})^{1/5}s^{4/5}$
. Hence,
$h(s,t)\leqslant 5({\textstyle \frac{6}{5}}s)^{1/5}({\textstyle \frac{11}{10}}st)^{1/5}\leqslant 5({\textstyle \frac{33}{25}})^{1/5}s^{4/5}$
. Hence,
![]() $4s-h(s,t)\geqslant s^{4/5}(4s^{1/5}-5({\textstyle \frac{33}{25}})^{1/5})$
. The right-hand side of this inequality is positive if
$4s-h(s,t)\geqslant s^{4/5}(4s^{1/5}-5({\textstyle \frac{33}{25}})^{1/5})$
. The right-hand side of this inequality is positive if
![]() $s>({\textstyle \frac{5}{4}})^{5}({\textstyle \frac{33}{25}})={\textstyle \frac{4125}{1024}}\approx 4.028$
, and so certainly
$s>({\textstyle \frac{5}{4}})^{5}({\textstyle \frac{33}{25}})={\textstyle \frac{4125}{1024}}\approx 4.028$
, and so certainly
![]() $(\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}t)(s,t)>0$
when
$(\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}t)(s,t)>0$
when
![]() $s\geqslant 5$
and
$s\geqslant 5$
and
![]() $s^{1/2}\leqslant t\leqslant s^{2}$
. Since
$s^{1/2}\leqslant t\leqslant s^{2}$
. Since
![]() $f(s,t)\geqslant f(s,s^{1/2})$
and
$f(s,t)\geqslant f(s,s^{1/2})$
and
![]() $f(s,s^{1/2})>0$
for
$f(s,s^{1/2})>0$
for
![]() $s\geqslant 5$
, it follows that
$s\geqslant 5$
, it follows that
![]() $f(s,t)>0$
for all
$f(s,t)>0$
for all
![]() $s\geqslant 5$
, for all
$s\geqslant 5$
, for all
![]() $s^{1/2}\leqslant t\leqslant s^{2}$
.
$s^{1/2}\leqslant t\leqslant s^{2}$
.
Now suppose that
![]() $s=2$
. Then
$s=2$
. Then
![]() $t\in \{2,4\}$
by Lemma 2.1. There exist unique generalized quadrangles of orders
$t\in \{2,4\}$
by Lemma 2.1. There exist unique generalized quadrangles of orders
![]() $(2,2)$
and
$(2,2)$
and
![]() $(2,4)$
, namely the symplectic space
$(2,4)$
, namely the symplectic space
![]() $\mathsf{W}(3,2)$
and the elliptic quadric
$\mathsf{W}(3,2)$
and the elliptic quadric
![]() $\mathsf{Q}^{-}(5,2)$
, respectively [Reference Payne and Thas21, 5.2.3 and 5.3.2]. The full collineation groups of these generalized quadrangles are
$\mathsf{Q}^{-}(5,2)$
, respectively [Reference Payne and Thas21, 5.2.3 and 5.3.2]. The full collineation groups of these generalized quadrangles are
![]() $\text{P}\unicode[STIX]{x1D6E4}\text{Sp}_{4}(2)$
and
$\text{P}\unicode[STIX]{x1D6E4}\text{Sp}_{4}(2)$
and
![]() $\text{P}\unicode[STIX]{x1D6E4}\text{U}_{4}(2)$
, respectively. One may use the package FinInG [Reference Bamberg, Betten, Cara, De Beule, Lavrauw and Neunhöffer3] in the computer algebra system GAP [15] to check that every nonidentity collineation of
$\text{P}\unicode[STIX]{x1D6E4}\text{U}_{4}(2)$
, respectively. One may use the package FinInG [Reference Bamberg, Betten, Cara, De Beule, Lavrauw and Neunhöffer3] in the computer algebra system GAP [15] to check that every nonidentity collineation of
![]() $\mathsf{W}(3,2)$
fixes at most
$\mathsf{W}(3,2)$
fixes at most
![]() $7$
points. Since
$7$
points. Since
![]() $\mathsf{W}(3,2)$
has a total of
$\mathsf{W}(3,2)$
has a total of
![]() $15$
points and
$15$
points and
![]() $15^{4/5}\approx 8.73>7$
, the claimed inequality
$15^{4/5}\approx 8.73>7$
, the claimed inequality
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<|{\mathcal{P}}|^{4/5}$
holds for every nonidentity collineation
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<|{\mathcal{P}}|^{4/5}$
holds for every nonidentity collineation
![]() $\unicode[STIX]{x1D703}$
in this case. On the other hand, there exist
$\unicode[STIX]{x1D703}$
in this case. On the other hand, there exist
![]() $36$
nonidentity collineations of
$36$
nonidentity collineations of
![]() $\mathsf{Q}^{-}(5,2)$
that fix
$\mathsf{Q}^{-}(5,2)$
that fix
![]() $15$
points, but the total number of points of
$15$
points, but the total number of points of
![]() $\mathsf{Q}^{-}(5,2)$
is
$\mathsf{Q}^{-}(5,2)$
is
![]() $27$
and
$27$
and
![]() $27^{4/5}\approx 13.97<15$
. We also remark that the substructure fixed by such a collineation is, in fact, a generalized quadrangle of order
$27^{4/5}\approx 13.97<15$
. We also remark that the substructure fixed by such a collineation is, in fact, a generalized quadrangle of order
![]() $(2,2)$
. Every other nonidentity collineation of
$(2,2)$
. Every other nonidentity collineation of
![]() $\mathsf{Q}^{-}(5,2)$
fixes at most
$\mathsf{Q}^{-}(5,2)$
fixes at most
![]() $9$
points.◻
$9$
points.◻
Proof of Theorem 1.2.
Since the action of
![]() $H_{1}$
on
$H_{1}$
on
![]() $\unicode[STIX]{x1D6FA}_{1}$
is not semiregular, there exists
$\unicode[STIX]{x1D6FA}_{1}$
is not semiregular, there exists
![]() $h_{1}\in H_{1}\setminus \{1\}$
fixing at least one point of
$h_{1}\in H_{1}\setminus \{1\}$
fixing at least one point of
![]() $\unicode[STIX]{x1D6FA}_{1}$
. Let
$\unicode[STIX]{x1D6FA}_{1}$
. Let
![]() $f_{1}$
be the number of points of
$f_{1}$
be the number of points of
![]() $\unicode[STIX]{x1D6FA}_{1}$
fixed by
$\unicode[STIX]{x1D6FA}_{1}$
fixed by
![]() $h_{1}$
. Let
$h_{1}$
. Let
![]() $\unicode[STIX]{x1D703}=(h_{1},1,\ldots ,1)\in N$
, and let
$\unicode[STIX]{x1D703}=(h_{1},1,\ldots ,1)\in N$
, and let
![]() $f$
be the number of points of
$f$
be the number of points of
![]() ${\mathcal{Q}}$
fixed by
${\mathcal{Q}}$
fixed by
![]() $\unicode[STIX]{x1D703}$
. If
$\unicode[STIX]{x1D703}$
. If
![]() $r=1$
then Theorem 1.3 implies that
$r=1$
then Theorem 1.3 implies that
![]() $f_{1}=f<|{\mathcal{P}}|^{4/5}=|\unicode[STIX]{x1D6FA}_{1}|^{4/5}$
. If
$f_{1}=f<|{\mathcal{P}}|^{4/5}=|\unicode[STIX]{x1D6FA}_{1}|^{4/5}$
. If
![]() $r\geqslant 2$
then Theorem 1.3 gives
$r\geqslant 2$
then Theorem 1.3 gives
![]() $f_{1}\prod _{i=2}^{r}|\unicode[STIX]{x1D6FA}_{i}|=f<|{\mathcal{P}}|^{4/5}=(\prod _{i=1}^{r}|\unicode[STIX]{x1D6FA}_{i}|)^{4/5}$
, so
$f_{1}\prod _{i=2}^{r}|\unicode[STIX]{x1D6FA}_{i}|=f<|{\mathcal{P}}|^{4/5}=(\prod _{i=1}^{r}|\unicode[STIX]{x1D6FA}_{i}|)^{4/5}$
, so
![]() $f_{1}(\prod _{i=2}^{r}|\unicode[STIX]{x1D6FA}_{i}|)^{1/5}<|\unicode[STIX]{x1D6FA}_{1}|^{4/5}$
. Since
$f_{1}(\prod _{i=2}^{r}|\unicode[STIX]{x1D6FA}_{i}|)^{1/5}<|\unicode[STIX]{x1D6FA}_{1}|^{4/5}$
. Since
![]() $(\prod _{i=2}^{r}|\unicode[STIX]{x1D6FA}_{i}|)^{1/5}\geqslant |\unicode[STIX]{x1D6FA}_{1}|^{(r-1)/5}$
, it follows that
$(\prod _{i=2}^{r}|\unicode[STIX]{x1D6FA}_{i}|)^{1/5}\geqslant |\unicode[STIX]{x1D6FA}_{1}|^{(r-1)/5}$
, it follows that
![]() $f_{1}<|\unicode[STIX]{x1D6FA}_{1}|^{1-r/5}$
. In particular,
$f_{1}<|\unicode[STIX]{x1D6FA}_{1}|^{1-r/5}$
. In particular,
![]() $1-r/5>0$
because
$1-r/5>0$
because
![]() $f_{1}\geqslant 1$
, and so
$f_{1}\geqslant 1$
, and so
![]() $r\leqslant 4$
.◻
$r\leqslant 4$
.◻
We also use Lemma 2.2 to sharpen the
![]() $4/5$
exponent bound in Theorem 1.3 in some special cases. The proofs are just modifications of the proof of Theorem 1.3, but since the details are somewhat tedious to check, we include them at the end of the paper, in Section 9, to save the reader having to reproduce them. We also remark that the exponent
$4/5$
exponent bound in Theorem 1.3 in some special cases. The proofs are just modifications of the proof of Theorem 1.3, but since the details are somewhat tedious to check, we include them at the end of the paper, in Section 9, to save the reader having to reproduce them. We also remark that the exponent
![]() $94/125=0.752$
in case (i) of Proposition 2.5 could be changed to
$94/125=0.752$
in case (i) of Proposition 2.5 could be changed to
![]() $3/4+\unicode[STIX]{x1D716}$
for any
$3/4+\unicode[STIX]{x1D716}$
for any
![]() $\unicode[STIX]{x1D716}>0$
at the expense of increasing the upper bound on
$\unicode[STIX]{x1D716}>0$
at the expense of increasing the upper bound on
![]() $s$
in case (ii), but that this would not have been useful for our arguments in Section 5.
$s$
in case (ii), but that this would not have been useful for our arguments in Section 5.
Proposition 2.4. Let
![]() ${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}})$
be a finite generalized quadrangle of order
${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}})$
be a finite generalized quadrangle of order
![]() $(s,t)$
, let
$(s,t)$
, let
![]() $\unicode[STIX]{x1D703}$
be any nonidentity collineation of
$\unicode[STIX]{x1D703}$
be any nonidentity collineation of
![]() ${\mathcal{Q}}$
, and let
${\mathcal{Q}}$
, and let
![]() ${\mathcal{Q}}_{\unicode[STIX]{x1D703}}=({\mathcal{P}}_{\unicode[STIX]{x1D703}},{\mathcal{L}}_{\unicode[STIX]{x1D703}})$
be the substructure of
${\mathcal{Q}}_{\unicode[STIX]{x1D703}}=({\mathcal{P}}_{\unicode[STIX]{x1D703}},{\mathcal{L}}_{\unicode[STIX]{x1D703}})$
be the substructure of
![]() ${\mathcal{Q}}$
fixed by
${\mathcal{Q}}$
fixed by
![]() $\unicode[STIX]{x1D703}$
. Then either
$\unicode[STIX]{x1D703}$
. Then either
(i)
 $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<|{\mathcal{P}}|^{7/9}$
,
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<|{\mathcal{P}}|^{7/9}$
,(ii)
 $s\in \{2,3\}$
,
$s\in \{2,3\}$
,
 $t=s^{2}$
and
$t=s^{2}$
and
 ${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
is a generalized quadrangle of order
${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
is a generalized quadrangle of order
 $(s,s)$
, or
$(s,s)$
, or(iii)
 $s\geqslant t+3$
,
$s\geqslant t+3$
,
 ${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
is a grid and
${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
is a grid and
 $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<s^{2}$
.
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<s^{2}$
.
Proposition 2.5. Let
![]() ${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}})$
be a finite generalized quadrangle of order
${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}})$
be a finite generalized quadrangle of order
![]() $(s,t)$
, let
$(s,t)$
, let
![]() $\unicode[STIX]{x1D703}$
be any nonidentity collineation of
$\unicode[STIX]{x1D703}$
be any nonidentity collineation of
![]() ${\mathcal{Q}}$
, and let
${\mathcal{Q}}$
, and let
![]() ${\mathcal{Q}}_{\unicode[STIX]{x1D703}}=({\mathcal{P}}_{\unicode[STIX]{x1D703}},{\mathcal{L}}_{\unicode[STIX]{x1D703}})$
be the substructure of
${\mathcal{Q}}_{\unicode[STIX]{x1D703}}=({\mathcal{P}}_{\unicode[STIX]{x1D703}},{\mathcal{L}}_{\unicode[STIX]{x1D703}})$
be the substructure of
![]() ${\mathcal{Q}}$
fixed by
${\mathcal{Q}}$
fixed by
![]() $\unicode[STIX]{x1D703}$
. Then either
$\unicode[STIX]{x1D703}$
. Then either
(i)
 $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<|{\mathcal{P}}|^{94/125}$
,
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<|{\mathcal{P}}|^{94/125}$
,(ii)
 $s<2.9701\times 10^{15}$
, or
$s<2.9701\times 10^{15}$
, or(iii)
 $s\geqslant t+3$
,
$s\geqslant t+3$
,
 ${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
is a grid and
${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
is a grid and
 $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<s^{2}$
.
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<s^{2}$
.
Proposition 2.6. Let
![]() ${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}})$
be a finite generalized quadrangle of order
${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}})$
be a finite generalized quadrangle of order
![]() $(s,t)$
, let
$(s,t)$
, let
![]() $\unicode[STIX]{x1D703}$
be any nonidentity collineation of
$\unicode[STIX]{x1D703}$
be any nonidentity collineation of
![]() ${\mathcal{Q}}$
, and let
${\mathcal{Q}}$
, and let
![]() ${\mathcal{P}}_{\unicode[STIX]{x1D703}}$
denote the set of points fixed by
${\mathcal{P}}_{\unicode[STIX]{x1D703}}$
denote the set of points fixed by
![]() $\unicode[STIX]{x1D703}$
. Suppose that
$\unicode[STIX]{x1D703}$
. Suppose that
![]() $t=s+2$
. Then
$t=s+2$
. Then
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<|{\mathcal{P}}|^{7/9}$
if
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<|{\mathcal{P}}|^{7/9}$
if
![]() $s\geqslant 3$
, and
$s\geqslant 3$
, and
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<|{\mathcal{P}}|^{13/18}$
if
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|<|{\mathcal{P}}|^{13/18}$
if
![]() $s\geqslant 5$
.
$s\geqslant 5$
.
3 Centralizer orders in nonabelian finite simple groups
Here we verify some lemmas about centralizer orders in nonabelian finite simple groups, from which Proposition 1.6 is immediately deduced. Specifically, we need to know which nonabelian finite simple groups
![]() $T$
contain nonidentity elements
$T$
contain nonidentity elements
![]() $x$
with “large” centralizers, in the sense that
$x$
with “large” centralizers, in the sense that
![]() $|C_{T}(x)|>|T|^{1-r/5}$
for
$|C_{T}(x)|>|T|^{1-r/5}$
for
![]() $r$
equal to one of
$r$
equal to one of
![]() $1$
,
$1$
,
![]() $2$
or
$2$
or
![]() $3$
. This question is readily and exactly answered for alternating groups and sporadic simple groups in the following two lemmas. Note that we treat the Tits group
$3$
. This question is readily and exactly answered for alternating groups and sporadic simple groups in the following two lemmas. Note that we treat the Tits group
![]() $^{2}\text{F}_{4}(2)^{\prime }$
in Lemma 3.2 along with the sporadic groups.
$^{2}\text{F}_{4}(2)^{\prime }$
in Lemma 3.2 along with the sporadic groups.
Lemma 3.1. Let
![]() $T\cong \text{Alt}_{n}$
with
$T\cong \text{Alt}_{n}$
with
![]() $n\geqslant 5$
. Then
$n\geqslant 5$
. Then
(i)
 $|C_{T}(x)|<|T|^{4/5}$
for all
$|C_{T}(x)|<|T|^{4/5}$
for all
 $x\in T\setminus \{1\}$
if and only if
$x\in T\setminus \{1\}$
if and only if
 $n\leqslant 18$
,
$n\leqslant 18$
,(ii)
 $|C_{T}(x)|<|T|^{3/5}$
for all
$|C_{T}(x)|<|T|^{3/5}$
for all
 $x\in T\setminus \{1\}$
if and only if
$x\in T\setminus \{1\}$
if and only if
 $n\leqslant 9$
,
$n\leqslant 9$
,(iii)
 $|C_{T}(x)|<|T|^{2/5}$
for all
$|C_{T}(x)|<|T|^{2/5}$
for all
 $x\in T\setminus \{1\}$
if and only if
$x\in T\setminus \{1\}$
if and only if
 $n\leqslant 6$
.
$n\leqslant 6$
.
Proof. If
![]() $n\geqslant 19$
and
$n\geqslant 19$
and
![]() $x\in T$
is a
$x\in T$
is a
![]() $3$
-cycle, then we have
$3$
-cycle, then we have
The remaining assertions are readily verified using GAP [15]. ◻
Lemma 3.2. Let
![]() $T$
be either a sporadic finite simple group or the Tits group
$T$
be either a sporadic finite simple group or the Tits group
![]() $^{2}\text{F}_{4}(2)^{\prime }$
. Then
$^{2}\text{F}_{4}(2)^{\prime }$
. Then
(i)
 $|C_{T}(x)|<|T|^{4/5}$
for all
$|C_{T}(x)|<|T|^{4/5}$
for all
 $x\in T\setminus \{1\}$
,
$x\in T\setminus \{1\}$
,(ii)
 $|C_{T}(x)|<|T|^{3/5}$
for all
$|C_{T}(x)|<|T|^{3/5}$
for all
 $x\in T\setminus \{1\}$
if and only if
$x\in T\setminus \{1\}$
if and only if
 $T\not \cong \text{Suz}$
,
$T\not \cong \text{Suz}$
,
 $\text{Co}_{2}$
,
$\text{Co}_{2}$
,
 $\text{Fi}_{22}$
,
$\text{Fi}_{22}$
,
 $\text{Fi}_{23}$
,
$\text{Fi}_{23}$
,
 $\text{B}$
or
$\text{B}$
or
 $\text{M}$
,
$\text{M}$
,(iii)
 $|C_{T}(x)|<|T|^{2/5}$
for all
$|C_{T}(x)|<|T|^{2/5}$
for all
 $x\in T\setminus \{1\}$
if and only if
$x\in T\setminus \{1\}$
if and only if
 $T\cong \text{J}_{1}$
.
$T\cong \text{J}_{1}$
.
Proof. This is readily verified by checking maximal centralizer orders in the ATLAS [Reference Conway, Curtis, Norton, Parker and Wilson10]. ◻
Next we consider the exceptional Lie type groups, namely those of type
![]() $\text{E}_{8}$
,
$\text{E}_{8}$
,
![]() $\text{E}_{7}$
,
$\text{E}_{7}$
,
![]() $\text{E}_{6}^{\unicode[STIX]{x1D700}}$
(where
$\text{E}_{6}^{\unicode[STIX]{x1D700}}$
(where
![]() $\unicode[STIX]{x1D700}=\pm$
),
$\unicode[STIX]{x1D700}=\pm$
),
![]() $\text{F}_{4}$
,
$\text{F}_{4}$
,
![]() $^{2}\text{F}_{4}$
,
$^{2}\text{F}_{4}$
,
![]() $\text{G}_{2}$
,
$\text{G}_{2}$
,
![]() $^{2}\text{G}_{2}$
,
$^{2}\text{G}_{2}$
,
![]() $^{3}\text{D}_{4}$
or
$^{3}\text{D}_{4}$
or
![]() $^{2}\text{B}_{2}$
. Note that we make no attempt to check the converse of assertion (i) (although this could be done using standard references including those cited here).
$^{2}\text{B}_{2}$
. Note that we make no attempt to check the converse of assertion (i) (although this could be done using standard references including those cited here).
Lemma 3.3. Let
![]() $T$
be a finite simple group of exceptional Lie type.
$T$
be a finite simple group of exceptional Lie type.
(i) If
 $T$
has type
$T$
has type
 $\text{E}_{8}$
,
$\text{E}_{8}$
,
 $\text{E}_{7}$
,
$\text{E}_{7}$
,
 $\text{E}_{6}^{\unicode[STIX]{x1D700}}$
,
$\text{E}_{6}^{\unicode[STIX]{x1D700}}$
,
 $\text{F}_{4}$
or
$\text{F}_{4}$
or
 $^{3}\text{D}_{4}$
, then there exists
$^{3}\text{D}_{4}$
, then there exists
 $x\in T\setminus \{1\}$
with
$x\in T\setminus \{1\}$
with
 $|C_{T}(x)|>|T|^{3/5}$
.
$|C_{T}(x)|>|T|^{3/5}$
.(ii)
 $|C_{T}(x)|<|T|^{2/5}$
for all
$|C_{T}(x)|<|T|^{2/5}$
for all
 $x\in T\setminus \{1\}$
if and only if
$x\in T\setminus \{1\}$
if and only if
 $T$
has type
$T$
has type
 $^{2}\text{B}_{2}$
.
$^{2}\text{B}_{2}$
.
Proof. (i) For
![]() $T\cong \text{E}_{8}(q)$
,
$T\cong \text{E}_{8}(q)$
,
![]() $\text{F}_{4}(q)$
or
$\text{F}_{4}(q)$
or
![]() $^{3}\text{D}_{4}(q)$
, take
$^{3}\text{D}_{4}(q)$
, take
![]() $x\in T$
to be a unipotent element of type
$x\in T$
to be a unipotent element of type
![]() $\text{A}_{1}$
in the sense of [Reference Liebeck and Seitz18, Tables 22.2.1 and 22.2.4] and [Reference Spaltenstein23], respectively. Then
$\text{A}_{1}$
in the sense of [Reference Liebeck and Seitz18, Tables 22.2.1 and 22.2.4] and [Reference Spaltenstein23], respectively. Then
![]() $|C_{T}(x)|=q^{57}|\text{E}_{7}(q)|$
,
$|C_{T}(x)|=q^{57}|\text{E}_{7}(q)|$
,
![]() $q^{15}|\text{C}_{3}(q)|$
or
$q^{15}|\text{C}_{3}(q)|$
or
![]() $q^{12}(q^{6}-1)$
, respectively, and it is readily checked that
$q^{12}(q^{6}-1)$
, respectively, and it is readily checked that
![]() $|C_{T}(x)|>|T|^{3/5}$
in each case. Now suppose that
$|C_{T}(x)|>|T|^{3/5}$
in each case. Now suppose that
![]() $T\cong \text{E}_{7}(q)$
or
$T\cong \text{E}_{7}(q)$
or
![]() $\text{E}_{6}^{\unicode[STIX]{x1D700}}(q)$
, and write
$\text{E}_{6}^{\unicode[STIX]{x1D700}}(q)$
, and write
![]() $G:=\text{Inndiag}(T)$
. Take
$G:=\text{Inndiag}(T)$
. Take
![]() $x\in T$
to be a unipotent element of type
$x\in T$
to be a unipotent element of type
![]() $\text{A}_{1}$
in the sense of [Reference Liebeck and Seitz18, Tables 22.2.2 and 22.2.3], respectively. Then
$\text{A}_{1}$
in the sense of [Reference Liebeck and Seitz18, Tables 22.2.2 and 22.2.3], respectively. Then
![]() $x^{T}=x^{G}$
by [Reference Burness and Giudici9, Corollary 17.10], so we have
$x^{T}=x^{G}$
by [Reference Burness and Giudici9, Corollary 17.10], so we have
![]() $|C_{T}(x)|=|C_{G}(x)|/|G:T|=q^{33}|\text{D}_{6}(q)|/\text{gcd}(2,q-1)$
or
$|C_{T}(x)|=|C_{G}(x)|/|G:T|=q^{33}|\text{D}_{6}(q)|/\text{gcd}(2,q-1)$
or
![]() $q^{21}|\text{A}_{5}^{\unicode[STIX]{x1D700}}(q)|/\text{gcd}(3,q-\unicode[STIX]{x1D700})$
, respectively, and again one can check that
$q^{21}|\text{A}_{5}^{\unicode[STIX]{x1D700}}(q)|/\text{gcd}(3,q-\unicode[STIX]{x1D700})$
, respectively, and again one can check that
![]() $|C_{T}(x)|>|T|^{3/5}$
in each case.
$|C_{T}(x)|>|T|^{3/5}$
in each case.
(ii) If
![]() $T\cong ^{2}\text{B}_{2}(q)$
then
$T\cong ^{2}\text{B}_{2}(q)$
then
![]() $|C_{T}(x)|\leqslant q^{2}<(q^{2}(q^{2}+1)(q-1))^{2/5}=|T|^{2/5}$
for all
$|C_{T}(x)|\leqslant q^{2}<(q^{2}(q^{2}+1)(q-1))^{2/5}=|T|^{2/5}$
for all
![]() $x\in T\setminus \{1\}$
[Reference Suzuki24]. It remains to check that
$x\in T\setminus \{1\}$
[Reference Suzuki24]. It remains to check that
![]() $|C_{T}(x)|>|T|^{2/5}$
for some
$|C_{T}(x)|>|T|^{2/5}$
for some
![]() $x\in T\setminus \{1\}$
when
$x\in T\setminus \{1\}$
when
![]() $T$
has type
$T$
has type
![]() $^{2}\text{F}_{4}$
,
$^{2}\text{F}_{4}$
,
![]() $\text{G}_{2}$
or
$\text{G}_{2}$
or
![]() $^{2}\text{G}_{2}$
. In these respective cases, take
$^{2}\text{G}_{2}$
. In these respective cases, take
![]() $x$
to be a unipotent element of type
$x$
to be a unipotent element of type
![]() $(\tilde{\text{A}}_{1})_{2}$
,
$(\tilde{\text{A}}_{1})_{2}$
,
![]() $\text{A}_{1}$
or
$\text{A}_{1}$
or
![]() $(\tilde{\text{A}}_{1})_{3}$
in the sense of [Reference Liebeck and Seitz18, Tables 22.2.5–22.2.7], so that
$(\tilde{\text{A}}_{1})_{3}$
in the sense of [Reference Liebeck and Seitz18, Tables 22.2.5–22.2.7], so that
![]() $|C_{T}(x)|=q^{10}|^{2}\text{B}_{2}(q)|$
,
$|C_{T}(x)|=q^{10}|^{2}\text{B}_{2}(q)|$
,
![]() $q^{5}|\text{A}_{1}(q)|$
or
$q^{5}|\text{A}_{1}(q)|$
or
![]() $q^{3}$
.◻
$q^{3}$
.◻
Finally, we consider the finite simple classical groups. Again, we do not check the converses of assertions (i) or (ii), remarking only that one could do so using the monograph [Reference Burness and Giudici9] of Burness and Giuidici, where the conjugacy classes of elements of prime order in these groups are classified.
Lemma 3.4. Let
![]() $T$
be a finite simple classical group.
$T$
be a finite simple classical group.
(i) If
 $T$
has type
$T$
has type
 $\text{A}_{n}^{\unicode[STIX]{x1D700}}$
,
$\text{A}_{n}^{\unicode[STIX]{x1D700}}$
,
 $\text{D}_{n}$
or
$\text{D}_{n}$
or
 $^{2}\text{D}_{n}$
with
$^{2}\text{D}_{n}$
with
 $n\geqslant 9$
, or type
$n\geqslant 9$
, or type
 $\text{B}_{n}$
or
$\text{B}_{n}$
or
 $\text{C}_{n}$
with
$\text{C}_{n}$
with
 $n\geqslant 5$
, then there exists
$n\geqslant 5$
, then there exists
 $x\in T\setminus \{1\}$
with
$x\in T\setminus \{1\}$
with
 $|C_{T}(x)|>|T|^{4/5}$
.
$|C_{T}(x)|>|T|^{4/5}$
.(ii) If
 $T$
has type
$T$
has type
 $\text{A}_{n}^{\unicode[STIX]{x1D700}}$
with
$\text{A}_{n}^{\unicode[STIX]{x1D700}}$
with
 $n\geqslant 4$
, type
$n\geqslant 4$
, type
 $\text{B}_{n}$
or
$\text{B}_{n}$
or
 $\text{C}_{n}$
with
$\text{C}_{n}$
with
 $n\geqslant 3$
, or type
$n\geqslant 3$
, or type
 $\text{D}_{n}$
or
$\text{D}_{n}$
or
 $^{2}\text{D}_{n}$
with
$^{2}\text{D}_{n}$
with
 $n\geqslant 4$
, then there exists
$n\geqslant 4$
, then there exists
 $x\in T\setminus \{1\}$
with
$x\in T\setminus \{1\}$
with
 $|C_{T}(x)|>|T|^{3/5}$
.
$|C_{T}(x)|>|T|^{3/5}$
.(iii)
 $|C_{T}(x)|<|T|^{2/5}$
for all
$|C_{T}(x)|<|T|^{2/5}$
for all
 $x\in T\setminus \{1\}$
if and only if
$x\in T\setminus \{1\}$
if and only if
 $T\cong \text{PSL}_{2}(q)$
with
$T\cong \text{PSL}_{2}(q)$
with
 $q\neq 7$
.
$q\neq 7$
.
Proof. Throughout the proof, we write
![]() $q=p^{f}$
with
$q=p^{f}$
with
![]() $p$
a prime and
$p$
a prime and
![]() $f\geqslant 1$
. First suppose that
$f\geqslant 1$
. First suppose that
![]() $T$
has type
$T$
has type
![]() $\text{A}_{1}$
. That is,
$\text{A}_{1}$
. That is,
![]() $T\cong \text{PSL}_{2}(q)$
, with
$T\cong \text{PSL}_{2}(q)$
, with
![]() $q\geqslant 4$
. The smallest nontrivial conjugacy class of
$q\geqslant 4$
. The smallest nontrivial conjugacy class of
![]() $T$
has size
$T$
has size
![]() $q(q-1)$
,
$q(q-1)$
,
![]() ${\textstyle \frac{1}{2}}(q^{2}-1)$
or
${\textstyle \frac{1}{2}}(q^{2}-1)$
or
![]() ${\textstyle \frac{1}{2}}q(q-1)$
according to whether
${\textstyle \frac{1}{2}}q(q-1)$
according to whether
![]() $p=2$
,
$p=2$
,
![]() $q\equiv 1\;(\text{mod}\;4)$
or
$q\equiv 1\;(\text{mod}\;4)$
or
![]() $q\equiv 3\;(\text{mod}\;4)$
. Hence, every nontrivial conjugacy class of
$q\equiv 3\;(\text{mod}\;4)$
. Hence, every nontrivial conjugacy class of
![]() $T$
has size greater than
$T$
has size greater than
![]() $|T|^{3/5}$
if and only if
$|T|^{3/5}$
if and only if
![]() $q\neq 7$
. Equivalently,
$q\neq 7$
. Equivalently,
![]() $|C_{T}(x)|<|T|^{2/5}$
for all
$|C_{T}(x)|<|T|^{2/5}$
for all
![]() $x\in T\setminus \{1\}$
if and only if
$x\in T\setminus \{1\}$
if and only if
![]() $q\neq 7$
.
$q\neq 7$
.
Now suppose that
![]() $T$
has type
$T$
has type
![]() $\text{A}_{n}^{\unicode[STIX]{x1D700}}$
with
$\text{A}_{n}^{\unicode[STIX]{x1D700}}$
with
![]() $n\geqslant 2$
. That is,
$n\geqslant 2$
. That is,
![]() $T\cong \text{PSL}_{n+1}^{\unicode[STIX]{x1D700}}(q)$
(where we write
$T\cong \text{PSL}_{n+1}^{\unicode[STIX]{x1D700}}(q)$
(where we write
![]() $\text{L}^{+}:=\text{L}$
and
$\text{L}^{+}:=\text{L}$
and
![]() $\text{L}^{-}:=\text{U}$
). Let
$\text{L}^{-}:=\text{U}$
). Let
![]() $x\in G:=\text{PGL}_{n+1}^{\unicode[STIX]{x1D700}}(q)$
be an element of order
$x\in G:=\text{PGL}_{n+1}^{\unicode[STIX]{x1D700}}(q)$
be an element of order
![]() $p$
with one Jordan block of size
$p$
with one Jordan block of size
![]() $2$
and
$2$
and
![]() $n-1$
Jordan blocks of size
$n-1$
Jordan blocks of size
![]() $1$
. That is,
$1$
. That is,
![]() $a_{1}=n-1$
,
$a_{1}=n-1$
,
![]() $a_{2}=1$
and
$a_{2}=1$
and
![]() $a_{3}=\cdots =a_{p}=0$
in the notation of [Reference Burness and Giudici9, Section 3.2.3]. Then
$a_{3}=\cdots =a_{p}=0$
in the notation of [Reference Burness and Giudici9, Section 3.2.3]. Then
![]() $x\in T$
, and
$x\in T$
, and
![]() $x^{T}=x^{G}$
by [Reference Burness and Giudici9, Propositions 3.2.7 and 3.3.10], so by [Reference Burness and Giudici9, Tables B.3 and B.4],
$x^{T}=x^{G}$
by [Reference Burness and Giudici9, Propositions 3.2.7 and 3.3.10], so by [Reference Burness and Giudici9, Tables B.3 and B.4],
![]() $|C_{T}(x)|=|C_{G}(x)|/|G:T|=(1/d)|C_{G}(x)|=(1/d)q^{2n-1}|\text{GL}_{n-1}^{\unicode[STIX]{x1D700}}(q)|$
, where
$|C_{T}(x)|=|C_{G}(x)|/|G:T|=(1/d)|C_{G}(x)|=(1/d)q^{2n-1}|\text{GL}_{n-1}^{\unicode[STIX]{x1D700}}(q)|$
, where
![]() $d:=\gcd (n+1,q-\unicode[STIX]{x1D700})$
. Hence
$d:=\gcd (n+1,q-\unicode[STIX]{x1D700})$
. Hence
For
![]() $n\in \{2,3\}$
we must show that
$n\in \{2,3\}$
we must show that
![]() $|C_{T}(x)|>|T|^{2/5}$
. If
$|C_{T}(x)|>|T|^{2/5}$
. If
![]() $n=2$
then
$n=2$
then
![]() $d\leqslant 3$
, so
$d\leqslant 3$
, so
![]() $|C_{T}(x)|\geqslant {\textstyle \frac{1}{3}}q^{3}(q-\unicode[STIX]{x1D700})$
while
$|C_{T}(x)|\geqslant {\textstyle \frac{1}{3}}q^{3}(q-\unicode[STIX]{x1D700})$
while
![]() $|T|\leqslant q^{3}(q^{2}-\unicode[STIX]{x1D700}^{2})(q^{3}-\unicode[STIX]{x1D700}^{3})$
. This implies that
$|T|\leqslant q^{3}(q^{2}-\unicode[STIX]{x1D700}^{2})(q^{3}-\unicode[STIX]{x1D700}^{3})$
. This implies that
![]() $|C_{T}(x)|>|T|^{2/5}$
for all
$|C_{T}(x)|>|T|^{2/5}$
for all
![]() $q\geqslant 7$
, and one may check directly that this inequality also holds for
$q\geqslant 7$
, and one may check directly that this inequality also holds for
![]() $q<7$
. If
$q<7$
. If
![]() $n=3$
then
$n=3$
then
![]() $d\leqslant 4$
, so
$d\leqslant 4$
, so
![]() $|C_{T}(x)|\geqslant {\textstyle \frac{1}{4}}q^{6}(q-\unicode[STIX]{x1D700})(q^{2}-\unicode[STIX]{x1D700}^{2})$
while
$|C_{T}(x)|\geqslant {\textstyle \frac{1}{4}}q^{6}(q-\unicode[STIX]{x1D700})(q^{2}-\unicode[STIX]{x1D700}^{2})$
while
![]() $|T|\leqslant q^{6}(q^{2}-\unicode[STIX]{x1D700}^{2})(q^{3}-\unicode[STIX]{x1D700}^{3})(q^{4}-\unicode[STIX]{x1D700}^{4})$
. This implies that
$|T|\leqslant q^{6}(q^{2}-\unicode[STIX]{x1D700}^{2})(q^{3}-\unicode[STIX]{x1D700}^{3})(q^{4}-\unicode[STIX]{x1D700}^{4})$
. This implies that
![]() $|C_{T}(x)|>|T|^{2/5}$
for all
$|C_{T}(x)|>|T|^{2/5}$
for all
![]() $q\geqslant 3$
, and a direct calculation shows that this inequality also holds for
$q\geqslant 3$
, and a direct calculation shows that this inequality also holds for
![]() $q=2$
. Now suppose that
$q=2$
. Now suppose that
![]() $4\leqslant n\leqslant 8$
. We must show that
$4\leqslant n\leqslant 8$
. We must show that
![]() $|C_{T}(x)|>|T|^{3/5}$
. Since
$|C_{T}(x)|>|T|^{3/5}$
. Since
![]() $q\geqslant 2$
, (1) gives
$q\geqslant 2$
, (1) gives
and so it suffices to show that
![]() $q^{2n^{2}-6n}>d^{2}2^{2n-5}3^{3n}$
. Indeed, since
$q^{2n^{2}-6n}>d^{2}2^{2n-5}3^{3n}$
. Indeed, since
![]() $d\leqslant n+1$
, it suffices to show that
$d\leqslant n+1$
, it suffices to show that
![]() $q^{2n^{2}-6n}>(n+1)^{2}2^{2n-5}3^{3n}$
. This inequality holds for all
$q^{2n^{2}-6n}>(n+1)^{2}2^{2n-5}3^{3n}$
. This inequality holds for all
![]() $q\geqslant 2$
if
$q\geqslant 2$
if
![]() $n\in \{7,8\}$
, for all
$n\in \{7,8\}$
, for all
![]() $q\geqslant 3$
if
$q\geqslant 3$
if
![]() $n=6$
, for all
$n=6$
, for all
![]() $q\geqslant 4$
if
$q\geqslant 4$
if
![]() $n=5$
, and for all
$n=5$
, and for all
![]() $q\geqslant 11$
if
$q\geqslant 11$
if
![]() $n=4$
. In the remaining cases, where
$n=4$
. In the remaining cases, where
![]() $(n,q)=(6,2)$
,
$(n,q)=(6,2)$
,
![]() $(5,2)$
,
$(5,2)$
,
![]() $(5,3)$
, or
$(5,3)$
, or
![]() $(4,q)$
with
$(4,q)$
with
![]() $q<11$
, one may check directly that
$q<11$
, one may check directly that
![]() $|C_{T}(x)|>|T|^{3/5}$
. It remains to show that
$|C_{T}(x)|>|T|^{3/5}$
. It remains to show that
![]() $|C_{T}(x)|>|T|^{4/5}$
for all
$|C_{T}(x)|>|T|^{4/5}$
for all
![]() $q\geqslant 2$
when
$q\geqslant 2$
when
![]() $n\geqslant 9$
. If
$n\geqslant 9$
. If
![]() $q\geqslant 3$
then (1) gives
$q\geqslant 3$
then (1) gives
so it suffices to show that
![]() $q^{n^{2}-8n}>d\cdot 2^{3n+5}3^{n-5}$
. Indeed, since
$q^{n^{2}-8n}>d\cdot 2^{3n+5}3^{n-5}$
. Indeed, since
![]() $d\leqslant n+1$
, we can just show that
$d\leqslant n+1$
, we can just show that
![]() $q^{n^{2}-8n}>(n+1)2^{3n+5}3^{n-5}$
. This inequality holds for all
$q^{n^{2}-8n}>(n+1)2^{3n+5}3^{n-5}$
. This inequality holds for all
![]() $q\geqslant 3$
if
$q\geqslant 3$
if
![]() $n\geqslant 11$
; if
$n\geqslant 11$
; if
![]() $n=10$
, it holds for all
$n=10$
, it holds for all
![]() $q\geqslant 5$
, and if
$q\geqslant 5$
, and if
![]() $n=9$
, it holds for all
$n=9$
, it holds for all
![]() $q\geqslant 29$
. For
$q\geqslant 29$
. For
![]() $n=10$
with
$n=10$
with
![]() $2\leqslant q<5$
, and
$2\leqslant q<5$
, and
![]() $n=9$
with
$n=9$
with
![]() $2\leqslant q<29$
, one may check directly that
$2\leqslant q<29$
, one may check directly that
![]() $|C_{T}(x)|>|T|^{4/5}$
. Finally, we must check that
$|C_{T}(x)|>|T|^{4/5}$
. Finally, we must check that
![]() $|C_{T}(x)|>|T|^{4/5}$
when
$|C_{T}(x)|>|T|^{4/5}$
when
![]() $q=2$
and
$q=2$
and
![]() $n\geqslant 9$
. Since
$n\geqslant 9$
. Since
![]() $n\geqslant 9$
, and since
$n\geqslant 9$
, and since
![]() ${\textstyle \frac{255}{256}}q^{i}\leqslant q^{i}-\unicode[STIX]{x1D700}\leqslant {\textstyle \frac{257}{256}}q^{i}$
for
${\textstyle \frac{255}{256}}q^{i}\leqslant q^{i}-\unicode[STIX]{x1D700}\leqslant {\textstyle \frac{257}{256}}q^{i}$
for
![]() $i\geqslant 8$
, (1) gives
$i\geqslant 8$
, (1) gives
and
Noting also that
![]() $d\leqslant 3$
, we see that it suffices to show that
$d\leqslant 3$
, we see that it suffices to show that
This holds for all
![]() $n\geqslant 9$
, and so the proof of the
$n\geqslant 9$
, and so the proof of the
![]() $\text{A}_{n}^{\unicode[STIX]{x1D700}}$
case is complete.
$\text{A}_{n}^{\unicode[STIX]{x1D700}}$
case is complete.
Next, suppose that
![]() $T$
has type
$T$
has type
![]() $\text{C}_{n}$
, where
$\text{C}_{n}$
, where
![]() $n\geqslant 2$
. That is,
$n\geqslant 2$
. That is,
![]() $T\cong \text{PSp}_{2n}(q)$
. Write
$T\cong \text{PSp}_{2n}(q)$
. Write
![]() $G:=\text{PGSp}_{2n}(q)$
, noting that
$G:=\text{PGSp}_{2n}(q)$
, noting that
![]() $|G:T|=\gcd (2,q-1)$
. If
$|G:T|=\gcd (2,q-1)$
. If
![]() $p>2$
, take
$p>2$
, take
![]() $x\in G$
of order
$x\in G$
of order
![]() $p$
with one Jordan block of size
$p$
with one Jordan block of size
![]() $2$
and
$2$
and
![]() $2(n-1)$
Jordan blocks of size
$2(n-1)$
Jordan blocks of size
![]() $1$
. That is,
$1$
. That is,
![]() $a_{1}=2(n-1)$
,
$a_{1}=2(n-1)$
,
![]() $a_{2}=1$
and
$a_{2}=1$
and
![]() $a_{3}=\cdots =a_{p}=0$
in the notation of [Reference Burness and Giudici9, Section 3.4.3]. Then
$a_{3}=\cdots =a_{p}=0$
in the notation of [Reference Burness and Giudici9, Section 3.4.3]. Then
![]() $x\in T$
, and by [Reference Burness and Giudici9, Proposition 3.4.12],
$x\in T$
, and by [Reference Burness and Giudici9, Proposition 3.4.12],
![]() $x^{G}$
splits into two
$x^{G}$
splits into two
![]() $T$
-conjugacy classes and hence
$T$
-conjugacy classes and hence
![]() $|C_{T}(x)|=2|C_{G}(x)|/|G:T|={\textstyle \frac{1}{2}}q^{2n-1}|\text{Sp}_{2(n-1)}(q)|$
. If
$|C_{T}(x)|=2|C_{G}(x)|/|G:T|={\textstyle \frac{1}{2}}q^{2n-1}|\text{Sp}_{2(n-1)}(q)|$
. If
![]() $p=2$
then
$p=2$
then
![]() $T=G$
and we take
$T=G$
and we take
![]() $x$
to be an involution of type
$x$
to be an involution of type
![]() $b_{1}$
as in [Reference Burness and Giudici9, Table 3.4.1], so that
$b_{1}$
as in [Reference Burness and Giudici9, Table 3.4.1], so that
![]() $|C_{T}(x)|=q^{2n-1}|\text{Sp}_{2(n-1)}(q)|$
. Hence, for every
$|C_{T}(x)|=q^{2n-1}|\text{Sp}_{2(n-1)}(q)|$
. Hence, for every
![]() $p$
, we have
$p$
, we have
where
![]() $d=\gcd (2,q-1)\leqslant 2$
. If
$d=\gcd (2,q-1)\leqslant 2$
. If
![]() $n=2$
then
$n=2$
then
![]() $|C_{T}(x)|\geqslant {\textstyle \frac{1}{2}}q^{4}(q^{2}-1)$
and
$|C_{T}(x)|\geqslant {\textstyle \frac{1}{2}}q^{4}(q^{2}-1)$
and
![]() $|T|\leqslant q^{4}(q^{2}-1)(q^{4}-1)$
, and it follows that
$|T|\leqslant q^{4}(q^{2}-1)(q^{4}-1)$
, and it follows that
![]() $|C_{T}(x)|>|T|^{2/5}$
for all
$|C_{T}(x)|>|T|^{2/5}$
for all
![]() $q\geqslant 2$
. Similarly, for
$q\geqslant 2$
. Similarly, for
![]() $n\in \{3,4\}$
one may check that
$n\in \{3,4\}$
one may check that
![]() $|C_{T}(x)|>|T|^{3/5}$
for all
$|C_{T}(x)|>|T|^{3/5}$
for all
![]() $q\geqslant 2$
. Now suppose that
$q\geqslant 2$
. Now suppose that
![]() $n\geqslant 5$
. Since
$n\geqslant 5$
. Since
![]() $q^{2i}\geqslant 4$
, we have
$q^{2i}\geqslant 4$
, we have
![]() $q^{2i}-1\geqslant {\textstyle \frac{3}{4}}q^{2i}$
for all
$q^{2i}-1\geqslant {\textstyle \frac{3}{4}}q^{2i}$
for all
![]() $i\geqslant 1$
, and so
$i\geqslant 1$
, and so
![]() $|C_{T}(x)|\geqslant {\textstyle \frac{1}{2}}({\textstyle \frac{3}{4}})^{n-1}q^{2n^{2}-n}$
, while
$|C_{T}(x)|\geqslant {\textstyle \frac{1}{2}}({\textstyle \frac{3}{4}})^{n-1}q^{2n^{2}-n}$
, while
![]() $|T|<q^{2n^{2}+n}$
. Hence, to show that
$|T|<q^{2n^{2}+n}$
. Hence, to show that
![]() $|C_{T}(x)|>|T|^{4/5}$
, it suffices to show that
$|C_{T}(x)|>|T|^{4/5}$
, it suffices to show that
![]() $({\textstyle \frac{3}{4}})^{5n-5}q^{2n^{2}-9n}>2$
. This inequality holds for all
$({\textstyle \frac{3}{4}})^{5n-5}q^{2n^{2}-9n}>2$
. This inequality holds for all
![]() $q\geqslant 2$
when
$q\geqslant 2$
when
![]() $n\geqslant 6$
, and for all
$n\geqslant 6$
, and for all
![]() $q\geqslant 4$
when
$q\geqslant 4$
when
![]() $n=5$
; for
$n=5$
; for
![]() $(n,q)=(5,2)$
and
$(n,q)=(5,2)$
and
![]() $(5,3)$
, one may check directly that
$(5,3)$
, one may check directly that
![]() $|C_{T}(x)|>|T|^{4/5}$
.
$|C_{T}(x)|>|T|^{4/5}$
.
Now suppose that
![]() $T$
has type
$T$
has type
![]() $\text{B}_{n}$
, where
$\text{B}_{n}$
, where
![]() $n\geqslant 2$
. That is,
$n\geqslant 2$
. That is,
![]() $T\cong \unicode[STIX]{x1D6FA}_{2n+1}(q)$
with
$T\cong \unicode[STIX]{x1D6FA}_{2n+1}(q)$
with
![]() $q$
odd. For
$q$
odd. For
![]() $q\equiv 1$
or
$q\equiv 1$
or
![]() $3\;(\text{mod}\;4)$
, let
$3\;(\text{mod}\;4)$
, let
![]() $x\in G:=\text{PGO}_{2n+1}(q)$
be an involution of type
$x\in G:=\text{PGO}_{2n+1}(q)$
be an involution of type
![]() $t_{n}$
or
$t_{n}$
or
![]() $t_{n}^{\prime }$
, respectively, in the sense of [Reference Burness and Giudici9, Sections 3.5.2.1 and 3.5.2.2]. Then
$t_{n}^{\prime }$
, respectively, in the sense of [Reference Burness and Giudici9, Sections 3.5.2.1 and 3.5.2.2]. Then
![]() $x\in T$
and
$x\in T$
and
![]() $x^{T}=x^{G}$
, so
$x^{T}=x^{G}$
, so
![]() $|C_{T}(x)|=|C_{G}(x)|/|G:T|={\textstyle \frac{1}{2}}|C_{G}(x)|=|\text{SO}_{2n}^{\pm }(q)|$
by [Reference Burness and Giudici9, Table B.8]. Now,
$|C_{T}(x)|=|C_{G}(x)|/|G:T|={\textstyle \frac{1}{2}}|C_{G}(x)|=|\text{SO}_{2n}^{\pm }(q)|$
by [Reference Burness and Giudici9, Table B.8]. Now,
and the right-hand side above is the value of
![]() $|C_{T}(x)|$
that we obtained in the
$|C_{T}(x)|$
that we obtained in the
![]() $\text{C}_{n}$
case. Since
$\text{C}_{n}$
case. Since
![]() $|\unicode[STIX]{x1D6FA}_{2n+1}(q)|=|\text{PSp}_{2n}(q)|$
, we therefore reach the same conclusions as for type
$|\unicode[STIX]{x1D6FA}_{2n+1}(q)|=|\text{PSp}_{2n}(q)|$
, we therefore reach the same conclusions as for type
![]() $\text{C}_{n}$
.
$\text{C}_{n}$
.
Now suppose that
![]() $T$
has type
$T$
has type
![]() $\text{D}_{n}^{\unicode[STIX]{x1D700}}$
, namely
$\text{D}_{n}^{\unicode[STIX]{x1D700}}$
, namely
![]() $T\cong \text{P}\unicode[STIX]{x1D6FA}_{2n}^{\unicode[STIX]{x1D700}}(q)$
with
$T\cong \text{P}\unicode[STIX]{x1D6FA}_{2n}^{\unicode[STIX]{x1D700}}(q)$
with
![]() $n\geqslant 4$
. Let
$n\geqslant 4$
. Let
![]() $G:=\text{Inndiag}(\text{P}\unicode[STIX]{x1D6FA}_{2n}^{\unicode[STIX]{x1D700}}(q))$
, as defined on [Reference Burness and Giudici9, page 56]. Assume first that
$G:=\text{Inndiag}(\text{P}\unicode[STIX]{x1D6FA}_{2n}^{\unicode[STIX]{x1D700}}(q))$
, as defined on [Reference Burness and Giudici9, page 56]. Assume first that
![]() $p>2$
, noting that
$p>2$
, noting that
![]() $|G:T|$
divides
$|G:T|$
divides
![]() $4$
. Take
$4$
. Take
![]() $x\in G$
of order
$x\in G$
of order
![]() $p$
with one Jordan block of size
$p$
with one Jordan block of size
![]() $2(n-2)$
and two Jordan blocks of size
$2(n-2)$
and two Jordan blocks of size
![]() $2$
. That is,
$2$
. That is,
![]() $a_{1}=2(n-2)$
,
$a_{1}=2(n-2)$
,
![]() $a_{2}=2$
and
$a_{2}=2$
and
![]() $a_{3}=\cdots =a_{p}=0$
in the notation of [Reference Burness and Giudici9, Section 3.5.3]. Then
$a_{3}=\cdots =a_{p}=0$
in the notation of [Reference Burness and Giudici9, Section 3.5.3]. Then
![]() $x\in T$
, and [Reference Burness and Giudici9, Propositions 3.5.14(i) and (ii,b)] imply that
$x\in T$
, and [Reference Burness and Giudici9, Propositions 3.5.14(i) and (ii,b)] imply that
![]() $x^{T}=x^{G}$
. Therefore, [Reference Burness and Giudici9, Table B.12] gives
$x^{T}=x^{G}$
. Therefore, [Reference Burness and Giudici9, Table B.12] gives
![]() $|C_{T}(x)|=|C_{G}(x)|/|G:T|\geqslant {\textstyle \frac{1}{4}}|C_{G}(x)|={\textstyle \frac{1}{8}}q^{4n-7}|\text{O}_{2(n-2)}^{\unicode[STIX]{x1D700}_{1}}(q)||\text{Sp}_{2}(q)|$
, where the value of
$|C_{T}(x)|=|C_{G}(x)|/|G:T|\geqslant {\textstyle \frac{1}{4}}|C_{G}(x)|={\textstyle \frac{1}{8}}q^{4n-7}|\text{O}_{2(n-2)}^{\unicode[STIX]{x1D700}_{1}}(q)||\text{Sp}_{2}(q)|$
, where the value of
![]() $\unicode[STIX]{x1D700}_{1}=\pm$
depends on
$\unicode[STIX]{x1D700}_{1}=\pm$
depends on
![]() $n$
and
$n$
and
![]() $q$
as described there. Multiplying the inequality in (3) by
$q$
as described there. Multiplying the inequality in (3) by
![]() $2$
to get a lower bound for
$2$
to get a lower bound for
![]() $|\text{O}_{2(n-2)}^{\unicode[STIX]{x1D700}_{1}}(q)|$
, it follows that
$|\text{O}_{2(n-2)}^{\unicode[STIX]{x1D700}_{1}}(q)|$
, it follows that
while
where
![]() $d=\gcd (4,q^{n}-\unicode[STIX]{x1D700})$
. Since
$d=\gcd (4,q^{n}-\unicode[STIX]{x1D700})$
. Since
![]() $q^{2i}\geqslant 9$
for all
$q^{2i}\geqslant 9$
for all
![]() $i\geqslant 1$
, and in particular
$i\geqslant 1$
, and in particular
![]() $q^{n}\geqslant 3^{4}=81$
, we have
$q^{n}\geqslant 3^{4}=81$
, we have
For
![]() $4\leqslant n\leqslant 8$
we need
$4\leqslant n\leqslant 8$
we need
![]() $|C_{T}(x)|>|T|^{3/5}$
, so by (6) it suffices to show that
$|C_{T}(x)|>|T|^{3/5}$
, so by (6) it suffices to show that
![]() $({\textstyle \frac{8}{9}})^{5n-10}q^{4n^{2}-22n+30}>8^{5}({\textstyle \frac{82}{81}})^{3}$
, which holds unless
$({\textstyle \frac{8}{9}})^{5n-10}q^{4n^{2}-22n+30}>8^{5}({\textstyle \frac{82}{81}})^{3}$
, which holds unless
![]() $(n,q)=(4,3)$
or
$(n,q)=(4,3)$
or
![]() $(4,5)$
. For
$(4,5)$
. For
![]() $(n,q)=(4,5)$
, (4)–(5) imply that
$(n,q)=(4,5)$
, (4)–(5) imply that
![]() $|C_{T}(x)|>|T|^{3/5}$
; for
$|C_{T}(x)|>|T|^{3/5}$
; for
![]() $(n,q)=(4,3)$
, a GAP [15] calculation shows that there exists an elements
$(n,q)=(4,3)$
, a GAP [15] calculation shows that there exists an elements
![]() $x\in T\setminus \{1\}$
for which this inequality holds. For
$x\in T\setminus \{1\}$
for which this inequality holds. For
![]() $n\geqslant 9$
we claim that
$n\geqslant 9$
we claim that
![]() $|C_{T}(x)|>|T|^{4/5}$
, and we now have
$|C_{T}(x)|>|T|^{4/5}$
, and we now have
![]() $q^{n}\geqslant 3^{9}=19683$
, so we can replace the
$q^{n}\geqslant 3^{9}=19683$
, so we can replace the
![]() ${\textstyle \frac{82}{81}}$
in (6) by
${\textstyle \frac{82}{81}}$
in (6) by
![]() ${\textstyle \frac{19684}{19683}}$
to see that it suffices to show that
${\textstyle \frac{19684}{19683}}$
to see that it suffices to show that
![]() $({\textstyle \frac{8}{9}})^{5n-10}q^{2n^{2}-21n+30}>8^{5}({\textstyle \frac{19684}{19683}})^{4}$
. If
$({\textstyle \frac{8}{9}})^{5n-10}q^{2n^{2}-21n+30}>8^{5}({\textstyle \frac{19684}{19683}})^{4}$
. If
![]() $n\geqslant 10$
then this inequality holds for all
$n\geqslant 10$
then this inequality holds for all
![]() $q\geqslant 3$
, and if
$q\geqslant 3$
, and if
![]() $n=9$
then it holds for
$n=9$
then it holds for
![]() $q\geqslant 127$
. For
$q\geqslant 127$
. For
![]() $n=9$
and
$n=9$
and
![]() $q<127$
, using the equality in (3) we obtain
$q<127$
, using the equality in (3) we obtain
which implies that
![]() $|C_{T}(x)|>|T|^{4/5}$
except when
$|C_{T}(x)|>|T|^{4/5}$
except when
![]() $q=3$
and
$q=3$
and
![]() $\unicode[STIX]{x1D700}=+$
. However, in this case we have
$\unicode[STIX]{x1D700}=+$
. However, in this case we have
![]() $|G:T|=2$
(compare [Reference Burness and Giudici9, Figure 2.5.1 and Lemma 2.2.9], noting that the discriminant of a hyperbolic quadratic form on
$|G:T|=2$
(compare [Reference Burness and Giudici9, Figure 2.5.1 and Lemma 2.2.9], noting that the discriminant of a hyperbolic quadratic form on
![]() $\mathbb{F}_{q}^{2n}$
with
$\mathbb{F}_{q}^{2n}$
with
![]() $(n,q)=(9,3)$
is
$(n,q)=(9,3)$
is
![]() $\boxtimes$
, in the notation used there, because
$\boxtimes$
, in the notation used there, because
![]() $n(q-1)/4=9$
is odd), so the
$n(q-1)/4=9$
is odd), so the
![]() ${\textstyle \frac{1}{4}}$
in the above estimate for
${\textstyle \frac{1}{4}}$
in the above estimate for
![]() $|C_{T}(x)|$
may be replaced by
$|C_{T}(x)|$
may be replaced by
![]() ${\textstyle \frac{1}{2}}$
, and we again obtain
${\textstyle \frac{1}{2}}$
, and we again obtain
![]() $|C_{T}(x)|>|T|^{4/5}$
.
$|C_{T}(x)|>|T|^{4/5}$
.
Finally, suppose that
![]() $T\cong \text{P}\unicode[STIX]{x1D6FA}_{2n}^{\unicode[STIX]{x1D700}}(q)$
with
$T\cong \text{P}\unicode[STIX]{x1D6FA}_{2n}^{\unicode[STIX]{x1D700}}(q)$
with
![]() $q$
even, noting that
$q$
even, noting that
![]() $T=G$
in this case. Take
$T=G$
in this case. Take
![]() $x\in G$
to be an involution of type
$x\in G$
to be an involution of type
![]() $a_{2}$
as in [Reference Burness and Giudici9, Table 3.5.1]. Then
$a_{2}$
as in [Reference Burness and Giudici9, Table 3.5.1]. Then
![]() $|C_{T}(x)|=q^{4n-7}|\unicode[STIX]{x1D6FA}_{2(n-2)}^{\unicode[STIX]{x1D700}}(q)||\text{Sp}_{2}(q)|$
and
$|C_{T}(x)|=q^{4n-7}|\unicode[STIX]{x1D6FA}_{2(n-2)}^{\unicode[STIX]{x1D700}}(q)||\text{Sp}_{2}(q)|$
and
![]() $\gcd (4,q^{n}-\unicode[STIX]{x1D700})=1$
, so instead of (4)–(5) we have
$\gcd (4,q^{n}-\unicode[STIX]{x1D700})=1$
, so instead of (4)–(5) we have
and
(In the bound for
![]() $|C_{T}(x)|$
we drop a factor of
$|C_{T}(x)|$
we drop a factor of
![]() ${\textstyle \frac{1}{4}}$
because
${\textstyle \frac{1}{4}}$
because
![]() $|G:T|=1$
for
$|G:T|=1$
for
![]() $q$
even, but pick up a factor of
$q$
even, but pick up a factor of
![]() ${\textstyle \frac{1}{2}}$
because
${\textstyle \frac{1}{2}}$
because
![]() $\unicode[STIX]{x1D6FA}_{2(n-2)}^{\unicode[STIX]{x1D700}}(q)$
has index
$\unicode[STIX]{x1D6FA}_{2(n-2)}^{\unicode[STIX]{x1D700}}(q)$
has index
![]() $2$
in
$2$
in
![]() $\text{SO}_{2(n-2)}^{\unicode[STIX]{x1D700}}(q)$
.) For
$\text{SO}_{2(n-2)}^{\unicode[STIX]{x1D700}}(q)$
.) For
![]() $4\leqslant n\leqslant 8$
we need
$4\leqslant n\leqslant 8$
we need
![]() $|C_{T}(x)|>|T|^{3/5}$
. As
$|C_{T}(x)|>|T|^{3/5}$
. As
![]() $q^{i}\geqslant 2$
for all
$q^{i}\geqslant 2$
for all
![]() $i\geqslant 1$
, and in particular
$i\geqslant 1$
, and in particular
![]() $q^{n}\geqslant 16$
, it suffices to show that
$q^{n}\geqslant 16$
, it suffices to show that
![]() $({\textstyle \frac{3}{4}})^{5n-10}q^{4n^{2}-22n+30}>4^{5}({\textstyle \frac{17}{16}})^{3}$
. This inequality holds unless
$({\textstyle \frac{3}{4}})^{5n-10}q^{4n^{2}-22n+30}>4^{5}({\textstyle \frac{17}{16}})^{3}$
. This inequality holds unless
![]() $(n,q)=(4,2)$
or
$(n,q)=(4,2)$
or
![]() $(4,4)$
, in which cases a direct calculation shows that
$(4,4)$
, in which cases a direct calculation shows that
![]() $|C_{T}(x)|>|T|^{3/5}$
. For
$|C_{T}(x)|>|T|^{3/5}$
. For
![]() $n\geqslant 9$
we must show that
$n\geqslant 9$
we must show that
![]() $|C_{T}(x)|>|T|^{4/5}$
. We now have
$|C_{T}(x)|>|T|^{4/5}$
. We now have
![]() $q^{n}\geqslant 512$
, and so it suffices to show that
$q^{n}\geqslant 512$
, and so it suffices to show that
![]() $({\textstyle \frac{3}{4}})^{5n-10}q^{2n^{2}-21n+30}>4^{5}({\textstyle \frac{513}{512}})^{4}$
. This inequality holds unless
$({\textstyle \frac{3}{4}})^{5n-10}q^{2n^{2}-21n+30}>4^{5}({\textstyle \frac{513}{512}})^{4}$
. This inequality holds unless
![]() $(n,q)=(10,2)$
, or
$(n,q)=(10,2)$
, or
![]() $n=9$
and
$n=9$
and
![]() $q\leqslant 2^{8}$
. One may use (7)–(8) to check that
$q\leqslant 2^{8}$
. One may use (7)–(8) to check that
![]() $|C_{T}(x)|>|T|^{4/5}$
in each of these cases except
$|C_{T}(x)|>|T|^{4/5}$
in each of these cases except
![]() $(n,q)=(9,2)$
, in which case the desired inequality may be verified by a direct calculation.◻
$(n,q)=(9,2)$
, in which case the desired inequality may be verified by a direct calculation.◻
4 Quasiprimitive point actions of type SD or CD
We now apply Corollary 1.5 to permutation groups
![]() $N$
that arise as subgroups of certain types of primitive groups. In some cases, we are also able to treat quasiprimitive groups, namely those in which every nontrivial normal subgroup is transitive. In this section, we consider the case where the group
$N$
that arise as subgroups of certain types of primitive groups. In some cases, we are also able to treat quasiprimitive groups, namely those in which every nontrivial normal subgroup is transitive. In this section, we consider the case where the group
![]() $N$
in Corollary 1.5 has a “diagonal” action. Specifically, we work under the following hypothesis.
$N$
in Corollary 1.5 has a “diagonal” action. Specifically, we work under the following hypothesis.
Hypothesis 4.1. Let
![]() $T$
be a nonabelian finite simple group, let
$T$
be a nonabelian finite simple group, let
![]() $k\geqslant 2$
, and write
$k\geqslant 2$
, and write
![]() $H=T^{k}$
. Let
$H=T^{k}$
. Let
![]() $\unicode[STIX]{x1D6FA}=\{(y_{1},\ldots ,y_{k-1},1)\mid y_{1},\ldots ,y_{k-1}\in T\}\leqslant H$
, and let
$\unicode[STIX]{x1D6FA}=\{(y_{1},\ldots ,y_{k-1},1)\mid y_{1},\ldots ,y_{k-1}\in T\}\leqslant H$
, and let
![]() $H$
act on
$H$
act on
![]() $\unicode[STIX]{x1D6FA}$
by
$\unicode[STIX]{x1D6FA}$
by
Suppose that
![]() $N=H^{r}$
is a collineation group of a thick finite generalized quadrangle
$N=H^{r}$
is a collineation group of a thick finite generalized quadrangle
![]() ${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}},\text{I})$
of order
${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}},\text{I})$
of order
![]() $(s,t)$
, such that
$(s,t)$
, such that
![]() ${\mathcal{P}}=\unicode[STIX]{x1D6FA}^{r}$
and
${\mathcal{P}}=\unicode[STIX]{x1D6FA}^{r}$
and
![]() $N$
has the product action on
$N$
has the product action on
![]() ${\mathcal{P}}$
.
${\mathcal{P}}$
.
This situation arises when
![]() $N$
is the socle of a primitive permutation group
$N$
is the socle of a primitive permutation group
![]() $G\leqslant \text{Sym}(\unicode[STIX]{x1D6FA})$
of type HS, HC, SD or CD. For type HS (resp. HC) we have
$G\leqslant \text{Sym}(\unicode[STIX]{x1D6FA})$
of type HS, HC, SD or CD. For type HS (resp. HC) we have
![]() $k=2$
and
$k=2$
and
![]() $r=1$
(resp.
$r=1$
(resp.
![]() $r\geqslant 2$
),
$r\geqslant 2$
),
![]() $G$
has two minimal normal subgroups, each isomorphic to
$G$
has two minimal normal subgroups, each isomorphic to
![]() $T^{r}$
, and the socle of
$T^{r}$
, and the socle of
![]() $G$
is
$G$
is
![]() $T^{r}\times T^{r}$
, which is isomorphic to
$T^{r}\times T^{r}$
, which is isomorphic to
![]() $N$
. For type SD (resp. CD) we have
$N$
. For type SD (resp. CD) we have
![]() $k\geqslant 2$
and
$k\geqslant 2$
and
![]() $r=1$
(resp.
$r=1$
(resp.
![]() $r\geqslant 2$
), and
$r\geqslant 2$
), and
![]() $G$
has a unique minimal normal subgroup, isomorphic to
$G$
has a unique minimal normal subgroup, isomorphic to
![]() $T^{kr}\cong N$
. Note that the notation
$T^{kr}\cong N$
. Note that the notation
![]() $k$
and
$k$
and
![]() $r$
is consistent with that of Table 1. Of course,
$r$
is consistent with that of Table 1. Of course,
![]() $G$
must (usually) satisfy certain other conditions [Reference Praeger, Li, Niemeyer, Hahn and Sabidussi22, Section 6] in order to actually be primitive, but these conditions are not needed for the proof of Proposition 4.2. It suffices that there is a subgroup of the form
$G$
must (usually) satisfy certain other conditions [Reference Praeger, Li, Niemeyer, Hahn and Sabidussi22, Section 6] in order to actually be primitive, but these conditions are not needed for the proof of Proposition 4.2. It suffices that there is a subgroup of the form
![]() $N$
. In particular, we are also able to treat quasiprimitive groups [Reference Praeger, Li, Niemeyer, Hahn and Sabidussi22, Section 12], because the (action of the) socle of
$N$
. In particular, we are also able to treat quasiprimitive groups [Reference Praeger, Li, Niemeyer, Hahn and Sabidussi22, Section 12], because the (action of the) socle of
![]() $G$
is the same as in the respective primitive types. (Note that a quasiprimitive group of type HS or HC is necessarily primitive, but a quasiprimitive group of type SD or CD need not be primitive.)
$G$
is the same as in the respective primitive types. (Note that a quasiprimitive group of type HS or HC is necessarily primitive, but a quasiprimitive group of type SD or CD need not be primitive.)
Proposition 4.2 shows, in particular, that the parameter
![]() $r$
in Hypothesis 4.1 can be at most
$r$
in Hypothesis 4.1 can be at most
![]() $3$
. As illustrated after Corollary 1.5, the proof relies on the information about centralizer orders in nonabelian finite simple groups given in Proposition 1.6. We also observe that when
$3$
. As illustrated after Corollary 1.5, the proof relies on the information about centralizer orders in nonabelian finite simple groups given in Proposition 1.6. We also observe that when
![]() $r=3$
, there always exists a solution
$r=3$
, there always exists a solution
![]() $(s,t)=(|\unicode[STIX]{x1D6FA}|-1,|\unicode[STIX]{x1D6FA}|+1)$
of the equation
$(s,t)=(|\unicode[STIX]{x1D6FA}|-1,|\unicode[STIX]{x1D6FA}|+1)$
of the equation
![]() $|\unicode[STIX]{x1D6FA}|^{3}=|\unicode[STIX]{x1D6FA}|^{r}=|{\mathcal{P}}|=(s+1)(st+1)$
, and this solution satisfies properties (ii) and (iii) of Lemma 2.1. Hence, although we are unable to rule out the case
$|\unicode[STIX]{x1D6FA}|^{3}=|\unicode[STIX]{x1D6FA}|^{r}=|{\mathcal{P}}|=(s+1)(st+1)$
, and this solution satisfies properties (ii) and (iii) of Lemma 2.1. Hence, although we are unable to rule out the case
![]() $r=3$
completely, we verify that this “obvious” situation cannot occur.
$r=3$
completely, we verify that this “obvious” situation cannot occur.
Proposition 4.2. If Hypothesis 4.1 holds then
![]() $r\leqslant 3$
and
$r\leqslant 3$
and
![]() $|C_{T}(x)|<|T|^{1-r/5}$
for all
$|C_{T}(x)|<|T|^{1-r/5}$
for all
![]() $x\in T\setminus \{1\}$
, and in particular
$x\in T\setminus \{1\}$
, and in particular
![]() $T$
must appear in Table 2. Moreover, if
$T$
must appear in Table 2. Moreover, if
![]() $r=3$
then
$r=3$
then
![]() $(s,t)\neq (|\unicode[STIX]{x1D6FA}|-1,|\unicode[STIX]{x1D6FA}|+1)$
.
$(s,t)\neq (|\unicode[STIX]{x1D6FA}|-1,|\unicode[STIX]{x1D6FA}|+1)$
.
Proof. Note first that
![]() $|{\mathcal{P}}|=|\unicode[STIX]{x1D6FA}|^{r}=|T|^{(k-1)r}$
. In particular, the excluded case
$|{\mathcal{P}}|=|\unicode[STIX]{x1D6FA}|^{r}=|T|^{(k-1)r}$
. In particular, the excluded case
![]() $(s,t)=(2,4)$
in Corollary 1.5 does not arise, because
$(s,t)=(2,4)$
in Corollary 1.5 does not arise, because
![]() $|{\mathcal{P}}|\geqslant |T|\geqslant |\text{Alt}_{5}|=60>(2+1)(2\cdot 4+1)$
. If we take
$|{\mathcal{P}}|\geqslant |T|\geqslant |\text{Alt}_{5}|=60>(2+1)(2\cdot 4+1)$
. If we take
![]() $x:=x_{1}=\cdots =x_{k}\neq 1$
in (9), then
$x:=x_{1}=\cdots =x_{k}\neq 1$
in (9), then
![]() $(y_{1},\ldots ,y_{k-1},1)\in \unicode[STIX]{x1D6FA}$
is fixed if and only if
$(y_{1},\ldots ,y_{k-1},1)\in \unicode[STIX]{x1D6FA}$
is fixed if and only if
![]() $y_{1},\ldots ,y_{k-1}\in C_{T}(x)$
. That is,
$y_{1},\ldots ,y_{k-1}\in C_{T}(x)$
. That is,
![]() $(x,\ldots ,x)\in H$
fixes precisely
$(x,\ldots ,x)\in H$
fixes precisely
![]() $|C_{T}(x)|^{k-1}$
elements of
$|C_{T}(x)|^{k-1}$
elements of
![]() $\unicode[STIX]{x1D6FA}$
(and, in particular, the action of
$\unicode[STIX]{x1D6FA}$
(and, in particular, the action of
![]() $H$
on
$H$
on
![]() $\unicode[STIX]{x1D6FA}$
is not semiregular). Corollary 1.5 therefore implies that
$\unicode[STIX]{x1D6FA}$
is not semiregular). Corollary 1.5 therefore implies that
![]() $r\leqslant 4$
and
$r\leqslant 4$
and
![]() $|C_{T}(x)|^{k-1}<|\unicode[STIX]{x1D6FA}|^{1-r/5}=|T|^{(k-1)(1-r/5)}$
, namely
$|C_{T}(x)|^{k-1}<|\unicode[STIX]{x1D6FA}|^{1-r/5}=|T|^{(k-1)(1-r/5)}$
, namely
![]() $|C_{T}(x)|<|T|^{1-r/5}$
, for all
$|C_{T}(x)|<|T|^{1-r/5}$
, for all
![]() $x\in T\setminus \{1\}$
. If
$x\in T\setminus \{1\}$
. If
![]() $r=4$
then we have a contradiction because every nonabelian finite simple group
$r=4$
then we have a contradiction because every nonabelian finite simple group
![]() $T$
contains a nonidentity element
$T$
contains a nonidentity element
![]() $x$
with
$x$
with
![]() $|C_{T}(x)|>|T|^{1/5}$
. For example, it is well known that
$|C_{T}(x)|>|T|^{1/5}$
. For example, it is well known that
![]() $T$
contains an involution
$T$
contains an involution
![]() $x$
with
$x$
with
![]() $|C_{T}(x)|>|T|^{1/3}$
(indeed, every involution has this property [Reference Liebeck and Shalev19, Proposition 2.4]). Therefore,
$|C_{T}(x)|>|T|^{1/3}$
(indeed, every involution has this property [Reference Liebeck and Shalev19, Proposition 2.4]). Therefore,
![]() $r\leqslant 3$
. In particular, Proposition 1.6 tells us that
$r\leqslant 3$
. In particular, Proposition 1.6 tells us that
![]() $T$
must be one of the groups appearing in Table 2. To prove the final assertion, suppose toward a contradiction that
$T$
must be one of the groups appearing in Table 2. To prove the final assertion, suppose toward a contradiction that
![]() $r=3$
and
$r=3$
and
![]() $(s,t)=(|\unicode[STIX]{x1D6FA}|-1,|\unicode[STIX]{x1D6FA}|+1)$
. Take any
$(s,t)=(|\unicode[STIX]{x1D6FA}|-1,|\unicode[STIX]{x1D6FA}|+1)$
. Take any
![]() $x\in T$
with
$x\in T$
with
![]() $|C_{T}(x)|>|T|^{1/3}$
. Then
$|C_{T}(x)|>|T|^{1/3}$
. Then
![]() $((x,\ldots ,x),(1,\ldots ,1),(1,\ldots ,1))\in H^{r}=H^{3}=N$
fixes
$((x,\ldots ,x),(1,\ldots ,1),(1,\ldots ,1))\in H^{r}=H^{3}=N$
fixes
![]() $|C_{T}(x)|^{k-1}|T|^{2(k-1)}>|T|^{7(k-1)/3}=|{\mathcal{P}}|^{7/9}$
points of
$|C_{T}(x)|^{k-1}|T|^{2(k-1)}>|T|^{7(k-1)/3}=|{\mathcal{P}}|^{7/9}$
points of
![]() ${\mathcal{Q}}$
, contradicting Proposition 2.6.◻
${\mathcal{Q}}$
, contradicting Proposition 2.6.◻
The following immediate consequence of Proposition 4.2 (and the preceding observations) implies the SD and CD cases of Theorem 1.1.
Proposition 4.3. Let
![]() ${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}})$
be a thick finite generalized quadrangle admitting a collineation group
${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}})$
be a thick finite generalized quadrangle admitting a collineation group
![]() $G$
that acts quasiprimitively of type SD or CD on
$G$
that acts quasiprimitively of type SD or CD on
![]() ${\mathcal{P}}$
. Then the conditions in Table 1 hold.
${\mathcal{P}}$
. Then the conditions in Table 1 hold.
5 Primitive point actions of type HS or HC
We now consider the case where
![]() $k=2$
in Hypothesis 4.1 in more detail. As explained above, this case arises when
$k=2$
in Hypothesis 4.1 in more detail. As explained above, this case arises when
![]() $N$
is the socle of a primitive permutation group
$N$
is the socle of a primitive permutation group
![]() $G\leqslant \text{Sym}(\unicode[STIX]{x1D6FA})$
of type HS (
$G\leqslant \text{Sym}(\unicode[STIX]{x1D6FA})$
of type HS (
![]() $r=1$
) or HC (
$r=1$
) or HC (
![]() $r\geqslant 2$
). When
$r\geqslant 2$
). When
![]() $k=2$
, it is natural to simplify the notation of Hypothesis 4.1 by identifying the set
$k=2$
, it is natural to simplify the notation of Hypothesis 4.1 by identifying the set
![]() $\unicode[STIX]{x1D6FA}$
with
$\unicode[STIX]{x1D6FA}$
with
![]() $T^{r}$
, so we first recast the hypothesis in this way and also establish some further notation.
$T^{r}$
, so we first recast the hypothesis in this way and also establish some further notation.
Hypothesis 5.1. Let
![]() $T$
be a nonabelian finite simple group and let
$T$
be a nonabelian finite simple group and let
![]() $N=T^{r}\times T^{r}$
act on
$N=T^{r}\times T^{r}$
act on
![]() $T^{r}$
by
$T^{r}$
by
Let
![]() $M=\{(u,1)\mid u\in T^{r}\}\leqslant N$
, so that
$M=\{(u,1)\mid u\in T^{r}\}\leqslant N$
, so that
![]() $M$
may be identified with
$M$
may be identified with
![]() $T^{r}$
acting regularly on itself by right multiplication. Suppose that
$T^{r}$
acting regularly on itself by right multiplication. Suppose that
![]() $N$
is a collineation group of a thick finite generalized quadrangle
$N$
is a collineation group of a thick finite generalized quadrangle
![]() ${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}},\text{I})$
of order
${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}},\text{I})$
of order
![]() $(s,t)$
with
$(s,t)$
with
![]() ${\mathcal{P}}=T^{r}$
. Let
${\mathcal{P}}=T^{r}$
. Let
![]() ${\mathcal{P}}_{1}\subset {\mathcal{P}}$
denote the set of points collinear with but not equal to the identity element
${\mathcal{P}}_{1}\subset {\mathcal{P}}$
denote the set of points collinear with but not equal to the identity element
![]() $1\in T^{r}={\mathcal{P}}$
, and let
$1\in T^{r}={\mathcal{P}}$
, and let
![]() ${\mathcal{L}}_{1}\subset {\mathcal{L}}$
denote the set of lines incident with
${\mathcal{L}}_{1}\subset {\mathcal{L}}$
denote the set of lines incident with
![]() $1$
. Given a line
$1$
. Given a line
![]() $\ell \in {\mathcal{L}}$
, let
$\ell \in {\mathcal{L}}$
, let
![]() $\bar{\ell }\subset {\mathcal{P}}$
denote the set of points incident with
$\bar{\ell }\subset {\mathcal{P}}$
denote the set of points incident with
![]() $\ell$
.
$\ell$
.
The following lemma may essentially be deduced from [Reference Yoshiara27, Lemma 10] upon observing that the assumption
![]() $\gcd (s,t)>1$
imposed there is not necessary (as far as we can tell, and at least not in our more restrictive setting). We include a proof to make it clear that we do not need to make this assumption. Our notation differs from that of [Reference Yoshiara27, page 654] as follows: the point-regular group
$\gcd (s,t)>1$
imposed there is not necessary (as far as we can tell, and at least not in our more restrictive setting). We include a proof to make it clear that we do not need to make this assumption. Our notation differs from that of [Reference Yoshiara27, page 654] as follows: the point-regular group
![]() $G$
is our
$G$
is our
![]() $M\cong T^{r}$
, and the point
$M\cong T^{r}$
, and the point
![]() $O$
is our point
$O$
is our point
![]() $1$
, so that
$1$
, so that
![]() $\unicode[STIX]{x1D6E5}$
is our
$\unicode[STIX]{x1D6E5}$
is our
![]() ${\mathcal{P}}_{1}$
.
${\mathcal{P}}_{1}$
.
Lemma 5.2. Suppose that Hypothesis 5.1 holds. Let
![]() $x\in {\mathcal{P}}_{1}$
, and let
$x\in {\mathcal{P}}_{1}$
, and let
![]() $\ell _{x}$
be the unique line in
$\ell _{x}$
be the unique line in
![]() ${\mathcal{L}}_{1}$
incident with
${\mathcal{L}}_{1}$
incident with
![]() $x$
. Then, for every
$x$
. Then, for every
![]() $i\in \{1,\ldots ,|x|-1\}$
, the conjugacy class
$i\in \{1,\ldots ,|x|-1\}$
, the conjugacy class
![]() $(x^{i})^{T^{r}}$
is contained in
$(x^{i})^{T^{r}}$
is contained in
![]() ${\mathcal{P}}_{1}$
. Moreover, the collineation
${\mathcal{P}}_{1}$
. Moreover, the collineation
![]() $(x,1)\in M$
fixes
$(x,1)\in M$
fixes
![]() $\ell _{x}$
.
$\ell _{x}$
.
Proof. Let us first establish some notation. Given
![]() $u\in T^{r}={\mathcal{P}}$
, write
$u\in T^{r}={\mathcal{P}}$
, write
 $$\begin{eqnarray}\displaystyle & \displaystyle \operatorname{fix}_{{\mathcal{P}}}(u)=\{P\in {\mathcal{P}}\mid P^{(u,1)}=P\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \operatorname{coll}_{{\mathcal{P}}}(u)=\{P\in {\mathcal{P}}\mid P^{(u,1)}\text{ is collinear with but not equal to }P\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \operatorname{fix}_{{\mathcal{L}}}(u)=\{\ell \in {\mathcal{L}}\mid \ell ^{(u,1)}=\ell \}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \operatorname{conc}_{{\mathcal{L}}}(u)=\{\ell \in {\mathcal{L}}\mid \ell ^{(u,1)}\text{ is concurrent with but not equal to }\ell \}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \operatorname{fix}_{{\mathcal{P}}}(u)=\{P\in {\mathcal{P}}\mid P^{(u,1)}=P\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \operatorname{coll}_{{\mathcal{P}}}(u)=\{P\in {\mathcal{P}}\mid P^{(u,1)}\text{ is collinear with but not equal to }P\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \operatorname{fix}_{{\mathcal{L}}}(u)=\{\ell \in {\mathcal{L}}\mid \ell ^{(u,1)}=\ell \}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \operatorname{conc}_{{\mathcal{L}}}(u)=\{\ell \in {\mathcal{L}}\mid \ell ^{(u,1)}\text{ is concurrent with but not equal to }\ell \}. & \displaystyle \nonumber\end{eqnarray}$$
Since the subgroup
![]() $M=\{(u,1)\mid u\in T^{r}\}$
of
$M=\{(u,1)\mid u\in T^{r}\}$
of
![]() $N$
acts regularly on
$N$
acts regularly on
![]() ${\mathcal{P}}$
,
${\mathcal{P}}$
,
![]() $\operatorname{fix}_{{\mathcal{P}}}(u)$
is empty. Moreover,
$\operatorname{fix}_{{\mathcal{P}}}(u)$
is empty. Moreover,
![]() $P\in \operatorname{coll}_{{\mathcal{P}}}(u)$
if and only if the points
$P\in \operatorname{coll}_{{\mathcal{P}}}(u)$
if and only if the points
![]() $P^{(P^{-1},1)}=1$
and
$P^{(P^{-1},1)}=1$
and
![]() $(Pu)^{(P^{-1},1)}=PuP^{-1}$
are collinear, which is if and only if
$(Pu)^{(P^{-1},1)}=PuP^{-1}$
are collinear, which is if and only if
![]() $PuP^{-1}\in u^{T^{r}}\cap {\mathcal{P}}_{1}$
. Since for
$PuP^{-1}\in u^{T^{r}}\cap {\mathcal{P}}_{1}$
. Since for
![]() $g,h\in T^{r}$
we have
$g,h\in T^{r}$
we have
![]() $gug^{-1}=huh^{-1}$
if and only if
$gug^{-1}=huh^{-1}$
if and only if
![]() $g^{-1}h\in C_{T^{r}}(u)$
, it follows that
$g^{-1}h\in C_{T^{r}}(u)$
, it follows that
as in the proof of [Reference Yoshiara27, Lemma 3]. Then (again, as in that proof) [Reference Payne and Thas21, 1.9.2] implies that
for every
![]() $u\in T^{r}$
.
$u\in T^{r}$
.
Now, since
![]() $x\in {\mathcal{P}}_{1}$
, we have
$x\in {\mathcal{P}}_{1}$
, we have
![]() $u^{-1}xu=x^{(u,u)}\in {\mathcal{P}}_{1}$
for every collineation of the form
$u^{-1}xu=x^{(u,u)}\in {\mathcal{P}}_{1}$
for every collineation of the form
![]() $(u,u)\in N$
, because such collineations (are precisely those that) fix the point
$(u,u)\in N$
, because such collineations (are precisely those that) fix the point
![]() $1$
. That is, every
$1$
. That is, every
![]() $T^{r}$
-conjugate of
$T^{r}$
-conjugate of
![]() $x$
is in
$x$
is in
![]() ${\mathcal{P}}_{1}$
. In other words,
${\mathcal{P}}_{1}$
. In other words,
![]() $x^{T^{r}}\cap {\mathcal{P}}_{1}=x^{T^{r}}$
, and so (10) implies that
$x^{T^{r}}\cap {\mathcal{P}}_{1}=x^{T^{r}}$
, and so (10) implies that
In particular, we have
![]() $\operatorname{coll}_{{\mathcal{P}}}(x)={\mathcal{P}}$
; that is, every point of
$\operatorname{coll}_{{\mathcal{P}}}(x)={\mathcal{P}}$
; that is, every point of
![]() ${\mathcal{Q}}$
is mapped to a collinear point under the collineation
${\mathcal{Q}}$
is mapped to a collinear point under the collineation
![]() $(x,1)\in M$
. We now claim that
$(x,1)\in M$
. We now claim that
![]() $\operatorname{conc}_{{\mathcal{L}}}(x)$
is empty. If not, then some line
$\operatorname{conc}_{{\mathcal{L}}}(x)$
is empty. If not, then some line
![]() $\ell$
is concurrent with its image under the collineation
$\ell$
is concurrent with its image under the collineation
![]() $(x,1)$
. Let
$(x,1)$
. Let
![]() $P$
denote the unique point incident with both
$P$
denote the unique point incident with both
![]() $\ell$
and
$\ell$
and
![]() $\ell ^{(x,1)}$
. Then
$\ell ^{(x,1)}$
. Then
![]() $Px^{-1}$
is incident with
$Px^{-1}$
is incident with
![]() $\ell$
, being the image of
$\ell$
, being the image of
![]() $P$
under the collineation
$P$
under the collineation
![]() $(x,1)^{-1}=(x^{-1},1)$
, and
$(x,1)^{-1}=(x^{-1},1)$
, and
![]() $Px^{-1}\neq P$
because
$Px^{-1}\neq P$
because
![]() $x\neq 1$
and
$x\neq 1$
and
![]() $M$
acts regularly on
$M$
acts regularly on
![]() ${\mathcal{P}}$
. Since
${\mathcal{P}}$
. Since
![]() ${\mathcal{Q}}$
is thick, there exists a third point
${\mathcal{Q}}$
is thick, there exists a third point
![]() $P_{3}$
incident with
$P_{3}$
incident with
![]() $\ell$
, distinct from
$\ell$
, distinct from
![]() $P$
and
$P$
and
![]() $Px^{-1}$
. Since
$Px^{-1}$
. Since
![]() $\operatorname{coll}_{{\mathcal{P}}}(x)={\mathcal{P}}$
, the points
$\operatorname{coll}_{{\mathcal{P}}}(x)={\mathcal{P}}$
, the points
![]() $P_{3}^{(x,1)}=P_{3}x$
and
$P_{3}^{(x,1)}=P_{3}x$
and
![]() $P_{3}$
are collinear. Moreover,
$P_{3}$
are collinear. Moreover,
![]() $P_{3}x$
is collinear with
$P_{3}x$
is collinear with
![]() $P$
, because both of these points are incident with
$P$
, because both of these points are incident with
![]() $\ell ^{(x,1)}$
. Therefore,
$\ell ^{(x,1)}$
. Therefore,
![]() $P_{3}x$
is collinear with two distinct points that are incident with
$P_{3}x$
is collinear with two distinct points that are incident with
![]() $\ell$
, namely
$\ell$
, namely
![]() $P_{3}$
and
$P_{3}$
and
![]() $P$
, and so
$P$
, and so
![]() $P_{3}x$
is itself incident with
$P_{3}x$
is itself incident with
![]() $\ell$
because
$\ell$
because
![]() ${\mathcal{Q}}$
contains no triangles. This, however, means that
${\mathcal{Q}}$
contains no triangles. This, however, means that
![]() $P_{3}x$
is incident with both
$P_{3}x$
is incident with both
![]() $\ell$
and
$\ell$
and
![]() $\ell ^{(x,1)}$
, which forces
$\ell ^{(x,1)}$
, which forces
![]() $P_{3}x=P$
and hence
$P_{3}x=P$
and hence
![]() $P_{3}=Px^{-1}$
, a contradiction. Therefore,
$P_{3}=Px^{-1}$
, a contradiction. Therefore,
![]() $|\text{conc}_{{\mathcal{L}}}(x)|=0$
as claimed, and so (11) implies that
$|\text{conc}_{{\mathcal{L}}}(x)|=0$
as claimed, and so (11) implies that
Next, we show that
![]() $(x^{i})^{T^{r}}\subseteq {\mathcal{P}}_{1}$
for all
$(x^{i})^{T^{r}}\subseteq {\mathcal{P}}_{1}$
for all
![]() $i\in \{1,\ldots ,|x|-1\}$
. For each such
$i\in \{1,\ldots ,|x|-1\}$
. For each such
![]() $i$
, we certainly have
$i$
, we certainly have
![]() $\operatorname{fix}_{{\mathcal{L}}}(x)\subseteq \operatorname{fix}_{{\mathcal{L}}}(x^{i})$
, because if the collineation
$\operatorname{fix}_{{\mathcal{L}}}(x)\subseteq \operatorname{fix}_{{\mathcal{L}}}(x^{i})$
, because if the collineation
![]() $(x,1)$
fixes a line then so too does
$(x,1)$
fixes a line then so too does
![]() $(x,1)^{i}=(x^{i},1)$
. In particular,
$(x,1)^{i}=(x^{i},1)$
. In particular,
![]() $|\text{fix}_{{\mathcal{L}}}(x^{i})|\geqslant |\text{fix}_{{\mathcal{L}}}(x)|=st+1$
, by (12). On the other hand, no two lines fixed by
$|\text{fix}_{{\mathcal{L}}}(x^{i})|\geqslant |\text{fix}_{{\mathcal{L}}}(x)|=st+1$
, by (12). On the other hand, no two lines fixed by
![]() $(x^{i},1)$
can be concurrent, because if they were, then the unique point incident with both of them would be fixed by
$(x^{i},1)$
can be concurrent, because if they were, then the unique point incident with both of them would be fixed by
![]() $(x^{i},1)$
, a contradiction since
$(x^{i},1)$
, a contradiction since
![]() $M$
acts regularly on
$M$
acts regularly on
![]() ${\mathcal{P}}$
. Hence, the total number of points that are incident with some line in
${\mathcal{P}}$
. Hence, the total number of points that are incident with some line in
![]() $\operatorname{fix}_{{\mathcal{L}}}(x^{i})$
is
$\operatorname{fix}_{{\mathcal{L}}}(x^{i})$
is
![]() $(s+1)|\text{fix}_{{\mathcal{L}}}(x^{i})|$
. As this number cannot exceed
$(s+1)|\text{fix}_{{\mathcal{L}}}(x^{i})|$
. As this number cannot exceed
![]() $|{\mathcal{P}}|=(s+1)(st+1)$
, we must also have
$|{\mathcal{P}}|=(s+1)(st+1)$
, we must also have
![]() $|\text{fix}_{{\mathcal{L}}}(x^{i})|\leqslant st+1$
. Therefore,
$|\text{fix}_{{\mathcal{L}}}(x^{i})|\leqslant st+1$
. Therefore,
![]() $|\text{fix}_{{\mathcal{L}}}(x^{i})|=st+1$
. Now (10) implies, on the one hand, that
$|\text{fix}_{{\mathcal{L}}}(x^{i})|=st+1$
. Now (10) implies, on the one hand, that
Since
![]() $|\text{coll}_{{\mathcal{P}}}(x^{i})|\leqslant |{\mathcal{P}}|$
, this implies that
$|\text{coll}_{{\mathcal{P}}}(x^{i})|\leqslant |{\mathcal{P}}|$
, this implies that
![]() $|\text{conc}_{{\mathcal{L}}}(x^{i})|=0$
, and then in turn that
$|\text{conc}_{{\mathcal{L}}}(x^{i})|=0$
, and then in turn that
![]() $|{\mathcal{P}}|=|\text{coll}_{{\mathcal{P}}}(x^{i})|$
. Appealing again to (10), we now deduce that
$|{\mathcal{P}}|=|\text{coll}_{{\mathcal{P}}}(x^{i})|$
. Appealing again to (10), we now deduce that
![]() $|(x^{i})^{T^{r}}\cap {\mathcal{P}}_{1}||C_{T^{r}}(x^{i})|=|{\mathcal{P}}|=|T^{r}|$
, which implies that
$|(x^{i})^{T^{r}}\cap {\mathcal{P}}_{1}||C_{T^{r}}(x^{i})|=|{\mathcal{P}}|=|T^{r}|$
, which implies that
![]() $(x^{i})^{T^{r}}\subseteq {\mathcal{P}}_{1}$
as required. The first assertion is therefore proved.
$(x^{i})^{T^{r}}\subseteq {\mathcal{P}}_{1}$
as required. The first assertion is therefore proved.
Finally, we must show that the collineation
![]() $(x,1)$
fixes the unique line
$(x,1)$
fixes the unique line
![]() $\ell _{x}\in {\mathcal{L}}_{1}$
incident with
$\ell _{x}\in {\mathcal{L}}_{1}$
incident with
![]() $x$
. If
$x$
. If
![]() $|x|=2$
, then
$|x|=2$
, then
![]() $(x,1)$
fixes
$(x,1)$
fixes
![]() $\ell _{x}$
because it fixes setwise the subset
$\ell _{x}$
because it fixes setwise the subset
![]() $\{1,x\}$
of points incident with
$\{1,x\}$
of points incident with
![]() $\ell _{x}$
. That is, it maps
$\ell _{x}$
. That is, it maps
![]() $1$
to
$1$
to
![]() $1^{(x,1)}=1x=x$
and
$1^{(x,1)}=1x=x$
and
![]() $x$
to
$x$
to
![]() $x^{(x,1)}=x^{2}=1$
. Now suppose that
$x^{(x,1)}=x^{2}=1$
. Now suppose that
![]() $|x|>2$
. Then the point
$|x|>2$
. Then the point
![]() $1^{(x,1)^{2}}=x^{2}\neq 1$
is collinear with
$1^{(x,1)^{2}}=x^{2}\neq 1$
is collinear with
![]() $x$
because
$x$
because
![]() $x$
is collinear with
$x$
is collinear with
![]() $1$
. On the other hand,
$1$
. On the other hand,
![]() $(x^{2})^{T_{r}}\subseteq {\mathcal{P}}_{1}$
by the first assertion, so in particular
$(x^{2})^{T_{r}}\subseteq {\mathcal{P}}_{1}$
by the first assertion, so in particular
![]() $x^{2}$
is collinear with
$x^{2}$
is collinear with
![]() $1$
. Therefore,
$1$
. Therefore,
![]() $x^{2}$
is collinear with two distinct points incident with
$x^{2}$
is collinear with two distinct points incident with
![]() $\ell _{x}$
(namely
$\ell _{x}$
(namely
![]() $1$
and
$1$
and
![]() $x$
), and so is itself incident with
$x$
), and so is itself incident with
![]() $\ell _{x}$
because
$\ell _{x}$
because
![]() ${\mathcal{Q}}$
contains no triangles. Hence,
${\mathcal{Q}}$
contains no triangles. Hence,
![]() $(x,1)$
fixes
$(x,1)$
fixes
![]() $\ell _{x}$
because it maps a pair of points incident with
$\ell _{x}$
because it maps a pair of points incident with
![]() $\ell _{x}$
, namely
$\ell _{x}$
, namely
![]() $1$
and
$1$
and
![]() $x$
, to another pair of points incident with
$x$
, to another pair of points incident with
![]() $\ell _{x}$
, namely
$\ell _{x}$
, namely
![]() $x$
and
$x$
and
![]() $x^{2}$
.◻
$x^{2}$
.◻
Hypothesis 5.1 imposes the following restrictions on the points and lines incident with the identity element of
![]() $T^{r}={\mathcal{P}}$
, and on the order
$T^{r}={\mathcal{P}}$
, and on the order
![]() $(s,t)$
of
$(s,t)$
of
![]() ${\mathcal{Q}}$
.
${\mathcal{Q}}$
.
Lemma 5.3. The following assertions hold under Hypothesis 5.1.
(i)
 ${\mathcal{P}}_{1}$
is a union of
${\mathcal{P}}_{1}$
is a union of
 $T^{r}$
-conjugacy classes.
$T^{r}$
-conjugacy classes.(ii) Every line
 $\ell \in {\mathcal{L}}_{1}$
has the property that
$\ell \in {\mathcal{L}}_{1}$
has the property that
 $\bar{\ell }$
is a subgroup of
$\bar{\ell }$
is a subgroup of
 $T^{r}$
. Specifically,
$T^{r}$
. Specifically,
 $\bar{\ell }=\{u\in T^{r}\mid (u,1)\in M\text{ fixes }\ell \}$
.
$\bar{\ell }=\{u\in T^{r}\mid (u,1)\in M\text{ fixes }\ell \}$
.(iii) Every line
 $\ell \in {\mathcal{L}}_{1}$
is incident with an involution.
$\ell \in {\mathcal{L}}_{1}$
is incident with an involution.(iv) If there exists a line in
 ${\mathcal{L}}_{1}$
incident with representatives of every
${\mathcal{L}}_{1}$
incident with representatives of every
 $T^{r}$
-conjugacy class of involutions in
$T^{r}$
-conjugacy class of involutions in
 ${\mathcal{P}}_{1}$
, then
${\mathcal{P}}_{1}$
, then
 $N$
acts transitively on the flags of
$N$
acts transitively on the flags of
 ${\mathcal{Q}}$
and
${\mathcal{Q}}$
and
 $r\geqslant 2$
.
$r\geqslant 2$
.(v)
 $T^{r}$
has at least three conjugacy classes of involutions.
$T^{r}$
has at least three conjugacy classes of involutions.(vi) If
 $T^{r}$
has exactly three conjugacy classes of involutions, then either
$T^{r}$
has exactly three conjugacy classes of involutions, then either
 ${\mathcal{P}}_{1}$
contains exactly two of these classes, or
${\mathcal{P}}_{1}$
contains exactly two of these classes, or
 $N$
acts transitively on the flags of
$N$
acts transitively on the flags of
 ${\mathcal{Q}}$
and
${\mathcal{Q}}$
and
 $r\geqslant 2$
.
$r\geqslant 2$
.(vii)
 $\gcd (s,t)=1$
and
$\gcd (s,t)=1$
and
 $t\geqslant s+1$
.
$t\geqslant s+1$
.
Proof. (i) This follows immediately from Lemma 5.2.
(ii) If
![]() $u\in \bar{\ell }$
then the collineation
$u\in \bar{\ell }$
then the collineation
![]() $(u,1)\in M$
fixes
$(u,1)\in M$
fixes
![]() $\ell$
by Lemma 5.2. Conversely, if
$\ell$
by Lemma 5.2. Conversely, if
![]() $(u,1)$
fixes
$(u,1)$
fixes
![]() $\ell$
then, because
$\ell$
then, because
![]() $1\in {\mathcal{P}}$
is incident with
$1\in {\mathcal{P}}$
is incident with
![]() $\ell$
, so too is
$\ell$
, so too is
![]() $1^{(u,1)}=u$
; that is,
$1^{(u,1)}=u$
; that is,
![]() $u\in \bar{\ell }$
.
$u\in \bar{\ell }$
.
(iii) If
![]() $\ell \in {\mathcal{L}}_{1}$
is not incident with any involution, then
$\ell \in {\mathcal{L}}_{1}$
is not incident with any involution, then
![]() $\bar{\ell }$
, which is a subgroup of
$\bar{\ell }$
, which is a subgroup of
![]() $T^{r}$
by (ii), must have odd order. That is,
$T^{r}$
by (ii), must have odd order. That is,
![]() $s+1=|\bar{\ell }|$
must be odd. However,
$s+1=|\bar{\ell }|$
must be odd. However,
![]() $(s+1)(st+1)=|T|^{r}$
is even by the Feit–Thompson theorem [Reference Feit and Thompson13], so
$(s+1)(st+1)=|T|^{r}$
is even by the Feit–Thompson theorem [Reference Feit and Thompson13], so
![]() $s$
must be odd and hence
$s$
must be odd and hence
![]() $s+1$
must be even, a contradiction.
$s+1$
must be even, a contradiction.
(iv) If
![]() $\ell \in {\mathcal{L}}_{1}$
is incident with representatives of every conjugacy class of involutions in
$\ell \in {\mathcal{L}}_{1}$
is incident with representatives of every conjugacy class of involutions in
![]() ${\mathcal{P}}_{1}$
, then
${\mathcal{P}}_{1}$
, then
![]() $\ell$
can be mapped to any other line in
$\ell$
can be mapped to any other line in
![]() ${\mathcal{L}}_{1}$
by some element of the stabilizer
${\mathcal{L}}_{1}$
by some element of the stabilizer
![]() $N_{1}=\{(u,u)\mid u\in T^{r}\}$
in
$N_{1}=\{(u,u)\mid u\in T^{r}\}$
in
![]() $N$
of the point
$N$
of the point
![]() $1\in {\mathcal{P}}=T^{r}$
. Since
$1\in {\mathcal{P}}=T^{r}$
. Since
![]() $N$
acts transitively on
$N$
acts transitively on
![]() ${\mathcal{P}}$
, this means that
${\mathcal{P}}$
, this means that
![]() $N$
acts transitively on the flags of
$N$
acts transitively on the flags of
![]() ${\mathcal{Q}}$
, and hence on
${\mathcal{Q}}$
, and hence on
![]() ${\mathcal{L}}$
. If
${\mathcal{L}}$
. If
![]() $r=1$
, this contradicts [Reference Bamberg, Popiel and Praeger8, Theorem 1.1], because
$r=1$
, this contradicts [Reference Bamberg, Popiel and Praeger8, Theorem 1.1], because
![]() $N$
acts primitively on
$N$
acts primitively on
![]() ${\mathcal{P}}$
in this case. Hence,
${\mathcal{P}}$
in this case. Hence,
![]() $r\geqslant 2$
.
$r\geqslant 2$
.
(v) Suppose toward a contradiction that
![]() $T^{r}$
contains at most two conjugacy classes of involutions. Then
$T^{r}$
contains at most two conjugacy classes of involutions. Then
![]() $r=1$
, because if
$r=1$
, because if
![]() $r\geqslant 2$
then any involution
$r\geqslant 2$
then any involution
![]() $x\in T$
gives rise to the three pairwise nonconjugate involutions
$x\in T$
gives rise to the three pairwise nonconjugate involutions
![]() $(x,1,\ldots ,1)$
,
$(x,1,\ldots ,1)$
,
![]() $(1,x,1,\ldots ,1)$
and
$(1,x,1,\ldots ,1)$
and
![]() $(x,x,1,\ldots ,1)$
in
$(x,x,1,\ldots ,1)$
in
![]() $T^{r}$
. Hence, by (iii),
$T^{r}$
. Hence, by (iii),
![]() $T$
must have exactly two conjugacy classes of involutions, say
$T$
must have exactly two conjugacy classes of involutions, say
![]() $x^{T}$
and
$x^{T}$
and
![]() $y^{T}$
, and both must be contained in
$y^{T}$
, and both must be contained in
![]() ${\mathcal{P}}_{1}$
. Without loss of generality,
${\mathcal{P}}_{1}$
. Without loss of generality,
![]() $x$
and
$x$
and
![]() $y$
commute, because at least one of them centralizes a Sylow
$y$
commute, because at least one of them centralizes a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $T$
. Therefore,
$T$
. Therefore,
![]() $xy$
is an involution, and so must be collinear with
$xy$
is an involution, and so must be collinear with
![]() $1\in {\mathcal{P}}$
. Since
$1\in {\mathcal{P}}$
. Since
![]() $1$
is collinear with
$1$
is collinear with
![]() $x$
, the images of
$x$
, the images of
![]() $1$
and
$1$
and
![]() $x$
under the collineation
$x$
under the collineation
![]() $(y,1)\in M$
are collinear. That is,
$(y,1)\in M$
are collinear. That is,
![]() $1^{(y,1)}=y$
is collinear with
$1^{(y,1)}=y$
is collinear with
![]() $x^{(y,1)}=xy$
. Similarly,
$x^{(y,1)}=xy$
. Similarly,
![]() $1$
and
$1$
and
![]() $y$
are collinear, and hence so too are
$y$
are collinear, and hence so too are
![]() $1^{(x,1)}=x$
and
$1^{(x,1)}=x$
and
![]() $y^{(x,1)}=yx=xy$
. Since the involution
$y^{(x,1)}=yx=xy$
. Since the involution
![]() $xy$
is also collinear with
$xy$
is also collinear with
![]() $1$
and
$1$
and
![]() ${\mathcal{Q}}$
contains no triangles, the points
${\mathcal{Q}}$
contains no triangles, the points
![]() $1$
,
$1$
,
![]() $x$
,
$x$
,
![]() $y$
and
$y$
and
![]() $xy$
must be incident with a common line. In particular,
$xy$
must be incident with a common line. In particular,
![]() $x$
and
$x$
and
![]() $y$
are incident with a common line in
$y$
are incident with a common line in
![]() ${\mathcal{L}}_{1}$
. Since
${\mathcal{L}}_{1}$
. Since
![]() $r=1$
, this contradicts (iv).
$r=1$
, this contradicts (iv).
(vi) Let
![]() $x$
,
$x$
,
![]() $y$
and
$y$
and
![]() $z$
denote representatives of the three
$z$
denote representatives of the three
![]() $T^{r}$
-conjugacy classes of involutions. If
$T^{r}$
-conjugacy classes of involutions. If
![]() ${\mathcal{P}}_{1}$
contains exactly one of these classes, then
${\mathcal{P}}_{1}$
contains exactly one of these classes, then
![]() $N$
acts flag-transitively by (iv), and it follows from [Reference Bamberg, Popiel and Praeger8, Theorem 1.1] that
$N$
acts flag-transitively by (iv), and it follows from [Reference Bamberg, Popiel and Praeger8, Theorem 1.1] that
![]() $r\geqslant 2$
. Now suppose that
$r\geqslant 2$
. Now suppose that
![]() ${\mathcal{P}}_{1}$
contains all three of
${\mathcal{P}}_{1}$
contains all three of
![]() $x^{T}$
,
$x^{T}$
,
![]() $y^{T}$
and
$y^{T}$
and
![]() $z^{T}$
. Without loss of generality,
$z^{T}$
. Without loss of generality,
![]() $x$
centralizes a Sylow
$x$
centralizes a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $T^{r}$
and both
$T^{r}$
and both
![]() $y$
and
$y$
and
![]() $z$
commute with
$z$
commute with
![]() $x$
, so
$x$
, so
![]() $xy=yx$
and
$xy=yx$
and
![]() $xz=zx$
are involutions. Arguing as in the proof of (iii), we deduce that
$xz=zx$
are involutions. Arguing as in the proof of (iii), we deduce that
![]() $1$
,
$1$
,
![]() $x$
,
$x$
,
![]() $y$
and
$y$
and
![]() $xy$
are incident with a common line
$xy$
are incident with a common line
![]() $\ell \in {\mathcal{L}}_{1}$
. Replacing
$\ell \in {\mathcal{L}}_{1}$
. Replacing
![]() $y$
by
$y$
by
![]() $z$
in this argument, we see that
$z$
in this argument, we see that
![]() $z$
is also incident with
$z$
is also incident with
![]() $\ell$
, so (iv) again implies that
$\ell$
, so (iv) again implies that
![]() $N$
acts flag-transitively, and it follows that
$N$
acts flag-transitively, and it follows that
![]() $r\geqslant 2$
.
$r\geqslant 2$
.
(vii) If
![]() $\gcd (s,t)>1$
then [Reference Yoshiara27, Lemma 6(1)] implies that every nontrivial
$\gcd (s,t)>1$
then [Reference Yoshiara27, Lemma 6(1)] implies that every nontrivial
![]() $T^{r}$
-conjugacy class intersects
$T^{r}$
-conjugacy class intersects
![]() ${\mathcal{P}}_{1}$
. However, assertion (i) then implies that
${\mathcal{P}}_{1}$
. However, assertion (i) then implies that
![]() ${\mathcal{P}}_{1}={\mathcal{P}}\setminus \{1\}$
, which is impossible. Therefore,
${\mathcal{P}}_{1}={\mathcal{P}}\setminus \{1\}$
, which is impossible. Therefore,
![]() $\gcd (s,t)=1$
. In particular, to show that
$\gcd (s,t)=1$
. In particular, to show that
![]() $t\geqslant s+1$
it suffices to show that
$t\geqslant s+1$
it suffices to show that
![]() $t\geqslant s$
. The proof of this assertion is adapted from that of [Reference Bamberg, Popiel and Praeger8, Corollary 2.3]. Choose two distinct lines
$t\geqslant s$
. The proof of this assertion is adapted from that of [Reference Bamberg, Popiel and Praeger8, Corollary 2.3]. Choose two distinct lines
![]() $\ell _{1},\ell _{2}\in {\mathcal{L}}_{1}$
, so that
$\ell _{1},\ell _{2}\in {\mathcal{L}}_{1}$
, so that
![]() $\bar{\ell }_{1}$
and
$\bar{\ell }_{1}$
and
![]() $\bar{\ell }_{2}$
are subgroups of
$\bar{\ell }_{2}$
are subgroups of
![]() $T^{r}$
by (ii). For brevity, we now abuse notation slightly and identify
$T^{r}$
by (ii). For brevity, we now abuse notation slightly and identify
![]() $\ell _{1}$
and
$\ell _{1}$
and
![]() $\ell _{2}$
with
$\ell _{2}$
with
![]() $\bar{\ell }_{1}$
and
$\bar{\ell }_{1}$
and
![]() $\bar{\ell }_{2}$
, respectively, dropping the “bar” notation. Since
$\bar{\ell }_{2}$
, respectively, dropping the “bar” notation. Since
![]() $\ell _{1}$
is a subgroup of
$\ell _{1}$
is a subgroup of
![]() $T^{r}$
and right multiplication by any element of
$T^{r}$
and right multiplication by any element of
![]() $T^{r}$
is a collineation of
$T^{r}$
is a collineation of
![]() ${\mathcal{Q}}$
(identified with an element of
${\mathcal{Q}}$
(identified with an element of
![]() $M$
), we have in particular that every right coset
$M$
), we have in particular that every right coset
![]() $\ell _{1}g_{2}$
of
$\ell _{1}g_{2}$
of
![]() $\ell _{1}$
with
$\ell _{1}$
with
![]() $g_{2}\in \ell _{2}$
corresponds precisely to the set of points incident with some line of
$g_{2}\in \ell _{2}$
corresponds precisely to the set of points incident with some line of
![]() ${\mathcal{Q}}$
. Similarly, left multiplications (identified with elements of
${\mathcal{Q}}$
. Similarly, left multiplications (identified with elements of
![]() $\{1\}\times T^{r}\leqslant N$
) are collineations, so every left coset
$\{1\}\times T^{r}\leqslant N$
) are collineations, so every left coset
![]() $g_{1}\ell _{2}$
of
$g_{1}\ell _{2}$
of
![]() $\ell _{2}$
with
$\ell _{2}$
with
![]() $g_{1}\in \ell _{1}$
is a line of
$g_{1}\in \ell _{1}$
is a line of
![]() ${\mathcal{Q}}$
. Therefore,
${\mathcal{Q}}$
. Therefore,
![]() ${\mathcal{L}}^{\prime }=\{g_{1}\ell _{2}\mid g_{1}\in \ell _{1}\}\cup \{\ell _{1}g_{2}\mid g_{2}\in \ell _{2}\}$
is a subset of
${\mathcal{L}}^{\prime }=\{g_{1}\ell _{2}\mid g_{1}\in \ell _{1}\}\cup \{\ell _{1}g_{2}\mid g_{2}\in \ell _{2}\}$
is a subset of
![]() ${\mathcal{L}}$
. Consider also the subset
${\mathcal{L}}$
. Consider also the subset
![]() ${\mathcal{P}}^{\prime }=\ell _{1}\ell _{2}$
of
${\mathcal{P}}^{\prime }=\ell _{1}\ell _{2}$
of
![]() ${\mathcal{P}}=T^{r}$
, and let
${\mathcal{P}}=T^{r}$
, and let
![]() $\text{I}^{\prime }$
be the restriction of
$\text{I}^{\prime }$
be the restriction of
![]() $\text{I}$
to
$\text{I}$
to
![]() $({\mathcal{P}}^{\prime }\times {\mathcal{L}}^{\prime })\cup ({\mathcal{L}}^{\prime }\times {\mathcal{P}}^{\prime })$
. If we can show that
$({\mathcal{P}}^{\prime }\times {\mathcal{L}}^{\prime })\cup ({\mathcal{L}}^{\prime }\times {\mathcal{P}}^{\prime })$
. If we can show that
![]() ${\mathcal{Q}}^{\prime }=({\mathcal{P}}^{\prime },{\mathcal{L}}^{\prime },\text{I}^{\prime })$
is a generalized quadrangle of
${\mathcal{Q}}^{\prime }=({\mathcal{P}}^{\prime },{\mathcal{L}}^{\prime },\text{I}^{\prime })$
is a generalized quadrangle of
![]() ${\mathcal{Q}}$
of order
${\mathcal{Q}}$
of order
![]() $(s,1)$
, then [Reference Payne and Thas21, 2.2.2(i)] will imply that
$(s,1)$
, then [Reference Payne and Thas21, 2.2.2(i)] will imply that
![]() $t\geqslant s$
. Let us first check that
$t\geqslant s$
. Let us first check that
![]() ${\mathcal{Q}}^{\prime }$
satisfies the generalized quadrangle axiom. Take
${\mathcal{Q}}^{\prime }$
satisfies the generalized quadrangle axiom. Take
![]() $\ell \in {\mathcal{L}}^{\prime }$
and
$\ell \in {\mathcal{L}}^{\prime }$
and
![]() $P\in {\mathcal{P}}^{\prime }$
not incident with
$P\in {\mathcal{P}}^{\prime }$
not incident with
![]() $\ell$
. Since
$\ell$
. Since
![]() ${\mathcal{Q}}$
satisfies the generalized quadrangle axiom, there is a unique point
${\mathcal{Q}}$
satisfies the generalized quadrangle axiom, there is a unique point
![]() $P_{0}\in {\mathcal{P}}$
incident with
$P_{0}\in {\mathcal{P}}$
incident with
![]() $\ell$
and collinear with
$\ell$
and collinear with
![]() $P$
. Since
$P$
. Since
![]() $\ell \subset {\mathcal{P}}^{\prime }$
, we have
$\ell \subset {\mathcal{P}}^{\prime }$
, we have
![]() $P_{0}\in {\mathcal{P}}^{\prime }$
, and so
$P_{0}\in {\mathcal{P}}^{\prime }$
, and so
![]() ${\mathcal{Q}}^{\prime }$
also satisfies the generalized quadrangle axiom. It remains to check that
${\mathcal{Q}}^{\prime }$
also satisfies the generalized quadrangle axiom. It remains to check that
![]() ${\mathcal{Q}}^{\prime }$
has order
${\mathcal{Q}}^{\prime }$
has order
![]() $(s,1)$
. Every line in
$(s,1)$
. Every line in
![]() ${\mathcal{L}}^{\prime }$
is incident with
${\mathcal{L}}^{\prime }$
is incident with
![]() $s+1$
points in
$s+1$
points in
![]() ${\mathcal{P}}^{\prime }$
, being a coset of either
${\mathcal{P}}^{\prime }$
, being a coset of either
![]() $\ell _{1}$
or
$\ell _{1}$
or
![]() $\ell _{2}$
, so it remains to show that every point in
$\ell _{2}$
, so it remains to show that every point in
![]() ${\mathcal{P}}^{\prime }$
is incident with exactly two lines in
${\mathcal{P}}^{\prime }$
is incident with exactly two lines in
![]() ${\mathcal{L}}^{\prime }$
. Given
${\mathcal{L}}^{\prime }$
. Given
![]() $P=g_{1}g_{2}\in {\mathcal{P}}^{\prime }$
, where
$P=g_{1}g_{2}\in {\mathcal{P}}^{\prime }$
, where
![]() $g_{1}\in \ell _{1}$
,
$g_{1}\in \ell _{1}$
,
![]() $g_{2}\in \ell _{2}$
, each line
$g_{2}\in \ell _{2}$
, each line
![]() $\ell \in {\mathcal{L}}^{\prime }$
incident with
$\ell \in {\mathcal{L}}^{\prime }$
incident with
![]() $P$
is either of the form
$P$
is either of the form
![]() $h_{1}\ell _{2}$
for some
$h_{1}\ell _{2}$
for some
![]() $h_{1}\in \ell _{1}$
or
$h_{1}\in \ell _{1}$
or
![]() $\ell _{1}h_{2}$
for some
$\ell _{1}h_{2}$
for some
![]() $h_{2}\in \ell _{2}$
, and since
$h_{2}\in \ell _{2}$
, and since
![]() $P\in \ell$
, we must have
$P\in \ell$
, we must have
![]() $h_{1}=g_{1}$
or
$h_{1}=g_{1}$
or
![]() $h_{2}=g_{2}$
, respectively. Therefore,
$h_{2}=g_{2}$
, respectively. Therefore,
![]() $P$
is incident with exactly two lines in
$P$
is incident with exactly two lines in
![]() ${\mathcal{L}}^{\prime }$
, namely
${\mathcal{L}}^{\prime }$
, namely
![]() $g_{1}\ell _{2}$
and
$g_{1}\ell _{2}$
and
![]() $\ell _{1}g_{2}$
.◻
$\ell _{1}g_{2}$
.◻
Proposition 4.2 restricts the possibilities for the simple group
![]() $T$
in Hypothesis 5.1 to those listed in Table 2. The following result shows that, moreover,
$T$
in Hypothesis 5.1 to those listed in Table 2. The following result shows that, moreover,
![]() $T$
must be a Lie type group.
$T$
must be a Lie type group.
Proposition 5.4. If Hypothesis 5.1 holds then
![]() $T$
is a Lie type group.
$T$
is a Lie type group.
Table 3. Alternating and sporadic groups in the proof of Proposition 5.4.

Proof. We have
![]() $|{\mathcal{P}}|=|T|^{r}$
, and
$|{\mathcal{P}}|=|T|^{r}$
, and
![]() $r\in \{1,2,3\}$
by Proposition 4.2. For each of the alternating and sporadic simple groups
$r\in \{1,2,3\}$
by Proposition 4.2. For each of the alternating and sporadic simple groups
![]() $T$
in Table 2, we check computationally for solutions of
$T$
in Table 2, we check computationally for solutions of
![]() $|T|^{r}=(s+1)(st+1)$
satisfying
$|T|^{r}=(s+1)(st+1)$
satisfying
![]() $s\geqslant 2$
,
$s\geqslant 2$
,
![]() $t\geqslant 2$
and properties (ii) and (iii) of Lemma 2.1 (see Remark 5.5). If
$t\geqslant 2$
and properties (ii) and (iii) of Lemma 2.1 (see Remark 5.5). If
![]() $r=3$
then the only such solutions have the form
$r=3$
then the only such solutions have the form
![]() $(s,t)=(|T|-1,|T|+1)=(|\unicode[STIX]{x1D6FA}|-1,|\unicode[STIX]{x1D6FA}|+1)$
, and this contradicts the final assertion of Proposition 4.2. If
$(s,t)=(|T|-1,|T|+1)=(|\unicode[STIX]{x1D6FA}|-1,|\unicode[STIX]{x1D6FA}|+1)$
, and this contradicts the final assertion of Proposition 4.2. If
![]() $r\in \{1,2\}$
then the possibilities for
$r\in \{1,2\}$
then the possibilities for
![]() $T$
and
$T$
and
![]() $(s,t)$
are as in Table 3. By Lemma 5.3(i),
$(s,t)$
are as in Table 3. By Lemma 5.3(i),
![]() ${\mathcal{P}}_{1}$
is a union of
${\mathcal{P}}_{1}$
is a union of
![]() $T^{r}$
-conjugacy classes, and so we must be able to partition
$T^{r}$
-conjugacy classes, and so we must be able to partition
![]() $|{\mathcal{P}}_{1}|=s(t+1)$
into a subset of the sizes of these classes (respecting multiplicities). When
$|{\mathcal{P}}_{1}|=s(t+1)$
into a subset of the sizes of these classes (respecting multiplicities). When
![]() $r=1$
and
$r=1$
and
![]() $T\cong \text{Alt}_{7}$
or
$T\cong \text{Alt}_{7}$
or
![]() $\text{Alt}_{8}$
, this is impossible: the nontrivial conjugacy class sizes not exceeding
$\text{Alt}_{8}$
, this is impossible: the nontrivial conjugacy class sizes not exceeding
![]() $s(t+1)$
are
$s(t+1)$
are
![]() $70$
,
$70$
,
![]() $105$
and
$105$
and
![]() $210$
in the first case, and
$210$
in the first case, and
![]() $105$
,
$105$
,
![]() $112$
and
$112$
and
![]() $210$
in the second (with each occurring exactly once). Similarly, if
$210$
in the second (with each occurring exactly once). Similarly, if
![]() $r=2$
and
$r=2$
and
![]() $T\cong \text{J}_{1}$
, one may check computationally that there is no partition of
$T\cong \text{J}_{1}$
, one may check computationally that there is no partition of
![]() $s(t+1)$
, where
$s(t+1)$
, where
![]() $(s,t)=(419,175141)$
, into nontrivial
$(s,t)=(419,175141)$
, into nontrivial
![]() $T^{2}$
-conjugacy class sizes. Hence, it remains to consider the cases where
$T^{2}$
-conjugacy class sizes. Hence, it remains to consider the cases where
![]() $r=2$
and
$r=2$
and
![]() $T\cong \text{Alt}_{6}$
or
$T\cong \text{Alt}_{6}$
or
![]() $\text{M}_{11}$
. Here we first determine computationally the possible partitions of
$\text{M}_{11}$
. Here we first determine computationally the possible partitions of
![]() $s(t+1)$
into nontrivial
$s(t+1)$
into nontrivial
![]() $T^{2}$
-conjugacy class sizes to obtain a list of possible partitions of
$T^{2}$
-conjugacy class sizes to obtain a list of possible partitions of
![]() ${\mathcal{P}}_{1}$
into
${\mathcal{P}}_{1}$
into
![]() $T^{2}$
-conjugacy classes. Now, because the point graph of
$T^{2}$
-conjugacy classes. Now, because the point graph of
![]() ${\mathcal{Q}}$
is a strongly regular graph in which adjacent vertices have
${\mathcal{Q}}$
is a strongly regular graph in which adjacent vertices have
![]() $\unicode[STIX]{x1D706}:=s-1$
common neighbors and nonadjacent vertices have
$\unicode[STIX]{x1D706}:=s-1$
common neighbors and nonadjacent vertices have
![]() $\unicode[STIX]{x1D707}:=t+1$
common neighbors,
$\unicode[STIX]{x1D707}:=t+1$
common neighbors,
![]() ${\mathcal{P}}_{1}$
must be a partial difference set of
${\mathcal{P}}_{1}$
must be a partial difference set of
![]() $T^{2}$
with these parameters. That is, each nonidentity element
$T^{2}$
with these parameters. That is, each nonidentity element
![]() $y\in T^{2}$
must have exactly
$y\in T^{2}$
must have exactly
![]() $\unicode[STIX]{x1D706}$
representations of the form
$\unicode[STIX]{x1D706}$
representations of the form
![]() $y=z_{i}z_{j}^{-1}$
for
$y=z_{i}z_{j}^{-1}$
for
![]() $z_{i},z_{j}\in {\mathcal{P}}_{1}$
if
$z_{i},z_{j}\in {\mathcal{P}}_{1}$
if
![]() $y\in {\mathcal{P}}_{1}$
, and exactly
$y\in {\mathcal{P}}_{1}$
, and exactly
![]() $\unicode[STIX]{x1D707}$
such representations if
$\unicode[STIX]{x1D707}$
such representations if
![]() $y\not \in {\mathcal{P}}_{1}$
. A computation verifies that this condition is violated for each of the partitions of
$y\not \in {\mathcal{P}}_{1}$
. A computation verifies that this condition is violated for each of the partitions of
![]() ${\mathcal{P}}_{1}$
determined in the previous step.◻
${\mathcal{P}}_{1}$
determined in the previous step.◻
Remark 5.5. In the proof of Proposition 5.4, and at several other points in Sections 5 and 6, we need to check computationally whether certain positive integers
![]() $X$
can be equal to the number of points of a thick finite generalized quadrangle. That is, we check for integral solutions
$X$
can be equal to the number of points of a thick finite generalized quadrangle. That is, we check for integral solutions
![]() $(s,t)$
of the equation
$(s,t)$
of the equation
![]() $(s+1)(st+1)=X$
subject to the constraints
$(s+1)(st+1)=X$
subject to the constraints
![]() $s\geqslant 2$
,
$s\geqslant 2$
,
![]() $t\geqslant 2$
,
$t\geqslant 2$
,
![]() $s^{1/2}\leqslant t\leqslant s^{2}\leqslant t^{4}$
and
$s^{1/2}\leqslant t\leqslant s^{2}\leqslant t^{4}$
and
![]() $s+t\mid st(st+1)$
imposed by Lemma 2.1. In Section 5,
$s+t\mid st(st+1)$
imposed by Lemma 2.1. In Section 5,
![]() $X$
has the form
$X$
has the form
![]() $|T|^{m}$
for some nonabelian finite simple group
$|T|^{m}$
for some nonabelian finite simple group
![]() $T$
and some
$T$
and some
![]() $m\leqslant 3$
, and in Section 6 we instead have
$m\leqslant 3$
, and in Section 6 we instead have
![]() $X=Y^{m}$
with
$X=Y^{m}$
with
![]() $m\leqslant 4$
and
$m\leqslant 4$
and
![]() $Y$
the index of a maximal subgroup of an almost simple group. The above inequalities imply that
$Y$
the index of a maximal subgroup of an almost simple group. The above inequalities imply that
![]() $s$
must lie between
$s$
must lie between
![]() $X^{1/4}-1$
and
$X^{1/4}-1$
and
![]() $X^{5/2}$
, so it suffices to consider every integer
$X^{5/2}$
, so it suffices to consider every integer
![]() $s$
in this range and determine whether
$s$
in this range and determine whether
![]() $t=((X-1)/s-1)/(s+1)$
is an integer and, if so, whether
$t=((X-1)/s-1)/(s+1)$
is an integer and, if so, whether
![]() $s+t\mid st(st+1)$
. We remark that we found it useful to also observe that
$s+t\mid st(st+1)$
. We remark that we found it useful to also observe that
![]() $s$
must divide
$s$
must divide
![]() $X-1$
, because it turned out that
$X-1$
, because it turned out that
![]() $X-1$
had only a very small number of divisors in many of the cases that we had to consider.
$X-1$
had only a very small number of divisors in many of the cases that we had to consider.
We now show that
![]() $r$
cannot equal
$r$
cannot equal
![]() $3$
, and deduce some further restrictions on
$3$
, and deduce some further restrictions on
![]() $T$
when
$T$
when
![]() $r\in \{1,2\}$
.
$r\in \{1,2\}$
.
Proposition 5.6. If Hypothesis 5.1 holds then
![]() $r\leqslant 2$
and
$r\leqslant 2$
and
![]() $T$
is a Lie type group with the property that
$T$
is a Lie type group with the property that
![]() $|C_{T}(x)|<|T|^{1-2r/9}$
for all
$|C_{T}(x)|<|T|^{1-2r/9}$
for all
![]() $x\in T\setminus \{1\}$
.
$x\in T\setminus \{1\}$
.
Proof. By Propositions 4.2 and 5.4,
![]() $T$
is a Lie type group and
$T$
is a Lie type group and
![]() $r\leqslant 3$
. We now show that
$r\leqslant 3$
. We now show that
![]() $|C_{T}(x)|<|T|^{1-2r/9}$
for all
$|C_{T}(x)|<|T|^{1-2r/9}$
for all
![]() $x\in T\setminus \{1\}$
and deduce from this that
$x\in T\setminus \{1\}$
and deduce from this that
![]() $r\neq 3$
. Suppose, toward a contradiction, that there exists
$r\neq 3$
. Suppose, toward a contradiction, that there exists
![]() $x\in T\setminus \{1\}$
with
$x\in T\setminus \{1\}$
with
![]() $|C_{T}(x)|\geqslant |T|^{1-2r/9}$
. Define
$|C_{T}(x)|\geqslant |T|^{1-2r/9}$
. Define
![]() $w=(x,1,\ldots ,1)\in T^{r}$
and let
$w=(x,1,\ldots ,1)\in T^{r}$
and let
![]() ${\mathcal{Q}}_{\unicode[STIX]{x1D703}}=({\mathcal{P}}_{\unicode[STIX]{x1D703}},{\mathcal{L}}_{\unicode[STIX]{x1D703}})$
be the substructure of
${\mathcal{Q}}_{\unicode[STIX]{x1D703}}=({\mathcal{P}}_{\unicode[STIX]{x1D703}},{\mathcal{L}}_{\unicode[STIX]{x1D703}})$
be the substructure of
![]() ${\mathcal{Q}}$
fixed by
${\mathcal{Q}}$
fixed by
![]() $\unicode[STIX]{x1D703}=(w,w)\in N_{1}$
. Then
$\unicode[STIX]{x1D703}=(w,w)\in N_{1}$
. Then
![]() ${\mathcal{P}}_{\unicode[STIX]{x1D703}}=C_{T}(x)\times T^{r-1}$
, and hence
${\mathcal{P}}_{\unicode[STIX]{x1D703}}=C_{T}(x)\times T^{r-1}$
, and hence
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\geqslant |T|^{(1-2r/9)+(r-1)}=|T|^{7r/9}=|{\mathcal{P}}|^{7/9}$
. Proposition 2.4 then says that either
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\geqslant |T|^{(1-2r/9)+(r-1)}=|T|^{7r/9}=|{\mathcal{P}}|^{7/9}$
. Proposition 2.4 then says that either
![]() $s\geqslant t+3$
, or
$s\geqslant t+3$
, or
![]() $(s,t)\in \{(2,4),(3,9)\}$
. The first of these conditions contradicts Lemma 5.3(vii); the second implies that
$(s,t)\in \{(2,4),(3,9)\}$
. The first of these conditions contradicts Lemma 5.3(vii); the second implies that
![]() $|T|^{r}=(s+1)(st+1)\in \{27,112\}$
, which is impossible because
$|T|^{r}=(s+1)(st+1)\in \{27,112\}$
, which is impossible because
![]() $|T|\geqslant 60$
. Hence, every
$|T|\geqslant 60$
. Hence, every
![]() $x\in T\setminus \{1\}$
must satisfy
$x\in T\setminus \{1\}$
must satisfy
![]() $|C_{T}(x)|<|T|^{1-2r/9}$
. For
$|C_{T}(x)|<|T|^{1-2r/9}$
. For
![]() $r=3$
, this says that
$r=3$
, this says that
![]() $|C_{T}(x)|<|T|^{1/3}$
for all
$|C_{T}(x)|<|T|^{1/3}$
for all
![]() $x\in T\setminus \{1\}$
, a contradiction because we can always find some
$x\in T\setminus \{1\}$
, a contradiction because we can always find some
![]() $x$
with
$x$
with
![]() $|C_{T}(x)|>|T|^{1/3}$
(as noted in the proof of Proposition 4.2). Therefore,
$|C_{T}(x)|>|T|^{1/3}$
(as noted in the proof of Proposition 4.2). Therefore,
![]() $r\leqslant 2$
.◻
$r\leqslant 2$
.◻
Proposition 5.6 allows us to further reduce the list of candidates for the simple group
![]() $T$
in Hypothesis 5.1 in the remaining cases, where
$T$
in Hypothesis 5.1 in the remaining cases, where
![]() $r\in \{1,2\}$
. Let us first consider the case
$r\in \{1,2\}$
. Let us first consider the case
![]() $r=2$
.
$r=2$
.
Corollary 5.7. If Hypothesis 5.1 holds with
![]() $r=2$
then
$r=2$
then
![]() $T$
has Lie type
$T$
has Lie type
![]() $\text{A}_{1}$
,
$\text{A}_{1}$
,
![]() $\text{A}_{2}^{\unicode[STIX]{x1D700}}$
,
$\text{A}_{2}^{\unicode[STIX]{x1D700}}$
,
![]() $^{2}\text{B}_{2}$
or
$^{2}\text{B}_{2}$
or
![]() $^{2}\text{G}_{2}$
. In particular,
$^{2}\text{G}_{2}$
. In particular,
![]() $T$
has a unique conjugacy class of involutions.
$T$
has a unique conjugacy class of involutions.
Proof. The result is verified by straightforward calculations involving the bound on centralizer orders imposed by Proposition 5.6, but we include the details in Section 9. ◻
We can now prove the HC case of Theorem 1.1.
Theorem 5.8. Suppose that
![]() ${\mathcal{Q}}$
is a thick finite generalized quadrangle with a collineation group
${\mathcal{Q}}$
is a thick finite generalized quadrangle with a collineation group
![]() $G$
that acts primitively on the point set
$G$
that acts primitively on the point set
![]() ${\mathcal{P}}$
of
${\mathcal{P}}$
of
![]() ${\mathcal{Q}}$
. Then the action of
${\mathcal{Q}}$
. Then the action of
![]() $G$
on
$G$
on
![]() ${\mathcal{P}}$
does not have O’Nan–Scott type HC.
${\mathcal{P}}$
does not have O’Nan–Scott type HC.
Proof. As explained above, the socle of
![]() $G$
is a group
$G$
is a group
![]() $N=T^{r}\times T^{r}$
as in Hypothesis 5.1, for some
$N=T^{r}\times T^{r}$
as in Hypothesis 5.1, for some
![]() $r\geqslant 2$
. However, Corollary 5.7 tells us that
$r\geqslant 2$
. However, Corollary 5.7 tells us that
![]() $r=2$
and that
$r=2$
and that
![]() $T$
has a unique conjugacy class of involutions. In particular,
$T$
has a unique conjugacy class of involutions. In particular,
![]() $T^{r}=T^{2}$
has exactly three conjugacy classes of involutions, with representatives
$T^{r}=T^{2}$
has exactly three conjugacy classes of involutions, with representatives
![]() $(x,1)$
,
$(x,1)$
,
![]() $(1,y)$
and
$(1,y)$
and
![]() $(x,y)$
, where
$(x,y)$
, where
![]() $x$
and
$x$
and
![]() $y$
are involutions in
$y$
are involutions in
![]() $T$
. Now, [Reference Bamberg, Popiel and Praeger8, Theorem 1.1] says that
$T$
. Now, [Reference Bamberg, Popiel and Praeger8, Theorem 1.1] says that
![]() $G$
cannot act transitively on the flags of
$G$
cannot act transitively on the flags of
![]() ${\mathcal{Q}}$
, so in particular
${\mathcal{Q}}$
, so in particular
![]() $N$
cannot act transitively on the flags of
$N$
cannot act transitively on the flags of
![]() ${\mathcal{Q}}$
. Lemma 5.3(vi) therefore implies that
${\mathcal{Q}}$
. Lemma 5.3(vi) therefore implies that
![]() ${\mathcal{P}}_{1}$
must contain exactly two
${\mathcal{P}}_{1}$
must contain exactly two
![]() $T^{2}$
-conjugacy classes of involutions. Hence, without loss of generality,
$T^{2}$
-conjugacy classes of involutions. Hence, without loss of generality,
![]() ${\mathcal{P}}_{1}$
contains the class
${\mathcal{P}}_{1}$
contains the class
![]() $(x,1)^{T^{2}}$
. Since
$(x,1)^{T^{2}}$
. Since
![]() $G$
acts primitively on
$G$
acts primitively on
![]() ${\mathcal{P}}$
, it induces a subgroup of
${\mathcal{P}}$
, it induces a subgroup of
![]() $\operatorname{Aut}(T^{2})=\operatorname{Aut}(T)\wr \text{Sym}_{2}$
that swaps the two simple direct factors of
$\operatorname{Aut}(T^{2})=\operatorname{Aut}(T)\wr \text{Sym}_{2}$
that swaps the two simple direct factors of
![]() $T^{2}$
. Therefore,
$T^{2}$
. Therefore,
![]() ${\mathcal{P}}_{1}$
also contains the class
${\mathcal{P}}_{1}$
also contains the class
![]() $(1,y)^{T^{2}}$
, and so does not contain the class
$(1,y)^{T^{2}}$
, and so does not contain the class
![]() $(x,y)^{T^{2}}$
. In particular, no line
$(x,y)^{T^{2}}$
. In particular, no line
![]() $\ell \in {\mathcal{L}}_{1}$
can be incident with both a conjugate of
$\ell \in {\mathcal{L}}_{1}$
can be incident with both a conjugate of
![]() $(x,1)$
and a conjugate of
$(x,1)$
and a conjugate of
![]() $(1,y)$
, because by Lemma 5.3(ii),
$(1,y)$
, because by Lemma 5.3(ii),
![]() $\ell$
would then also be incident with the product of these elements, a conjugate of
$\ell$
would then also be incident with the product of these elements, a conjugate of
![]() $(x,y)$
. Hence,
$(x,y)$
. Hence,
![]() ${\mathcal{L}}_{1}$
is partitioned into two sets of lines: those incident with conjugates of
${\mathcal{L}}_{1}$
is partitioned into two sets of lines: those incident with conjugates of
![]() $(x,1)$
, and those incident with conjugates of
$(x,1)$
, and those incident with conjugates of
![]() $(1,y)$
. Since
$(1,y)$
. Since
![]() $G_{1}$
swaps these sets,
$G_{1}$
swaps these sets,
![]() $G$
acts flag-transitively, in contradiction with [Reference Bamberg, Popiel and Praeger8, Theorem 1.1].◻
$G$
acts flag-transitively, in contradiction with [Reference Bamberg, Popiel and Praeger8, Theorem 1.1].◻
For
![]() $r=1$
we are left with the following list of candidates for
$r=1$
we are left with the following list of candidates for
![]() $T$
.
$T$
.
Corollary 5.9. Suppose that Hypothesis 5.1 holds with
![]() $r=1$
. Then
$r=1$
. Then
![]() $T$
is of Lie type
$T$
is of Lie type
![]() $\text{A}_{1}$
,
$\text{A}_{1}$
,
![]() $\text{A}_{n}^{\unicode[STIX]{x1D700}}$
with
$\text{A}_{n}^{\unicode[STIX]{x1D700}}$
with
![]() $2\leqslant n\leqslant 6$
,
$2\leqslant n\leqslant 6$
,
![]() $\text{B}_{2}$
,
$\text{B}_{2}$
,
![]() $\text{C}_{2}$
,
$\text{C}_{2}$
,
![]() $\text{C}_{3}$
,
$\text{C}_{3}$
,
![]() $\text{D}_{n}^{\unicode[STIX]{x1D700}}$
with
$\text{D}_{n}^{\unicode[STIX]{x1D700}}$
with
![]() $4\leqslant n\leqslant 6$
, or exceptional Lie type other than
$4\leqslant n\leqslant 6$
, or exceptional Lie type other than
![]() $\text{E}_{8}$
.
$\text{E}_{8}$
.
Proof. By Propositions 4.2 and 5.4,
![]() $T$
is one of the Lie type groups in the first column of Table 2. By arguing as in the proof of Proposition 5.6 but applying Proposition 2.5 instead of Proposition 2.4 in the first paragraph, we conclude that one of the following conditions must also hold:
$T$
is one of the Lie type groups in the first column of Table 2. By arguing as in the proof of Proposition 5.6 but applying Proposition 2.5 instead of Proposition 2.4 in the first paragraph, we conclude that one of the following conditions must also hold:
(i) every nonidentity element
 $x\in T$
satisfies
$x\in T$
satisfies
 $|C_{T}(x)|<|T|^{94/125}$
, or
$|C_{T}(x)|<|T|^{94/125}$
, or(ii)
 $s\leqslant 2.9701\times 10^{15}$
.
$s\leqslant 2.9701\times 10^{15}$
.
By choosing appropriate elements
![]() $x\in T$
as in the proofs in Section 3, we are able to use this to deduce that
$x\in T$
as in the proofs in Section 3, we are able to use this to deduce that
![]() $T$
does not have type
$T$
does not have type
![]() $\text{A}_{7}^{\unicode[STIX]{x1D700}}$
,
$\text{A}_{7}^{\unicode[STIX]{x1D700}}$
,
![]() $\text{A}_{8}^{\unicode[STIX]{x1D700}}$
,
$\text{A}_{8}^{\unicode[STIX]{x1D700}}$
,
![]() $\text{B}_{4}$
,
$\text{B}_{4}$
,
![]() $\text{C}_{4}$
,
$\text{C}_{4}$
,
![]() $\text{D}_{7}^{\unicode[STIX]{x1D700}}$
,
$\text{D}_{7}^{\unicode[STIX]{x1D700}}$
,
![]() $\text{D}_{8}^{\unicode[STIX]{x1D700}}$
or
$\text{D}_{8}^{\unicode[STIX]{x1D700}}$
or
![]() $\text{E}_{8}$
. We rule out
$\text{E}_{8}$
. We rule out
![]() $\text{E}_{8}$
here as an example, and include details of the remaining cases in Section 9. If
$\text{E}_{8}$
here as an example, and include details of the remaining cases in Section 9. If
![]() $T\cong \text{E}_{8}(q)$
then
$T\cong \text{E}_{8}(q)$
then
![]() $(s+1)^{4}>|{\mathcal{P}}|=|T|\geqslant |\text{E}_{8}(2)|\approx 3.378\times 10^{74}$
and hence
$(s+1)^{4}>|{\mathcal{P}}|=|T|\geqslant |\text{E}_{8}(2)|\approx 3.378\times 10^{74}$
and hence
![]() $s>|\text{E}_{8}(2)|^{1/4}-1\approx 4.287\times 10^{18}$
, contradicting (ii), so (i) must hold. However, as noted in the proof of Lemma 3.3, there exists
$s>|\text{E}_{8}(2)|^{1/4}-1\approx 4.287\times 10^{18}$
, contradicting (ii), so (i) must hold. However, as noted in the proof of Lemma 3.3, there exists
![]() $x\in T\cong \text{E}_{8}(q)$
with
$x\in T\cong \text{E}_{8}(q)$
with
![]() $|C_{T}(x)|=q^{57}|\text{E}_{7}(q)|\sim q^{190}$
, while
$|C_{T}(x)|=q^{57}|\text{E}_{7}(q)|\sim q^{190}$
, while
![]() $|T|^{94/125}\sim (q^{248})^{94/125}<q^{187}$
. Indeed, one may check that
$|T|^{94/125}\sim (q^{248})^{94/125}<q^{187}$
. Indeed, one may check that
![]() $|C_{T}(x)|>|T|^{94/125}$
for all
$|C_{T}(x)|>|T|^{94/125}$
for all
![]() $q\geqslant 2$
.◻
$q\geqslant 2$
.◻
Finally, we use Lemma 5.3 to reduce the list of candidates for
![]() $T$
in Corollary 5.9 to those given in the first row of Table 1, thereby proving the HS case of Theorem 1.1.
$T$
in Corollary 5.9 to those given in the first row of Table 1, thereby proving the HS case of Theorem 1.1.
Proposition 5.10. Let
![]() ${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}})$
be a thick finite generalized quadrangle admitting a collineation group
${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}})$
be a thick finite generalized quadrangle admitting a collineation group
![]() $G$
that acts primitively of type HS on
$G$
that acts primitively of type HS on
![]() ${\mathcal{P}}$
, with socle
${\mathcal{P}}$
, with socle
![]() $T\times T$
for some nonabelian finite simple group
$T\times T$
for some nonabelian finite simple group
![]() $T$
. Then
$T$
. Then
![]() $T$
has Lie type
$T$
has Lie type
![]() $\text{A}_{5}^{\unicode[STIX]{x1D700}}$
,
$\text{A}_{5}^{\unicode[STIX]{x1D700}}$
,
![]() $\text{A}_{6}^{\unicode[STIX]{x1D700}}$
,
$\text{A}_{6}^{\unicode[STIX]{x1D700}}$
,
![]() $\text{B}_{3}$
,
$\text{B}_{3}$
,
![]() $\text{C}_{2}$
,
$\text{C}_{2}$
,
![]() $\text{C}_{3}$
,
$\text{C}_{3}$
,
![]() $\text{D}_{4}^{\unicode[STIX]{x1D700}}$
,
$\text{D}_{4}^{\unicode[STIX]{x1D700}}$
,
![]() $\text{D}_{5}^{\unicode[STIX]{x1D700}}$
,
$\text{D}_{5}^{\unicode[STIX]{x1D700}}$
,
![]() $\text{D}_{6}^{\unicode[STIX]{x1D700}}$
,
$\text{D}_{6}^{\unicode[STIX]{x1D700}}$
,
![]() $\text{E}_{6}^{\unicode[STIX]{x1D700}}$
,
$\text{E}_{6}^{\unicode[STIX]{x1D700}}$
,
![]() $\text{E}_{7}$
or
$\text{E}_{7}$
or
![]() $\text{F}_{4}$
.
$\text{F}_{4}$
.
Proof. We are assuming that Hypothesis 5.1 holds with
![]() $r=1$
, so
$r=1$
, so
![]() $T$
must be one of the groups listed in Corollary 5.9. It remains to show that, moreover,
$T$
must be one of the groups listed in Corollary 5.9. It remains to show that, moreover,
![]() $T$
cannot have type
$T$
cannot have type
![]() $\text{A}_{1}$
,
$\text{A}_{1}$
,
![]() $\text{A}_{2}^{\unicode[STIX]{x1D700}}$
,
$\text{A}_{2}^{\unicode[STIX]{x1D700}}$
,
![]() $\text{A}_{3}^{\unicode[STIX]{x1D700}}$
,
$\text{A}_{3}^{\unicode[STIX]{x1D700}}$
,
![]() $\text{A}_{4}^{\unicode[STIX]{x1D700}}$
,
$\text{A}_{4}^{\unicode[STIX]{x1D700}}$
,
![]() $^{2}\text{B}_{2}$
,
$^{2}\text{B}_{2}$
,
![]() $^{2}\text{G}_{2}$
,
$^{2}\text{G}_{2}$
,
![]() $^{2}\text{F}_{4}$
,
$^{2}\text{F}_{4}$
,
![]() $\text{G}_{2}$
or
$\text{G}_{2}$
or
![]() $^{3}\text{D}_{4}$
. This follows from Lemma 5.3(v), because in each of these cases
$^{3}\text{D}_{4}$
. This follows from Lemma 5.3(v), because in each of these cases
![]() $T$
has at most two conjugacy classes of involutions. (This may be verified using, for example, [Reference Gorenstein, Lyons and Solomon17, Table 4.5.1] for odd characteristic and [Reference Liebeck and Seitz18] for even characteristic.)◻
$T$
has at most two conjugacy classes of involutions. (This may be verified using, for example, [Reference Gorenstein, Lyons and Solomon17, Table 4.5.1] for odd characteristic and [Reference Liebeck and Seitz18] for even characteristic.)◻
Remark 5.11. Proposition 5.10 begs the obvious question of whether we can rule out the last remaining candidates for
![]() $T$
listed there. We are confident that we will be able to do this, but it seems that it will require even more new ideas and a detailed case-by-case analysis. Of course, some of the remaining groups can be ruled out in certain cases using Lemma 5.3(v); in particular, if
$T$
listed there. We are confident that we will be able to do this, but it seems that it will require even more new ideas and a detailed case-by-case analysis. Of course, some of the remaining groups can be ruled out in certain cases using Lemma 5.3(v); in particular, if
![]() $T$
has Lie type
$T$
has Lie type
![]() $\text{C}_{2}$
,
$\text{C}_{2}$
,
![]() $\text{C}_{3}$
,
$\text{C}_{3}$
,
![]() $\text{F}_{4}$
or
$\text{F}_{4}$
or
![]() $\text{E}_{6}^{\unicode[STIX]{x1D700}}$
in characteristic
$\text{E}_{6}^{\unicode[STIX]{x1D700}}$
in characteristic
![]() $p$
, then we must have
$p$
, then we must have
![]() $p=2$
, because in odd characteristic these groups have only two conjugacy classes of involutions. When
$p=2$
, because in odd characteristic these groups have only two conjugacy classes of involutions. When
![]() $T$
has exactly three conjugacy classes of involutions, we can begin by applying Lemma 5.3(v) (because we know from [Reference Bamberg, Popiel and Praeger8] that
$T$
has exactly three conjugacy classes of involutions, we can begin by applying Lemma 5.3(v) (because we know from [Reference Bamberg, Popiel and Praeger8] that
![]() $N$
cannot act transitively on the flags of
$N$
cannot act transitively on the flags of
![]() ${\mathcal{Q}}$
), and then the arguments in the proof of Lemma 5.3(iv)–(vi) can be extended to deduce some restrictions on which involutions can appear in
${\mathcal{Q}}$
), and then the arguments in the proof of Lemma 5.3(iv)–(vi) can be extended to deduce some restrictions on which involutions can appear in
![]() ${\mathcal{P}}_{1}$
. However, even with this extra information, we have thus far been unable to completely rule out any of the remaining candidates for
${\mathcal{P}}_{1}$
. However, even with this extra information, we have thus far been unable to completely rule out any of the remaining candidates for
![]() $T$
. These kinds of arguments become more difficult when
$T$
. These kinds of arguments become more difficult when
![]() $T$
has more than three conjugacy classes of involutions, and in any case, it seems that it will be necessary to treat each group individually, and to use the structure of its involution centralizers in some detail. Although not an ideal state of affairs, we therefore leave the remaining cases for a future project.
$T$
has more than three conjugacy classes of involutions, and in any case, it seems that it will be necessary to treat each group individually, and to use the structure of its involution centralizers in some detail. Although not an ideal state of affairs, we therefore leave the remaining cases for a future project.
6 Primitive point actions of type PA
We now apply Corollary 1.5 to the case where
![]() $N$
is the socle of a primitive permutation group
$N$
is the socle of a primitive permutation group
![]() $G$
of O’Nan–Scott type PA. The notation of Hypothesis 6.1 coincides with that of Table 1.
$G$
of O’Nan–Scott type PA. The notation of Hypothesis 6.1 coincides with that of Table 1.
Hypothesis 6.1. Let
![]() ${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}})$
be a thick finite generalized quadrangle of order
${\mathcal{Q}}=({\mathcal{P}},{\mathcal{L}})$
be a thick finite generalized quadrangle of order
![]() $(s,t)$
admitting a collineation group
$(s,t)$
admitting a collineation group
![]() $G$
that acts primitively of type PA on
$G$
that acts primitively of type PA on
![]() ${\mathcal{P}}$
, writing
${\mathcal{P}}$
, writing
![]() $T^{r}\leqslant G\leqslant H\wr \text{Sym}_{r}$
for some almost simple primitive group
$T^{r}\leqslant G\leqslant H\wr \text{Sym}_{r}$
for some almost simple primitive group
![]() $H\leqslant \text{Sym}(\unicode[STIX]{x1D6FA})$
with socle
$H\leqslant \text{Sym}(\unicode[STIX]{x1D6FA})$
with socle
![]() $T$
, where
$T$
, where
![]() $r\geqslant 2$
.
$r\geqslant 2$
.
Proposition 6.2. If Hypothesis 6.1 holds then
![]() $2\leqslant r\leqslant 4$
and every nonidentity element of
$2\leqslant r\leqslant 4$
and every nonidentity element of
![]() $H$
fixes less than
$H$
fixes less than
![]() $|\unicode[STIX]{x1D6FA}|^{1-r/5}$
points of
$|\unicode[STIX]{x1D6FA}|^{1-r/5}$
points of
![]() $\unicode[STIX]{x1D6FA}$
.
$\unicode[STIX]{x1D6FA}$
.
Proof. The socle of
![]() $G$
is
$G$
is
![]() $N=T^{r}$
and the action of
$N=T^{r}$
and the action of
![]() $H$
on
$H$
on
![]() $\unicode[STIX]{x1D6FA}$
is not semiregular, so the result follows immediately from Corollary 1.5.◻
$\unicode[STIX]{x1D6FA}$
is not semiregular, so the result follows immediately from Corollary 1.5.◻
To say more than this, we would like to have generic lower bounds for the fixity
![]() $f(H)$
, namely the maximum number of fixed points of a nonidentity element, of an almost simple primitive group
$f(H)$
, namely the maximum number of fixed points of a nonidentity element, of an almost simple primitive group
![]() $H\leqslant \text{Sym}(\unicode[STIX]{x1D6FA})$
. This problem was investigated in a recent paper of Liebeck and Shalev [Reference Liebeck and Shalev19], who proved that
$H\leqslant \text{Sym}(\unicode[STIX]{x1D6FA})$
. This problem was investigated in a recent paper of Liebeck and Shalev [Reference Liebeck and Shalev19], who proved that
![]() $f(H)\geqslant |\unicode[STIX]{x1D6FA}|^{1/6}$
except in a short list of exceptions. This lower bound is not quite large enough to force further restrictions on
$f(H)\geqslant |\unicode[STIX]{x1D6FA}|^{1/6}$
except in a short list of exceptions. This lower bound is not quite large enough to force further restrictions on
![]() $r$
in Proposition 6.2, because to rule out
$r$
in Proposition 6.2, because to rule out
![]() $r=4$
(as we did for types HC and CD) we would need
$r=4$
(as we did for types HC and CD) we would need
![]() $f(H)$
to be at least
$f(H)$
to be at least
![]() $|\unicode[STIX]{x1D6FA}|^{1/5}$
. However, Liebeck and Shalev remark (after [Reference Liebeck and Shalev19, Theorem 4]) that their
$|\unicode[STIX]{x1D6FA}|^{1/5}$
. However, Liebeck and Shalev remark (after [Reference Liebeck and Shalev19, Theorem 4]) that their
![]() $|\unicode[STIX]{x1D6FA}|^{1/6}$
bound could potentially be improved generically to around
$|\unicode[STIX]{x1D6FA}|^{1/6}$
bound could potentially be improved generically to around
![]() $|\unicode[STIX]{x1D6FA}|^{1/3}$
, which would be sufficient for this purpose. Work in this direction is currently being undertaken by Elisa Covato at the University of Bristol as part of her PhD research [Reference Covato11], with the aim of classifying the almost simple primitive permutation groups
$|\unicode[STIX]{x1D6FA}|^{1/3}$
, which would be sufficient for this purpose. Work in this direction is currently being undertaken by Elisa Covato at the University of Bristol as part of her PhD research [Reference Covato11], with the aim of classifying the almost simple primitive permutation groups
![]() $H\leqslant \text{Sym}(\unicode[STIX]{x1D6FA})$
containing an involution that fixes at least
$H\leqslant \text{Sym}(\unicode[STIX]{x1D6FA})$
containing an involution that fixes at least
![]() $|\unicode[STIX]{x1D6FA}|^{4/9}$
points. As of this writing, the alternating and sporadic cases have been completed, and so we are able to apply these results to sharpen Proposition 6.2 as follows.
$|\unicode[STIX]{x1D6FA}|^{4/9}$
points. As of this writing, the alternating and sporadic cases have been completed, and so we are able to apply these results to sharpen Proposition 6.2 as follows.
Proposition 6.3. Suppose that Hypothesis 6.1 holds with
![]() $r>2$
and
$r>2$
and
![]() $T$
an alternating group or a sporadic simple group, and let
$T$
an alternating group or a sporadic simple group, and let
![]() $S\leqslant H$
denote the point stabilizer in the action of
$S\leqslant H$
denote the point stabilizer in the action of
![]() $H$
on
$H$
on
![]() $\unicode[STIX]{x1D6FA}$
. Then
$\unicode[STIX]{x1D6FA}$
. Then
![]() $r\in \{3,4\}$
,
$r\in \{3,4\}$
,
![]() $H=T\cong \text{Alt}_{p}$
with
$H=T\cong \text{Alt}_{p}$
with
![]() $p$
a prime congruent to
$p$
a prime congruent to
![]() $3$
modulo
$3$
modulo
![]() $4$
, and
$4$
, and
![]() $S\cap T=p\cdot (p-1)/2$
.
$S\cap T=p\cdot (p-1)/2$
.
Proof. Since
![]() $r>2$
, Proposition 6.2 tells us that
$r>2$
, Proposition 6.2 tells us that
![]() $r\in \{3,4\}$
, and that the fixity
$r\in \{3,4\}$
, and that the fixity
![]() $f(H)$
of
$f(H)$
of
![]() $H$
must be at most
$H$
must be at most
![]() $|\unicode[STIX]{x1D6FA}|^{1-r/5}$
. If
$|\unicode[STIX]{x1D6FA}|^{1-r/5}$
. If
![]() $f(H)\leqslant |\unicode[STIX]{x1D6FA}|^{1-3/5}=|\unicode[STIX]{x1D6FA}|^{2/5}$
then Covato’s results [Reference Covato11] imply that either (i)
$f(H)\leqslant |\unicode[STIX]{x1D6FA}|^{1-3/5}=|\unicode[STIX]{x1D6FA}|^{2/5}$
then Covato’s results [Reference Covato11] imply that either (i)
![]() $T\cong \text{Alt}_{p}$
with
$T\cong \text{Alt}_{p}$
with
![]() $p\equiv 3\;(\text{mod}\;4)$
a prime and
$p\equiv 3\;(\text{mod}\;4)$
a prime and
![]() $S\cap T=p\cdot (p-1)/2$
, or (ii)
$S\cap T=p\cdot (p-1)/2$
, or (ii)
![]() $H$
and
$H$
and
![]() $S$
are in Table 4.
$S$
are in Table 4.
In case (i) we can at least deal with the situation where
![]() $H=\text{Sym}_{p}$
. Indeed, by the argument in [Reference Liebeck and Shalev19, Section 6], there is an involution
$H=\text{Sym}_{p}$
. Indeed, by the argument in [Reference Liebeck and Shalev19, Section 6], there is an involution
![]() $u\in S=p\cdot (p-1)$
fixing
$u\in S=p\cdot (p-1)$
fixing
![]() $2^{(p-3)/2}((p-3)/2)!$
elements of
$2^{(p-3)/2}((p-3)/2)!$
elements of
![]() $\unicode[STIX]{x1D6FA}$
, which is greater than
$\unicode[STIX]{x1D6FA}$
, which is greater than
![]() $|\unicode[STIX]{x1D6FA}|^{2/5}=(2(p-2)!)^{2/5}$
provided that
$|\unicode[STIX]{x1D6FA}|^{2/5}=(2(p-2)!)^{2/5}$
provided that
![]() $p>7$
. If
$p>7$
. If
![]() $p=7$
then we observe that
$p=7$
then we observe that
![]() $u$
still fixes more than
$u$
still fixes more than
![]() $|\unicode[STIX]{x1D6FA}|^{1/3}$
elements. This rules out
$|\unicode[STIX]{x1D6FA}|^{1/3}$
elements. This rules out
![]() $r=4$
, because then
$r=4$
, because then
![]() $1/3>1-r/5=1/5$
. For
$1/3>1-r/5=1/5$
. For
![]() $r=3$
we apply Proposition 2.6. We have
$r=3$
we apply Proposition 2.6. We have
![]() $|\unicode[STIX]{x1D6FA}|=2\cdot 5!=120$
and hence
$|\unicode[STIX]{x1D6FA}|=2\cdot 5!=120$
and hence
![]() $|{\mathcal{P}}|=|\unicode[STIX]{x1D6FA}|^{3}=120^{3}$
, and the only solution of
$|{\mathcal{P}}|=|\unicode[STIX]{x1D6FA}|^{3}=120^{3}$
, and the only solution of
![]() $120^{3}=(s+1)(st+1)$
satisfying
$120^{3}=(s+1)(st+1)$
satisfying
![]() $s\geqslant 2$
,
$s\geqslant 2$
,
![]() $t\geqslant 2$
and properties (ii) and (iii) of Lemma 2.1 is
$t\geqslant 2$
and properties (ii) and (iii) of Lemma 2.1 is
![]() $(s,t)=(119,121)$
, so Proposition 2.6 implies that every nonidentity collineation of
$(s,t)=(119,121)$
, so Proposition 2.6 implies that every nonidentity collineation of
![]() ${\mathcal{Q}}$
fixes at most
${\mathcal{Q}}$
fixes at most
![]() $|{\mathcal{P}}|^{7/9}$
points. However, the collineation
$|{\mathcal{P}}|^{7/9}$
points. However, the collineation
![]() $(u,1,1)\in G$
fixes more than
$(u,1,1)\in G$
fixes more than
![]() $|\unicode[STIX]{x1D6FA}|^{1/3}|\unicode[STIX]{x1D6FA}|^{2}=|{\mathcal{P}}|^{7/9}$
points, a contradiction. Therefore, if we are in case (i) then we must have
$|\unicode[STIX]{x1D6FA}|^{1/3}|\unicode[STIX]{x1D6FA}|^{2}=|{\mathcal{P}}|^{7/9}$
points, a contradiction. Therefore, if we are in case (i) then we must have
![]() $H=\text{Alt}_{p}$
, as per the assertion.
$H=\text{Alt}_{p}$
, as per the assertion.
Table 4. Actions with small fixity in Proposition 6.3.

Now suppose that
![]() $H$
and
$H$
and
![]() $S$
are in Table 4. First consider the six cases on the left-hand side of the table. In each of these cases,
$S$
are in Table 4. First consider the six cases on the left-hand side of the table. In each of these cases,
![]() $f(H)$
is at least
$f(H)$
is at least
![]() $|\unicode[STIX]{x1D6FA}|^{1/5}$
, so
$|\unicode[STIX]{x1D6FA}|^{1/5}$
, so
![]() $r=4$
is ruled out. For
$r=4$
is ruled out. For
![]() $r=3$
, we apply Proposition 2.6 as above. Since
$r=3$
, we apply Proposition 2.6 as above. Since
![]() $f(H)>|\unicode[STIX]{x1D6FA}|^{1/5}$
, we have in particular
$f(H)>|\unicode[STIX]{x1D6FA}|^{1/5}$
, we have in particular
![]() $f(H)>|\unicode[STIX]{x1D6FA}|^{1/6}$
. Choose
$f(H)>|\unicode[STIX]{x1D6FA}|^{1/6}$
. Choose
![]() $u\in H$
fixing at least
$u\in H$
fixing at least
![]() $|\unicode[STIX]{x1D6FA}|^{1/6}$
elements of
$|\unicode[STIX]{x1D6FA}|^{1/6}$
elements of
![]() $\unicode[STIX]{x1D6FA}$
, and consider the collineation
$\unicode[STIX]{x1D6FA}$
, and consider the collineation
![]() $(u,1,1)\in G$
, which fixes at least
$(u,1,1)\in G$
, which fixes at least
![]() $|\unicode[STIX]{x1D6FA}|^{1/6+2}=|\unicode[STIX]{x1D6FA}|^{13/6}=|{\mathcal{P}}|^{13/18}$
points of
$|\unicode[STIX]{x1D6FA}|^{1/6+2}=|\unicode[STIX]{x1D6FA}|^{13/6}=|{\mathcal{P}}|^{13/18}$
points of
![]() ${\mathcal{Q}}$
. Since the only solutions of
${\mathcal{Q}}$
. Since the only solutions of
![]() $|\unicode[STIX]{x1D6FA}|^{3}=(s+1)(st+1)$
satisfying
$|\unicode[STIX]{x1D6FA}|^{3}=(s+1)(st+1)$
satisfying
![]() $s\geqslant 2$
,
$s\geqslant 2$
,
![]() $t\geqslant 2$
and properties (ii) and (iii) of Lemma 2.1 are those with
$t\geqslant 2$
and properties (ii) and (iii) of Lemma 2.1 are those with
![]() $t=s+2$
, Proposition 2.6 provides a contradiction. Now consider the five cases on the right-hand side of Table 4. The actions of
$t=s+2$
, Proposition 2.6 provides a contradiction. Now consider the five cases on the right-hand side of Table 4. The actions of
![]() $\text{J}_{3}.2$
,
$\text{J}_{3}.2$
,
![]() $\text{O'N}.2$
and
$\text{O'N}.2$
and
![]() $\text{Th}$
all have fixity greater than
$\text{Th}$
all have fixity greater than
![]() $|\unicode[STIX]{x1D6FA}|^{1/6}$
[Reference Liebeck and Shalev19, Lemma 5.3], so these are ruled out for both
$|\unicode[STIX]{x1D6FA}|^{1/6}$
[Reference Liebeck and Shalev19, Lemma 5.3], so these are ruled out for both
![]() $r=3$
and
$r=3$
and
![]() $r=4$
by the same arguments as above. Now consider the action of
$r=4$
by the same arguments as above. Now consider the action of
![]() $\text{M}_{23}$
. Here
$\text{M}_{23}$
. Here
![]() $|\unicode[STIX]{x1D6FA}|=40320$
, and for
$|\unicode[STIX]{x1D6FA}|=40320$
, and for
![]() $r=4$
there are no solutions of
$r=4$
there are no solutions of
![]() $|\unicode[STIX]{x1D6FA}|^{r}=(s+1)(st+1)$
satisfying
$|\unicode[STIX]{x1D6FA}|^{r}=(s+1)(st+1)$
satisfying
![]() $s\geqslant 2$
,
$s\geqslant 2$
,
![]() $t\geqslant 2$
and properties (ii) and (iii) of Lemma 2.1. If
$t\geqslant 2$
and properties (ii) and (iii) of Lemma 2.1. If
![]() $r=3$
, the only such solution is
$r=3$
, the only such solution is
![]() $(s,t)=(40319,40321)$
. By [Reference Liebeck and Shalev19, Lemma 5.3], we have
$(s,t)=(40319,40321)$
. By [Reference Liebeck and Shalev19, Lemma 5.3], we have
![]() $f(H)=5$
, realized by an element
$f(H)=5$
, realized by an element
![]() $u$
of order
$u$
of order
![]() $11$
, and so we can construct a collineation
$11$
, and so we can construct a collineation
![]() $\unicode[STIX]{x1D703}=(u,1,1)\in G$
of
$\unicode[STIX]{x1D703}=(u,1,1)\in G$
of
![]() ${\mathcal{Q}}$
fixing
${\mathcal{Q}}$
fixing
![]() $5|\unicode[STIX]{x1D6FA}|^{2}=8128512000$
points. However,
$5|\unicode[STIX]{x1D6FA}|^{2}=8128512000$
points. However,
![]() $s=t-2<t+3$
, so the final assertion of Lemma 2.2 implies that
$s=t-2<t+3$
, so the final assertion of Lemma 2.2 implies that
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant (s+1)(s+3)=1988752683<8128512000$
, and we have a contradiction. Finally, consider the given action of
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant (s+1)(s+3)=1988752683<8128512000$
, and we have a contradiction. Finally, consider the given action of
![]() $\text{B}$
, for which
$\text{B}$
, for which
![]() $|\unicode[STIX]{x1D6FA}|=3843461129719173164826624000000$
. For
$|\unicode[STIX]{x1D6FA}|=3843461129719173164826624000000$
. For
![]() $r=4$
, there is no solution of
$r=4$
, there is no solution of
![]() $|\unicode[STIX]{x1D6FA}|^{r}=(s+1)(st+1)$
satisfying
$|\unicode[STIX]{x1D6FA}|^{r}=(s+1)(st+1)$
satisfying
![]() $s\geqslant 2$
,
$s\geqslant 2$
,
![]() $t\geqslant 2$
and properties (ii) and (iii) of Lemma 2.1. For
$t\geqslant 2$
and properties (ii) and (iii) of Lemma 2.1. For
![]() $r=3$
, the only such solution is
$r=3$
, the only such solution is
![]() $(s,t)=(|\unicode[STIX]{x1D6FA}|-1,|\unicode[STIX]{x1D6FA}|+1)$
, and so the final assertion of Lemma 2.2 implies that any nonidentity collineation of
$(s,t)=(|\unicode[STIX]{x1D6FA}|-1,|\unicode[STIX]{x1D6FA}|+1)$
, and so the final assertion of Lemma 2.2 implies that any nonidentity collineation of
![]() ${\mathcal{Q}}$
fixes at most
${\mathcal{Q}}$
fixes at most
![]() $(|\unicode[STIX]{x1D6FA}|+1)(|\unicode[STIX]{x1D6FA}|+3)$
points. However, [Reference Liebeck and Shalev19, Lemma 5.3] tells us that
$(|\unicode[STIX]{x1D6FA}|+1)(|\unicode[STIX]{x1D6FA}|+3)$
points. However, [Reference Liebeck and Shalev19, Lemma 5.3] tells us that
![]() $f(H)=22$
, so we can construct a collineation with
$f(H)=22$
, so we can construct a collineation with
![]() $22|\unicode[STIX]{x1D6FA}|^{2}$
points to yield a contradiction.◻
$22|\unicode[STIX]{x1D6FA}|^{2}$
points to yield a contradiction.◻
Remark 6.4. Further improvements to Proposition 6.2 will be made in a future project. In the first instance, we hope to use Covato’s results [Reference Covato11] on fixities of Lie type groups (once available), to complete our treatment of the cases
![]() $r=3$
and
$r=3$
and
![]() $r=4$
. We also note that it is straightforward to handle the case
$r=4$
. We also note that it is straightforward to handle the case
![]() $r=2$
with
$r=2$
with
![]() $T$
a sporadic simple group, and likewise the almost simple case with sporadic socle, computationally along the lines of [Reference Bamberg, Giudici, Morris, Royle and Spiga5, Section 6] (but assuming only point primitivity and not line primitivity). However, we omit these computations from the present paper for brevity.
$T$
a sporadic simple group, and likewise the almost simple case with sporadic socle, computationally along the lines of [Reference Bamberg, Giudici, Morris, Royle and Spiga5, Section 6] (but assuming only point primitivity and not line primitivity). However, we omit these computations from the present paper for brevity.
7 Proof of Theorem 1.1
Let us now summarize the proof of Theorem 1.1. If the primitive action of
![]() $G$
on
$G$
on
![]() ${\mathcal{P}}$
has O’Nan–Scott type AS or TW, then the conditions stated in Table 1 follow immediately from Theorem 1.3. Types HS, HC and PA are treated in Proposition 5.10, Theorem 5.8 and Proposition 6.3, respectively. Types SD and CD are treated together in Proposition 4.3.
${\mathcal{P}}$
has O’Nan–Scott type AS or TW, then the conditions stated in Table 1 follow immediately from Theorem 1.3. Types HS, HC and PA are treated in Proposition 5.10, Theorem 5.8 and Proposition 6.3, respectively. Types SD and CD are treated together in Proposition 4.3.
8 Discussion and open problems
We feel that the results presented in this paper represent a substantial amount of progress toward the classification of point-primitive generalized quadrangles, but there is evidently still a good deal of work to do. We conclude the paper with a brief discussion, and outline some open problems that could be investigated independently and then potentially applied to our classification program.
As discussed in Remark 5.11, we are confident that we will be able to finish the HS case, and it is at least somewhat clear how this might be done. However, the SD and CD cases would appear to be more difficult. The arguments used in Section 5 do not work in these cases, because the proof of Lemma 5.2 (and therefore Lemma 5.3) relies in a crucial way on having
![]() $k=2$
in Hypothesis 4.1, so that conjugation by an element of the point-regular subgroup
$k=2$
in Hypothesis 4.1, so that conjugation by an element of the point-regular subgroup
![]() $M$
is a collineation. We have thus far been unable to find a way to work around this difficulty in any sort of generality. On the other hand, a primitive (resp. quasiprimitive) group of type SD must induce a primitive (resp. transitive) permutation group on the set of simple direct factors of its socle
$M$
is a collineation. We have thus far been unable to find a way to work around this difficulty in any sort of generality. On the other hand, a primitive (resp. quasiprimitive) group of type SD must induce a primitive (resp. transitive) permutation group on the set of simple direct factors of its socle
![]() $T^{k}$
, and it seems that it should be possible to use this extra structure to say more about the SD and CD types, at least in the primitive case (especially since we have already reduced the list of candidates for
$T^{k}$
, and it seems that it should be possible to use this extra structure to say more about the SD and CD types, at least in the primitive case (especially since we have already reduced the list of candidates for
![]() $T$
to those in Table 1). Although we have made some preliminary investigations along these lines, we do not yet know how to finish the SD and CD cases, and so we leave this task for a future project.
$T$
to those in Table 1). Although we have made some preliminary investigations along these lines, we do not yet know how to finish the SD and CD cases, and so we leave this task for a future project.
8.1 Point-regular groups and number theory
There is, of course, a potential, but apparently extremely challenging, way to deal with all of the types HS, SD and CD, and also with type TW, in one fell swoop. In each of these cases, the full collineation group must have a point-regular subgroup of the form
![]() $T^{m}$
, for some
$T^{m}$
, for some
![]() $m$
, with
$m$
, with
![]() $T$
a nonabelian finite simple group. Hence, it would certainly be sufficient to show that such a group cannot act regularly on the points of a generalized quadrangle. However, this would appear to be a very difficult problem in light of the (limited) existing literature. Yoshiara [Reference Yoshiara27] managed to show that a generalized quadrangle of order
$T$
a nonabelian finite simple group. Hence, it would certainly be sufficient to show that such a group cannot act regularly on the points of a generalized quadrangle. However, this would appear to be a very difficult problem in light of the (limited) existing literature. Yoshiara [Reference Yoshiara27] managed to show that a generalized quadrangle of order
![]() $(s,t)$
with
$(s,t)$
with
![]() $s=t^{2}$
cannot have a point-regular collineation group, while Ghinelli [Reference Ghinelli16] considered the case where
$s=t^{2}$
cannot have a point-regular collineation group, while Ghinelli [Reference Ghinelli16] considered the case where
![]() $s$
is even and
$s$
is even and
![]() $t=s$
, showing that such a group must have trivial center and cannot be a Frobenius group. Beyond this, not much else seems to be known in the way of restrictions on groups that can act regularly on the points of a generalized quadrangle (though certainly many of the known generalized quadrangles admit point-regular groups [Reference Bamberg and Giudici4], and the abelian case is understood [Reference De Winter and Thas12]). Although Yoshiara [Reference Yoshiara27] has an extensive suite of lemmas that one might attempt to use to investigate (in particular) the possibility that a group of the form
$t=s$
, showing that such a group must have trivial center and cannot be a Frobenius group. Beyond this, not much else seems to be known in the way of restrictions on groups that can act regularly on the points of a generalized quadrangle (though certainly many of the known generalized quadrangles admit point-regular groups [Reference Bamberg and Giudici4], and the abelian case is understood [Reference De Winter and Thas12]). Although Yoshiara [Reference Yoshiara27] has an extensive suite of lemmas that one might attempt to use to investigate (in particular) the possibility that a group of the form
![]() $T^{m}$
acts point-regularly on a generalized quadrangle
$T^{m}$
acts point-regularly on a generalized quadrangle
![]() ${\mathcal{Q}}$
, the bulk of these lemmas assume that the order
${\mathcal{Q}}$
, the bulk of these lemmas assume that the order
![]() $(s,t)$
of
$(s,t)$
of
![]() ${\mathcal{Q}}$
satisfies
${\mathcal{Q}}$
satisfies
![]() $\gcd (s,t)\neq 1$
. Although this condition holds under Yoshiara’s intended assumption that
$\gcd (s,t)\neq 1$
. Although this condition holds under Yoshiara’s intended assumption that
![]() $s=t^{2}$
, it seems to be difficult to guarantee in general. Indeed, according to Lemma 5.3(ii) (and perhaps not surprisingly), it must fail in our HS case. On the other hand, one might seek a contradiction by examining the arithmetic nature of the equation
$s=t^{2}$
, it seems to be difficult to guarantee in general. Indeed, according to Lemma 5.3(ii) (and perhaps not surprisingly), it must fail in our HS case. On the other hand, one might seek a contradiction by examining the arithmetic nature of the equation
![]() $|T|^{m}=(s+1)(st+1)$
subject to the constraints imposed by Lemma 2.1, and asking when it can be guaranteed that a solution must satisfy
$|T|^{m}=(s+1)(st+1)$
subject to the constraints imposed by Lemma 2.1, and asking when it can be guaranteed that a solution must satisfy
![]() $\gcd (s,t)\neq 1$
. More generally, one might simply ask whether this equation can have any such solutions at all. This motivates the following problem.
$\gcd (s,t)\neq 1$
. More generally, one might simply ask whether this equation can have any such solutions at all. This motivates the following problem.
Problem 8.1. Determine for which nonabelian finite simple groups
![]() $T$
, and which positive integers
$T$
, and which positive integers
![]() $m$
, there exist integral solutions
$m$
, there exist integral solutions
![]() $(s,t)$
of the equation
$(s,t)$
of the equation
subject to the constraints
Failing this, determine when such a solution must satisfy
![]() $\gcd (s,t)\neq 1$
.
$\gcd (s,t)\neq 1$
.
As noted before Proposition 4.2, there is always an “obvious” solution of (13)–(14) when
![]() $m$
is divisible by
$m$
is divisible by
![]() $3$
, namely
$3$
, namely
![]() $(s,t)=(|T|^{m/3}-1,|T|^{m/3}+1)$
, and
$(s,t)=(|T|^{m/3}-1,|T|^{m/3}+1)$
, and
![]() $\gcd (s,t)=1$
in this case because
$\gcd (s,t)=1$
in this case because
![]() $|T|$
is even. It would be useful even to know whether this is the unique solution in this particular situation. We do know that (13)–(14) has solutions for certain groups
$|T|$
is even. It would be useful even to know whether this is the unique solution in this particular situation. We do know that (13)–(14) has solutions for certain groups
![]() $T$
when
$T$
when
![]() $m=1$
or
$m=1$
or
![]() $2$
, as demonstrated by Table 3, but we do not recall encountering any solutions apart from the aforementioned “obvious” ones when
$2$
, as demonstrated by Table 3, but we do not recall encountering any solutions apart from the aforementioned “obvious” ones when
![]() $m\geqslant 3$
. Moreover, it is straightforward to run numerical computations that suggest that certain combinations of families of
$m\geqslant 3$
. Moreover, it is straightforward to run numerical computations that suggest that certain combinations of families of
![]() $T$
and values of
$T$
and values of
![]() $m$
will never yield a solution of (13)–(14). For example, if
$m$
will never yield a solution of (13)–(14). For example, if
![]() $T\cong \text{PSL}_{2}(q)$
and
$T\cong \text{PSL}_{2}(q)$
and
![]() $m=1$
then there is no solution if
$m=1$
then there is no solution if
![]() $q<10^{6}$
, but we do not see how to go about proving that there is no solution for any
$q<10^{6}$
, but we do not see how to go about proving that there is no solution for any
![]() $q$
.
$q$
.
One might also ask about gearing Problem 8.1 toward the PA and AS cases, by seeking solutions of (13)–(14) with
![]() $|T|$
replaced by
$|T|$
replaced by
![]() $|H:S|$
for
$|H:S|$
for
![]() $H$
an almost simple group with socle
$H$
an almost simple group with socle
![]() $T$
and
$T$
and
![]() $S$
a maximal subgroup of
$S$
a maximal subgroup of
![]() $H$
(compare with Hypothesis 6.1, which reduces to the AS case if
$H$
(compare with Hypothesis 6.1, which reduces to the AS case if
![]() $r$
is taken to be
$r$
is taken to be
![]() $1$
). However, solutions of (13)–(14) seem to be rather more common in this setting, and so other methods are needed to rule out cases where solutions arise. For example, if we take
$1$
). However, solutions of (13)–(14) seem to be rather more common in this setting, and so other methods are needed to rule out cases where solutions arise. For example, if we take
![]() $H=T=\text{McL}$
(the McLaughlin sporadic simple group) then there are five (classes of) maximal subgroups
$H=T=\text{McL}$
(the McLaughlin sporadic simple group) then there are five (classes of) maximal subgroups
![]() $S$
of
$S$
of
![]() $H$
for which
$H$
for which
![]() $|H:S|^{2}=(s+1)(st+1)$
has a solution subject to (14): four maximal subgroups of order
$|H:S|^{2}=(s+1)(st+1)$
has a solution subject to (14): four maximal subgroups of order
![]() $40320$
, for which
$40320$
, for which
![]() $(s,t)=(296,5644)$
, and the maximal subgroup
$(s,t)=(296,5644)$
, and the maximal subgroup
![]() $\text{PSU}_{4}(3)$
, for which
$\text{PSU}_{4}(3)$
, for which
![]() $(s,t)=(24,126)$
.
$(s,t)=(24,126)$
.
8.2 Fixities of primitive groups of type TW
Let us conclude with a brief discussion of the TW case. Write
![]() $N=T_{1}\times \cdots \times T_{r}$
, where
$N=T_{1}\times \cdots \times T_{r}$
, where
![]() $T_{1}\cong \cdots \cong T_{r}\cong T$
for some nonabelian finite simple group
$T_{1}\cong \cdots \cong T_{r}\cong T$
for some nonabelian finite simple group
![]() $T$
. A primitive permutation group
$T$
. A primitive permutation group
![]() $G\leqslant \text{Sym}(\unicode[STIX]{x1D6FA})$
of type TW is a semidirect product
$G\leqslant \text{Sym}(\unicode[STIX]{x1D6FA})$
of type TW is a semidirect product
![]() $N\rtimes P$
with socle
$N\rtimes P$
with socle
![]() $N$
acting regularly by right multiplication, and
$N$
acting regularly by right multiplication, and
![]() $P\leqslant \text{Sym}_{r}$
acting by conjugation in such a way that
$P\leqslant \text{Sym}_{r}$
acting by conjugation in such a way that
![]() $T_{1},\ldots ,T_{r}$
are permuted transitively. Certain other rather complicated conditions must also hold [Reference Baddeley2], and in particular
$T_{1},\ldots ,T_{r}$
are permuted transitively. Certain other rather complicated conditions must also hold [Reference Baddeley2], and in particular
![]() $T$
must be a section of
$T$
must be a section of
![]() $P$
. If we intend to apply Theorem 1.1 to classify the generalized quadrangles with a point-primitive collineation group of TW type, then we will need “good” lower bounds for fixities of primitive TW-type groups. Liebeck and Shalev [Reference Liebeck and Shalev19, Section 4] showed that, for every
$P$
. If we intend to apply Theorem 1.1 to classify the generalized quadrangles with a point-primitive collineation group of TW type, then we will need “good” lower bounds for fixities of primitive TW-type groups. Liebeck and Shalev [Reference Liebeck and Shalev19, Section 4] showed that, for every
![]() $T$
and
$T$
and
![]() $r$
, the fixity of
$r$
, the fixity of
![]() $G$
is at least
$G$
is at least
![]() $|T|^{r/3}$
. Although this is very far away from the
$|T|^{r/3}$
. Although this is very far away from the
![]() $4/5$
exponent bound imposed by Theorem 1.1, we would be interested to know under what conditions the exponent could be improved to something “close” to
$4/5$
exponent bound imposed by Theorem 1.1, we would be interested to know under what conditions the exponent could be improved to something “close” to
![]() $4/5$
, so that we could at least rule out some of the subgeometries listed in Lemma 2.2 and then perhaps use other ideas to say more. In [Reference Liebeck and Shalev19, Section 4], Liebeck and Shalev considered an involution
$4/5$
, so that we could at least rule out some of the subgeometries listed in Lemma 2.2 and then perhaps use other ideas to say more. In [Reference Liebeck and Shalev19, Section 4], Liebeck and Shalev considered an involution
![]() $x\in P$
(which must exist because
$x\in P$
(which must exist because
![]() $T$
is a section of
$T$
is a section of
![]() $P$
and
$P$
and
![]() $|T|$
is even) and observed that
$|T|$
is even) and observed that
![]() $x$
induces a permutation of
$x$
induces a permutation of
![]() $\{T_{1},\ldots ,T_{r}\}$
that fixes at least
$\{T_{1},\ldots ,T_{r}\}$
that fixes at least
![]() $|T|^{ca+b}$
elements of
$|T|^{ca+b}$
elements of
![]() $\unicode[STIX]{x1D6FA}\equiv T^{r}$
, where the induced permutation has cycle structure
$\unicode[STIX]{x1D6FA}\equiv T^{r}$
, where the induced permutation has cycle structure
![]() $(1^{a},2^{b})$
and every involution
$(1^{a},2^{b})$
and every involution
![]() $g\in \operatorname{Aut}(T)$
satisfies
$g\in \operatorname{Aut}(T)$
satisfies
![]() $|C_{T}(g)|\geqslant |T|^{c}$
. By [Reference Liebeck and Shalev19, Proposition 2.4], we can take
$|C_{T}(g)|\geqslant |T|^{c}$
. By [Reference Liebeck and Shalev19, Proposition 2.4], we can take
![]() $c=1/3$
independently of
$c=1/3$
independently of
![]() $T$
, and so because
$T$
, and so because
![]() $a/3+b\geqslant (r-2)/3+2/3=r/3$
, it follows that
$a/3+b\geqslant (r-2)/3+2/3=r/3$
, it follows that
![]() $x$
fixes at least
$x$
fixes at least
![]() $|T|^{r/3}$
elements. Now,
$|T|^{r/3}$
elements. Now,
![]() $c$
can certainly be taken larger than
$c$
can certainly be taken larger than
![]() $1/3$
in at least some nonabelian finite simple groups
$1/3$
in at least some nonabelian finite simple groups
![]() $T$
(though presumably never as large as
$T$
(though presumably never as large as
![]() $4/5$
), and if we happen to have
$4/5$
), and if we happen to have
![]() $c>1/2$
then
$c>1/2$
then
![]() $ca+b$
is maximized when
$ca+b$
is maximized when
![]() $b=1$
(else it is maximized when
$b=1$
(else it is maximized when
![]() $a=0$
). Hence, roughly speaking, if
$a=0$
). Hence, roughly speaking, if
![]() $c$
happens to be somewhat large (for a given
$c$
happens to be somewhat large (for a given
![]() $T$
) and we happen to be able to guarantee that
$T$
) and we happen to be able to guarantee that
![]() $x$
can be chosen with
$x$
can be chosen with
![]() $b$
quite small, then we might have a useful bound on the fixity of
$b$
quite small, then we might have a useful bound on the fixity of
![]() $G$
to work with. Bounds on
$G$
to work with. Bounds on
![]() $c$
can certainly be determined on a case-by-case basis from standard results about involution centralizers, but in light of the rather involved necessary and sufficient conditions for
$c$
can certainly be determined on a case-by-case basis from standard results about involution centralizers, but in light of the rather involved necessary and sufficient conditions for
![]() $P$
to be a maximal subgroup of
$P$
to be a maximal subgroup of
![]() $G$
, it is not clear to us what can be said about the cycle structure of permutations of
$G$
, it is not clear to us what can be said about the cycle structure of permutations of
![]() $\{T_{1},\ldots ,T_{r}\}$
induced by involutions in
$\{T_{1},\ldots ,T_{r}\}$
induced by involutions in
![]() $P$
. We therefore pose the following (somewhat vaguely worded) problem.
$P$
. We therefore pose the following (somewhat vaguely worded) problem.
Problem 8.2. Under what conditions can it be guaranteed that a primitive permutation group of type TW and degree
![]() $d$
has large fixity, where by “large” we mean, say,
$d$
has large fixity, where by “large” we mean, say,
![]() $d^{3/4}$
or more?
$d^{3/4}$
or more?
9 Additional proofs
Proof of Proposition 2.4.
Suppose that we are not in case (iii). Then, by the final assertion of Lemma 2.2,
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant (s+1)(t+1)$
, and we argue as in the proof of Theorem 1.3. We must show that we are either in case (ii), or that
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant (s+1)(t+1)$
, and we argue as in the proof of Theorem 1.3. We must show that we are either in case (ii), or that
![]() $f(s,t)=((s+1)(st+1))^{7/9}-(s+1)(t+1)$
is positive. We have
$f(s,t)=((s+1)(st+1))^{7/9}-(s+1)(t+1)$
is positive. We have
![]() $\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}t(s,t)=(s+1)(7s-h(s,t))/h(s,t)$
, where
$\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}t(s,t)=(s+1)(7s-h(s,t))/h(s,t)$
, where
![]() $h(s,t)=9((s+1)(st+1))^{2/9}$
. If
$h(s,t)=9((s+1)(st+1))^{2/9}$
. If
![]() $s\geqslant 13$
then (using also
$s\geqslant 13$
then (using also
![]() $2\leqslant t\leqslant s^{2}$
) we have
$2\leqslant t\leqslant s^{2}$
) we have
![]() $h(s,t)\leqslant 9({\textstyle \frac{14}{13}}s)^{2/9}({\textstyle \frac{27}{26}}st)^{2/9}\leqslant 9({\textstyle \frac{189}{169}})^{2/9}s^{8/9}$
, so
$h(s,t)\leqslant 9({\textstyle \frac{14}{13}}s)^{2/9}({\textstyle \frac{27}{26}}st)^{2/9}\leqslant 9({\textstyle \frac{189}{169}})^{2/9}s^{8/9}$
, so
![]() $7s-h(s,t)\geqslant s^{8/9}(7s^{1/9}-9({\textstyle \frac{189}{169}})^{2/9})$
. The right-hand side is positive if and only if
$7s-h(s,t)\geqslant s^{8/9}(7s^{1/9}-9({\textstyle \frac{189}{169}})^{2/9})$
. The right-hand side is positive if and only if
![]() $s>({\textstyle \frac{9}{7}})^{9}({\textstyle \frac{189}{169}})^{2}\approx 12.01>12$
, and so it follows that
$s>({\textstyle \frac{9}{7}})^{9}({\textstyle \frac{189}{169}})^{2}\approx 12.01>12$
, and so it follows that
![]() $f(s,t)>0$
for all
$f(s,t)>0$
for all
![]() $s\geqslant 13$
, for all
$s\geqslant 13$
, for all
![]() $s^{1/2}\leqslant t\leqslant s^{2}$
. If
$s^{1/2}\leqslant t\leqslant s^{2}$
. If
![]() $4\leqslant s\leqslant 12$
then a direct calculation shows that
$4\leqslant s\leqslant 12$
then a direct calculation shows that
![]() $f(s,t)>0$
for all
$f(s,t)>0$
for all
![]() $s^{1/2}\leqslant t\leqslant s^{2}$
, so it remains to consider
$s^{1/2}\leqslant t\leqslant s^{2}$
, so it remains to consider
![]() $s\in \{2,3\}$
. If
$s\in \{2,3\}$
. If
![]() $s=2$
then, by the final paragraph of the proof of Theorem 1.3, either
$s=2$
then, by the final paragraph of the proof of Theorem 1.3, either
![]() $t=2$
and every nonidentity collineation of
$t=2$
and every nonidentity collineation of
![]() ${\mathcal{Q}}$
fixes at most
${\mathcal{Q}}$
fixes at most
![]() $7<|{\mathcal{P}}|^{7/9}=15^{7/9}\approx 8.22$
points, or
$7<|{\mathcal{P}}|^{7/9}=15^{7/9}\approx 8.22$
points, or
![]() $t=4$
and we are in case (ii). Finally, if
$t=4$
and we are in case (ii). Finally, if
![]() $s=3$
then
$s=3$
then
![]() $3^{1/2}\leqslant t\leqslant 3^{2}$
, and a direct calculation shows that
$3^{1/2}\leqslant t\leqslant 3^{2}$
, and a direct calculation shows that
![]() $f(3,t)>0$
for
$f(3,t)>0$
for
![]() $3^{1/2}\leqslant t\leqslant 7$
. Moreover,
$3^{1/2}\leqslant t\leqslant 7$
. Moreover,
![]() ${\mathcal{Q}}$
cannot have order
${\mathcal{Q}}$
cannot have order
![]() $(s,t)=(3,8)$
by Lemma 2.1(iii). If
$(s,t)=(3,8)$
by Lemma 2.1(iii). If
![]() $(s,t)=(3,9)$
then
$(s,t)=(3,9)$
then
![]() ${\mathcal{Q}}$
is the elliptic quadric
${\mathcal{Q}}$
is the elliptic quadric
![]() $\mathsf{Q}^{-}(5,3)$
[Reference Payne and Thas21, 5.3.2], and a FinInG [Reference Bamberg, Betten, Cara, De Beule, Lavrauw and Neunhöffer3] calculation shows that (up to conjugacy) there is a unique nonidentity collineation
$\mathsf{Q}^{-}(5,3)$
[Reference Payne and Thas21, 5.3.2], and a FinInG [Reference Bamberg, Betten, Cara, De Beule, Lavrauw and Neunhöffer3] calculation shows that (up to conjugacy) there is a unique nonidentity collineation
![]() $\unicode[STIX]{x1D703}$
fixing
$\unicode[STIX]{x1D703}$
fixing
![]() $40>|{\mathcal{P}}|^{7/9}=112^{7/9}\approx 39.25$
points. Moreover,
$40>|{\mathcal{P}}|^{7/9}=112^{7/9}\approx 39.25$
points. Moreover,
![]() ${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
is a generalized quadrangle of order
${\mathcal{Q}}_{\unicode[STIX]{x1D703}}$
is a generalized quadrangle of order
![]() $(3,3)$
, and every other nonidentity collineation of
$(3,3)$
, and every other nonidentity collineation of
![]() ${\mathcal{Q}}$
fixes at most
${\mathcal{Q}}$
fixes at most
![]() $16<112^{7/9}$
points.◻
$16<112^{7/9}$
points.◻
Proof of Proposition 2.5.
Suppose that we are not in case (ii) or (iii). Then
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant (s+1)(t+1)$
by the final assertion of Lemma 2.2. We show that
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant (s+1)(t+1)$
by the final assertion of Lemma 2.2. We show that
![]() $f(s,t)=((s+1)(st+1))^{94/125}-(s+1)(t+1)$
is positive. We have
$f(s,t)=((s+1)(st+1))^{94/125}-(s+1)(t+1)$
is positive. We have
where
![]() $h(s,t)=125((s+1)(st+1))^{31/125}$
. Let
$h(s,t)=125((s+1)(st+1))^{31/125}$
. Let
![]() $a=2.9701\times 10^{15}$
. Then
$a=2.9701\times 10^{15}$
. Then
![]() $s\geqslant a$
, so (using also
$s\geqslant a$
, so (using also
![]() $2\leqslant t\leqslant s^{2}$
) we have
$2\leqslant t\leqslant s^{2}$
) we have
 $$\begin{eqnarray}\displaystyle h(s,t) & {\leqslant} & \displaystyle 125\biggl(\frac{a+1}{a}s\biggr)^{31/125}\biggl(\frac{2a+1}{2a}st\biggr)^{31/125}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 9\biggl(\frac{(2a+1)(a+1)}{2a^{2}}\biggr)^{31/125}s^{124/125},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h(s,t) & {\leqslant} & \displaystyle 125\biggl(\frac{a+1}{a}s\biggr)^{31/125}\biggl(\frac{2a+1}{2a}st\biggr)^{31/125}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 9\biggl(\frac{(2a+1)(a+1)}{2a^{2}}\biggr)^{31/125}s^{124/125},\nonumber\end{eqnarray}$$
and hence
The right-hand side is positive because
and it follows that
![]() $f(s,t)>0$
for all
$f(s,t)>0$
for all
![]() $s\geqslant a$
, for all
$s\geqslant a$
, for all
![]() $s^{1/2}\leqslant t\leqslant s^{2}$
.◻
$s^{1/2}\leqslant t\leqslant s^{2}$
.◻
Proof of Proposition 2.6.
Since
![]() $s=t-2<t+3$
, the final assertion of Lemma 2.2 implies that
$s=t-2<t+3$
, the final assertion of Lemma 2.2 implies that
![]() $|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant (s+1)(t+1)=(s+1)(s+3)$
. The result follows upon comparing this with
$|{\mathcal{P}}_{\unicode[STIX]{x1D703}}|\leqslant (s+1)(t+1)=(s+1)(s+3)$
. The result follows upon comparing this with
![]() $|{\mathcal{P}}|=(s+1)^{3}$
.◻
$|{\mathcal{P}}|=(s+1)^{3}$
.◻
Proof of Corollary 5.7.
By Propositions 4.2 and 5.4,
![]() $T$
is one of the Lie type groups in the second column of Table 2. However, by Proposition 5.6, we must also have
$T$
is one of the Lie type groups in the second column of Table 2. However, by Proposition 5.6, we must also have
![]() $|C_{T}(x)|<|T|^{5/9}$
for all
$|C_{T}(x)|<|T|^{5/9}$
for all
![]() $x\in T\setminus \{1\}$
. We use this to show that
$x\in T\setminus \{1\}$
. We use this to show that
![]() $T$
cannot have type
$T$
cannot have type
![]() $\text{A}_{3}^{\unicode[STIX]{x1D700}}$
,
$\text{A}_{3}^{\unicode[STIX]{x1D700}}$
,
![]() $\text{B}_{2}=\text{C}_{2}$
,
$\text{B}_{2}=\text{C}_{2}$
,
![]() $^{2}\text{F}_{4}$
or
$^{2}\text{F}_{4}$
or
![]() $\text{G}_{2}$
.
$\text{G}_{2}$
.
If
![]() $T\cong \text{G}_{2}(q)$
then
$T\cong \text{G}_{2}(q)$
then
![]() $|T|=q^{6}(q^{6}-1)(q^{2}-1)$
, and we can choose
$|T|=q^{6}(q^{6}-1)(q^{2}-1)$
, and we can choose
![]() $x\in T$
with
$x\in T$
with
![]() $|C_{T}(x)|=q|\text{A}_{1}(q)|=q^{6}(q^{2}-1)/\text{gcd}(2,q-1)$
as in the proof of Lemma 3.3(ii). Note also that
$|C_{T}(x)|=q|\text{A}_{1}(q)|=q^{6}(q^{2}-1)/\text{gcd}(2,q-1)$
as in the proof of Lemma 3.3(ii). Note also that
![]() $q\geqslant 3$
because
$q\geqslant 3$
because
![]() $\text{G}_{2}(2)$
is not simple. If
$\text{G}_{2}(2)$
is not simple. If
![]() $q$
is even or
$q$
is even or
![]() $q>19$
then
$q>19$
then
![]() $|C_{T}(x)|>|T|^{5/9}$
, and if
$|C_{T}(x)|>|T|^{5/9}$
, and if
![]() $q\in \{3,5,7,9,11,13,17,19\}$
then there is no solution of
$q\in \{3,5,7,9,11,13,17,19\}$
then there is no solution of
![]() $|T|^{2}=(s+1)(st+1)$
satisfying
$|T|^{2}=(s+1)(st+1)$
satisfying
![]() $s\geqslant 2,t\geqslant 2$
and properties (ii) and (iii) of Lemma 2.1. If
$s\geqslant 2,t\geqslant 2$
and properties (ii) and (iii) of Lemma 2.1. If
![]() $T\cong ^{2}\text{F}_{4}(q)$
then
$T\cong ^{2}\text{F}_{4}(q)$
then
![]() $q=2^{2n+1}$
with
$q=2^{2n+1}$
with
![]() $n\geqslant 1$
(because
$n\geqslant 1$
(because
![]() $^{2}\text{F}_{4}(2)$
is not simple and
$^{2}\text{F}_{4}(2)$
is not simple and
![]() $^{2}\text{F}_{4}(2)^{\prime }$
was treated in Proposition 5.4),
$^{2}\text{F}_{4}(2)^{\prime }$
was treated in Proposition 5.4),
![]() $|T|=q^{12}(q^{6}+1)(q^{4}-1)(q^{3}+1)(q-1)$
and, as in the proof of Lemma 3.3(ii), we can choose
$|T|=q^{12}(q^{6}+1)(q^{4}-1)(q^{3}+1)(q-1)$
and, as in the proof of Lemma 3.3(ii), we can choose
![]() $x\in T$
with
$x\in T$
with
![]() $|C_{T}(x)|=q^{10}|^{2}\text{B}_{2}(q)|$
$|C_{T}(x)|=q^{10}|^{2}\text{B}_{2}(q)|$
![]() $=q^{12}(q^{2}+1)(q-1)$
. This yields
$=q^{12}(q^{2}+1)(q-1)$
. This yields
![]() $|C_{T}(x)|>|T|^{5/9}$
for all
$|C_{T}(x)|>|T|^{5/9}$
for all
![]() $q$
. If
$q$
. If
![]() $T\cong \text{PSp}_{4}(q)$
$T\cong \text{PSp}_{4}(q)$
![]() $\cong \unicode[STIX]{x1D6FA}_{5}(q)$
then
$\cong \unicode[STIX]{x1D6FA}_{5}(q)$
then
![]() $q\geqslant 3$
(because
$q\geqslant 3$
(because
![]() $\text{PSp}_{2}(2)\cong \text{Sym}_{6}$
is not simple),
$\text{PSp}_{2}(2)\cong \text{Sym}_{6}$
is not simple),
![]() $|T|=$
$|T|=$
![]() $q^{4}(q^{4}-1)(q^{2}-1)/\text{gcd}(2,q-1)$
, and taking
$q^{4}(q^{4}-1)(q^{2}-1)/\text{gcd}(2,q-1)$
, and taking
![]() $x\in T$
with
$x\in T$
with
![]() $|C_{T}(x)|=q^{4}(q^{2}-1)/\text{gcd}(2,q-1)$
as in the proof of Lemma 3.4 yields
$|C_{T}(x)|=q^{4}(q^{2}-1)/\text{gcd}(2,q-1)$
as in the proof of Lemma 3.4 yields
![]() $|C_{T}(x)|\geqslant |T|^{5/9}$
for all
$|C_{T}(x)|\geqslant |T|^{5/9}$
for all
![]() $q\geqslant 3$
. Finally, if
$q\geqslant 3$
. Finally, if
![]() $T\cong \text{PSL}_{4}^{\unicode[STIX]{x1D700}}(q)$
then
$T\cong \text{PSL}_{4}^{\unicode[STIX]{x1D700}}(q)$
then
and we can choose
![]() $x\in T$
with
$x\in T$
with
![]() $|C_{T}(x)|=q^{5}|\text{GL}_{2}^{\unicode[STIX]{x1D700}}(q)|/\text{gcd}(4,q-\unicode[STIX]{x1D700})=$
$|C_{T}(x)|=q^{5}|\text{GL}_{2}^{\unicode[STIX]{x1D700}}(q)|/\text{gcd}(4,q-\unicode[STIX]{x1D700})=$
![]() $q^{6}(q^{2}-1)(q-\unicode[STIX]{x1D700})/\text{gcd}(4,q-\unicode[STIX]{x1D700})$
as in the proof of Lemma 3.4. This yields
$q^{6}(q^{2}-1)(q-\unicode[STIX]{x1D700})/\text{gcd}(4,q-\unicode[STIX]{x1D700})$
as in the proof of Lemma 3.4. This yields
![]() $|C_{T}(x)|>|T|^{5/9}$
unless
$|C_{T}(x)|>|T|^{5/9}$
unless
![]() $\unicode[STIX]{x1D716}=+$
and
$\unicode[STIX]{x1D716}=+$
and
![]() $q=2$
, and in this case there is no solution of
$q=2$
, and in this case there is no solution of
![]() $|T|^{2}=(s+1)(st+1)$
satisfying
$|T|^{2}=(s+1)(st+1)$
satisfying
![]() $s\geqslant 2$
,
$s\geqslant 2$
,
![]() $t\geqslant 2$
and properties (ii) and (iii) of Lemma 2.1.◻
$t\geqslant 2$
and properties (ii) and (iii) of Lemma 2.1.◻
Proof of Corollary 5.9 (continued).
Now suppose that
![]() $T\cong \text{PSL}_{n+1}^{\unicode[STIX]{x1D700}}(q)$
with
$T\cong \text{PSL}_{n+1}^{\unicode[STIX]{x1D700}}(q)$
with
![]() $n\in \{7,8\}$
, and choose
$n\in \{7,8\}$
, and choose
![]() $x\in T$
as in the proof of Lemma 3.4, so that (1) holds. If
$x\in T$
as in the proof of Lemma 3.4, so that (1) holds. If
![]() $n=8$
then
$n=8$
then
![]() $|C_{T}(x)|>|T|^{7/9}$
for all
$|C_{T}(x)|>|T|^{7/9}$
for all
![]() $q\geqslant 2$
, so Proposition 5.6 gives a contradiction. If
$q\geqslant 2$
, so Proposition 5.6 gives a contradiction. If
![]() $n=7$
then
$n=7$
then
![]() $|C_{T}(x)|>|T|^{94/125}$
for all
$|C_{T}(x)|>|T|^{94/125}$
for all
![]() $q\geqslant 2$
, so condition (ii) must hold. That is,
$q\geqslant 2$
, so condition (ii) must hold. That is,
![]() $s\leqslant 2.9701\times 10^{15}$
, so
$s\leqslant 2.9701\times 10^{15}$
, so
This forces
![]() $q\leqslant 9$
, in which case there is no solution of
$q\leqslant 9$
, in which case there is no solution of
![]() $|T|=(s+1)(st+1)$
satisfying
$|T|=(s+1)(st+1)$
satisfying
![]() $s\geqslant 2$
,
$s\geqslant 2$
,
![]() $t\geqslant 2$
and properties (ii) and (iii) of Lemma 2.1.
$t\geqslant 2$
and properties (ii) and (iii) of Lemma 2.1.
If
![]() $T\cong \text{PSp}_{8}(q)$
then
$T\cong \text{PSp}_{8}(q)$
then
and we take
![]() $x\in T$
with
$x\in T$
with
![]() $|C_{T}(x)|=q^{16}(q^{2}-1)(q^{4}-1)(q^{6}-1)/\text{gcd}(2,q-1)$
, as per (2). This yields
$|C_{T}(x)|=q^{16}(q^{2}-1)(q^{4}-1)(q^{6}-1)/\text{gcd}(2,q-1)$
, as per (2). This yields
![]() $|C_{T}(x)|>|T|^{94/125}$
for all
$|C_{T}(x)|>|T|^{94/125}$
for all
![]() $q\geqslant 2$
, so again (15) must hold. This implies that
$q\geqslant 2$
, so again (15) must hold. This implies that
![]() $q\leqslant 53$
, in which case there is no solution of
$q\leqslant 53$
, in which case there is no solution of
![]() $|T|=(s+1)(st+1)$
satisfying
$|T|=(s+1)(st+1)$
satisfying
![]() $s\geqslant 2$
,
$s\geqslant 2$
,
![]() $t\geqslant 2$
and properties (ii) and (iii) of Lemma 2.1. Similarly, for
$t\geqslant 2$
and properties (ii) and (iii) of Lemma 2.1. Similarly, for
![]() $T\cong \unicode[STIX]{x1D6FA}_{9}(q)$
take
$T\cong \unicode[STIX]{x1D6FA}_{9}(q)$
take
![]() $x\in T$
as in the proof of Lemma 3.4, so that
$x\in T$
as in the proof of Lemma 3.4, so that
![]() $|C_{T}(x)|=|\text{SO}_{2n}^{\pm }(q)|=q^{12}(q^{4}\pm 1)(q^{2}-1)(q^{4}-1)(q^{6}-1)$
as in (3). This yields
$|C_{T}(x)|=|\text{SO}_{2n}^{\pm }(q)|=q^{12}(q^{4}\pm 1)(q^{2}-1)(q^{4}-1)(q^{6}-1)$
as in (3). This yields
![]() $|C_{T}(x)|>|T|^{94/125}$
for all
$|C_{T}(x)|>|T|^{94/125}$
for all
![]() $q\geqslant 2$
, so (15) must hold, and we immediately have a contradiction because
$q\geqslant 2$
, so (15) must hold, and we immediately have a contradiction because
![]() $|\unicode[STIX]{x1D6FA}_{9}(q)|=|\text{PSp}_{8}(q)|$
.
$|\unicode[STIX]{x1D6FA}_{9}(q)|=|\text{PSp}_{8}(q)|$
.
Finally, suppose that
![]() $T\cong \text{P}\unicode[STIX]{x1D6FA}_{2n}^{\pm }(q)$
with
$T\cong \text{P}\unicode[STIX]{x1D6FA}_{2n}^{\pm }(q)$
with
![]() $n\in \{7,8\}$
, and choose
$n\in \{7,8\}$
, and choose
![]() $x\in T$
as in the proof of Lemma 3.4. If
$x\in T$
as in the proof of Lemma 3.4. If
![]() $n=8$
then by using (4)–(5) (for
$n=8$
then by using (4)–(5) (for
![]() $q$
odd) and (7)–(8) (for
$q$
odd) and (7)–(8) (for
![]() $q$
even), one may check that
$q$
even), one may check that
![]() $|C_{T}(x)|>|T|^{94/125}$
for all
$|C_{T}(x)|>|T|^{94/125}$
for all
![]() $q\geqslant 2$
. Hence, (15) must hold, and this implies that
$q\geqslant 2$
. Hence, (15) must hold, and this implies that
![]() $q\in \{2,3\}$
, in which case there is no solution of
$q\in \{2,3\}$
, in which case there is no solution of
![]() $|T|=(s+1)(st+1)$
satisfying
$|T|=(s+1)(st+1)$
satisfying
![]() $s\geqslant 2$
,
$s\geqslant 2$
,
![]() $t\geqslant 2$
and properties (ii) and (iii) of Lemma 2.1. Now suppose that
$t\geqslant 2$
and properties (ii) and (iii) of Lemma 2.1. Now suppose that
![]() $n=7$
. Then (15) holds if and only if
$n=7$
. Then (15) holds if and only if
![]() $q\leqslant 4$
, and in this case there is no solution of
$q\leqslant 4$
, and in this case there is no solution of
![]() $|T|=$
$|T|=$
![]() $(s+1)(st+1)$
satisfying
$(s+1)(st+1)$
satisfying
![]() $s\geqslant 2$
,
$s\geqslant 2$
,
![]() $t\geqslant 2$
and properties (ii) and (iii) of Lemma 2.1. Therefore, we must have
$t\geqslant 2$
and properties (ii) and (iii) of Lemma 2.1. Therefore, we must have
![]() $q\geqslant 5$
. However, in this case
$q\geqslant 5$
. However, in this case
![]() $|C_{T}(x)|>|T|^{94/125}$
, so we have a contradiction. (To check this, note that
$|C_{T}(x)|>|T|^{94/125}$
, so we have a contradiction. (To check this, note that
![]() $|C_{T}(x)|\geqslant c\cdot q^{42}(q^{5}-1)(q^{2}-1)^{2}(q^{4}-1)(q^{6}-1)(q^{8}-1)$
where
$|C_{T}(x)|\geqslant c\cdot q^{42}(q^{5}-1)(q^{2}-1)^{2}(q^{4}-1)(q^{6}-1)(q^{8}-1)$
where
![]() $c={\textstyle \frac{1}{2}}$
or
$c={\textstyle \frac{1}{2}}$
or
![]() ${\textstyle \frac{1}{4}}$
according to whether
${\textstyle \frac{1}{4}}$
according to whether
![]() $q$
is even or odd.)◻
$q$
is even or odd.)◻
Acknowledgments
We thank Elisa Covato and Tim Burness for making available to us the results quoted in Section 6, and Luke Morgan for helpful discussions.