Evidence of viscosity drop and heat turning fibrous material into flocculent precipitate

Strong and consistent evidence of DNA thermal degradation resulting in the fragmentation into much smaller molecular products (thus incompatible with a hypothesis of orderly disassociation or with one of unchanged molecular weight) had clearly emerged in several papers between 1950 and 1960. Milestone results of experiments on thermal depolymerization showing this fragmentation evidence were described by Goldstein and Stern in 1950. The Authors report the following settling experimental observation: ‘Preliminary tests showed that a highly viscous aqueous solution of sodium desoxyribosenucleinate loses its viscosity when it is heated almost to the boiling point and then permitted to cool to room temperature. Upon adding the solution to 1.5 volumes of ethyl alcohol a flocculent precipitate is formed instead of the fibrous material yielded by “native” nucleic acid preparations’. Concerning viscosity, Figure 12 therein (reproduced in Figure 10) shows that a 0.1% solution of purified calf thymus DNA in a barbital buffer at pH 7.2, heated just 1 minute at 100 °C, experiments an irreversible drop of relative viscosity, from a value of 3.4 to a value below 1.4 (see Figure 10). Besides, the same figure shows a similar drop to a value, close to 1.4, is obtained by a 2 minutes heating at 90 °C.

Notably, Goldstein and Stern warn that an experiment that fails in detecting evidences of depolymerization (produced either sonically or thermally) is ultraviolet absorption spectrophotometry. Specifically, concerning changes upon heating in ultraviolet spectrum absorption of solutions of tetrasodium salt of DNA (therein indicated by the acronym STN), they report: ‘The examination in the Beckman spectrophotometer of a 0.048% STN solution in distilled water (after dilution to 0.008%) which had been heated for 15 minutes at 100 °C showed no change in the position of the maximum at 259 mμ or of the minimum at 231 mμ, although the relative viscosity had fallen from 3.11 to 1.35 as a result of this treatment. The rise in optical density from 1.28 to 1.46 at 259 mμ which was observed in this experiment may possibly be due to the fact that it was performed in the absence of a buffer system’.

Goldstein and Stern (Reference Goldstein and Stern1950) also warn (see section therein ‘Effect on absorption spectrum’) that when the optical density absorption spectrum is observed in the wavelengths range from 225 to 300 mμ, changes are detected only if the solvent is distilled water (‘unbuffered’ solution) while in the buffered solutions, no changes are observed. Such findings find confirmation in a study by Blout and Asadourian (Reference Blout and Asadourian1954) showing that the intensity of ultraviolet absorption of the sodium salt of DNA is dependent on the ionic strength. The intensity of absorption is highly pH dependent, in the absence of salt, in the pH range 3 to 12. These and other results therein reported, concerning various heating tests between 60 and 100 °C, lead the Authors to the conclusive observation: ‘The depolymerization of deoxyribonucleic acid by thermal treatment is of special interest in view of the high-temperature coefficient and, hence, large energy of activation, observed in the range between 60 and 100 °C (see Figure 12 therein). While this phenomenon is similar to the heat inactivation and denaturation of proteins (cf. ref. 22), there exist important differences. Thus, the nucleic acid molecules appear to be split into many small fragments on heating while the thermal denaturation of proteins, as a rule, does not lead to a significant alteration of their molecular weight, although in some instances aggregation will occur under these conditions (cf. ref. 22). This would seem to indicate that the bond strength of the sugar-phosphate links in the polynucleotide chain is smaller than that of the peptide bonds in proteins’.

In the same year, Miyaji and Price (Reference Miyaji and Price1950) found confirmation of the viscosity drop induced by heating. They also study the effect of NaCl addition coming to the following conclusion: ‘The viscosity of aqueous solutions of sodium thymonucleate is reduced both by heating and by addition of sodium chloride and other salts. If, however, the nucleate solution is heated in the presence of a sufficiently high concentration of salt, there is no further decrease in viscosity beyond that induced by the salt. The protective effect of the salt is reversible, for if the salt is removed by dialysis from the heated nucleate-salt mixture, the residual aqueous solution of nucleate again suffers a marked reduction in viscosity on heating’. They also find the singular phenomenon above 85 °C that ‘At temperatures over 85 °C, mixtures of nucleate and salt sometimes yielded a small amount of white precipitate’.

Miyaji and Price highlight the importance of discriminating whether the drop in viscosity is due to either (1) fragmentation of the DNA molecule or (2) to coiling of the DNA molecule with reduction of molecular radius yet in the absence of fragmentation, or even to a combination of the two phenomena.

Evidence of thixotropy induced by heating

Zamenhof and Chargaff (Reference Zamenhof and Chargaff1950) found that heating a 0.3 percent solution of DNA at 86 °C for 90 minutes makes the specific viscosity, $ {\eta}_{\mathrm{sp}} $ , drop from 30.3 to 3.9. They find that the solution degraded by heating can repolymerize but show that a DNA preparation degraded by heat (similar to the degradation produced by other agents such as acid and alkali) acquires a marked thixotropy (i.e., reduction of viscosity determined by forced flow and viscosity recovery as the forced flow is arrested). They also show, conversely, that an intact DNA preparation exhibits no thixotropy since its viscosity remains unaltered upon subjecting it to forced flow. They observe that this effect of induced thixotropy is irreversible since it cannot be removed by repolymerization. They conclude that their experiments show that ‘original preparations of desoxypentose nucleic acids possess unique physical properties (non-thixotropic viscosity, regular temperature-viscosity relationship) which, once lost, cannot be regained by repolymerization’. They specify that such phenomena of irreversible acquisition of thixotropy ‘were observed with desoxypentose nucleic acid preparations from calf thymus and from yeast, depolymerized not only by acid or alkali but also by heat’. Also, with Goldstein and Stern, they are among the first who ‘extend the concept of irreversible denaturation from the field of proteins to that of another group of macromolecules, the nucleic acids’ and likewise remark the irreversible character of the transformations produced in DNA by heating.

Evidence of vanishing of transforming activity paired with viscosity drop

A biological confirmation of the simultaneous onset, at heating temperatures higher than $ {T}_{\mathrm{td}} $ = 81 °C, of irreversible viscosity drop phenomena paired with biological inactivation phenomena was reported by Zamenhof, Alexander, and Leidy in 1953. The Authors extract and purify DNA from a culture of Hemophilus influenzae that has resistance to streptomycin. They add dilutions of these aqueous solutions of purified DNA from streptomycin-resistant colonies to bacterial suspensions obtained from cultures derived from strains characterized by initial absence of resistance to streptomycin, under controlled 37 °C temperature and time. Subsequently, they add streptomycin (SM) and detect, by observing the quantity of surviving bacteria, the degree of resistance to streptomycin induced in the non SM-resistant colonies by DNA addition. Thanks to dilutions they can also measure the degree of biological activity of the extracted DNA solutions.

As well known, biology interprets this phenomenon of induced resistance as a parasexual phenomenon, known as Griffith bacterial transformation activity, thanks to which the bacterium that initially does not have resistance to streptomycin, upon entering in contact with the purified DNA solution «acquires» the genetic code contained in the DNA molecules thus receiving the necessary instructions to build the polysaccharide bacterial capsule that gives the increase in resistance to streptomycin, and transmits it to its own lineage. They perform part of their experiments with H. influenzae after subjecting the DNA extract to heating at a variable T temperature in a pH 7.4 buffer with 0.14 M NaC1 and 0.015 M sodium citrate (upon reporting the temperature to 23 °C before each activity assay). They find that viscosity and activity are practically unaffected by 1 hour heating to temperatures (T) as high as 76–81 °C while, in a temperature range (T) between 81 and 90 °C heating, induces a more than significant reduction and, by further increasing (T), they see a drop to practically zero of the phenomenon of bacterial transformation activity.

Points on the graph of Figure 1 by the Authors on page 379 (Zamenhof et al., Reference Zamenhof, Alexander and Leidy1953), concerning measures of relative bacterial transformative activity (in percentage), have been digitized; the resulting numerical values, converted from logarithmic scale, are reported in Table 1 herein. The values of Table 1 are plotted in Figure 1 herein, reporting on the x horizontal axis the heating temperature of DNA in °C and, on the ordinates, the percentage of residual bacterial transformation activity employing a linear scale in place of the logarithmic scale of the original figure.

Table 1. Numerical values obtained by digitalization of points in Figure 1 in Zamenhof et al. (Reference Zamenhof, Alexander and Leidy1953) concerning the stability of the transforming principle preparation to heat

Figure 1. Activity versus temperature after 1 hour heating, according to Figure 1 in Zamenhof et al. (Reference Zamenhof, Alexander and Leidy1953). Ordinates are represented by an ordinary linear scale in place of the logarithmic scale of the original figure.

The evidence found in Zamenhof et al. (Reference Zamenhof, Alexander and Leidy1953), clearly represented by Figure 1 herein, is that, upon subjecting a purified DNA aqueous solution to a preliminary heating/cooling cycle bringing it to a variable temperature (T) and back again to 23 °C, the residual bacterial transformation activity is stable when T ranges between 25 and 80.9 °C. When the heating temperature T reaches 81.4 °C, the transforming activity is reduced to 15%, and, by increasing the heating temperature, the activity continues to decay rapidly to zero, so that at 90 °C it is basically absent.

A further fundamental result in Zamenhof et al. (Reference Zamenhof, Alexander and Leidy1953) concerns the stability of DNA viscosity after heating. Upon measuring viscosity in the same pH 7.4 buffer at 23 °C, the Authors find that ‘the viscosity and the activity are practically unaffected by 1 hour heating to temperatures as high as 76–81 °C’.

Concerning the possibility that heating or acidity may just induce molecular contraction and not depolymerization Zamenhof et al. also write: ‘It has recently been suggested (22, 26, 27) that the decrease in viscosity of DNA solution upon mild H⁺ treatment is due to the change in asymmetry caused by the contracting of the molecule rather than by actual depolymerization. This may also be true for the mild heating. The contraction may be made possible by the breakage of labile bonds (such as hydrogen bonds) under the action of thermal oscillations (40, 41). At higher temperatures, actual depolymerization may occur (32)’.

Evidence of depolimerization by ultraviolet light measurements

Thomas, in his 1954 publication on the study of the ultraviolet absorption spectrum of neutral saline NaCl (unbuffered) solution of desoxyribonucleic acids (DNA) isolated from calf thymus, starfish (Asterias glacialis) testicles, and red frog (Rana temporaria) testicle, devotes an entire section, titled ‘Effets irreversibles de la temperature sur le spectre U.V.’, on the effects of heating on changes of optical density measures. Besides finding that this measure is strongly sensitive to the NaCl concentration, he plots the graphs of the function relating the absorption at 260 mμ versus the preheating temperature and he finds sudden increases of the optical density at temperatures ranging between 55 °C and 80 °C with intermediate plateau regions in which the absorption remains constant. For calf thymus DNA he finds a maximum upper limit for stability against depolymerization corresponding to a temperature around 80 °C, in agreement with Goldstein and Stern (although these authors are not quoted by Thomas).

It is worth observing that the detection by Thomas of changes in optical density as a function of heating temperature is also in agreement with the explanation by Goldstein and Stern since Thomas employs unbuffered solutions.

Detection of depolymerization by staining

Measurements indicating depolymerization of DNA are summarized by Kurnick (Reference Kurnick1954a) and recalled in the following list:

• – reduction in viscosity;

• – reduction in the rate of sedimentation in the ultracentrifuge;

• – increase in ultraviolet absorption (detectable in unbuffered solutions);

• – lowering of PH;

• – formation of acid-soluble and dialyzable products.

Based on his previous study (Kurnick, Reference Kurnick1954b), where he showed that methyl green selectively stains only highly polymerized desoxyribonucleic acid and fails to stain, to any significant extent, depolymerized desoxyribonucleic acid and ribonucleic acid, Kurnick introduces a new methodology for studying depolymerization induced by heat (Kurnick, Reference Kurnick1954a). From experiments on calf thymus DNA, among which ultracentrifugation patterns of DNA solutions, with and without 0.02% methyl green, heated to 80° for 7 hours, and to 100° for 1 hour or 2 hours as well as on unheated DNA, he finds that ‘Heat and enzymatic depolymerization of DNA produce certain effects in common: both reduce the viscosity of the solution rapidly […], increase the ultraviolet absorption […] and reduce methyl green affinity’. He remarks that ‘These changes are maximal before any dialyzable, acid-soluble oligonucleotides are formed […] and nearly maximal before reduction in sedimentation rate appears’. He adds: ‘The products of heat and initial enzymatic digestion (and of sonic depolymerization) are large molecules which, as judged by their sedimentation velocity, are probably still quite asymmetric rods. This hypothesis is in better accord with the unaltered sedimentation rate (despite marked reduction in viscosity) than the alternative suggestion (citation of Creeth et al., Reference Creeth, Gulland and Jordan1947 and Conway and Butler, Reference Conway and Butler1952) that heat has produced collapsed molecules of the original molecular weights. Such collapsed molecules would show a great reduction in viscosity, but would also show considerable change in sedimentability’.

He conclusively provides an explanation of the heating degradation at 100 °C in terms of ‘bombardment by the solvent molecules’: ‘Thus, at l00°C, a molecule with very low intrinsic viscosity, but of a considerable size as characterized by its non-dialyzability, sedimentability, and affinity for methyl green […] is stable. This suggests that the increased bombardment by the solvent molecules at elevated temperature snaps the rigid molecule into still large units, but of such lesser size as to be stable when subjected to the bombardment characteristic of this temperature’.

From the background above on the studies on thermal depolymerization published between 1950 and 1954, it consistently emerges that heating at temperatures above 81°, or just above 81°, ordinarily produces depolymerization (or disaggregation) in purified DNA solutions. For completeness, it is worth adding that a residual possibly conceivable alternative justification explaining the drop in viscosity could be the hypothesis considered by Creeth et al. (Reference Creeth, Gulland and Jordan1947) of a coiling of the DNA molecule capable of ‘reducing the molecular asymmetry but not the molecular weight’. It should be pointed out, however, that such a coiling hypothesis is drawn in Conway and Butler (Reference Conway and Butler1952) to explain a decrease in viscosity observed after the addition of NaCl, occurring without production of titratable groups and that in Creeth et al. (Reference Creeth, Gulland and Jordan1947) no heating experiments are carried out.

Estimates of molecular weight from viscosity-sedimentation experiments

An important contribution comprehensively accounting for most of the previously published literature on the effect of DNA heating, confirming Goldstein and Stern’s conclusion on DNA fragmentation above 81°, is a physical chemical study by Dekker and Schachman (Reference Dekker and Schachman1954). This study, while essentially focused on the assessment of different investigated models for the possible macromolecular structure of DNA (among which also models differing from the Watson and Crick double helical chain (Watson and Crick, Reference Watson and Crick1953)), is important for the sake of understanding the effect of heating, since it reports a simple quantitative estimate of the molecular weight change before and after heating due to fragmentation, by a calculation from sedimentation and viscosity data before and after heating.

Dekker and Schachman do not exclude ab initio a possible coiling of the DNA molecule determined by heating and they are the first to point out that paired measurements of viscosity and sedimentation rate of dilute solutions of DNA and heated DNA could differentiate between a disorganization of the DNA molecule without a change in molecular weight (coiling), on one side, and a process in which there is a degradation into much smaller pieces, on the other side. Their key reasoning is that if, upon heating, the DNA molecule is divided into smaller fragments, the viscosity must decrease and the sedimentation coefficient must decrease as well, while, in case heating should produce just a coiling of the molecule, unlike viscosity the sedimentation must instead increase.

Based on their experimental measurements, the Authors make the fundamental observation which compels them to exclude a hypothesis of thermal coiling as they write: ‘The reduced viscosity of a 0.005 percent solution heated at pH 7 for 15 minutes at 100 °C. decreased from 30 (gm/100 cc)⁻¹ to less than 1.0 (gm/100 cc)⁻¹. Instead of an increase in the sedimentation rate, which would be expected from the amount of coiling necessary to produce such a large drop in viscosity, we found that measurements at 0.005 percent DNA showed that the heated material had a sedimentation coefficient of about 6S, whereas the unheated preparation had a value of nearly 20S. These experiments provide proof that the molecular weight of DNA changes from about 5 $ \times $ 10⁶ to 5 $ \times $ 10⁴ as a result of this mild heating procedure’. In the previous quotation, uppercase S indicates the Svedberg unit which corresponds to $ s\times {10}^{-13} $ where $ s $ stands here for seconds. It is also worth recalling that the reduced viscosity, $ {\eta}_{\mathrm{red}} $ , is related to the viscosity $ \eta $ through the following relations: $ {\eta}_{\mathrm{red}}={\eta}_{\mathrm{sp}}/c $ where $ c $ is the concentration and $ {\eta}_{\mathrm{sp}} $ is the specific viscosity $ {\eta}_{\mathrm{sp}}={\eta}_r-1 $ , being $ {\eta}_r=\eta /{\eta}_0 $ the relative viscosity defined as the ratio of solution viscosity $ \eta $ to solvent viscosity $ {\eta}_0 $ . The intrinsic viscosity $ \left[\eta \right] $ is obtained by extrapolation of reduced viscosity against concentration at infinite dilution, $ c=0 $ , viz.: $ \left[\eta \right]=\underset{c\to 0}{\lim }{\eta}_{\mathrm{sp}}/c $ (Cox et al., Reference Cox, Overend, Peacocke and Wilson1958; Perry et al., Reference Perry, Chilton, Kirkpatrick, Perry, Chilton and Kirkpatrick1963).

The proportion behind this simple quantitative estimate by Dekker and Schachman can be presented as follows. Denoting by $ M $ the average weight of the DNA molecule, or of its fragment produced upon heating (assuming here introductively and simplistically that all molecules or fragments have the same weight and molecular hydrodynamic radius $ {r}_s $ ), the following direct proportionality holds

(1) $$ M\hskip0.4em \propto \hskip0.4em \left({r}_s\times s\times \eta \right), $$

where $ s $ is now the sedimentation constant, $ \eta $ the viscosity, and $ \hskip0.4em \propto \hskip0.4em $ is the symbol of direct proportionality. References for the proportion above, which is obtained by combining Svedberg’s equation (Svedberg, Reference Svedberg1938) with Stokes-Einstein’s equation, can be found in treatises of physical chemistry of macromolecules such as Barrow’s treatise (see, e.g., Barrow, Reference Barrow1966, Chap. 20 and, in particular, p. 659, Equation (23)). Fundamental more advanced investigations, contemporary to those years, based on careful consideration of the hydrodynamic Stokes’s law, empirical data for long-chain polymers, dimensionless analysis, and investigation of universal constant for flexible long chain polymers such as DNA can be found in Mandelkern et al. (Reference Mandelkern, Krigbaum, Sheraga and Flory1952) and related references.

Dekker and Schachman’s estimate (Dekker and Schachman, Reference Dekker and Schachman1954) stems from the simplistic consideration that the hydrodynamic radius remains unchanged upon heating so that, denoting by subscripts $ N $ and $ H $ the quantities relevant to native DNA and to DNA possibly fragmented by heating, respectively, one infers from Eq. (1) setting $ {r_s}_N={r_s}_H $ :

(2) $$ \frac{M_N}{M_H}=\frac{{r_s}_N}{{r_s}_H}\times \frac{s_N}{s_H}\times \frac{\eta_N}{\eta_H}=1\times \frac{20}{6}\times \frac{30}{1}=100. $$

Shooter et al. (Reference Shooter, Pain and Butler1956) also dedicate a study to examining the effect of thermal degradation above 80 °C on DNA. Based on their experiments they propose some simple graphical models suggesting the effects of heating on DNA (see the reproduction in current Figure 2).

Figure 2. Suggested effect of heating, Figure 4 in Shooter et al. (Reference Shooter, Pain and Butler1956). (a) fraying out of single strands from main structure; (b) collapse of main structure about the more flexible parts of the molecule which are joined only by single strands of nucleotides; (c) molecule breaking up into smaller units. Reprinted from Shooter et al. (Reference Shooter, Pain and Butler1956, p. 501), Copyright (1956), with permission from Elsevier.

They conclude their study stating that after 15 minutes heating at 100 °C, DNA samples always produce thermal degradation. They remark that the extent of degradation and the distribution of the size and shape of the fragments produced depends on how DNA is prepared.

Evidence of irreversibility of heating degradation from titration analyses

Titration analyses although do not provide direct quantification of molecular weight decrease and direct evidence of possible onset of disruptive longitudinal sequence-breaking random fragmentation of DNA molecules, can detect however some irreversible features occurring during the heating process and the quantity of broken hydrogen bonds. For these reasons, part of these works on titration relevant to DNA heating are hereafter reviewed.

The study by Cavalieri and Rosenberg (Reference Cavalieri and Rosenberg1957) reports potentiometric titration analyses on DNA solutions using calomel and glass electrodes. The study ascertains the conditions under which hydrogen bonds in DNA can be cleaved reversibly by heat, and the conditions under which hydrogen bonds cleave spontaneously and irreversibly. Concerning the temperature at which irreversible phenomena are observed the Authors report: ‘A temperature is finally reached (about 70° in 0.017 M NaCl, for example) at which denaturation occurs without titrating any bases, and cannot be prevented by heating in buffers of any pH. In such cases, the original H-bonds of DNA must all be thermally and irreversibly cleaved’.

Cox and Peacocke (Reference Cox and Peacocke1956) prior to presenting their results on electrometric titration well summarize the contemporary debate on the stability of the molecular weight to heating: ‘When sodium deoxyribonucleate is heated in neutral aqueous solution, irreversible changes occur above a critical temperature which varies with the source of the deoxyribonucleate and its method of extraction. These irreversible changes, which often take place over a temperature range of only a few degrees, include a drop in the viscosity; an increase in the ultraviolet absorption; a displacement of the spectrophotometric titration curves; the appearance of new infrared absorption bands; changes in sedimentation constant; and displacement of the titration curves. Some investigators deduced a decrease in molecular weight from sedimentation and viscosity measurements after the nucleate had been heated in water (Dekker and Schachman, Reference Dekker and Schachman1954; Sadron, Reference Sadron1955), and in salt (Shooter et al., Reference Shooter, Pain and Butler1956), whereas others reported (Doty and Rice, Reference Doty and Rice1955; Sadron, Reference Sadron1955) no change in molecular weight after heating in the presence of sufficient sodium chloride’ (notice that, in the quotation above, text references originally reported in superscript format have been converted into the current squared brackets format adding also author and year). They summarize in Figure 2 therein that the percentage of ruptured hydrogen bonds in herring-sperm in a (0.15%, 0.05 M -NaCl) solution heated for 1 hour at 95 °C is 100%. Moreover, on the basis of these titration experiments the Authors infer evidence for ‘the random nature of the heat-denaturation process’.

We incidentally remark that the statement by Cox and Peacocke (Reference Cox and Peacocke1956), according to which Sadron (Reference Sadron1955) would report no change in molecular weight after heating in the presence of sufficient sodium chloride, appears to be incorrect as the data in this publication by Sadron show in all cases a decrease of the molecular weight after heating except for just one case where it is reported even an increment of molecular weight. This issue is examined in detail in section ‘Evidence from light scattering of DNA fragmentation upon heating’ dedicated to the light scattering measurements by Sadron on heated DNA.

Cox and Peacocke (Reference Cox and Peacocke1957) specify the limit of titration in detecting changes in molecular weight: ‘ionizing radiations invariably and heat, under certain conditions, also cause changes in molecular weight but this degradative aspect of their action will not be considered further here, if only for the reason that the titration curves can only just detect a release of one secondary phosphoryl end group in 50 nucleotides’.

Most importantly, Cox, Overend, Peacocke, and Wilson (Reference Cox, Overend, Peacocke and Wilson1955) in their publication on Nature, reaffirm that ‘it is only changes in the intrinsic viscosity which are of significance in the estimation of molecular size and shape’ and propose the employment of the following expression, usual for high weight polymers, relating intrinsic viscosity $ \left[\eta \right] $ to the viscosity-average molecular weight, $ {M}_v\hskip-0.2em : $

(3) $$ \left[\eta \right]=K{\left({M}_v\right)}^{\alpha }, $$

where $ K $ and $ \alpha $ are constants for homologous polymers. Based on their experimental data the Authors compute $ \alpha =0.93 $ . Remarkably, agreement with this value is found by the same Doty and coworkers who later computed in 1960 from two DNA preparations from Diplococcus Pneumoniae DNA and Escherichia coli two determinations of $ \alpha $ and $ K $ whose average value is $ \alpha =0.923 $ and $ K=3.28 $ . The exponent close to unity signifies that the relation between viscosity-average molecular weight and intrinsic viscosity is almost linear.

Use of this formula with the intrinsic viscosity data, measured before and after a heating treatment, allows to compute the drops from the molecular weight of the unheated molecule $ {M}_N $ to the weight of the molecule after heating, $ {M}_H $ , by the following formula:

(4) $$ \frac{M_H}{M_N}={\left(\frac{{\left[\eta \right]}_H}{{\left[\eta \right]}_N}\right)}^{1/0.923}={\left(\frac{{\left[\eta \right]}_H}{{\left[\eta \right]}_N}\right)}^{1.083}. $$

On the basis of light-scattering experiments and viscosity measurements on DNA degraded by gamma rays, Peacocke and Preston (Reference Peacocke and Preston1958) improve the precision of the determination of coefficients $ \alpha $ and $ K $ in Eq. (3). They find a round value $ \alpha =1.0 $ for the exponent and find $ K=3.28. $ They also find that the weight-average molecular weight $ {M}_w $ is related to intrinsic viscosity by:

(5) $$ \left[\eta \right]=4.26\times {\left({M}_w\right)}^{1.00}. $$

Most importantly, they find a remarkable consistency of the value $ {M}_w $ obtained from Eq. (5) with countercheck values obtained by light scattering measures, so that Eq. (5) can be considered a reliable choice for determining molecular weight from intrinsic viscosity, substitutive of light scattering measurements.

Employing the data reported by Shooter et al. (Reference Shooter, Pain and Butler1956) concerning measurements before and after 15 minutes heating at 100 °C on different samples and also in the absence of salt (see Table I therein), the viscosity-based average weight of the heated DNA molecules is computed from Eq. (4) to range between 1.45% and 5.01% of the average weight before heating, what signifies a depolymerization in considerably shorter fragments.

Models for random degradation matching experimental data

Kinetic molecular models provide a valuable mean for computing the number of scissions (fragmentations in shorter segments) that the DNA molecule undergoes during a heating experiment and the rate of fragmentations, that is the number of fragmentations per unit of time, based on diagrams of molecular weight plotted versus time.

Peacocke and Preston (Reference Peacocke and Preston1958), proceeding from viscosity and light scattering experiments on DNA samples degraded after exposure at different doses of gamma rays, find that internucleotide phosphodiester bonds in DNA are ruptured by a random fragmentation process. Fragmentation is the process which divides the molecule into shorter segments of lower molecular weight. They experimentally find for DNA an almost quadratic relation (exponent 1.85) between the radiation dose $ R $ and the intrinsic viscosity $ \left[\eta \right] $ instead of the linear relation characteristic of single-strand polymers. From such fundamental difference, they infer that in DNA (and in any other similar double-stranded polymer) the fragmentation of the molecule in a fragmentation process must be generated by a double breakage mechanism. This mechanism consists of the breakage of two intra-chain longitudinal bonds each located at two facing nucleotides situated at the same longitudinal position of the molecule but belonging to opposite strands. This mechanism is mathematized in the context of molecular weight distributions (Charlesby, Reference Charlesby1954). In this context, the distinction is made between the number-average molecular weight $ {M}_n $ (which is the arithmetic mean of the weights) and the weight-average molecular weight $ {M}_w $ (which is the weighted arithmetic mean in which the molecular weights themselves are taken as the averaging weights). For a uniform distribution $ {M}_w={M}_n $ while for a random distribution (i.e., a distribution generated from random fracture of an infinite chain) $ {M}_w=2{M}_n $ .

The considerations of Peacocke and Preston are conveniently summarized hereafter in the format of proportionality relations. The weight-average molecular weight $ {M}_w $ and number-average molecular weight $ {M}_n $ are related to the number of fragmentations $ F $ per original number-average molecule:

(6) $$ F=\frac{{\left({M}_w\right)}_0}{\left({M}_w\right)}-1=\frac{{\left({M}_n\right)}_0}{\left({M}_n\right)}-1, $$

where the 0 subscript indicates the original molecular weight of the molecule before fragmentation starts. We recall that in special cases for a higher number of molecules and fractures ( $ F\gg 1\Big) $ relation above can be represented as the proportionality relation:

(7) $$ F\hskip0.4em \propto \hskip0.4em \frac{1}{M_n}. $$

For degradation by radiation of single-strand polymer chains it is ordinarily expected that the probability of single chain break $ {p}_s $ and the radiation dose $ R $ are related to fragmentation by:

(8) $$ F\hskip0.4em \propto \hskip0.4em {p}_s\hskip0.4em \propto \hskip0.4em R $$

what should imply from (7) that $ \frac{1}{M_n}\hskip0.4em \propto \hskip0.4em R $ . Peacocke and coworkers find instead, experimentally, that after a transitory range of exposition, the proportionality holds: $ \frac{1}{M_n}\hskip0.4em \propto \hskip0.4em {R}^2 $ . They explain in terms of probability distributions such evidence, unusual for single-stranded polymers, to be the consequence of a fragmentation process in which a fragmentation is produced when two intra-chain scissions at opposite strands in two facing nucleotides occur (or in two proximal nucleotides). The probability of this double-step process is shown to follow the proportionality $ {p}_D\hskip0.4em \propto \hskip0.4em {p}_s^2 $ , so that, owing to the previous proportionality relations, one has:

(9) $$ F\hskip0.4em \propto \hskip0.4em {p}_D\hskip0.4em \propto \hskip0.4em {p}_s^2\hskip0.4em \propto \hskip0.4em {R}^2. $$

Owing to the previous equation and to (7) one finally has for DNA and any double-stranded polymer the theoretical prediction:

(10) $$ \frac{1}{M_n}\hskip0.4em \propto \hskip0.4em {R}^2\hskip0.5em \mathrm{or}\ \mathrm{equivalently}\hskip0.5em \frac{1}{\sqrt{M_n}}\hskip0.4em \propto \hskip0.4em R. $$

It is important to highlight the difference between the previous relation (10) and the corresponding relation for single-stranded polymers which reads instead:

(11) $$ \frac{1}{M_n}\hskip0.4em \propto \hskip0.4em R. $$

Peacocke and Preston find that, for gamma-rays degradation of DNA, Eq. (10) is closely respected and consider this as evidence that the fragments ensuing from gamma-ray degradations are always double-stranded.

The Authors also investigate the effect on the molecular weight of heat degradation (100 °C along 15 minutes in a 0.1 M NaCl solution) applied to fragments obtained by previous gamma-ray degradation. Their data shows this thermal treatment yields a decrease in molecular weight, but the Authors underline that quantitative appreciation of the entity of molecular weight decrease and number of fractures is made difficult by the ‘the known tendency for the polynucleotide chains to remain entangled, in spite of the removal of hydrogen bonding, and for separated chains to re-aggregate on cooling’.

A kinetic statistical model for random degradation of a two-stranded polymer, specifically devised by Applequist (Reference Applequist1961) to analyze DNA degradation, provides a more detailed description of the kinetics of double fracture proposed by Peacocke and Preston. This model by Applequist accounts for independent probabilities of intrachain fractures (termed P-bonds by the Author) and crosslinking hydrogen bonds (H-bonds).

Denoting by $ p $ the fraction of broken P-bonds, by $ q $ the fraction of broken H-bonds, and by $ p^{\prime } $ the probability that a pair of facing nucleotides is followed by a double chain break, they compute that at the beginning of the degradation process, when almost all P-bonds are unbroken, the relation holds:

(12) $$ {p}_D=\frac{\left(1+q\right){p}_s^2}{\left(1-q\right)}. $$

This relation is a more explicit determination of the proportionality relation highlighted by Peacocke and Preston and contained in Eq. (9). By further introducing the simplest assumption that P-bonds are broken by a first-order rate process, namely, $ 1-p=\left(1-{p}_0\right)\bullet {e}^{-\mathrm{kt}} $ corresponding in the early stages of degradation when $ \mathrm{kt}\ll 1 $ to the linearized law $ p={p}_0+\left(1-{p}_0\right)\bullet \mathrm{kt} $ , they find that the linear relation:

(13) $$ {\left(\frac{M_{w0}}{M_w}\right)}^{1/2}=1+\frac{1-{p}_0}{p_0}\mathrm{kt} $$

excellently fits the asymptotic trend in experimental data $ {M}_w(t) $ obtained from enzymatic degradation (Schumaker et al., Reference Schumaker, Richards and Schachman1956), acidic degradation (Thomas and Doty, Reference Thomas and Doty1956), and thermal degradation (Doty et al., Reference Doty, Marmur, Eigner and Schildkraut1960). The data for thermal degradation is reported together with the fit provided by Eq. (13) (divided by $ {\left({M}_{w0}\right)}^{1/2} $ ) in Figure 3a,b, respectively.

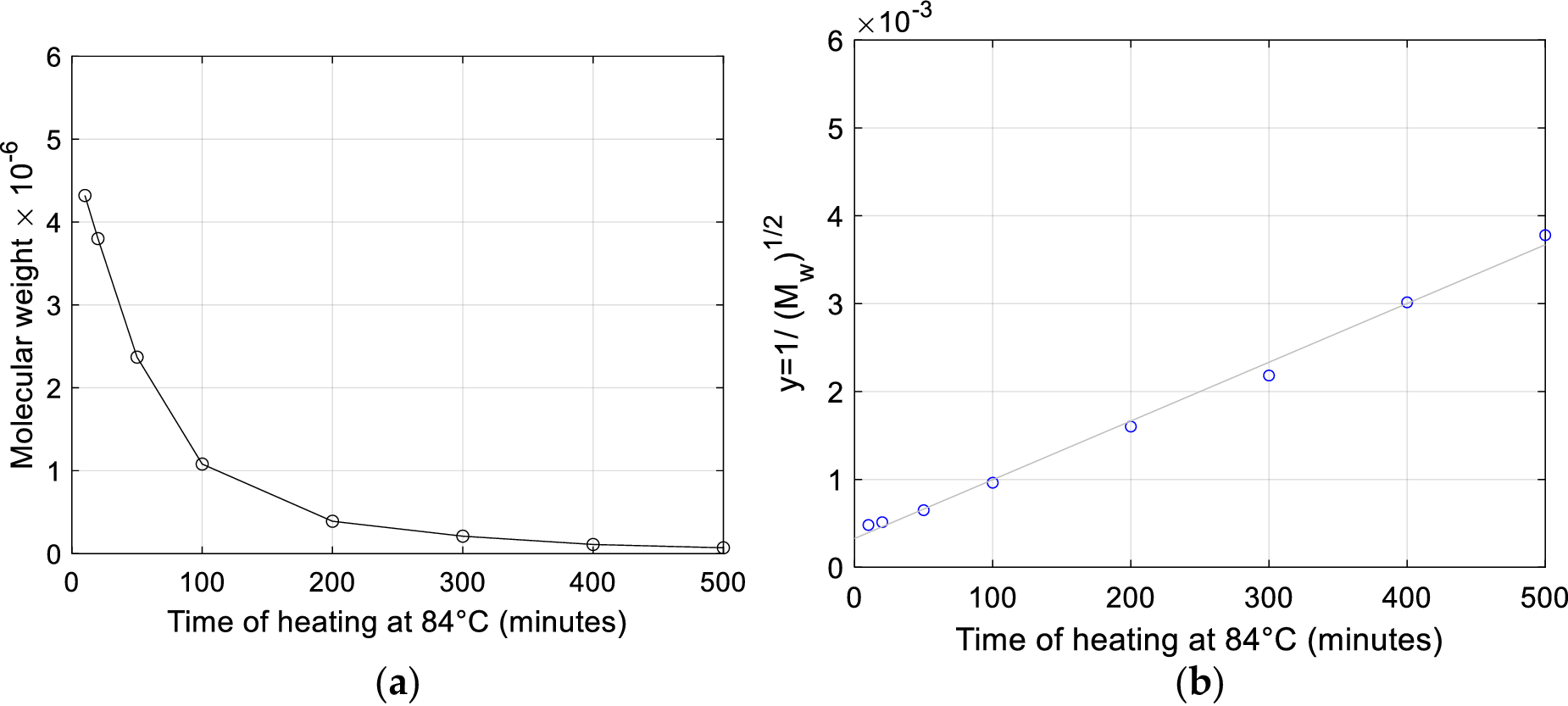
Figure 3. (a) Thermal degradation of diplococcus pneumoniae DNA; data digitized from Doty et al. (Reference Doty, Marmur, Eigner and Schildkraut1960). (b) Same data represented in the format of Eq. (13) and corresponding least-square linear fit.

This very close fit constitutes a strong proof that the DNA remains actually two-stranded during the thermal degradation process investigated by Doty et al. (Reference Doty, Marmur, Eigner and Schildkraut1960). This observation is pivotal for the focus of our study for three reasons:

1. 1) Fragmentation rules out also the plausibility of the 100 °C stable molecular weight claim.

2. 2) Doty et al. (Reference Doty, Marmur, Eigner and Schildkraut1960), based on the circumstance that one of their determination of the molecular weight of the DNA heated at 84° is approximately decreased by a factor of two (from 10.5 million to 5.0 million), advance the claim that ‘with aggregation eliminated and depolymerization taken into account it can be said that strand separation did occur in the very early stages of the exposure to the elevated temperature’. Conversely, the fit in Figure 3b shows the two-stranded character of the heated DNA and points to the clear evidence that the continuous fall of molecular weight is the result of progressive fragmentation into pieces that substantially remain two-stranded, so that the molecular weight halving recorded by Doty et al. is only fortuitously in agreement with the value of ½, as remarkably first pointed out by Applequist (Reference Applequist1961). In this respect it is worth acknowledging that also Doty et al. (Reference Doty, Marmur, Eigner and Schildkraut1960) in the statement above mention the necessity to account for ‘depolymerization’, thus duly excluding the possibility that halving of molecular might correspond to separation of intact single strands.

3. 3) The elucidation of the substantial two-stranded character of the material produced by heating, besides confuting the 100 °C dissociation claim, as advanced by Doty et al. in the same paper (Doty et al., Reference Doty, Marmur, Eigner and Schildkraut1960), raises the question of the very meaningfulness of heating denaturation for the purpose of strand separation.

A second important highlight in the contribution by Applequist is the role of the initial induction relatable to the presence of an initially uniform distribution of molecular weights and the determination based on the data by Shumaker et al. of the presence of initially broken P-bonds corresponding to $ {p}_0=1.57\times {10}^{-2} $ . This numerical determination will be recalled in the discussion of section ‘What really happens during DNA thermal fragmentation?’.

An examination of the type of intra-strand bond breakage is reported in the fourth main section ‘Discussion on the structural resilience of DNA chains after reiterated PCR cycles’ based on a closer review of the insightful analysis by Dekker and Schachman (Reference Dekker and Schachman1954).

Evidence from light scattering of DNA fragmentation upon heating

This subsection reviews determinations of DNA degradation by heating via light-scattering experiments reported in publications other than those by Doty and Rice of 1955 and 1957, which are instead more closely reviewed in the dedicated third main section ‘Review of the experiments on DNA heating by Doty and Rice (Reference Doty and Rice1955, Reference Rice and Doty1957)’.

Peacocke and Preston (Reference Peacocke and Preston1958) also perform light scattering measurements on DNA degraded by combined exposure to gamma rays and heating at 100 °C for 15 minutes. They confirm the observation of a decrease in molecular weight but highlight that the observation of the effect of heating degradation in larger DNA molecules is less pronounced and emphasize that the interpretation of the entity of this decrease is affected by the observed tendency of the polynucleotide chains to remain entangled, despite the removal of hydrogen bonding, and by the tendency of separated chains to re-aggregate on cooling, which has been recalled above.

Sadron performed measurements of molecular weights by light scattering after heating alone (in absence of gamma-rays exposure) and reported his findings in several publications between 1955 and 1959 (Sadron, Reference Sadron1955, Reference Sadron1959; Freund et al., Reference Freund, Pouyet and Sadron1958). In the 1955 biochemistry congress proceedings (see addendum on page 134 therein) he reports the effect of heating at 100 °C for 15 minutes on two DNA preparations of initial molecular weight $ {M}_0=6.0\times {10}^6 $ . The weights he determines by light scattering on heated DNA at different NaCl concentrations show that DNA weight is always reduced as a confirmation that DNA is the more degraded the less is the NaCl content.

In particular, the table on the 1955 addendum on page 134 by Sadron (Reference Sadron1955) reports that just 15 minutes heating in the absence of salt brings the molecular weight from $ 6\times {10}^6 $ to $ 0.28\times {10}^6 $ and $ 0.35\times {10}^6 $ . In just one experiment with 1 M NaCl, he finds, in one of the two preparations, a weight increment to an average value $ M=7.0\times {10}^6 $ . Later, Freund et al. (Reference Freund, Pouyet and Sadron1958) reported tests of calf thymus DNA (CV71) in 1 M NaCl solutions where they obtain by light scattering for the unheated preparation the molecular weight $ {M}_0=7.4\times {10}^6 $ . They measure by light scattering the molecular weight $ M $ in a 0.01 M NaCl solution after thermal degradation produced by heating at temperatures of 75°, 80°, 85°, and 98 °C during a variable time $ \theta $ . They find that by heating at temperatures of 80°, 85°, and 98 °C the ratio $ R=M/{M}_0 $ as a function of $ \theta $ first increases, reaches a maximum, and then drops to a residual value $ R=0.047 $ corresponding to $ M={M}_2=350000 $ . The point data in the original figure have been digitized and those corresponding to temperatures of 85 °C and 98 °C are reported in Figure 4 herein. The only correction applied to the digitized number is that minutes have been rounded to the closest simple fractions of one hour (multiples of 5 minutes) and that ordinates reached at the horizontal asymptote have been rounded to the value 0.047 explicitly reported by Freund et al. (Reference Freund, Pouyet and Sadron1958).

Figure 4. Ratio $ R=M/{M}_0 $ versus heating time $ \theta $ . Datapoints digitized from Figure 1 in Freund et al. (Reference Freund, Pouyet and Sadron1958). Only data for 98 °C and 85 °C are reported.

The Authors find that the higher is the heating temperature the higher is the maximum, as shown in Figure 4. This figure shows that heating at 98 °C brings this maximum above 1.4 and then makes $ R $ suddenly drop at approximately 10 minutes to a value below 0.35. It is also seen that at 15 minutes the interpolation reaches 10% of the native weight. This measure brings further quantitative straightforward evidence of the sudden fragmentation that the DNA molecule undergoes when heated at temperatures above 90 °C.

DNA heating experiments in the presence of different electrolytes

Hamaguchi and Geiduschek (Reference Hamaguchi and Geiduschek1962) perform a broad analysis of thermal stability of DNA in aqueous solution in the presence of many different electrolytes and under many different pH conditions and temperature ranges. They confirm that the thermal stability of DNA has a relatively broad maximum at pH 7–8 in 0.1 M NaCl and that in any concentration of any of the many electrolytes therein investigated the upper bounds of the temperature threshold of thermal stability can be never above 92.6 °C (see Table I and Figure 4 therein), irrespective of the electrolytes content and type.

Brief notes on the fundamentals of light scattering

Before examining Rice and Doty’s light scattering results, a brief introduction is reported of the measurement principle and measurement technique of the light scattering method and of the related turbidimetry method.

Fundamental advancements to optical methods of turbidity and light-scattering have been contributed by Debye (Reference Debye1944, Reference Debye1946, Reference Debye1947) and by Zimm (Reference Zimm1948a, Reference Zimm1948b). In brief, the essential physical principle of these optical techniques applied to molecules in solution, as first described by Debye (Reference Debye1944), is based on the following relation expressing the turbidity $ \tau $ of diluted solutions as a function of the refractive index of the solvent, $ {\mu}_0 $ , of the refractive index $ \mu $ of the solution, of the wave-length $ \lambda $ , and of the number $ n $ of molecules per $ {\mathrm{cm}}^3 $ :

(22) $$ \tau =\frac{32{\pi}^3}{3}\frac{{\mu_0}^2{\left(\mu -{\mu}_0\right)}^2}{\lambda^4}\frac{1}{n}. $$

If $ {\mu}_0 $ for the solvent is known, $ n $ can thus be measured, in the first instance, on the basis of two experiments, a first one giving $ \mu $ and a second one giving $ \tau $ . Once $ n $ is determined, the mass of the particle $ u $ and its molecular weight $ M $ follow from the concentration $ c $ as $ u=c/n $ and $ M= cN/n $ , being as usual $ N $ Avogadro’s number. For practical purposes, the quantity $ K=\tau /(Mc) $ is introduced by Debye. This quantity, on account of Eq. (22) and of relation $ nM= cN $ , achieves the expression:

(23) $$ K=\frac{32{\pi}^3}{3}\frac{{\mu_0}^2}{N{\lambda}^4}\frac{{(\mu -{\mu}_0)}^2}{c^2}. $$

$ K $ is thus for turbidity, in a first approximation, a refraction constant which, once determined, permits to compute $ M $ as $ M=\tau / Kc $ or, equivalently:

(24) $$ \frac{K\bullet c}{\tau }=\frac{1}{M}. $$

However, Debye discusses in 1947 that, for solutions of high-polymer substances, such as the case of DNA, even at high dilutions $ K $ cannot be treated as a constant with respect to concentration $ c $ but is found to be a function $ K(c) $ of the concentration $ c $ , and the same occurs for turbidity $ \tau $ which is similarly a function $ \tau (c) $ of concentration. He advises to employ the linear interpolation:

(25) $$ \frac{K(c)\bullet c}{\tau (c)}=\frac{1}{M}+2B\bullet c, $$

in which $ B $ is a constant depending on the solvent so that in the limit of zero concentration, $ c\to 0 $ , Eq. (24) is recovered and $ M $ is computed. This corresponds to the following two-dimensional plot extrapolation:

• • the refraction term $ K $ and the dilution $ \tau $ are determined for different concentrations $ {c}_1,{c}_2,{c}_3,\dots $ obtaining several determinations $ K\left({c}_1\right),K\left({c}_2\right),K\left({c}_3\right),\dots $ and $ \tau \left({c}_1\right),\tau \left({c}_2\right),\tau \left({c}_3\right),\dots $ ;

• • from these determinations the left-hand side of Eq. (25) as a function of the independent variable $ c $ , $ L(c)=K(c)\bullet c/\tau (c), $ is interpolated (in Debye, Reference Debye1946, in particular, the method of least squares is employed);

• • function $ L(c) $ is extrapolated to zero concentration obtaining the limit $ \underset{c\to 0}{\lim }L(c)=\underset{c\to 0}{\lim}\frac{K(c)\bullet c}{\tau (c)} $ ; this limit is equal to the limit of the right-hand side $ \underset{c\to 0}{\lim}\left(\frac{1}{M}+2B\bullet c\right)=1/M $ ;

• • eventually, this method graphically provides the molecular weight $ M $ as the intercept at $ c=0 $ of curve $ L(c) $ .

The method described so far for determining $ M $ only involves measurement of the turbidity $ \tau $ and not of light scattered at different angles. For larger thread-like polymerized molecules, such as DNA, a more refined measurement technique which is based on the additional information obtainable from measurement of the angular distribution of the scattered light is further devised by Debye (Reference Debye1947). Debye derives a fundamental analytical relation for the intensity $ I $ of scattered light as a function of the angle $ \theta $ between the primary beam and the scattered beam. The function $ I\left(\theta, c\right) $ , accounting for such dependency upon $ \theta $ and upon the concentration $ c $ of solute in each experiment, is theoretically elaborated by Debye through an averaging procedure accounting for all conceivable particle configurations (since the particles are statistically free to rotate and fluctuate in the optical model). The expression of $ I\left(\theta, c\right) $ resulting from this theoretical elaboration depends on the employed model for the particle. Debye presents specific analytical expressions for particles modeled as having spherical or ellipsoidal shape and, additionally, considers a third model (a so-called random coil model, essentially devised for schematizing the optical behavior of polymers) in which thread polymers are schematized as a flexible number of links, each one able to rotate freely. Debye finds that, for this set of molecular models (random coils, spherical shapes, or ellipsoidal shapes), the relevant function $ I\left(\theta, c\right) $ turns out to be conveniently expressed in a relatively simpler analytical closed form of the following type: $ I\left({\sin}^2\left(\theta /2\right),c\right) $ , that is, by an analytical expression in which $ {\sin}^2\left(\theta /2\right) $ is the first independent variable. A convenient alternate series expansion expression of function $ I\left(\theta, c\right) $ , applicable to a variety of molecular shapes and typologies and under some respects analogous to Eq. (12), is contextually elaborated by Debye one year later. A more explicit expansion of this form is also presented by Zimm (Reference Zimm1948a, see Equation (26) therein). Zimm’s series expansion yields a determination of the molecular weight $ M $ from light scattering measurements at different angles and is similarly applicable to different particle models. The first three terms of this expansion are:

(26) $$ \frac{K\bullet c}{I\left(\theta, c\right)}=\frac{1}{M}\bullet \frac{1}{P\left(\theta \right)}+2{A}_2\bullet c+f\left(\theta \right)\bullet {c}^2+\dots . $$

In the previous relation, $ I\left(\theta, c\right) $ is the intensity of the excess scattering (over that of the solvent alone) at a given concentration, $ P\left(\theta \right) $ is a probability function such that $ P(0)=1 $ , $ {A}_2 $ is a constant independent from $ \theta $ and $ c $ , and $ f\left(\theta \right) $ is a term independent from $ c. $ Owing to these properties, it is seen that extrapolation of the left-hand term in Eq. (19) at zero concentration and zero angle $ \theta $ gives again the reciprocal of the molecular weight:

(27) $$ {\left(\frac{K\bullet c}{I\left(\theta, c\right)}\right)}_{\begin{array}{c}c\to 0\\ {}\theta \to 0\end{array}}=\frac{1}{M}. $$

Debye also shows (1947) that the slope of the plots (as a function of $ c $ ) in proximity of $ c=0 $ defined by coefficient $ 2{A}_2 $ in Eq. (26) defines the square of the average size of the particle in terms of distance from its center of gravity (also termed radius of gyration by some authors (Doty and Bunce, Reference Doty and Bunce1952; Alexander and Stacey, Reference Alexander and Stacey1955)). For clarity in the employed terminology, it is recalled that the function $ \frac{K\bullet c}{I\left(\theta, c\right)} $ is also called by Alexander and Stacey (Reference Alexander and Stacey1955) and by Doty and Bunce (Reference Doty and Bunce1952) ‘reciprocal reduced intensity’ and the Zimm plots are also denominated reciprocal reduced intensity plots.

The accuracy of the extrapolation procedure stated by Eq. (27) is understood to be critical for the accuracy of the determination of the molecular weight. The extrapolation is operatively carried out by graphical construction of a grid-like plot (denominated Zimm plot) in the plane having the quantity $ {\sin}^2\left(\theta /2\right) $ on the horizontal axis and the quantity $ K\bullet c/I\left(\theta, c\right) $ on the vertical axis.

For the problem of interest, which is the determination of the weight of the DNA molecule by light scattering, the construction of a Zimm plot has been well exemplified and explained by Alexander and Stacey (Reference Alexander and Stacey1955) who, aside to Doty and coworkers, have been among the first researchers performing such a measure. Figure 5 is a reproduction of the plot performed by Alexander and Stacey for determining the molecular weight of herring sperm DNA at PH 6.8. On the horizontal axis of the graph in Figure 5 it can be read $ {\sin}^2\left(\theta /2\right)+2000\bullet c $ since the addition of the term $ 2000\bullet c $ is simply a mean for graphically shifting in the horizontal direction the curves, function of $ {\sin}^2\left(\theta /2\right) $ , obtained at each constant value for $ c $ . The intercept at $ c=0 $ is seen to be $ \frac{1}{M}=1.7\bullet {10}^{-7} $ and from this value the result $ M=5.9\bullet {10}^6 $ is computed by these Authors. Observe that the slope of the horizontal segments of the plot represents the sensitivity of this method to the solute concentration and that the property of these segments of being almost horizontal in the vicinity of the intercept with the vertical axis ensures the independence of evaluation of the molecular weight from the concentration employed in the experiments.

Figure 5. Figure 1 in Alexander and Stacey (Reference Alexander and Stacey1955). Zimm plot for determining the molecular weight of herring sperm DNA at PH 6.8. Used with permission of Portland Press, Ltd. from Alexander and Stacey (Reference Alexander and Stacey1955), Copyright (1984), permission conveyed through Copyright Clearance Center, Inc.

We briefly recall now the light scattering results that Doty and coworkers published in the years 1953–1957. With these data, Doty supports two claims:

• • the claim of unchanged DNA molecular weight upon acidification to pH 2.6 (Reichmann et al., Reference Reichmann, Bunce and Doty1953);

• • the claim of unchanged DNA molecular weight after 15 minutes heating at 100 °C (Rice and Doty, Reference Rice and Doty1957).

A fundamental digression on the detection of DNA acidic degradation by light scattering with a confutation

Although the central object of discussion of this subsection is on possible evidences from the light scattering measurements by Doty and Rice of the molecular weight stability of DNA to heating, a brief digression on the close examination of the light scattering data relevant to the assessment of stability upon pH 2.6 acidification of DNA, presented by Reichmann et al. (Reference Reichmann, Bunce and Doty1953), is carried out hereafter to duly highlight possible sources of fallacious, or diverging, interpretation of data from light scattering. Such a digression is revealed to be important by the existence of an ongoing debate in the thread of publications (Alexander and Stacey, Reference Alexander and Stacey1955; Chargaff, Reference Chargaff, Chargaff and Davidson1955; Rice and Doty, Reference Rice and Doty1957), concerning the question of whether the molecular weight of DNA changes or not after acidification at pH 2.6 in aqueous solution with 0.2 M NaCl. Such debate is very instructive for discerning in heating degradation the situations s1), s2), s3), and s4) enumerated at the beginning of the present subsection ‘DNA molecular weight from light scattering’.

The apparatus employed by Reichmann et al. (Reference Reichmann, Bunce and Doty1953) for light-scattering experiments is not described in detail, as the reader is referred to (Doty and Bunce, Reference Doty and Bunce1952) where it is specified that measurements were made by a Brice-Speiser photometer.

Reichmann et al. (Reference Reichmann, Bunce and Doty1953) perform two sets of light scattering experiments for determining the molecular weight of calf thymus DNA in 0.2 M NaCl, at pH 6.5 and at pH 2.6 obtaining the two Zimm plots in Figure 6, reproducing Figure 1 by Reichmann et al. These Authors interpret these plots as the evidence of unchanged molecular weight, ostensibly given by the common intercept attained by these grids in the limit of zero angle and zero concentration.

Figure 6. Zimm plots presented by Reichmann et al. (Reference Reichmann, Bunce and Doty1953) for determining the molecular weight of calf thymus DNA in 0.2 M NaCl at pH 6.5 and 2.6. As reported, tested concentrations vary from 0.005 to 0.05 mg./cc. Used with permission of Interscience Publishers, Inc. from Reichmann et al. (Reference Reichmann, Bunce and Doty1953), Copyright (1946), permission conveyed through Copyright Clearance Center, Inc.

Reichmann et al. pair this possible evidence of stable molecular weight with the interpretation that the fall in viscosity would be the result of a contraction of the coiled molecule as the solution is acidified. They do not consider any possibility of the effect of disaggregation and reaggregation evidenced by Shooter et al. (Reference Shooter, Pain and Butler1956). However, this conclusion of stable molecular weight under pH 2.6 has been challenged by contrary evidence shown by Alexander and Stacey who employed the same method of light scattering to analyze the behavior of this molecule in a broader set of similar experiments. The light-scattering analyses of DNA by these Authors are characterized by a specific view toward possible evidence of depolymerization and toward the delicate discernment of antagonist effects due to fragmentation and fragments reaggregation highlighted in the previous subsection ‘Molecular weight from combined sedimentation/viscosity measurements and the scientific debate among Doty, Shooter and coworkers’. In this study, the Authors examine DNA depolymerization due to acid treatment under conditions similar to those of Reichmann et al. (Reference Reichmann, Bunce and Doty1953) while encompassing a countercheck of particle weight and particle size at different pH values and even in the presence of renetraulization. Their results relevant to the analysis of possible depolymerization due to acidification down below pH 2.6 are recalled hereafter.

The apparatus for the light scattering experiments by Alexander and Stacey is described in Alexander and Stacey (Reference Alexander and Stacey1955) and is similar in design to the one used by Carr and Zimm (Reference Carr and Zimm1950). Also, the experimental conditions examined by these Authors and by Reichmann et al. are readily comparable (solutions of 0.10 to 0.2 M NaCl).

In examining and confronting the experimental results, it is convenient to introductively recall that evidence of acid depolymerization below pH 5 in terms of viscosity reduction and decreased sedimentation has been already highlighted by Cecil and Ogston (Reference Cecil and Ogston1948b) who had reported that at pH 3.5 ‘Treatment with acid leads to the formation of two fractions, one of which is relatively homogeneous and resembles the original material except that it is altered by reprecipitation. The formation of the heterogeneous component is probably the result of disaggregation. The changes brought about at pH 3.5 proceed to a limit, and no further important change follows subsequent neutralization. Reprecipitation of the neutralized solution causes a further large change, the homogeneous component disappearing and a gel-forming material appearing in its place: this change is likely to be due to a re-aggregation’. Evidence in terms of viscosity reduction and of decreased transformation activity in bacteria similarly pointing toward depolymerization has been also reported by Zamenhof et al. (Reference Zamenhof, Alexander and Leidy1953) (with a different buffer) and is synthesized in the following Figure 7 taken from such reference.

Figure 7. Effects of pH on viscosity and transforming activity according to experiments by Zamenhof et al. (Reference Zamenhof, Alexander and Leidy1953). Datapoints digitized from Figure 2 therein. Dots: measured viscosity; crosses: measured transforming activity; for further details on buffer composition refer to the original publication.

The data showing the effect of molecular weight decrease, as determined by the Zimm plot, and showing a spurious molecular weight increase due to fragments reaggregation, are shown in Table 4 and Figure 8 (data and image taken from Alexander and Stacey, Reference Alexander and Stacey1955).

Table 4. Influence of acid treatment on the weight and shape of DNA in solution as determined by light scattering measurements by Alexander and Stacey (Reference Alexander and Stacey1955)

Figure 8. Reciprocal reduced intensity plots after different acid and neutralization treatments, according to experiments by Alexander and Stacey (Reference Alexander and Stacey1955). Datapoints and lines digitized from Figure 3 therein. (a) No treatments, pH 6.8; (b) pH 4.0; (c) pH 3.0; (d) pH 7.0 after re-neutralization from pH 2.6; (e) pH 2.6. See also corresponding values in Table 4 herein. In the original source, only the curve corresponding to the extrapolation to $ c\to 0 $ is plotted and not the entire Zimm grids. pH labels and arrows on the right side are the only addition to the data points and lines of the original figure.

We recall that, as the intercept gives $ 1/M $ , when the intercepts of the curves in Figure 8 are lifted up after a treatment, the molecular weight of the particle (or of the aggregate of particles) decreases. The opposite is true when the intercept decreases: the weight of the particle increases (as observed by the Authors this phenomenon can result from aggregation revealed by the observed precipitation). The curves are best examined following the sequence of incremental acidification $ (a)\to (b)\to (c)\to (e) $ and next considering the re-neutralization $ (e)\to (d) $ from pH 2.6 to pH 7.0. What is seen is that in step $ (a)\to (b) $ $ M $ remains the same. Next in step (b) $ \to (c) $ , from pH 4.0 to pH 3.0, the lowering of the intercept corresponds to an increase of $ M $ from 5.9 $ \bullet {10}^6 $ to 6.6 $ \bullet {10}^6 $ . This increase can be interpreted as a first sign of fragmentation and reaggregation. Such a picture is confirmed in step $ (c)\to (e) $ where pH is lowered from pH 3.0 to pH 2.6 and $ M $ rises from 6.6 $ \bullet {10}^6 $ to 15.9 $ \bullet {10}^6 $ showing a clear sign of reaggregation. The evidence that aggregation is reduced comes from step $ (e)\to (d) $ (from pH 2.6 to pH 7.0) when $ M $ is lowered back again to 5.9, possibly giving the fallacious feeling of the molecule being undegraded since 5.9 is the same molecular weight of the best-preserved DNA samples. Any misinterpretation is ruled out by examining data in the last row of Table 4 showing that reneutralization to pH 7.0 from pH 2.2 yields a molecular weight of 2.45.

Concerning the completeness of the dataset of measurements behind Figure 8, it is important to remark that the authors report to have performed the extrapolation by ordinarily testing the solution at different concentration (as required by the proper execution of the grid-plot methodology devised by Debie and Zimm) although only the curves corresponding to the extrapolation to $ c\to 0 $ are plotted by Alexander and Stacey in their figures and not the entire Zimm grids (this for avoiding data superposition and for permitting clear readability to the reader).

Altogether the data by Alexander and Stacey (Reference Alexander and Stacey1955) recalled in Table 4 and Figure 8 herein disproof the claim by Reichmann et al. (Reference Reichmann, Bunce and Doty1953) that the DNA molecule recovers its original size and shape upon the pH being returned to pH 6.5 from pH 2.6 and the fallacious explanation that the large decreases in viscosity observed by several researchers upon adding acid to DNA solutions are due primarily to the contraction of the DNA molecules, the contribution of degradation being only secondary.

Referring to media more acid than pH 3.0 the Authors explicitly report the following evidence: ‘In more media, there was a rapid aggregation until precipitation occurred. At pH 2.6 apparently stable aggregates with molecular weights of about 15 $ \times $ 10⁶ were produced (Figure 3). This material is polydisperse and no significance can be attached to this numerical value since the weight-average molecular weight varies somewhat with slight changes in experimental conditions in this pH range’ (Alexander and Stacey, Reference Alexander and Stacey1955).

It is thus recognized that the evidence obtained by Alexander and Stacey (Reference Alexander and Stacey1955) which has been herein recalled provides five elements of understanding:

• ▪ it rules out the possibility of DNA not being fragmented at pH 2.6 under the experimental conditions considered by Reichmann et al. (Reference Reichmann, Bunce and Doty1953);

• ▪ it confirms by the independent method of light scattering, also for the acidic treatment (not yet for heating), the effect of disaggregation and reaggregation highlighted by Shooter et al. (Reference Shooter, Pain and Butler1956), among others, by ultracentrifuge and viscosity analysis of heated DNA, previously recalled in the subsection of the scientific background titled ‘Evidence of viscosity drop and of heat turning fibrous material into flocculent precipitate’;

• ▪ it invalidates the hypothesis drawn by the group of Doty that the decrease in viscosity can be justified by the sole effect of contraction of the coiled DNA molecule;

• ▪ it confirms the existing evidence for acidic degradation with disaggregation and reaggregation already at pH 3.5 found by Cecil and Ogston (Reference Cecil and Ogston1948b) recalled above;

• ▪ most importantly, it points out the tangible risk of possible fallacious misdetection of increased molecular weight, or even of unchanged molecular weight, by light scattering in the presence of a limited set of data.

Questioned light-scattering evidence by Rice and Doty of stable molecular weight at 100° (with a second confutation)

Once the elements of knowledge in the bullet list above are acquired, the examination of the light scattering data by Rice and Doty (Reference Rice and Doty1957) on DNA subjected to heating at 94 °C and 100 °C can be carried out in an unbiased way able to separate the ‘wheat from the chaff’, that is, of separating a fallacious evidence of increased or stable molecular weight in front of an incomplete set of measurements. These results are presented hereafter.

For information on the methods and apparatus employed for the light scattering experiments, Rice and Doty refer to the experimental methods reported in Reichmann et al. (Reference Reichmann, Rice, Thomas and Doty1954). In this last publication, the apparatus is not described in detail and outer reference is made again to Reichmann et al. (Reference Reichmann, Bunce and Doty1953) and, transitively, to Doty and Bunce (Reference Doty and Bunce1952). In this last publication, as already recalled, it is specified that the light scattering measurements were made by a Brice-Speiser photometer. The Authors report that a saline-citrate solvent (0.015 M sodium citrate and 0.15 M NaCl) had been used in all light scattering experiments. The concentration of DNA solutions is reported to be of ‘about 6 mg/dl’ corresponding to 0.06 mg/cc. The employed DNA sample is again the one coded SB-11.

The study by Rice and Doty proceeds from the premise referred to the publication by Reichmann et al. (Reference Reichmann, Bunce and Doty1953) that: ‘When dissolved in 0.2 M NaCl, DNA can be exposed to PH values as low as 2.6 for several hours without significant chemical degradation’. Such a premise has been just shown in the previous subsection ‘A fundamental digression on the detection of DNA acidic degradation by light scattering with a confutation’ to be disproved by Alexander and Stacey (Reference Alexander and Stacey1955) showing that what had been detected at pH 2.6 are joint phenomena of fragmentation and reaggregation, in confirmation of Cecil and Ogston’s (Reference Cecil and Ogston1948b) early findings and of the multiplicity of evidences so far collected in the subsections titled ‘The pivotal papers of Doty et al. of the years 1955–1960’ and ‘Evidence of viscosity drop and of heat turning fibrous material into flocculent precipitate’ of the scientific background.

The data which Rice and Doty claim would show that heating at 100 °C during 15 minutes leaves the molecular weight unchanged are contained in Figure 5 therein. Such figure has been digitized and reproduced in current Figure 9b.

Figure 9. Figures 4 and 5 in Rice and Doty (Reference Rice and Doty1957). Angular distribution of scattered light for calf thymus DNA sample SB-11: (a) Measurements at 25° after the sample is heated at 94° during 0, 15, 30, 60, and 120 minutes. (b) Measurements at 25 °C after the sample is heated at 100 °C for 0, 15, 35, 60, and 120 minutes. Reprinted (adapted) with permission from Rice and Doty (Reference Rice and Doty1957), Copyright (1957), American Chemical Society.

Concerning the completeness of the dataset of measurements behind Figure 9, it is important to remark on the following key circumstance. The Authors report that ‘the molecular weight can be obtained from measurements at a single concentration’ and employ the value of 0.06 mg/cc, so that they do report of not having performed measurements at different solute concentrations and report of not having performed an ordinary extrapolation procedure with respect to concentration to obtain these curves. This choice appears to be non-compliant with the standard Zimm-plot methodology (devised by Reference ZimmZimm, 1948b and Debye, Reference Debye1947 and described in the subsection ‘Brief notes on the fundamentals of light scattering’ above) ordinarily applied, for instance, by Alexander and Stacey (Reference Alexander and Stacey1955) with the graphical construction shown in Figure 5 herein and ordinarily applied to obtain the plots in Figure 8. The non-compliant methodology deployed by Rice and Doty to obtain the plots and the molecular weight determination in Figure 9 can be promptly criticized based on the following consideration. From Figure 6 herein, which reproduces the complete Zimm plot extrapolation concerning a previous similar light scattering experiment by the same group of Doty over a similar DNA sample tested at pH 2.6 (Reichmann et al., Reference Reichmann, Bunce and Doty1953, Figure 1 therein), it is seen that the employment of one concentration, in place of the ordinary construction of the complete Zimm grids, is prone to considerable error. Actually, owing to the apparent variability of the curves upon concentration (see the subvertical curves therein intercepting the filled dots) by passing, for instance, from 0.005 to 0.05 mg./cc, the use of the single arbitrarily selected value of 0.06 mg/cc, indicated by the Authors, is prone to arbitrarily affect the particular point where the curve at the selected concentration intercepts the vertical axis. This approach is clearly prone to yielding a considerably large experimental error or even room for arbitrariness in selecting the concentration. Stated differently, if the curve reported by the Authors were to be determined at a different concentration – say of 0.005 mg/cc – it cannot be excluded that the intercept on the vertical axis and the corresponding determination for the molecular weight would have been considerably different. The criticality just highlighted deprives this measure of intersubjectivity and points to the necessity of rejecting this measure as scientific evidence supporting the 100 °C stable molecular weight claim.

It is worth to point out that, after having recalled and remarked in subsection ‘Molecular weight from combined sedimentation/viscosity measurements and the scientific debate among Doty, Shooter and coworkers’ the absence of scientific probative value of the arguments by Rice and Doty from sedimentation-viscosity measures in support of their 100 °C stable molecular weight claim, the light scattering data reproduced in the plots of Figure 9a,b remained the last possible surviving evidence from those contributed by Rice and Doty (Reference Rice and Doty1957) in support of such claim. It is also worth recalling that, as reviewed in subsection ‘Evidence from light scattering of DNA fragmentation upon heating’, all light scattering experiments on DNA heated at elevated temperatures, from all retrievable scientific publications of the decade 1950–1960 on such argument, show consistent and coherent evidence disproving the 100 °C stable molecular weight claim. Also, to the authors’ knowledge, there exists no other element of evidence from light scattering published in the literature of the decade 1950–1960 in possible support of the 100 °C stable molecular weight claim.

In the light of the considerations above and of the elements highlighted in subsection ‘Pioneering pre-1961 studies on DNA heating not authored by Doty’ of the scientific background, the confutation provided in the present subsection of a measurement of stable molecular weight from the light-scattering data of Doty and Rice brings to an end the review of the papers by Doty possibly supporting such claim and brings to zero the number of unconfuted elements of evidence in possible support of the 100 °C stable molecular weight claim.

Considerations on PCR buffers

Even if one resorts to appealing to a possible remedial protective action of the electrolytes in the PCR buffer reported by Mullis and Faloona, the data reported by Hamaguchi and Geiduschek (Reference Hamaguchi and Geiduschek1962) indicate that conditions provided for in the PCR buffer are prone to thermal instability at the PCR temperatures (of 95 °C and 100 °C) and that such conditions are less stable to thermal disruption than those of most of the DNA solutions employed in the many works herein reviewed. Moreover, data reported by Hamaguchi and Geiduschek (Reference Hamaguchi and Geiduschek1962) show that at any concentration of any of the many electrolytes therein investigated, upper bounds of thermal instability onset temperatures (defined as midpoints of thermal denaturation curves) cannot be, in any case, above 92.6 °C, so that a protective action of some electrolyte cannot be argued at 95 °C and 100 °C. To make matters worse, these data also show that thermal stability in sodium acetate (which is the prevalent solute in the PCR buffers) is even lower than in sodium chloride (see Table I therein) as the midpoint temperature of irreversible thermal denaturation curves viscometrically determined by these authors (which turns out to be always an upper bound of the temperature of thermal depolymerization onset) is lowered from 90.0 °C to 83.5 °C.

Most remarkably, the absence of NaCl in the PCR buffers deprives these solutions of the protective effect of salt against thermal degradation which the reviewed literature has shown to be fundamental.

Considerations on the known degrading effect of depurination by heating are not carried out but could be also taken into account. The addition of dithiothreitol (DTT) (the three isomer of 2,3-dihydroxy-1,4-dithiolbutane), which is a strong reducing agent, provided for in two PCR buffers (methods I and II) can be considered anything but a stabilizing component considering the capability of thiols of generating mercaptylated derivatives of DNA, as shown for instance by Tamm and Chargaff (Reference Tamm and Chargaff1953) employing phenylmethanethiol (benzyl mercaptan). The effect of addition of DTT is also not contemplated in the subsequent analyses.

Optimistic computations of the number of DNA fragmentations consequent to PCR heating

According to Mullis and Faloona (Reference Mullis and Faloona1987), PCR heating temperatures are 95 °C and 100 °C. The number of heating cycles in PCR multiplied by the duration of each heating process ranges approximately from a minimum overall time of exposure to heating of $ 10\times 1\;\mathrm{minute}=10 $ minutes (in methods I and II, prescribing addition of DTT) to maximum overall heating times higher than 40 minutes (in methods III, IV, V, and VI and in absence of DTT) and as high as $ 27\times 2=54 $ minutes in particular in method V.

The most promptly employable information for estimating the entity of fragmentation of PCR short heating cycles, among those herein reviewed, is represented by the five sequence-breaking fragmentations computed in the above subsection ‘A summary of evidence of DNA thermal disruption’ from Goldstein and Stern’s data on the viscosity drop consequent to 1 minute heating at 100 °C followed by cooling. We recall from the reviewed literature that the optimistical significance of this estimate from viscosity data in representing a reliable lower bound to the weight-average number of fragmentations and number-average number of fragmentations experimented by the distribution of DNA molecules during 1 minute heating at 100° is supported, among many others, by the following elements:

• • ‘the random nature of the heat-denaturation process’ (Cox and Peacocke, Reference Cox and Peacocke1956);

• • the knowledge that ‘it is only changes in the intrinsic viscosity which are of significance in the estimation of molecular size and shape’ reaffirmed, for instance, in Nature by Cox, Overend, Peacocke, and Wilson;

• • the partial fragments reaggregation on cooling which determines a regain in viscosity (in part of thixotropic nature) so that what is actually determined by measuring a lower bound of the viscosity drop upon cooling of the heated solution is just a lower bound of the number of fragmentations really experimented by the molecule;

• • the evidence, shown by Peacocke and Preston (Reference Peacocke and Preston1958) and by Applequist (Reference Applequist1961), that single-strand fragmentation is a first-order rate process and that the number of single-strand sequence-breaking ruptures by heating is linear with time all through the heating degradation.

• • the evidence, shown by the same Authors, that the number of single-strand sequence-breaking ruptures by heating is much higher than the number of complete fragmentations of the molecule (requiring each a double longitudinal rupture), since it is a quadratic function of time.

Lower bound estimate of the probability of survival of a sequence of nucleotides after repeated heating/cooling 1 minute, 100 °C cycles

Based on the two models described in the above subsection ‘What really happens during DNA thermal fragmentation?’ (USH and ISH-93) and on the conservative assumption that one heating/cooling for 1 minute at 100 °C produces 5 fragmentations, a highly optimistic computation of the probability of survival (integrity preservation of molecular information) of a selected sequence of nucleotides contained in the main single-strand sequence after repeated cycles is carried out. As discussed above such a computation provides a lower bound of the degree of disordering and rupture experimented by a nucleotide sequence during such a cycle. We recall that:

• • the USH model consists of the abstraction of uninterrupted strands of 7000 nucleotides assumed to have thermally labile longitudinal bonds;

• • the ISH-93 model is an abstraction in which each strand is made of 75 sub-chains whose internal intranucleotide bonds are not thermally labile.

To perform a computation, the length of the sequence intended for PCR ‘amplification’ must be introduced. Mullis and Faloona (Reference Mullis and Faloona1987) write: ‘The sequence to be synthesized can be present initially as a discrete molecule or it can be part of a larger molecule.’

As far as the integrity of the full sequence is concerned, the computation is the same for the USH model and the ISH-93 model. Five random thermal longitudinal fragmentations occurring in 1 minute heating correspond to randomly dividing the main sequence into five subsequences each preserving its internal order of nucleotides. In the optimistic abstraction herein followed of cooling always being able to restore a sequential reaggregation of fragments, cooling corresponds to randomly reassembling these five ordered subsequences into one out of $ \left(5+1\right)!=720 $ new possible main sequences each obtainable as a random permutation, so that the probability of reobtaining the original full sequence is 1/720. Already after only 3 cycles, this probability becomes very low dropping to $ \frac{1}{{\left(6!\right)}^3}=1/\left(2.6874\times {10}^{11}\right) $ . After the total number of 10 cycles provided for by PCR, corresponding to $ {n}_{\mathrm{Tfrag}}=10\times 5=50 $ overall fragmentations, the optimistic estimate of the probability of preserving the integrity of the molecule is $ 3.1097\times {10}^{-32} $ .

The integrity of smaller contained sequences after 10 heating cycles is now examined. This issue is important, for instance, when the possible employment of PCR is intended by its users for searching for information possibly relatable to the gene expression of a protein. The length of the subsequence is indicated by $ {n}_{\mathrm{sub}} $ . A documented representative value of $ {n}_{\mathrm{sub}} $ can be set to $ {n}_{\mathrm{sub}}=1000 $ adopting, for instance, an optimistic lower bound of the typical lengths retrievable in public databases for the so-called spike protein (US National Center for Biotechnology Information, European Bioinformatics Institute, 2021).

For the USH model, denoting by $ {n}_T=7000 $ the total number of nucleotides, by $ {n}_{\mathrm{sub}}=1000 $ the number of consecutive nucleotides of a subsequence, and by $ {n}_{\mathrm{Tfrag}}=10\times 5=5 $ 0 the total number of fragmentations after 10 cycles, the number of combinations by which the main sequence can be fragmented in 50 subsequences is computed as:

(34) $$ {\displaystyle \begin{array}{rcl}{N}_m& =& \frac{n_T!}{\left({n}_T-{n}_{\mathrm{Tfrag}}\right)!{n}_{\mathrm{Tfrag}}!}=\frac{7000!}{\left(7000-50\right)!50!}\\ {}& =& \frac{7000\bullet 6999\bullet \dots \bullet 6952\bullet 6951}{50!},\end{array}} $$

where $ n! $ indicates the factorial of number $ n $ . The number of combinations by which the main sequence can be fragmented into 50 subsequences preserving the integrity of the main sequence is

(35) $$ {\displaystyle \begin{array}{c}{N}_{\mathrm{int}}=\frac{\left({n}_T-{n}_{\mathrm{sub}}\right)!}{\left({n}_T-{n}_{\mathrm{sub}}-{n}_{\mathrm{Tfrag}}\right)!{n}_{\mathrm{Tfrag}}!}=\frac{\left(7000-1000\right)!}{\left(7000-1000-50\right)!50!}=\\ {}=\frac{(6000)!}{(5950)!50!}=\frac{6000\bullet 5999\bullet \dots \bullet 5952\bullet 5951}{50!}.\end{array}} $$

The probability of preserving the integrity of the main sequence is thus computed to be:

(36) $$ {P}_{\mathrm{int}\mathrm{egr}}=\frac{N_{\mathrm{int}}}{N_m}=\frac{6000\bullet 5999\bullet \dots \bullet 5952\bullet 5951}{7000\bullet 6999\bullet \dots \bullet 6952\bullet 6951}\cong 0.00044. $$

The same computation can be carried out with the ISH-93 model in the same way by just converting in number of subchains elements (we recall, each sub-chain being composed of 93 nucleotides, see Table 5) the lengths of 7000 and 1000 in sub-tokens of 93, while the number of total fragmentations remains $ {n}_{\mathrm{Tfrag}}=10\times 5=5 $ 0. Accordingly, one computes:

(37) $$ {n}_T:= \frac{n_T}{93}=\frac{7000}{93}\cong 75\hskip0.4em \mathrm{and}\hskip0.52em {n}_{\mathrm{sub}}:= \frac{n_{\mathrm{sub}}}{93}=\frac{1000}{93}\hskip0.4em \cong \hskip0.4em 11. $$

Table 5. Test molecule models USH, and ISH with equally spaced sub-chains of 56 and 93 nucleotides

The probability of preserving the integrity of the main sequence is thus computed to be for the ISH-93 model:

(38) $$ {P}_{\mathrm{int}\mathrm{egr}}=\frac{N_{\mathrm{int}}}{N_m}=\frac{64\bullet 63\bullet \dots \bullet 16\bullet 15}{75\bullet 74\bullet \dots \bullet 27\bullet 26}\hskip0.4em \cong \hskip0.4em 0.00000091, $$

so that computations elucidate that the ‘ISH-93 model’ at hand, although composed of longer sub-chains (hypothesized thermally unbreakable), turns out to be, as a matter of fact, less thermally stable, as far as the integrity of a sequence of 1000 nucleobases is concerned.

The above computations well exemplify and illustrate the remarkable proneness of PCR to entropy-related error determined by the presence of heating steps in such procedure, even more so if it is considered that all simplifying hypotheses introduced to arrive at such computations do have a lower-bound optimistic character, that is, they all contribute to the benefit of reducing the computed probability of disruption produced by the PCR heating cycles. The considerations above raise a serious concern toward longitudinal sequence-breaking degradation, even more so when the action of the randomizing effect of fragments reaggregation upon cooling is contemplated in addition to the randomization effect produced by thermal degradation at the end of each PCR heating cycle (ranging between 1 and 5 minutes). A critical factor related to this statement is the length of the sequence to be amplified and whether this sequence is larger than the sub-chain elements with uninterrupted phosphodiester bonds identified by Dekker and Schachman (Reference Dekker and Schachman1954). If the sequence to be amplified or to be detected is larger than the average length of the Dekker and Schachman sub-chains (93 in our simplified computations), as it is the case of a sequence of more than 100 nucleobases such as the length reported by NIH under the denomination spike protein, the probability of preserving integrity is thus computed to be very low.

In this regard, it is worth recalling that the abstraction of the physical phenomena of heating and cooling leading the computational models adopted for the calculations above have speculatively excluded the possibility of translation and rotation of the molecular fragments and the possibility of formation, upon reaggregation, of a more topologically complex-and more disordered nonsequential arrangement, like, for instance, a net.

Perhaps fewer words and fewer computations are necessary to represent to the reader the degree of disorder which can be achieved after just one heating–cooling cycle at 60 °C, by showing here in Figure 12 the electron micrograph taken by Williams (Reference Williams1952) of a sprayed 0.01% water solution of DNA prepared by the method by Schwander and Signer subjected to a process consisting of (1) freezing at −78 °C, (2) 60 °C heating for drying, and (3) rapid cooling.

Figure 12. Reproduction of Figure 1 by Williams (Reference Williams1952). (a) ‘Low-magnification ( $ \times \mathrm{13,500} $ ) electron micrograph of a freeze-dried water solution of DNA. Three-dimensional character of specimen is well shown by the separation of fibers and their shadows in the region marked with an arrow. The horizontal fibers here are about 0.5 μ above substrate. Spherical particles are of polystyrene latex’. (b) ‘High magnification ( $ \times \mathrm{100,000} $ ) electron micrograph of DNA. Region indicated with an arrow shows fibril about 15 A in diameter’. Reprinted from Williams (Reference Williams1952, pp. 237–239), Copyright (1952), with permission from Elsevier Science and Technology Journals.

It may be argued that Figure 12 may not be representative of the degree of disorder induced by PCR cycles because the DNA freeze-drying process, with 60 °C heating, leading to the micrograph of Figure 12 may have induced disordering factors that cannot be comparable with the effect in PCR of multiple 95 °C or 100 °C heating steps followed by quick cooling. It is undeniable that, while the milder 60 °C heating must have induced a significantly lower degradation, concentration and drying have a significant role in determining the picture of densely agglomerated fibers in Figure 12.

On the other hand, micrographs of the molecules in the material produced after DNA heating at 100 °C have been taken by Doty et al. (Reference Doty, Marmur, Eigner and Schildkraut1960). Figure 3 in the same paper shows the electron micrograph with a magnification factor $ \left(\times \mathrm{95,000}\right) $ of DNA molecules from a solution heated in saline-citrate at 100 °C for 10 minutes, and then diluted, slowly cooled, and dialyzed. Such micrograph shows longer molecules having all, with no exceptions, a cross-linked, non-sequential, topologically complex, and involuted structure, appearing in large part quite intricately coiled and, as observed by the Authors, with ‘irregular patches at the ends of cylindrical threads’. Figure 4 in Doty et al. (Reference Doty, Marmur, Eigner and Schildkraut1960) shows a micrograph obtained with exactly the same methodology with the only difference that the cooling step was instead performed quickly. The description given by the Authors is that the figure ‘shows only irregularly coiled molecules with clustered regions’. As this second micrograph has the same magnification factor as the first Figure 3, relevant to slowly cooled DNA, the lengths of the observable molecular threads in the two figures can be compared. By comparing the two figures, it is evident that the visible aggregates in Figure 4, besides being in some part clustered, are also much smaller in length and few individual thread-like fragments, even up to 20 times shorter than the thread-like structures of Figure 3, can be almost clearly discerned.

Altogether the evidences recapitulated in this section, and in particular the ascertainment by Applequist (Reference Applequist1961) that the molecular weight halving reported by Doty et al. (Reference Doty, Marmur, Eigner and Schildkraut1960) is only ‘fortuitously in agreement’ with the value of ½, should recommend caution in verifying the true nature of the phenomena observed when slow cooling is applied after heating, as described by Doty et al. (Reference Doty, Marmur, Eigner and Schildkraut1960) (frequently referred to as ‘annealing’). Caution should be applied to verify whether these annealing phenomena truly consist of an ordered reformation of a two-stranded material from the association of two one-stranded chains, or also involve the other much less ordered combined fragmentation-aggregation phenomena, elucidated by the researches of Sadron and coworkers (Sadron, Reference Sadron1955; Reference Sadron1959; Freund et al., Reference Freund, Pouyet and Sadron1958) and Shooter et al. (Reference Shooter, Pain and Butler1956). As shown in this review, these phenomena are instead mainly ascribable to some combination of thermal degradation and possible aggregation/agglomeration, during the subsequent cooling stage, into clusters made of many shorter degraded two-stranded molecules of lower molecular weight.

The possible occurrence of these degradation and reaggregation phenomena should be considered also in the interpretation of data from experiments which have employed heat-denaturing processes inspired by those proposed by Doty et al. (Reference Doty, Marmur, Eigner and Schildkraut1960). One of these interpretative problems is raised, for instance, with the results presented by Hall and Spiegelman (Reference Hall and Spiegelman1961) who have applied heat-denaturing processes at 95 °C along 15 minutes to investigate the possible formation of helices pairings or helices complexes made of DNA and RNA looking forward to a confirmation of the interpretations suggested by previous X-ray diffraction studies (Rich and Davies, Reference Rich and Davies1956; Felsenfeld et al., Reference Felsenfeld, Davies and Rich1957; Rich, Reference Rich, By and Glass1957, Reference Rich1958, Reference Rich2006).

Summarizing, as elucidated by the elements of empirical evidence and by the conservative quantitative lower-bound predictions collected in the present section, it would not be an exaggeration to argue that achieving a faithful amplification, and even before detection, of a long nucleobase sequence after reiterated cooling and uncooling cycles of PCR, may appear to be as much plausible as pretending to faithfully reconstitute at the Ångströms scale a complete long celery stalk of the size of few thousands Ångströms from a soup of randomly aggregated and very similar vegetable fragments, with each fragment being dozens of times smaller in size. Such a duty would be burdensome enough for a nanoscale Maxwell’s demon with tweezers capable of seeing and reconstructing the searched nucleobase sequence, even more so in the absence of such a demon and by just reiterating the thermal bombardment by heating/cooling cycles.