1. INTRODUCTION
The Greenland ice sheet sheds mass in two ways: through surface ablation and through dynamic ice loss into the ocean. The former includes the sublimation and meltwater runoff components of the surface mass balance (SMB), while the latter encompasses all direct ice discharge to the ocean (i.e. outlet glacier calving). Both of these processes have contributed to increased mass loss from Greenland since the 1990s, with SMB-related losses now contributing approximately twice as much mass loss as ice discharge does (Enderlin and others, Reference Enderlin2014). Understanding these sources of mass loss is necessary if we are to quantify and project the mass balance of the Greenland ice sheet, which is an important contributor to global sea-level rise (Vaughan and others, Reference Vaughan2013). Interactions between increased SMB-related mass loss and ice discharge have received particular attention recently due to their potential influence on ice-sheet mass balance (Phillips and others, Reference Phillips, Rajaram and Steffen2010; Colgan and others, Reference Colgan, Sommers, Rajaram and Abdalati2015).
Surface melt and subsequent runoff is the major source of SMB-related ice loss, contributing 90% of ablation versus 10% from sublimation (Ettema and others, Reference Ettema2009). Not all surface melt is lost as runoff, however: an estimated 45% of the annual surface melt refreezes within the firn (Ettema and others, Reference Ettema2009), and an additional fraction of melt refreezes englacially (i.e. in crevasses). Although this refrozen melt does not contribute directly to sea-level rise, it may affect ice discharge indirectly by releasing latent heat: cold (temperature below the melting point) firn and ice can absorb the latent heat of the refrozen meltwater and consequently become warmer and softer. This process in turn affects ice dynamics, since under a given driving stress, softer ice will flow more quickly downslope, enhancing dynamic mass loss (Cuffey and Paterson, Reference Cuffey and Paterson2010). Such changes in ice dynamics are likely to be greatest when the ice warms quickly, since over longer periods (centuries to millennia), the ice sheet will evolve to a shape consistent with its rheology (Nye, Reference Nye1951).
Refreezing can occur both in firn (Mock and Weeks, Reference Mock and Weeks1965) and in glacial ice (Jarvis and Clarke, Reference Jarvis and Clarke1974). It has been argued that the latter, sometimes called cryo-hydrologic warming, can quickly and substantially enhance the velocity of the ice sheet in certain areas (Phillips and others, Reference Phillips, Rajaram and Steffen2010, Reference Phillips, Rajaram, Colgan, Steffen and Abdalati2013). Recently, Colgan and others (Reference Colgan, Sommers, Rajaram and Abdalati2015) calculated that cryo-hydrologic warming occurring over the entire Greenland ice sheet could discharge tens of centimetres of sea-level equivalent over the coming centuries, although they did not evaluate the likelihood of this end-member scenario actually occurring. In this paper, we assess the influence on englacial temperature of refreezing in the firn and deeper within the ice sheet along specific flowlines, and then generalise the results to larger areas of the ice sheet.
Above the equilibrium line altitude (ELA), in the percolation and wet snow zones, most of the meltwater percolates downward into the firn, where it refreezes (Benson, Reference Benson1962; Mock and Weeks, Reference Mock and Weeks1965; Greuell and Konzelmann, Reference Greuell and Konzelmann1994; Humphrey and others, Reference Humphrey, Harper and Pfeffer2012; Machguth and others, Reference Machguth2016). Recently, Humphrey and others (Reference Humphrey, Harper and Pfeffer2012) observed that this process warms the top 10 m of firn in western Greenland by as much as 12°C above the mean annual surface temperature. Over many hundreds of years, this warmth in the firn heats the underlying ice column through downward advection as new snow accumulates and, to a lesser extent, through thermal diffusion (Lüthi and others, Reference Lüthi2015). Such warmth sourced from the surface of the ice sheet can, in some places, have a greater effect on ice temperature at depth than the basal geothermal flux (Lüthi and others, Reference Lüthi2015; Meierbachtol and others, Reference Meierbachtol, Harper, Johnson, Humphrey and Brinkerhoff2015). In Svalbard, this heat source may even be responsible for sustained fast ice flow in outlet glaciers by melting the bed, which is hundreds of metres below the firn (Schäfer and others, Reference Schäfer2014).
Below the ELA, where bare ice is exposed by the end of the summer, meltwater collects in crevasses and supraglacial lakes. Lakes can hydrofracture to the bottom of the ice sheet and deliver the meltwater to the bed, through vertical shafts known as moulins, over a period of hours (Das and others, Reference Das2008). Moulins can remain active for multiple years, but they ultimately are closed by creep as they are advected away from their water sources (Catania and Neumann, Reference Catania and Neumann2010). This limited lifetime, along with their small size (<~10 m diameter) and low spatial density (Phillips and others, Reference Phillips2011), suggests that moulins should have only a limited thermal effect. Indeed, results from a numeric model that incorporates moulins confirm this (Vorkauf, Reference Vorkauf2014).
Some supraglacial lakes, however, do not form moulins; instead, their water refreezes in place (Darnell and others, Reference Darnell, Amundson, Cathles and MacAyeal2013). This transfers latent heat onto the ice-sheet surface and diffusively warms the upper portion of the ice column. Lakes also insulate the ice-sheet surface from low wintertime temperatures. The thermal influence of such lakes, however, is limited by the relatively short time it takes the ice beneath them to advect through the lake basin. For typical flow speeds of 100 m a−1 and typical lake widths of 1–3 km, this amounts to a few decades, limiting the diffusion depth to tens of metres. Furthermore, this downward diffusion of heat competes with summer ice ablation rates in the upper ablation zone (~1 m a−1). Thus, the thermal influence of refreezing within supraglacial lakes generally is limited to the top ~10 m of the ice sheet. Overall, moulins and supraglacial lakes alter near-surface ice temperatures considerably but influence englacial temperatures only marginally. Thus, we exclude supraglacial lakes from this analysis.
Meltwater that enters crevasses can accumulate and may reach depths of hundreds of metres over a period of weeks (van der Veen, Reference van der Veen2007). The meltwater can refreeze onto the walls of crevasses at rates approaching millimetres per day (Alley and others, Reference Alley, Dupont, Parizek and Anandakrishnan2005), thus contributing a substantial amount of latent heat to the ice at depth over even a relatively short time period. Therefore, latent-heat transfer through crevasses in the ablation zone (cryo-hydrologic warming) can have a considerable effect on ice temperature at the depths to which they penetrate, particularly with recent increases in surface melt (Phillips and others, Reference Phillips, Rajaram, Colgan, Steffen and Abdalati2013). Model analyses suggest that this englacial refreezing process, under certain conditions, could warm the ice at 500 m depth by 10°C in fewer than 10 a (Phillips and others, Reference Phillips, Rajaram and Steffen2010; Lüthi and others, Reference Lüthi2015). Temperature observations in Greenland boreholes suggest that the ice has warmed englacially via latent-heat transfer in crevasses (Thomsen, Reference Thomsen1988; Thomsen and Olesen, Reference Thomsen and Olesen1990; Harrington and others, Reference Harrington, Humphrey and Harper2015; Lüthi and others, Reference Lüthi2015; Meierbachtol and others, Reference Meierbachtol, Harper, Johnson, Humphrey and Brinkerhoff2015), though such field evidence does not constrain the timescale over which such warming has occurred.
In this study, we investigate the current magnitude of the effect that englacial refreezing of meltwater has on ice dynamics in western Greenland. We study both the accumulation zone, which warms primarily through refreezing in firn (Machguth and others, Reference Machguth2016), and the ablation zone, where crevasse-based cryo-hydrologic warming dominates. We choose central western Greenland because its ablation zone is comparatively extensive, stretching up to 100 km into the interior, compared with only 0–10 km in south-eastern Greenland (Ettema and others, Reference Ettema2009). The breadth of the ablation zone in central western Greenland allows the ice ample transit time to warm through latent-heat transfer. Although the area lacks extensive firn aquifers such as those found in south-eastern Greenland (Forster and others, Reference Forster2013), the wide percolation zone extends up from the ELA to at least 2300 m elevation (Machguth and others, Reference Machguth2016) and allows extensive refreezing within the firn. Modest accumulation rates then push this shallow warmth downwards into the ice sheet, affecting ice temperatures downstream. Overall, studying central western Greenland, where strong melting occurs, allows us to determine the potential for englacial refreezing to affect the dynamics of the ice sheet and thus changes in global sea level.
2. STUDY AREA IN WESTERN GREENLAND
Our study area in western Greenland spans 64.5°–72.0°N and extends from the coast to the ice-sheet divide. Because englacial temperature data are available only in a few regions within this area, we focus our modelling effort on those regions where observations of englacial temperatures are most plentiful. We then extend our conclusions over the larger study area using climatological and remote-sensing-derived observations of travel time and ice balance fluxes.
Boreholes were drilled in the Jakobshavn Isbræ catchment in 1988/89 (Iken and others, Reference Iken, Echelmeyer, Harrison and Funk1993) and in 1995 (Lüthi and others, Reference Lüthi, Funk, Iken, Gogineni and Truffer2002) and instrumented with thermistors. These thermistors overwintered and their data provided, after processing (Humphrey, Reference Humphrey1991), near-equilibrium englacial temperatures at various depths. We also use temperature data from boreholes drilled in the Pâkitsoq area, a slow-moving region of divergent ice flow 20 km north of Jakobshavn, downstream of Swiss Camp (69.57°N, 49.28°W). Temperature measurements in Pâkitsoq were made in the late 1980s (Thomsen, Reference Thomsen1988; Thomsen and Olesen, Reference Thomsen and Olesen1990) and in 2011 (Ryser and others, Reference Ryser2014a; Lüthi and others, Reference Lüthi2015).
SMB estimates (Ettema and others, Reference Ettema2009) and catchments drawn from velocity data (Joughin and others, Reference Joughin, Smith, Howat, Scambos and Moon2010) indicate that the Jakobshavn catchment collects ~5% of the steady-state discharge of the ice sheet. In comparison, the Pâkitsoq area and its adjacent outlet glacier Sermeq Avannarleq account for ~0.03% of Greenland's steady-state ice discharge.
Ice flow differs substantially between the Jakobshavn and Pâkitsoq areas. The 110 000 km2 Jakobshavn catchment (the size of Pennsylvania) funnels ice from a ~300 km-wide section of the divide into a 5-km-wide outlet glacier. This convergence of ice results in a deeply incised bedrock trough (Clarke and Echelmeyer, Reference Clarke and Echelmeyer1996) and flow velocities up to 17 km a−1 (Joughin and others, Reference Joughin, Smith, Shean and Floricioiu2014). In contrast, ice in the neighbouring Pâkitsoq area originates at a point on the flank of the ice sheet where its neighbouring catchments converge (Fig. 1). This ice gradually spreads out to form a 20-km-wide catchment, with flow speeds of <~100 m a−1 that generally slow along flow (Joughin and others, Reference Joughin, Smith, Howat, Scambos and Moon2010). The flowlines plotted in Figure 1a illustrate these contrasting regional velocity patterns. In addition, the ice in the Jakobshavn catchment is much thicker (Clarke and Echelmeyer, Reference Clarke and Echelmeyer1996) than the ice in the Pâkitsoq catchment (Bamber and others, Reference Bamber2013).
Fig. 1. (a) Modelled flowlines (coloured lines) and borehole sites (coloured dots) in the Jakobshavn and Pâkitsoq catchments. Red flowlines travel through boreholes on Jakobshavn while other colours show flowlines in Pâkitsoq. Surface elevations from Howat and others (Reference Howat, Negrete and Smith2014) and the ELA from RACMO2 (pink) are shown atop a Landsat image from 3 July 2014. Regions of divergent flow are hatched. (b) Study area in western Greenland, with surface velocity from Joughin and others (Reference Joughin, Smith, Howat, Scambos and Moon2010) shown west of the divide, and major outlet glaciers labelled. Regions of divergent flow are hatched. (c) Locations of panels a (black box) and b (blue box).
Both the Jakobshavn and Pâkitsoq regions host crevasse fields. The fast flow of Jakobshavn produces extensive local crevassing. In Pâkitsoq, although the speeds are much lower, the surface is heavily crevassed because bedrock bumps produce cracks in the relatively thin ice as it stretches to flow over them. The ELA is relatively constant across these two regions, at ~1500–1600 m (averaged over 1960–2011), as indicated by RACMO2 SMB output (van Angelen and others, Reference van Angelen, van den Broeke, Wouters and Lenaerts2013). It is important to note that although the ELA is the elevation at which snowfall balances runoff and sublimation on average, snowmelt does occur above the ELA in most years.
3. METHODS
We assess the effect that surface melt has on ice temperature and viscosity through its refreezing within the firn in the accumulation zone and within glacial ice in the ablation zone. To quantify the effect of latent-heat transfer, we represent refreezing processes in a numeric model for ice temperature and compare the model output with existing measurements of englacial temperatures in the ablation zone of western Greenland. This allows us to delineate and characterise regions where englacial refreezing substantially affects ice flow. Based on these results, we evaluate the overall importance of these two refreezing processes on ice flow in western Greenland. Here we describe the model used in this study.
3.1. Temperature model without englacial latent-heat transfer
We use an existing thermal model to determine englacial temperature within vertical columns linked to form flowlines (Poinar, Reference Poinar2015). The model is polythermal: it includes physics for sub-temperate ice (ice colder than its melting point), temperate ice (ice at its melting point) and liquid water within the temperate ice (located between ice grains and produced by shear heating). For cold ice within each vertical column, the model solves the heat equation using the fully implicit finite-difference method with a 5 a time step on a 400-point vertical grid (∆z ~ 1–10 m), which is adaptable to accommodate the basal temperate ice layer. Where ice is temperate, the model calculates its internal water content and the consequent latent heat flux into cold-ice areas above and downstream of the temperate ice. The heat flux associated with this phase transition is described more fully by MacAyeal (Reference MacAyeal1997), Funk and others (Reference Funk, Echelmeyer and Iken1994) and Greve (Reference Greve1997), studies which form the basis for inclusion of polythermal ice in our model.
The model assumes the modern-day geometry of the ice sheet (surface and basal topography, geothermal flux and surface velocities) but also incorporates palaeoclimate information (temperature and SMB) from the last glacial period, extending back to 50 ka (Cuffey and Clow, Reference Cuffey and Clow1997). To simulate dynamic thinning since the last glacial maximum, we enhance accumulation rates by 30% during the Holocene, following Lüthi and others (Reference Lüthi, Funk, Iken, Gogineni and Truffer2002).
3.2. Calculation of velocity field and strain heating
The model applies a standard Dansgaard and Johnsen (Reference Dansgaard and Johnsen1969) formulation for vertical velocity, constrained by the SMB (from RACMO2) at the upper surface and the basal melt rate (computed from temperature gradients) at the bed. Details are provided in Poinar (Reference Poinar2015).
The model advects ice downstream at horizontal velocity u, which is the sum of the calculated deformational velocity u d and the basal (sliding) velocity u b.
$$u(x,z) = \; u_{\rm d}(x,z) + u_{\rm b}(x)$$
We calculate the deformational velocity as follows:
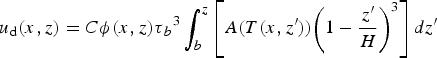$$u_{\rm d}(x,z) = C\phi (x,z)\tau{_b}{^3}\mathop \int_b^z \left[ {A(T(x,{z}^{\prime})){\left( {1 - \displaystyle{{{z}^{\prime}} \over H}} \right)}^3} \right]dz^{\prime}$$
Here, τ b is basal shear stress, which Shapero and others (Reference Shapero, Joughin, Poinar, Morlighem and Gillet-Chaulet2016) calculated for the downstream portion of the Jakobshavn catchment; we set basal shear stress equal to the driving stress in other areas. The quantity b is the elevation of the bed, and A(T) is the temperature-dependent rate factor, which we calculate using a standard Arrhenius relationship (Cuffey and Paterson, Reference Cuffey and Paterson2010) that evolves with the model. The constant C is a tuning parameter and ϕ(x,z) is a shape function, which describes the distribution of horizontal velocity as a function of z and the rate factor. The shape function has the properties ϕ(x,b) = 0 and ϕ(x,s) = 1, where s is the elevation of the ice-sheet surface. Poinar (Reference Poinar2015) provides further details.
We enforce the observed surface velocity field (Joughin and others, Reference Joughin, Smith, Howat, Scambos and Moon2010) along each flowline, but we partition that velocity between deformation and sliding according to the rheology of the ice at each grid point:
$$u_{\rm b}(x)\, = \,\; u_{\rm s}(x) - u_{\rm d}(x,s)$$
where u s is the observed along-flow surface velocity. In sum, the deformational velocity in our model is sensitive to changes in ice temperature, but the overall horizontal velocity is pinned to observations.
The model calculates along-flow vertical shear heating as a function of shear strain rate and vertical shear stress, which we compute from basal shear stress:
$$W(z) = \displaystyle{{\partial u_{\rm d}} \over {\partial z}}\left( {1 - \displaystyle{z \over H}} \right)\tau _{\rm b}$$
Ice rheology, A(T), is implicit here through Eqn (2), as is the tuning parameter C, which is constant with x and z within a flowline but is allowed to vary between flowlines. We use C to represent multiple factors not included in our model, including the viscosity contrast between ice-age ice and harder Holocene ice (Lüthi and others, Reference Lüthi, Funk, Iken, Gogineni and Truffer2002; Cuffey and Paterson, Reference Cuffey and Paterson2010), locally enhanced shear heating due to lateral stress transfer (Lüthi and others, Reference Lüthi, Funk and Iken2003), and other factors, such as grain size and fabrics, that are commonly incorporated into such factors.
3.3. Tuning to match borehole temperature observations
We used ice temperatures measured in the Jakobshavn boreholes to constrain the tuning parameter C. Because C controls the magnitude of shear heating (Eqns (2) and (4)), which is concentrated at the bed, its influence is greatest at the bed. Thus, tuning C to capture temperatures near the bed has little influence on the refreezing processes we examine here, which have the greatest effects higher in the ice column.
For each Jakobshavn borehole, we adjusted C along the corresponding flowline to best match the measured temperatures in the bottom third of the ice column. We found that C = 1.5 along the flowlines for Sites A and B and 4.0 at Site D produced the best match. Field measurements at Site C did not access the deeper ice, precluding tuning there, so we also use 1.5 for Site C. Varying C from 1 to 5 for the ice feeding these four borehole sites affected temperatures in the bottom 1000 m of the ice column by up to 5°C, due to enhanced shear heating there, but changed temperatures in the upper half of the ice column by <0.4°C. With C tuned to these values, we find temperate ice layers with thicknesses of 15, 211, 0 and 30 m at Jakobshavn drill sites A, B, C and D, respectively. In part due to our tuning process, these values are in good agreement with direct and indirect borehole measurements of temperate ice thickness, of 0–100 m at Site A, ~230–300 m at Site B and 31 m at Site D (Iken and others, Reference Iken, Echelmeyer, Harrison and Funk1993; Lüthi and others, Reference Lüthi, Funk, Iken, Gogineni and Truffer2002). The inferred value at Site B was generated with a thicker DEM (Clarke and Echelmeyer, Reference Clarke and Echelmeyer1996) than we use here (Bamber and others, Reference Bamber2013); the reduced vertical stretching required in our model geometry may explain the thinner temperate ice that we find (Funk and others, Reference Funk, Echelmeyer and Iken1994). In Pâkitsoq, we used C = 3 based on the enhancement factor found by Schøtt and others (Reference Schøtt, Waddington and Raymond1992), as shown in Table 1. We found that ice temperatures in Pâkitsoq, where basal temperate ice layers are uncommon, were not especially sensitive to the value of this parameter.
Table 1. Model parameters and results at the 12 borehole sites studied
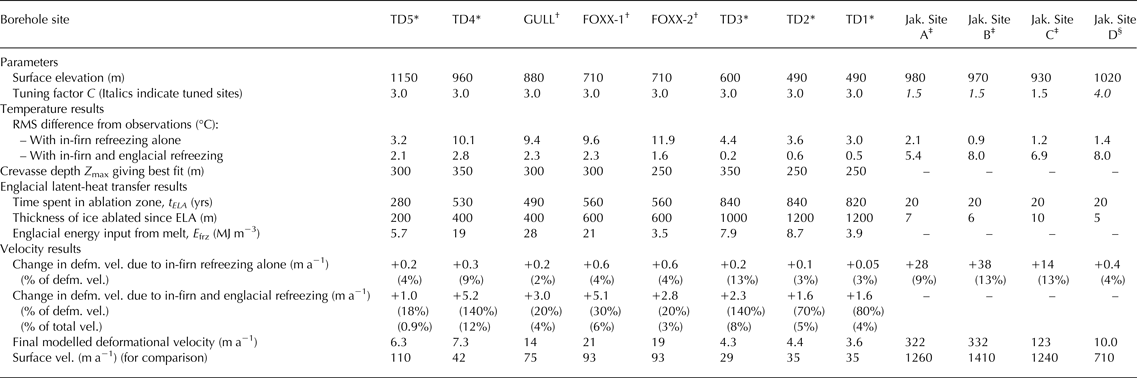
* Thomsen and others (Reference Thomsen and Olesen1990).
† Ryser and others (Reference Ryser2014a) and Lüthi and others (Reference Lüthi2015).
‡ Iken and others (Reference Iken, Echelmeyer, Harrison and Funk1993).
§ Lüthi and others (Reference Lüthi, Funk, Iken, Gogineni and Truffer2002).
This reference temperature model provides a platform from which to investigate the effect that added latent heat has on ice temperature. In the next two subsections, we describe how we adapt the model to include latent heat from refreezing in the firn and crevasse fields.
3.4. Model representation of near-surface latent-heat transfer in firn
Most large-scale ice-sheet models do not incorporate the thermal effects of latent heat from refreezing in firn. Here we explore the sensitivity of temperature at depth to thermal conditions within the firn by applying three distinct sets of surface (≤15 m depth) boundary conditions (BCs) to our model:
-
(BC 1) Skin temperature (mean annual temperature at the ice-sheet surface) from the RACMO2 regional climate model,
-
(BC 2) Near-surface temperature measurements from 1955 to 1980s, collated by Reeh (Reference Reeh1989), that reflect the warming effect of refreezing of meltwater within the firn,
-
(BC 3) Temperatures at 15 m depth calculated from the SMB routine of the RACMO2 regional climate model (van Angelen and others, Reference van Angelen, van den Broeke, Wouters and Lenaerts2013) and supplemented by field measurements (Humphrey and others, Reference Humphrey, Harper and Pfeffer2012), as described below.
Figure 2 illustrates these surface boundary conditions and their application to the model.
Fig. 2. Illustration of surface and basal boundary conditions used in the model, englacial temperature prescriptions (0°C) applied to the idealised crevasse fields, and the consequent diffusive warming (pink) from the englacial temperature prescription.
Figure 3 shows the spatial variation of each of these boundary conditions along a flowline within the Jakobshavn catchment. We use the skin temperature (BC 1) as a control case and BC 3 as an end-member case. In general, BC 2 temperatures are intermediate between BCs 1 and 3. Although BCs 2–3 represent subsurface temperatures (depths of 3–20 m), we apply them directly to the surface of the modelled ice sheet.
Fig. 3. Surface boundary conditions (BCs 1–3) versus surface elevation along the flowline through the TD5 borehole, in the Pâkitsoq catchment. Location of the TD5 borehole is indicated by the black horizontal line at 1150 m. Dots indicate observations (other studies) and lines indicate the boundary conditions applied in our model. The green line is a smoothed fit through the Reeh (Reference Reeh1989) measurements that we apply. The thin orange line at ~1400–1700 m elevation indicates the RACMO2 output that we replace with field observations (purple) from Humphrey and others (Reference Humphrey, Harper and Pfeffer2012), where available, to make the solid orange curve that we applied in our model.
The first two boundary conditions are unmodified from their original sources (Reeh, Reference Reeh1989; van Angelen and others, Reference van Angelen, van den Broeke, Wouters and Lenaerts2013). We found some substantial differences, however, when we compared the RACMO2 firn temperature estimates with field measurements acquired along an elevation transect directly upstream of our Pâkitsoq study region (Humphrey and others, Reference Humphrey, Harper and Pfeffer2012). These data indicate that surface meltwater warms the firn to temperatures as much as 14°C above the mean-annual air temperature, which is higher than the RACMO2 model predicts (thin orange curve in Fig. 3). This is likely because RACMO2 does not allow heterogeneous refreezing within the firn column, and as a result, the RACMO2 meltwater refreezes higher in the firn column than the field measurements indicate (Kuipers Munneke and others, Reference Kuipers Munneke2015). Consequently, in RACMO2, latent heat can more easily escape into the atmosphere, causing modelled firn temperatures up to 7°C lower than observed. To account for the model-data differences, we used a combination of the observations and the model results. Specifically, where the two near-surface modelled and observed temperatures disagree, we take the higher of the two (solid orange curve in Fig. 3).
3.5. Model representation of englacial latent-heat transfer in crevasses
In the ablation zone, meltwater collects in crevasse fields and supraglacial lakes. We focus on meltwater in crevasses, which can refreeze at tens to hundreds of metres depth within the ice sheet and contribute latent heat toward warming the surrounding ice. We simplify this latent-heat-transfer problem by assigning englacial temperatures of 0°C to areas we identify as crevasse fields. In these areas, we prescribe 0°C temperatures from the surface to some assigned depth, which we vary across crevasse fields.
We generalise the nature of the ice-sheet surface by randomising the locations of modelled crevasse fields along our flowlines. We give each grid point below 1700 m elevation a 50% chance of being assigned as a ‘crevasse field’ (0°C temperature prescribed from the surface to some controlled random depth of tens to hundreds of metres) and a 50% chance of being ‘bare ice’ (BC 3 assigned at the surface). This distribution reflects the observations of Colgan and others (Reference Colgan2011), who identified ~50% of the Pâkitsoq area as crevasse fields. We chose the 1700 m contour for our model because satellite images indicate that some englacial fractures exist above the ELA, although they are relatively sparse.
Our model has a horizontal resolution of 3 km, which is comparable in scale to a typical crevasse field (Joughin and others, Reference Joughin2013), but much coarser than the width of a single crevasse. Thus, within the area represented by one grid element, we would expect hundreds of crevasses to be present that might extend to many different depths, yet we can only specify one such depth per grid element. Figure 4a illustrates how temperatures may look within such a crevasse field, where crevasses spaced by 50 m penetrate to random depths between 0 and 350 m. The temperature field is heterogeneous at small scales, with ice at or near 0°C near each crevasse but significantly colder at depth and between crevasses. Representing this full variation of ice temperature within a crevasse field would be computationally expensive; furthermore, quantifying the depth of each crevasse is beyond our observational abilities. Yet as the ice advects through and out of the crevasse field, thermal diffusion begins to homogenise the ice temperature (Fig. 4a). Further diffusion will continue to smooth out the temperature distribution downstream.
Fig. 4. (a) Representation of a 3 km-wide crevasse field, with crevasses spaced by 50 m and penetrating to Z max = 350 m. Ice initiates at the GULL borehole and advects rightward at 100 m a−1. Crevasse walls are set to 0°C; this warmth advects and diffuses over time. This temperature field was calculated using a separate model (Poinar, Reference Poinar2015) than that used for the rest of this work. The leftmost boundary condition (initialisation temperature) is the model result with BC 3 (heat deposition within the firn), shown on panel b in orange. (b) Results of representing this crevasse field in our model as a single crevassed point (black dashed line and grey shading) with Z max = 300 m. The coloured profile shows the mean temperature of panel a. The panel a average is slightly cooler than the model mean because the model mean (black / grey) also feels the influence of all additional crevassed points upstream of this site.
Thus, in our model, we represent crevasses coarsely, assigning either zero or one crevasse per 3 km grid point (Fig. 4b) with a 50% probability. This scheme is, on average, equivalent to 3 km-wide areas of uncrevassed ice that collect no latent heat, alternating with 3 km-wide crevasse fields that collect 100% of the latent heat from local meltwater. To represent the variety of depths that meltwater likely reaches within a single crevasse field, we run multiple realisations of our model and allow the crevasse depths to vary among realisations (black and grey curves in Fig. 4b). Averaging these realisations has a similar smoothing effect as that of horizontal diffusive processes (Fig. 4a) on true englacial temperatures within crevasse fields (Phillips and others, Reference Phillips, Rajaram and Steffen2010).
We assign crevasse depths in a controlled random fashion. For each set of runs, we use a value Z max to represent the deepest possible crevasse along the flowline. We vary Z max from 20 to 500 m between sets of runs. At each ‘crevasse field’ model grid point, we enforce a 0°C englacial temperature from the surface to some depth Z, where Z is chosen from a uniform random distribution spanning the domain [0, Z max]. Thus, the expected average crevasse depth in each run is Z max/2. We do not prescribe any pattern of crevasse depth along the flowline. We perform eleven sets of model runs, where each run within a set of 10 runs has the same parameter Z max but randomly located crevasse fields, each with a randomised depth Z. We chose this approach for its ease of implementation and ad hoc simplicity in investigating sensitivity to melt, rather than as a model that incorporates the full physics of the problem.
4. RESULTS
We ran our model, varying the thermal surface boundary condition and the englacial meltwater penetration depth, to find the values that produce the best fit to the temperatures observed in boreholes in the Jakobshavn and Pâkitsoq areas of western Greenland.
4.1. Model results from Jakobshavn Isbræ
We modelled flowlines that pass through the three boreholes drilled within the main trunk of Jakobshavn Isbræ in 1988/89 (Iken and others, Reference Iken, Echelmeyer, Harrison and Funk1993) and the one borehole drilled 4 km outboard of the centre of the trunk in 1995 (Lüthi and others, Reference Lüthi, Funk, Iken, Gogineni and Truffer2002). Using the skin temperature from RACMO2 as the surface boundary condition (BC 1), the modelled temperature profiles shown in Figure 5 (blue curves) are all lower than the observations. This difference is greatest within approximately 200 m of the surface, where modelled temperatures are as much as 7°C lower than observations (e.g. Site A). More typically, modelled temperatures are 3–5°C lower than observations.
Fig. 5. Model results at the four Jakobshavn boreholes (by panel) for the three surface boundary conditions tested (coloured lines), plotted alongside measured englacial temperatures (black dots). (a–c) Sites A–C (Iken and others, Reference Iken, Echelmeyer, Harrison and Funk1993); (d) Site D (Lüthi and others, Reference Lüthi, Funk, Iken, Gogineni and Truffer2002). Modelled temperate ice thicknesses with the 15 m depth boundary condition (BC 3, orange) are (a) 14 m, (b) 211 m, (c) 0 m and (d) 30 m. The dashed black lines show these modelled temperate ice thicknesses at each borehole site.
Using the near-surface temperature measurements compiled by Reeh (Reference Reeh1989) (BC 2; green curves in Fig. 5) also yields englacial temperatures that are substantially colder than the borehole measurements. The temperature profiles computed using 15-m depth temperatures from RACMO2 and Humphrey and others (Reference Humphrey, Harper and Pfeffer2012) (BC 3) fit the borehole measurements to within a root-mean-square (RMS) difference of 2°C. All of the surface boundary conditions produce similar fits to the deepest temperatures due to our adjustment of the turning factor. The overall fit using BC 3 is best at Site B (RMS difference 0.9°C) and poorest at Site A (RMS difference 2.1°C). We consider ~2°C an acceptable margin consistent with anticipated uncertainties in the model and observations. Furthermore, the differences show no systematic variation with depth. Experimental model runs that included crevasse-based latent-heat transfer in the Jakobshavn flowlines yielded temperature profiles that were substantially warmer (up to 8°C; Table 1) than observations. Thus, for the Jakobshavn drill sites, we find that the model is best able to reproduce observations using BC 3. Our model results are not consistent with the occurrence of crevasse-based latent-heat transfer in the catchment.
4.2. Model results from Pâkitsoq
In the Pâkitsoq area, we modelled flowlines that pass through five boreholes (TD1–5) drilled in 1988–1990 (Thomsen and Olesen, Reference Thomsen and Olesen1990) and three boreholes drilled at two sites (FOXX and GULL) in 2011 (Ryser and others, Reference Ryser2014a; Lüthi and others, Reference Lüthi2015). The FOXX site includes two boreholes with distinctly different temperatures; we model them each in turn. We performed separate sets of runs along each flowline through the seven borehole sites we studied. Figure 1 shows these flowlines. We compared the results for each Z max with measured borehole temperatures and chose the Z max with the best match (lowest RMS error) as being representative of the typical crevasse depth in the areas near each borehole.
We tested all three boundary conditions as well as a suite of model runs incorporating englacial latent-heat transfer, with crevasses carrying meltwater to a variety of depths.
4.2.1. Firn refreezing boundary condition
The results of the model at the seven Pâkitsoq borehole sites are shown in Figures 6, 7. Coloured solid lines indicate model output using the three surface boundary conditions. As in the Jakobshavn catchment, all seven boreholes are warmer than the model predicts using our control run with skin temperature (BC 1). The RMS differences at Pâkitsoq, however, are larger than at Jakobshavn, reaching as high as 19°C at the GULL borehole and at least 5°C at all other Pâkitsoq boreholes. Furthermore, the firn heating boundary conditions (BCs 2–3), which we successfully used to model the Jakobshavn temperatures, add only ~3°C at most to the englacial temperatures and thus are unable to explain the observed englacial warmth.
Fig. 6. Model results at four of the Pâkitsoq boreholes (TD5, TD4, GULL and FOXX-1). These four boreholes are located nearer to the ELA (farther upstream) than the other boreholes (Fig. 7). Shown are model results using the three surface boundary conditions tested (blue, green, and orange lines), model results incorporating both BC 3 and the thermal effects of crevasses (black dashed lines and shading), and measured englacial temperatures (coloured dots; references shown on each panel). The model gave all grid points with s <1700 m a 50% chance of crevassing, except for ice along the TD5 flowline, where we prescribed a 20% chance of crevassing. Tick marks on the left side of each panel indicate depths at 100 m intervals.
Fig. 7. Model results at four of the Pâkitsoq boreholes (FOXX-2, TD3, TD2 and TD1). These boreholes are at lower elevations than those in Figure 6. Shown are model results using the three surface boundary conditions tested (blue, green and orange lines), model results incorporating both BC 3 and the thermal effects of crevasses (black dashed lines and shading), and measured englacial temperatures (coloured dots; references shown on each panel). The model gave all grid points with s <1700 m along each flowline shown here a 50% chance of crevassing. Tick marks on the left side of each panel indicate depths at 100 m intervals.
As in the Jakobshavn catchment, BC 3 produces the best match to the temperatures observed in the Pâkitsoq boreholes. Using BC 3, the overall discrepancy between measured and modelled temperatures in Pâkitsoq is largest (RMS difference 12°C) at the FOXX-2 borehole site. This site is located well within the ablation zone (surface elevation s = 710 m; ELA at 1500 m). The discrepancy is also large at the TD4, FOXX-2 and GULL boreholes (observations ~10°C higher than the model). The fit generally improves with distance downstream, through the lower-elevation boreholes TD3, TD2, and TD1. The ice in these boreholes is, on average, 4°C warmer than modelled. The fit is better at the lower-elevation boreholes largely because most of the cold ice in the upper column has melted away (Table 1), leaving only the warmer layers below; the relatively narrow range between the surface temperatures and the melting point here (~7°C) effectively limits the possible RMS difference. The model still does a poor job, however, of capturing the overall shape of the temperature distribution. This suggests that englacial latent heat sources (refreezing in crevasses) play a significant role in warming the ice.
4.2.2. Effect of englacial refreezing
Next we assess the role of englacial latent-heat transfer through crevasses at the Pâkitsoq borehole sites. To examine sensitivity of the temperature response to crevasse depth, we tested eleven different upper bounds on crevasse depth, Z max, spanning 20–500 m. For each Z max, we performed 10 model runs in which we varied the locations and depths of crevasse fields. We represent the modelled ice temperature at each borehole by the mean output temperature among these runs. By varying Z max, our model was able to produce temperature profiles that approximately match the observations at all eight Pâkitsoq boreholes. At the neighbouring boreholes FOXX-1 and FOXX-2, matching the temperature observations required slightly different Z max (300 and 250 m, respectively, as shown in Table 1). The model-observation RMS difference is ~2°C at upper-elevation sites (TD5, TD4, FOXX-1, FOXX-2, and GULL, surface elevation s >700 m) and <1°C at lower-elevation sites (TD1–3, s <600 m).
Along six of our seven flowlines, each grid point below 1700 m elevation had a 50% chance of being assigned as a ‘crevasse field’ and a 50% chance of being ‘bare ice’, as described above. We tested multiple such crevassed-area parameters, ranging from 20% to 90% crevassed, and found little influence on the overall results, except at the highest-elevation borehole (TD5). There, a 20% crevassed-area parameter provided a markedly better fit than did a value of 50%. This may be indicative of sparser crevassing at higher elevations (Poinar and others, Reference Poinar2015). In general, however, we found a lack of sensitivity of ice temperature to crevasse density. This is likely due to our model setup, wherein once a crevasse has warmed the ice at depth, the upper ice column advects downstream faster than it can diffusively cool, making the presence or absence of additional crevassing downstream less influential on ice temperatures. Thus, for all flowlines except TD5, we use a 50% crevassed-area parameter.
4.2.3. Relative crevasse depth
Table 1 shows the best-fit maximum crevasse depths Z max identified for each Pâkitsoq borehole site. These depths average ~300 m and span a relatively narrow range (250–350 m), despite the wide range tested (20–500 m). There is no apparent relationship between elevation on the ice sheet and Z max. The relative penetration depth of the crevasses into the ice sheet does, however, increase downstream, as the thickness of the ice columns generally decreases. For instance, at TD1 and TD3, the best-fit crevasse depths Z max represent the full ice thickness at the borehole sites. Note that Z max is the maximum crevasse depth over a uniform distribution; the average depth of crevasses is half of this value. Thus, crevasses penetrate, on average, through half of the ice thickness there. At the high-elevation site TD5, however, typical crevasses (Z max/2~150 m) penetrate only the top 10–15% of the ice sheet. Crevasses penetrate through 50–60% of the ice thickness at the remaining four borehole sites.
While our model is relatively simple, the match to the data suggests that penetration of the water-filled crevasses that allow englacial refreezing is generally limited to ~300 m.
4.2.4. Spatial distribution of englacial refreezing rates
Crevasse fields warm the ice sheet by giving meltwater access to the cold ice at depth, where it refreezes. Lüthi and others (Reference Lüthi2015) calculated that such refreezing had deposited approximately 25 MJ m−3 of energy into the ice upstream of the FOXX and GULL borehole sites. To compare the results of our model to their value, we calculate an apparent energy deposition density E frz for each borehole:
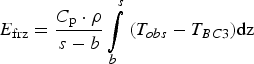$$E_{{\rm frz}} = \displaystyle{{C_{\rm p} \cdot \rho} \over {s - b}}\int\limits_b^s {(T_{obs} - T_{BC3})} {\rm dz}$$
This quantity takes the column-averaged difference between the observations (T obs) and our profiles modelled without englacial, crevasse-type refreezing, but with the near-surface boundary condition (BC 3) adapted to represent in-firn refreezing (T BC3), and scales it to an energy density (E frz). We use E frz to interpret the amount of water that evidently refroze englacially.
The results of this calculation are shown in Table 1. Some sites (TD4, FOXX-1, GULL) have apparent energy inputs in excess of ~20 MJ m−3, in agreement with Lüthi and others (Reference Lüthi2015), while values for the other sites are a factor of two less. Interestingly, these high-energy-input sites are not especially warm compared with other Pâkitsoq boreholes (e.g. TD1–3). The ice columns at the high-energy-input sites are thicker and the modelled crevasse depths are slightly greater (Z max of 300–350 m), though, so that although these sites collect larger volumes of meltwater, they also distribute the heat over a larger depth range. Furthermore, the lower-elevation boreholes (TD1–3) have experienced more cumulative ablation (Table 1), thus shedding some of the warmth that they may have absorbed upstream.
4.2.5. Effect on ice velocity
An anticipated consequence of the cryo-hydrologic warming seen in the Pâkitsoq boreholes is an increase in ice velocity, since the warmed and rheologically softened ice should flow faster in response to a given driving stress. We calculate the expected speedup from a base case (BC 3; no englacial refreezing) based on the temperature change at the site of each borehole, using Eqn (2). We assume no change in driving stress or basal shear stress. The results are shown in Table 1. The velocity increases range from 1 m a−1 at TD5 to 5 m a−1 at TD4, for final deformational velocities of 6.3 and 7.3 m a−1, respectively. These increases represent 20% and 140% of the base-case deformational velocity at these sites, respectively. The observed motion, however, is much greater than the computed deformational velocity, due to basal sliding (Joughin and others, Reference Joughin, Smith, Howat, Scambos and Moon2010): 110 and 42 and m a−1, respectively. Thus, the increase due to enhanced deformation relative to the observed speed is only 1% and 12%, respectively.
While englacial warming may substantially affect ice rheology, it appears that it increases the total ice velocity only modestly. This is because of the prevalence of basal slip and because the rheology of the upper ice column, where our work and previous work (Ryser and others, Reference Ryser2014a; Lüthi and others, Reference Lüthi2015) shows that latent-heat transfer is occurring, is less important to ice flow than the rheology of the lower ice column. The full partition of ice motion into deformation and sliding components is notoriously complex in the Pâkitsoq region and is influenced by processes outside of what we have modelled here (Ryser and others, Reference Ryser2014b). Our simple model gives a general approximation of the response of ice speed to englacial latent-heat transfer.
5. GENERALISATION TO WESTERN GREENLAND
Next we generalise the importance of deep englacial refreezing, of the type observed in Pâkitsoq, to a broader scale. We use the central western sector of the Greenland ice sheet, from 64.5° to 72.0°N latitude, as our study area. This area is bounded by a local ice divide to the north and a steep change in the ELA location to the south. Although this area contains a number of major outlet glaciers, including Jakobshavn, Store and Rink Glaciers, it also has high surface melt rates and a comparatively large fraction of land-terminating ice. These attributes make it the region of the ice sheet most broadly similar to the Pâkitsoq catchment.
5.1. Generalisation metric: time spent in the ablation zone
Latent-heat deposition in crevasses was required to make our model match observations in the Pâkitsoq catchment, but including this worsened the model-data fit within Jakobshavn (Table 1). This apparent absence of crevasse-based heating in Jakobshavn may, in part, reflect a limitation of our model with respect to the residence time of ice in crevasse fields. In the model, we add englacial latent heat to each crevassed node instantaneously, i.e. as soon as the ice moves into a crevasse field. In reality, it takes some time for crevasses to reach the depths we instantaneously prescribe, as each crevasse must collect water, often from a limited local catchment, in order to hydrofracture (van der Veen, Reference van der Veen2007). In general, ice spending more melt seasons in a crevasse field (i.e. slower-moving ice) can absorb more latent heat, due to higher cumulative meltwater volumes and increased time to conduct the latent heat into the ice sheet (Phillips and others, Reference Phillips, Rajaram and Steffen2010). Thus, ice that flows through a 3 km wide crevasse field at 1000 m a−1 (e.g. Jakobshavn) would, in reality, absorb approximately one tenth the latent heat of ice that flows through a similar crevasse field at 100 m a−1 (e.g. Pâkitsoq). Our model, however, deposits identical amounts of latent heat in these two cases. Thus, the difference in observed behaviour between the two regions may reflect the fact that residence time in a crevasse field, which is inversely proportional to speed, plays a critical role in determining how much englacial warming occurs.
Rather than computing ice residence time in each individual crevasse field across western Greenland, we use the residence time in the ablation zone as a simpler proxy for the amount of warming ice will experience from englacial latent-heat transfer. Ice with a longer tenure in the ablation zone will, in general, also have longer tenures in crevasse fields, and will thus collect and refreeze more water, as described above. As detailed in Table 1, the travel time of ice through the ablation zone is much greater in Pâkitsoq (~300–800 a) than it is in Jakobshavn (20 a). This is also apparent from Figure 1a, which shows the catchment boundaries for these and other regions. In Pâkitsoq, the ice flow diverges laterally (the catchment widens downstream), which tends to slow speeds along a flowline and thus produce long residence times. By contrast, in the Jakobshavn catchment, flow is laterally convergent, which implies a narrowing catchment, increasing speed and short residence times.
We use the time spent in the ablation zone (or, equivalently, t ELA , the time elapsed since crossing the ELA) to distinguish between fast-moving Jakobshavn-like ice and slow-moving Pâkitsoq-like ice. We calculate the amount of time spent in the ablation zone for each point on the surface of the ice sheet within the central western Greenland region (Fig. 1b) by integrating the along-flow surface velocities (Joughin and others, Reference Joughin, Smith, Howat, Scambos and Moon2010) beginning at the ELA, as derived from RACMO2 (1960–2011):
$$t_{ELA}(x) = \mathop \int_{ELA}^x \displaystyle{{dx^{\prime}} \over {u_{\rm s}({x}^{\prime})}}$$
Because we are looking at warming in the top part of the ice column and because sliding accounts for much of the speed, we do not correct for speed as a function of depth. Furthermore, the wintertime speeds we use, which are ~10% slower than summertime speeds (Bartholomew and others, Reference Bartholomew2011), bias our residence times long by approximately the same margin. Residence times in the ablation zone for all points in our central western Greenland study area are shown in Figure 8a. To put this region in context, we also show residence times for the remainder of the ice sheet in Figure 8b.
Fig. 8. (a) Time elapsed since crossing the equilibrium line for all points within the 64.5°–72.0°N study area. Blue data on the leftmost axis show the ice flux across 2-km gates along the ELA. These fluxes were computed by summing the average SMB (1960–2011, from RACMO2) within the catchment upstream of each gate, which we delineated with flowlines generated from observed surface velocities (Joughin and others, Reference Joughin, Smith, Howat, Scambos and Moon2010). Numbers in parentheses indicate the fraction of the central western Greenland balance flux that each labelled glacier catchment contributes. (b) Time elapsed since crossing the equilibrium line for the entire ablation zone of the Greenland ice sheet. The box indicates the area of focus in panel (a). Arrows in north-western and north-eastern Greenland point to the largest areas outside western Greenland where ice spends >1000 a in the ablation zone.
To the south of Jakobshavn Isbræ, residence times typically are >1000 a. The ice at the seven Pâkitsoq borehole sites has spent 280–840 a in the ablation zone before arriving at each drill site (Table 1), which suggests that this area should experience substantial cryo-hydrologic warming (~10°C or greater), as has been observed. Of the seven Pâkitsoq sites, the TD5 borehole (t ELA = 280 a) shows the least evidence of englacial latent-heat transfer and represents an approximate midpoint between cold, Jakobshavn-like englacial temperatures and cryo-hydrologically warmed, Pâkitsoq-like temperatures. Thus, we use t ELA = 250 a as an approximate threshold for cryo-hydrologic warming.
5.2. Weighting for ice flux
Figure 8a shows that ice in a large swath of the ice sheet with low ice flux and divergent flow has relatively long ablation-zone residence times (>~1000 a). By contrast, convergent, fast-flowing, high-flux glaciers cover relatively little area in the ablation zone. For instance, Jakobshavn Isbræ, which outputs more ice than any other western Greenland glacier, has a disproportionately small footprint in Figure 8a. Thus, the information in Figure 8a should be weighted in terms of ice flux before its potential sea-level contribution is interpreted. We calculate balance ice fluxes by integrating the SMB, which we average over 1960–2011 from RACMO2, within the catchments of multiple 2-km-wide gates along the ELA. These fluxes are shown in Figure 8a in blue. Fast-moving ice in Jakobshavn Isbræ and in many glaciers north of it (including Store Glacier and Rink Glacier) generally moves through the ablation zone in <100 a. Together, the catchments of these three glaciers contribute >50% of the balance ice flux across our study area, as noted in Figure 8a. In contrast, Isunnguata Sermia, a slower-moving, land-terminating outlet glacier where field measurements indicate englacial warming (Harrington and others, Reference Harrington, Humphrey and Harper2015), contributes just 1% of the total balance flux.
We weight the residence-time estimates by the balance flux to assess the fraction of ice flux that flows quickly through the ablation zone. As shown in Table 1, the fastest-moving ice in Jakobshavn Isbræ spends only 20 a in the ablation zone; such ice (t ELA ≤ 20 a) accounts for a full 15% of the ice flux through central western Greenland, despite its small areal extent (Fig. 8a). We find that ~63% of the ice flux across the equilibrium line in central western Greenland occurs in regions where the ice spends <250 a in the ablation zone. Thus, the majority of the ice does not spend enough time exposed to melt to experience substantial cryo-hydrologic warming.
6. DISCUSSION
Here we discuss our results in the context of the boundary conditions used in ice-sheet models as well as the implications of cryo-hydrologic warming for sea-level rise predictions.
6.1. Latent-heat transfer in firn
Our model results for Jakobshavn Isbræ (Fig. 5) clearly show that it is necessary to include the latent heat of refreezing in firn to model englacial temperatures. Ice temperatures modelled using RACMO2 skin temperature (BC 1) are as much as ~9°C lower than observations in the top few hundred metres of the ice column, although the difference dwindles with depth and is <1°C by depths of ~1000 m.
6.1.1. Variations among boundary conditions
The results using the Reeh (Reference Reeh1989) boundary condition (BC 2) are also substantially cooler than observations, even though this surface temperature parameterisation was developed to reflect the refreezing of meltwater within firn. Reeh (Reference Reeh1989) used temperatures measured at depths of 3 m (in snow pits) and 7–20 m (in shallow ice cores) at various elevations in western Greenland from 1955 through the 1980s. We speculate that these field measurements may underrepresent refreezing due to the nature of the local site selection: melt-free locations on local highs may have been chosen over lower-lying areas, where slush and surface water tend to inhibit sampling operations. Thus, the poorer agreement of Jakobshavn boreholes with the simulations using BC 2 could suggest that the Reeh (Reference Reeh1989) parameterisation may be colder than the true spatial average due to sparse sites that undersampled the true influence of percolating meltwater.
6.1.2. Inferred near-surface temperature history
The Jakobshavn temperature profiles modelled using the near-surface RACMO2 boundary condition (BC 3) show warm inflections at ~60–130 m depth (Fig. 5). There, the ice is ~3°C warmer than expected from the otherwise smooth curve. A simple analysis using present-day SMB and surface velocities shows that the ice at ~100 m depth originated at the surface approximately at the elevation of the warmest firn temperatures (s ~1550 m, Fig. 3). It is unclear, however, whether this specific output of our model is actually observable in the Jakobshavn ice because the near-surface temperature measurements there are too sparse (~100 m vertical spacing) to indicate this level of detail.
Near-surface observations in the TD5 borehole show a similar pattern to the near-surface warmth we modelled in the Jakobshavn boreholes: temperatures in the top 200 m are ~5°C higher than expected with BC 3, as also observed by Lüthi and others (Reference Lüthi2015). Our model with englacial latent-heat transfer occurring at 50% of the ice-sheet area, however, finds ice temperatures another ~8°C higher than observed (not shown). With a sparser distribution of crevasses (20% of the ice-sheet surface), the model produces a more satisfactory fit to the data (Fig. 6a). Lüthi and others (Reference Lüthi2015), however, excluded englacial latent-heat transfer at this site and instead identified a past localised warm period to explain this near-surface warmth. While we do not rule out a past warm period, we consider that crevasse-based englacial warming is a viable alternative for explaining near-surface warmth at the TD5 drill site.
6.2. Englacial temperatures in Pâkitsoq
In Pâkitsoq, our results suggest that at elevations below ~1700 m, crevasses carry water to an average of ~150 m depth (Z max ~ 300 m) within the ice sheet, where it has a substantial (~2–10°C) influence on englacial temperatures. The high temperatures and the consequent inferred energy deposition density E frz (Eqn (5)) indicate that 0.3–15% of the available local meltwater has refrozen since the ice around each borehole crossed the equilibrium line. This range is similar to the ice-sheet-wide refreezing rate of 7% assumed by Colgan and others (Reference Colgan, Sommers, Rajaram and Abdalati2015), although with some contrast because our results reflect only the ablation zone, where deep englacial meltwater retention should be maximised. In comparison, most meltwater in the accumulation zone refreezes within the top tens of metres of the firn (Machguth and others, Reference Machguth2016), which prevents it from reaching deep into the ice sheet. RACMO2 output indicates that slightly more than half of the total Greenland snowmelt occurs within the accumulation zone, which limits the depth to which this melt can percolate. Thus, our results, which focus on the ablation zone, should be taken as an upper bound on overall Greenland refreezing rates.
Our results agree well with those of Lüthi and others (Reference Lüthi2015), who used a similar approach but different techniques to model a subset of the Pâkitsoq boreholes. They assumed a spatially constant crevasse depth of 400 m and allowed each crevasse to persist for 50 a before returning its ice to a standard surface boundary condition. For comparison, with our model grid spacing of 3 km, surface velocities of ~100 m a−1, and 50% of grid points hosting crevasses, our model has an effective crevasse lifetime of 45 a. Along the TD5 flowline, this decreases to 36 a because of the sparser crevasse distribution there (20% of grid points).
Lüthi and others (Reference Lüthi2015) assigned a substantially greater penetration depth (400 m) than we found (Z max/2 ~150 m). We note that their zone of crevassing begins at Swiss Camp (s = 1150 m), whereas ours begins at s = 1700 m, a horizontal difference of 50 km. We speculate that our expanded area of crevassing compensates for our shallower and slightly shorter-lived crevasses compared with Lüthi and others (Reference Lüthi2015).
Lüthi and others (Reference Lüthi2015) excluded the TD4 borehole from their analysis. Indeed, our work suggests that this site is anomalous: it requires the deepest crevasses (Z max = 350 m) but has a temperature profile that our model could not recreate and whose shape is different from the other sites (Fig. 6). Field reports suggest drilling difficulties here (Thomsen and Olesen, Reference Thomsen and Olesen1990), so it is possible that the reported temperatures at TD4 are inaccurate. It is also possible that the drill site was close to a relict moulin or anomalously deep crevasse. Indeed, the heterogeneity of observed ice temperatures at the FOXX site (Ryser and others, Reference Ryser2014a; Lüthi and others, Reference Lüthi2015) suggests that heat sources can vary substantially, even over very short spatial scales (86 m). This highlights one limitation of our model approach: the assumption that crevasse depth varies randomly along a flowline. In fact, field measurements, such as those at the neighbouring FOXX boreholes, could be used to constrain crevasse depths locally, as done by Jarvis and Clarke (Reference Jarvis and Clarke1974).
6.3. Model limitations
The warm ice observed in the Pâkitsoq catchment has analogues elsewhere in Greenland. For example, Harrington and others (Reference Harrington, Humphrey and Harper2015) found ice substantially warmer than the mean-annual air temperature in Isunnguata Sermia, south-western Greenland. Their five drill sites spanned a similar range of elevations and showed comparable, though slightly higher, englacial temperatures to the Pâkitsoq sites we studied. The Isunnguata sites, however, have all spent substantially longer in the ablation zone (850–1200 a) than the Pâkitsoq ice has (Fig. 8a). These tenures represent roughly the 75th percentile of tELA in western Greenland. The warmth in those boreholes is not surprising given the long period over which the ice has been able to collect meltwater. The rate of warming is evidently lower in the Isunnguata catchment, though, perhaps due to differences in the surface hydrology (e.g. a greater presence of moulins, a sparser distribution of crevasses, or shallower depths of water-filled crevasses). Indeed, modelling work by Harrington and others (Reference Harrington, Humphrey and Harper2015) suggests that crevasses in this area penetrate to just 20–120 m, as compared with the ~300 or 400 m found in Pâkitsoq, by this work and Lüthi and others (Reference Lüthi2015), respectively. Thus, the degree of englacial warming appears to vary regionally in ways that our t ELA metric may not always capture.
Our temperature model is limited in that it does not quantitatively incorporate the t ELA metric. The growing body of field studies (Ryser and others, Reference Ryser2014a; Lüthi and others, Reference Lüthi2015) suggests that areas with long residence times consistently show evidence of englacial latent-heat transfer. By contrast, our model can accurately reproduce the temperature of ice with short residence times (Iken and others, Reference Iken, Echelmeyer, Harrison and Funk1993; Funk and others, Reference Funk, Echelmeyer and Iken1994; Lüthi and others, Reference Lüthi, Funk, Iken, Gogineni and Truffer2002) without this process. From these limited observations, we reason that t ELA ~250 a represents an approximate threshold for substantial latent-heat transfer. Thus, we hypothesise that areas with shorter residence times do not experience substantial englacial latent-heat transfer, while areas with longer residence times do. A model with a more explicit treatment of englacial latent-heat transfer (Phillips and others, Reference Phillips, Rajaram and Steffen2010, Reference Phillips, Rajaram, Colgan, Steffen and Abdalati2013) may be able to better constrain this threshold. While we cannot confirm our hypothesis with our present model, additional borehole temperature measurements or more sophisticated modelling could test our residence time hypothesis.
6.4. Context for field measurements of cryo-hydrologic warming
Given the continuum of warmth observed in boreholes in Pâkitsoq and on other land-terminating ice (Harrington and others, Reference Harrington, Humphrey and Harper2015), it seems unlikely that englacial latent-heat transfer through surface crevasses has begun recently or that a sudden transition has occurred. Our results suggest that englacial temperatures are in equilibrium with a surface meltwater supply that has regularly reached up to ~300 m depth and has been operating continuously over the past few thousands of years. Although englacial latent-heat transfer may migrate to higher elevations over time, our results at the TD5 borehole suggest that the effect largely will be limited to the upper ice column, where warming has little influence on flow (Ryser and others, Reference Ryser2014a; Lüthi and others, Reference Lüthi2015).
Our conclusion of near-equilibrium englacial temperatures contrasts with that of Phillips and others (Reference Phillips, Rajaram, Colgan, Steffen and Abdalati2013), who identified a recent rapid increase in englacial latent-heat transfer as evidenced by the apparent acceleration of ice motion in western Greenland. Unfortunately, their conclusion was reached through interpreting artefacts in velocity measurements, which have since been corrected (http://nsidc.org/data/docs/measures/nsidc0478_joughin). The updated measurements suggest no such acceleration. This lack of acceleration supports our hypothesis that any recent cryo-hydrologic warming has had little effect on flow.
The influence of cryo-hydrologic warming largely is limited to slow-flowing regions, many of which have divergent flow and mostly lose mass in situ via surface melting rather than by iceberg calving. As it is likely that latent heat from meltwater has been warming this ice over much of the Holocene, the ice sheet should have evolved to have a lower surface slope that would produce balance velocities (including both deformation and sliding) consistent with this warmer, softer ice. Indeed, the shape of the ice sheet in our study area has been in steady state over approximately the past 4000 a (Lecavalier and others, Reference Lecavalier2014), which suggests that the present-day rate of englacial warming has likely been occurring in the lower ablation zone for millennia.
Higher on the ice sheet where the ice is cold, inland migration of the ELA could newly warm and soften the ice, which would modestly (up to ~10%) increase flow speed. Our results suggest that such warming, however, would not have a sudden, catastrophic effect on ice flow, as has sometimes been suggested (Phillips and others, Reference Phillips, Rajaram and Steffen2010). Rather, the upper ice column would warm, but this would have a moderate effect on ice flow and would occur gradually, over decadal or longer timescales. It would take additional decades to centuries to warm the full ice column (Colgan and others, Reference Colgan, Sommers, Rajaram and Abdalati2015), and over these timescales, other influences on ice flow are likely to have a larger effect (e.g., ice-sheet thinning directly due to surface melt).
6.5. Ice-sheet-wide interpretation
Central western Greenland hosts a considerable amount of land-terminating ice that spends hundreds of years in the ablation zone: ~50% by area, as shown in Figure 8a. Surface ablation, as opposed to outlet glacier calving, is the primary control on mass balance in these areas. We compare the concentration of such ice in central western Greenland to other regions of the ice sheet. Figure 8b shows the time elapsed since crossing the ELA for ice over all of Greenland. Like Figure 8a, this map highlights areas where significant cryo-hydrologic warming likely occurs viz. a long tenure in the ablation zone. The largest such area is our study area in central western Greenland (20 000 km2), but ice in certain pockets of northern and north-eastern Greenland (~5000 km2 each) spends thousands of years in the ablation zone before ultimately ablating. These pockets, located near Humboldt Glacier (t ELA ~2000 a) and Nioghalvfjerdsfjorden (t ELA ~8000 a), are particular examples where surface melt is the dominant mode of ice loss. Elsewhere in Greenland, especially along its east and west coasts, outlet glacier calving, characterised by short t ELA (<~250 a), is the primary ice loss mechanism, so that cryo-hydrologic warming likely has little influence.
Figure 8b does not give a complete picture of the effects of melt. For example, south-eastern Greenland experiences similar annual melt rates to central western Greenland. High snowfall rates there make the net SMB positive (Ettema and others, Reference Ettema2009; van Angelen and others, Reference van Angelen, van den Broeke, Wouters and Lenaerts2013), however, causing it not to appear on the map, which only includes areas below the ELA. Field evidence and remote-sensing data indicate that meltwater in these areas is stored in aquifers within the firn (Forster and others, Reference Forster2013), although it remains unclear whether such water may enter sub-surface crevasses.
7. CONCLUSION
Our model incorporates a computationally inexpensive parameterisation of firn thermal processes into its surface boundary condition. Our results suggest that this greatly improves estimates of englacial temperatures, particularly in areas of fast-moving ice.
Our model also shows that in certain areas, englacial refreezing of surface meltwater can substantially increase ice temperatures at depth, which can translate to a substantial increase in softness. Our results in the Pâkitsoq area show that although considerable englacial refreezing is increasing ice temperatures by as much as ~10°C, the effect on ice flow is small (<10%) because this effect largely occurs in the upper ice column.
Furthermore, our study of ice flux suggests that divergent, slow-flowing areas, where such englacial warming is likely to occur, are only modest contributors to outlet glacier calving. This is because most of the ice flux across the central western Greenland ELA (~63%) occurs through laterally convergent ice that moves too quickly through the ablation zone to experience appreciable cryo-hydrologic warming. This region represents the area of Greenland with greatest vulnerability to cryo-hydrologic warming, due to its large extent of land-terminating ice that spends many hundreds of years in the ablation zone. Thus, we conclude that cryo-hydrologic warming likely does not pose a significant threat to the stability of the Greenland ice sheet.
ACKNOWLEDGEMENTS
This material is based upon work supported by the National Science Foundation Graduate Research Fellowship Program under Grant No. DGE-0718124 (K.P.) and through CReSIS (NSF ANT-0424589, I.J. and K.P.). The Polar Program of the Netherlands Organisation for Scientific Research and the Netherlands Earth System Science Center (NESSC) supported J.T.M.L. and M.R.v.d.B. We are grateful to Michelle Koutnik, Ben Smith and Ed Waddington for helpful comments on drafts of this manuscript and to Martin Lüthi and two anonymous reviewers for their insightful and constructive criticism of this work.
Open access
