The function remdup (also called mkset in some functional languages) removes duplicates from a given list. The following definition of remdup is standard and leads to a quadratic time algorithm

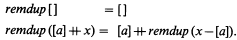
The operator (—) used in the last expression subtracts one list from another; its definition is

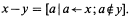
Defined in this way remdup x returns the list of distinct elements of x in the order in which they first appear in x. In other words, the position of remdup JC as a subsequence of x is lexically the smallest among all possible solutions.

Now let us change the problem and ask that remdup simply return the lexically least solution. Note the subtle difference between this version and the previous one: before, it was the position of the subsequence that was lexically the least, now it is the subsequence itself. To make the distinction clear, consider x = [1,4,2,4,3]. With the original definition remdup x returns [1,4,2,3]; the lexically least subsequence, however, is [1,2,4,3].

The question we are interested in is this: can we also find a quadratic time algorithm for the new problem? The answer turns out to be yes, but justifying it requires a bit of work.