Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T03:30:22.976Z Has data issue: false hasContentIssue false
  • English
  • Français

OPTIMAL MIXING OF MARKOV DECISION RULES FOR MDP CONTROL

Published online by Cambridge University Press:  17 May 2011

Dinard van der Laan
Dinard van der Laan
Affiliation:
Tinbergen Institute and Department of Econometrics and Operations Research, VU University, De Boelelaan 1105, 1081 HV Amsterdam, The Netherlands E-mail: dalaan@feweb.vu.nl
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article we study Markov decision process (MDP) problems with the restriction that at decision epochs, only a finite number of given Markov decision rules are admissible. For example, the set of admissible Markov decision rules 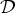could consist of some easy-implementable decision rules. Additionally, many open-loop control problems can be modeled as an MDP with such a restriction on the admissible decision rules. Within the class of available policies, optimal policies are generally nonstationary and it is difficult to prove that some policy is optimal. We give an example with two admissible decision rules—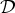={d1, d2} —for which we conjecture that the nonstationary periodic Markov policy determined by its period cycle (d1, d1, d2, d1, d2, d1, d2, d1, d2) is optimal. This conjecture is supported by results that we obtain on the structure of optimal 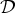Markov policies in general. We also present some numerical results that give additional confirmation for the conjecture for the particular example we consider.

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 25 , Issue 3 , July 2011 , pp. 307 - 342
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1.Altman, B., Gaujal, E. & Hordijk, A. (2003). Discrete-event control of stochastic networks: Multimodularity and regularity. Lecture Notes in Mathematics. New York: Springer Verlag.CrossRefGoogle Scholar
2.Altman, E., Gaujal, B. & Hordijk, A. (2000). Balanced sequences and optimal routing. Journal of the ACM 47: 752–775.CrossRefGoogle Scholar
3.Altman, E., Gaujal, B. & Hordijk, A. (2000). Multimodularity, convexity and optimization properties. Mathematics of Operations Research 25: 324–347.CrossRefGoogle Scholar
4.Altman, E., Gaujal, B., Hordijk, A. & Koole, G. (1998) Optimal admission, routing and service assignment control: the case of single buffer queues. In the 37th IEEE Conference on Decision and Control, Tampa, FL, Vol. 2, pp. 2119–2124.CrossRefGoogle Scholar
5.Altman, E. & Shwartz, A. (1991). Markov decision problems and state-action frequencies. SIAM Journal on Control and Optimization 29: 786–809.CrossRefGoogle Scholar
6.Bhulai, S., Farenhorst-Yuan, T., Heidergott, B. & van der Laan, D.A. (2010). Optimal balanced control for call centers. Technical report, Tinbergen Institute.CrossRefGoogle Scholar
7.Cao, X.R. (1998). The MacLaurin series for performance functions of Markov chains. Advances in Applied Probability 30: 676–692.CrossRefGoogle Scholar
8.Fernández-Gaucherand, E., Araposthathis, A. & Marcus, S.I. (1991). On the average cost optimality equation and the structure of optimal policies for partially observable Markov decision processes. Annals of Operations Research 29: 439–470.CrossRefGoogle Scholar
9.Fernández-Gaucherand, E., Araposthathis, A. & Marcus, S.I. (1991). Remarks on the existence of solutions to the average cost optimality equation in Markov decision processes. Systems and Control Letters 15: 425–432.CrossRefGoogle Scholar
10.Gaujal, B., Hordijk, A. & van der Laan, D.A. (2007). On the optimal policy for deterministic and exponential polling systems. Probability in the Engineering and Informational Sciences 21: 157–187.CrossRefGoogle Scholar
11.Hajek, B. (1985). Extremal splittings of point processes. Mathematics of Operations Research 10(4): 543–556.CrossRefGoogle Scholar
12.Heidergott, B. & Hordijk, A. (2003). Taylor series expansions for stationary Markov chains. Advances in Applied Probability 35: 1046–1070.CrossRefGoogle Scholar
13.Heidergott, B. & Vázquez-Abad, F. (2008). Measure valued differentiation for Markov chains. Journal of Optimization and Applications 136: 187–209.CrossRefGoogle Scholar
14.Heidergott, B., Vázquez-Abad, F.J., Pflug, G. & Farenhorst-Yuan, T. (2010). Gradient estimation for discrete-event systems by measure-valued differentiation. ACM Transactions on Modeling and Computer Simulation (TOMACS) 20: 1–28.CrossRefGoogle Scholar
15.Hernández-Lerma, O. & Lasserre, J.B. (1996). Discrete-time Markov control processes: Basic optimality criteria. New York: Springer.CrossRefGoogle Scholar
16.Hordijk, A. & van der Laan, D.A. (2005). On the average waiting time for regular routing to deterministic queues. Mathematics of Operations Research 30: 521–544.CrossRefGoogle Scholar
17.Koole, G. (1999). On the static assignment to parallel servers. IEEE Transactions on Automatic Control 44: 1588–1592.CrossRefGoogle Scholar
18.Lothaire, M. (2002). Algebraic combinatorics on words. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
19.MacPhee, I.M. & Jordan, B.P. (1995). Optimal search for a moving target. Probability in the Engineering and Informational Sciences 9: 159–182.CrossRefGoogle Scholar
20.Morse, M. & Hedlund, G.A. (1940). Symbolic dynamics II — sturmian trajectories. American Journal of Mathematics 62: 1–42.CrossRefGoogle Scholar
21.Pflug, G.C. (1996). Optimization of stochastic models. Amsterdam: Kluwer Academic.CrossRefGoogle Scholar
22.Puterman, M. (1994). Markov decision processes: Discrete stochastic dynamic programming. New York: John Wiley and Sons.CrossRefGoogle Scholar
23.Ross, K.W. (1989). Randomized and past-dependent policies for Markov decision processes with multiple constraints. Operations Research 37: 474–477.CrossRefGoogle Scholar
24.Ross, S.M. (1983). Introduction to stochastic dynamic programming. New York: Academic Press.Google Scholar
25.Tijdeman, R. (2000). Fraenkel's conjecture for six sequences. Discrete Mathematics 222: 223–234.CrossRefGoogle Scholar