Article contents
Weyl chamber length compactification of the 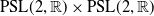 $\textrm{PSL}(2,{\mathbb{R}})\times \textrm{PSL}(2,{\mathbb{R}})$ maximal character variety
$\textrm{PSL}(2,{\mathbb{R}})\times \textrm{PSL}(2,{\mathbb{R}})$ maximal character variety
Published online by Cambridge University Press: 27 September 2024
Abstract
We study the vectorial length compactification of the space of conjugacy classes of maximal representations of the fundamental group  $\Gamma$ of a closed hyperbolic surface
$\Gamma$ of a closed hyperbolic surface 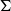 $\Sigma$ in
$\Sigma$ in 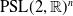 $\textrm{PSL}(2,{\mathbb{R}})^n$. We identify the boundary with the sphere
$\textrm{PSL}(2,{\mathbb{R}})^n$. We identify the boundary with the sphere  ${\mathbb{P}}(({\mathcal{ML}})^n)$, where
${\mathbb{P}}(({\mathcal{ML}})^n)$, where 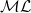 $\mathcal{ML}$ is the space of measured geodesic laminations on
$\mathcal{ML}$ is the space of measured geodesic laminations on 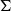 $\Sigma$. In the case
$\Sigma$. In the case 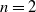 $n=2$, we give a geometric interpretation of the boundary as the space of homothety classes of
$n=2$, we give a geometric interpretation of the boundary as the space of homothety classes of 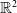 ${\mathbb{R}}^2$-mixed structures on
${\mathbb{R}}^2$-mixed structures on 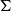 $\Sigma$. We associate to such a structure a dual tree-graded space endowed with an
$\Sigma$. We associate to such a structure a dual tree-graded space endowed with an 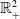 ${\mathbb{R}}_+^2$-valued metric, which we show to be universal with respect to actions on products of two
${\mathbb{R}}_+^2$-valued metric, which we show to be universal with respect to actions on products of two 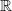 $\mathbb{R}$-trees with the given length spectrum.
$\mathbb{R}$-trees with the given length spectrum.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust
References
- 1
- Cited by


