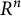1 Introduction
The notion of projectively flat metrics in Finsler geometry originated from the famous Hilbert’s fourth problem, that is, to characterize Finsler metrics on an open subset of
![]() $\mathbf {R}^n$
whose geodesics are straight lines as sets of points. By Beltrami’s theorem, a Riemannian metric is locally projectively flat if and only if it is of constant sectional curvature. However, things are much more complicated in Finsler geometry. Although every locally projectively flat Finsler metric is of scalar flag curvature, many are not of constant flag curvature [Reference Huang and Mo5, Reference Song and Zhou12]. There are also Finsler metrics of scalar flag curvature but are not locally projectively flat. Therefore, the study of locally projectively flat metrics is of its own interest. The characterization of locally projectively flat Finsler metrics dates back to Hamel’s work [Reference Hamel4] at the beginning of 20th century. In recent years, many more explicit constructions have been found for special types of Finsler metrics. For example, a Randers metric
$\mathbf {R}^n$
whose geodesics are straight lines as sets of points. By Beltrami’s theorem, a Riemannian metric is locally projectively flat if and only if it is of constant sectional curvature. However, things are much more complicated in Finsler geometry. Although every locally projectively flat Finsler metric is of scalar flag curvature, many are not of constant flag curvature [Reference Huang and Mo5, Reference Song and Zhou12]. There are also Finsler metrics of scalar flag curvature but are not locally projectively flat. Therefore, the study of locally projectively flat metrics is of its own interest. The characterization of locally projectively flat Finsler metrics dates back to Hamel’s work [Reference Hamel4] at the beginning of 20th century. In recent years, many more explicit constructions have been found for special types of Finsler metrics. For example, a Randers metric
![]() $F = \alpha + \beta $
is locally projectively flat if and only if
$F = \alpha + \beta $
is locally projectively flat if and only if
![]() $\alpha $
is a locally projectively flat Riemannian metric and
$\alpha $
is a locally projectively flat Riemannian metric and
![]() $\beta $
is a closed one-form [Reference Báscó and Matsumoto1]. Locally projectively flat
$\beta $
is a closed one-form [Reference Báscó and Matsumoto1]. Locally projectively flat
![]() $(\alpha , \beta )$
metrics [Reference Shen10] and general
$(\alpha , \beta )$
metrics [Reference Shen10] and general
![]() $(\alpha ,\beta )$
metrics are also studied intensively. In [Reference Yu and Zhu14], Yu and Zhu constructed a class of locally projectively flat general
$(\alpha ,\beta )$
metrics are also studied intensively. In [Reference Yu and Zhu14], Yu and Zhu constructed a class of locally projectively flat general
![]() $(\alpha ,\beta )$
metrics. In [Reference Li and Shen6], the first author and Li gave the equivalent conditions for a general
$(\alpha ,\beta )$
metrics. In [Reference Li and Shen6], the first author and Li gave the equivalent conditions for a general
![]() $(\alpha , \beta )$
metrics to be locally projectively flat, and constructed some interesting local examples.
$(\alpha , \beta )$
metrics to be locally projectively flat, and constructed some interesting local examples.
Every Finsler metric induces a spray via geodesics. The study of sprays on a manifold will lead to a better understanding on Finsler metrics. The notion of projective flatness can be extended naturally to sprays. We would like to know any topological obstruction to the existence of locally projectively flat sprays on a manifold.
Theorem 1.1 Let G be a locally projectively flat spray on a n-manifold M. Then the Pontrjagin classes
![]() $p_k$
of M with rational coefficients are all zero for
$p_k$
of M with rational coefficients are all zero for
![]() $k\ne 0$
.
$k\ne 0$
.
This gives a topological obstruction to the existence of locally projectively flat sprays on a manifold.
Example 1.2 It is well known that spheres have trivial Pontrjagin classes. The standard Riemannian metric
![]() $g_{\mathbf {S}^n}$
on an n-dimensional unit sphere has constant sectional curvature
$g_{\mathbf {S}^n}$
on an n-dimensional unit sphere has constant sectional curvature
![]() $1$
, hence is locally projectively flat. Let
$1$
, hence is locally projectively flat. Let
![]() $G_0$
be the spray of this metric, a family of locally projectively flat sprays can be constructed using positively homogeneous functions P on the slit tangent bundle
$G_0$
be the spray of this metric, a family of locally projectively flat sprays can be constructed using positively homogeneous functions P on the slit tangent bundle
![]() $T\mathbf {S}^n{\,\setminus\,} 0$
. See Section 5 for more detailed constructions.
$T\mathbf {S}^n{\,\setminus\,} 0$
. See Section 5 for more detailed constructions.
Example 1.3 The cohomology of the complex projective space
![]() $\mathbf {C}P^n$
with coefficient G is
$\mathbf {C}P^n$
with coefficient G is
 $$\begin{align*}H^l(\mathbf{C}P^n,G) = \begin{cases} G, & \text{if }l\text{ is even and }0 \le l \le n, \\ 0, & \text{otherwise,}\end{cases} \end{align*}$$
$$\begin{align*}H^l(\mathbf{C}P^n,G) = \begin{cases} G, & \text{if }l\text{ is even and }0 \le l \le n, \\ 0, & \text{otherwise,}\end{cases} \end{align*}$$
and the total Pontrjagin class of
![]() $\mathbf {C}P^n$
is
$\mathbf {C}P^n$
is
![]() $p = (1+c^2)^{n+1}$
, where c is the image of the generator of
$p = (1+c^2)^{n+1}$
, where c is the image of the generator of
![]() $H^2(\mathbf {C}P^n,\mathbf {Z})$
under the natural map
$H^2(\mathbf {C}P^n,\mathbf {Z})$
under the natural map
![]() $H^2(\mathbf {C}P^n,\mathbf {Z}) \to H^2(\mathbf {C}P^n,G)$
. In particular, the Pontrjagin classes of
$H^2(\mathbf {C}P^n,\mathbf {Z}) \to H^2(\mathbf {C}P^n,G)$
. In particular, the Pontrjagin classes of
![]() $\mathbf {C}P^n(n\ge 2)$
are not zero, hence
$\mathbf {C}P^n(n\ge 2)$
are not zero, hence
![]() $\mathbf {C}P^n(n\ge 2)$
does not admit a locally projectively flat spray.
$\mathbf {C}P^n(n\ge 2)$
does not admit a locally projectively flat spray.
2 Preliminaries
A spray G on a manifold M is a smooth vector field on the slit tangent bundle
![]() $TM{\,\setminus\,} 0$
expressed in a standard local coordinate system
$TM{\,\setminus\,} 0$
expressed in a standard local coordinate system
![]() $(x^i, y^i)$
on
$(x^i, y^i)$
on
![]() $TM$
as
$TM$
as
 $$ \begin{align} G = y^i \frac\partial{\partial x^i} - 2G^i(x,y)\frac\partial{\partial y^i}, \end{align} $$
$$ \begin{align} G = y^i \frac\partial{\partial x^i} - 2G^i(x,y)\frac\partial{\partial y^i}, \end{align} $$
where
![]() $G^i(y)$
are local functions on
$G^i(y)$
are local functions on
![]() $TM$
satisfying
$TM$
satisfying
for all
![]() $\lambda> 0$
. The
$\lambda> 0$
. The
![]() $G^i$
s are also called the spray coefficients.
$G^i$
s are also called the spray coefficients.
Let
![]() $\tilde {\gamma }$
be an integral curve of G on
$\tilde {\gamma }$
be an integral curve of G on
![]() $TM{\,\setminus\,} 0$
, and
$TM{\,\setminus\,} 0$
, and
![]() $\gamma = \pi \circ \tilde {\gamma }$
be its projection on M, where
$\gamma = \pi \circ \tilde {\gamma }$
be its projection on M, where
![]() $\pi : TM{\,\setminus\,} 0\to M$
is the canonical projection.
$\pi : TM{\,\setminus\,} 0\to M$
is the canonical projection.
![]() $\gamma $
satisfies the equation
$\gamma $
satisfies the equation
and it is called a geodesic of G. We say that two sprays G and
![]() $\tilde {G}$
are (pointwise) projectively related if their geodesics are the same as sets of points on the manifold. Equivalently, this is characterized by the condition
$\tilde {G}$
are (pointwise) projectively related if their geodesics are the same as sets of points on the manifold. Equivalently, this is characterized by the condition
where
![]() $P = P(x,y)$
satisfies the homogeneity property
$P = P(x,y)$
satisfies the homogeneity property
for
![]() $\lambda> 0$
. A spray G is said to be flat if at every point, there is a local coordinate system in which
$\lambda> 0$
. A spray G is said to be flat if at every point, there is a local coordinate system in which
It is said to be locally projectively flat if it is projectively related to a flat spray. A quantity is said to be projectively invariant if it is the same for projectively related sprays.
In order to study the Pontrjagin classes of
![]() $\pi ^*TM$
and
$\pi ^*TM$
and
![]() $TM$
, we shall use the Berwald connection on the pullback bundle
$TM$
, we shall use the Berwald connection on the pullback bundle
![]() $\pi ^*TM$
. Let
$\pi ^*TM$
. Let
 $$\begin{align*}N^i_j := \frac{\partial G^i}{\partial y^j}, \quad\Gamma^i_{jk} := \frac{\partial^2 G^i}{\partial y^j\partial y^k}, \end{align*}$$
$$\begin{align*}N^i_j := \frac{\partial G^i}{\partial y^j}, \quad\Gamma^i_{jk} := \frac{\partial^2 G^i}{\partial y^j\partial y^k}, \end{align*}$$
the local connection one-forms of the Berwald connection are given by
and its curvature forms are
Put
![]() $\omega ^i := dx^i$
and
$\omega ^i := dx^i$
and
![]() $\omega ^{n+i} := dy^i + N^i_jdx^j$
, we have
$\omega ^{n+i} := dy^i + N^i_jdx^j$
, we have
and
where R is the Riemann curvature and B is the Berwald curvature. In local coordinates, they are given by
 $$ \begin{align*} &R_{j\;kl}^{\;i} = \frac{\delta\Gamma^i_{jl}}{\delta x^k} - \frac{\delta\Gamma^i_{jk}}{\delta x^l} + \Gamma^i_{km}\Gamma^m_{jl} - \Gamma^i_{lm}\Gamma^m_{jk}, \\ &B_{j\;kl}^{\;i} = \frac{\partial^3G^i}{\partial y^j\partial y^k\partial y^l}, \end{align*} $$
$$ \begin{align*} &R_{j\;kl}^{\;i} = \frac{\delta\Gamma^i_{jl}}{\delta x^k} - \frac{\delta\Gamma^i_{jk}}{\delta x^l} + \Gamma^i_{km}\Gamma^m_{jl} - \Gamma^i_{lm}\Gamma^m_{jk}, \\ &B_{j\;kl}^{\;i} = \frac{\partial^3G^i}{\partial y^j\partial y^k\partial y^l}, \end{align*} $$
where
![]() $\frac {\delta }{\delta x^i} = \frac {\partial }{\partial x^i} - N^j_i\frac {\partial }{\partial y^j}$
is the horizontal covariant derivative. For the simplicity of notation, we will denote
$\frac {\delta }{\delta x^i} = \frac {\partial }{\partial x^i} - N^j_i\frac {\partial }{\partial y^j}$
is the horizontal covariant derivative. For the simplicity of notation, we will denote
![]() $A^*_{\;*|j} = \frac {\delta }{\delta x^j}A^*_{\;*}$
and
$A^*_{\;*|j} = \frac {\delta }{\delta x^j}A^*_{\;*}$
and
![]() $A^*_{\;*\cdot j} = \frac {\partial }{\partial y^j}A^*_{\;*}$
.
$A^*_{\;*\cdot j} = \frac {\partial }{\partial y^j}A^*_{\;*}$
.
The two-index Riemannian curvature tensor is then given by
![]() $R^i_{\;k} = R^{\;i}_{j\;kl}y^jy^l$
. We have
$R^i_{\;k} = R^{\;i}_{j\;kl}y^jy^l$
. We have
so the two-index Riemann curvature tensor and the four-index Riemann curvature tensor basically contain the same geometric data. The Riemann curvature can be computed directly using the spray coefficients as
 $$ \begin{align} R^i_{\;k} = 2\frac{\partial G^i}{\partial x^k} - y^j\frac{\partial^2G^i}{\partial x^j\partial y^k} + 2G^j\frac{\partial^2G^i}{\partial y^j\partial y^k} - \frac{\partial G^i}{\partial y^j}\frac{\partial G^j}{\partial y^k}. \end{align} $$
$$ \begin{align} R^i_{\;k} = 2\frac{\partial G^i}{\partial x^k} - y^j\frac{\partial^2G^i}{\partial x^j\partial y^k} + 2G^j\frac{\partial^2G^i}{\partial y^j\partial y^k} - \frac{\partial G^i}{\partial y^j}\frac{\partial G^j}{\partial y^k}. \end{align} $$
We will also use
![]() $R = \frac 1{n-1}R^m_{\;m}$
.
$R = \frac 1{n-1}R^m_{\;m}$
.
In the case when G is a Berwald spray, where
![]() $B_{j\;kl}^{\;i} = 0$
, the spray coefficients
$B_{j\;kl}^{\;i} = 0$
, the spray coefficients
![]() $G^i$
s are quadratic in
$G^i$
s are quadratic in
![]() $y^i$
s, and so are the Riemann curvature
$y^i$
s, and so are the Riemann curvature
![]() $R^i_{\;k}$
. In particular,
$R^i_{\;k}$
. In particular,
![]() $\Gamma ^i_{jk}$
and
$\Gamma ^i_{jk}$
and
![]() $R^{\;i}_{j\;kl}$
are independent of
$R^{\;i}_{j\;kl}$
are independent of
![]() $y^i$
s. Therefore, the differential forms
$y^i$
s. Therefore, the differential forms
![]() $\omega ^{\;i}_j$
and
$\omega ^{\;i}_j$
and
![]() $\Omega ^{\;i}_j$
can be viewed as differential forms on M, and the connection can be viewed as a connection of the tangent bundle
$\Omega ^{\;i}_j$
can be viewed as differential forms on M, and the connection can be viewed as a connection of the tangent bundle
![]() $TM$
. In fact, we have
$TM$
. In fact, we have
In dimension
![]() $n \geq 3$
, locally projectively flat sprays are characterized by two projectively invariant quantities. The Douglas curvature is constructed from the Berwald curvature:
$n \geq 3$
, locally projectively flat sprays are characterized by two projectively invariant quantities. The Douglas curvature is constructed from the Berwald curvature:
 $$ \begin{align} D_{j\;kl}^{\;i} = B_{j\;kl}^{\;i} - \frac2{n+1}\left[ E_{jk}\delta^i_l + E_{jl}\delta^i_k + E_{kl}\delta^i_j + \frac{\partial E_{jk}}{\partial y^l}y^i \right]\!, \end{align} $$
$$ \begin{align} D_{j\;kl}^{\;i} = B_{j\;kl}^{\;i} - \frac2{n+1}\left[ E_{jk}\delta^i_l + E_{jl}\delta^i_k + E_{kl}\delta^i_j + \frac{\partial E_{jk}}{\partial y^l}y^i \right]\!, \end{align} $$
where
![]() $E_{ij} =\frac {1}{2} B^{\;m}_{m\;ij}$
is called the mean Berwald curvature.
$E_{ij} =\frac {1}{2} B^{\;m}_{m\;ij}$
is called the mean Berwald curvature.
The Weyl tensor is the spray analog of the projective curvature tensor in Riemannian geometry. It is defined by
 $$ \begin{align} W^i_{\;k} = A^i_{\;k} - \frac1{n+1}\frac{\partial A^m_{\;k}}{\partial y^m}y^i, \end{align} $$
$$ \begin{align} W^i_{\;k} = A^i_{\;k} - \frac1{n+1}\frac{\partial A^m_{\;k}}{\partial y^m}y^i, \end{align} $$
where
![]() $A^i_{\;k} = R^i_{\;k} - R\delta ^i_k$
. The followings are well-known [Reference Shen8].
$A^i_{\;k} = R^i_{\;k} - R\delta ^i_k$
. The followings are well-known [Reference Shen8].
Lemma 2.1 A spray G is of scalar curvature, in the sense that
for some one-form
![]() $\tau $
on
$\tau $
on
![]() $TM{\,\setminus\,} 0$
with
$TM{\,\setminus\,} 0$
with
![]() $\tau _k y^k = R$
, if and only if
$\tau _k y^k = R$
, if and only if
![]() $W = 0$
.
$W = 0$
.
Lemma 2.2 A spray G on a manifold M of dimension
![]() $\ge 3$
is locally projectively flat if and only if
$\ge 3$
is locally projectively flat if and only if
![]() $W = 0$
and
$W = 0$
and
![]() $D = 0$
.
$D = 0$
.
For convenience in discussing the projective change by the S-curvature, we will also use another formula for the Weyl tensor. Let
![]() $dV = \sigma (x)dx^1\wedge \cdots \wedge dx^n$
be a volume form on M, the quantity
$dV = \sigma (x)dx^1\wedge \cdots \wedge dx^n$
be a volume form on M, the quantity
 $$\begin{align*}\tau(x,y) := \ln \frac{\sqrt{\det g_{ij}(x,y)}}{\sigma(x)} \end{align*}$$
$$\begin{align*}\tau(x,y) := \ln \frac{\sqrt{\det g_{ij}(x,y)}}{\sigma(x)} \end{align*}$$
is called the distortion and its rate of change along geodesics is measured by S-curvature. Namely, let
![]() $\gamma (t)$
be a geodesic with
$\gamma (t)$
be a geodesic with
![]() $\gamma (0) = x$
and
$\gamma (0) = x$
and
![]() $\dot {\gamma }(0) = y\in T_xM{\,\setminus\,} 0$
, we have
$\dot {\gamma }(0) = y\in T_xM{\,\setminus\,} 0$
, we have
The S-curvature can be expressed as
 $$\begin{align*}S(x,y) = \frac{\partial G^m}{\partial y^m}(x,y) - y^m\frac{\partial}{\partial x^m}[\ln \sigma ](x) \end{align*}$$
$$\begin{align*}S(x,y) = \frac{\partial G^m}{\partial y^m}(x,y) - y^m\frac{\partial}{\partial x^m}[\ln \sigma ](x) \end{align*}$$
and satisfies the homogeneity property
for
![]() $\lambda> 0$
. The non-Riemannian quantity
$\lambda> 0$
. The non-Riemannian quantity
![]() $\chi $
-curvature
$\chi $
-curvature
relates the S-curvature and the Weyl tensor. Indeed, it can be computed using the S-curvature by
and the Weyl tensor can be expressed as
Thus, for a spray
![]() $(G, dV)$
whose S-curvature is vanishing, we have
$(G, dV)$
whose S-curvature is vanishing, we have
![]() $\chi _k = 0$
and
$\chi _k = 0$
and
3 Pontrjagin classes
The Pontrjagin classes were originally introduced by Lev Pontrjagin in 1940s in the study of the Grassmannian manifolds. In modern texts, it is most often described using the Chern class of a complexified bundle. Let
![]() $\xi $
be a real vector bundle, and let
$\xi $
be a real vector bundle, and let
![]() $\xi _{\mathbf {C}} := \xi \otimes _{\mathbf {R}}\mathbf {C}$
be its complexification, then the ith Pontrjagin class of
$\xi _{\mathbf {C}} := \xi \otimes _{\mathbf {R}}\mathbf {C}$
be its complexification, then the ith Pontrjagin class of
![]() $\xi $
is given by
$\xi $
is given by
where
![]() $c_{j}(\xi _{\mathbf {C}})$
is the jth Chern class of the complex vector bundle
$c_{j}(\xi _{\mathbf {C}})$
is the jth Chern class of the complex vector bundle
![]() $\xi _{\mathbf {C}}$
.
$\xi _{\mathbf {C}}$
.
Using a connection D on the vector bundle
![]() $\xi $
, we can express the Pontrjagin classes of
$\xi $
, we can express the Pontrjagin classes of
![]() $\xi $
as a differential form representing a de Rham cohomology class. Let
$\xi $
as a differential form representing a de Rham cohomology class. Let
![]() $U\subset M$
be an open subset on which there is trivialization
$U\subset M$
be an open subset on which there is trivialization
![]() $\psi : \xi |_U \cong U\times \mathbf {R}^n$
of the bundle
$\psi : \xi |_U \cong U\times \mathbf {R}^n$
of the bundle
![]() $\xi $
, and
$\xi $
, and
![]() $e_i = \psi ^{-1}\partial _i$
. The connection D, viewed as a covariant derivative, can be described by
$e_i = \psi ^{-1}\partial _i$
. The connection D, viewed as a covariant derivative, can be described by
where X is a vector field on U,
![]() $\eta $
is a section of
$\eta $
is a section of
![]() $\xi $
given by
$\xi $
given by
![]() $\eta = \eta ^ie_i$
on U, and the
$\eta = \eta ^ie_i$
on U, and the
![]() $\omega _j^{\;i}$
s are
$\omega _j^{\;i}$
s are
![]() $n^2$
local one-forms on U. The curvature of D is hence described by an
$n^2$
local one-forms on U. The curvature of D is hence described by an
![]() $n\times n$
matrix of (real-valued) two-forms
$n\times n$
matrix of (real-valued) two-forms
where
![]() $\Omega _j^{\;i}$
s are given as in (3). The differential forms
$\Omega _j^{\;i}$
s are given as in (3). The differential forms
![]() $\omega _j^{\;i}$
s and
$\omega _j^{\;i}$
s and
![]() $\Omega _j^{\;i}$
s, viewed as complex-valued forms, define a connection on the complexified bundle
$\Omega _j^{\;i}$
s, viewed as complex-valued forms, define a connection on the complexified bundle
![]() $\xi _{\mathbf {C}}$
and its curvature, which we will still denote by D and
$\xi _{\mathbf {C}}$
and its curvature, which we will still denote by D and
![]() $\Omega $
, respectively.
$\Omega $
, respectively.
Given an
![]() $n\times n$
complex matrix T, we have
$n\times n$
complex matrix T, we have
where
![]() $\sigma _i(T)$
is the ith elementary symmetric polynomial evaluated on the n eigenvalues of T. The following can be found on most textbooks covering characteristic classes (see, for example, [Reference Milnor and Stasheff7]).
$\sigma _i(T)$
is the ith elementary symmetric polynomial evaluated on the n eigenvalues of T. The following can be found on most textbooks covering characteristic classes (see, for example, [Reference Milnor and Stasheff7]).
Theorem 3.1 Let
![]() $\xi $
be a complex vector bundle of rank n with connection D. Then the cohomology class
$\xi $
be a complex vector bundle of rank n with connection D. Then the cohomology class
![]() $[\sigma _r(\Omega )]\in H^{2r}(X;\mathbf {C})$
is equal to
$[\sigma _r(\Omega )]\in H^{2r}(X;\mathbf {C})$
is equal to
![]() $(2\pi i)^rc_r(\xi )$
, for all
$(2\pi i)^rc_r(\xi )$
, for all
![]() $r = 1, \ldots , n$
, where
$r = 1, \ldots , n$
, where
![]() $c_r(\xi )$
is the rth Chern class with coefficient
$c_r(\xi )$
is the rth Chern class with coefficient
![]() $\mathbf {C}$
.
$\mathbf {C}$
.
In the study of Riemannian manifolds of constant curvature, Chern obtained a consequence of this theorem [Reference Chern3, Reference Milnor and Stasheff7].
Corollary 3.2 Let
![]() $\xi $
be a real vector bundle of rank n with connection D. Then the de Rham cocycle
$\xi $
be a real vector bundle of rank n with connection D. Then the de Rham cocycle
![]() $\sigma _{2k}(\Omega )$
represents the cohomology class
$\sigma _{2k}(\Omega )$
represents the cohomology class
![]() $(2\pi )^{2k}p_k(\xi )\in H^{4k}(M;\mathbf {R})$
, while
$(2\pi )^{2k}p_k(\xi )\in H^{4k}(M;\mathbf {R})$
, while
![]() $[\sigma _{2k+1}(\Omega )] = 0$
in
$[\sigma _{2k+1}(\Omega )] = 0$
in
![]() $H^{4k+2}(M;\mathbf {R})$
, where
$H^{4k+2}(M;\mathbf {R})$
, where
![]() $p_k(\xi )$
is the kth Pontrjagin class of
$p_k(\xi )$
is the kth Pontrjagin class of
![]() $\xi $
with coefficient
$\xi $
with coefficient
![]() $\mathbf {R}$
.
$\mathbf {R}$
.
Chern proved the following.
Theorem 3.3 Suppose that for a Riemannian manifold M, the sectional curvature
![]() $K(V_x, W_x)$
of the plane
$K(V_x, W_x)$
of the plane
![]() $\mathrm{span}\{V_x, W_x\}\subset T_xM$
depends on the point
$\mathrm{span}\{V_x, W_x\}\subset T_xM$
depends on the point
![]() $x\in M$
only. Then all its Pontrjagin classes with rational coefficients are zero.
$x\in M$
only. Then all its Pontrjagin classes with rational coefficients are zero.
We shall remark that such manifolds are said to have isotropic curvature in Finsler geometry.
In terms of the local curvature forms
![]() $\Omega _j^{\;i}$
s defined in some neighborhood of
$\Omega _j^{\;i}$
s defined in some neighborhood of
![]() $x\in M$
, a direct computation using (11) gives
$x\in M$
, a direct computation using (11) gives
 $$ \begin{align*} \sigma_{2k}(\Omega)(x) =& \sum_{i_1 < \cdots < i_{2k}, \sigma\in S_{2k}} \operatorname{\mathrm{sign}}{\sigma}\cdot \Omega_{i_1}^{\;i_{\sigma(1)}}(x) \wedge \cdots\wedge \Omega_{i_{2k}}^{\;i_{\sigma(2k)}}(x) \\ =& \dfrac1{(2k)!}\sum_{i_1, \ldots, i_{2k}, \sigma\in S_{2k}}\operatorname{\mathrm{sign}}{\sigma}\cdot \Omega_{i_1}^{\;i_{\sigma(1)}}(x) \wedge \cdots\wedge \Omega_{i_{2k}}^{\;i_{\sigma(2k)}}(x), \end{align*} $$
$$ \begin{align*} \sigma_{2k}(\Omega)(x) =& \sum_{i_1 < \cdots < i_{2k}, \sigma\in S_{2k}} \operatorname{\mathrm{sign}}{\sigma}\cdot \Omega_{i_1}^{\;i_{\sigma(1)}}(x) \wedge \cdots\wedge \Omega_{i_{2k}}^{\;i_{\sigma(2k)}}(x) \\ =& \dfrac1{(2k)!}\sum_{i_1, \ldots, i_{2k}, \sigma\in S_{2k}}\operatorname{\mathrm{sign}}{\sigma}\cdot \Omega_{i_1}^{\;i_{\sigma(1)}}(x) \wedge \cdots\wedge \Omega_{i_{2k}}^{\;i_{\sigma(2k)}}(x), \end{align*} $$
where
![]() $S_{2k}$
is the symmetric group on
$S_{2k}$
is the symmetric group on
![]() $2k$
elements.
$2k$
elements.
4 Pontrjagin classes of Douglas sprays
In this section, we study the Pontrjagin classes of Douglas sprays. The main tool will be a projective change by the S-curvature.
Let G be a spray, and let
![]() $dV$
be a volume form on an n-dimensional manifold M. We define another spray
$dV$
be a volume form on an n-dimensional manifold M. We define another spray
![]() $\hat {G}$
by
$\hat {G}$
by
where S is the S-curvature of
![]() $(G, dV)$
. In the sequel, a letter with a hat over it will always represent a quantity of the spray
$(G, dV)$
. In the sequel, a letter with a hat over it will always represent a quantity of the spray
![]() $\hat {G}$
. We have the following.
$\hat {G}$
. We have the following.
Lemma 4.1 [Reference Shen11]
 $$ \begin{align} \hat{B}_{j\;kl}^{\;i} =& D_{j\;kl}^{\;i}, \nonumber\\ \hat{S} =& 0. \end{align} $$
$$ \begin{align} \hat{B}_{j\;kl}^{\;i} =& D_{j\;kl}^{\;i}, \nonumber\\ \hat{S} =& 0. \end{align} $$
Thus, if G is Douglas, then
![]() $\hat {G}$
is a Berwald spray. As an immediate consequence, we have the following lemma.
$\hat {G}$
is a Berwald spray. As an immediate consequence, we have the following lemma.
Lemma 4.2 Let G be a Douglas spray on a manifold M. The Pontrjagin classes of M with coefficient
![]() $\mathbf {R}$
are represented by the forms
$\mathbf {R}$
are represented by the forms
 $$\begin{align*}\frac1{(4\pi)^{2k}(2k)!}\sum_{i_1, \ldots ,i_{2k}, \sigma\in S_{2k}} \operatorname{\mathrm{sign}} \sigma\cdot \prod_{s=1}^{2k}\hat{R}^{\;i_{\sigma(s)}}_{i_s\;m_sl_l}\bigwedge_{s=1}^{2k}dx^{m_s}\wedge dx^{l_s}, \end{align*}$$
$$\begin{align*}\frac1{(4\pi)^{2k}(2k)!}\sum_{i_1, \ldots ,i_{2k}, \sigma\in S_{2k}} \operatorname{\mathrm{sign}} \sigma\cdot \prod_{s=1}^{2k}\hat{R}^{\;i_{\sigma(s)}}_{i_s\;m_sl_l}\bigwedge_{s=1}^{2k}dx^{m_s}\wedge dx^{l_s}, \end{align*}$$
where
![]() $\hat {R}$
is the Riemann curvature of the associated spray
$\hat {R}$
is the Riemann curvature of the associated spray
![]() $\hat {G}$
.
$\hat {G}$
.
Proof of Theorem 1.1
We will assume that the dimension of the manifold is
![]() $n\ge 4$
, for otherwise, there is nothing to prove. We already have that
$n\ge 4$
, for otherwise, there is nothing to prove. We already have that
![]() $\hat {G}$
is a Berwald spray. On the other hand,
$\hat {G}$
is a Berwald spray. On the other hand,
![]() $\hat {S} = 0$
implies that
$\hat {S} = 0$
implies that
![]() $\hat {\chi }_k = 0$
for the spray
$\hat {\chi }_k = 0$
for the spray
![]() $\hat {G}$
. The expression for the Weyl tensor (10) now becomes
$\hat {G}$
. The expression for the Weyl tensor (10) now becomes
hence
A straightforward calculation yields
It follows that the curvature forms of the Berwald connection of
![]() $\hat {G}$
is given by
$\hat {G}$
is given by
Then
 $$ \begin{align*} \sigma_{2k}(\hat{\Omega}) &= \frac1{(2k!)}\sum_{i_1, \ldots ,i_{2k}, \sigma\in S_{2k}} \operatorname{\mathrm{sign}}{\sigma}\cdot \hat{\Omega}_{i_1}^{\;i_{\sigma(1)}} \wedge \cdots\wedge \hat{\Omega}_{i_{2k}}^{\;i_{\sigma(2k)}} \\ & = \frac{1}{2^{2k}(2k)!} \sum_{i_1, \ldots ,i_{2k}, \sigma\in S_{2k}} \operatorname{\mathrm{sign}}{\sigma} \cdot \hat{R}_{\cdot l_1\cdot i_1} \ldots \hat{R}_{\cdot l_{2k}\cdot i_{2k}} dx^{i_{\sigma(1)}}\wedge dx^{l_1} \ldots dx^{i_{\sigma(2k)}}\wedge dx^{l_{2k}}\\ & = \frac{(-1)^{k}}{2^{2k}(2k)!} \sum_{i_1, \ldots ,i_{2k}, \sigma\in S_{2k}} \operatorname{\mathrm{sign}}\sigma \cdot \hat{R}_{\cdot l_1\cdot i_1} \ldots \hat{R}_{\cdot l_{2k}\cdot i_{2k}} dx^{i_{\sigma(1)}}\wedge\cdots \wedge dx^{i_{\sigma(2k)}}\wedge dx^{l_1}\wedge \cdots \wedge dx^{l_{2k}}\\ & = \frac{(-1)^{k}}{2^{2k}} \sum_{i_1, \ldots ,i_{2k}} \hat{R}_{\cdot l_1\cdot i_1} \ldots \hat{R}_{\cdot l_{2k}\cdot i_{2k}} dx^{i_{1}}\wedge\cdots \wedge dx^{i_{2k}} \wedge dx^{l_1}\wedge \cdots \wedge dx^{l_{2k}}. \end{align*} $$
$$ \begin{align*} \sigma_{2k}(\hat{\Omega}) &= \frac1{(2k!)}\sum_{i_1, \ldots ,i_{2k}, \sigma\in S_{2k}} \operatorname{\mathrm{sign}}{\sigma}\cdot \hat{\Omega}_{i_1}^{\;i_{\sigma(1)}} \wedge \cdots\wedge \hat{\Omega}_{i_{2k}}^{\;i_{\sigma(2k)}} \\ & = \frac{1}{2^{2k}(2k)!} \sum_{i_1, \ldots ,i_{2k}, \sigma\in S_{2k}} \operatorname{\mathrm{sign}}{\sigma} \cdot \hat{R}_{\cdot l_1\cdot i_1} \ldots \hat{R}_{\cdot l_{2k}\cdot i_{2k}} dx^{i_{\sigma(1)}}\wedge dx^{l_1} \ldots dx^{i_{\sigma(2k)}}\wedge dx^{l_{2k}}\\ & = \frac{(-1)^{k}}{2^{2k}(2k)!} \sum_{i_1, \ldots ,i_{2k}, \sigma\in S_{2k}} \operatorname{\mathrm{sign}}\sigma \cdot \hat{R}_{\cdot l_1\cdot i_1} \ldots \hat{R}_{\cdot l_{2k}\cdot i_{2k}} dx^{i_{\sigma(1)}}\wedge\cdots \wedge dx^{i_{\sigma(2k)}}\wedge dx^{l_1}\wedge \cdots \wedge dx^{l_{2k}}\\ & = \frac{(-1)^{k}}{2^{2k}} \sum_{i_1, \ldots ,i_{2k}} \hat{R}_{\cdot l_1\cdot i_1} \ldots \hat{R}_{\cdot l_{2k}\cdot i_{2k}} dx^{i_{1}}\wedge\cdots \wedge dx^{i_{2k}} \wedge dx^{l_1}\wedge \cdots \wedge dx^{l_{2k}}. \end{align*} $$
Since
![]() $\hat {R}_{\cdot i\cdot j} = \hat {R}_{\cdot j\cdot i}$
, we obtain
$\hat {R}_{\cdot i\cdot j} = \hat {R}_{\cdot j\cdot i}$
, we obtain
![]() $0$
after summing over
$0$
after summing over
![]() $i_1$
and
$i_1$
and
![]() $l_1$
. We conclude that
$l_1$
. We conclude that
Since
![]() $\hat {G}$
is Berwald, these curvature forms can be viewed as curvature forms on
$\hat {G}$
is Berwald, these curvature forms can be viewed as curvature forms on
![]() $TM$
. Therefore, the Pontrjagin classes of M with real coefficients are identically zero. It follows from naturality of cohomology in coefficients that the Pontrjagin classes of M with rational coefficients are zero.
$TM$
. Therefore, the Pontrjagin classes of M with real coefficients are identically zero. It follows from naturality of cohomology in coefficients that the Pontrjagin classes of M with rational coefficients are zero.
5 Locally projectively flat sprays on the sphere
In this section, we describe in more detail, some known locally projectively flat sprays on the unit sphere.
Example 5.1 Let
![]() $G_0$
be the spray of the standard Riemannian metric on the unit sphere, and let
$G_0$
be the spray of the standard Riemannian metric on the unit sphere, and let
![]() $P: T\mathbf {S}^n{\,\setminus\,} 0\to \mathbf {R}$
be a smooth function satisfying
$P: T\mathbf {S}^n{\,\setminus\,} 0\to \mathbf {R}$
be a smooth function satisfying
for all
![]() $x\in \mathbf {S}^n$
,
$x\in \mathbf {S}^n$
,
![]() $y\in T_x\mathbf {S}^n{\,\setminus\,} \{0\}$
, and
$y\in T_x\mathbf {S}^n{\,\setminus\,} \{0\}$
, and
![]() $\lambda> 0$
. Then the spray
$\lambda> 0$
. Then the spray
![]() $G_P = G_0 - 2PY$
is locally projectively flat, where Y is the vector field expressed as
$G_P = G_0 - 2PY$
is locally projectively flat, where Y is the vector field expressed as
![]() $y^i\frac {\partial }{\partial x^i}$
in local coordinates
$y^i\frac {\partial }{\partial x^i}$
in local coordinates
![]() $(x^i, y^i)$
for the slit tangent bundle
$(x^i, y^i)$
for the slit tangent bundle
![]() $T\mathbf {S}^n{\,\setminus\,} 0$
.
$T\mathbf {S}^n{\,\setminus\,} 0$
.
Among this family are a collection of sprays induced by Randers metrics
![]() $F(y) = \sqrt {g_{\mathbf {S}^n}(y,y)} + df(y),$
where f is a smooth function on
$F(y) = \sqrt {g_{\mathbf {S}^n}(y,y)} + df(y),$
where f is a smooth function on
![]() $\mathbf {S}^n$
and
$\mathbf {S}^n$
and
![]() $y\in T\mathbf {S}^n{\,\setminus\,} 0$
. In this case, we have
$y\in T\mathbf {S}^n{\,\setminus\,} 0$
. In this case, we have
 $$\begin{align*}P(y) = \dfrac{\operatorname{\mathrm{Hess}} f(y,y)}{2F(y)}. \end{align*}$$
$$\begin{align*}P(y) = \dfrac{\operatorname{\mathrm{Hess}} f(y,y)}{2F(y)}. \end{align*}$$
Example 5.2 According to the characterizations of locally projectively flat general
![]() $(\alpha ,\beta )$
metrics studied in [Reference Li and Shen6, Reference Yu and Zhu14], a general
$(\alpha ,\beta )$
metrics studied in [Reference Li and Shen6, Reference Yu and Zhu14], a general
![]() $(\alpha ,\beta )$
metric
$(\alpha ,\beta )$
metric
![]() $F = \alpha \phi \left (b^2,\frac {\beta }{\alpha } \right )$
is locally projectively flat if
$F = \alpha \phi \left (b^2,\frac {\beta }{\alpha } \right )$
is locally projectively flat if
![]() $\alpha $
is locally projectively flat,
$\alpha $
is locally projectively flat,
![]() $\beta $
is closed and conformal with respect to
$\beta $
is closed and conformal with respect to
![]() $\alpha $
, and
$\alpha $
, and
![]() $\phi = \phi (b^2, s)$
satisfies
$\phi = \phi (b^2, s)$
satisfies
On the sphere
![]() $\mathbf {S}^n$
, let
$\mathbf {S}^n$
, let
![]() $\alpha $
be the standard Riemannian metric of constant sectional curvature
$\alpha $
be the standard Riemannian metric of constant sectional curvature
![]() $1$
, written as
$1$
, written as
where
![]() $r\in [0,\pi ]$
and
$r\in [0,\pi ]$
and
![]() $ds_{n-1}^2$
is the standard Riemannian metric on the
$ds_{n-1}^2$
is the standard Riemannian metric on the
![]() $(n-1)$
-dimensional sphere
$(n-1)$
-dimensional sphere
![]() $\mathbf {S}^{n-1}$
. It is well known that the one-form
$\mathbf {S}^{n-1}$
. It is well known that the one-form
![]() $\beta = \sin rdr$
is closed and conformal with
$\beta = \sin rdr$
is closed and conformal with
Using the example constructed in [Reference Yu and Zhu14], namely
which satisfies the equation (14), we see that the general
![]() $(\alpha ,\beta )$
metric
$(\alpha ,\beta )$
metric
 $$\begin{align*}F(y) = \alpha(y)\left(\sqrt{1+\sin^2r} + \frac{\sin rdr(y)}{\alpha(y)}\right)^2 \end{align*}$$
$$\begin{align*}F(y) = \alpha(y)\left(\sqrt{1+\sin^2r} + \frac{\sin rdr(y)}{\alpha(y)}\right)^2 \end{align*}$$
is locally projective flat with the projective factor
 $$\begin{align*}P(y) = \frac{2\alpha(y)\cos r}{\sqrt{1+\sin^2r}}. \end{align*}$$
$$\begin{align*}P(y) = \frac{2\alpha(y)\cos r}{\sqrt{1+\sin^2r}}. \end{align*}$$
Example 5.3 Another interesting class of locally projectively flat Finsler metrics on the sphere are the Bryant metrics [Reference Bryant, Bao, Chern and Shen2, Reference Shen9]. In gnomonic coordinates, it is given by
 $$\begin{align*}F(y) = \sqrt{\dfrac{\sqrt{A}+B}{2D}+\left(\dfrac{C}{D}\right)^2} + \dfrac{C}{D}, \end{align*}$$
$$\begin{align*}F(y) = \sqrt{\dfrac{\sqrt{A}+B}{2D}+\left(\dfrac{C}{D}\right)^2} + \dfrac{C}{D}, \end{align*}$$
where
 $$ \begin{align*} A =& \left(\cos (2\alpha) {\left|{y}\right|}^2 +\left({\left|{x}\right|}^2{\left|{y}\right|}^2 - \langle x,y\rangle^2\right)\right)^2 + \left(\sin (2\alpha) {\left|{y}\right|}^2\right)^2\!, \\ B =& \cos (2\alpha) {\left|{y}\right|}^2 +\left({\left|{x}\right|}^2{\left|{y}\right|}^2 - \langle x,y\rangle^2\right), \\ C =& \sin (2\alpha) \langle x,y\rangle, \\ D =& {\left|{x}\right|}^4 + 2\cos (2\alpha) {\left|{x}\right|}^2 + 1, \end{align*} $$
$$ \begin{align*} A =& \left(\cos (2\alpha) {\left|{y}\right|}^2 +\left({\left|{x}\right|}^2{\left|{y}\right|}^2 - \langle x,y\rangle^2\right)\right)^2 + \left(\sin (2\alpha) {\left|{y}\right|}^2\right)^2\!, \\ B =& \cos (2\alpha) {\left|{y}\right|}^2 +\left({\left|{x}\right|}^2{\left|{y}\right|}^2 - \langle x,y\rangle^2\right), \\ C =& \sin (2\alpha) \langle x,y\rangle, \\ D =& {\left|{x}\right|}^4 + 2\cos (2\alpha) {\left|{x}\right|}^2 + 1, \end{align*} $$
with
![]() $\langle \cdot ,\cdot \rangle $
being the standard inner product in the Euclidean space
$\langle \cdot ,\cdot \rangle $
being the standard inner product in the Euclidean space
![]() $\mathbf {R}^n$
and
$\mathbf {R}^n$
and
![]() ${\left |{\cdot }\right |}$
being the induced norm. The spray induced by a Bryant metric can also be written in the form
${\left |{\cdot }\right |}$
being the induced norm. The spray induced by a Bryant metric can also be written in the form
![]() $G_0 - 2PY$
, with the function P satisfying
$G_0 - 2PY$
, with the function P satisfying
where
![]() $y\in T\mathbf {S}^n{\,\setminus\,} 0$
and the functions
$y\in T\mathbf {S}^n{\,\setminus\,} 0$
and the functions
![]() $p,q,s$
can be expressed in the gnomonic coordinates as
$p,q,s$
can be expressed in the gnomonic coordinates as
 $$ \begin{align*} p(x) &= \dfrac14\ln \dfrac{1+2\cos(2\alpha) {\left|{x}\right|}^2 + {\left|{x}\right|}^4}{1 + 2{\left|{x}\right|}^2 + {\left|{x}\right|}^4}, \\q(x) &= \dfrac1{2}\tan^{-1}\dfrac{{\left|{x}\right|}^2 + \cos(2\alpha)}{\sin(2\alpha)}, \\s(x) &= s({\left|{x}\right|}^2) = 4(1+{\left|{x}\right|}^2)^2r"({\left|{x}\right|}^2) + 4(1+{\left|{x}\right|}^2)r'({\left|{x}\right|}^2), \end{align*} $$
$$ \begin{align*} p(x) &= \dfrac14\ln \dfrac{1+2\cos(2\alpha) {\left|{x}\right|}^2 + {\left|{x}\right|}^4}{1 + 2{\left|{x}\right|}^2 + {\left|{x}\right|}^4}, \\q(x) &= \dfrac1{2}\tan^{-1}\dfrac{{\left|{x}\right|}^2 + \cos(2\alpha)}{\sin(2\alpha)}, \\s(x) &= s({\left|{x}\right|}^2) = 4(1+{\left|{x}\right|}^2)^2r"({\left|{x}\right|}^2) + 4(1+{\left|{x}\right|}^2)r'({\left|{x}\right|}^2), \end{align*} $$
and
![]() $r = r({\left |{x}\right |}^2)$
satisfies the differential equation
$r = r({\left |{x}\right |}^2)$
satisfies the differential equation
 $$ \begin{align} 4r"({\left|{x}\right|}^2)(1+{\left|{x}\right|}^2) + 6r'({\left|{x}\right|}^2) = \dfrac{\sin(2\alpha)}{2(1+2\cos(2\alpha){\left|{x}\right|}^2 + {\left|{x}\right|}^4)}. \end{align} $$
$$ \begin{align} 4r"({\left|{x}\right|}^2)(1+{\left|{x}\right|}^2) + 6r'({\left|{x}\right|}^2) = \dfrac{\sin(2\alpha)}{2(1+2\cos(2\alpha){\left|{x}\right|}^2 + {\left|{x}\right|}^4)}. \end{align} $$
One may check that these functions are indeed smooth on the whole sphere as follows. Let
![]() $\varphi $
be the inclination angle in the spherical coordinate. Since the Bryant metrics are invariant under vertical reflection
$\varphi $
be the inclination angle in the spherical coordinate. Since the Bryant metrics are invariant under vertical reflection
![]() $\varphi \mapsto \pi - \varphi $
, it suffices to check that these functions extend to even smooth functions in
$\varphi \mapsto \pi - \varphi $
, it suffices to check that these functions extend to even smooth functions in
![]() $u = 1/\tan \varphi = 1/{\left |{x}\right |}$
. For p and q, this is clear. For s, we have
$u = 1/\tan \varphi = 1/{\left |{x}\right |}$
. For p and q, this is clear. For s, we have
so s is even and smooth as long as r is. Finally, the differential equation (15) reads
 $$\begin{align*}(1+u^2)\dfrac{d^2r}{du^2} + 3u\dfrac{dr}{du} = \dfrac{\sin (2\alpha)}{2(1 + 2\cos(2\alpha)u^2 + u^4)}. \end{align*}$$
$$\begin{align*}(1+u^2)\dfrac{d^2r}{du^2} + 3u\dfrac{dr}{du} = \dfrac{\sin (2\alpha)}{2(1 + 2\cos(2\alpha)u^2 + u^4)}. \end{align*}$$
Note that it can be written as
 $$\begin{align*}\dfrac{d}{du}\begin{pmatrix} \dot{r} \\ r \end{pmatrix} = f(u,r,\dot{r}) := \begin{pmatrix} \dfrac{3u}{1+u^2}\dot{r} \\ \dot{r} \end{pmatrix} + \begin{pmatrix} \dfrac{\sin (2\alpha)}{2(1 + 2\cos(2\alpha)u^2 + u^4)(1+u^2)} \\ 0 \end{pmatrix}. \end{align*}$$
$$\begin{align*}\dfrac{d}{du}\begin{pmatrix} \dot{r} \\ r \end{pmatrix} = f(u,r,\dot{r}) := \begin{pmatrix} \dfrac{3u}{1+u^2}\dot{r} \\ \dot{r} \end{pmatrix} + \begin{pmatrix} \dfrac{\sin (2\alpha)}{2(1 + 2\cos(2\alpha)u^2 + u^4)(1+u^2)} \\ 0 \end{pmatrix}. \end{align*}$$
Since f is uniformly Lipschitz in
![]() $(r,\dot {r})$
for all
$(r,\dot {r})$
for all
![]() $u\in \mathbf {R}$
, an improved Picard–Lindelöf theorem (see, e.g., [Reference Teschl13]) implies the existence of an even solution for all
$u\in \mathbf {R}$
, an improved Picard–Lindelöf theorem (see, e.g., [Reference Teschl13]) implies the existence of an even solution for all
![]() $u\in \mathbf {R}$
. The solution is smooth since f is smooth. Another application of the theorem to the original equation (15) shows that this solution extends smoothly to the north and south poles of the sphere.
$u\in \mathbf {R}$
. The solution is smooth since f is smooth. Another application of the theorem to the original equation (15) shows that this solution extends smoothly to the north and south poles of the sphere.