1 Introduction
First introduced in the 1970s (Green and Rao Reference Green and Rao1971; Jasso and Rossi Reference Jasso and Rossi1977), conjoint experiments ask survey respondents to rate or rank profiles which vary across multiple dimensions. This research design has critical strengths: It allows researchers to make causal inferences about a variety of potentially relevant attributes simultaneously, and so to compare the treatment effects of various attributes (Hainmueller, Hopkins, and Yamamoto Reference Hainmueller, Hopkins and Yamamoto2014). Conjoint designs also mirror many real-world choices in which people must evaluate bundles of attributes, which can greatly enhance their external validity (Hainmueller, Hangartner, and Yamamoto Reference Hainmueller, Hangartner and Yamamoto2015). These characteristics, together with the increasing number of surveys administered via computers, have led to a surge in the use of conjoint designs in political science. Conjoint designs are now being used to answer far-ranging questions, including those about where people choose to live, whom they wish to admit to their countries, and which political candidates they support.Footnote 1
While research proceeds on the statistical properties of conjoint designs (Raghavarao, Wiley, and Chitturi Reference Raghavarao, Wiley and Chitturi2011; Hainmueller, Hopkins, and Yamamoto Reference Hainmueller, Hopkins and Yamamoto2014; Egami and Imai Reference Egami and Imai2015; Acharya, Blackwell, and Sen Reference Acharya, Blackwell and Sen2016), there has been little attention on how to optimize conjoint survey designs given well-known challenges in survey research. Here, we integrate research on survey design with work on conjoint experiments to examine a central design question facing those fielding conjoint experiments: How many conjoint tasks can respondents perform with the needed levels of attention?
Underlying the question is the threat of survey satisficing. Research on survey taking indicates that as survey tasks become more onerous, respondents become increasingly likely to satisfice, meaning that they adapt by using cognitive shortcuts which can degrade response quality (Krosnick Reference Krosnick1999).Footnote 2 Satisficing respondents are more likely to rush through surveys, ignore or skip instructions, choose response options because of their placement, and use other effort-saving heuristics (Berinsky, Margolis, and Sances Reference Berinsky, Margolis and Sances2014).
In this paper, we conduct a series of conjoint survey experiments to empirically examine the degree of satisficing when respondents are faced with a large number of choice tasks. In our experiments, we ask respondents to complete many more tasks than in a typical conjoint study and estimate the degree of degradation in response quality over those tasks. Specifically, respondents are asked to evaluate as many as 30 conjoint tables, where the tables are comprised of two core attributes that are included for all respondents and two to 18 additional attributes that are randomly assigned for each respondent. We find that conjoint designs are remarkably robust as a tool for eliciting preferences about multidimensional objects. Using samples from two common online sources of survey respondents—Amazon’s Mechanical Turk (MT) and Survey Sampling International (SSI)—we see no significant decline in the core attributes’ effects as the number of tasks increases.
2 Problem: Satisficing in Conjoint Experiments
Conjoint experiments are one variant of survey research, meaning that many insights about survey design generally should apply. However, the growing research on conjoint surveys has not yet incorporated the insights of the highly developed literature on survey measurement (e.g. Groves et al. Reference Groves, Fowler, Couper, Lepkowski, Singer and Tourangeau2011). Here, we focus on the issue of survey satisficing and how it might undermine conjoint experiments.
A key element of conjoint designs that has the potential to increase satisficing beyond acceptable levels is the number of discrete evaluation tasks requested of respondents. Should respondents perform just one evaluation in a given survey, or should they be asked to perform 5, 10, or even 50? Conjoint experiments typically require respondents to complete the same task repeatedly. In fact, in traditional conjoint designs, respondents are often asked to evaluate the entire set of possible combinations from an orthogonalized array of attribute levels, a number which can easily grow above 50 (Raghavarao, Wiley, and Chitturi Reference Raghavarao, Wiley and Chitturi2011). While fully randomized designs allow researchers more discretion in choosing the number of tasks, researchers still have an incentive to assign numerous tasks so as to increase their statistical power.
However, research on survey response indicates that satisficing is likely to be a function of the total survey length. For example, Galesic and Bosnjak (Reference Galesic and Bosnjak2009) find that when answering questions placed later in a questionnaire, respondents take less time and provide more uniform answers. Similarly, respondents are more likely to give the same response to blocks of questions when those questions are found later in a questionnaire (Herzog and Bachman Reference Herzog and Bachman1981), another indication of increased satisficing. Findings like these fuel the “longstanding view that long questionnaires or interviews should be avoided,” even as others contend that the evidence underpinning that view is weaker than many suspect (De Vaus Reference De Vaus2014, p. 111). Still, concerns about questionnaire length may be particularly acute when choosing the number of conjoint tasks, as fatigue may set in more rapidly when performing the same task repeatedly.
In short, researchers have good reason to expect that conjoint designs with a large number of tasks could produce significant levels of survey satisficing, but to date, there has been little empirical evidence as to the severity of this problem. Researchers are often tempted to ask respondents to complete many conjoint tasks in a single survey so as to maximize their statistical power. But this temptation carries risks, as researchers may well induce suboptimal levels of survey satisficing. Below, we provide an empirical assessment of this trade-off.
3 Empirical Evidence on the Number of Choice Tasks and Satisficing
Our goal is to investigate whether asking respondents to complete many repeated conjoint tasks will degrade their response quality due to satisficing, and if so when the degradation tends to kick in. In this section, we report the result of the six conjoint experiments we conducted for this purpose.
3.1 Design and methodology
The main portion of our study—the first five of the six experiments—was fielded on a total of 4,921 respondents we recruited via MT for payments of $1.25.Footnote 3 Our last, sixth survey was conducted on 1,613 respondents from SSI to confirm that key findings were not specific to MT respondents. These surveys occurred between February and May, 2015. While both use opt-in survey samples, MT draws from a small, highly experienced population (e.g. Stewart et al. Reference Stewart, Ungemach, Harris, Bartels, Newell, Paolacci and Chandler2015). As a result, by conducting our study via both MT and SSI, we can observe the role of fatigue for populations with different levels of survey-taking experience.Footnote 4
After a few introductory demographic questions about their own education, partisanship, and ideology, we told respondents: “This study is about voting and about your views on potential candidates for President. We are going to present pairs of hypothetical presidential candidates in the United States. For each pair, please indicate which of the two candidates you would prefer to see as President.” One example of the resulting conjoint task is available in Figure 1. We developed a set of twenty possible attributes that could define U.S. presidential candidates, including everything from their education, income, religion, and political partisanship to their positions on key issues (e.g. gay marriage, health care, abortion) and personal facts such as their favorite professional sport and car. The full list of attributes is provided in Table A.1 in the supplementary materials.
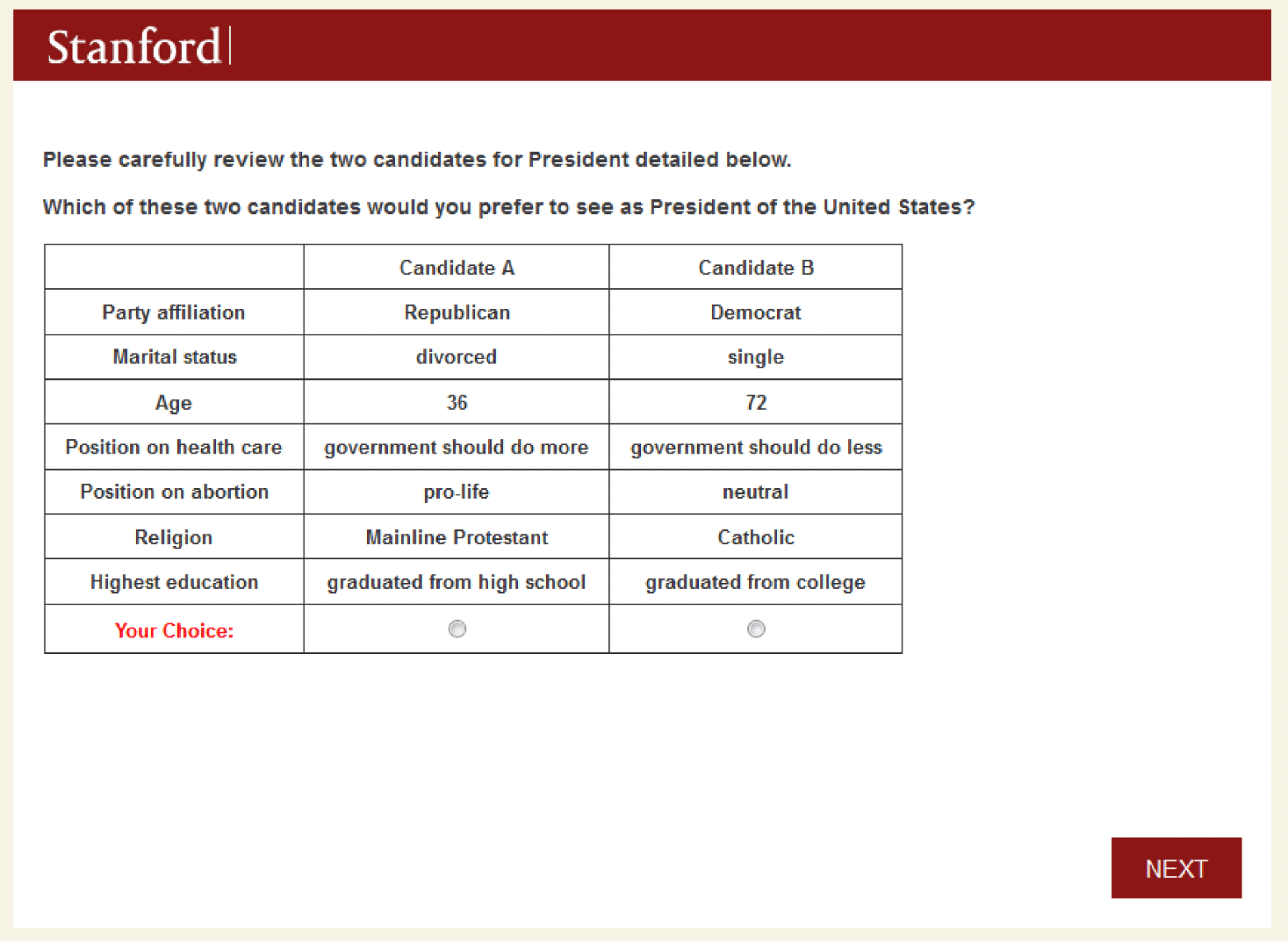
Figure 1. An example choice task from the study. Respondents are asked to assess two hypothetical presidential candidates.
We employed several randomizations, some of which we report elsewhere. For one thing, we randomly varied the total number of attributes presented to respondents. Specifically, each respondent was randomly assigned to 4, 5, 6, 7, 8, 10, 15, or 20 attributes. Of those, the two “core” attributes—candidates’ education and partisanship—were always included in each respondent’s table regardless of their assigned number of attributes, and the rest were randomly drawn from the master list of 20 attributes. Once a specific number and set of attributes was assigned to a respondent it was fixed for the duration of her survey. We also randomized the attributes’ order within the conjoint table and then fixed that order across tasks for each respondent. For example, if a respondent saw the candidate’s income at the top of the conjoint table, it remained in that position for the duration of her tasks.Footnote 5
Most importantly for our purposes here, we asked respondents to complete 30 of these conjoint tasks, which is much more than typical recent applications of randomized conjoint analysis. The purpose of this design choice, of course, was to study how response quality might change as respondents went through numerous screens of conjoint tables (which also consisted of a large number of attributes for some).
As the number of tasks increases, do respondents adapt by being less discerning in their choices? Our expectation is that any increased survey satisficing will induce respondents to pay less attention to the task, and so will attenuate the predictive power of the core attributes. We employ two metrics to measure the predictive power of the attributes. First, we estimate the Average Marginal Component Effects (AMCEs) of the two core attributes and compare the estimates across tasks.
Second, we calculate the coefficient of determination (i.e.
$R^{2}$
) from the regression of conjoint responses on the core attributes,Footnote
6
and compare those
$R^{2}$
s across tasks. Because the
$R^{2}$
is a function of the regression-based estimates of the AMCEs under the fully randomized conjoint design, any changes in the
$R^{2}$
across tasks can be attributed to changes in satisficing. In other words, the
$R^{2}$
can be interpreted as a summary measure of the explanatory power of the two core attributes combined, and its change as the overall variation in satisficing.
3.2 Results
We first present results from five surveys on MT respondents. Figure 2 shows the estimated AMCEs for the two core attributes that were always included in the conjoint table—education and party affiliation—across the number of completed tasks along with their 95% confidence intervals clustered by respondent. Remarkably, the results suggest a surprising degree of robustness over a large number of choice tasks. For both attributes, the estimated AMCEs are substantively large and statistically significant in the respondents’ first task (0.186 and 0.263 for education and party, respectively, with
$SE=0.01$
for both attributes). The AMCEs then drop slightly for the second task (0.152 and 0.238,
$SE=0.01$
for both) but remain stable and close to that level throughout the duration of the survey, even occasionally jumping back to the original level. Even at the 30th task, the estimated AMCEs barely differ from those for the second task (0.140 and 0.233,
$SE=0.01$
for both). We note that the rate of sample attrition over the course of the 30 tasks is negligibly small, as is typical in surveys fielded on MT.
Figure 2. The AMCEs for our core attributes of interest from the five MT surveys as the number of completed choice tasks increases.
Figure 3. The partial
$R^{2}$
values for our core attributes for the pooled MT data as a function of the number of completed tasks.
The result for the partial
$R^{2}$
values, presented in Figure 3, confirms the stability of conjoint responses across the 30 tasks for our MT respondents. The partial
$R^{2}$
for the two core attributes is about 0.104 in the respondents’ first task, with a 95% block-bootstrapped confidence interval of [0.091, 0.118].Footnote
7
The coefficient drops slightly to 0.079 in the second task (with the 95% CI of [0.068, 0.092]) and remains remarkably stable around that value throughout the remaining 28 tasks. The two core attributes meaningfully explain the choice responses even at the very end of the lengthy conjoint exercises (
$R^{2}=0.075$
, with 95% CI [0.063, 0.087]). These findings are replicated in our SSI sample, as shown in Figures A.1 and A.2 in Section A.2 of the supplementary materials.
In additional analyses reported in the supplementary materials, we also find that our results hold when evaluating the effects of other attributes included in our conjoint design, such as the candidates’ age, military service, and policy positions (see Supplementary Figures A.3–A.6 in Section A.3). Overall, our study suggests that conjoint designs are remarkably impervious to threats from survey fatigue and satisfying when applied to respondents on MT and SSI, two of the most frequently used populations in experimental research.
4 Conclusion
The rapid growth of survey research conducted via computers has enabled researchers to employ increasingly complex research designs at little added cost. Conjoint experiments are one such design, and they have seen a renaissance within political science in the past few years. However, research on survey methods has to date been focused on the change in sampling frames that accompanies the shift toward online survey administration (e.g. Chang and Krosnick Reference Chang and Krosnick2009; Yeager et al. Reference Yeager, Krosnick, Chang, Javitz, Levendusky, Simpser and Wang2011). For those administering surveys via computer, there is surprisingly little guidance about the extent to which insights developed for phone and in-person surveys hold up (but see Gooch and Vavreck Reference Gooch and Vavreck2015).
In this paper, we sought to advance our understanding of response behavior in surveys administered by computer by probing one breaking point of conjoint designs. Specifically, we considered an important decision confronting researchers who seek to implement conjoint experiments: how many tasks can one assign per respondent without inducing survey fatigue and excessive satisficing? Through a series of experiments, we find conjoint designs to be surprisingly robust, at least with the opt-in samples employed here (and in many other contemporary survey experiments). Even after completing 30 tasks, respondents continue to process the conjoint profiles in similar ways and to provide similar, sensible results.
These results allow us to make design recommendations for researchers interested in using conjoint survey experiments. While the results do not point to an optimal number of tasks, they show that the number of tasks is not a binding constraint for the experimental design in terms of satisficing—at least within the 30-task limit explored in this study. While we would not necessarily recommend researchers to use as many as 30 tasks, we have shown that within that limit, satisficing is not a serious concern that should dictate the number of tasks. Instead, researchers are free to make their decisions on the number of tasks on the basis of other design considerations, such as the survey length, cost constraints, and statistical power.
Certainly, the results from this study may differ for populations with little to no experience taking surveys via computer, or with reduced incentives to pay attention. The results may also differ in cases where the conjoint survey covers different subject matter. Making comparisons that are more familiar to respondents—such as between presidential candidates, job applicants, or consumer products—is likely to be easier than evaluating, for example, the elements of a complex policy proposal. Survey fatigue may be more pronounced and/or set in more quickly in a more complex context.
Conjoint experiments undoubtedly have breaking points—but our analyses suggest that at least for surveys administered with experienced and motivated survey takers, the breaking point in terms of the number of tasks appears to be beyond the range of common practice. Important questions remain about other aspects of conjoint design and their implications for survey response quality. In a companion study, we investigate the extent to which increasing the number of attributes in a conjoint design affects response quality (Bansak et al. Reference Bansak, Hainmueller, Hopkins and Yamamoto2017a). Broader questions include whether conjoint experiments might have advantages over alternative designs such as vignettes in terms of satisficing, to which Hainmueller, Hangartner, and Yamamoto (Reference Hainmueller, Hangartner and Yamamoto2015) provide some partial answers.
Supplementary material
For supplementary material accompanying this paper, please visit https://doi.org/10.1017/pan.2017.40.
