Hostname: page-component-89b8bd64d-5bvrz Total loading time: 0 Render date: 2026-05-06T23:52:17.814Z Has data issue: false hasContentIssue false
  • English
  • Français

ORDERING CONVOLUTIONS OF HETEROGENEOUS EXPONENTIAL AND GEOMETRIC DISTRIBUTIONS REVISITED

Published online by Cambridge University Press:  23 April 2010

Tiantian Mao ,
Taizhong Hu  and
Peng Zhao
Tiantian Mao
Affiliation:
Department of Statistics and Finance, University of Science and Technology of China, Hefei, Anhui 230026, People's Republic of ChinaE-mail: mttiy@mail.ustc.edu.cn; thu@ustc.edu.cn
Taizhong Hu
Affiliation:
Department of Statistics and Finance, University of Science and Technology of China, Hefei, Anhui 230026, People's Republic of ChinaE-mail: mttiy@mail.ustc.edu.cn; thu@ustc.edu.cn
Peng Zhao
Affiliation:
School of Mathematics and Statistics, Lanzhou University, Lanzhou 730000, People's Republic of China, E-mail: zhaop07@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let Sn(a1, …, an) be the sum of n independent exponential random variables with respective hazard rates a1, …, an or the sum of n independent geometric random variables with respective parameters a1, …, an. In this article, we investigate sufficient conditions on parameter vectors (a1, …, an) and 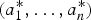under which Sn(a1, …, an) and 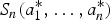are ordered in terms of the increasing convex and the reversed hazard rate orders for both exponential and geometric random variables and in terms of the mean residual life order for geometric variables. For the bivariate case, all of these sufficient conditions are also necessary. These characterizations are used to compare fail-safe systems with heterogeneous exponential components in the sense of the increasing convex and the reversed hazard rate orders. The main results complement several known ones in the literature.

Information

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 24 , Issue 3 , July 2010 , pp. 329 - 348
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

1.Balakrishnan, N. & Iliopoulos, G. (2009). Stochastic monotonicity of the MLE of exponential mean under different censoring schemes. Annals of the Institute of Statistical Mathematics 61: 753–772.CrossRefGoogle Scholar
2.Boland, P.J., El-Neweihi, E. & Proschan, F. (1994). Schur properties of convolutions of exponential and geometric random variables. Journal of Multivariate Analysis 48: 157–167.CrossRefGoogle Scholar
3.Bon, J.L. & Păltănea, E. (1999). Ordering properties of convolutions of exponential random variables. Lifetime Data Analysis 5: 185–192.CrossRefGoogle ScholarPubMed
4.Bon, J.L. & Păltănea, E. (2006). Comparisons of order statistics in a random sequence to the same statistics with i.i.d. variables. ESAIM: Probability and Statistics 10: 1–10.CrossRefGoogle Scholar
5.Genest, C., Kochar, S. & Xu, M. (2009). On the range of heterogeneous samples. Journal of Multivariate Analysis 100: 1587–1592.CrossRefGoogle Scholar
6.Jorswieck, E. & Boche, H. (2006). Majorization and matrix-monotone functions in wireless communications. Foundations and Trends in Communications and Information Theory 3: 553–701.CrossRefGoogle Scholar
7.Kochar, S. & Ma, C. (1999). Dispersive ordering of convolutions of exponential random variables. Statistics and Probability Letters 43: 321–324.CrossRefGoogle Scholar
8.Kochar, S. & Xu, M. (2009a). Comparisons of parallel systems according to the convex transform order. Journal of Applied Probability 46: 342–352.CrossRefGoogle Scholar
9.Kochar, S. & Xu, M. (2009b). On the right spread order of convolutions of heterogeneous exponential random variables. Journal of Multivariate Analysis 101: 165–176.CrossRefGoogle Scholar
10.Korwar, R.M. (2002). On stochastic orders for sums of independent random variables. Journal of Multivariate Analysis 80: 344–357.CrossRefGoogle Scholar
11.Ma, C. (2000). Convex orders for linear combinations of random variables. Journal of Statistical Planning and Inference 84: 11–25.CrossRefGoogle Scholar
12.Marshall, A.W. & Olkin, I. (1979). Inequalities: Theory of majorization and its applications. New York: Academic Press.Google Scholar
13.Marshall, A.W. & Proschan, F. (1965). An inequality for convex functions involving majorization. Journal of Mathematical Analysis and Applications, 12: 87–90.CrossRefGoogle Scholar
14.Müller, A. & Stoyan, D. (2002). Comparison methods for stochastic models and risks. West Sussex, UK: Wiley.Google Scholar
15.Păltănea, E. (2008). On the comparison in hazard rate ordering of fail-safe systems. Journal of Statistical Planning and Inference 138: 1993–1997.CrossRefGoogle Scholar
16.Sen, A. & Balakrishnan, N. (1999). Convolution of geometrics and a reliability problem. Statistics and Probability Letters 43: 421–426.CrossRefGoogle Scholar
17.Shaked, M. & Shanthikumar, J.G. (2007). Stochastic orders. New York: Springer.CrossRefGoogle Scholar
18.Yu, Y. (2008). On an inequality of Karlin and Rinott concerning weighted sums of i.i.d. random variables. Advances in Applied Probability 40: 1223–1226.CrossRefGoogle Scholar
19.Zhao, P. & Balakrishnan, N. (2009). Characterization of MRL order of fail-safe systems with heterogeneous exponential components. Journal of Statistical Planning and Inference 139: 3027–3037.CrossRefGoogle Scholar
20.Zhao, P. & Balakrishnan, N. (2009). Likelihood ratio ordering of convolutions of heterogeneous exponential and geometric random variables. Statistics and Probability Letters 79: 1717–1723.CrossRefGoogle Scholar
21.Zhao, P. & Balakrishnan, N. (2009). Mean residual life order of convolutions of heterogeneous exponential random variables. Journal of Multivariate Analysis 100: 1792–1801.CrossRefGoogle Scholar
22.Zhao, P. & Hu, T. (2009). On hazard rate ordering of the sums of heterogeneous geometric random variables. Journal of Multivariate Analysis 101: 44–51.CrossRefGoogle Scholar
23.Zhao, P. & Li, X. (2009). Stochastic order of sample range from heterogeneous exponential random variables. Probability in the Engineering and Informational Sciences 23: 17–29.CrossRefGoogle Scholar
24.Zhao, P., Li, X. & Balakrishnan, N. (2009). Likelihood ratio order of the second order statistic from independent heterogeneous exponential random variables. Journal of Multivariate Analysis 100: 952–962.CrossRefGoogle Scholar