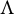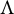1 Introduction and statements
A map f on a (non-degenerate) compact interval
![]() $X\subset \mathbb R$
is called piecewise contracting interval map (PCIM), if there exists a finite collection
$X\subset \mathbb R$
is called piecewise contracting interval map (PCIM), if there exists a finite collection
![]() $\mathcal Z$
of pairwise disjoint open subintervals of X such that
$\mathcal Z$
of pairwise disjoint open subintervals of X such that
![]() $X=\bigcup _{\scriptscriptstyle Z\in \mathcal Z}\overline {Z}$
and
$X=\bigcup _{\scriptscriptstyle Z\in \mathcal Z}\overline {Z}$
and
![]() $f|Z:Z\to X$
is a contraction (with respect to Euclidean metric) for all
$f|Z:Z\to X$
is a contraction (with respect to Euclidean metric) for all
![]() $Z\in \mathcal Z$
. It suffices to define f on
$Z\in \mathcal Z$
. It suffices to define f on
![]() $X^*:=\bigcup _{\scriptscriptstyle Z\in \mathcal Z}Z$
and study the dynamics of f on
$X^*:=\bigcup _{\scriptscriptstyle Z\in \mathcal Z}Z$
and study the dynamics of f on
![]() $\widetilde X:=\bigcap _{j=0}^\infty f^{-j}(X^*)$
, the set of points for which all iterates of f are well defined; therefore, there is no problem when considering the orbit of points in
$\widetilde X:=\bigcap _{j=0}^\infty f^{-j}(X^*)$
, the set of points for which all iterates of f are well defined; therefore, there is no problem when considering the orbit of points in
![]() $\widetilde X$
. It is not difficult to see that
$\widetilde X$
. It is not difficult to see that
![]() $\widetilde X$
is dense on X when f is piecewise monotonic (i.e.,
$\widetilde X$
is dense on X when f is piecewise monotonic (i.e.,
![]() $f|Z$
is strictly monotone for all
$f|Z$
is strictly monotone for all
![]() $Z\in \mathcal Z$
).
$Z\in \mathcal Z$
).
We consider the attractor
![]() $\Lambda $
of f, which is defined as the asymptotic set that attracts all orbits of points in
$\Lambda $
of f, which is defined as the asymptotic set that attracts all orbits of points in
![]() $\widetilde X$
(a formal definition of
$\widetilde X$
(a formal definition of
![]() $\Lambda $
will be provided in the next section). It is known that the
$\Lambda $
will be provided in the next section). It is known that the
![]() $\omega $
-limit set of any point in
$\omega $
-limit set of any point in
![]() $\widetilde X$
is nonempty, compact, and is contained in
$\widetilde X$
is nonempty, compact, and is contained in
![]() $\Lambda $
(see Lemma 2.1 in [Reference Calderón, Catsigeras and Guiraud1]), but it is not necessarily invariant if it contains points of the finite set
$\Lambda $
(see Lemma 2.1 in [Reference Calderón, Catsigeras and Guiraud1]), but it is not necessarily invariant if it contains points of the finite set
![]() $\Delta :=X\backslash X^*$
(as usual, for every
$\Delta :=X\backslash X^*$
(as usual, for every
![]() $x\in \widetilde X$
, we denote by
$x\in \widetilde X$
, we denote by
![]() $\omega (x)$
its
$\omega (x)$
its
![]() $\omega $
-limit set). For this reason, it is convenient to work with a concept of invariance that does not depend on how f is defined on
$\omega $
-limit set). For this reason, it is convenient to work with a concept of invariance that does not depend on how f is defined on
![]() $\Delta $
. We say that a set
$\Delta $
. We say that a set
![]() $A\subset X$
is f-pseudo-invariant if, for every
$A\subset X$
is f-pseudo-invariant if, for every
![]() $x\in A$
,
$x\in A$
,
Note that if
![]() $A \subset X$
is f-pseudo-invariant, then
$A \subset X$
is f-pseudo-invariant, then
![]() $A \cap \widetilde X$
is invariant by f, i.e.,
$A \cap \widetilde X$
is invariant by f, i.e.,
![]() $f(A \cap \widetilde X)\subset A \cap \widetilde X$
. As we will see next, it is possible to guarantee that every pseudo-invariant set intersects
$f(A \cap \widetilde X)\subset A \cap \widetilde X$
. As we will see next, it is possible to guarantee that every pseudo-invariant set intersects
![]() $\widetilde X$
provided that the collection of one-sided limits of points in
$\widetilde X$
provided that the collection of one-sided limits of points in
![]() $\Delta $
– which we denote by D – is contained in
$\Delta $
– which we denote by D – is contained in
![]() $\widetilde X$
.
$\widetilde X$
.
Lemma 1.1 Suppose that
![]() $D\subset \widetilde X$
. If
$D\subset \widetilde X$
. If
![]() $A \subset X$
is a nonempty f-pseudo-invariant set, then
$A \subset X$
is a nonempty f-pseudo-invariant set, then
![]() $A\cap \widetilde X$
is a nonempty f-invariant set.
$A\cap \widetilde X$
is a nonempty f-invariant set.
Proof If
![]() $A\subset \widetilde X$
, the result follows. Otherwise, let
$A\subset \widetilde X$
, the result follows. Otherwise, let
![]() $y\in A\backslash \widetilde X\neq \emptyset $
and consider the smallest integer
$y\in A\backslash \widetilde X\neq \emptyset $
and consider the smallest integer
![]() $t\geq 0$
such that
$t\geq 0$
such that
![]() $c:=f^t(y)\in A\cap \Delta $
. Since A is a pseudo-invariant set, we have that at least one of the one-sided limits of f at c belongs to A. Thus, as
$c:=f^t(y)\in A\cap \Delta $
. Since A is a pseudo-invariant set, we have that at least one of the one-sided limits of f at c belongs to A. Thus, as
![]() $D\subset \widetilde X$
, we deduce that
$D\subset \widetilde X$
, we deduce that
![]() $A\cap \widetilde X\neq \emptyset $
.
$A\cap \widetilde X\neq \emptyset $
.
Lemma 1.1 is also useful for redefining other concepts in dynamics such as minimality. If
![]() $D\subset \widetilde X$
, we say that a compact and pseudo-invariant set
$D\subset \widetilde X$
, we say that a compact and pseudo-invariant set
![]() $A\subset X$
is
$A\subset X$
is
![]() $\widetilde X$
-minimal if the orbit of every point in
$\widetilde X$
-minimal if the orbit of every point in
![]() $A\cap \widetilde X$
is dense in A. In fact, if
$A\cap \widetilde X$
is dense in A. In fact, if
![]() $D\subset \widetilde X$
, then it is also possible to completely describe the attractor of f.
$D\subset \widetilde X$
, then it is also possible to completely describe the attractor of f.
Theorem 1.2 [Reference Calderón, Catsigeras and Guiraud1]
If f is piecewise monotonic and
![]() $D\subset \widetilde X$
, then there exist two natural numbers
$D\subset \widetilde X$
, then there exist two natural numbers
![]() $N_1,N_2\geq 0$
such that
$N_1,N_2\geq 0$
such that
![]() $N_1+N_2\geq 1$
and the attractor
$N_1+N_2\geq 1$
and the attractor
![]() $\Lambda $
of f can be decomposed as follows:
$\Lambda $
of f can be decomposed as follows:
 $$ \begin{align} \Lambda=\left(\bigcup\limits_{i=1}^{N_1}\mathcal O_i\right)\cup\left(\bigcup\limits_{j=1}^{N_2}K_j\right)\!, \end{align} $$
$$ \begin{align} \Lambda=\left(\bigcup\limits_{i=1}^{N_1}\mathcal O_i\right)\cup\left(\bigcup\limits_{j=1}^{N_2}K_j\right)\!, \end{align} $$
where
![]() $\mathcal O_1,\mathcal O_2,\ldots ,\mathcal O_{N_1}\subset \widetilde {X}$
are pairwise disjoint periodic orbits and
$\mathcal O_1,\mathcal O_2,\ldots ,\mathcal O_{N_1}\subset \widetilde {X}$
are pairwise disjoint periodic orbits and
![]() $K_1,K_2,\ldots ,K_{N_2}$
are different pseudo-invariant and
$K_1,K_2,\ldots ,K_{N_2}$
are different pseudo-invariant and
![]() $\widetilde X$
-minimal Cantor sets of X. Moreover, for any
$\widetilde X$
-minimal Cantor sets of X. Moreover, for any
![]() $x\in \widetilde X$
, either there exists
$x\in \widetilde X$
, either there exists
![]() $i\in \{1,\dots ,N_1\}$
such that
$i\in \{1,\dots ,N_1\}$
such that
![]() $\omega (x)=\mathcal O_i$
or there exists
$\omega (x)=\mathcal O_i$
or there exists
![]() $j\in \{1,\dots ,N_2\}$
such that
$j\in \{1,\dots ,N_2\}$
such that
![]() $\omega (x)=K_j$
.
$\omega (x)=K_j$
.
To establish our main result, we will require a global injectivity condition that does not depend on how f is defined on
![]() $\Delta $
. We say that f satisfies the separation property if f is piecewise monotonic and
$\Delta $
. We say that f satisfies the separation property if f is piecewise monotonic and
![]() $\overline {f(Z)}\cap \overline {f(Z')}=\emptyset $
for all
$\overline {f(Z)}\cap \overline {f(Z')}=\emptyset $
for all
![]() $Z,Z'\in \mathcal Z$
such that
$Z,Z'\in \mathcal Z$
such that
![]() $Z\neq Z'$
. A PCIM that satisfies the separation property is injective on
$Z\neq Z'$
. A PCIM that satisfies the separation property is injective on
![]() $X^*$
, but not necessarily on the whole set X (consider the case in which f is not injective on
$X^*$
, but not necessarily on the whole set X (consider the case in which f is not injective on
![]() $\Delta $
). Also, not every injective PCIM on
$\Delta $
). Also, not every injective PCIM on
![]() $X^*$
satisfies the separation property. However, every injective PCIM on
$X^*$
satisfies the separation property. However, every injective PCIM on
![]() $X^*$
such that its set
$X^*$
such that its set
![]() $\Delta $
contains only jump-discontinuities satisfies it. Our main result is the following.
$\Delta $
contains only jump-discontinuities satisfies it. Our main result is the following.
Theorem 1.3 Suppose that f satisfies the separation property and
![]() $D\subset \widetilde X$
. Then, the Hausdorff dimension of
$D\subset \widetilde X$
. Then, the Hausdorff dimension of
![]() $\Lambda $
and the topological entropy of
$\Lambda $
and the topological entropy of
![]() $f|(\Lambda \cap \widetilde X)$
are equal to zero.
$f|(\Lambda \cap \widetilde X)$
are equal to zero.
The concept of topological entropy in Theorem 1.3 refers to the quantity:
 $$\begin{align*}h_{\mathrm{top}}\big(f|(\Lambda\cap\widetilde X)\big)=\lim_{\epsilon\to0}\limsup_{n\to\infty}\frac{\log r_n(\epsilon,\Lambda\cap\widetilde X)}{n}, \end{align*}$$
$$\begin{align*}h_{\mathrm{top}}\big(f|(\Lambda\cap\widetilde X)\big)=\lim_{\epsilon\to0}\limsup_{n\to\infty}\frac{\log r_n(\epsilon,\Lambda\cap\widetilde X)}{n}, \end{align*}$$
where
![]() $r_n(\epsilon ,\Lambda \cap \widetilde X)$
denotes the smallest cardinality of every
$r_n(\epsilon ,\Lambda \cap \widetilde X)$
denotes the smallest cardinality of every
![]() $(n,\epsilon )$
-spanning set for
$(n,\epsilon )$
-spanning set for
![]() $\Lambda \cap \widetilde X$
with respect to f (see Definition 7.8 in [Reference Walters12]). Although the number
$\Lambda \cap \widetilde X$
with respect to f (see Definition 7.8 in [Reference Walters12]). Although the number
![]() $r_n(\epsilon ,K)$
is defined for a compact set K in the continuous context, it will be shown that
$r_n(\epsilon ,K)$
is defined for a compact set K in the continuous context, it will be shown that
![]() $r_n(\epsilon ,\Lambda \cap \widetilde X)$
is well defined for all
$r_n(\epsilon ,\Lambda \cap \widetilde X)$
is well defined for all
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $\epsilon>0$
. Also, note that if
$\epsilon>0$
. Also, note that if
![]() $D \subset \widetilde X$
and f is piecewise monotonic, then Theorem 1.2 implies that
$D \subset \widetilde X$
and f is piecewise monotonic, then Theorem 1.2 implies that
![]() $\Lambda $
is an f-pseudo-invariant set. Thus, using Lemma 1.1, we deduce that
$\Lambda $
is an f-pseudo-invariant set. Thus, using Lemma 1.1, we deduce that
![]() $\Lambda \cap \widetilde X$
is a nonempty and f-invariant set.
$\Lambda \cap \widetilde X$
is a nonempty and f-invariant set.
Remark 1.4 The results presented in Theorem 1.3 are also proven in [Reference Gaivão and Nogueira6] under the hypotheses of global injectivity and assuming that the map is strictly increasing on each continuity piece. Another difference is that the authors work with the concept of singular entropy, which was introduced in [Reference Misiurewicz and Ziemian11] as an alternative for calculating the entropy according to Bowen’s formula for continuous piecewise monotone systems of the interval.
Paper organization: In Section 2, we set the notation that we will use throughout this work. Section 3 is devoted to defining the concept of complexity and its relationship with the atoms of the system, which allow us to characterize the attractor of f. Finally, in Section 4, we prove Theorem 1.3.
2 Convenient notation
In what follows, we always assume that
![]() $f:X\to X$
is a PCIM and that the topology on X is the one induced by the Euclidean metric. Then, there exist
$f:X\to X$
is a PCIM and that the topology on X is the one induced by the Euclidean metric. Then, there exist
![]() $\lambda \in (0,1)$
and a collection of
$\lambda \in (0,1)$
and a collection of
![]() $N\geq 1$
open nonempty disjoint subintervals
$N\geq 1$
open nonempty disjoint subintervals
![]() $X_1,X_2,\ldots ,X_N$
such that
$X_1,X_2,\ldots ,X_N$
such that
![]() ${X=\bigcup _{i=1}^N\overline {X_i}}$
and
${X=\bigcup _{i=1}^N\overline {X_i}}$
and
The real number
![]() $\lambda $
is called contraction rate of f, and the elements of the collection
$\lambda $
is called contraction rate of f, and the elements of the collection
![]() $\{X_i\}_{i=1}^N$
are called contraction pieces. We will consider them to be sorted. In particular, let
$\{X_i\}_{i=1}^N$
are called contraction pieces. We will consider them to be sorted. In particular, let
![]() $c_0,c_N$
denote the extreme points of X and
$c_0,c_N$
denote the extreme points of X and
![]() $\Delta =\{c_1<c_2<\dots <c_{N-1}\}$
the set of the boundaries of the contraction pieces of f; that is,
$\Delta =\{c_1<c_2<\dots <c_{N-1}\}$
the set of the boundaries of the contraction pieces of f; that is,
For notational convenience, we assume that
![]() $X_1$
and
$X_1$
and
![]() $X_N$
are half-closed, but one may also consider the case where one or both pieces are open by adding
$X_N$
are half-closed, but one may also consider the case where one or both pieces are open by adding
![]() $c_0$
and/or
$c_0$
and/or
![]() $c_N$
to
$c_N$
to
![]() $\Delta $
. In other words,
$\Delta $
. In other words,
![]() $\Delta $
must contain all the discontinuity points of the map.
$\Delta $
must contain all the discontinuity points of the map.
As we said before, the attractor
![]() $\Lambda $
of f is nonempty, compact, pseudo-invariant, and
$\Lambda $
of f is nonempty, compact, pseudo-invariant, and
![]() $\widetilde X$
-minimal provided that f is piecewise monotonic and
$\widetilde X$
-minimal provided that f is piecewise monotonic and
![]() $D\subset \widetilde X$
. The formal definition of the attractor
$D\subset \widetilde X$
. The formal definition of the attractor
![]() $\Lambda $
is given by
$\Lambda $
is given by
We are interested in computing the topological entropy of
![]() $f|(\Lambda \cap \widetilde X)$
and the Hausdorff dimension of
$f|(\Lambda \cap \widetilde X)$
and the Hausdorff dimension of
![]() $\Lambda $
. For the latter, it will be necessary to recall some concepts. If
$\Lambda $
. For the latter, it will be necessary to recall some concepts. If
![]() $\delta \geq 0$
and
$\delta \geq 0$
and
![]() $E\subset X$
, a
$E\subset X$
, a
![]() $\delta $
-cover of E is a countable collection of subsets of X that covers E and the diameter of each of which is smaller than or equal to
$\delta $
-cover of E is a countable collection of subsets of X that covers E and the diameter of each of which is smaller than or equal to
![]() $\delta $
. Thus, for any
$\delta $
. Thus, for any
![]() $E\subset X$
, and every
$E\subset X$
, and every
![]() $s\geq 0$
and
$s\geq 0$
and
![]() $\delta>0$
, we consider the numbers
$\delta>0$
, we consider the numbers
 $$\begin{align*}\mathcal H_\delta^s(E):=\inf\left\{\sum_{C\in\mathcal C}\big(\!\operatorname{\mathrm{diam}}(C)\big)^s\ :\ \mathcal C \text{ is a } \delta\text{-cover of } E\right\} \end{align*}$$
$$\begin{align*}\mathcal H_\delta^s(E):=\inf\left\{\sum_{C\in\mathcal C}\big(\!\operatorname{\mathrm{diam}}(C)\big)^s\ :\ \mathcal C \text{ is a } \delta\text{-cover of } E\right\} \end{align*}$$
and
It is known that
![]() $\mathcal H^s_\delta $
and
$\mathcal H^s_\delta $
and
![]() $\mathcal H^s$
define an outer measure and a measure on X, respectively. Furthermore,
$\mathcal H^s$
define an outer measure and a measure on X, respectively. Furthermore,
![]() $\mathcal H^s$
is called s-dimensional Hausdorff measure on X. The Hausdorff dimension of a set
$\mathcal H^s$
is called s-dimensional Hausdorff measure on X. The Hausdorff dimension of a set
![]() $E\subset X$
, which we denote by
$E\subset X$
, which we denote by
![]() $\dim _{\mathcal H}(E)$
, is the critical value
$\dim _{\mathcal H}(E)$
, is the critical value
![]() $s\geq 0$
where
$s\geq 0$
where
![]() $\mathcal H^s(E)$
jumps from infinity to zero. This number satisfies, for example, that
$\mathcal H^s(E)$
jumps from infinity to zero. This number satisfies, for example, that
![]() $\dim _{\mathcal H}(E)=0$
for every
$\dim _{\mathcal H}(E)=0$
for every
![]() $E\subset X$
such that
$E\subset X$
such that
![]() $\#E\leq \aleph _0$
. Moreover, if
$\#E\leq \aleph _0$
. Moreover, if
![]() $s_0:=\dim _{\mathcal H}(E)\geq 1$
is a positive integer, then
$s_0:=\dim _{\mathcal H}(E)\geq 1$
is a positive integer, then
![]() $\mathcal H^{s_0}$
coincides with the Lebesgue measure on
$\mathcal H^{s_0}$
coincides with the Lebesgue measure on
![]() $\mathbb R^{s_0}$
. If
$\mathbb R^{s_0}$
. If
![]() $s_0=0$
, then it is known that E is totally disconnected (the reciprocal is not true!). In practical terms, the Hausdorff dimension provides a general notion of the size of a set in a metric space.
$s_0=0$
, then it is known that E is totally disconnected (the reciprocal is not true!). In practical terms, the Hausdorff dimension provides a general notion of the size of a set in a metric space.
Additionally, we can consider another fractal dimension that allows us to describe the “size” of sets. Given
![]() $E\subset X$
and
$E\subset X$
and
![]() $\epsilon>0$
, let
$\epsilon>0$
, let
![]() $\ell (E,\epsilon )$
be the smallest number of intervals with diameter at most
$\ell (E,\epsilon )$
be the smallest number of intervals with diameter at most
![]() $\epsilon $
covering E. Then, we can define the box dimension of E to be
$\epsilon $
covering E. Then, we can define the box dimension of E to be
 $$\begin{align*}\dim_B(E):=\liminf_{\epsilon\to0^+}\frac{\log \ell(E,\epsilon)}{\log(1/\epsilon)}. \end{align*}$$
$$\begin{align*}\dim_B(E):=\liminf_{\epsilon\to0^+}\frac{\log \ell(E,\epsilon)}{\log(1/\epsilon)}. \end{align*}$$
Here, we use the lower limit to avoid problems with the convergence. Strictly speaking, this is usually called the lower box dimension and the box dimension is usually said to exist when the limit
![]() $\lim _{\epsilon \to 0^+}$
exists. Next, we give the existing comparison between the Hausdorff and box dimensions.
$\lim _{\epsilon \to 0^+}$
exists. Next, we give the existing comparison between the Hausdorff and box dimensions.
Lemma 2.1 (Inequality (3.17) in [Reference Falconer4])
For every
![]() $E\subset X$
,
$E\subset X$
,
![]() $\dim _{\mathcal H}(E)\leq \dim _B(E)$
.
$\dim _{\mathcal H}(E)\leq \dim _B(E)$
.
We recall that the previous result is valid in a general metric space, after adapting the definitions accordingly.
3 Complexity and atoms
Let
![]() $\mathbb N$
be the set of natural numbers starting at 0. We say that the sequence
$\mathbb N$
be the set of natural numbers starting at 0. We say that the sequence
![]() $\theta =(\theta _t)_{t\geq 0}\in \{1,\ldots ,N\}^{\mathbb N}$
is the itinerary of a point
$\theta =(\theta _t)_{t\geq 0}\in \{1,\ldots ,N\}^{\mathbb N}$
is the itinerary of a point
![]() $x\in \widetilde X$
if, for every
$x\in \widetilde X$
if, for every
![]() $t\in \mathbb N$
and
$t\in \mathbb N$
and
![]() $i\in \{1,\ldots ,N\}$
, we have that
$i\in \{1,\ldots ,N\}$
, we have that
![]() $\theta _t=i$
if and only if
$\theta _t=i$
if and only if
![]() $f^t(x)\in X_i$
. Also, the complexity function of a sequence
$f^t(x)\in X_i$
. Also, the complexity function of a sequence
![]() $\theta =(\theta _t)_{t\geq 0}$
is the function
$\theta =(\theta _t)_{t\geq 0}$
is the function
![]() $p_\theta (n):=\#L_n(\theta )$
defined for every
$p_\theta (n):=\#L_n(\theta )$
defined for every
![]() $n\geq 1$
, where
$n\geq 1$
, where
Thus,
![]() $p_\theta (n)$
gives the number of different words of length n contained in
$p_\theta (n)$
gives the number of different words of length n contained in
![]() $\theta $
. The complexity function of any sequence is a non-decreasing function of n. Also, if there exists
$\theta $
. The complexity function of any sequence is a non-decreasing function of n. Also, if there exists
![]() $n_0\geq 1$
such that
$n_0\geq 1$
such that
![]() $p_\theta (n_0+1)=p_\theta (n_0)$
, it can be shown that
$p_\theta (n_0+1)=p_\theta (n_0)$
, it can be shown that
![]() $p_\theta (n)=p_\theta (n_0)$
for all
$p_\theta (n)=p_\theta (n_0)$
for all
![]() $n\geq n_0$
. Theorem 1.2 is the result of classifying the orbits of points in
$n\geq n_0$
. Theorem 1.2 is the result of classifying the orbits of points in
![]() $\widetilde X$
according to the complexity associated with their itineraries.
$\widetilde X$
according to the complexity associated with their itineraries.
Note that it is possible to associate the concept of complexity with each point of
![]() $\widetilde X$
via its itinerary. It could happen that the complexity associated with orbits of a PCIM grows exponentially. However, when a PCIM satisfies the separation property, the complexity growth is at most affine for each itinerary of the system and n sufficiently large. Specifically, we have the following result.
$\widetilde X$
via its itinerary. It could happen that the complexity associated with orbits of a PCIM grows exponentially. However, when a PCIM satisfies the separation property, the complexity growth is at most affine for each itinerary of the system and n sufficiently large. Specifically, we have the following result.
Theorem 3.1 [Reference Catsigeras, Guiraud and Meyroneinc2]
Suppose that f satisfies the separation property. Let
![]() $x\in \widetilde X$
and
$x\in \widetilde X$
and
![]() $\theta \in \{1,\ldots ,N\}^{\mathbb N}$
be its itinerary, then there exist
$\theta \in \{1,\ldots ,N\}^{\mathbb N}$
be its itinerary, then there exist
![]() $m_0\geq 1$
,
$m_0\geq 1$
,
![]() $\alpha \in \{0,\ldots ,N-1\}$
, and
$\alpha \in \{0,\ldots ,N-1\}$
, and
![]() $\beta \in \big \{1,\ldots ,1+m_0(N-1-\alpha )\big \}$
such that
$\beta \in \big \{1,\ldots ,1+m_0(N-1-\alpha )\big \}$
such that
Under the assumptions of Theorem 1.2, it can be proved that, for every
![]() $x\in \widetilde X$
,
$x\in \widetilde X$
,
![]() $\omega (x)$
is a periodic orbit if and only if the complexity associated with x is eventually constant; that is,
$\omega (x)$
is a periodic orbit if and only if the complexity associated with x is eventually constant; that is,
![]() $\alpha =0$
(see Theorem 2.2 in [Reference Calderón, Catsigeras and Guiraud1]). Furthermore,
$\alpha =0$
(see Theorem 2.2 in [Reference Calderón, Catsigeras and Guiraud1]). Furthermore,
![]() $\omega (x)$
is an
$\omega (x)$
is an
![]() $\widetilde X$
-minimal Cantor set if and only if the complexity associated with x is eventually affine with
$\widetilde X$
-minimal Cantor set if and only if the complexity associated with x is eventually affine with
![]() $\alpha \neq 0$
(see Theorem 2.3 in [Reference Calderón, Catsigeras and Guiraud1]). One of the important tools that allowed the establishment of these results is the so-called atom.
$\alpha \neq 0$
(see Theorem 2.3 in [Reference Calderón, Catsigeras and Guiraud1]). One of the important tools that allowed the establishment of these results is the so-called atom.
Let
![]() $\mathcal P(X)$
be the power set of X. For every
$\mathcal P(X)$
be the power set of X. For every
![]() $i\in \{1,\ldots ,N\}$
, let
$i\in \{1,\ldots ,N\}$
, let
![]() $F_i:\mathcal P(X)\to \mathcal P(X)$
be defined by
$F_i:\mathcal P(X)\to \mathcal P(X)$
be defined by
![]() $F_i(A)=\overline {f(A\cap X_i)}$
for
$F_i(A)=\overline {f(A\cap X_i)}$
for
![]() $A\in \mathcal P(X)$
. Let
$A\in \mathcal P(X)$
. Let
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $(i_1,\ldots ,i_n)\in \{1,\ldots ,N\}^n$
. We say that
$(i_1,\ldots ,i_n)\in \{1,\ldots ,N\}^n$
. We say that
is an atom of generation n if it is nonempty. We denote
![]() $\mathcal A_n$
the set of all atoms of generation n. Every atom of generation
$\mathcal A_n$
the set of all atoms of generation n. Every atom of generation
![]() $n\geq 2$
is contained in an atom of previous generation. Precisely, for all
$n\geq 2$
is contained in an atom of previous generation. Precisely, for all
![]() $n\geq 2$
and
$n\geq 2$
and
![]() $(i_1,\ldots ,i_n)\in \{1,\ldots ,N\}^n$
, we have that
$(i_1,\ldots ,i_n)\in \{1,\ldots ,N\}^n$
, we have that
Also, each atom of any generation is a compact interval contained in X. Moreover, note that the attractor of f can be defined in terms of atoms as
We are interested in relating the code associated with an atom to the itinerary of points in X. The following result is relevant for this purpose.
Lemma 3.2 (Lemma 2.3 in [Reference Catsigeras, Guiraud and Meyroneinc2])
Suppose that f satisfies the separation property. Then, for every
![]() $n\geq 1$
,
$n\geq 1$
,
-
(1) the collection of atoms of generation n is pairwise disjoint. Precisely, if
 $A,B\in \mathcal A_n$
are such that
$A,B\in \mathcal A_n$
are such that
 $A\cap B\neq \emptyset $
, then
$A\cap B\neq \emptyset $
, then
 $A=B$
;
$A=B$
; -
(2) if
 $A_{i_1\ldots i_n},A_{j_1\ldots j_n}\in \mathcal A_n$
are such that
$A_{i_1\ldots i_n},A_{j_1\ldots j_n}\in \mathcal A_n$
are such that
 $A_{i_1\ldots i_n}=A_{j_1\ldots j_n}$
, then
$A_{i_1\ldots i_n}=A_{j_1\ldots j_n}$
, then
 $(i_1,\ldots ,i_n)=(j_1,\ldots ,j_n)$
.
$(i_1,\ldots ,i_n)=(j_1,\ldots ,j_n)$
.
Next, we list some basic properties of atoms. The proof of each property is straightforward and is left as an exercise to the reader. Recall that
![]() $\lambda \in (0,1)$
is the contraction rate of f.
$\lambda \in (0,1)$
is the contraction rate of f.
Lemma 3.3 Each one of the following statements holds:
-
(1) For all
 $n\geq 1$
,
$n\geq 1$
,  $$\begin{align*}\max_{A\in\mathcal A_{n+1}}\operatorname{\mathrm{diam}}(A)\leq \lambda \max_{A\in\mathcal A_{n}}\operatorname{\mathrm{diam}}(A)\,. \end{align*}$$
$$\begin{align*}\max_{A\in\mathcal A_{n+1}}\operatorname{\mathrm{diam}}(A)\leq \lambda \max_{A\in\mathcal A_{n}}\operatorname{\mathrm{diam}}(A)\,. \end{align*}$$
-
(2) For all
 $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
 $n_0\geq 1$
such that
$n_0\geq 1$
such that
 $\operatorname {\mathrm {diam}}(A)<\epsilon $
for every
$\operatorname {\mathrm {diam}}(A)<\epsilon $
for every
 $A\in \mathcal A_{n}$
with
$A\in \mathcal A_{n}$
with
 ${n\geq n_0}$
.
${n\geq n_0}$
. -
(3) For all
 $x\in \Lambda $
, there exists a decreasing sequence
$x\in \Lambda $
, there exists a decreasing sequence
 $\{B_k\}_{k\geq 1}$
of atoms (i.e.,
$\{B_k\}_{k\geq 1}$
of atoms (i.e.,
 $B_k\supset B_{k+1}$
for all
$B_k\supset B_{k+1}$
for all
 $k\geq 1$
) such that
$k\geq 1$
) such that
 $x\in B_k\in \mathcal A_k$
for all
$x\in B_k\in \mathcal A_k$
for all
 $k\geq 1$
and (3.3)
$k\geq 1$
and (3.3) $$ \begin{align} \bigcap_{k\geq1}B_k=\{x\}\,. \end{align} $$
$$ \begin{align} \bigcap_{k\geq1}B_k=\{x\}\,. \end{align} $$
-
(4) If f satisfies the separation property, the sequence
 $\{B_n\}_{n\geq 1}$
defined in item 3 is unique for each
$\{B_n\}_{n\geq 1}$
defined in item 3 is unique for each
 $x\in \Lambda $
.
$x\in \Lambda $
.
Note that the existence of the sequence of atoms
![]() $\{B_k\}_{k \geq 1}$
in Lemma 3.3 is guaranteed by (3.2). Besides, the uniqueness in item 4 of the same lemma follows directly from Lemma 3.2. Finally, the relationship between atoms, orbits, and itineraries is established in the following result.
$\{B_k\}_{k \geq 1}$
in Lemma 3.3 is guaranteed by (3.2). Besides, the uniqueness in item 4 of the same lemma follows directly from Lemma 3.2. Finally, the relationship between atoms, orbits, and itineraries is established in the following result.
Lemma 3.4 (Lemmas 2.4 and 2.5 in [Reference Catsigeras, Guiraud and Meyroneinc2])
Let
![]() $x\in \widetilde X$
, and let
$x\in \widetilde X$
, and let
![]() $\theta \in \{1,\ldots ,N\}^{\mathbb N}$
be its itinerary, then
$\theta \in \{1,\ldots ,N\}^{\mathbb N}$
be its itinerary, then
![]() $f^{t+n}(x)\in A_{\theta _t\theta _{t+1}\ldots \theta _{t+n-1}}$
for every
$f^{t+n}(x)\in A_{\theta _t\theta _{t+1}\ldots \theta _{t+n-1}}$
for every
![]() $t\geq 0$
and
$t\geq 0$
and
![]() $n\geq 1$
. Moreover, if f also satisfies the separation property and
$n\geq 1$
. Moreover, if f also satisfies the separation property and
![]() $f^{t+n}(x)\in A_{i_1i_2\ldots i_n}$
for some
$f^{t+n}(x)\in A_{i_1i_2\ldots i_n}$
for some
![]() $t\geq 0$
and
$t\geq 0$
and
![]() $n\geq 1$
, then
$n\geq 1$
, then
![]() $(i_1,\ldots ,i_n)=(\theta _t,\ldots ,\theta _{t+n-1})$
.
$(i_1,\ldots ,i_n)=(\theta _t,\ldots ,\theta _{t+n-1})$
.
Remark 3.5 In a more general setting, atoms also allow defining the attractor of a piecewise contracting map (PCM) on a compact subset of
![]() $\mathbb R^k$
,
$\mathbb R^k$
,
![]() $k\geq 1$
. In [Reference Catsigeras, Guiraud, Meyroneinc and Ugalde3], the authors use a condition on the growth of the number of atoms of generation n with respect to the contraction rate establishing, in that case, that the attractor of a PCM has zero Hausdorff dimension. Furthermore, an example of a PCM on
$k\geq 1$
. In [Reference Catsigeras, Guiraud, Meyroneinc and Ugalde3], the authors use a condition on the growth of the number of atoms of generation n with respect to the contraction rate establishing, in that case, that the attractor of a PCM has zero Hausdorff dimension. Furthermore, an example of a PCM on
![]() $\mathbb R^3$
with positive topological entropy is exhibited in the same article. Moreover, in [Reference Gaivão5, Reference Gaivão and Nogueira6, Reference Janson and Öberg8 – Reference Laurent and Nogueira10], the authors study the asymptotic dynamics of parametrized families of piecewise affine contractions on the interval and circle using different approaches, without considering the concept of atom. Specifically, the authors of [Reference Gaivão5, Reference Gaivão and Nogueira6, Reference Janson and Öberg8, Reference Laurent and Nogueira9] prove that certain sets of real parameters for which those families admit non-periodic asymptotic dynamics have zero Hausdorff dimension. For the 3-parametric family studied in [Reference Laurent and Nogueira10], the computation of the Hausdorff dimension for the set of parameters associated with non-periodic dynamics was not carried out.
$\mathbb R^3$
with positive topological entropy is exhibited in the same article. Moreover, in [Reference Gaivão5, Reference Gaivão and Nogueira6, Reference Janson and Öberg8 – Reference Laurent and Nogueira10], the authors study the asymptotic dynamics of parametrized families of piecewise affine contractions on the interval and circle using different approaches, without considering the concept of atom. Specifically, the authors of [Reference Gaivão5, Reference Gaivão and Nogueira6, Reference Janson and Öberg8, Reference Laurent and Nogueira9] prove that certain sets of real parameters for which those families admit non-periodic asymptotic dynamics have zero Hausdorff dimension. For the 3-parametric family studied in [Reference Laurent and Nogueira10], the computation of the Hausdorff dimension for the set of parameters associated with non-periodic dynamics was not carried out.
4 Proof of Theorem 1.3
We say that C is a basic piece of
![]() $\Lambda $
if C is an
$\Lambda $
if C is an
![]() $\widetilde X$
-minimal component of the attractor of f; that is,
$\widetilde X$
-minimal component of the attractor of f; that is,
![]() $C\in \{\mathcal O_1,\ldots ,\mathcal O_{N_1},K_1,\ldots ,K_{N_2}\}$
(see Theorem 1.2). Also, if C is a basic piece of
$C\in \{\mathcal O_1,\ldots ,\mathcal O_{N_1},K_1,\ldots ,K_{N_2}\}$
(see Theorem 1.2). Also, if C is a basic piece of
![]() $\Lambda $
, we denote by
$\Lambda $
, we denote by
![]() $\mathcal A_n(C)$
the set of all atoms of generation n that intersect C. Because of (3.2), for every
$\mathcal A_n(C)$
the set of all atoms of generation n that intersect C. Because of (3.2), for every
![]() $n\geq 1$
, every basic piece is contained in the union of atoms of generation n.
$n\geq 1$
, every basic piece is contained in the union of atoms of generation n.
Lemma 4.1 Suppose that f satisfies the separation property and
![]() $D\subset \widetilde X$
. If K is a non-periodic basic piece of
$D\subset \widetilde X$
. If K is a non-periodic basic piece of
![]() $\Lambda $
and
$\Lambda $
and
![]() $\theta $
the itinerary of a point
$\theta $
the itinerary of a point
![]() $x\in K\cap \widetilde X$
, then
$x\in K\cap \widetilde X$
, then
In particular,
![]() $\#\mathcal A_n(K) = p_\theta (n)$
.
$\#\mathcal A_n(K) = p_\theta (n)$
.
Proof Let
![]() $n\geq 1$
. Consider
$n\geq 1$
. Consider
![]() $A\in \mathcal A_n(K)$
and let
$A\in \mathcal A_n(K)$
and let
![]() $y\in A$
. By the separation property, there exists
$y\in A$
. By the separation property, there exists
![]() $\epsilon>0$
such that
$\epsilon>0$
such that
![]() $\epsilon <\min \!\big \{\!\operatorname {\mathrm {dist}}(A_1,A_2)\ :\ A_1,A_2\in \mathcal A_n\,\text { and }\,A_1\neq A_2\big \}$
, where
$\epsilon <\min \!\big \{\!\operatorname {\mathrm {dist}}(A_1,A_2)\ :\ A_1,A_2\in \mathcal A_n\,\text { and }\,A_1\neq A_2\big \}$
, where
![]() $\operatorname {\mathrm {dist}}$
denotes the Euclidean metric on X. Next, by the
$\operatorname {\mathrm {dist}}$
denotes the Euclidean metric on X. Next, by the
![]() $\widetilde X$
-minimality of K, there exist
$\widetilde X$
-minimality of K, there exist
![]() $m\geq n$
and
$m\geq n$
and
![]() $x\in K\cap \widetilde X$
such that
$x\in K\cap \widetilde X$
such that
Thus, we deduce that
![]() $f^m(x)\in A$
. If
$f^m(x)\in A$
. If
![]() $\theta $
is the itinerary of x, from Lemma 3.4 and item (1) of Lemma 3.2, we deduce that
$\theta $
is the itinerary of x, from Lemma 3.4 and item (1) of Lemma 3.2, we deduce that
Then, we conclude that
![]() $y\in A_{\theta _{m-n}\ldots \theta _{m-1}}$
, where
$y\in A_{\theta _{m-n}\ldots \theta _{m-1}}$
, where
![]() $\theta _{m-n}\ldots \theta _{m-1}\in L_n(\theta )$
. Thus, we have that
$\theta _{m-n}\ldots \theta _{m-1}\in L_n(\theta )$
. Thus, we have that
In addition, the reciprocal contention of (4.1) is clearly valid.
Remark 4.2 Note that Lemma 4.1 is also valid for periodic basic pieces. In this case, the number of atoms that contain the periodic orbit is eventually constant equal to its period, which also coincides with its complexity.
Lemma 4.3 Suppose that f satisfies the separation property and
![]() $D\subset \widetilde X$
. Then, there exist
$D\subset \widetilde X$
. Then, there exist
![]() $k\geq 1$
and
$k\geq 1$
and
![]() $x_1,\ldots ,x_k\in \Lambda \cap \widetilde X$
such that
$x_1,\ldots ,x_k\in \Lambda \cap \widetilde X$
such that
 $$\begin{align*}\Lambda\subset \bigcup_{j=1}^k\left(\bigcup_{w\in L_n(\theta_j)}A_{w}\!\right)\qquad\forall\,n\geq1, \end{align*}$$
$$\begin{align*}\Lambda\subset \bigcup_{j=1}^k\left(\bigcup_{w\in L_n(\theta_j)}A_{w}\!\right)\qquad\forall\,n\geq1, \end{align*}$$
where
![]() $\theta _j$
is the itinerary of
$\theta _j$
is the itinerary of
![]() $x_j$
for every
$x_j$
for every
![]() $j\in \{1,\ldots ,k\}$
. In particular, we have that
$j\in \{1,\ldots ,k\}$
. In particular, we have that
![]() ${\#\mathcal A_n=p_{\theta _1}(n)+\cdots +p_{\theta _k}(n)}$
.
${\#\mathcal A_n=p_{\theta _1}(n)+\cdots +p_{\theta _k}(n)}$
.
Proof By Theorem 1.2, there exist a finite number
![]() $k:=N_1+N_2$
of different basic pieces of
$k:=N_1+N_2$
of different basic pieces of
![]() $\Lambda $
, which we sort by
$\Lambda $
, which we sort by
![]() $C_1,\ldots ,C_k$
. For every
$C_1,\ldots ,C_k$
. For every
![]() $i\in \{1,\ldots ,k\}$
, we choose a point
$i\in \{1,\ldots ,k\}$
, we choose a point
![]() $x_i\in C_i\cap \widetilde X$
. If
$x_i\in C_i\cap \widetilde X$
. If
![]() $\theta _i$
is the itinerary of
$\theta _i$
is the itinerary of
![]() $x_i$
for every
$x_i$
for every
![]() $i\in \{1,\ldots ,k\}$
, from Lemma 4.1 and Remark 4.2, we obtain the result.
$i\in \{1,\ldots ,k\}$
, from Lemma 4.1 and Remark 4.2, we obtain the result.
We want to have a notion of the attractor size of a PCIM. For this purpose, we will compute the Hausdorff dimension of
![]() $\Lambda $
using the comparison given in Lemma 2.1. Also, we will need the following elementary inequality.
$\Lambda $
using the comparison given in Lemma 2.1. Also, we will need the following elementary inequality.
Lemma 4.4 (log-sum inequality, Theorem 2.3 in [Reference Han and Kobayashi7])
Let
![]() $k\geq 1$
, and let
$k\geq 1$
, and let
![]() $a_1,\ldots ,a_k$
be nonnegative real numbers, then
$a_1,\ldots ,a_k$
be nonnegative real numbers, then
 $$\begin{align*}\left(\sum_{i=1}^k a_i\right)\log\!\left(\frac{1}{k}\sum_{i=1}^k a_i\right)\leq \sum_{i=1}^ka_i \log a_i. \end{align*}$$
$$\begin{align*}\left(\sum_{i=1}^k a_i\right)\log\!\left(\frac{1}{k}\sum_{i=1}^k a_i\right)\leq \sum_{i=1}^ka_i \log a_i. \end{align*}$$
The previous lemma will allow us to establish an upper bound for the box dimension and, therefore, for the Hausdorff dimension. With this idea, we can prove the following result.
Theorem 4.5 Suppose that f satisfies the separation property and
![]() $D\subset \widetilde X$
. Then,
$D\subset \widetilde X$
. Then,
![]() $\dim _{\mathcal H}(\Lambda ) \ =\dim _B(\Lambda )=0$
.
$\dim _{\mathcal H}(\Lambda ) \ =\dim _B(\Lambda )=0$
.
Proof Thanks to Lemma 2.1, it is enough to prove that
![]() $\dim _B(\Lambda )=0$
. By (3.2), we have that
$\dim _B(\Lambda )=0$
. By (3.2), we have that
Let
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $\epsilon _n:=\lambda ^n\operatorname {\mathrm {diam}}(X)$
. From item 1 of Lemma 3.3, we deduce that
$\epsilon _n:=\lambda ^n\operatorname {\mathrm {diam}}(X)$
. From item 1 of Lemma 3.3, we deduce that
![]() $\operatorname {\mathrm {diam}}(A)<\epsilon _n$
for every
$\operatorname {\mathrm {diam}}(A)<\epsilon _n$
for every
![]() $A\in \mathcal A_n$
. Next, from (4.2) and Lemma 4.3, there exist
$A\in \mathcal A_n$
. Next, from (4.2) and Lemma 4.3, there exist
![]() $x_1,\ldots ,x_k\in \Lambda \cap \widetilde X$
such that
$x_1,\ldots ,x_k\in \Lambda \cap \widetilde X$
such that
 $$\begin{align*}\ell(\Lambda,\epsilon_n)\leq \#\mathcal A_{n}=\sum_{j=1}^k p_{\theta_j}(n), \end{align*}$$
$$\begin{align*}\ell(\Lambda,\epsilon_n)\leq \#\mathcal A_{n}=\sum_{j=1}^k p_{\theta_j}(n), \end{align*}$$
where
![]() $\theta _j$
is the itinerary of
$\theta _j$
is the itinerary of
![]() $x_j$
for every
$x_j$
for every
![]() $j\in \{1,\ldots ,k\}$
. Now, applying the log-sum inequality to the nonnegative numbers
$j\in \{1,\ldots ,k\}$
. Now, applying the log-sum inequality to the nonnegative numbers
![]() $k\,p_{\theta _1}(n),\ldots ,k\,p_{\theta _k}(n)$
, we obtain
$k\,p_{\theta _1}(n),\ldots ,k\,p_{\theta _k}(n)$
, we obtain
 $$\begin{align*}\log \ell(\Lambda,\epsilon_n)\leq \log\!\left(\frac{1}{k}\sum_{j=1}^k k\,p_{\theta_j}(n)\!\right)\leq \frac{\sum\limits_{j=1}^k p_{\theta_j}(n)\log \!\big(k\,p_{\theta_j}(n)\big)}{\sum\limits_{j=1}^k p_{\theta_j}(n)}\leq \sum_{j=1}^k \log \!\big(k\,p_{\theta_j}(n)\big). \end{align*}$$
$$\begin{align*}\log \ell(\Lambda,\epsilon_n)\leq \log\!\left(\frac{1}{k}\sum_{j=1}^k k\,p_{\theta_j}(n)\!\right)\leq \frac{\sum\limits_{j=1}^k p_{\theta_j}(n)\log \!\big(k\,p_{\theta_j}(n)\big)}{\sum\limits_{j=1}^k p_{\theta_j}(n)}\leq \sum_{j=1}^k \log \!\big(k\,p_{\theta_j}(n)\big). \end{align*}$$
Thus, we deduce that
 $$ \begin{align} \frac{\log \ell(\Lambda,\epsilon_n)}{\log(1/\epsilon_n)}\leq \sum_{j=1}^k\frac{\log \!\big(k\,p_{\theta_j}(n)\big)}{\log(1/\epsilon_n)}=\sum_{j=1}^k\frac{\log \!\big(k\,p_{\theta_j}(n)\big)}{n\log(1/\lambda)+\log(1/\operatorname{\mathrm{diam}}(X))}. \end{align} $$
$$ \begin{align} \frac{\log \ell(\Lambda,\epsilon_n)}{\log(1/\epsilon_n)}\leq \sum_{j=1}^k\frac{\log \!\big(k\,p_{\theta_j}(n)\big)}{\log(1/\epsilon_n)}=\sum_{j=1}^k\frac{\log \!\big(k\,p_{\theta_j}(n)\big)}{n\log(1/\lambda)+\log(1/\operatorname{\mathrm{diam}}(X))}. \end{align} $$
By Theorem 3.1, we have that
![]() $p_{\theta _j}(n)$
is at most an affine function for n sufficiently large. Therefore,
$p_{\theta _j}(n)$
is at most an affine function for n sufficiently large. Therefore,
 $$\begin{align*}\frac{\log\!\big(k\,p_{\theta_j}(n)\big)}{n\log(1/\lambda)+\log(1/\operatorname{\mathrm{diam}}(X))}\;\stackrel{n\to\infty}\longrightarrow\; 0\qquad\forall\,j\in\{1,\ldots,k\}. \end{align*}$$
$$\begin{align*}\frac{\log\!\big(k\,p_{\theta_j}(n)\big)}{n\log(1/\lambda)+\log(1/\operatorname{\mathrm{diam}}(X))}\;\stackrel{n\to\infty}\longrightarrow\; 0\qquad\forall\,j\in\{1,\ldots,k\}. \end{align*}$$
Thus, from (4.3), we deduce that
![]() $\liminf _{\epsilon \to 0^+} \frac {\log \ell (\Lambda ,\epsilon )}{\log (1/\epsilon )}\leq 0$
, concluding that
$\liminf _{\epsilon \to 0^+} \frac {\log \ell (\Lambda ,\epsilon )}{\log (1/\epsilon )}\leq 0$
, concluding that
![]() ${\dim _B(\Lambda )=0}$
. Thus, by Lemma 2.1, we have that
${\dim _B(\Lambda )=0}$
. Thus, by Lemma 2.1, we have that
![]() $\dim _{\mathcal H}(\Lambda )=0$
.
$\dim _{\mathcal H}(\Lambda )=0$
.
Theorem 4.5 corresponds to the first part of Theorem 1.3. Now, we are going to prove the second and final part. Recall that
![]() $\Lambda \cap \widetilde X$
is a nonempty and f-invariant set whenever f is piecewise monotonic and
$\Lambda \cap \widetilde X$
is a nonempty and f-invariant set whenever f is piecewise monotonic and
![]() $D\subset \widetilde X$
. Given
$D\subset \widetilde X$
. Given
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $\epsilon>0$
, we say that a set
$\epsilon>0$
, we say that a set
![]() $E\subset \Lambda \cap \widetilde X$
is an
$E\subset \Lambda \cap \widetilde X$
is an
![]() $(n,\epsilon )$
-spanning set for
$(n,\epsilon )$
-spanning set for
![]() $\Lambda \cap \widetilde X$
if, for every
$\Lambda \cap \widetilde X$
if, for every
![]() $x\in \Lambda \cap \widetilde X$
, there exists
$x\in \Lambda \cap \widetilde X$
, there exists
![]() $y\in E$
such that
$y\in E$
such that
Thus, we define
![]() $r_n(\epsilon ,\Lambda \cap \widetilde X)$
as the smallest cardinality of every
$r_n(\epsilon ,\Lambda \cap \widetilde X)$
as the smallest cardinality of every
![]() $(n,\epsilon )$
-spanning set for
$(n,\epsilon )$
-spanning set for
![]() $\Lambda \cap \widetilde X$
with respect to f. The number
$\Lambda \cap \widetilde X$
with respect to f. The number
![]() $r_n(\epsilon ,K)$
is well defined when K is a compact set over which f is continuous; however, this is not the usual case for PCIMs.
$r_n(\epsilon ,K)$
is well defined when K is a compact set over which f is continuous; however, this is not the usual case for PCIMs.
Lemma 4.6 Suppose that f is piecewise monotonic and
![]() $D\subset \widetilde X$
. Then, for every
$D\subset \widetilde X$
. Then, for every
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $\epsilon>0$
,
$\epsilon>0$
,
![]() $r_n(\epsilon ,\Lambda \cap \widetilde X)$
is a finite number.
$r_n(\epsilon ,\Lambda \cap \widetilde X)$
is a finite number.
Proof Let
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $\epsilon>0$
. From item 2 of Lemma 3.3, there exists
$\epsilon>0$
. From item 2 of Lemma 3.3, there exists
![]() $n_0\geq n$
such that
$n_0\geq n$
such that
Next, denote by
![]() $\mathcal C(\mathcal A_{n_0},n)$
the collection of all connected components of
$\mathcal C(\mathcal A_{n_0},n)$
the collection of all connected components of
Since f is piecewise monotonic, the collection
![]() $\mathcal C(\mathcal A_{n_0},n)$
is finite. Furthermore, from (3.2), we can consider the subcollection
$\mathcal C(\mathcal A_{n_0},n)$
is finite. Furthermore, from (3.2), we can consider the subcollection
![]() $\mathcal C^*(\mathcal A_{n_0},n)\subset \mathcal C(\mathcal A_{n_0},n)$
of connected components that intersect
$\mathcal C^*(\mathcal A_{n_0},n)\subset \mathcal C(\mathcal A_{n_0},n)$
of connected components that intersect
![]() $\Lambda \cap \widetilde X$
, whose union covers said set. Thus, for every
$\Lambda \cap \widetilde X$
, whose union covers said set. Thus, for every
![]() $B\in \mathcal C^*(\mathcal A_{n_0},n)$
, we can take
$B\in \mathcal C^*(\mathcal A_{n_0},n)$
, we can take
![]() $x_B\in B\cap \Lambda \cap \widetilde X\neq \emptyset $
. It is clear that
$x_B\in B\cap \Lambda \cap \widetilde X\neq \emptyset $
. It is clear that
![]() $E_{n,\epsilon }:=\{x_B\ :\ B\in \mathcal C^*(\mathcal A_{n_0},n)\}\subset \Lambda \cap \widetilde X$
is a finite
$E_{n,\epsilon }:=\{x_B\ :\ B\in \mathcal C^*(\mathcal A_{n_0},n)\}\subset \Lambda \cap \widetilde X$
is a finite
![]() $(n,\epsilon )$
-spanning set. This implies that
$(n,\epsilon )$
-spanning set. This implies that
![]() $r_n(\epsilon ,\Lambda \cap \widetilde X)<\infty $
, concluding the proof.
$r_n(\epsilon ,\Lambda \cap \widetilde X)<\infty $
, concluding the proof.
Next, we establish and prove the last part of Theorem 1.3.
Theorem 4.7 If f satisfies the separation property and
![]() $D\kern1.2pt{\subset}\kern1.2pt \widetilde X$
, then
$D\kern1.2pt{\subset}\kern1.2pt \widetilde X$
, then
![]() ${h_{top}\big (f|(\Lambda \kern1.2pt{\cap}\kern1.2pt \widetilde X)\kern-1pt\big )\kern1pt{=}\kern1.2pt0}$
.
${h_{top}\big (f|(\Lambda \kern1.2pt{\cap}\kern1.2pt \widetilde X)\kern-1pt\big )\kern1pt{=}\kern1.2pt0}$
.
Proof Let
![]() $n\geq 1$
, and let
$n\geq 1$
, and let
![]() $\epsilon>0$
be such that
$\epsilon>0$
be such that
Consider
![]() $n_0\geq n$
such that (4.4) holds. Note that every atom of generation
$n_0\geq n$
such that (4.4) holds. Note that every atom of generation
![]() $n_0$
or higher has at most one element of
$n_0$
or higher has at most one element of
![]() $\Delta $
. Since f satisfies the separation property, we deduce, from (3.1) and Lemma 4.3, that
$\Delta $
. Since f satisfies the separation property, we deduce, from (3.1) and Lemma 4.3, that
 $$\begin{align*}\#\mathcal A_{n+n_0}-\#\mathcal A_{n_0}=\sum_{m=n_0}^{n_0+n-1}\big(\#\mathcal A_{m+1}-\#\mathcal A_{m}\big)\leq n(N-1). \end{align*}$$
$$\begin{align*}\#\mathcal A_{n+n_0}-\#\mathcal A_{n_0}=\sum_{m=n_0}^{n_0+n-1}\big(\#\mathcal A_{m+1}-\#\mathcal A_{m}\big)\leq n(N-1). \end{align*}$$
Next, noting that
![]() $\#\mathcal C(\mathcal A_{n_0},n)=\#\mathcal A_{n+n_0}$
, we have the following inequalities:
$\#\mathcal C(\mathcal A_{n_0},n)=\#\mathcal A_{n+n_0}$
, we have the following inequalities:
Thus, we obtain that
 $$\begin{align*}h_{top}\big(f|(\Lambda\cap\widetilde X)\big)\leq \lim_{\epsilon\to0}\limsup_{n\to\infty}\frac{\log \big(n(N-1)+\#\mathcal A_{n_0}\big)}{n}=0, \end{align*}$$
$$\begin{align*}h_{top}\big(f|(\Lambda\cap\widetilde X)\big)\leq \lim_{\epsilon\to0}\limsup_{n\to\infty}\frac{\log \big(n(N-1)+\#\mathcal A_{n_0}\big)}{n}=0, \end{align*}$$
which concludes the proof.
Remark 4.8 From Lemma 4.3, we know that the number of atoms of generation
![]() $n\geq 1$
is directly related to the complexity of the system. In fact, it can be said that the eventual affine linear growth of the complexity associated with f allows us to prove Theorem 4.7. If f is not injective, the relationship between topological entropy and the complexity is not clear. Still, it is common to define the topological entropy of piecewise continuous maps of the interval using the complexity associated with the orbits of the system.
$n\geq 1$
is directly related to the complexity of the system. In fact, it can be said that the eventual affine linear growth of the complexity associated with f allows us to prove Theorem 4.7. If f is not injective, the relationship between topological entropy and the complexity is not clear. Still, it is common to define the topological entropy of piecewise continuous maps of the interval using the complexity associated with the orbits of the system.
Acknowledgment
We sincerely thank P. Guiraud and E. Ugalde for their valuable support and guidance in the initial ideas of this study. Also, we would like to thank the anonymous referee for the careful review of this manuscript; their comments greatly improved our work.