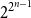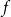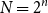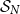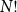1. Introduction
We consider feedback shift registers, linear in the eldest bit (in
![]() $\mathbb{F}_2$
), given as
$\mathbb{F}_2$
), given as
Here
is an arbitrary
![]() $n-1$
bit Boolean function (the ‘feedback’ or ‘logic’), and we will consider all
$n-1$
bit Boolean function (the ‘feedback’ or ‘logic’), and we will consider all
![]() $2^{2^{n-1}}$
possible
$2^{2^{n-1}}$
possible
![]() $f$
to be equally likely. We write
$f$
to be equally likely. We write
and note that the map
 \begin{eqnarray} \pi _f\;:\;\mathbb{F}_2^n & \to &\mathbb{F}_2^n \nonumber \\[5pt] (x_0,x_1,\ldots,x_{n-1}) & \mapsto & (x_1,\ldots,x_{n-1},x_n) \\[5pt] & = & (x_1,\ldots,x_{n-1},x_0 \oplus f(x_1,\ldots,x_{n-1})). \nonumber \end{eqnarray}
\begin{eqnarray} \pi _f\;:\;\mathbb{F}_2^n & \to &\mathbb{F}_2^n \nonumber \\[5pt] (x_0,x_1,\ldots,x_{n-1}) & \mapsto & (x_1,\ldots,x_{n-1},x_n) \\[5pt] & = & (x_1,\ldots,x_{n-1},x_0 \oplus f(x_1,\ldots,x_{n-1})). \nonumber \end{eqnarray}
is a permutation on
![]() $N$
objects.
$N$
objects.
In 1959 [Reference Golomb, Welch and Goldstein17], see also Chapter VII of [Reference Golomb16], Golomb, Welch and Goldstein suggest that the flat random permutation in
![]() ${\mathcal{S}}_N$
, with all
${\mathcal{S}}_N$
, with all
![]() $N!$
permutations
$N!$
permutations
![]() $\pi$
equally likely, gives a good approximation to the cycle structure of
$\pi$
equally likely, gives a good approximation to the cycle structure of
![]() $\pi _f$
, in the sense that the cycle structure of
$\pi _f$
, in the sense that the cycle structure of
![]() $\pi _f$
is close to the cycle structure of
$\pi _f$
is close to the cycle structure of
![]() $\pi$
, in various aspects of distribution, such as the average length of the longest cycle. See [Reference Wolfram and Golomb21], especially the section ‘Cellular Automata and Nonlinear Shift Registers’, which includes an anecdote that Golomb used custom hardware modules in 1956 to experiment on this conjecture, and these ran about 3 million times faster than the general purpose computer on the same problem.
$\pi$
, in various aspects of distribution, such as the average length of the longest cycle. See [Reference Wolfram and Golomb21], especially the section ‘Cellular Automata and Nonlinear Shift Registers’, which includes an anecdote that Golomb used custom hardware modules in 1956 to experiment on this conjecture, and these ran about 3 million times faster than the general purpose computer on the same problem.
We prove that the longest cycle part of this conjecture is true, and more, namely that
![]() $\pi$
and
$\pi$
and
![]() $\pi _f$
have the same limit distributions in the infinite-dimensional simplex
$\pi _f$
have the same limit distributions in the infinite-dimensional simplex
![]() $\Delta$
, for the processesFootnote
1
of long cycle lengths, scaled by
$\Delta$
, for the processesFootnote
1
of long cycle lengths, scaled by
![]() $N$
. This does not answer other aspects of Golomb’s conjecture, involving the distribution of the number of cycles, or behaviour of short cycles.
$N$
. This does not answer other aspects of Golomb’s conjecture, involving the distribution of the number of cycles, or behaviour of short cycles.
There are two natural ways to view the large cycles of the random permutation
![]() $\pi _f$
, which we now describe briefly. First, there is the process of largest cycle lengths: write
$\pi _f$
, which we now describe briefly. First, there is the process of largest cycle lengths: write
![]() $L_i$
for the length of the
$L_i$
for the length of the
![]() $i^{\mathrm{th}}$
longest cycle of
$i^{\mathrm{th}}$
longest cycle of
![]() $\pi _f$
, with
$\pi _f$
, with
![]() $L_i \;:\!=\; 0$
if the permutation has fewer than
$L_i \;:\!=\; 0$
if the permutation has fewer than
![]() $i$
cycles, so that always
$i$
cycles, so that always
![]() $L_1+L_2+\cdots = N$
, where
$L_1+L_2+\cdots = N$
, where
![]() $N=2^n$
. Write
$N=2^n$
. Write
![]() ${\overline{{\boldsymbol{{L}}}}}={\overline{{\boldsymbol{{L}}}}}(N)$
for the process of scaled cycle lengths,
${\overline{{\boldsymbol{{L}}}}}={\overline{{\boldsymbol{{L}}}}}(N)$
for the process of scaled cycle lengths,
![]() ${\overline{{\boldsymbol{{L}}}}}=(L_1/N,L_2/N,\ldots\!)$
. Second, there is the process of cycle lengths taken in age order: pick a random
${\overline{{\boldsymbol{{L}}}}}=(L_1/N,L_2/N,\ldots\!)$
. Second, there is the process of cycle lengths taken in age order: pick a random
![]() $n$
-tuple, take
$n$
-tuple, take
![]() $A_1$
to be the length of the cycle of
$A_1$
to be the length of the cycle of
![]() $\pi _f$
containing that first
$\pi _f$
containing that first
![]() $n$
-tuple, then pick a random
$n$
-tuple, then pick a random
![]() $n$
-tuple from among those not on the first cycle, take
$n$
-tuple from among those not on the first cycle, take
![]() $A_2$
to be the length of the cycle of
$A_2$
to be the length of the cycle of
![]() $\pi _f$
containing that second
$\pi _f$
containing that second
![]() $n$
-tuple, and so on. Write
$n$
-tuple, and so on. Write
![]() ${\overline{{\boldsymbol{{A}}}}}={\overline{{\boldsymbol{{A}}}}}(N)=(A_1/N,A_2/N,\ldots\!)$
for the process of scaled cycle lengths in age order. For flat random permutations
${\overline{{\boldsymbol{{A}}}}}={\overline{{\boldsymbol{{A}}}}}(N)=(A_1/N,A_2/N,\ldots\!)$
for the process of scaled cycle lengths in age order. For flat random permutations
![]() $\pi$
in place of
$\pi$
in place of
![]() $\pi _f$
, the limit of
$\pi _f$
, the limit of
![]() $\overline{{\boldsymbol{{A}}}}$
is called the GEM process (after Griffiths [Reference Griffiths18], Engen [Reference Engen15] and McCloskey [Reference McCloskey20]); it is the distribution of
$\overline{{\boldsymbol{{A}}}}$
is called the GEM process (after Griffiths [Reference Griffiths18], Engen [Reference Engen15] and McCloskey [Reference McCloskey20]); it is the distribution of
![]() $(1-U_1,U_1(1-U_2),U_1U_2(1-U_3),\ldots\!)$
, where
$(1-U_1,U_1(1-U_2),U_1U_2(1-U_3),\ldots\!)$
, where
![]() $U,U_1,U_2,\ldots$
are independent and uniformly distributed in
$U,U_1,U_2,\ldots$
are independent and uniformly distributed in
![]() $(0,1)$
. The Poisson–Dirichlet process is
$(0,1)$
. The Poisson–Dirichlet process is
![]() $(X_1,X_2,\ldots\!)$
where
$(X_1,X_2,\ldots\!)$
where
![]() $X_i$
is the
$X_i$
is the
![]() $i^{{th}}$
largest of
$i^{{th}}$
largest of
![]() $1-U_1,U_1(1-U_2),U_1U_2(1-U_3),\ldots$
. This construction gives the simplest way to characterise the Poisson–Dirichlet process, PD. For flat random permutations, the limit of
$1-U_1,U_1(1-U_2),U_1U_2(1-U_3),\ldots$
. This construction gives the simplest way to characterise the Poisson–Dirichlet process, PD. For flat random permutations, the limit of
![]() $\overline{{\boldsymbol{{L}}}}$
is PD.Footnote
2
See Section 5.1 for a review of these concepts, including more discussion of age-order and the GEM limit as used in (5). See also [Reference Arratia, Barbour and Tavaré3]. Formally, our result is the following:
$\overline{{\boldsymbol{{L}}}}$
is PD.Footnote
2
See Section 5.1 for a review of these concepts, including more discussion of age-order and the GEM limit as used in (5). See also [Reference Arratia, Barbour and Tavaré3]. Formally, our result is the following:
Theorem 1.
Consider the random permutation
![]() $\pi _f$
given by (3), where all
$\pi _f$
given by (3), where all
![]() $2^{2^{n-1}}$
possible
$2^{2^{n-1}}$
possible
![]() $f$
in (2) are equally likely. Then, as
$f$
in (2) are equally likely. Then, as
![]() $n \to \infty$
,
$n \to \infty$
,
![]() ${\overline{{\boldsymbol{{L}}}}}(N)$
converges in distribution to
${\overline{{\boldsymbol{{L}}}}}(N)$
converges in distribution to
![]() $(X_1,X_2,\ldots\!)$
with PD distribution.
$(X_1,X_2,\ldots\!)$
with PD distribution.
Writing
![]() $\to ^d$
to denote convergence in distribution, we can succinctly summarise the conclusion of Theorem 1 by writing
$\to ^d$
to denote convergence in distribution, we can succinctly summarise the conclusion of Theorem 1 by writing
We note some easy consequences of Theorem 1. Theorem 1 is equivalent to
with GEM distribution, by a soft argument involving size-biased permutations, originally given by [Reference Donnelly and Joyce13]. By projecting onto the first coordinate,Footnote 3 we see
By taking expectations, we see
Of course, the uniform distributional limit in (6) makes no local limit claim; it is plausible that
![]() $N \,{\mathbb{P}}(A_1 = i) \to 1$
holds uniformly in
$N \,{\mathbb{P}}(A_1 = i) \to 1$
holds uniformly in
![]() $n \lt i \lt N-n$
. For any fixed
$n \lt i \lt N-n$
. For any fixed
![]() $i \gt 1$
, the statement
$i \gt 1$
, the statement
![]() $N \,{\mathbb{P}}(A_1 = i) \to 1$
is false. It is true that
$N \,{\mathbb{P}}(A_1 = i) \to 1$
is false. It is true that
![]() $N \,{\mathbb{P}}(A_1 = 1) = N \,{\mathbb{P}}(A_1 = N) =1$
. And for any fixed
$N \,{\mathbb{P}}(A_1 = 1) = N \,{\mathbb{P}}(A_1 = N) =1$
. And for any fixed
![]() $j\gt 0$
the statement
$j\gt 0$
the statement
![]() $N \,{\mathbb{P}}(A_1 = N-j) \to 1$
is false; see [Reference Coppersmith, Rhoades and VanderKam10].
$N \,{\mathbb{P}}(A_1 = N-j) \to 1$
is false; see [Reference Coppersmith, Rhoades and VanderKam10].
We work with the de Bruijn graph
![]() $D_{n-1}$
, with edge set
$D_{n-1}$
, with edge set
![]() $\mathbb{F}_2^n$
and vertex set
$\mathbb{F}_2^n$
and vertex set
![]() $\mathbb{F}_2^{n-1}$
; edge
$\mathbb{F}_2^{n-1}$
; edge
![]() $e = (y_0,y_1,\ldots,y_{n-1})$
goes from vertex
$e = (y_0,y_1,\ldots,y_{n-1})$
goes from vertex
![]() $v= (y_0,y_1,\ldots,y_{n-2})$
to vertex
$v= (y_0,y_1,\ldots,y_{n-2})$
to vertex
![]() $v'= (y_1,\ldots,y_{n-1})$
. The graph
$v'= (y_1,\ldots,y_{n-1})$
. The graph
![]() $D_{n-1}$
is 2-in, 2-out regular, and a random feedback logic
$D_{n-1}$
is 2-in, 2-out regular, and a random feedback logic
![]() $f$
corresponds to a random resolution of all vertices; the resolution at a vertex
$f$
corresponds to a random resolution of all vertices; the resolution at a vertex
![]() $v$
pairs the incoming edges,
$v$
pairs the incoming edges,
![]() $0v$
and
$0v$
and
![]() $1v$
, with the outgoing edges
$1v$
, with the outgoing edges
![]() $v0$
and
$v0$
and
![]() $v1$
. The cycles of a random permutation
$v1$
. The cycles of a random permutation
![]() $\pi _f$
correspond exactly to the edge-disjoint cycles in a random circuit decomposition of the Eulerian graph
$\pi _f$
correspond exactly to the edge-disjoint cycles in a random circuit decomposition of the Eulerian graph
![]() $D_{n-1}$
.
$D_{n-1}$
.
2. A survey of the Proof of Theorem 1
In this section we survey the proof of Theorem 1 while omitting many necessary technicalities. It is hoped the reader will thus have a better notion of what is happening, and why, as s/he reads the later sections. We begin with the notion of relativisation. Suppose, as for example in the hypotheses of Theorem 1, that one has for each
![]() $n=1,2,\dots$
a probability
$n=1,2,\dots$
a probability
![]() $P_n$
on the permutations of a set
$P_n$
on the permutations of a set
![]() ${\mathcal{E}}_n$
. Let
${\mathcal{E}}_n$
. Let
![]() $\pi \in{\mathcal{S}}({\mathcal{E}}_n)$
be one such permutation, and let
$\pi \in{\mathcal{S}}({\mathcal{E}}_n)$
be one such permutation, and let
![]() $\boldsymbol{{e}}=(e_1,\dots,e_k)$
be a
$\boldsymbol{{e}}=(e_1,\dots,e_k)$
be a
![]() $k$
-tuple of, for now, distinct elements from the domain
$k$
-tuple of, for now, distinct elements from the domain
![]() ${\mathcal{E}}_n$
. Picturing the permutation
${\mathcal{E}}_n$
. Picturing the permutation
![]() $\pi$
as a collection of disjoint cycles, one sees that by ignoring all elements of
$\pi$
as a collection of disjoint cycles, one sees that by ignoring all elements of
![]() ${\mathcal{E}}_n$
except for the
${\mathcal{E}}_n$
except for the
![]() $e_i$
, these latter are permuted among themselves. That is, starting with
$e_i$
, these latter are permuted among themselves. That is, starting with
![]() $e_i$
, traverse the cycle of
$e_i$
, traverse the cycle of
![]() $\pi$
containing this element: –
$\pi$
containing this element: –
until after one or more steps an element
![]() $e_j$
is encountered. (It is possible for the first element so encountered to be
$e_j$
is encountered. (It is possible for the first element so encountered to be
![]() $e_i$
, which happens when the traversed cycle contains only a single member of the
$e_i$
, which happens when the traversed cycle contains only a single member of the
![]() $k$
-tuple
$k$
-tuple
![]() $\boldsymbol{{e}}$
.) Since the
$\boldsymbol{{e}}$
.) Since the
![]() $e_i$
are given in a definite order, the induced permutation among these elements is readily identified with an element of
$e_i$
are given in a definite order, the induced permutation among these elements is readily identified with an element of
![]() ${\mathcal{S}}_k$
, the permutations of the set
${\mathcal{S}}_k$
, the permutations of the set
![]() $\{1,2,\dots,k\}$
. Altogether, we have a function
$\{1,2,\dots,k\}$
. Altogether, we have a function
which we call relativisation. Here,
![]() $({\mathcal{E}}_n)_k$
denotes the ordered
$({\mathcal{E}}_n)_k$
denotes the ordered
![]() $k$
-tuples drawn from
$k$
-tuples drawn from
![]() ${\mathcal{E}}_n$
without replacement. We shall prove: Suppose that for every fixed
${\mathcal{E}}_n$
without replacement. We shall prove: Suppose that for every fixed
![]() $k\ge 1$
the sequence of distributions induced on
$k\ge 1$
the sequence of distributions induced on
![]() ${\mathcal{S}}_k$
by the functions
${\mathcal{S}}_k$
by the functions
![]() ${\textit{rel}}_{n,k}$
and the probability distributions
${\textit{rel}}_{n,k}$
and the probability distributions
![]() $P_n$
tends to the uniform distribution. (For brevity, we say ‘
$P_n$
tends to the uniform distribution. (For brevity, we say ‘
![]() $P_n$
has the uniform relativisation property’.) Then the large cycle process associated with
$P_n$
has the uniform relativisation property’.) Then the large cycle process associated with
![]() $P_n$
tends to Poisson–Dirichlet. The proof that the uniform relativisation property implies the Poisson–Dirichlet property appears in Section 5.3, as Lemma 10.
$P_n$
tends to Poisson–Dirichlet. The proof that the uniform relativisation property implies the Poisson–Dirichlet property appears in Section 5.3, as Lemma 10.
Henceforth we specialise to the particular sequence
![]() $P_n$
of interest: the sets
$P_n$
of interest: the sets
![]() ${\mathcal{E}}_n$
are the binary
${\mathcal{E}}_n$
are the binary
![]() $n$
-tuples
$n$
-tuples
![]() ${\mathbb{F}_2}^n$
, and
${\mathbb{F}_2}^n$
, and
![]() $P_n$
assigns equal weight to each of the
$P_n$
assigns equal weight to each of the
![]() $2^{N/2}$
shift register permutations
$2^{N/2}$
shift register permutations
![]() $\pi _f$
(and no weight to other permutations), where
$\pi _f$
(and no weight to other permutations), where
![]() $N=2^n$
. Let
$N=2^n$
. Let
![]() $S_{n,k}$
denote the Cartesian product
$S_{n,k}$
denote the Cartesian product
For technical reasons we define the relativisation function
![]() ${\textit{rel}}_{n,k}$
on the set
${\textit{rel}}_{n,k}$
on the set
![]() $S_{n,k}$
, see Definition (8) in Section 4.10. Nevertheless, pairs
$S_{n,k}$
, see Definition (8) in Section 4.10. Nevertheless, pairs
![]() $(f,{\mathbb{E}\,})$
in which
$(f,{\mathbb{E}\,})$
in which
![]() $\boldsymbol{{e}}$
contains a repeated element may be safely ignored by the reader for now, and only the primary objective be kept in mind: to show that as
$\boldsymbol{{e}}$
contains a repeated element may be safely ignored by the reader for now, and only the primary objective be kept in mind: to show that as
![]() $(f,\boldsymbol{{e}})$
varies over
$(f,\boldsymbol{{e}})$
varies over
![]() $S_{n,k}$
the coverage of
$S_{n,k}$
the coverage of
![]() ${\mathcal{S}}_k$
under the relativisation function
${\mathcal{S}}_k$
under the relativisation function
![]() ${\textit{rel}}_{n,k}$
is approximately uniform.
${\textit{rel}}_{n,k}$
is approximately uniform.
Roughly speaking, this objective is accomplished by partitioning the set
![]() $S_{n,k}$
into blocks such that the restriction of
$S_{n,k}$
into blocks such that the restriction of
![]() ${\textit{rel}}_{n,k}$
to each block of the partition yields an almost uniform coverage of
${\textit{rel}}_{n,k}$
to each block of the partition yields an almost uniform coverage of
![]() ${\mathcal{S}}_k$
. The description of these blocks involves the notion of toggle. Let
${\mathcal{S}}_k$
. The description of these blocks involves the notion of toggle. Let
![]() $v\in{\mathbb{F}_2}^{n-1}$
and
$v\in{\mathbb{F}_2}^{n-1}$
and
![]() $f$
be a feedback function; then the toggle of the function
$f$
be a feedback function; then the toggle of the function
![]() $f$
at the point
$f$
at the point
![]() $v$
is the function
$v$
is the function
![]() $f_v$
which disagrees with
$f_v$
which disagrees with
![]() $f$
only at the argument
$f$
only at the argument
![]() $v$
:
$v$
:
 \begin{equation*} f_v(w) = \begin {cases} f(w) & w\neq v \\[5pt] 1\oplus f(w) & w=v \, . \end {cases} \end{equation*}
\begin{equation*} f_v(w) = \begin {cases} f(w) & w\neq v \\[5pt] 1\oplus f(w) & w=v \, . \end {cases} \end{equation*}
That is, we have toggled a single bit in the truth table of
![]() $f$
. Toggling a feedback function has a predictable effect on
$f$
. Toggling a feedback function has a predictable effect on
![]() ${\textit{rel}}_{n,k}(\pi _f,\boldsymbol{{e}})$
. In particular, for
${\textit{rel}}_{n,k}(\pi _f,\boldsymbol{{e}})$
. In particular, for
![]() $x\in{\mathbb{F}_2}, v\in{\mathbb{F}_2}^{n-1}$
, if
$x\in{\mathbb{F}_2}, v\in{\mathbb{F}_2}^{n-1}$
, if
![]() $xv=\pi _f^i(e_a)$
and
$xv=\pi _f^i(e_a)$
and
and, (with
![]() $a\lt b$
),
$a\lt b$
),
![]() $\bar{x}v=\pi _f^j(e_b)$
, and
$\bar{x}v=\pi _f^j(e_b)$
, and
then (let the reader check by drawing a picture)
where
![]() $(a,b)$
denotes a transposition in
$(a,b)$
denotes a transposition in
![]() ${\mathcal{S}}_k$
. The blocks in our partition of
${\mathcal{S}}_k$
. The blocks in our partition of
![]() $S_{n,k}$
arise as follows: given
$S_{n,k}$
arise as follows: given
![]() $(f,\boldsymbol{{e}})\in{S_{n,k}}$
, we determine, in a way explained below, a subset of size
$(f,\boldsymbol{{e}})\in{S_{n,k}}$
, we determine, in a way explained below, a subset of size
![]() $m$
,
$m$
,
and define the block containing
![]() $(f,\boldsymbol{{e}})$
to be the
$(f,\boldsymbol{{e}})$
to be the
![]() $2^m$
different toggles
$2^m$
different toggles
![]() $(f_U,\boldsymbol{{e}})$
,
$(f_U,\boldsymbol{{e}})$
,
![]() $U$
ranging over subsets of
$U$
ranging over subsets of
![]() $V$
. Here,
$V$
. Here,
![]() $f_U$
denotes function
$f_U$
denotes function
![]() $f$
toggled at all
$f$
toggled at all
![]() $v\in U$
. For the block to be well defined, it must be the case that the choice of
$v\in U$
. For the block to be well defined, it must be the case that the choice of
![]() $V$
will be the same for all
$V$
will be the same for all
![]() $f_U$
as for
$f_U$
as for
![]() $f$
. This necessitates the introduction of a subset
$f$
. This necessitates the introduction of a subset
![]() $H\subseteq{S_{n,k}}$
, the ‘happy event’, see equation (42) in Section 4.8. It turns out that the happy event is almost all of
$H\subseteq{S_{n,k}}$
, the ‘happy event’, see equation (42) in Section 4.8. It turns out that the happy event is almost all of
![]() $S_{n,k}$
,
$S_{n,k}$
,
![]() $|H|/|{S_{n,k}}|\to 1$
, and for
$|H|/|{S_{n,k}}|\to 1$
, and for
![]() $(f,\boldsymbol{{e}})\in H$
the blocks are well defined. Moreover for each such block we have an ordered sequence of transpositions
$(f,\boldsymbol{{e}})\in H$
the blocks are well defined. Moreover for each such block we have an ordered sequence of transpositions
![]() $(a_i, b_i)\in{\mathcal{S}}_k$
(
$(a_i, b_i)\in{\mathcal{S}}_k$
(
![]() $1\le i\le m)$
with
$1\le i\le m)$
with
where
![]() $U=\{i_1,\dots,i_{\ell }\}$
. For
$U=\{i_1,\dots,i_{\ell }\}$
. For
![]() $m$
sufficiently large, almost all such sequences of transpositions yield
$m$
sufficiently large, almost all such sequences of transpositions yield
![]() $2^m$
compositions which cover
$2^m$
compositions which cover
![]() ${\mathcal{S}}_k$
almost uniformly. (Lemma 7 in Section 4.9 proves that for all
${\mathcal{S}}_k$
almost uniformly. (Lemma 7 in Section 4.9 proves that for all
![]() $k,\epsilon$
there is an
$k,\epsilon$
there is an
![]() $m$
such that the distribution induced on
$m$
such that the distribution induced on
![]() ${\mathcal{S}}_k$
is within
${\mathcal{S}}_k$
is within
![]() $\epsilon$
of uniform in total variation for all but an
$\epsilon$
of uniform in total variation for all but an
![]() $\epsilon$
fraction of possible sequences.)
$\epsilon$
fraction of possible sequences.)
Let us say something about how, given
![]() $(f,\boldsymbol{{e}})\in{S_{n,k}}$
, the
$(f,\boldsymbol{{e}})\in{S_{n,k}}$
, the
![]() $m$
-subset
$m$
-subset
![]() $V$
of
$V$
of
![]() ${\mathbb{F}_2}^{n-1}$
is chosen. The pair
${\mathbb{F}_2}^{n-1}$
is chosen. The pair
![]() $(f,\boldsymbol{{e}})$
determines
$(f,\boldsymbol{{e}})$
determines
![]() $k$
segments
$k$
segments
in which the length
![]() $t$
is taken to be approximately
$t$
is taken to be approximately
![]() $N^{3/5}$
. For this length it is almost certain that not only are the initial edges
$N^{3/5}$
. For this length it is almost certain that not only are the initial edges
![]() $e_a$
distinct, but in fact all
$e_a$
distinct, but in fact all
![]() $k\times (t+1)$
of the edges
$k\times (t+1)$
of the edges
![]() $\pi _f^i(e_a)$
are distinct. This feature is included in the definition (42) of event
$\pi _f^i(e_a)$
are distinct. This feature is included in the definition (42) of event
![]() $H$
. Given that
$H$
. Given that
![]() $\pi _f$
acts by shifting left and bringing in one new bit on the right, each sequence (8) is equivalent to a binary sequence
$\pi _f$
acts by shifting left and bringing in one new bit on the right, each sequence (8) is equivalent to a binary sequence
of length
![]() $n+t$
. To be considered for membership in
$n+t$
. To be considered for membership in
![]() $V$
, an
$V$
, an
![]() $(n-1)$
-tuple
$(n-1)$
-tuple
![]() $v^{\#}$
must appear in two of these binary sequences; that is, for some
$v^{\#}$
must appear in two of these binary sequences; that is, for some
![]() $a\lt b$
and some bit
$a\lt b$
and some bit
![]() $x\in \{0,1\}$
$x\in \{0,1\}$
One may ask as
![]() $(f,\boldsymbol{{e}})$
varies uniformly over
$(f,\boldsymbol{{e}})$
varies uniformly over
![]() $S_{n,k}$
what is the probability of finding such leftmost
$S_{n,k}$
what is the probability of finding such leftmost
![]() $(n-1)$
-repeats
$(n-1)$
-repeats
![]() $(i,j)$
in various regions of the plane? Remarkably, such points when rescaled as
$(i,j)$
in various regions of the plane? Remarkably, such points when rescaled as
![]() $(i/N^{1/2},j/N^{1/2})$
constitute, in the limit with respect to total variation distance, a familiar Poisson process. Thanks to this limiting behaviour we can estimate not only the probability of finding
$(i/N^{1/2},j/N^{1/2})$
constitute, in the limit with respect to total variation distance, a familiar Poisson process. Thanks to this limiting behaviour we can estimate not only the probability of finding
![]() $v^{\#}$
’s which satisfy the above minimal constraint for
$v^{\#}$
’s which satisfy the above minimal constraint for
![]() $V$
-membership, but also the probability of finding
$V$
-membership, but also the probability of finding
![]() $m$
$m$
![]() $v^{\#}$
’s lying in a much more stringently constrained geometry, which geometry implies
$v^{\#}$
’s lying in a much more stringently constrained geometry, which geometry implies
![]() $(f,\boldsymbol{{e}})\in H$
. Section 4 is devoted to proving these properties of
$(f,\boldsymbol{{e}})\in H$
. Section 4 is devoted to proving these properties of
![]() $H$
and
$H$
and
![]() $V$
under the assumption that the probabilities in question can be approximated by a Poisson process.
$V$
under the assumption that the probabilities in question can be approximated by a Poisson process.
We conclude our survey by saying how this last assumption is justified. We present in Section 3 an algorithm called sequential editing which begins with
![]() $k$
random binary sequences (referred to as coin toss sequences) and edits them in such a way that the result of the editing is a set of
$k$
random binary sequences (referred to as coin toss sequences) and edits them in such a way that the result of the editing is a set of
![]() $k$
sequences which could have been produced by choosing
$k$
sequences which could have been produced by choosing
![]() $(f,\boldsymbol{{e}})\in{S_{n,k}}$
and forming the
$(f,\boldsymbol{{e}})\in{S_{n,k}}$
and forming the
![]() $k$
segments (8). Even more, the probability of obtaining a particular set of sequences is exactly the same, whether we choose
$k$
segments (8). Even more, the probability of obtaining a particular set of sequences is exactly the same, whether we choose
![]() $(f,\boldsymbol{{e}})$
and form (8), or flip
$(f,\boldsymbol{{e}})$
and form (8), or flip
![]() $k(n+t)$
coins and perform sequential editing. (This is proven in Theorem 5 of Section 3.6).
$k(n+t)$
coins and perform sequential editing. (This is proven in Theorem 5 of Section 3.6).
Moreover, there is a ‘good event’
![]() $G$
,
$G$
,
![]() $G\subseteq{\mathbb{F}_2}^{(n+t)k}$
, such that when the initial coin toss sequence
$G\subseteq{\mathbb{F}_2}^{(n+t)k}$
, such that when the initial coin toss sequence
![]() $C$
belongs to
$C$
belongs to
![]() $G$
the leftmost
$G$
the leftmost
![]() $(n-1)$
-repeats in the edited sequence appear in exactly the same locations
$(n-1)$
-repeats in the edited sequence appear in exactly the same locations
![]() $(i,j)$
as they do in
$(i,j)$
as they do in
![]() $C$
. Since
$C$
. Since
![]() $G$
is almost all of
$G$
is almost all of
![]() ${\mathbb{F}_2}^{(n+t)k}$
(Theorem 4 in Section 3), the study of the
${\mathbb{F}_2}^{(n+t)k}$
(Theorem 4 in Section 3), the study of the
![]() $(f,\boldsymbol{{e}})$
-induced pairs is reduced to the study of leftmost
$(f,\boldsymbol{{e}})$
-induced pairs is reduced to the study of leftmost
![]() $(n-1)$
-repeats in
$(n-1)$
-repeats in
![]() $k$
random sequences. This new process is by no means easily evaluated, but fortunately it is in the realm of the Chen–Stein method as presented and extended in [Reference Arratia, Goldstein and Gordon6]. In such a manner the above described approximation is justified.
$k$
random sequences. This new process is by no means easily evaluated, but fortunately it is in the realm of the Chen–Stein method as presented and extended in [Reference Arratia, Goldstein and Gordon6]. In such a manner the above described approximation is justified.
Looking back at this survey, it appears that the components in the proof of Theorem 1 have been described almost in the reverse order that they appear in the sequel. May we wish that in the end the determined reader will understand the proof forwards and backwards.
3. Comparisons with coin tossing sequences
Throughout this section these conventions will be observed:
![]() $a_i,b_i,C_i$
denote bits;
$a_i,b_i,C_i$
denote bits;
![]() $v_i$
denotes an
$v_i$
denotes an
![]() $(n-1)$
-long sequence of bits; and
$(n-1)$
-long sequence of bits; and
![]() $e_i$
denotes an
$e_i$
denotes an
![]() $n$
-long sequence of bits. A tool used in the proof of Theorem 1 is to compare the bit sequence
$n$
-long sequence of bits. A tool used in the proof of Theorem 1 is to compare the bit sequence
![]() $b_0,b_1,\dots b_{n+t}$
generated by a randomly chosen feedback logic
$b_0,b_1,\dots b_{n+t}$
generated by a randomly chosen feedback logic
![]() $f$
with a coin toss sequence, denoted in this section
$f$
with a coin toss sequence, denoted in this section
![]() $C_0,C_1,\dots, C_{n+t}$
. A bit sequence
$C_0,C_1,\dots, C_{n+t}$
. A bit sequence
![]() $b_i$
generated by a feedback logic has what we refer to as the de Bruijn property: it satisfies a recursion of the form
$b_i$
generated by a feedback logic has what we refer to as the de Bruijn property: it satisfies a recursion of the form
![]() $b_{t+n} = b_t + f(b_{t+1},\dots,b_{t+n-1})$
. In a sequence with the de Bruijn property the
$b_{t+n} = b_t + f(b_{t+1},\dots,b_{t+n-1})$
. In a sequence with the de Bruijn property the
![]() $n$
-long words
$n$
-long words
![]() $0v$
and
$0v$
and
![]() $1v$
must be followed by different bits. Of course, not every coin toss sequence has the de Bruijn property. The sequential edit, defined below, of a coin toss sequence
$1v$
must be followed by different bits. Of course, not every coin toss sequence has the de Bruijn property. The sequential edit, defined below, of a coin toss sequence
![]() $C_i$
is obtained in a left-to-right bit-by-bit manner and adheres as closely as possible to
$C_i$
is obtained in a left-to-right bit-by-bit manner and adheres as closely as possible to
![]() $C_i$
, changes being made only when forced by the desire to respect the de Bruijn property. On the other hand, the shotgun edit, also defined below, of a sequence
$C_i$
, changes being made only when forced by the desire to respect the de Bruijn property. On the other hand, the shotgun edit, also defined below, of a sequence
![]() $C_i$
is a naive imitation of a sequential edit. In a sense and circumstances to be made precise, by the combination of Theorems 2 and 4, with high probability, these two produce the same output.
$C_i$
is a naive imitation of a sequential edit. In a sense and circumstances to be made precise, by the combination of Theorems 2 and 4, with high probability, these two produce the same output.
3.1. Sequential editing
We begin with an
![]() $n+t$
long bit sequence
$n+t$
long bit sequence
The new bit sequence of the same length,
is produced by following two rules:
-
Rule 1:
 \begin{equation*} b_i = C_i, 0 \le i \le n-1; \end{equation*}
\begin{equation*} b_i = C_i, 0 \le i \le n-1; \end{equation*}
-
Rule 2: For
 $i\ge 0$
determine bit
$i\ge 0$
determine bit
 $b_{i+n}$
by first asking if the feedback logic bit
$b_{i+n}$
by first asking if the feedback logic bit
 $f(b_{i+1},\dots,b_{i+n-1})$
has been previously defined; if so, set
$f(b_{i+1},\dots,b_{i+n-1})$
has been previously defined; if so, set
 $b_{i+n}$
accordingly:otherwise, define (and remember) the feedback logic bit in such a way that
$b_{i+n}$
accordingly:otherwise, define (and remember) the feedback logic bit in such a way that \begin{equation*} b_{i+n} = b_{i} \oplus f(b_{i+1},\dots,b_{i+n-1}); \end{equation*}
\begin{equation*} b_{i+n} = b_{i} \oplus f(b_{i+1},\dots,b_{i+n-1}); \end{equation*}
 $b_{i+n}$
and
$b_{i+n}$
and
 $C_{i+n}$
agree.
$C_{i+n}$
agree.
Here, we give some terminology and indexing practice. We say that the sequence
![]() $b$
is obtained from the coin toss sequence
$b$
is obtained from the coin toss sequence
![]() $C$
by sequential editing. Each time a
$C$
by sequential editing. Each time a
![]() $b_{i+n}$
has freedom – because the necessary feedback bit has not yet been set – we set the feedback bit so that
$b_{i+n}$
has freedom – because the necessary feedback bit has not yet been set – we set the feedback bit so that
![]() $b_{i+n}=C_{i+n}$
; but at any time the bit
$b_{i+n}=C_{i+n}$
; but at any time the bit
![]() $b_{i+n}$
‘has no choice’, we assign it the forced value. Such a time
$b_{i+n}$
‘has no choice’, we assign it the forced value. Such a time
![]() $i$
is a time of a potential edit; if it turns out (by chance) that
$i$
is a time of a potential edit; if it turns out (by chance) that
![]() $b_{i+n}$
and
$b_{i+n}$
and
![]() $C_{i+n}$
agree, then no actual edit has taken place; if it is forced to take
$C_{i+n}$
agree, then no actual edit has taken place; if it is forced to take
![]() $b_{i+n}$
equal to
$b_{i+n}$
equal to
![]() $\overline{C_{i+n}}$
then an actual edit has taken place, and we label the time of this actual edit as
$\overline{C_{i+n}}$
then an actual edit has taken place, and we label the time of this actual edit as
![]() $i$
rather than
$i$
rather than
![]() $i+n$
. The sequence
$i+n$
. The sequence
![]() $b$
obtained by this process always has the de Bruijn property. In terms of the de Bruijn graph with all vertices resolved, a potential edit occurs at time
$b$
obtained by this process always has the de Bruijn property. In terms of the de Bruijn graph with all vertices resolved, a potential edit occurs at time
![]() $i$
when
$i$
when
![]() $e_{i}$
, the edge from
$e_{i}$
, the edge from
![]() $v_{i}$
to
$v_{i}$
to
![]() $v_{i+1}$
, is going in to a vertex
$v_{i+1}$
, is going in to a vertex
![]() $v=v_{i+1}$
where
$v=v_{i+1}$
where
![]() $f(v)$
, the resolution of that vertex, is already known, so that the successor edge,
$f(v)$
, the resolution of that vertex, is already known, so that the successor edge,
![]() $e_{i+1}=\pi _f(e_i)$
is determined — this is equivalent to determining
$e_{i+1}=\pi _f(e_i)$
is determined — this is equivalent to determining
![]() $b_{i+n}$
, the rightmost bit of
$b_{i+n}$
, the rightmost bit of
![]() $e_{i+1}$
.
$e_{i+1}$
.
3.2. Shotgun editing
Now we define a second, generally different, way to edit the coin toss sequence
![]() $C_i$
to produce a sequence
$C_i$
to produce a sequence
![]() $a_i$
. We call this the shotgun edit. Unlike
$a_i$
. We call this the shotgun edit. Unlike
![]() $b_i$
obtained by sequential editing, the sequence
$b_i$
obtained by sequential editing, the sequence
![]() $a_i$
obtained by shotgun editing may not have the de Bruijn property.
$a_i$
obtained by shotgun editing may not have the de Bruijn property.
The symbols
![]() $I$
,
$I$
,
![]() $J$
,
$J$
,
![]() $I_k$
,
$I_k$
,
![]() $J_k$
denote intervals of integers contained in the
$J_k$
denote intervals of integers contained in the
![]() $(n+t)$
-long interval
$(n+t)$
-long interval
![]() $[0,1,2,\dots,t+n-1]$
. We use
$[0,1,2,\dots,t+n-1]$
. We use
![]() $\ell (I)$
and
$\ell (I)$
and
![]() $r(I)$
to denote the left- and right- endpoints of the interval
$r(I)$
to denote the left- and right- endpoints of the interval
![]() $I$
. A binary sequence
$I$
. A binary sequence
has an
![]() $m$
-long repeat at
$m$
-long repeat at
![]() $(I,J)$
if
$(I,J)$
if
![]() $\ell (I)\lt \ell (J)$
,
$\ell (I)\lt \ell (J)$
,
![]() $|I|=m=|J|$
and the two ordered
$|I|=m=|J|$
and the two ordered
![]() $m$
-tuples
$m$
-tuples
![]() $(C_i\;:\;i\in I)$
and
$(C_i\;:\;i\in I)$
and
![]() $(C_j\;:\;j\in J)$
are equal. We say that (9) has a leftmost
Footnote
4
$(C_j\;:\;j\in J)$
are equal. We say that (9) has a leftmost
Footnote
4
![]() $m$
-long repeat at
$m$
-long repeat at
![]() $(I,J)$
if, in addition, either
$(I,J)$
if, in addition, either
![]() $\ell (I)=0$
or
$\ell (I)=0$
or
This given, the shotgun edit of coin toss (9) is readily defined: make a list
![]() $(I_1,J_1),(I_2,J_2),\dots$
of all the leftmost
$(I_1,J_1),(I_2,J_2),\dots$
of all the leftmost
![]() $n$
-long repeats found in (9). Let
$n$
-long repeats found in (9). Let
 \begin{equation*} a_i = \begin {cases} \overline {C_i} & \textit {if} i=r(J_k) \textit {some} k\\[5pt] C_i & \textit {otherwise.} \end {cases} \end{equation*}
\begin{equation*} a_i = \begin {cases} \overline {C_i} & \textit {if} i=r(J_k) \textit {some} k\\[5pt] C_i & \textit {otherwise.} \end {cases} \end{equation*}
3.3. Zero and first generation words
Let
be a coin toss sequence whose leftmost
![]() $n$
-tuple repeats occur at
$n$
-tuple repeats occur at
![]() $(I_1,J_1),(I_2,J_2),\dots$
. The zero-generation words of length
$(I_1,J_1),(I_2,J_2),\dots$
. The zero-generation words of length
![]() $h$
are simply words of the form:
$h$
are simply words of the form:
A first-generation word is a zero-generation word with exactly one bit complemented, with the index of the complemented bit required to be
![]() $r(J_k)$
for some
$r(J_k)$
for some
![]() $k$
:
$k$
:
3.4. The good event
 $G_{(t)}$
$G_{(t)}$
We always consider
![]() $n$
to be understood, but sometimes we will not want to emphasise the role of
$n$
to be understood, but sometimes we will not want to emphasise the role of
![]() $t$
, hence writing
$t$
, hence writing
![]() $G \equiv{G_{(t)}}$
. Henceforth we shall always assume that
$G \equiv{G_{(t)}}$
. Henceforth we shall always assume that
![]() $t$
is at most
$t$
is at most
![]() $N=2^n$
, since we are interested in cycle lengths for permutations on a set of size
$N=2^n$
, since we are interested in cycle lengths for permutations on a set of size
![]() $N$
. Let
$N$
. Let
be a length
![]() $n+t$
coin toss sequence whose leftmost
$n+t$
coin toss sequence whose leftmost
![]() $n$
-repeats occur at
$n$
-repeats occur at
![]() $(I_1,J_1),(I_2,J_2),\dots$
. Then the good event
$(I_1,J_1),(I_2,J_2),\dots$
. Then the good event
![]() $G_{(t)}$
is defined to be the conjunction of these six conditions:
$G_{(t)}$
is defined to be the conjunction of these six conditions:
-
(a) neither the initial
 $n$
-long word of the coin toss sequence, nor any of its
$n$
-long word of the coin toss sequence, nor any of its
 $1$
-offsFootnote
5
is repeated (probability of failure
$1$
-offsFootnote
5
is repeated (probability of failure
 $O(tn/N)$
);
$O(tn/N)$
); -
(b) all intersections of the form
 $I_k\cap J_{k^{\prime }}$
are empty (probability of failure
$I_k\cap J_{k^{\prime }}$
are empty (probability of failure
 $O(t^3n/N^2+tn^3/N)$
);
$O(t^3n/N^2+tn^3/N)$
); -
(c) the sets
 $I_1,I_2,\dots$
are pairwise disjoint; likewise
$I_1,I_2,\dots$
are pairwise disjoint; likewise
 $J_1,J_2,\dots$
(probability of failure
$J_1,J_2,\dots$
(probability of failure
 $O(t^2n^2/N^2+t^3n/N^2+tn^3/N)$
);
$O(t^2n^2/N^2+t^3n/N^2+tn^3/N)$
); -
(d) no first-generation word of length
 $n-1$
equals a zero-generation word of length
$n-1$
equals a zero-generation word of length
 $n-1$
, or another first-generation word of length
$n-1$
, or another first-generation word of length
 $n-1$
(probability of failure
$n-1$
(probability of failure
 $O(t^4n^2/N^3+t^3n^3/N^2+tn^3/N)$
);
$O(t^4n^2/N^3+t^3n^3/N^2+tn^3/N)$
); -
(e) for every leftmost
 $(n-1)$
-repeat
$(n-1)$
-repeat
 $(I,J)$
we havefor all
$(I,J)$
we havefor all \begin{equation*} r(J_k)\notin I \cup J \cup \{\ell (I)-1,\ell (J)-1\}, \end{equation*}
\begin{equation*} r(J_k)\notin I \cup J \cup \{\ell (I)-1,\ell (J)-1\}, \end{equation*}
 $k$
(probability of failure
$k$
(probability of failure
 $O(t^3n/N^2+t^2n^2/N^2+tn^3/N)$
);
$O(t^3n/N^2+t^2n^2/N^2+tn^3/N)$
);
-
(f) there is no
 $(2n-1)$
-repeat (probability of failure
$(2n-1)$
-repeat (probability of failure
 $O(t^2/N^2)$
).
$O(t^2/N^2)$
).
The indicated probabilities of failure will be proven below in Theorem 4. First, though, we will prove a theorem that explains why
![]() $G$
is called the ‘good event’.
$G$
is called the ‘good event’.
Theorem 2. If the coin toss sequence
belongs to the good event
![]() $G$
, then
$G$
, then
Conclusion 1.
The sequentially edited sequence
![]() $b_i$
and the shotgun edited sequence
$b_i$
and the shotgun edited sequence
![]() $a_i$
agree; and
$a_i$
agree; and
Conclusion 2.
The sequentially edited sequence
![]() $b_i$
and the coin toss sequence have their leftmost
$b_i$
and the coin toss sequence have their leftmost
![]() $(n-1)$
repeats at exactly the same positions.
$(n-1)$
repeats at exactly the same positions.
These conclusions, along with Theorem 4 in the next subsection, will provide substantial control of the prevalence of
![]() $(n-1)$
-tuple repeats
$(n-1)$
-tuple repeats
Proof of Conclusion
1. Assume, to the contrary, that the
![]() $a$
and
$a$
and
![]() $b$
sequences differ; let
$b$
sequences differ; let
![]() $i$
be the first position of disagreement:
$i$
be the first position of disagreement:
There are two possibilities: (1)
![]() $a_i\neq b_i$
and
$a_i\neq b_i$
and
![]() $b_i=C_i$
; or (2)
$b_i=C_i$
; or (2)
![]() $a_i\neq b_i$
and
$a_i\neq b_i$
and
![]() $a_i=C_i$
.
$a_i=C_i$
.
Case (1). Since
![]() $a_i\neq C_i$
we have
$a_i\neq C_i$
we have
![]() $i=r(J_k)$
for some
$i=r(J_k)$
for some
![]() $k$
, and there is a leftmost
$k$
, and there is a leftmost
![]() $n$
-repeat in the
$n$
-repeat in the
![]() $C$
sequence at
$C$
sequence at
![]() $(I_k,J_k)$
. But
$(I_k,J_k)$
. But
![]() $a_j=C_j$
for
$a_j=C_j$
for
![]() $j\in I_k$
(condition(b)); and
$j\in I_k$
(condition(b)); and
![]() $a_j=C_j$
for
$a_j=C_j$
for
![]() $j\in J_k\setminus \{i\}$
(condition (c)). Hence
$j\in J_k\setminus \{i\}$
(condition (c)). Hence
![]() $b_j=a_j=C_j$
for
$b_j=a_j=C_j$
for
![]() $j \in I_k\cup J_k\setminus \{i\}$
. But
$j \in I_k\cup J_k\setminus \{i\}$
. But
![]() $b_i\neq a_i \neq C_i$
, so in fact the
$b_i\neq a_i \neq C_i$
, so in fact the
![]() $b$
-sequence itself has an
$b$
-sequence itself has an
![]() $n$
-repeat at
$n$
-repeat at
![]() $(I_k,J_k)$
. But the
$(I_k,J_k)$
. But the
![]() $b$
-sequence has the de Bruijn property, and so the
$b$
-sequence has the de Bruijn property, and so the
![]() $(I_k,J_k)$
repeat can be backed up
$(I_k,J_k)$
repeat can be backed up
![]() $d=\ell (I_k)\gt 0$
steps to reveal
$d=\ell (I_k)\gt 0$
steps to reveal
Since
![]() $i-d\lt i$
,
$i-d\lt i$
,
so in fact
The word on the right side of the last equality is either a zero-generation or a first-generation word; either case contradicts condition (a).
Case (2). Because
![]() $i$
is a sequential edit point, (
$i$
is a sequential edit point, (
![]() $b_i\neq C_i$
), it must be that the
$b_i\neq C_i$
), it must be that the
![]() $(n-1)$
-long word
$(n-1)$
-long word
![]() $(b_{i-n+1},\dots, b_{i-1})$
is appearing for a second or later time, say
$(b_{i-n+1},\dots, b_{i-1})$
is appearing for a second or later time, say
We must have
![]() $b_{\ell }=C_{\ell }$
, since no sequential editing took place at time
$b_{\ell }=C_{\ell }$
, since no sequential editing took place at time
![]() $\ell$
. (The relevant bit of the feedback logic had not yet been determined.) We know that
$\ell$
. (The relevant bit of the feedback logic had not yet been determined.) We know that
![]() $b_i\neq b_{\ell }$
, else the
$b_i\neq b_{\ell }$
, else the
![]() $b$
-sequence contains an
$b$
-sequence contains an
![]() $n$
-repeat which, as was explained in Case (1), backs up to yield the contradictory (10). So,
$n$
-repeat which, as was explained in Case (1), backs up to yield the contradictory (10). So,
![]() $C_i\neq b_i \neq b_{\ell } = C_{\ell }$
; that is,
$C_i\neq b_i \neq b_{\ell } = C_{\ell }$
; that is,
![]() $C_i=C_{\ell }$
and
$C_i=C_{\ell }$
and
Because
![]() $i$
is the first point at which the
$i$
is the first point at which the
![]() $b$
and
$b$
and
![]() $a$
sequences disagree,
$a$
sequences disagree,
Suppose (for the sake of a contradiction) that none of the
![]() $a$
bits appearing on either side of this last Equation (11) was edited by the shotgun process. Then we have
$a$
bits appearing on either side of this last Equation (11) was edited by the shotgun process. Then we have
We have thus discovered an
![]() $n$
-long repeat in the coin toss sequence, but it might not be a leftmost
$n$
-long repeat in the coin toss sequence, but it might not be a leftmost
![]() $n$
-long repeat. So, we look left to determine the least
$n$
-long repeat. So, we look left to determine the least
![]() $m\ge 1$
such that either
$m\ge 1$
such that either
![]() $\ell -n+1-m\lt 0$
(i.e., you’ve gone ‘off the board’) or the run of equalities is broken:
$\ell -n+1-m\lt 0$
(i.e., you’ve gone ‘off the board’) or the run of equalities is broken:
One of these two will happen for
![]() $m\lt n$
or else the
$m\lt n$
or else the
![]() $C$
-sequence is found to contain a
$C$
-sequence is found to contain a
![]() $2n$
-repeat, contradicting assumption (f). But then we have found a leftmost
$2n$
-repeat, contradicting assumption (f). But then we have found a leftmost
![]() $n$
-repeat in the
$n$
-repeat in the
![]() $C$
-sequence beginning at
$C$
-sequence beginning at
![]() $\ell -n+1-m+1$
and
$\ell -n+1-m+1$
and
![]() $i-n+1-m+1$
; shotgun editing would consequently modify the
$i-n+1-m+1$
; shotgun editing would consequently modify the
![]() $C$
-bit at position
$C$
-bit at position
![]() $i-n+1-m+1+n-1=i-m+1$
. Since
$i-n+1-m+1+n-1=i-m+1$
. Since
we have found that one of the
![]() $C$
-bits on the right side of equation (12), namely the one whose index is
$C$
-bits on the right side of equation (12), namely the one whose index is
![]() $i-m+1$
, is changed by shotgun editing, contrary to our earlier supposition that none of the
$i-m+1$
, is changed by shotgun editing, contrary to our earlier supposition that none of the
![]() $a$
bits appearing on either side of the equality (11) was edited by the shotgun process.
$a$
bits appearing on either side of the equality (11) was edited by the shotgun process.
By condition (c), every
![]() $n$
-long word in the
$n$
-long word in the
![]() $a$
sequence either is a zero-generation word (matches exactly the corresponding
$a$
sequence either is a zero-generation word (matches exactly the corresponding
![]() $C$
-bits) or is a first-generation word (matches the corresponding
$C$
-bits) or is a first-generation word (matches the corresponding
![]() $C$
-bits with exactly one change). Thus, at least one of the
$C$
-bits with exactly one change). Thus, at least one of the
![]() $n$
-long words appearing in (11) is a first-generation word, and this contradicts condition (d).
$n$
-long words appearing in (11) is a first-generation word, and this contradicts condition (d).
Proof of Conclusion
2. We will make use of the
![]() $a$
and
$a$
and
![]() $b$
sequences being equal. Suppose we have a leftmost
$b$
sequences being equal. Suppose we have a leftmost
![]() $(n-1)$
repeat in the coin toss sequence,
$(n-1)$
repeat in the coin toss sequence,
By condition (e), none of these
![]() $2n$
bits (or
$2n$
bits (or
![]() $2n-2$
in case
$2n-2$
in case
![]() $i=0$
) can be edited by the shotgun edit. Hence, we have a leftmost
$i=0$
) can be edited by the shotgun edit. Hence, we have a leftmost
![]() $(n-1)$
-repeat at the same place in the
$(n-1)$
-repeat at the same place in the
![]() $a$
sequence, whence also the
$a$
sequence, whence also the
![]() $b$
sequence.
$b$
sequence.
On the other hand, suppose we have a leftmost
![]() $(n-1)$
-repeat in the
$(n-1)$
-repeat in the
![]() $a$
sequence,
$a$
sequence,
and
If
then
![]() $(a_{i},\dots,a_{i+n-2})$
is a first-generation word of length
$(a_{i},\dots,a_{i+n-2})$
is a first-generation word of length
![]() $n-1$
which equals the first- or zero-generation word
$n-1$
which equals the first- or zero-generation word
![]() $(a_{\ell },\dots,a_{\ell +n-2})$
, which is forbidden by condition (d). So,
$(a_{\ell },\dots,a_{\ell +n-2})$
, which is forbidden by condition (d). So,
Similarly,
Altogether by (14),(15),(16) we have
If
![]() $i=0$
, then the last is a leftmost
$i=0$
, then the last is a leftmost
![]() $(n-1)$
-repeat in the
$(n-1)$
-repeat in the
![]() $C$
sequence, as asserted. So, to conclude, suppose for the sake of a contradiction that
$C$
sequence, as asserted. So, to conclude, suppose for the sake of a contradiction that
![]() $i\gt 0$
and that
$i\gt 0$
and that
![]() $C_{i-1}= C_{\ell -1}$
. Then, we have an
$C_{i-1}= C_{\ell -1}$
. Then, we have an
![]() $n$
-long repeat
$n$
-long repeat
Sliding left for
![]() $m$
steps, we will encounter a leftmost
$m$
steps, we will encounter a leftmost
![]() $n$
-repeat in the coin toss sequence
$n$
-repeat in the coin toss sequence
with
![]() $0\le m\lt n-1$
by condition (f). But in such a case
$0\le m\lt n-1$
by condition (f). But in such a case
![]() $a_{\ell +n-2-m} \neq C_{\ell +n-2-m}$
by the definition of shotgun editing. However, for
$a_{\ell +n-2-m} \neq C_{\ell +n-2-m}$
by the definition of shotgun editing. However, for
![]() $0\le m\lt n-1$
$0\le m\lt n-1$
and by (16)
![]() $a_{\ell +n-2-m} = C_{\ell +n-2-m}$
The supposition that
$a_{\ell +n-2-m} = C_{\ell +n-2-m}$
The supposition that
![]() $i\gt 0$
and that
$i\gt 0$
and that
![]() $C_{i-1}= C_{\ell -1}$
has been contradicted, and so (17) is, indeed, a leftmost
$C_{i-1}= C_{\ell -1}$
has been contradicted, and so (17) is, indeed, a leftmost
![]() $(n-1)$
-repeat as needed.
$(n-1)$
-repeat as needed.
3.5. Probability
In this section we bound the probability of failure of any one of the conditions (a)–(f) appearing in Theorem 2. Let
![]() $S$
be a set of relations, each of the form
$S$
be a set of relations, each of the form
![]() $C_i=C_j$
or
$C_i=C_j$
or
![]() $C_i \neq C_j$
with
$C_i \neq C_j$
with
![]() $i\lt j$
. We assume always that
$i\lt j$
. We assume always that
![]() $S$
has at most one relation for a given
$S$
has at most one relation for a given
![]() $(i,j)$
; that is, we don’t allow both
$(i,j)$
; that is, we don’t allow both
![]() $C_i=C_j$
and
$C_i=C_j$
and
![]() $C_i \neq C_j$
. What is the probability that a coin toss sequence
$C_i \neq C_j$
. What is the probability that a coin toss sequence
![]() $C$
will satisfy such a set of relations? The desired probability is
$C$
will satisfy such a set of relations? The desired probability is
![]() $2^{-|S|}$
provided the graph associated with
$2^{-|S|}$
provided the graph associated with
![]() $S$
is cycle free. The graph we have in mind here is
$S$
is cycle free. The graph we have in mind here is
![]() $(V,E)$
where
$(V,E)$
where
![]() $V$
is the set
$V$
is the set
![]() $0,1,2,\dots$
and
$0,1,2,\dots$
and
![]() $E$
is the set of pairs
$E$
is the set of pairs
![]() $\{i,j\}$
such that at least one (and by convention exactly one) of the relations
$\{i,j\}$
such that at least one (and by convention exactly one) of the relations
![]() $C_i=C_j$
or
$C_i=C_j$
or
![]() $C_i \neq C_j$
belongs to
$C_i \neq C_j$
belongs to
![]() $S$
.
$S$
.
In particular, if the graph of
![]() $S$
consists of the
$S$
consists of the
![]() $n$
pairs
$n$
pairs
![]() $(i,j),(i+1,j+1),\dots,(i+n-1,\, j+n-1)$
the probability is
$(i,j),(i+1,j+1),\dots,(i+n-1,\, j+n-1)$
the probability is
![]() $2^{-n}=1/N$
. This is quite clear if
$2^{-n}=1/N$
. This is quite clear if
![]() $I=\{i,\dots,i+n-1\}$
and
$I=\{i,\dots,i+n-1\}$
and
![]() $J=\{j,\dots,j+n-1\}$
are disjoint, since then the underlying graph has no vertex of degree 2. It is also true if
$J=\{j,\dots,j+n-1\}$
are disjoint, since then the underlying graph has no vertex of degree 2. It is also true if
![]() $I$
and
$I$
and
![]() $J$
overlap, (of course
$J$
overlap, (of course
![]() $I\neq J$
): every vertex of degree
$I\neq J$
): every vertex of degree
![]() $2$
in the graph (i.e., every element of
$2$
in the graph (i.e., every element of
![]() $I\cap J$
) has one larger neighbour and one smaller neighbour. But a cycle would require at least one vertex with two smaller neighbours.
$I\cap J$
) has one larger neighbour and one smaller neighbour. But a cycle would require at least one vertex with two smaller neighbours.
We will have frequent occasion below, in the proof of Theorem 4, to consider sets
![]() $S$
whose graphs are the union of two such
$S$
whose graphs are the union of two such
![]() $n$
-sets of pairs
$n$
-sets of pairs
![]() $(i_1,j_1)$
,
$(i_1,j_1)$
,
![]() $(i_1+1,j_1+1), \dots, (i_1+n-1,j_1+n-1)$
and
$(i_1+1,j_1+1), \dots, (i_1+n-1,j_1+n-1)$
and
![]() $(i_2,j_2)$
,
$(i_2,j_2)$
,
![]() $(i_2+1,j_2+1), \dots$
$(i_2+1,j_2+1), \dots$
![]() $(i_2+n-1,j_2+n-1)$
. We begin with a lemma which shows that in many situations which arise in these proofs the probability in question is
$(i_2+n-1,j_2+n-1)$
. We begin with a lemma which shows that in many situations which arise in these proofs the probability in question is
![]() $1/N^2$
.
$1/N^2$
.
Lemma 3.
Let
![]() $\mathcal{G}$
be the graph whose edges consist of two sets of pairs
$\mathcal{G}$
be the graph whose edges consist of two sets of pairs
and
Then
![]() $\mathcal{G}$
is cycle free if any one of the following three conditions holds, where we assume
$\mathcal{G}$
is cycle free if any one of the following three conditions holds, where we assume
![]() $i_1\lt j_1$
and
$i_1\lt j_1$
and
![]() $i_2\lt j_2$
:
$i_2\lt j_2$
:
-
(i)
 $I_1\cap I_2 =\emptyset$
$I_1\cap I_2 =\emptyset$
-
(ii)
 $J_1\cap J_2 =\emptyset$
$J_1\cap J_2 =\emptyset$
-
(iii)
 $(I_1\cup I_2) \cap (J_1\cup J_2) = \emptyset$
and
$(I_1\cup I_2) \cap (J_1\cup J_2) = \emptyset$
and
 $j_2-i_2 \neq j_1-i_1$
.
$j_2-i_2 \neq j_1-i_1$
.
Proof. If
![]() $I_1\cap I_2=\emptyset$
then no vertex has two neighbours larger than it. If
$I_1\cap I_2=\emptyset$
then no vertex has two neighbours larger than it. If
![]() $J_1\cap J_2=\emptyset$
then no vertex has two neighbours smaller than it. In case (iii), all edges out of
$J_1\cap J_2=\emptyset$
then no vertex has two neighbours smaller than it. In case (iii), all edges out of
![]() $I_1\cup I_2$
go to
$I_1\cup I_2$
go to
![]() $J_1\cup J_2$
, and vice versa. A cycle, if there is one, lies within the bipartite graph whose parts are
$J_1\cup J_2$
, and vice versa. A cycle, if there is one, lies within the bipartite graph whose parts are
![]() $I_1\cup I_2$
and
$I_1\cup I_2$
and
![]() $J_1\cup J_2$
, and clearly the cycle must alternate edges between
$J_1\cup J_2$
, and clearly the cycle must alternate edges between
![]() $(I_1,J_1)$
and
$(I_1,J_1)$
and
![]() $(I_2,J_2)$
types. If the cycle (of necessity even in length) uses
$(I_2,J_2)$
types. If the cycle (of necessity even in length) uses
![]() $\ell$
edges of the first sort and
$\ell$
edges of the first sort and
![]() $\ell$
of the second, then it has travelled
$\ell$
of the second, then it has travelled
![]() $\ell \times (j_1-i_1)$
in one direction and
$\ell \times (j_1-i_1)$
in one direction and
![]() $\ell \times (j_2-i_2)$
in the other. The last part of condition (iii) makes it impossible for the cycle to have returned to its starting point.
$\ell \times (j_2-i_2)$
in the other. The last part of condition (iii) makes it impossible for the cycle to have returned to its starting point.
Theorem 4.
Let
![]() $G$
be the good event. Then,
$G$
be the good event. Then,
Proof. We shall show that the probability that a random coin toss sequence of length
![]() $t+n$
fails any one of the conditions (a) through (f) in the definition of
$t+n$
fails any one of the conditions (a) through (f) in the definition of
![]() $G$
is
$G$
is
![]() $O(t^4n^2/N^3+t^3n^3/N^2+tn^3/N)$
. (More explicitly, each will be shown to fail with the probability indicated in the definition of
$O(t^4n^2/N^3+t^3n^3/N^2+tn^3/N)$
. (More explicitly, each will be shown to fail with the probability indicated in the definition of
![]() $G$
.) We invoke the above Lemma during the proof by citing Lemma (i), Lemma (ii) and Lemma (iii).
$G$
.) We invoke the above Lemma during the proof by citing Lemma (i), Lemma (ii) and Lemma (iii).
Condition (a): [neither the initial
![]() $n$
-long word of the coin toss sequence, nor any of its
$n$
-long word of the coin toss sequence, nor any of its
![]() $1$
-offs, is repeated.] Consider first an exact repetition. There are
$1$
-offs, is repeated.] Consider first an exact repetition. There are
![]() $t-1$
places where the repeated sequence can start, and by earlier remarks the probability that the second sequence repeats the first is
$t-1$
places where the repeated sequence can start, and by earlier remarks the probability that the second sequence repeats the first is
![]() $1/N$
. The same argument applies to the
$1/N$
. The same argument applies to the
![]() $1$
-offs of the initial pattern, and we conclude that the probability for condition (a) to fail is less than
$1$
-offs of the initial pattern, and we conclude that the probability for condition (a) to fail is less than
![]() $t(n+1)/N$
.
$t(n+1)/N$
.
Condition (b): [all intersections
![]() $I_k\cap J_{k^{\prime }}$
are empty.] For
$I_k\cap J_{k^{\prime }}$
are empty.] For
![]() $k=k^{\prime }$
we bound the probability of failure by
$k=k^{\prime }$
we bound the probability of failure by
![]() $tn/N$
using the same technique as in case (a). Suppose that
$tn/N$
using the same technique as in case (a). Suppose that
![]() $I_1\cap J_2 \neq \emptyset$
. By the
$I_1\cap J_2 \neq \emptyset$
. By the
![]() $k=k^{\prime }$
case of the proof we may assume
$k=k^{\prime }$
case of the proof we may assume
![]() $J_1$
disjoint from
$J_1$
disjoint from
![]() $I_1$
and to its right; and
$I_1$
and to its right; and
![]() $I_2$
disjoint from
$I_2$
disjoint from
![]() $J_2$
and to its left. If
$J_2$
and to its left. If
![]() $I_1\cap I_2=\emptyset$
then Lemma (i) yields the upper bound
$I_1\cap I_2=\emptyset$
then Lemma (i) yields the upper bound
![]() $O(t^3n/N^2)$
. If
$O(t^3n/N^2)$
. If
![]() $J_1\cap J_2=\emptyset$
then Lemma (ii) yields
$J_1\cap J_2=\emptyset$
then Lemma (ii) yields
![]() $O(t^3n/N^2)$
. In the remaining case
$O(t^3n/N^2)$
. In the remaining case
![]() $I_1$
meets
$I_1$
meets
![]() $I_2$
,
$I_2$
,
![]() $J_1$
meets
$J_1$
meets
![]() $J_2$
, and
$J_2$
, and
![]() $I_1$
meets
$I_1$
meets
![]() $J_2$
. Thus the union
$J_2$
. Thus the union
![]() $I_1\cup I_2\cup J_1\cup J_2$
is an interval, and a bound of
$I_1\cup I_2\cup J_1\cup J_2$
is an interval, and a bound of
![]() $O(tn^3/N)$
results.
$O(tn^3/N)$
results.
Condition (c): [the sets
![]() $I_1,I_2,\dots$
are pairwise disjoint; likewise
$I_1,I_2,\dots$
are pairwise disjoint; likewise
![]() $J_1,J_2,\dots$
.] We will prove the assertion regarding
$J_1,J_2,\dots$
.] We will prove the assertion regarding
![]() $I_1,I_2,\dots$
; the other assertion is proven in an entirely similar manner. Suppose
$I_1,I_2,\dots$
; the other assertion is proven in an entirely similar manner. Suppose
![]() $I_1\cap I_2\neq \emptyset$
. We may assume
$I_1\cap I_2\neq \emptyset$
. We may assume
![]() $J_1\cap J_2\neq \emptyset$
; otherwise Lemma (ii) implies an upper bound of
$J_1\cap J_2\neq \emptyset$
; otherwise Lemma (ii) implies an upper bound of
![]() $O(t^3n/N^2)$
. So now, both intersections
$O(t^3n/N^2)$
. So now, both intersections
![]() $I_1\cap I_2$
and
$I_1\cap I_2$
and
![]() $J_1\cap J_2$
are nonempty. If any one of the four intersections
$J_1\cap J_2$
are nonempty. If any one of the four intersections
![]() $I_a\cap J_b$
is nonempty, then again the union
$I_a\cap J_b$
is nonempty, then again the union
![]() $I_1\cup I_2\cup J_1 \cup J_2$
is an interval, and we have the upper bound
$I_1\cup I_2\cup J_1 \cup J_2$
is an interval, and we have the upper bound
![]() $O(tn^3/N)$
. So assume
$O(tn^3/N)$
. So assume
![]() $(I_1\cup I_2) \cap (J_1 \cup J_2) = \emptyset$
. Assume, for the sake of a contradiction, that
$(I_1\cup I_2) \cap (J_1 \cup J_2) = \emptyset$
. Assume, for the sake of a contradiction, that
![]() $r(J_2)-r(I_2)=d=r(J_1)-r(I_1)$
. Then we have
$r(J_2)-r(I_2)=d=r(J_1)-r(I_1)$
. Then we have
![]() $I_1\neq I_2$
and
$I_1\neq I_2$
and
![]() $J_1\neq J_2$
. Without loss, let us say
$J_1\neq J_2$
. Without loss, let us say
![]() $I_1$
is left of
$I_1$
is left of
![]() $I_2$
and
$I_2$
and
![]() $J_1$
is left of
$J_1$
is left of
![]() $J_2$
. We have
$J_2$
. We have
![]() $C_{\ell (I_2)-1} \neq C_{\ell (J_2)-1}$
because
$C_{\ell (I_2)-1} \neq C_{\ell (J_2)-1}$
because
![]() $(I_2,J_2)$
is assumed to be a leftmost
$(I_2,J_2)$
is assumed to be a leftmost
![]() $n$
-repeat. Since
$n$
-repeat. Since
![]() $I_1$
is left of
$I_1$
is left of
![]() $I_2$
,
$I_2$
,
![]() $\ell (I_2)-1\in I_1$
; but then
$\ell (I_2)-1\in I_1$
; but then
![]() $C_{\ell (I_2)-1} = C_{\ell (J_2)-1}$
, the contradiction. So,
$C_{\ell (I_2)-1} = C_{\ell (J_2)-1}$
, the contradiction. So,
![]() $r(J_2)-r(I_2)=d=r(J_1)-r(I_1)$
is untenable and now Lemma (iii) implies an upper bound of
$r(J_2)-r(I_2)=d=r(J_1)-r(I_1)$
is untenable and now Lemma (iii) implies an upper bound of
![]() $O(t^2n^2/N^2)$
.
$O(t^2n^2/N^2)$
.
Condition (d): [no First-generation word of length
![]() $n-1$
equals a Zero-generation word of length
$n-1$
equals a Zero-generation word of length
![]() $n-1$
, or another First-generation word of length
$n-1$
, or another First-generation word of length
![]() $n-1$
]. Suppose the first assertion is violated. Then we have, for some
$n-1$
]. Suppose the first assertion is violated. Then we have, for some
![]() $i$
, some
$i$
, some
![]() $d\gt 0$
and some
$d\gt 0$
and some
![]() $j\in \{i,i+1,\dots,i+n-2\}$
,
$j\in \{i,i+1,\dots,i+n-2\}$
,
with
![]() $r(J_k) \in \{j,j+d\}$
and with
$r(J_k) \in \{j,j+d\}$
and with
![]() $(I_k,J_k)$
a leftmost
$(I_k,J_k)$
a leftmost
![]() $n$
-repeat. Let
$n$
-repeat. Let
![]() $I = \{i,i+1,\ldots,i+n-2\}$
and let
$I = \{i,i+1,\ldots,i+n-2\}$
and let
![]() $J = \{i+d,i+d+1,\ldots,i+d+n-2\}$
. If
$J = \{i+d,i+d+1,\ldots,i+d+n-2\}$
. If
![]() $I$
and
$I$
and
![]() $I_k$
are disjoint then using Lemma (i) the probability is bounded by
$I_k$
are disjoint then using Lemma (i) the probability is bounded by
![]() $O(t^3 \, n/N^2)$
. So assume they intersect, so their union is an interval. Similarly we can assume, using Lemma (ii), that
$O(t^3 \, n/N^2)$
. So assume they intersect, so their union is an interval. Similarly we can assume, using Lemma (ii), that
![]() $J$
and
$J$
and
![]() $J_k$
also intersect so their union is another interval. If these two intervals intersect, forming another interval, we have a probability bound of
$J_k$
also intersect so their union is another interval. If these two intervals intersect, forming another interval, we have a probability bound of
![]() $O(t \, n^3/N)$
. Otherwise
$O(t \, n^3/N)$
. Otherwise
![]() $( I \cup I_k) \cap (J \cup J_k)$
is empty. If
$( I \cup I_k) \cap (J \cup J_k)$
is empty. If
![]() $r(J_k) - r(I_k) = d$
then
$r(J_k) - r(I_k) = d$
then
![]() $C_j = C_{j+d}$
, contradicting (18). So Lemma (iii) implies
$C_j = C_{j+d}$
, contradicting (18). So Lemma (iii) implies
![]() $O(t^2 \, n^2/N^2)$
for the probability. This gives an overall bound of
$O(t^2 \, n^2/N^2)$
for the probability. This gives an overall bound of
![]() $O(t \, n^3/N +t^2 \, n^2/N^2 +t^3 \,n/N^2)$
.
$O(t \, n^3/N +t^2 \, n^2/N^2 +t^3 \,n/N^2)$
.
Next, suppose the second assertion of (d) is violated. Then we have, for some
![]() $i$
, some
$i$
, some
![]() $d\gt 0$
and some
$d\gt 0$
and some
![]() $j_1,j_2\in \{i,i+1,\dots,i+n-2\}$
,
$j_1,j_2\in \{i,i+1,\dots,i+n-2\}$
,
with
![]() $j_1=r(J_1)$
,
$j_1=r(J_1)$
,
![]() $j_2+d=r(J_2)$
and
$j_2+d=r(J_2)$
and
![]() $(I_1,J_1), (I_2,J_2)$
leftmost
$(I_1,J_1), (I_2,J_2)$
leftmost
![]() $n$
-repeats. As reasoned before we have
$n$
-repeats. As reasoned before we have
![]() $I\cap J$
,
$I\cap J$
,
![]() $I_1\cap J_1$
and
$I_1\cap J_1$
and
![]() $I_2\cap J_2$
all empty with probability at least
$I_2\cap J_2$
all empty with probability at least
![]() $1-O(tn^2/N)$
. It follows, from the sheer geometry of the situation, that
$1-O(tn^2/N)$
. It follows, from the sheer geometry of the situation, that
![]() $I\cap I_1=\emptyset$
. We may assume that
$I\cap I_1=\emptyset$
. We may assume that
![]() $I_1\cap I_2=\emptyset$
, since (as proven in (c) above) the probability of failure is
$I_1\cap I_2=\emptyset$
, since (as proven in (c) above) the probability of failure is
![]() $O(t^3n/N^2+t^2n^2/N^2+tn^3/N)$
. We may assume that
$O(t^3n/N^2+t^2n^2/N^2+tn^3/N)$
. We may assume that
![]() $I_1\cap I=\emptyset$
, for otherwise the union of
$I_1\cap I=\emptyset$
, for otherwise the union of
![]() $I_1$
and
$I_1$
and
![]() $I$
and
$I$
and
![]() $J_1$
is a connected interval, and then by reasoning as above a bound of
$J_1$
is a connected interval, and then by reasoning as above a bound of
![]() $O( t^3n^3/N^2)$
results. We now have all three intersections
$O( t^3n^3/N^2)$
results. We now have all three intersections
![]() $I\cap I_1$
,
$I\cap I_1$
,
![]() $I\cap I_2$
and
$I\cap I_2$
and
![]() $I_1\cap I_2$
being empty; and by an obvious embellishment of Lemma (i) the probability of the remaining case is
$I_1\cap I_2$
being empty; and by an obvious embellishment of Lemma (i) the probability of the remaining case is
![]() $O( t^4n^2/N^3)$
.
$O( t^4n^2/N^3)$
.
Condition (e): [for every leftmost
![]() $(n-1)$
-repeat
$(n-1)$
-repeat
![]() $(I,J)$
we have
$(I,J)$
we have
for all
![]() $k$
.] Say
$k$
.] Say
![]() $I=\{i,i+1,\dots,i+n-2\}$
and
$I=\{i,i+1,\dots,i+n-2\}$
and
![]() $J=\{i+d,i+d+1,\dots,i+d+n-2\}$
. The probability that
$J=\{i+d,i+d+1,\dots,i+d+n-2\}$
. The probability that
![]() $I_k\cap J_k$
is not empty is
$I_k\cap J_k$
is not empty is
![]() $O(tn/N)$
, so assume
$O(tn/N)$
, so assume
![]() $I_k\cap J_k=\emptyset$
. If
$I_k\cap J_k=\emptyset$
. If
![]() $r(J_k) \in I\cup \{i-1\}$
, then, since
$r(J_k) \in I\cup \{i-1\}$
, then, since
![]() $I_k$
lies entirely to the left of
$I_k$
lies entirely to the left of
![]() $J_k$
,
$J_k$
,
![]() $I_k\cap I=\emptyset$
. By Lemma (i) the probability of this is
$I_k\cap I=\emptyset$
. By Lemma (i) the probability of this is
![]() $O(t^3n/N^2)$
.
$O(t^3n/N^2)$
.
The probability that
![]() $I\cap J$
is not empty is
$I\cap J$
is not empty is
![]() $O(tn/N)$
, so assume both
$O(tn/N)$
, so assume both
![]() $I_k\cap J_k$
and
$I_k\cap J_k$
and
![]() $I\cap J$
are empty. The probability that
$I\cap J$
are empty. The probability that
![]() $I_k\cap I$
is empty is, by Lemma (i),
$I_k\cap I$
is empty is, by Lemma (i),
![]() $O(t^3n/N^2)$
, so assume
$O(t^3n/N^2)$
, so assume
![]() $I_k\cap I\neq \emptyset$
. If
$I_k\cap I\neq \emptyset$
. If
![]() $I\cap J_k$
or
$I\cap J_k$
or
![]() $I_k\cap J$
is nonempty then
$I_k\cap J$
is nonempty then
![]() $I_k\cup I \cup J_k \cup J$
is an interval, and the probability of this is
$I_k\cup I \cup J_k \cup J$
is an interval, and the probability of this is
![]() $O(tn^3/N)$
. So, assume
$O(tn^3/N)$
. So, assume
![]() $(I\cup I_k) \cap (I_k\cup J) = \emptyset$
. If
$(I\cup I_k) \cap (I_k\cup J) = \emptyset$
. If
![]() $r(J_k)-r(I_k)=r(J)-r(I)$
, then
$r(J_k)-r(I_k)=r(J)-r(I)$
, then
 \begin{align*} C_{\ell (I)-1} = C_{\ell (J)-1} & \quad \textit{by}\; \ell (I)-1 \in I_k \\[5pt] C_{\ell (I)-1} \neq C_{\ell (J)-1} & \quad \textit{by}\; (I,J)\; \textit{being a leftmost }\; (n-1)-\textit{repeat}, \end{align*}
\begin{align*} C_{\ell (I)-1} = C_{\ell (J)-1} & \quad \textit{by}\; \ell (I)-1 \in I_k \\[5pt] C_{\ell (I)-1} \neq C_{\ell (J)-1} & \quad \textit{by}\; (I,J)\; \textit{being a leftmost }\; (n-1)-\textit{repeat}, \end{align*}
an impossibility. So,
![]() $r(J_k)-r(I_k)\neq r(J)-r(I)$
and Lemma (iii) gives the bound
$r(J_k)-r(I_k)\neq r(J)-r(I)$
and Lemma (iii) gives the bound
![]() $O(t^2n^2/N^2)$
for this final scenario.
$O(t^2n^2/N^2)$
for this final scenario.
Condition (f): [there is no
![]() $(2n-1)$
-repeat.] Easily, the failure probability is at most
$(2n-1)$
-repeat.] Easily, the failure probability is at most
![]() $2t^2/N^2$
.
$2t^2/N^2$
.
3.6. Coin tossing versus paths in the de Bruijn graph
Theorem 5.
Let
![]() $b_0,\dots,b_{t+n-1}$
be a bit string. Then, the probability that this string arose by the sequential editing of an
$b_0,\dots,b_{t+n-1}$
be a bit string. Then, the probability that this string arose by the sequential editing of an
![]() $n+t$
long coin toss sequence is the same as the probability that it arose by choosing a logic
$n+t$
long coin toss sequence is the same as the probability that it arose by choosing a logic
![]() $f\;:\;V^{n-1}\rightarrow V$
and starting position
$f\;:\;V^{n-1}\rightarrow V$
and starting position
![]() $(b_0,\dots,b_{n-1})$
each uniformly at random.
$(b_0,\dots,b_{n-1})$
each uniformly at random.
Proof. Without loss of generality we assume the given string has the de Bruijn property. (Else, the two probabilities are both zero.) First, let’s compute the probability that
![]() $b$
arose by sequential editing of a
$b$
arose by sequential editing of a
![]() $(t+n)$
-long coin toss. The probability of the coin toss yielding
$(t+n)$
-long coin toss. The probability of the coin toss yielding
![]() $b_0,\dots,b_{n-1}$
is
$b_0,\dots,b_{n-1}$
is
![]() $(1/2)^n$
. Consider
$(1/2)^n$
. Consider
![]() $b_i$
, with
$b_i$
, with
![]() $i\ge n$
. If
$i\ge n$
. If
![]() $(b_{i-n+1},\dots,b_{i-1})$
is equal to
$(b_{i-n+1},\dots,b_{i-1})$
is equal to
![]() $(b_{j-n+1},\dots,b_{j-1})$
for some
$(b_{j-n+1},\dots,b_{j-1})$
for some
![]() $j$
in the range
$j$
in the range
![]() $n\le j\lt i$
, then sequential editing says to let
$n\le j\lt i$
, then sequential editing says to let
![]() $b_i$
be what it ought to be:
$b_i$
be what it ought to be:
![]() $b_{i-n}\oplus f(b_{i-n+1},\dots,b_{i-1})$
. In which case, it does not matter what value
$b_{i-n}\oplus f(b_{i-n+1},\dots,b_{i-1})$
. In which case, it does not matter what value
![]() $C_i$
has. But if
$C_i$
has. But if
![]() $i\ge n$
and
$i\ge n$
and
![]() $(b_{i-n+1},\dots,b_{i-1})$
has not been seen before (among
$(b_{i-n+1},\dots,b_{i-1})$
has not been seen before (among
![]() $(n-1)$
-long words ending at a position greater then or equal to
$(n-1)$
-long words ending at a position greater then or equal to
![]() $n$
), then
$n$
), then
![]() $C_i$
must be equal to
$C_i$
must be equal to
![]() $b_i$
. (And, we remember henceforward the value of
$b_i$
. (And, we remember henceforward the value of
![]() $f(b_{i-n+1},\dots,b_{i-1})$
is
$f(b_{i-n+1},\dots,b_{i-1})$
is
![]() $b_i\oplus b_{i-n}$
.) Altogether, then, the probability that a length
$b_i\oplus b_{i-n}$
.) Altogether, then, the probability that a length
![]() $t+n$
coin toss will yield a given sequence
$t+n$
coin toss will yield a given sequence
![]() $b_0,b_1,\dots,b_{t+n-1}$
by sequential editing is
$b_0,b_1,\dots,b_{t+n-1}$
by sequential editing is
![]() $2^{-r}$
where
$2^{-r}$
where
Now let’s compute the probability that
![]() $b$
arose by choosing a starting position and logic at random. Classify each position
$b$
arose by choosing a starting position and logic at random. Classify each position
![]() $i$
,
$i$
,
![]() $0\le i\le t+n-1$
, as Type I or Type II. The position is Type I if
$0\le i\le t+n-1$
, as Type I or Type II. The position is Type I if
![]() $i\ge n$
and the preceding
$i\ge n$
and the preceding
![]() $(n-1)$
long word
$(n-1)$
long word
![]() $(b_{i-n+1},\dots,b_{i-1})$
is appearing for the first time in the
$(b_{i-n+1},\dots,b_{i-1})$
is appearing for the first time in the
![]() $b$
-sequence. The position is Type II otherwise: either
$b$
-sequence. The position is Type II otherwise: either
![]() $i\lt n$
, or the preceding
$i\lt n$
, or the preceding
![]() $(n-1)$
long word
$(n-1)$
long word
![]() $(b_{i-n+1},\dots,b_{i-1})$
is appearing for the second or later time. It should be clear that the probability in question is
$(b_{i-n+1},\dots,b_{i-1})$
is appearing for the second or later time. It should be clear that the probability in question is
The two probabilities just calculated agree.Footnote 6
3.7. Notation for paths starting at
 $k$
random
$k$
random
 $n$
-tuples
$n$
-tuples
We now fix
![]() $k \ge 1$
and use the notation
$k \ge 1$
and use the notation
![]() $e_1,\ldots,e_k$
to name
$e_1,\ldots,e_k$
to name
![]() $k$
random
$k$
random
![]() $n$
-tuples. Collectively, these
$n$
-tuples. Collectively, these
![]() $k$
edges of
$k$
edges of
![]() $D_{n-1}$
are denoted
$D_{n-1}$
are denoted
Picking a random feedback
![]() $f$
, and
$f$
, and
![]() $k$
random
$k$
random
![]() $n$
-tuples, independent of
$n$
-tuples, independent of
![]() $f$
, is equivalent to picking one element, uniformly at random from the space
$f$
, is equivalent to picking one element, uniformly at random from the space
The choice of
![]() $(f,\boldsymbol{{e}})$
from
$(f,\boldsymbol{{e}})$
from
![]() $S_{n,k}$
determines
$S_{n,k}$
determines
![]() $k$
infinite periodic sequences of edges: for
$k$
infinite periodic sequences of edges: for
![]() $a=1$
to
$a=1$
to
![]() $k$
,
$k$
,
For the sake of comparison with coin tossing, we often look at such paths only up to time
![]() $t$
(this is what motivated our terminology segment):
$t$
(this is what motivated our terminology segment):
3.8.
 $(k,t)$
-sequential editing
$(k,t)$
-sequential editing
Now we will define a modification of the sequential editing process that was discussed earlier in Section 3.1. The reader should bear in mind our ultimate goal. We wish to study what happens when a feedback logic
![]() $f$
is chosen at random;
$f$
is chosen at random;
![]() $k$
different starting
$k$
different starting
![]() $n$
-tuples
$n$
-tuples
![]() $e_1,\dots,e_k$
are chosen at random; and
$e_1,\dots,e_k$
are chosen at random; and
![]() $k$
walks of length
$k$
walks of length
![]() $t$
are generated, the first starting from
$t$
are generated, the first starting from
![]() $e_1$
and using the logic
$e_1$
and using the logic
![]() $f$
to continue for
$f$
to continue for
![]() $t$
steps; the second starting from
$t$
steps; the second starting from
![]() $e_2$
, etc. As in Section 3.1, we wish to generate these walks using
$e_2$
, etc. As in Section 3.1, we wish to generate these walks using
![]() $k(n+t)$
coin tosses, and we would like to have an analogue to Theorem 5 saying that our procedure for passing from the coin toss to the
$k(n+t)$
coin tosses, and we would like to have an analogue to Theorem 5 saying that our procedure for passing from the coin toss to the
![]() $k$
walks perfectly simulates the process of choosing a logic and starting points at random. The reader can almost certainly envision the natural way to achieve this, but we will write out the details.
$k$
walks perfectly simulates the process of choosing a logic and starting points at random. The reader can almost certainly envision the natural way to achieve this, but we will write out the details.
The first
![]() $n+t$
coins are used exactly as in Section 3.1: Rule 1 is applied to the first
$n+t$
coins are used exactly as in Section 3.1: Rule 1 is applied to the first
![]() $n$
coin tosses to yield starting point
$n$
coin tosses to yield starting point
![]() $e_1$
, and then Rule 2 is applied
$e_1$
, and then Rule 2 is applied
![]() $t$
times to get the overlapping
$t$
times to get the overlapping
![]() $n$
-tuples
$n$
-tuples
![]() $e_1=e_{1,0}, e_{1,1}, \ldots, e_{1,t}$
that form the first walk. Equivalently, this segment is spelled out by the
$e_1=e_{1,0}, e_{1,1}, \ldots, e_{1,t}$
that form the first walk. Equivalently, this segment is spelled out by the
![]() $(n+t)$
de Bruijn bits
$(n+t)$
de Bruijn bits
![]() $b_0 \ldots b_{t+n-1}$
, and along the way, some feedback logic bits have been defined.
$b_0 \ldots b_{t+n-1}$
, and along the way, some feedback logic bits have been defined.
Then, for the next
![]() $n$
coin tosses,
$n$
coin tosses,
![]() $C_i$
for
$C_i$
for
![]() $i=t+n$
to
$i=t+n$
to
![]() $i=t+2n-1$
inclusive, sequential editing is suspended; again Rule 1 is applied, to give
$i=t+2n-1$
inclusive, sequential editing is suspended; again Rule 1 is applied, to give
with no new feedback logic bits learned. Then, Rule 2 is applied for the next
![]() $t$
input bits,
$t$
input bits,
![]() $C_i$
for
$C_i$
for
![]() $i=t+2n$
to
$i=t+2n$
to
![]() $i=2t+2n-1$
to create the second walk of length
$i=2t+2n-1$
to create the second walk of length
![]() $t$
,
$t$
,
![]() ${\textrm{Seg}}(f,e_2,t)$
— remembering of course those feedback logic bits that were learned during the creation of
${\textrm{Seg}}(f,e_2,t)$
— remembering of course those feedback logic bits that were learned during the creation of
![]() ${\textrm{Seg}}(f,e_1,t)$
, and (most likely) learning some new feedback logic bits in the process. (It might be the case that
${\textrm{Seg}}(f,e_1,t)$
, and (most likely) learning some new feedback logic bits in the process. (It might be the case that
![]() $e_2=e_1$
, or that
$e_2=e_1$
, or that
![]() $e_2$
appears in the first walk, in which case, we don’t learn any new feedback logic bits.) If
$e_2$
appears in the first walk, in which case, we don’t learn any new feedback logic bits.) If
![]() $k\gt 2$
, we continue in a similar fashion, first suspending editing for time
$k\gt 2$
, we continue in a similar fashion, first suspending editing for time
![]() $n$
, during which time we learn no new feedback logic bits and we form
$n$
, during which time we learn no new feedback logic bits and we form
![]() $e_a \;:\!=\; (b_{(a-1)(t+n)},\ldots,b_{(a-1)t+an-1}) \;:\!=\; (C_{(a-1)(t+n)},\ldots,C_{(a-1)t+an-1})$
, then returning to Rule 2 for the next
$e_a \;:\!=\; (b_{(a-1)(t+n)},\ldots,b_{(a-1)t+an-1}) \;:\!=\; (C_{(a-1)(t+n)},\ldots,C_{(a-1)t+an-1})$
, then returning to Rule 2 for the next
![]() $t$
bits, to fill out
$t$
bits, to fill out
![]() ${\textrm{Seg}}(f,e_a,t)$
.
${\textrm{Seg}}(f,e_a,t)$
.
For
![]() $k,t \ge 1$
we define
$k,t \ge 1$
we define
as given by the above procedure.
It may, or should, seem intuitively obvious that
![]() ${Q-EDIT_{k,t}}$
, applied to an input uniformly chosen from
${Q-EDIT_{k,t}}$
, applied to an input uniformly chosen from
![]() $ \{0,1\}^{k(n+t)}$
, induces the same distribution on the
$ \{0,1\}^{k(n+t)}$
, induces the same distribution on the
![]() $k$
segments of length
$k$
segments of length
![]() $t$
in (22), as does a uniform pick from
$t$
in (22), as does a uniform pick from
![]() $S_{n,k}$
and iteration of
$S_{n,k}$
and iteration of
![]() $\pi _f$
from each of
$\pi _f$
from each of
![]() $e_1,\ldots,e_k$
. We claim that the argument given in the proof of Theorem 5 can be adapted to show this.
$e_1,\ldots,e_k$
. We claim that the argument given in the proof of Theorem 5 can be adapted to show this.
3.9. The good event
 $G_{(k,t)}$
for
$G_{(k,t)}$
for
 $(k,t)$
-sequential editing
$(k,t)$
-sequential editing
There are two different ways to produce
![]() $k$
walks each of length
$k$
walks each of length
![]() $t$
out of a sequence of
$t$
out of a sequence of
![]() $k(n+t)$
coin tosses. The first, with
$k(n+t)$
coin tosses. The first, with
![]() $t'=(k-1)n+kt$
playing the role of
$t'=(k-1)n+kt$
playing the role of
![]() $t$
, is simple sequential edit, to determine a starting
$t$
, is simple sequential edit, to determine a starting
![]() $n$
-tuple
$n$
-tuple
![]() $e$
, and one path
$e$
, and one path
![]() $e_0,e_1,\ldots,e_{t'}$
corresponding to
$e_0,e_1,\ldots,e_{t'}$
corresponding to
![]() $t'=(k-1)n+kt$
iterates of
$t'=(k-1)n+kt$
iterates of
![]() $\pi _f$
starting from
$\pi _f$
starting from
![]() $e$
. The good event, regarding this first procedure, is really
$e$
. The good event, regarding this first procedure, is really
![]() $G \equiv G_{((k-1)n+kt)}$
. We can then cut the path of length
$G \equiv G_{((k-1)n+kt)}$
. We can then cut the path of length
![]() $t'$
to produce
$t'$
to produce
![]() $k$
paths of length
$k$
paths of length
![]() $t$
; see (31) to see the natural notation associated with such cutting. The second procedure is is to apply
$t$
; see (31) to see the natural notation associated with such cutting. The second procedure is is to apply
![]() ${Q-EDIT_{k,t}}$
, defined in the previous section, to produce a
${Q-EDIT_{k,t}}$
, defined in the previous section, to produce a
![]() $k$
-tuple of starting edges,
$k$
-tuple of starting edges,
![]() $\boldsymbol{{e}}$
, and
$\boldsymbol{{e}}$
, and
![]() $k$
segments of length
$k$
segments of length
![]() $t$
, as in (23). The good event, regarding this second procedure, to be called
$t$
, as in (23). The good event, regarding this second procedure, to be called
![]() $G_{(k,t)}$
, is designed so that the two procedures agree. We simply take all of the demands of the good event for simple editing on
$G_{(k,t)}$
, is designed so that the two procedures agree. We simply take all of the demands of the good event for simple editing on
![]() $k(n+t)$
coins, and throw in additional requirements to ensure the suspensions of editing involved in the definition of
$k(n+t)$
coins, and throw in additional requirements to ensure the suspensions of editing involved in the definition of
![]() ${Q-EDIT_{k,t}}$
. Informally, these additional requirements are that every
${Q-EDIT_{k,t}}$
. Informally, these additional requirements are that every
![]() $(n-1)$
tuple which appears at some time
$(n-1)$
tuple which appears at some time
![]() $j$
involved in suspension occurs at no other time
$j$
involved in suspension occurs at no other time
![]() $i$
in the coin toss sequence. Formally, given
$i$
in the coin toss sequence. Formally, given
![]() $n,k,t$
, the bad event
$n,k,t$
, the bad event
![]() $B$
is given by
$B$
is given by
where the event
![]() $M_{ij} = \emptyset$
if
$M_{ij} = \emptyset$
if
![]() $i=j$
, and otherwise
$i=j$
, and otherwise
and the good event is then
Since a word of length
![]() $n-1$
has
$n-1$
has
![]() $n$
neighbours at Hamming distance 1 or less,
$n$
neighbours at Hamming distance 1 or less,
![]() ${\mathbb{P}}(M_{ij}) = n/2^{n-1}$
for
${\mathbb{P}}(M_{ij}) = n/2^{n-1}$
for
![]() $i \ne j$
, so that
$i \ne j$
, so that
![]() ${\mathbb{P}}(B) \le (n+t)k^2n^2 \times 2/N$
, for the sake of extending Theorem 4.
${\mathbb{P}}(B) \le (n+t)k^2n^2 \times 2/N$
, for the sake of extending Theorem 4.
We now consider the following to have been proved; it is a single theorem, to give the extensions of Theorems 2 and 4 and 5, appropriate to
![]() $k,t$
sequential editing. Note that in the final conclusion of Theorem 6 we treat
$k,t$
sequential editing. Note that in the final conclusion of Theorem 6 we treat
![]() $k$
as fixed while
$k$
as fixed while
![]() $n,t \to \infty$
, so that
$n,t \to \infty$
, so that
![]() $t$
and
$t$
and
![]() $kt$
are of the same order, and we take the assumption
$kt$
are of the same order, and we take the assumption
![]() $t/\sqrt{N} \to \infty$
so that the three terms in the bound from Theorem 4 are covered by a single term.
$t/\sqrt{N} \to \infty$
so that the three terms in the bound from Theorem 4 are covered by a single term.
Theorem 6.
-
(i) The procedure
 ${Q-EDIT_{k,t}}$
, applied to a coin toss sequence
chosen uniformly at random from
${Q-EDIT_{k,t}}$
, applied to a coin toss sequence
chosen uniformly at random from \begin{equation*} (C_0,C_1,\ldots,C_{k(n+t)-1}), \end{equation*}
\begin{equation*} (C_0,C_1,\ldots,C_{k(n+t)-1}), \end{equation*}
 $\{0,1\}^{k(n+t)}$
, yields
$\{0,1\}^{k(n+t)}$
, yields
 $k$
segments of length
$k$
segments of length
 $t$
,
$t$
,
 $({\operatorname{Seg}}(f,e_1,t),\ldots,{\operatorname{Seg}}(f,e_k,t) )$
with exactly the same distribution as obtained by a random feedback logic
$({\operatorname{Seg}}(f,e_1,t),\ldots,{\operatorname{Seg}}(f,e_k,t) )$
with exactly the same distribution as obtained by a random feedback logic
 $f$
and
$f$
and
 $k$
starting
$k$
starting
 $n$
-tuples,
$n$
-tuples,
 $\boldsymbol{{e}} = (e_1,\ldots,e_k)$
.
$\boldsymbol{{e}} = (e_1,\ldots,e_k)$
.
-
(ii) The good event
 ${G_{(k,t)}} \subset \{0,1\}^{k(n+t)}$
, defined by (27) — which ultimately involves conditions (a) through (f) from Section 3.4, applied with
${G_{(k,t)}} \subset \{0,1\}^{k(n+t)}$
, defined by (27) — which ultimately involves conditions (a) through (f) from Section 3.4, applied with
 $t'=(k-1)n+kt$
in the role of
$t'=(k-1)n+kt$
in the role of
 $t$
, is such that for every outcome in
$t$
, is such that for every outcome in
 $G_{(k,t)}$
, the bit sequence
$G_{(k,t)}$
, the bit sequence
 $b_0b_1 \cdots b_{k(n+t)-1}$
(and the equivalent sequence of overlapping
$b_0b_1 \cdots b_{k(n+t)-1}$
(and the equivalent sequence of overlapping
 $n$
-tuples,
$n$
-tuples,
 $e_0e_1\cdots e_{(k-1)n+kt}$
) formed by single sequential edit agrees with the shotgun edit of the
$e_0e_1\cdots e_{(k-1)n+kt}$
) formed by single sequential edit agrees with the shotgun edit of the
 $k(n+t)$
coins, and leftmost
$k(n+t)$
coins, and leftmost
 $(n-1)$
-tuple repeats have the same locations in
$(n-1)$
-tuple repeats have the same locations in
 $b_0b_1 \cdots b_{k(n+t)-1}$
and in
$b_0b_1 \cdots b_{k(n+t)-1}$
and in
 $(C_0,C_1,\ldots,C_{k(n+t)-1})$
.
$(C_0,C_1,\ldots,C_{k(n+t)-1})$
. -
(iii) Also, on the good event
 $G_{(k,t)}$
, the
$G_{(k,t)}$
, the
 $k$
segments of length
$k$
segments of length
 $t$
, produced by
$t$
, produced by
 ${Q-EDIT_{k,t}}$
and notated as in (23) match exactly with
${Q-EDIT_{k,t}}$
and notated as in (23) match exactly with
 $e_0\cdots e_t, e_{t+n}\cdots e_{2t+n}, \ldots, e_{(k-1)(t+n)} \cdots e_{(k-1)n+kt}$
, produced by cutting the output of the single sequential edit of
$e_0\cdots e_t, e_{t+n}\cdots e_{2t+n}, \ldots, e_{(k-1)(t+n)} \cdots e_{(k-1)n+kt}$
, produced by cutting the output of the single sequential edit of
 $k(n+t)$
coins.
$k(n+t)$
coins.
-
(iv) Finally, if
 $t/\sqrt{N} \to \infty$
with
$t/\sqrt{N} \to \infty$
with
 $k$
fixed, then
$k$
fixed, then
 ${\mathbb{P}}({G_{(k,t)}}) \ge 1 - O(n^3 \, t^3/N^2)$
.
${\mathbb{P}}({G_{(k,t)}}) \ge 1 - O(n^3 \, t^3/N^2)$
.
We summarise: there is an exact operation, sequential editing of
![]() $n+t$
coin tosses, which achieves the exact distribution of
$n+t$
coin tosses, which achieves the exact distribution of
![]() ${\textrm{Seg}}(f,e,t)$
, as induced by a uniform choice of
${\textrm{Seg}}(f,e,t)$
, as induced by a uniform choice of
![]() $(f,e)$
from its
$(f,e)$
from its
![]() $2^{2^{n-1}} 2^n$
possible values, followed by starting at
$2^{2^{n-1}} 2^n$
possible values, followed by starting at
![]() $e$
and taking
$e$
and taking
![]() $t$
iterates of the permutation
$t$
iterates of the permutation
![]() $\pi _f$
. There is a good event
$\pi _f$
. There is a good event
![]() $G \equiv G_{t}$
, with
$G \equiv G_{t}$
, with
![]() ${\mathbb{P}}(G) \to 1$
provided that
${\mathbb{P}}(G) \to 1$
provided that
![]() $t^3n^3/N^2 \to 0$
, for which the sequential edit agrees with the shotgun edit, and
$t^3n^3/N^2 \to 0$
, for which the sequential edit agrees with the shotgun edit, and
![]() $v_i=v_j$
iff the coins have a leftmost
$v_i=v_j$
iff the coins have a leftmost
![]() $(n-1)$
-tuple repeat at
$(n-1)$
-tuple repeat at
![]() $(i,j)$
. This sequential edit can be used with
$(i,j)$
. This sequential edit can be used with
![]() $k(n+t)$
in place of
$k(n+t)$
in place of
![]() $n+t$
, to create one long segment; there is the corresponding good event
$n+t$
, to create one long segment; there is the corresponding good event
![]() $G_{t^{\prime }}$
,
$G_{t^{\prime }}$
,
![]() $t^{\prime }=(k-1)n+kt$
. There is a second, distinct operation,
$t^{\prime }=(k-1)n+kt$
. There is a second, distinct operation,
![]() ${Q-EDIT_{k,t}}$
, for editing
${Q-EDIT_{k,t}}$
, for editing
![]() $k(n+t)$
coin tosses, to yield the exact distribution of
$k(n+t)$
coin tosses, to yield the exact distribution of
![]() $k$
segments of length
$k$
segments of length
![]() $t$
under a single logic
$t$
under a single logic
![]() $f$
and
$f$
and
![]() $k$
starting
$k$
starting
![]() $n$
-tuples,
$n$
-tuples,
![]() $\boldsymbol{{e}} = (e_1,\ldots,e_k)$
; that is, the distribution of
$\boldsymbol{{e}} = (e_1,\ldots,e_k)$
; that is, the distribution of
![]() $({\textrm{Seg}}(f,e_1,t),\ldots,{\textrm{Seg}}(f,e_k,t))$
as induced by a uniform choice of
$({\textrm{Seg}}(f,e_1,t),\ldots,{\textrm{Seg}}(f,e_k,t))$
as induced by a uniform choice of
![]() $(f,{\mathbb{E}\,})$
from its
$(f,{\mathbb{E}\,})$
from its
![]() $2^{2^{n-1}} 2^{kn}$
possible values. And there is a corresponding good event
$2^{2^{n-1}} 2^{kn}$
possible values. And there is a corresponding good event
![]() ${G_{(k,t)}} \subset G_{t^{\prime }}$
, with
${G_{(k,t)}} \subset G_{t^{\prime }}$
, with
formed by adding the constraint that
![]() $i$
or
$i$
or
![]() $j \in \cup _{0 \le a \lt k} [a(n+t)-n+2,a(n+t)]$
implies that there is not an
$j \in \cup _{0 \le a \lt k} [a(n+t)-n+2,a(n+t)]$
implies that there is not an
![]() $(n-1)$
tuple repeat at
$(n-1)$
tuple repeat at
![]() $(i,j)$
. On the event
$(i,j)$
. On the event
![]() $G_{(k,t)}$
, the
$G_{(k,t)}$
, the
![]() $k$
-sequential edit agrees exactly with the cutting of
$k$
-sequential edit agrees exactly with the cutting of
![]() ${\textrm{Seg}}(f,e_1,k(n+t)-n)$
.
${\textrm{Seg}}(f,e_1,k(n+t)-n)$
.

Figure 1. An example, one segment of length 290, where there are three leftmost
![]() $(n-1)$
-tuple repeats, at (56,153), (120,260) and (135,175).
$(n-1)$
-tuple repeats, at (56,153), (120,260) and (135,175).

Figure 2. The same example: one segment of length 290, where there are three leftmost
![]() $(n-1)$
-tuple repeats, at locations (56,153), (120,260) and (135,175). Now, the locations are plotted in standard Cartesian coordinates.
$(n-1)$
-tuple repeats, at locations (56,153), (120,260) and (135,175). Now, the locations are plotted in standard Cartesian coordinates.

Figure 3. Coloring. An example, with
![]() $k=3$
,
$k=3$
,
![]() $n=10,t=90$
. The same one segment of length 290, as in Figure 1, where there are three leftmost
$n=10,t=90$
. The same one segment of length 290, as in Figure 1, where there are three leftmost
![]() $(n-1)$
-tuple repeats, at (56,153), (120,260) and (135,175). Now the first segment is coloured red, the second yellow and the third blue.
$(n-1)$
-tuple repeats, at (56,153), (120,260) and (135,175). Now the first segment is coloured red, the second yellow and the third blue.

Figure 4. Coloring and cutting; a succinct way to visualise both. The
![]() $k$
segments of length
$k$
segments of length
![]() $t$
are still shown as they appear along the single segment of length
$t$
are still shown as they appear along the single segment of length
![]() $k(t+n)-n$
. We also show the
$k(t+n)-n$
. We also show the
![]() $\left(\substack{k \\[3pt] 2}\right)$
$\left(\substack{k \\[3pt] 2}\right)$
![]() $t$
by
$t$
by
![]() $t$
squares where matches may occur between two differently coloured length
$t$
squares where matches may occur between two differently coloured length
![]() $t$
segments. Note the repeat at (56,153) is a vertex coloured both red and yellow, hence orange. The repeat at (120,260) is a vertex coloured both yellow and blue, hence green. The vertex at (135,175) is coloured yellow twice - we could show it as an extra-saturated yellow but did not. The significance of the diagonals of the small squares is explained in Section 4.3.
$t$
segments. Note the repeat at (56,153) is a vertex coloured both red and yellow, hence orange. The repeat at (120,260) is a vertex coloured both yellow and blue, hence green. The vertex at (135,175) is coloured yellow twice - we could show it as an extra-saturated yellow but did not. The significance of the diagonals of the small squares is explained in Section 4.3.
3.10. A cutting example
We now illustrate some of the concepts just introduced, with an example and with Figures 1, 2, 3 and 4. Take
![]() $n=10,t=90,k=3$
. So, to generate
$n=10,t=90,k=3$
. So, to generate
![]() $k=3$
segments of length
$k=3$
segments of length
![]() $t=90$
, we start with
$t=90$
, we start with
![]() $k(n+t)=300$
coin tosses, used to generate one segment of length
$k(n+t)=300$
coin tosses, used to generate one segment of length
![]() $k(n+t)-n=290$
. When we have in mind a single segment of length
$k(n+t)-n=290$
. When we have in mind a single segment of length
![]() $t$
, we will use a single subscript to label the edges, so that with
$t$
, we will use a single subscript to label the edges, so that with
![]() $e=e_0$
, the segment is a list of
$e=e_0$
, the segment is a list of
![]() $t+1$
edges
$t+1$
edges
The coin tosses, indexed from
![]() $i=0$
to
$i=0$
to
![]() $i=299$
, are labelled
$i=299$
, are labelled
![]() $C_i$
, the de Bruijn bits formed by sequential edit are labelled
$C_i$
, the de Bruijn bits formed by sequential edit are labelled
![]() $b_i$
, and the bits formed by shotgun edit are labelled
$b_i$
, and the bits formed by shotgun edit are labelled
![]() $a_i$
. On the good event
$a_i$
. On the good event
![]() $G$
, we will have
$G$
, we will have
![]() $a_i=b_i$
for all
$a_i=b_i$
for all
![]() $i$
. The vertex
$i$
. The vertex
![]() $v_i$
is the
$v_i$
is the
![]() $(n-1)$
- tuple of bits starting with
$(n-1)$
- tuple of bits starting with
![]() $b_i$
, the edge
$b_i$
, the edge
![]() $e_i$
is the
$e_i$
is the
![]() $n$
-tuple of bits starting with
$n$
-tuple of bits starting with
![]() $b_i$
and edge
$b_i$
and edge
![]() $e_i$
at time
$e_i$
at time
![]() $i$
goes from vertex
$i$
goes from vertex
![]() $v_{i}$
to
$v_{i}$
to
![]() $v_{i+1}$
:
$v_{i+1}$
:
We also view the segment in (28) as a list of
![]() $t+2$
vertices, or as a list of
$t+2$
vertices, or as a list of
![]() $t+n$
bits, and abuse notation by writing equality, so that
$t+n$
bits, and abuse notation by writing equality, so that
Since we are particularly interested in leftmost
![]() $(n-1)$
-tuple repeats, we shall suppose that we are in the good event
$(n-1)$
-tuple repeats, we shall suppose that we are in the good event
![]() $G$
, and the leftmost
$G$
, and the leftmost
![]() $(n-1)$
-tuple repeats in the coin toss sequence are at (56,153), (120,260) and (135,175). Thanks to
$(n-1)$
-tuple repeats in the coin toss sequence are at (56,153), (120,260) and (135,175). Thanks to
![]() $G$
occurring, we know that all 291 edges
$G$
occurring, we know that all 291 edges
![]() $e_0$
to
$e_0$
to
![]() $e_{290}$
are distinct, and the only vertex repetitions are
$e_{290}$
are distinct, and the only vertex repetitions are
![]() $v_{56}=v_{153}, v_{120}=v_{260}$
and
$v_{56}=v_{153}, v_{120}=v_{260}$
and
![]() $v_{135}=v_{175}$
. One way of indicating where these vertex repeats occur is to draw some auxiliary lines pointing to the locations, as in Figure 1. Figure 2 gives a two-dimensional (‘spatial’) view of the same situation.
$v_{135}=v_{175}$
. One way of indicating where these vertex repeats occur is to draw some auxiliary lines pointing to the locations, as in Figure 1. Figure 2 gives a two-dimensional (‘spatial’) view of the same situation.
When we cut the single long segment in (28) into
![]() $k=3$
segments, we use two indices; the first runs from 1 to
$k=3$
segments, we use two indices; the first runs from 1 to
![]() $k$
, and the second runs from 0 to
$k$
, and the second runs from 0 to
![]() $t$
. Including the relation with (28), for Example 1, but with the labels
$t$
. Including the relation with (28), for Example 1, but with the labels
![]() $e_1,\ldots,e_k$
overloaded — since they also appear on the left side, naming the starting edges for the
$e_1,\ldots,e_k$
overloaded — since they also appear on the left side, naming the starting edges for the
![]() $k$
segments — this will give
$k$
segments — this will give
 \begin{equation*} \begin {array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} {\textrm {Seg}}(f,e_1,t) & = & e_{1,0}\cdots e_{1,90} & = & e_0\cdots e_{90} \\[5pt] {\textrm {Seg}}(f,e_2,t) & = & e_{2,0}\cdots e_{2,90} & = & e_{100}\cdots e_{190} \\[5pt] {\textrm {Seg}}(f,e_3,t) & = & e_{3,0}\cdots e_{3,90} & = & e_{200}\cdots e_{290}. \end {array} \end{equation*}
\begin{equation*} \begin {array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} {\textrm {Seg}}(f,e_1,t) & = & e_{1,0}\cdots e_{1,90} & = & e_0\cdots e_{90} \\[5pt] {\textrm {Seg}}(f,e_2,t) & = & e_{2,0}\cdots e_{2,90} & = & e_{100}\cdots e_{190} \\[5pt] {\textrm {Seg}}(f,e_3,t) & = & e_{3,0}\cdots e_{3,90} & = & e_{200}\cdots e_{290}. \end {array} \end{equation*}
The same
![]() $k=3$
segments of length
$k=3$
segments of length
![]() $t=90$
, presented as lists of vertices (which here are 9-tuples) are notated as
$t=90$
, presented as lists of vertices (which here are 9-tuples) are notated as
 \begin{equation} \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c}{\textrm{Seg}}(f,e_1,t) & = & v_{1,0}v_{1,1}\cdots v_{1,90}v_{1,91} & = & v_0v_1\cdots v_{90}v_{91} \\[5pt] {\textrm{Seg}}(f,e_2,t) & = & v_{2,0}v_{2,1}\cdots v_{2,90}v_{2,91} & = & v_{100}v_{101}\cdots v_{190}v_{191} \\[5pt] {\textrm{Seg}}(f,e_3,t) & = & v_{3,0}v_{3,1}\cdots v_{3,90} v_{3,91} & = & v_{200}v_{201}\cdots v_{290}v_{291}. \end{array} \end{equation}
\begin{equation} \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c}{\textrm{Seg}}(f,e_1,t) & = & v_{1,0}v_{1,1}\cdots v_{1,90}v_{1,91} & = & v_0v_1\cdots v_{90}v_{91} \\[5pt] {\textrm{Seg}}(f,e_2,t) & = & v_{2,0}v_{2,1}\cdots v_{2,90}v_{2,91} & = & v_{100}v_{101}\cdots v_{190}v_{191} \\[5pt] {\textrm{Seg}}(f,e_3,t) & = & v_{3,0}v_{3,1}\cdots v_{3,90} v_{3,91} & = & v_{200}v_{201}\cdots v_{290}v_{291}. \end{array} \end{equation}
Collectively, these
![]() $k$
segments are given by a deterministic function of
$k$
segments are given by a deterministic function of
![]() $(f,\boldsymbol{{e}})$
, where
$(f,\boldsymbol{{e}})$
, where
![]() $\boldsymbol{{e}}=(e_1,e_2,\ldots,e_k)$
names all
$\boldsymbol{{e}}=(e_1,e_2,\ldots,e_k)$
names all
![]() $k$
starting points.
$k$
starting points.
3.11. Coloring
Imagine the
![]() $k$
segments of length
$k$
segments of length
![]() $t$
as pieces of (directed) yarn, with
$t$
as pieces of (directed) yarn, with
![]() $k$
different ‘primary’ colours. Vertices that appear only once get the primary colour of the segment they come from; vertices that appear twice on the same segment might be visualised as having a more saturated version of the primary colour of that segment. The interesting case occurs when a vertex appears on two different segments; such a vertex, call it
$k$
different ‘primary’ colours. Vertices that appear only once get the primary colour of the segment they come from; vertices that appear twice on the same segment might be visualised as having a more saturated version of the primary colour of that segment. The interesting case occurs when a vertex appears on two different segments; such a vertex, call it
![]() $v^{\#}$
, gets each of two primary colours — and its secondary colour shows which two segments this vertex lies on; for example imagine that the two strands are red and yellow, so that
$v^{\#}$
, gets each of two primary colours — and its secondary colour shows which two segments this vertex lies on; for example imagine that the two strands are red and yellow, so that
![]() $v^{\#}$
is coloured orange. Figure 3 on page 31 and Figure 4 illustrate this colouring.
$v^{\#}$
is coloured orange. Figure 3 on page 31 and Figure 4 illustrate this colouring.
4. Toggling
To toggle a logic
![]() $ f\;:\;\mathbb{F}_2^{n-1} \to \mathbb{F}_2$
at a vertex
$ f\;:\;\mathbb{F}_2^{n-1} \to \mathbb{F}_2$
at a vertex
![]() $v \in \mathbb{F}_2^{n-1}$
is simply to get a new
$v \in \mathbb{F}_2^{n-1}$
is simply to get a new
![]() $f$
from the old, by changing the value at
$f$
from the old, by changing the value at
![]() $v$
. This is called a ‘cross-join step’ and is studied extensively in the context of cycle joining algorithms to create a full cycle logic. Our interest in toggling is different: we have
$v$
. This is called a ‘cross-join step’ and is studied extensively in the context of cycle joining algorithms to create a full cycle logic. Our interest in toggling is different: we have
![]() $k \ge 2$
segments induced by a logic
$k \ge 2$
segments induced by a logic
![]() $f$
and
$f$
and
![]() $k$
starting
$k$
starting
![]() $n$
-tuples,
$n$
-tuples,
![]() $e_1,\ldots,e_k$
, and we want to choose
$e_1,\ldots,e_k$
, and we want to choose
![]() $m$
different ‘toggle points’ in the role of
$m$
different ‘toggle points’ in the role of
![]() $v$
, to get a nice family of
$v$
, to get a nice family of
![]() $2^m$
related logics. All this is done in the interest of showing that the chance that
$2^m$
related logics. All this is done in the interest of showing that the chance that
![]() $e_1$
and
$e_1$
and
![]() $e_2$
lie on the same cycle of
$e_2$
lie on the same cycle of
![]() $\pi _f$
is approximately one-half, for large
$\pi _f$
is approximately one-half, for large
![]() $n$
, and more generally, that the chance
$n$
, and more generally, that the chance
![]() $e_1,\ldots,e_k$
all lie on the same cycle is approximately
$e_1,\ldots,e_k$
all lie on the same cycle is approximately
![]() $1/k$
, and even more, that the permutation
$1/k$
, and even more, that the permutation
![]() $\pi _f$
, relativised to
$\pi _f$
, relativised to
![]() $e_1,\ldots,e_k$
, is approximately uniformly distributed over all
$e_1,\ldots,e_k$
, is approximately uniformly distributed over all
![]() $k!$
permutations. This introductory paragraph is intentionally short and vague; the full details use all of Sections 3–6. Section 4.1 gives a longer attempt at introduction, including Figure 5, showing the huge collection of candidate toggle vertices, using
$k!$
permutations. This introductory paragraph is intentionally short and vague; the full details use all of Sections 3–6. Section 4.1 gives a longer attempt at introduction, including Figure 5, showing the huge collection of candidate toggle vertices, using
![]() $k$
colours to help visualise the
$k$
colours to help visualise the
![]() $k$
segments of interest.
$k$
segments of interest.

Figure 5. Take
![]() $n=34$
,
$n=34$
,
![]() $N=2^n$
and
$N=2^n$
and
![]() $t=3 \times (n+N^{.6})-n$
. The expected number of leftmost
$t=3 \times (n+N^{.6})-n$
. The expected number of leftmost
![]() $(n-1)$
-tuple repeats is about
$(n-1)$
-tuple repeats is about
![]() $\left(\substack{t \\[3pt] 2}\right)/N\doteq 501.4$
. The picture shows 500 ‘arrival’ points, giving the locations of repeats, plotted as for one segment of long length
$\left(\substack{t \\[3pt] 2}\right)/N\doteq 501.4$
. The picture shows 500 ‘arrival’ points, giving the locations of repeats, plotted as for one segment of long length
![]() $t$
. In each
$t$
. In each
![]() $N^{.6}$
by
$N^{.6}$
by
![]() $N^{.6}$
square, the expected number of points is
$N^{.6}$
square, the expected number of points is
![]() $N^{.2}\doteq 111.4$
. The colour scheme is intended to be purple, green, blue across the top row, orange, yellow for the middle and red (magenta) for the bottom.
$N^{.2}\doteq 111.4$
. The colour scheme is intended to be purple, green, blue across the top row, orange, yellow for the middle and red (magenta) for the bottom.
4.1. Big picture perspective:
 $k$
coloured segments,
$k$
coloured segments,
 $m$
toggle points
$m$
toggle points
We will have
![]() $k$
segments each of length
$k$
segments each of length
![]() $t=N^{.6}$
. The expected number of leftmost
$t=N^{.6}$
. The expected number of leftmost
![]() $(n-1)$
-tuple repeats within a single segment is about
$(n-1)$
-tuple repeats within a single segment is about
![]() $\left(\substack{t \\[3pt] 2}\right)/N\doteq .5 N^{.2}$
. The expected number of repeats between two different given segments is about
$\left(\substack{t \\[3pt] 2}\right)/N\doteq .5 N^{.2}$
. The expected number of repeats between two different given segments is about
![]() $t^2/ N = N^{.2}$
, so the expected number of repeats between two different segments, combined over all
$t^2/ N = N^{.2}$
, so the expected number of repeats between two different segments, combined over all
![]() $\left(\substack{k \\[3pt] 2}\right)$
choices for which two segments, is about
$\left(\substack{k \\[3pt] 2}\right)$
choices for which two segments, is about
![]() $\left(\substack{k \\[3pt] 2}\right) \times N^{.2}$
. This is a huge number of repeats (each based on one vertex having a secondary colouring), and we intend to find
$\left(\substack{k \\[3pt] 2}\right) \times N^{.2}$
. This is a huge number of repeats (each based on one vertex having a secondary colouring), and we intend to find
![]() $m$
such repeats, say at
$m$
such repeats, say at
![]() $v^{\#}_1,\ldots,v^{\#}_m$
in narrowly constrained spatial positions. The goal is to show that, with high probability, for all
$v^{\#}_1,\ldots,v^{\#}_m$
in narrowly constrained spatial positions. The goal is to show that, with high probability, for all
![]() $2^m$
choices of how to change
$2^m$
choices of how to change
![]() $f$
by toggling the values of
$f$
by toggling the values of
![]() $f(v^{\#}_i)$
for
$f(v^{\#}_i)$
for
![]() $i \in I \subset \{1,2,\ldots,m\}$
, the same
$i \in I \subset \{1,2,\ldots,m\}$
, the same
![]() $m$
vertices will be picked out by the narrow two-dimensional spatial constraints.
$m$
vertices will be picked out by the narrow two-dimensional spatial constraints.
In this section we present further figures intended to assist the reader’s intuition. We also give an algorithm which for a given logic
![]() $f$
and starting edges
$f$
and starting edges
![]() $e_i$
finds
$e_i$
finds
![]() $m$
vertices
$m$
vertices
![]() $v^{\#}_1$
, …,
$v^{\#}_1$
, …,
![]() $v^{\#}_m$
. These points—we call them toggle points—give rise to a family of
$v^{\#}_m$
. These points—we call them toggle points—give rise to a family of
![]() $2^m$
functions. We also define (in Section 4.10) a process called relativisation which associates with
$2^m$
functions. We also define (in Section 4.10) a process called relativisation which associates with
![]() $\pi _f$
in
$\pi _f$
in
![]() $S_N$
a permutation
$S_N$
a permutation
![]() $\sigma$
in
$\sigma$
in
![]() $S_k$
,
$S_k$
,
![]() $k$
being fixed and
$k$
being fixed and
![]() $N \to \infty$
. It will be shown that as
$N \to \infty$
. It will be shown that as
![]() $f$
varies over the
$f$
varies over the
![]() $2^m$
functions in a ‘toggle class’, the resulting
$2^m$
functions in a ‘toggle class’, the resulting
![]() $\sigma ’s$
cover
$\sigma ’s$
cover
![]() $S_k$
almost uniformly. In Section 5, it will be shown that this uniform coverage of
$S_k$
almost uniformly. In Section 5, it will be shown that this uniform coverage of
![]() $S_k$
(for each fixed
$S_k$
(for each fixed
![]() $k$
) is a sufficient condition to prove Theorem 1.
$k$
) is a sufficient condition to prove Theorem 1.
A critical issue is that the algorithm for choosing the toggle points must be such that, if the feedback
![]() $f$
is replaced by any one of the
$f$
is replaced by any one of the
![]() $2^m$
functions in the toggle class, the algorithm would find the same toggle points and the same class.Footnote
7
However this is not necessarily the case and the probability of success for the algorithm must be estimated; this leads to the definition of an event
$2^m$
functions in the toggle class, the algorithm would find the same toggle points and the same class.Footnote
7
However this is not necessarily the case and the probability of success for the algorithm must be estimated; this leads to the definition of an event
![]() $H$
.
$H$
.
4.2. Toggling: The case
 $k=2$
and
$k=2$
and
 $m=1$
$m=1$
We show what can happen when we toggle one bit of a logic
![]() $f$
. We have two segments of length
$f$
. We have two segments of length
![]() $t$
, which share a vertex
$t$
, which share a vertex
![]() $v^{\#}$
. Toggling changes the value of
$v^{\#}$
. Toggling changes the value of
![]() $f$
, only at
$f$
, only at
![]() $v^{\#}$
, and gives a new logic
$v^{\#}$
, and gives a new logic
![]() ${f^{*}}$
. Suppose that the segments under
${f^{*}}$
. Suppose that the segments under
![]() $f$
were red and yellow, and that
$f$
were red and yellow, and that
![]() $v^{\#}$
appears at position
$v^{\#}$
appears at position
![]() $i$
on the red segment, and position
$i$
on the red segment, and position
![]() $j$
on the yellow segment. Overall, this repeat has spatial location
$j$
on the yellow segment. Overall, this repeat has spatial location
![]() $(i,j)$
and colour orange. Exactly one such repeat was visualised in Figures 2 and 3; it occurred with
$(i,j)$
and colour orange. Exactly one such repeat was visualised in Figures 2 and 3; it occurred with
![]() $(i,j)=(56,53)$
. The displacement is
$(i,j)=(56,53)$
. The displacement is
![]() $i-j$
— we have a preferred sequence of colours, (derived from the rainbow ROY G. BIV) where red comes before yellow — hence the displacement is 3, rather than
$i-j$
— we have a preferred sequence of colours, (derived from the rainbow ROY G. BIV) where red comes before yellow — hence the displacement is 3, rather than
![]() $-3$
, in this example.
$-3$
, in this example.
4.3. Picking the ‘earliest’ toggle with a small displacement
Consider the case where we have
![]() $k=2$
segments and want to find a single vertex
$k=2$
segments and want to find a single vertex
![]() $v^{\#}$
via a recipe which, when applied to the segments under the toggled logic
$v^{\#}$
via a recipe which, when applied to the segments under the toggled logic
![]() ${f^{*}}$
, still picks out the same vertex. A good recipe involves naming a small bound
${f^{*}}$
, still picks out the same vertex. A good recipe involves naming a small bound
![]() $d$
on the absolute displacement
$d$
on the absolute displacement
![]() $|i-j|$
(thus staying close to the ‘diagonal’), and then picking the ‘earliest’ pair
$|i-j|$
(thus staying close to the ‘diagonal’), and then picking the ‘earliest’ pair
![]() $(i,j)$
that satisfies the displacement bound. This was the key to overcoming the ‘fallacy’ described in Footnote 7.
$(i,j)$
that satisfies the displacement bound. This was the key to overcoming the ‘fallacy’ described in Footnote 7.
The specific choice of how to define earliest is somewhat arbitrary; we will take smallest
![]() $(i+j)$
as the first criterion for earliest, with ties to be broken according to smallest value of
$(i+j)$
as the first criterion for earliest, with ties to be broken according to smallest value of
![]() $\max\!(i,j)$
— given that
$\max\!(i,j)$
— given that
![]() $i+j = i'+j'$
, this is equivalent to taking smallest absolute displacement for the tie-break criterion. For use in the case of
$i+j = i'+j'$
, this is equivalent to taking smallest absolute displacement for the tie-break criterion. For use in the case of
![]() $k$
colours and
$k$
colours and
![]() $\left(\substack{k \\[3pt] 2}\right)$
colour pairs
$\left(\substack{k \\[3pt] 2}\right)$
colour pairs
![]() $\alpha =(a,b)$
, break further ties according to
$\alpha =(a,b)$
, break further ties according to
![]() $\min\!(a,b)$
and then
$\min\!(a,b)$
and then
![]() $\max\!(a,b)$
.
$\max\!(a,b)$
.
The logic
![]() $f$
, with value at
$f$
, with value at
![]() $v^{\#}$
complemented, gives a new logic
$v^{\#}$
complemented, gives a new logic
![]() ${{f^{*}}}={\textrm{Toggle}}(f,\{v^{\#} \})$
, so that
${{f^{*}}}={\textrm{Toggle}}(f,\{v^{\#} \})$
, so that
![]() ${{f^{*}}}(v^{\#})=1-f(v^{\#})$
, while
${{f^{*}}}(v^{\#})=1-f(v^{\#})$
, while
![]() ${{f^{*}}}(v)=f(v) \ \ \forall v \ne v^{\#}$
. It is possible that changing the logic bit at
${{f^{*}}}(v)=f(v) \ \ \forall v \ne v^{\#}$
. It is possible that changing the logic bit at
![]() $v^{\#}$
, will cause an earlier pair to become available as the location of a match between the two segments; so that the recipe for picking the earliest small displacement match, applied to
$v^{\#}$
, will cause an earlier pair to become available as the location of a match between the two segments; so that the recipe for picking the earliest small displacement match, applied to
![]() ${f^{*}}$
, picks out a different vertex instead of
${f^{*}}$
, picks out a different vertex instead of
![]() $v^{\#}$
. In this case, the word toggle is very misleading: the overall operation (find
$v^{\#}$
. In this case, the word toggle is very misleading: the overall operation (find
![]() $v^{\#}$
, then complement the logic at that vertex) is not an involution. Our programme is to specify a displacement bound
$v^{\#}$
, then complement the logic at that vertex) is not an involution. Our programme is to specify a displacement bound
![]() $d$
that varies with
$d$
that varies with
![]() $n$
, in such a way that 1) with high probability, at least one small displacement match can be found, and 2) with high probability, the vertex for the earliest small displacement match is the same in the logic
$n$
, in such a way that 1) with high probability, at least one small displacement match can be found, and 2) with high probability, the vertex for the earliest small displacement match is the same in the logic
![]() ${{f^{*}}} ={\textrm{Toggle}}(f,\{v^{\#} \})$
at the vertex selected for
${{f^{*}}} ={\textrm{Toggle}}(f,\{v^{\#} \})$
at the vertex selected for
![]() $f$
. The example in Figure 8, viewed with any
$f$
. The example in Figure 8, viewed with any
![]() $d \ge 3$
, illustrates what might go wrong with respect to 2).
$d \ge 3$
, illustrates what might go wrong with respect to 2).

Figure 6. About 333 of the 500 occurrences of repeats from Figure 5, but now viewed as among
![]() $k=3$
segments of length
$k=3$
segments of length
![]() $t=N^{.6}\doteq 1.38 \times 10^6$
. The
$t=N^{.6}\doteq 1.38 \times 10^6$
. The
![]() $\left(\substack{k \\[3pt] 2}\right)$
$\left(\substack{k \\[3pt] 2}\right)$
![]() $t$
by
$t$
by
![]() $t$
above-diagonal squares from Figure 5 are superimposed, so the expected number of points is about
$t$
above-diagonal squares from Figure 5 are superimposed, so the expected number of points is about
![]() $\left(\substack{k \\[3pt] 2}\right) \times N^{.2}\doteq 334.3$
. The approximately 167.1 repeats where both occurrences lie in the same segment, corresponding to the
$\left(\substack{k \\[3pt] 2}\right) \times N^{.2}\doteq 334.3$
. The approximately 167.1 repeats where both occurrences lie in the same segment, corresponding to the
![]() $k$
right triangles hugging the diagonal in Figure 5, are not shown. In Section 4.5 we discuss this picture, suggesting scaling for the axes, so that in each colour, the picture is approximately a standard (rate 1 per unit area) two-dimensional Poisson process. The colour scheme is intended to be purple, green, orange.
$k$
right triangles hugging the diagonal in Figure 5, are not shown. In Section 4.5 we discuss this picture, suggesting scaling for the axes, so that in each colour, the picture is approximately a standard (rate 1 per unit area) two-dimensional Poisson process. The colour scheme is intended to be purple, green, orange.

Figure 7. Toggling. An example with
![]() $t=90$
and displacement
$t=90$
and displacement
![]() $d=3$
. The same repeat as shown in Figure 3 with location (56,153) and shown by the orange dot in Figure 4. When all
$d=3$
. The same repeat as shown in Figure 3 with location (56,153) and shown by the orange dot in Figure 4. When all
![]() $\left(\substack{k \\[3pt] 2}\right)$
squares are superimposed, as in Figure 6, the spatial location becomes
$\left(\substack{k \\[3pt] 2}\right)$
squares are superimposed, as in Figure 6, the spatial location becomes
![]() $(i,j)=(56,53)$
. Before the toggle, we have two segments of length
$(i,j)=(56,53)$
. Before the toggle, we have two segments of length
![]() $t=90$
; after the toggle, the segments have length
$t=90$
; after the toggle, the segments have length
![]() $t \pm d$
, that is, 93 and 87.
$t \pm d$
, that is, 93 and 87.

Figure 8. Toggling. This is a continuation of the example in Figure 7, with one repeat with location (56,153), shown by the orange dot in Figure 4. When all
![]() $\left(\substack{k \\[3pt] 2}\right)$
squares are superimposed, as in Figure 6, the spatial location becomes
$\left(\substack{k \\[3pt] 2}\right)$
squares are superimposed, as in Figure 6, the spatial location becomes
![]() $(i,j)=(56,53)$
. Now suppose there were an additional repeat, (which would have been shown by a red dot at (53,58) in Figure 4,) shown here in Figure 8 by the pair of red dots for
$(i,j)=(56,53)$
. Now suppose there were an additional repeat, (which would have been shown by a red dot at (53,58) in Figure 4,) shown here in Figure 8 by the pair of red dots for
![]() $f$
. After the toggle at the orange vertex, vertex 53, along the segment that starts red and finishes yellow, is the same as vertex 55, along the segment that start yellow and finishes red. So, in the logic
$f$
. After the toggle at the orange vertex, vertex 53, along the segment that starts red and finishes yellow, is the same as vertex 55, along the segment that start yellow and finishes red. So, in the logic
![]() ${f^{*}}$
, we have two matches between the two segments: the original, at (56,53), shown by the orange dots, and a new one, at (53,55), shown by the red dots.
${f^{*}}$
, we have two matches between the two segments: the original, at (56,53), shown by the orange dots, and a new one, at (53,55), shown by the red dots.
Recall, from Section 3, that
![]() $t$
is the length of our segments. To get high probability in 1), a necessary and sufficient condition is that
$t$
is the length of our segments. To get high probability in 1), a necessary and sufficient condition is that
To get high probability in 2), a necessary and sufficient condition is that
The argument that (33) suffices is somewhat delicate, akin to a stopping time argument; it is easier to prove — see (37) — that a sufficient condition is that
and then it will be easy to arrange for situations corresponding to pairs
![]() $(t,d)$
satisfying both (32) and (34).
$(t,d)$
satisfying both (32) and (34).
4.4. Displacements caused by toggles
Suppose we have
![]() $k=3$
colours, as shown in Figure 9. There are three segments of length
$k=3$
colours, as shown in Figure 9. There are three segments of length
![]() $t=90$
, with respect to
$t=90$
, with respect to
![]() $f$
. The segment with respect to
$f$
. The segment with respect to
![]() $f$
, starting with
$f$
, starting with
![]() $e_{1}$
, coloured red, has
$e_{1}$
, coloured red, has
![]() $v^{\#}_1$
in position 6 and
$v^{\#}_1$
in position 6 and
![]() $v^{\#}_2$
in position 35 — so the red segment, of length 90, is divided into an initial red path of length 6, followed by a red path of length 29, followed by a red path of length 55.
$v^{\#}_2$
in position 35 — so the red segment, of length 90, is divided into an initial red path of length 6, followed by a red path of length 29, followed by a red path of length 55.

Figure 9. With starting edges
![]() $e_1,e_2,e_3$
, three segments under the logic
$e_1,e_2,e_3$
, three segments under the logic
![]() $f$
are shown in the top part of the display; the red and yellow segments share a vertex
$f$
are shown in the top part of the display; the red and yellow segments share a vertex
![]() $v^{\#}_1$
, coloured orange, early on, the red and blue segments share a vertex
$v^{\#}_1$
, coloured orange, early on, the red and blue segments share a vertex
![]() $v^{\#}_2$
, coloured purple, at a intermediate time, and the yellow and blue segments share a vertex
$v^{\#}_2$
, coloured purple, at a intermediate time, and the yellow and blue segments share a vertex
![]() $v^{\#}_3$
, coloured green, at a late time. We take
$v^{\#}_3$
, coloured green, at a late time. We take
![]() ${{f^{*}}}={\textrm{Toggle}}(f,\{v^{\#}_1 \})$
and
${{f^{*}}}={\textrm{Toggle}}(f,\{v^{\#}_1 \})$
and
![]() ${{f^{**}}}={\textrm{Toggle}}(f,\{v^{\#}_1,v^{\#}_2 \})$
to be the logics formed by toggling at
${{f^{**}}}={\textrm{Toggle}}(f,\{v^{\#}_1,v^{\#}_2 \})$
to be the logics formed by toggling at
![]() $v^{\#}_1$
, and at both
$v^{\#}_1$
, and at both
![]() $v^{\#}_1$
and
$v^{\#}_1$
and
![]() $v^{\#}_2$
. The middle part of the display shows the three segments under
$v^{\#}_2$
. The middle part of the display shows the three segments under
![]() ${f^{*}}$
, and the bottom part of the display shows the three segments under
${f^{*}}$
, and the bottom part of the display shows the three segments under
![]() ${f^{**}}$
.
${f^{**}}$
.
The
![]() $f$
segment starting with
$f$
segment starting with
![]() $e_{2}$
, coloured yellow, has
$e_{2}$
, coloured yellow, has
![]() $v^{\#}_1$
in position 3 and
$v^{\#}_1$
in position 3 and
![]() $v^{\#}_3$
in position 75; hence, it is divided into yellow paths of lengths 3, 72, 15, in that order.
$v^{\#}_3$
in position 75; hence, it is divided into yellow paths of lengths 3, 72, 15, in that order.
The
![]() $f$
segment starting with
$f$
segment starting with
![]() $e_{3}$
, coloured blue, has
$e_{3}$
, coloured blue, has
![]() $v^{\#}_2$
in position 37 and
$v^{\#}_2$
in position 37 and
![]() $v^{\#}_3$
in position 71; hence, it is divided into blue paths of lengths 37, 34, 19, in that order.
$v^{\#}_3$
in position 71; hence, it is divided into blue paths of lengths 37, 34, 19, in that order.
Next, consider
![]() ${{f^{*}}} \;:\!=\; f$
, toggled at
${{f^{*}}} \;:\!=\; f$
, toggled at
![]() $v^{\#}_1$
. Its segment starting from
$v^{\#}_1$
. Its segment starting from
![]() $e_{1}$
has length 6 red followed by length (72 + 15) = 87, for a total length of 93. Its segment starting from
$e_{1}$
has length 6 red followed by length (72 + 15) = 87, for a total length of 93. Its segment starting from
![]() $e_{2}$
has length 3 yellow, followed by length (29 + 55) = 84, for a total length of 87. The
$e_{2}$
has length 3 yellow, followed by length (29 + 55) = 84, for a total length of 87. The
![]() ${f^{*}}$
segment starting from
${f^{*}}$
segment starting from
![]() $e_{3}$
is still length 90, all blue. More importantly,
$e_{3}$
is still length 90, all blue. More importantly,
![]() $v^{\#}_2$
has moved from position 35 on
$v^{\#}_2$
has moved from position 35 on
![]() ${\textrm{Seg}}(f, e_1)$
to position 32 on
${\textrm{Seg}}(f, e_1)$
to position 32 on
![]() ${\textrm{Seg}}(f,e_2)$
, and
${\textrm{Seg}}(f,e_2)$
, and
![]() $v^{\#}_3$
has moved from position 75 on
$v^{\#}_3$
has moved from position 75 on
![]() ${\textrm{Seg}}(f, e_2)$
to position 78 on
${\textrm{Seg}}(f, e_2)$
to position 78 on
![]() ${\textrm{Seg}}(f,e_1)$
, so these have new positions under
${\textrm{Seg}}(f,e_1)$
, so these have new positions under
![]() ${f^{*}}$
, i.e., have been displaced.
${f^{*}}$
, i.e., have been displaced.
Now consider the full effect of changing from
![]() $f$
to
$f$
to
![]() ${f^{*}}$
, by toggling the logic at the bit
${f^{*}}$
, by toggling the logic at the bit
![]() $v^{\#}_1$
which appeared at positions
$v^{\#}_1$
which appeared at positions
![]() $(i,j)=(i,i-d) = (6,3)$
, with
$(i,j)=(i,i-d) = (6,3)$
, with
![]() $d=3$
, for the red and yellow segments: every red vertex later than 6 gets displaced by
$d=3$
, for the red and yellow segments: every red vertex later than 6 gets displaced by
![]() $-d$
, and every yellow vertex later than 3 gets displaced by
$-d$
, and every yellow vertex later than 3 gets displaced by
![]() $+d$
. If a match occurs at
$+d$
. If a match occurs at
![]() $(I,J)$
in the
$(I,J)$
in the
![]() $f$
segments, and the colours involved are red, and some colour, call it
$f$
segments, and the colours involved are red, and some colour, call it
![]() $a$
, with
$a$
, with
![]() $a$
not equal to yellow, then:
$a$
not equal to yellow, then:
Case 1. Color
 $a$
comes after red, in the list of
$a$
comes after red, in the list of
 $k$
colours: the ordered colour pair is (red,
$k$
colours: the ordered colour pair is (red,
 $a)$
. The index
$a)$
. The index
 $I\gt i$
belongs to a red vertex in position
$I\gt i$
belongs to a red vertex in position
 $I$
under the logic
$I$
under the logic
 $f$
, and this vertex has position
$f$
, and this vertex has position
 $I-d$
under the logic
$I-d$
under the logic
 ${f^{*}}$
. So the point at
${f^{*}}$
. So the point at
 $(I,J)$
moves to position
$(I,J)$
moves to position
 $(I-d,J)$
.Footnote
8
$(I-d,J)$
.Footnote
8
Case 2. Color
 $a$
comes before red, in the list of
$a$
comes before red, in the list of
 $k$
colours; the colour pair is
$k$
colours; the colour pair is
 $(a,$
red). The index
$(a,$
red). The index
 $J\gt i$
belongs to a red vertex, in position
$J\gt i$
belongs to a red vertex, in position
 $J$
under the logic
$J$
under the logic
 $f$
, but in position
$f$
, but in position
 $J-d$
under the logic
$J-d$
under the logic
 ${f^{*}}$
. So the point at
${f^{*}}$
. So the point at
 $(I,J)$
moves to position
$(I,J)$
moves to position
 $(I,J-d)$
.
$(I,J-d)$
.
If there is an orange match at
![]() $(I,J)$
for the
$(I,J)$
for the
![]() $f$
segments, with
$f$
segments, with
![]() $I\gt i$
and
$I\gt i$
and
![]() $J\gt j$
, this match will move to
$J\gt j$
, this match will move to
![]() $(I-d,J+d)$
.
$(I-d,J+d)$
.
Similarly, a match between yellow, and some
![]() $a$
not equal to red, occurring at
$a$
not equal to red, occurring at
![]() $(I,J)$
under the logic
$(I,J)$
under the logic
![]() $f$
, moves to
$f$
, moves to
![]() $(I+3,J)$
or
$(I+3,J)$
or
![]() $(I,J+3)$
under the logic
$(I,J+3)$
under the logic
![]() ${f^{*}}$
, according to whether
${f^{*}}$
, according to whether
![]() $a$
comes after or before yellow, in the list of all
$a$
comes after or before yellow, in the list of all
![]() $k$
colours.
$k$
colours.
This effect can be seen in Figure 9: the orange dot is at (6,3) with displacement
![]() $d=3$
, the purple dot occurs at (35,37) under
$d=3$
, the purple dot occurs at (35,37) under
![]() $f$
, but at (32,37) under
$f$
, but at (32,37) under
![]() ${f^{*}}$
and
${f^{*}}$
and
![]() ${f^{**}}$
.
${f^{**}}$
.
More cases can be seen in Figure 10.

Figure 10. Displacements caused by a single toggle. An example with
![]() $t=90$
, and three colours, red, yellow, and blue. Say the toggle is at
$t=90$
, and three colours, red, yellow, and blue. Say the toggle is at
![]() $v^{\#}_2$
occurring at (red,blue) time
$v^{\#}_2$
occurring at (red,blue) time
![]() $(35,40)$
, similar to the purple vertex at (
$(35,40)$
, similar to the purple vertex at (
![]() $35,37)$
in Figure 9, but with the displacement changed from −2 to −5, for the sake of being easier to see in the two-dimensional picture. We have thrown in several more matches between two different colours, at various earlier and later times, to show the resulting two-dimensional displacements. Red vertices at times greater than 35 have their time increased by 5, and blue vertices at times greater than 40 have their time decreased by 5. Two-dimensional match locations are indicated by a solid circle for the logic
$35,37)$
in Figure 9, but with the displacement changed from −2 to −5, for the sake of being easier to see in the two-dimensional picture. We have thrown in several more matches between two different colours, at various earlier and later times, to show the resulting two-dimensional displacements. Red vertices at times greater than 35 have their time increased by 5, and blue vertices at times greater than 40 have their time decreased by 5. Two-dimensional match locations are indicated by a solid circle for the logic
![]() $f$
and an open circle for the logic
$f$
and an open circle for the logic
![]() ${f^{*}}$
.
${f^{*}}$
.
4.5. The natural scale: by
 $1/\sqrt{N}$
for length, by
$1/\sqrt{N}$
for length, by
 $1/N$
for area
$1/N$
for area
One gets an intuitive grasp of the process of spatial locations of places
![]() $(i,j)$
where two segments of different colours share a vertex, by looking at a picture such as that in Figure 6 — even though the axes are unlabelled.
$(i,j)$
where two segments of different colours share a vertex, by looking at a picture such as that in Figure 6 — even though the axes are unlabelled.
One view would be that the square is
![]() $t$
by
$t$
by
![]() $t$
, with
$t$
, with
![]() $n=34, N=2^n,t=N^{.6}$
, i.e., about 1.3 million by 1.3 million. The other natural view is that the square is about
$n=34, N=2^n,t=N^{.6}$
, i.e., about 1.3 million by 1.3 million. The other natural view is that the square is about
![]() $t/\sqrt{N}$
by
$t/\sqrt{N}$
by
![]() $t/\sqrt{N}$
, i.e., about 10.556 by 10.556, with area 111.43.
$t/\sqrt{N}$
, i.e., about 10.556 by 10.556, with area 111.43.
The latter point of view is natural, since at each
![]() $(i,j)$
, for each colour pair
$(i,j)$
, for each colour pair
![]() $(a,b)$
,
$(a,b)$
,
![]() $1 \le a \lt b \le k$
, with
$1 \le a \lt b \le k$
, with
![]() $\doteq$
to allow a small discrepancy for the failure of the good event,
$\doteq$
to allow a small discrepancy for the failure of the good event,
![]() ${\mathbb{P}}($
an arrival
Footnote
9
at
${\mathbb{P}}($
an arrival
Footnote
9
at
![]() $(i,j)$
in those colours)
$(i,j)$
in those colours)
![]() $ \;:\!=\;{\mathbb{P}}(v_{a,i}=v_{b,j}$
and
$ \;:\!=\;{\mathbb{P}}(v_{a,i}=v_{b,j}$
and
![]() $v_{a,i-1} \ne v_{b,j-1})$
$v_{a,i-1} \ne v_{b,j-1})$
![]() $\doteq{\mathbb{P}}($
there is a leftmost
$\doteq{\mathbb{P}}($
there is a leftmost
![]() $(n-1)$
-tuple repeat at a specific locationFootnote
10
in the coin tossing sequence)
$(n-1)$
-tuple repeat at a specific locationFootnote
10
in the coin tossing sequence)
![]() $= 1/N$
. Hence, scaling length by
$= 1/N$
. Hence, scaling length by
![]() $1/\sqrt{N}$
, so that area is scaled by
$1/\sqrt{N}$
, so that area is scaled by
![]() $1/N$
, leads to
$1/N$
, leads to
The picture in Figure 6, viewed as occurring on a 10.556 by 10.556 square, closely resembles a (standard, rate
![]() $1 \, dy \, dx$
) two-dimensional Poisson process, in each secondary colour pair. And overall, ignoring colour, the picture resembles the rate
$1 \, dy \, dx$
) two-dimensional Poisson process, in each secondary colour pair. And overall, ignoring colour, the picture resembles the rate
![]() $\left(\substack{k \\[3pt] 2}\right) \, dy \, dx$
Poisson process on the
$\left(\substack{k \\[3pt] 2}\right) \, dy \, dx$
Poisson process on the
![]() $t/ \sqrt{N}$
by
$t/ \sqrt{N}$
by
![]() $t/ \sqrt{N}$
square.
$t/ \sqrt{N}$
square.
There are additional requirements for the Poisson process, beyond having intensity
![]() $1 \, dy \, dx$
. Namely, probabilistic independence for the counts in disjoint regions. We do have a good Poisson process approximation, for a combination of two reasons. First, the good event
$1 \, dy \, dx$
. Namely, probabilistic independence for the counts in disjoint regions. We do have a good Poisson process approximation, for a combination of two reasons. First, the good event
![]() $G={G_{(k,t)}}$
from Theorem 6 gives a high-probability coupling (since
$G={G_{(k,t)}}$
from Theorem 6 gives a high-probability coupling (since
![]() $t=N^{.6}$
entails
$t=N^{.6}$
entails
![]() $t^3n^3/N^2 \to 0$
) between coin tossing and the
$t^3n^3/N^2 \to 0$
) between coin tossing and the
![]() $k$
de Bruijn segments of length
$k$
de Bruijn segments of length
![]() $t$
. Second, the Chen–Stein method, Theorem 3 of [Reference Arratia, Goldstein and Gordon6], gives a total variation distance upper bound (tending to zero since
$t$
. Second, the Chen–Stein method, Theorem 3 of [Reference Arratia, Goldstein and Gordon6], gives a total variation distance upper bound (tending to zero since
![]() $t=N^{.6}$
entails
$t=N^{.6}$
entails
![]() $t^3n/N^2 \to 0$
) between the process of indicators of leftmost
$t^3n/N^2 \to 0$
) between the process of indicators of leftmost
![]() $(n-1)$
-tuple repeats for coin tossing, and a process with the same intensity, but mutually independent coordinates.
$(n-1)$
-tuple repeats for coin tossing, and a process with the same intensity, but mutually independent coordinates.
We get our intuition from the Poisson process. But for our proofs, we will work directly with the discrete, dependent processes.
4.6. Controlled regions for
 $m$
successive potential toggle vertices
$m$
successive potential toggle vertices
4.6.1. Quick motivation for the geometric progression
We will construct choice functions in (40), based on regions, defined in (36), which in turn are based on a geometric progression in (35). Here we give some motivation for this elaborate construction.
If we search for a single toggle point, in a thin and long rectangle along the diagonal,
![]() $\{ (i,j)\;:\;|i-j| \le d, 0\le i,j \le t \}$
, then, in the natural scale of Section 4.5, (and ignoring factors of
$\{ (i,j)\;:\;|i-j| \le d, 0\le i,j \le t \}$
, then, in the natural scale of Section 4.5, (and ignoring factors of
![]() $\sqrt{2}$
related to the 45 degree rotation, and of 2 for
$\sqrt{2}$
related to the 45 degree rotation, and of 2 for
![]() $\pm d$
), the rectangle is
$\pm d$
), the rectangle is
![]() $d_1 = d/\sqrt{N}$
by
$d_1 = d/\sqrt{N}$
by
![]() $w_1= \ t/\sqrt{N}$
. Condition (32) can be interpreted as meaning that the (natural scale) area,
$w_1= \ t/\sqrt{N}$
. Condition (32) can be interpreted as meaning that the (natural scale) area,
![]() $d_1w_1$
, tends to infinity — so that with high probability, matches can be found in this rectangle, and condition (33) can similarly be interpreted as meaning that
$d_1w_1$
, tends to infinity — so that with high probability, matches can be found in this rectangle, and condition (33) can similarly be interpreted as meaning that
![]() $d_1 \to 0$
, so that no matches will be found in the two-dimensional set, of area on the order of
$d_1 \to 0$
, so that no matches will be found in the two-dimensional set, of area on the order of
![]() $d_1^2$
, of points within
$d_1^2$
, of points within
![]() $\ell _\infty$
distance
$\ell _\infty$
distance
![]() $d_1$
of the chosen location
$d_1$
of the chosen location
![]() $(i,j)$
.
$(i,j)$
.
Now in choosing
![]() $m$
toggle points, displacements caused by earlier toggles might change the search result, and we wish to make this unlikely. In more detail: as seen in Section 4.4, toggling a logic
$m$
toggle points, displacements caused by earlier toggles might change the search result, and we wish to make this unlikely. In more detail: as seen in Section 4.4, toggling a logic
![]() $f$
at a vertex
$f$
at a vertex
![]() $v^{\#}$
which appears on two different colours, at times
$v^{\#}$
which appears on two different colours, at times
![]() $i,j$
with
$i,j$
with
![]() $|i-j| \le d$
causes displacements in the time indices of vertices occurring later on those segments, by amounts up to
$|i-j| \le d$
causes displacements in the time indices of vertices occurring later on those segments, by amounts up to
![]() $d$
. Our
$d$
. Our
![]() $m$
potential toggle points,
$m$
potential toggle points,
![]() $v^{\#}_1,\ldots,v^{\#}_m$
, are controlled so that on any segment,
$v^{\#}_1,\ldots,v^{\#}_m$
, are controlled so that on any segment,
![]() $v^{\#}_\ell$
is preceded by toggle points from among the
$v^{\#}_\ell$
is preceded by toggle points from among the
![]() $v^{\#}_1,\ldots,v^{\#}_{\ell -1}$
. If the displacement caused by toggling at
$v^{\#}_1,\ldots,v^{\#}_{\ell -1}$
. If the displacement caused by toggling at
![]() $v^{\#}_i$
is at most
$v^{\#}_i$
is at most
![]() $d_i$
, then in choosing
$d_i$
, then in choosing
![]() $v^{\#}_\ell$
, the accumulated displacements from previous toggles is at most
$v^{\#}_\ell$
, the accumulated displacements from previous toggles is at most
![]() $d_1+\cdots +d_{\ell -1}$
. By taking the
$d_1+\cdots +d_{\ell -1}$
. By taking the
![]() $d_i$
in geometric progression, with large ratio
$d_i$
in geometric progression, with large ratio
![]() $r^2$
, this accumulated displacement in the search for
$r^2$
, this accumulated displacement in the search for
![]() $v^{\#}_\ell$
is at most order of
$v^{\#}_\ell$
is at most order of
![]() $d_{\ell -1}$
. The rectangle where we search for
$d_{\ell -1}$
. The rectangle where we search for
![]() $v^{\#}_\ell$
is thin and long,
$v^{\#}_\ell$
is thin and long,
![]() $d_\ell$
by
$d_\ell$
by
![]() $w_\ell = r/d_\ell$
; the length of its boundary is order of
$w_\ell = r/d_\ell$
; the length of its boundary is order of
![]() $w_\ell$
, so the area involved in points at a distance at most
$w_\ell$
, so the area involved in points at a distance at most
![]() $d_{\ell -1} = d_\ell/r^2$
from the boundary is order of
$d_{\ell -1} = d_\ell/r^2$
from the boundary is order of
![]() $1/r =o(1)$
. Hence with high probability, displaced indices have no effect.
$1/r =o(1)$
. Hence with high probability, displaced indices have no effect.
4.6.2. The search regions
We divide the time interval
![]() $[0,t]$
into
$[0,t]$
into
![]() $m$
equal length pieces. On the earliest piece, with times in [0,t/m], we demand that we can find a match
$m$
equal length pieces. On the earliest piece, with times in [0,t/m], we demand that we can find a match
![]() $(i,j)$
with
$(i,j)$
with
![]() $|i-j|$
very very very small, but no upper bound on
$|i-j|$
very very very small, but no upper bound on
![]() $\max\!(i,j)$
other than
$\max\!(i,j)$
other than
![]() $\max\!(i,j) \lt t/m$
. In the natural scale of Section 4.5 we are searching for matches in a very very very thin and very very long rectangle surrounding the diagonal line
$\max\!(i,j) \lt t/m$
. In the natural scale of Section 4.5 we are searching for matches in a very very very thin and very very long rectangle surrounding the diagonal line
![]() $i=j$
; this rectangle has a large area. On the second piece, with times in
$i=j$
; this rectangle has a large area. On the second piece, with times in
![]() $[t/m,2t/m]$
, we relax the notion of thin, expanding by a large factor
$[t/m,2t/m]$
, we relax the notion of thin, expanding by a large factor
![]() $r^2$
, relax the notion of long, dividing by the factor
$r^2$
, relax the notion of long, dividing by the factor
![]() $r^2$
, thus keeping the area constant. We continue this pair of geometric progressions, so the
$r^2$
, thus keeping the area constant. We continue this pair of geometric progressions, so the
![]() $m$
th region is a thin long rectangle — but still with the same area.
$m$
th region is a thin long rectangle — but still with the same area.
Here is a concrete way to accomplish the above, together with
![]() $t^3n^3/N^2 \to 0$
and with
$t^3n^3/N^2 \to 0$
and with
![]() $k$
fixed. Let
$k$
fixed. Let
The last condition should be understood as ‘in the natural scale from Section 4.5, the
![]() $t$
by
$t$
by
![]() $t$
rectangle is
$t$
rectangle is
![]() $ma$
by
$ma$
by
![]() $ma$
, and length
$ma$
, and length
![]() $t/m$
for the discrete
$t/m$
for the discrete
![]() $i$
and
$i$
and
![]() $j$
corresponds to length
$j$
corresponds to length
![]() $a$
’. Let
$a$
’. Let
and, ignoring the factors of
![]() $\sqrt{2}$
involved in the 45 degree rotation, take the thin long rectangles to have shapes
$\sqrt{2}$
involved in the 45 degree rotation, take the thin long rectangles to have shapes
 \begin{eqnarray} d_1 = \frac{1}{r^{2m}} & \textrm{ by } & w_1 = r^{2m+1} = (t/m)/\sqrt{N} \nonumber \\[5pt] d_2 = \frac{1}{r^{2m-2}} & \textrm{ by } & w_2 = r^{2m-1} \\[5pt] & \vdots & \nonumber \\[5pt] d_m = \frac{1}{r^2} & \textrm{ by } & w_m = r^{3} \nonumber \end{eqnarray}
\begin{eqnarray} d_1 = \frac{1}{r^{2m}} & \textrm{ by } & w_1 = r^{2m+1} = (t/m)/\sqrt{N} \nonumber \\[5pt] d_2 = \frac{1}{r^{2m-2}} & \textrm{ by } & w_2 = r^{2m-1} \\[5pt] & \vdots & \nonumber \\[5pt] d_m = \frac{1}{r^2} & \textrm{ by } & w_m = r^{3} \nonumber \end{eqnarray}
Indexing by
![]() $\ell =1$
to
$\ell =1$
to
![]() $m$
, the
$m$
, the
![]() $\ell$
th rectangle is
$\ell$
th rectangle is
![]() $d_\ell \;:\!=\; r^{2\ell -2m-2}$
by
$d_\ell \;:\!=\; r^{2\ell -2m-2}$
by
![]() $w_\ell \;:\!=\; r^{2m-2\ell +3}$
on the natural scale. Directly in terms of the discrete
$w_\ell \;:\!=\; r^{2m-2\ell +3}$
on the natural scale. Directly in terms of the discrete
![]() $i$
and
$i$
and
![]() $j$
, we define
$j$
, we define
 \begin{eqnarray}{\textit{Region}}_\ell =\left \{ (i,j)\;:\;\frac{|i-j|}{\sqrt{N}} \lt r^{2\ell -2m-2} \right . & \textrm{ and } & \\[5pt] \left . \frac{(\ell -1)t}{m} \le \min\!(i,j) \le \max\!(i,j) \le \frac{(\ell -1)t}{m} + \frac{t/m}{r^{2(\ell -1)}} \right \}, & & \nonumber \end{eqnarray}
\begin{eqnarray}{\textit{Region}}_\ell =\left \{ (i,j)\;:\;\frac{|i-j|}{\sqrt{N}} \lt r^{2\ell -2m-2} \right . & \textrm{ and } & \\[5pt] \left . \frac{(\ell -1)t}{m} \le \min\!(i,j) \le \max\!(i,j) \le \frac{(\ell -1)t}{m} + \frac{t/m}{r^{2(\ell -1)}} \right \}, & & \nonumber \end{eqnarray}
so one checks that 1) as
![]() $\ell$
increases by 1, the thinness constraint relaxes by a factor of
$\ell$
increases by 1, the thinness constraint relaxes by a factor of
![]() $r^2$
, while the width constraint becomes more severe by a factor of
$r^2$
, while the width constraint becomes more severe by a factor of
![]() $r^2$
, so the area stays constant, 2) the first region, with
$r^2$
, so the area stays constant, 2) the first region, with
![]() $\ell =1$
, allows
$\ell =1$
, allows
![]() $i,j \in [0,t/m]$
and 3) the last region, with
$i,j \in [0,t/m]$
and 3) the last region, with
![]() $\ell =m$
, has
$\ell =m$
, has
![]() $|i-j|/\sqrt{N} \le 1/r^2 = o(1)$
as
$|i-j|/\sqrt{N} \le 1/r^2 = o(1)$
as
![]() $n \to \infty$
.
$n \to \infty$
.
Consider the possibility discussed in Section 4.3, where a toggle at a vertex appearing in two differently coloured segment enables a match within a single segment to become, after the toggle, an earlier match between two different segments. For each
![]() $\ell =1$
to
$\ell =1$
to
![]() $m$
, with the
$m$
, with the
![]() $(t,d)$
in (34) given by
$(t,d)$
in (34) given by
![]() $t=w_\ell \sqrt{N}, d= d_\ell \sqrt{N}$
, the condition in (34) is indeed satisfied by our specific choice in (35). On the natural scale, and ignoring rotation, we are searching for a match in a
$t=w_\ell \sqrt{N}, d= d_\ell \sqrt{N}$
, the condition in (34) is indeed satisfied by our specific choice in (35). On the natural scale, and ignoring rotation, we are searching for a match in a
![]() $\delta = d_\ell$
by
$\delta = d_\ell$
by
![]() $W=w_\ell$
rectangle, thin and long, with
$W=w_\ell$
rectangle, thin and long, with
![]() $\delta \to 0$
and area
$\delta \to 0$
and area
![]() $\delta W \to \infty$
. The condition (34), on the natural scale, means that
$\delta W \to \infty$
. The condition (34), on the natural scale, means that
![]() $\delta ^3 W \to 0$
. It implies that, with high probability, we do not find a match between two differently coloured segments (at
$\delta ^3 W \to 0$
. It implies that, with high probability, we do not find a match between two differently coloured segments (at
![]() $(i,j)$
in the rectangle, with
$(i,j)$
in the rectangle, with
![]() $|i-j|/\sqrt{N}\lt \delta$
,) and simultaneously a nearby match within a single segment. Here, nearby means with both indices within distance
$|i-j|/\sqrt{N}\lt \delta$
,) and simultaneously a nearby match within a single segment. Here, nearby means with both indices within distance
![]() $\delta \sqrt{N}$
from
$\delta \sqrt{N}$
from
![]() $i$
or
$i$
or
![]() $j$
. Now, the
$j$
. Now, the
![]() $\delta$
by
$\delta$
by
![]() $W$
rectangle can be covered by
$W$
rectangle can be covered by
![]() $W/\delta$
squares, each square of size
$W/\delta$
squares, each square of size
![]() $4 \delta$
by
$4 \delta$
by
![]() $4 \delta$
, and with each successive square being a translate, by
$4 \delta$
, and with each successive square being a translate, by
![]() $\delta$
, of the previous square. Ignoring constant factors,Footnote
11
the expected number of arrivals in one square is order of
$\delta$
, of the previous square. Ignoring constant factors,Footnote
11
the expected number of arrivals in one square is order of
![]() $\delta ^2$
, and the chance of two or more arrivals in that one square is order of
$\delta ^2$
, and the chance of two or more arrivals in that one square is order of
![]() $\delta ^4.$
Thus the expected number of squares with two or more arrivals is order of
$\delta ^4.$
Thus the expected number of squares with two or more arrivals is order of
4.7. Definition of the choice functions
Write
![]() $V = \mathbb{F}_2^{n-1}$
for the set of vertices in
$V = \mathbb{F}_2^{n-1}$
for the set of vertices in
![]() $D_{n-1}$
, and write ‘null’ for a special value, not in
$D_{n-1}$
, and write ‘null’ for a special value, not in
![]() $V$
, used to encode ‘undefined’. Recall that we write
$V$
, used to encode ‘undefined’. Recall that we write
![]() $\boldsymbol{{e}} = (e_1,\ldots,e_k)$
for the starting
$\boldsymbol{{e}} = (e_1,\ldots,e_k)$
for the starting
![]() $n$
-tuples for
$n$
-tuples for
![]() $k$
segments, and
$k$
segments, and
![]() $S_{n,k} = \{(f,\boldsymbol{{e}}) \}$
for the space in which we make a uniform choice of logic and starting edges. Also recall our notation (31) for vertices along the
$S_{n,k} = \{(f,\boldsymbol{{e}}) \}$
for the space in which we make a uniform choice of logic and starting edges. Also recall our notation (31) for vertices along the
![]() $k$
segments. Note that we have both
$k$
segments. Note that we have both
![]() $k$
segments and
$k$
segments and
![]() $k$
colours; these are different concepts, and ultimately, colours will be labelled according to the segment labels under
$k$
colours; these are different concepts, and ultimately, colours will be labelled according to the segment labels under
![]() $f$
— but on the soon to be defined ‘happy’ event
$f$
— but on the soon to be defined ‘happy’ event
![]() $H$
, finding
$H$
, finding
![]() $v^{\#}_i$
on two different segments of
$v^{\#}_i$
on two different segments of
![]() $f$
will be equivalent to finding
$f$
will be equivalent to finding
![]() $v^{\#}_i$
on two different colours. To keep track of the colours, let
$v^{\#}_i$
on two different colours. To keep track of the colours, let
For
![]() $\ell =1$
to
$\ell =1$
to
![]() $m$
, we define
$m$
, we define
where
![]() ${\textit{Region}}_\ell$
is defined by (36).
${\textit{Region}}_\ell$
is defined by (36).
For
![]() $\ell =1$
to
$\ell =1$
to
![]() $m$
, we define
$m$
, we define
where the value is
![]() $\textit{null}$
if the set of candidates is empty, and otherwise, picking the first
$\textit{null}$
if the set of candidates is empty, and otherwise, picking the first
![]() $(i,j,a,b)$
in
$(i,j,a,b)$
in
![]() ${\textrm{Candidates}}_\ell (f,\boldsymbol{{e}})$
,
${\textrm{Candidates}}_\ell (f,\boldsymbol{{e}})$
,
![]() $v^{\#}_\ell$
is the vertex with
$v^{\#}_\ell$
is the vertex with
![]() $v^{\#}_\ell =v_{a,i} = v_{b,j}$
. To be very careful, the order for first is the lex-first order on
$v^{\#}_\ell =v_{a,i} = v_{b,j}$
. To be very careful, the order for first is the lex-first order on
![]() $(i+j, \max\!(i,j), a,b)$
.
$(i+j, \max\!(i,j), a,b)$
.
4.8. The happy event
 $H = H(k,m,n)$
$H = H(k,m,n)$
We now describe a subset of
![]() $S_{n,k}$
and refer to this subset as the happy event
$S_{n,k}$
and refer to this subset as the happy event
![]() $H$
. One requirement for
$H$
. One requirement for
![]() $(f,\boldsymbol{{e}}) \in H$
is that, for
$(f,\boldsymbol{{e}}) \in H$
is that, for
![]() $\ell =1$
to
$\ell =1$
to
![]() $m$
, each of the values
$m$
, each of the values
![]() ${\textit{Choice}}_\ell (f,\boldsymbol{{e}}) \ne{\textit{null}}$
. Starting with such an
${\textit{Choice}}_\ell (f,\boldsymbol{{e}}) \ne{\textit{null}}$
. Starting with such an
![]() $(f,\boldsymbol{{e}})$
, the choice functions pick out a set of
$(f,\boldsymbol{{e}})$
, the choice functions pick out a set of
![]() $m$
distinct vertices; call them
$m$
distinct vertices; call them
![]() $v^{\#}_1,\ldots, v^{\#}_m$
, and name the set,
$v^{\#}_1,\ldots, v^{\#}_m$
, and name the set,
![]() ${{V^{\#}}} = \{ v^{\#}_1,\ldots, v^{\#}_m \}$
— we will use this notation in (42) below.
${{V^{\#}}} = \{ v^{\#}_1,\ldots, v^{\#}_m \}$
— we will use this notation in (42) below.
Given a set of vertices,
![]() $U \subset V$
, we denote the logic
$U \subset V$
, we denote the logic
![]() $f$
toggled at the vertices in
$f$
toggled at the vertices in
![]() $U$
as
$U$
as
![]() ${\textrm{Toggle}}(f,U)$
, defined by
${\textrm{Toggle}}(f,U)$
, defined by
 \begin{equation} {\textrm{Toggle}}(f,U) \;:\!=\;{{f^{*}}}, \textrm{ where }{{f^{*}}}(v) = \left \{ \begin{array}{l@{\quad}l} 1-f(v) & \mbox{if $v \in U$} \\[5pt] f(v) & \mbox{if $v \in V \setminus U$} \end{array} \right . . \end{equation}
\begin{equation} {\textrm{Toggle}}(f,U) \;:\!=\;{{f^{*}}}, \textrm{ where }{{f^{*}}}(v) = \left \{ \begin{array}{l@{\quad}l} 1-f(v) & \mbox{if $v \in U$} \\[5pt] f(v) & \mbox{if $v \in V \setminus U$} \end{array} \right . . \end{equation}
We define
![]() $H$
as follows:
$H$
as follows:
Informally,
![]() $(f,\boldsymbol{{e}})$
is in the happy event iff the
$(f,\boldsymbol{{e}})$
is in the happy event iff the
![]() $k$
segments involve no
$k$
segments involve no
![]() $n$
-repeats, and the choice recipes find
$n$
-repeats, and the choice recipes find
![]() $m$
potential toggle vertices, and all
$m$
potential toggle vertices, and all
![]() $2^m$
cousins
$2^m$
cousins
![]() ${f^{*}}$
, formed by toggling at a subset of those vertices, give rise to the same
${f^{*}}$
, formed by toggling at a subset of those vertices, give rise to the same
![]() $v^{\#}_1,\ldots,v^{\#}_m$
.
$v^{\#}_1,\ldots,v^{\#}_m$
.
The definition above creates an equivalence relation on
![]() $H$
, in which all classes have size
$H$
, in which all classes have size
![]() $2^m$
, and all
$2^m$
, and all
![]() $({{f^{*}}},\boldsymbol{{e}}) \in [(f,\boldsymbol{{e}})]$
share the same sequence
$({{f^{*}}},\boldsymbol{{e}}) \in [(f,\boldsymbol{{e}})]$
share the same sequence
![]() $v^{\#}_1,\ldots,v^{\#}_m$
. Using the calculations given in Section 4.6.1 one may show that for fixed
$v^{\#}_1,\ldots,v^{\#}_m$
. Using the calculations given in Section 4.6.1 one may show that for fixed
![]() $k,m$
,
$k,m$
,
![]() $|H|/|S_{n,k}| \to 1$
; that it, that
$|H|/|S_{n,k}| \to 1$
; that it, that
![]() ${\mathbb{P}}(H) \to 1$
as
${\mathbb{P}}(H) \to 1$
as
![]() $n \to \infty$
.
$n \to \infty$
.
4.9. Definition and likelihood of an
 $\varepsilon$
-good schedule
$\varepsilon$
-good schedule
Given
![]() $k$
, view
$k$
, view
![]() $\mathcal{A}$
, defined by (38) as an alphabet of size
$\mathcal{A}$
, defined by (38) as an alphabet of size
A schedule of length
![]() $m$
is a word
$m$
is a word
![]() $\alpha _1 \alpha _2 \cdots \alpha _m \in{\mathcal{A}}^m$
. Given a schedule of length
$\alpha _1 \alpha _2 \cdots \alpha _m \in{\mathcal{A}}^m$
. Given a schedule of length
![]() $m$
, and
$m$
, and
![]() $m$
coin tosses
$m$
coin tosses
![]() $D_1,\ldots,D_m$
, for
$D_1,\ldots,D_m$
, for
![]() $i=1$
to
$i=1$
to
![]() $m$
define permutations in
$m$
define permutations in
![]() ${\mathcal{S}}_k$
by
${\mathcal{S}}_k$
by
 \begin{equation*} \tau _i = \left \{ \begin {array}{l@{\quad}l} \text {the transposition } (a b) & \mbox {if $\alpha _i=(a,b)$ and $D_i=\text { heads }$} \\[5pt] \text { the identity } & \mbox {if $D_i=\text { tails }$} \end {array} \right ., \end{equation*}
\begin{equation*} \tau _i = \left \{ \begin {array}{l@{\quad}l} \text {the transposition } (a b) & \mbox {if $\alpha _i=(a,b)$ and $D_i=\text { heads }$} \\[5pt] \text { the identity } & \mbox {if $D_i=\text { tails }$} \end {array} \right ., \end{equation*}
and let
![]() $\tau = \tau (\alpha _1 \alpha _2 \cdots \alpha _m,D_1,\ldots,D_m)$
be the product, with
$\tau = \tau (\alpha _1 \alpha _2 \cdots \alpha _m,D_1,\ldots,D_m)$
be the product, with
![]() $\tau _1$
applied first,
$\tau _1$
applied first,
Write
![]() $\sigma$
for an arbitrary permutation in
$\sigma$
for an arbitrary permutation in
![]() ${\mathcal{S}}_k$
, and let
${\mathcal{S}}_k$
, and let
be the conditional probability of getting
![]() $\sigma$
for the value of
$\sigma$
for the value of
![]() $\tau$
, given the schedule
$\tau$
, given the schedule
![]() $\alpha _1 \alpha _2 \cdots \alpha _m$
— these are values of the form
$\alpha _1 \alpha _2 \cdots \alpha _m$
— these are values of the form
![]() $z/2^m$
with
$z/2^m$
with
![]() $z$
in
$z$
in
![]() $Z$
. The total variation distance to the uniform distribution on
$Z$
. The total variation distance to the uniform distribution on
![]() ${\mathcal{S}}_k$
is
${\mathcal{S}}_k$
is
Given
![]() $\varepsilon \gt 0$
, a schedule
$\varepsilon \gt 0$
, a schedule
![]() $\alpha _1 \alpha _2 \cdots \alpha _m$
is
$\alpha _1 \alpha _2 \cdots \alpha _m$
is
![]() $\varepsilon$
-good if
$\varepsilon$
-good if
![]() ${\textrm{Distance}}(\alpha _1 \alpha _2 \cdots \alpha _m) \lt \varepsilon$
.
${\textrm{Distance}}(\alpha _1 \alpha _2 \cdots \alpha _m) \lt \varepsilon$
.
Lemma 7.
Given
![]() $k$
, and
$k$
, and
![]() $\varepsilon \gt 0$
, there exists
$\varepsilon \gt 0$
, there exists
![]() $m$
such that, for a random schedule of length
$m$
such that, for a random schedule of length
![]() $m$
, with all
$m$
, with all
![]() $\left(\substack{k \\[3pt] 2}\right)^m$
equally likely,
$\left(\substack{k \\[3pt] 2}\right)^m$
equally likely,
Proof. There is a well-known bijection between
![]() ${\mathcal{S}}_k$
and the set
${\mathcal{S}}_k$
and the set
![]() $C_k \;:\!=\; [1] \times [2] \times \cdots \times [k]\;$
: given
$C_k \;:\!=\; [1] \times [2] \times \cdots \times [k]\;$
: given
![]() $c=(c_1,c_2,\ldots,c_k)$
with
$c=(c_1,c_2,\ldots,c_k)$
with
![]() $1 \le c_i \le i$
, take
$1 \le c_i \le i$
, take
where
![]() $(a \ b)$
denotes the transposition
$(a \ b)$
denotes the transposition
![]() $(a \ b) \in{\mathcal{S}}_k$
if
$(a \ b) \in{\mathcal{S}}_k$
if
![]() $a \ne b$
, and the identity map otherwise. (The corresponding algorithm, to generate uniformly distributed random permutations, is known as the ‘Fisher-Yates shuffle’ or ‘Knuth shuffle’.)
$a \ne b$
, and the identity map otherwise. (The corresponding algorithm, to generate uniformly distributed random permutations, is known as the ‘Fisher-Yates shuffle’ or ‘Knuth shuffle’.)
Now consider the particular word
![]() $w$
of length
$w$
of length
![]() $K$
over the alphabet
$K$
over the alphabet
![]() $\mathcal{A}$
defined in (38), given by
$\mathcal{A}$
defined in (38), given by
If we had
![]() $m=K$
and the schedule is
$m=K$
and the schedule is
![]() $\alpha _1 \alpha _2 \cdots \alpha _m=w$
, then
$\alpha _1 \alpha _2 \cdots \alpha _m=w$
, then
![]() ${\textrm{Distance}}(\alpha _1 \alpha _2 \cdots \alpha _m) \le 1-2^{-K}$
, because for each
${\textrm{Distance}}(\alpha _1 \alpha _2 \cdots \alpha _m) \le 1-2^{-K}$
, because for each
![]() $\sigma$
in (45), one assignment of the coin values
$\sigma$
in (45), one assignment of the coin values
![]() $(D_1,\ldots,D_m)$
yields
$(D_1,\ldots,D_m)$
yields
![]() $\tau =\sigma$
, via the coins for the genuine transpositions among the
$\tau =\sigma$
, via the coins for the genuine transpositions among the
![]() $(i \ c_i)$
on the right side of (45) being heads, and all others coins being tails. When the word
$(i \ c_i)$
on the right side of (45) being heads, and all others coins being tails. When the word
![]() $w$
appears
$w$
appears
![]() $\ell$
times inside a long word
$\ell$
times inside a long word
![]() $\alpha _1 \alpha _2 \cdots \alpha _m$
, we have, using a standard result,
$\alpha _1 \alpha _2 \cdots \alpha _m$
, we have, using a standard result,
For historical interest, we note that similar results are in [Reference Diaconis11, Thm. 1, p. 23]; see also [Reference Diaconis and Shahshahani12]. In a very long random word
![]() $\alpha _1 \alpha _2 \cdots \alpha _m$
, the number of occurrences of
$\alpha _1 \alpha _2 \cdots \alpha _m$
, the number of occurrences of
![]() $w$
is random, with mean and variance roughly
$w$
is random, with mean and variance roughly
![]() $m \ K^{-K}$
, so a sufficiently large
$m \ K^{-K}$
, so a sufficiently large
![]() $m$
guarantees that
$m$
guarantees that
![]() $\ell$
is sufficiently large, with high probability.
$\ell$
is sufficiently large, with high probability.
4.10. Relativized permutations
We will define ‘
![]() $\pi _f$
relativized to
$\pi _f$
relativized to
![]() $e_1,\ldots,e_k$
’ to be a specific permutation in
$e_1,\ldots,e_k$
’ to be a specific permutation in
![]() ${\mathcal{S}}_1 \cup \cdots{\mathcal{S}}_{k-1} \cup{\mathcal{S}}_k$
, where
${\mathcal{S}}_1 \cup \cdots{\mathcal{S}}_{k-1} \cup{\mathcal{S}}_k$
, where
![]() ${\mathcal{S}}_j$
denotes the set of all permutations on
${\mathcal{S}}_j$
denotes the set of all permutations on
![]() $\{1,2,\ldots,j\}$
. For use in Lemma 10, we need to allow for the possibility that
$\{1,2,\ldots,j\}$
. For use in Lemma 10, we need to allow for the possibility that
![]() $e_1,\ldots,e_k$
are not
$e_1,\ldots,e_k$
are not
![]() $k$
distinct
$k$
distinct
![]() $n$
-tuples.
$n$
-tuples.
Definition 8.
Let
![]() $\pi$
be a permutation on a finite set
$\pi$
be a permutation on a finite set
![]() $S$
, and let
$S$
, and let
![]() $\boldsymbol{{e}} = (e_1,\ldots,e_k) \in S^k$
. In case
$\boldsymbol{{e}} = (e_1,\ldots,e_k) \in S^k$
. In case
![]() $e_1,\ldots,e_k$
are all distinct, write the full cycle notation for
$e_1,\ldots,e_k$
are all distinct, write the full cycle notation for
![]() $\pi$
, erase all symbols not in
$\pi$
, erase all symbols not in
![]() $\{e_1,\ldots,e_k\}$
, and then relabel
$\{e_1,\ldots,e_k\}$
, and then relabel
![]() $e_1,\ldots,e_k$
as
$e_1,\ldots,e_k$
as
![]() $1,\ldots,k$
. This yields the cycle notation for a permutation
$1,\ldots,k$
. This yields the cycle notation for a permutation
![]() $\sigma = \sigma (\pi,\boldsymbol{{e}}) \in{\mathcal{S}}_k$
, and we call
$\sigma = \sigma (\pi,\boldsymbol{{e}}) \in{\mathcal{S}}_k$
, and we call
![]() $\sigma$
‘
$\sigma$
‘
![]() $\pi$
relativized to
$\pi$
relativized to
![]() $\boldsymbol{{e}}$
’. In case
$\boldsymbol{{e}}$
’. In case
![]() $j \;:\!=\; | \{e_1,\ldots,e_k\}| \lt k$
, edit the list
$j \;:\!=\; | \{e_1,\ldots,e_k\}| \lt k$
, edit the list
![]() $(e_1,\ldots,e_k)$
by deleting repeats, from left to right, to get a new list
$(e_1,\ldots,e_k)$
by deleting repeats, from left to right, to get a new list
![]() $\boldsymbol{{e}}' =(e_1',\ldots,e_j') \in S^j$
, with no repeats. Now we take ‘
$\boldsymbol{{e}}' =(e_1',\ldots,e_j') \in S^j$
, with no repeats. Now we take ‘
![]() $\pi$
relativized to
$\pi$
relativized to
![]() $\boldsymbol{{e}}$
’ to be
$\boldsymbol{{e}}$
’ to be
![]() $ \sigma (\pi,\boldsymbol{{e}}') \in{\mathcal{S}}_j$
.
$ \sigma (\pi,\boldsymbol{{e}}') \in{\mathcal{S}}_j$
.
On the happy event
![]() $H$
from (42), consider an equivalence class
$H$
from (42), consider an equivalence class
![]() $[(f,\boldsymbol{{e}})]$
. We want to name a canonical choice of class leader, and since all
$[(f,\boldsymbol{{e}})]$
. We want to name a canonical choice of class leader, and since all
![]() $2^m$
elements
$2^m$
elements
![]() $({{f^{*}}},\boldsymbol{{e}})$
in the class share the same
$({{f^{*}}},\boldsymbol{{e}})$
in the class share the same
![]() $v^{\#}_1,\ldots,v^{\#}_m$
, and differ only in the values of the
$v^{\#}_1,\ldots,v^{\#}_m$
, and differ only in the values of the
![]() ${f^{*}}$
at those vertices, the natural choice of leader is
${f^{*}}$
at those vertices, the natural choice of leader is
![]() $(f_0,\boldsymbol{{e}})$
where
$(f_0,\boldsymbol{{e}})$
where
Finally, we can say what colours are: for
![]() $a=1$
to
$a=1$
to
![]() $k$
, the vertices along
$k$
, the vertices along
![]() ${\textrm{Seg}}(f_0,e_a,t)$
have colour
${\textrm{Seg}}(f_0,e_a,t)$
have colour
![]() $a$
. Among the various
$a$
. Among the various
![]() $({{f^{*}}},\boldsymbol{{e}})$
in the equivalence class
$({{f^{*}}},\boldsymbol{{e}})$
in the equivalence class
![]() $[(f_0,\boldsymbol{{e}})]$
, except for the case
$[(f_0,\boldsymbol{{e}})]$
, except for the case
![]() ${{f^{*}}}=f_0$
, at least some of the
${{f^{*}}}=f_0$
, at least some of the
![]() $k$
segments start with one colour and end with another.
$k$
segments start with one colour and end with another.
The schedule corresponding to the equivalence class
![]() $[(f,\boldsymbol{{e}})]$
is the word
$[(f,\boldsymbol{{e}})]$
is the word
![]() $\alpha _1 \alpha _2 \cdots \alpha _m$
where
$\alpha _1 \alpha _2 \cdots \alpha _m$
where
![]() $\alpha _i = (a_i,b_i)$
where
$\alpha _i = (a_i,b_i)$
where
![]() $1 \le a_i \lt b_i \le k$
and
$1 \le a_i \lt b_i \le k$
and
![]() $v^{\#}_i$
appears on colours
$v^{\#}_i$
appears on colours
![]() $a_i$
and
$a_i$
and
![]() $b_i$
, that is,
$b_i$
, that is,
![]() $v^{\#}_i$
is a vertex of both
$v^{\#}_i$
is a vertex of both
![]() ${\textrm{Seg}}(f_0,e_{a_i},t)$
and
${\textrm{Seg}}(f_0,e_{a_i},t)$
and
![]() ${\textrm{Seg}}(f_0,e_{b_i},t)$
. We visualiseFootnote
12
${\textrm{Seg}}(f_0,e_{b_i},t)$
. We visualiseFootnote
12
![]() $f(v^{\#}_i)=1$
as meaning that the strands of colours
$f(v^{\#}_i)=1$
as meaning that the strands of colours
![]() $a_i$
and
$a_i$
and
![]() $b_i$
are cut (at
$b_i$
are cut (at
![]() $v^{\#}_i$
) and glued together to create a colour jump, as in Figs. 8 and 9.
$v^{\#}_i$
) and glued together to create a colour jump, as in Figs. 8 and 9.
For
![]() $a=1$
to
$a=1$
to
![]() $k$
, write
$k$
, write
![]() ${e'}_a \;:\!=\;$
the final edge
${e'}_a \;:\!=\;$
the final edge
![]() $e_{a,t}$
of
$e_{a,t}$
of
![]() ${\textrm{Seg}}(f_0,e_a,t)$
, so that, under the logic
${\textrm{Seg}}(f_0,e_a,t)$
, so that, under the logic
![]() $f_0$
,
$f_0$
,
![]() ${\textrm{Seg}}(f_0,e_a,t)$
is a directed path (in colour
${\textrm{Seg}}(f_0,e_a,t)$
is a directed path (in colour
![]() $a$
) from its female end
$a$
) from its female end
![]() $e_a$
to its male end
$e_a$
to its male end
![]() ${e'}_a$
. Note that being in
${e'}_a$
. Note that being in
![]() $H$
implies that the starting edges
$H$
implies that the starting edges
![]() $e_1,\ldots,e_k$
are distinct, and the final edges
$e_1,\ldots,e_k$
are distinct, and the final edges
![]() ${e'}_1,\ldots,{e'}_k$
are distinct.
${e'}_1,\ldots,{e'}_k$
are distinct.
It is clear — from the relative timing of the appearances of the
![]() $v^{\#}_1,\ldots,v^{\#}_m$
along the segments
$v^{\#}_1,\ldots,v^{\#}_m$
along the segments
![]() ${\textrm{Seg}}(f_0,e_a,t)$
— that under the logic
${\textrm{Seg}}(f_0,e_a,t)$
— that under the logic
![]() ${f^{*}}$
,
${f^{*}}$
,
![]() ${\textrm{Seg}}({{f^{*}}},e_a,t)$
is a directed path from its female end
${\textrm{Seg}}({{f^{*}}},e_a,t)$
is a directed path from its female end
![]() $e_a$
to its male end
$e_a$
to its male end
![]() $e'_{\!\!g(a)}$
, where
$e'_{\!\!g(a)}$
, where
![]() $g \equiv g({{f^{*}}})$
is the permutation in
$g \equiv g({{f^{*}}})$
is the permutation in
![]() ${\mathcal{S}}_k$
given by
${\mathcal{S}}_k$
given by
 \begin{equation*} \tau _i = \left \{ \begin {array}{l@{\quad}l} \text {the transposition } (a b) & \mbox {if $\alpha _i=(a,b)$ and ${{f^{*}}}(v^{\#}_i)=1$ } \\[5pt] \text { the identity } & \mbox {if ${{f^{*}}}(v^{\#}_i)=0 $} \end {array} \right.\!\!, \end{equation*}
\begin{equation*} \tau _i = \left \{ \begin {array}{l@{\quad}l} \text {the transposition } (a b) & \mbox {if $\alpha _i=(a,b)$ and ${{f^{*}}}(v^{\#}_i)=1$ } \\[5pt] \text { the identity } & \mbox {if ${{f^{*}}}(v^{\#}_i)=0 $} \end {array} \right.\!\!, \end{equation*}
compare with (43).
Take the usual notation from Hall-style matching theory, and abbreviate the female ends as
![]() $\{1,2,\ldots,k\}$
and the male ends as
$\{1,2,\ldots,k\}$
and the male ends as
![]() $\{1',2',\ldots,k' \}$
. Then
$\{1',2',\ldots,k' \}$
. Then
![]() $f_0$
induces the matching from
$f_0$
induces the matching from
![]() $\{1,2,\ldots,k\}$
to
$\{1,2,\ldots,k\}$
to
![]() $\{1',2',\ldots,k' \}$
with
$\{1',2',\ldots,k' \}$
with
![]() $a \mapsto a'$
. Now the
$a \mapsto a'$
. Now the
![]() $k$
paths under
$k$
paths under
![]() $f_0$
starting from the male ends
$f_0$
starting from the male ends
![]() $\{1',2',\ldots,k' \}$
must eventually arrive at female ends
$\{1',2',\ldots,k' \}$
must eventually arrive at female ends
![]() $\{1,2,\ldots,k\}$
. Define the return matching
$\{1,2,\ldots,k\}$
. Define the return matching
![]() $\hat{g}$
by
$\hat{g}$
by
![]() $\hat{g}(a')=b$
if the path starting from the male end
$\hat{g}(a')=b$
if the path starting from the male end
![]() $a'$
first arrives at the female end
$a'$
first arrives at the female end
![]() $b$
. This return matching
$b$
. This return matching
![]() $\hat{g}$
is the same under all logics
$\hat{g}$
is the same under all logics
![]() ${f^{*}}$
with
${f^{*}}$
with
![]() $({{f^{*}}},\boldsymbol{{e}}) \in [(f_0,\boldsymbol{{e}})]$
.
$({{f^{*}}},\boldsymbol{{e}}) \in [(f_0,\boldsymbol{{e}})]$
.
Finally, for
![]() $(f,\boldsymbol{{e}}) \in H$
,
$(f,\boldsymbol{{e}}) \in H$
,
and of course, on each toggle class
With hindsight, we observe that the estimates of this section, and the previous Section 4.9, have enabled us to dodge a very difficult consideration of interlacement (of the
![]() $e_1,\ldots,e_k$
and
$e_1,\ldots,e_k$
and
![]() $v^{\#}_1,\ldots,v^{\#}_1$
); see [Reference Arratia, Bollobás and Sorkin5] for a study of interlacement.
$v^{\#}_1,\ldots,v^{\#}_1$
); see [Reference Arratia, Bollobás and Sorkin5] for a study of interlacement.
5. Sampling with
 $k$
starts, to prove poisson–Dirichlet convergence
$k$
starts, to prove poisson–Dirichlet convergence
5.1. Background, and notation, for flat random permutations
An overall reference for the following material and history is [Reference Arratia, Barbour and Tavaré3]. For a random permutation in
![]() ${\mathcal{S}}_k$
, with all
${\mathcal{S}}_k$
, with all
![]() $k!$
possible permutations equally likely, for j = 1,2,…, let
$k!$
possible permutations equally likely, for j = 1,2,…, let
with
![]() $L_j = 0$
if the permutation has fewer than
$L_j = 0$
if the permutation has fewer than
![]() $j$
cycles, so that always
$j$
cycles, so that always
![]() $L_1(k)+L_2(k)+\cdots = k$
. The notation
$L_1(k)+L_2(k)+\cdots = k$
. The notation
![]() $L_j \equiv L_j(k)$
means that we consider the two notations equivalent, so that we can use either, depending on whether or not we wish to emphasise the parameter
$L_j \equiv L_j(k)$
means that we consider the two notations equivalent, so that we can use either, depending on whether or not we wish to emphasise the parameter
![]() $k$
. Write
$k$
. Write
so that
![]() ${\overline{L}}_i \equiv{\overline{L}}_i(k) \;:\!=\; L_i/k$
. We use notation analogous to the above, systematically: boldface gives a process, and overline specifies normalising, so that the sum of the components is 1.
${\overline{L}}_i \equiv{\overline{L}}_i(k) \;:\!=\; L_i/k$
. We use notation analogous to the above, systematically: boldface gives a process, and overline specifies normalising, so that the sum of the components is 1.
This paragraph, summarising the convoluted history of the limit distribution for the length of the longest cycle, begins with Dickman’s 1930 study of the largest prime factor of a random integer. Dickman proved that for each fixed
![]() $u \ge 1$
,
$u \ge 1$
,
![]() $\Psi (x,x^{1/u})/x \to \rho (u)$
, where
$\Psi (x,x^{1/u})/x \to \rho (u)$
, where
![]() $\Psi (x,y)$
counts the
$\Psi (x,y)$
counts the
![]() $y$
-smooth integers from 1 to
$y$
-smooth integers from 1 to
![]() $x$
. The function
$x$
. The function
![]() $\rho$
is characterised by
$\rho$
is characterised by
![]() $\rho (u)=0$
for
$\rho (u)=0$
for
![]() $u\lt 0$
,
$u\lt 0$
,
![]() $\rho (u)=1$
for
$\rho (u)=1$
for
![]() $0 \le u \le 1$
and for all
$0 \le u \le 1$
and for all
![]() $u$
,
$u$
,
![]() $u \rho (u)=\int _{u-1}^u \rho (t) \ dt$
. In modern language, writing
$u \rho (u)=\int _{u-1}^u \rho (t) \ dt$
. In modern language, writing
![]() $P^+ = P^+(x)$
for the largest prime factor of an random integer chosen from 1 to
$P^+ = P^+(x)$
for the largest prime factor of an random integer chosen from 1 to
![]() $\lfloor x \rfloor$
, Dickman’s result is that
$\lfloor x \rfloor$
, Dickman’s result is that
Later work by Goncharov (1944) and Shepp and Lloyd (1966) showed the corresponding result for random permutations, that for every fixed
![]() $u \ge 1$
,
$u \ge 1$
,
![]() ${\mathbb{P}}(L_1(k) \lt k/u) \to \rho (u)$
. In modern language this is
${\mathbb{P}}(L_1(k) \lt k/u) \to \rho (u)$
. In modern language this is
The random variable
![]() $X_1$
appearing in (49) and (50) is the first coordinate of the Poisson–Dirichlet process; the second coordinate corresponds to the second largest prime factor, or second largest cycle length, and so on. For primes, the joint limit was proved by Billingsley (1972) [Reference Billingsley9], and for permutations, the joint limit was discussed by Vershik and Shmidt (1977) and Kingman (1977). In these early studies, the Poisson–Dirichlet process appears as the limit, but not in a form easily recognisable as either (54) or (55). A fun exercise for the reader would be to prove that the distribution of
$X_1$
appearing in (49) and (50) is the first coordinate of the Poisson–Dirichlet process; the second coordinate corresponds to the second largest prime factor, or second largest cycle length, and so on. For primes, the joint limit was proved by Billingsley (1972) [Reference Billingsley9], and for permutations, the joint limit was discussed by Vershik and Shmidt (1977) and Kingman (1977). In these early studies, the Poisson–Dirichlet process appears as the limit, but not in a form easily recognisable as either (54) or (55). A fun exercise for the reader would be to prove that the distribution of
![]() $X_1$
, as given by the cumulative distribution function in (49), together with the integral equation characterising
$X_1$
, as given by the cumulative distribution function in (49), together with the integral equation characterising
![]() $\rho$
, is the same as the distribution of
$\rho$
, is the same as the distribution of
![]() $X_1$
as given by its density, which is the special case
$X_1$
as given by its density, which is the special case
![]() $k=1$
of (54). See [Reference Arratia2] for more on the Poisson–Dirichlet in relation to prime factorizations and [Reference Arratia, Barbour and Tavaré4] for more on the Poisson–Dirichlet in relation to flat random permutations.
$k=1$
of (54). See [Reference Arratia2] for more on the Poisson–Dirichlet in relation to prime factorizations and [Reference Arratia, Barbour and Tavaré4] for more on the Poisson–Dirichlet in relation to flat random permutations.
Returning to the process of longest cycle lengths in (48), the joint distribution is most easily understood by taking the cycles in ‘age order’. Let
Our notation convention has already told the reader that
![]() ${\boldsymbol{{A}}} \equiv{\boldsymbol{{A}}}(k) \;:\!=\; (A_1(k),A_2(k),\cdots )$
, and that
${\boldsymbol{{A}}} \equiv{\boldsymbol{{A}}}(k) \;:\!=\; (A_1(k),A_2(k),\cdots )$
, and that
![]() ${\overline{{\boldsymbol{{A}}}}}(k)={\boldsymbol{{A}}}(k)/k$
. Here, the notion of age comes from canonical cycle notation: 1 is written as the start of the first (eldest) cycle, whose length is
${\overline{{\boldsymbol{{A}}}}}(k)={\boldsymbol{{A}}}(k)/k$
. Here, the notion of age comes from canonical cycle notation: 1 is written as the start of the first (eldest) cycle, whose length is
![]() $A_1$
, then the smallest
$A_1$
, then the smallest
![]() $i$
not on this first cycle is the start of the second cycle, whose length is
$i$
not on this first cycle is the start of the second cycle, whose length is
![]() $A_2$
, and so on — with
$A_2$
, and so on — with
![]() $A_j \;:\!=\; 0$
if the permutation has fewer than
$A_j \;:\!=\; 0$
if the permutation has fewer than
![]() $j$
cycles.Footnote
13
It is easy to see that
$j$
cycles.Footnote
13
It is easy to see that
![]() $A_1$
is uniformly distributed in
$A_1$
is uniformly distributed in
![]() $\{1,2,\ldots,k\}$
, and for each
$\{1,2,\ldots,k\}$
, and for each
![]() $j=1,2,\ldots$
, if there are at least
$j=1,2,\ldots$
, if there are at least
![]() $j$
cycles, then
$j$
cycles, then
This very easily leads to a description of the limit proportions: with
![]() $U,U_1,U_2,\ldots$
independent, uniformly distributed in (0,1),
$U,U_1,U_2,\ldots$
independent, uniformly distributed in (0,1),
We write
![]() $\to ^d$
to denote convergence in distribution, and we note that
$\to ^d$
to denote convergence in distribution, and we note that
![]() $U =^d 1-U$
, where
$U =^d 1-U$
, where
![]() $=^d$
denotes equality in distribution. The distribution of the process on the right side of (52) is named GEM, after Griffiths [Reference Griffiths18], Engen [Reference Engen15] and McCloskey [Reference McCloskey20]; its construction is popularly referred to as ‘stick breaking’ although stick breaking in general allows
$=^d$
denotes equality in distribution. The distribution of the process on the right side of (52) is named GEM, after Griffiths [Reference Griffiths18], Engen [Reference Engen15] and McCloskey [Reference McCloskey20]; its construction is popularly referred to as ‘stick breaking’ although stick breaking in general allows
![]() $U$
to take any distribution on (0,1), not just the uniform.
$U$
to take any distribution on (0,1), not just the uniform.
Convergence of processes, such as (52) and (56), and our Theorem 1 and Lemmas 9 and 10, are instances of convergence for stochastic processes with values in
![]() $\mathbb{R}^\infty$
, with the usual compact-open topology, and as such, convergence of processes is equivalent to convergence to the finite-dimensional-distributions, of the first
$\mathbb{R}^\infty$
, with the usual compact-open topology, and as such, convergence of processes is equivalent to convergence to the finite-dimensional-distributions, of the first
![]() $r$
coordinates, for each
$r$
coordinates, for each
![]() $r=1,2,\ldots$
.
$r=1,2,\ldots$
.
Define
The (usual subspace) topology on
![]() $\Delta$
is the same as the metric topology from the
$\Delta$
is the same as the metric topology from the
![]() $\ell _1$
distance,
$\ell _1$
distance,
We write
![]() $\rm{\small{ RANK}}$
for the function on
$\rm{\small{ RANK}}$
for the function on
![]() $\Delta$
which sorts, with largest first. An example shows some of the subtlety of the preceeding considerations: let
$\Delta$
which sorts, with largest first. An example shows some of the subtlety of the preceeding considerations: let
![]() $\boldsymbol{{e}}_i \in \Delta$
be the
$\boldsymbol{{e}}_i \in \Delta$
be the
![]() $i^{th}$
standard basis vector — all zeros apart from a 1 in the
$i^{th}$
standard basis vector — all zeros apart from a 1 in the
![]() $i^{th}$
coordinate, and let
$i^{th}$
coordinate, and let
![]() $\textbf{0}$
be the all zeros vector. Note that
$\textbf{0}$
be the all zeros vector. Note that
![]() $\textbf{0} \in [0,1]^\infty \setminus \Delta$
, and in the larger space
$\textbf{0} \in [0,1]^\infty \setminus \Delta$
, and in the larger space
![]() $[0,1]^\infty$
,
$[0,1]^\infty$
,
![]() $\boldsymbol{{e}}_n \to \textbf{0}$
. But for
$\boldsymbol{{e}}_n \to \textbf{0}$
. But for
![]() $i \ne j, d(\boldsymbol{{e}}_i,\boldsymbol{{e}}_j)=1$
, and the sequence
$i \ne j, d(\boldsymbol{{e}}_i,\boldsymbol{{e}}_j)=1$
, and the sequence
![]() $\boldsymbol{{e}}_1,\boldsymbol{{e}}_2,\ldots$
does not converge in
$\boldsymbol{{e}}_1,\boldsymbol{{e}}_2,\ldots$
does not converge in
![]() $\Delta$
. The closure of
$\Delta$
. The closure of
![]() $\Delta$
is the compact set
$\Delta$
is the compact set
![]() $\overline{\Delta } = \{(x_1,x_2,\dots ) \in [0,1]^\infty \;:\;x_1+x_2+\cdots \le 1\}$
, and
$\overline{\Delta } = \{(x_1,x_2,\dots ) \in [0,1]^\infty \;:\;x_1+x_2+\cdots \le 1\}$
, and
![]() $\rm{{\small RANK}}$
is also definedFootnote
14
on
$\rm{{\small RANK}}$
is also definedFootnote
14
on
![]() $\overline{\Delta }$
; note that
$\overline{\Delta }$
; note that
![]() $\textbf{0} \in \overline{\Delta }$
, and our
$\textbf{0} \in \overline{\Delta }$
, and our
![]() $\boldsymbol{{e}}_n$
example shows that
$\boldsymbol{{e}}_n$
example shows that
![]() $\rm{{\small RANK}}$
is not continuous on
$\rm{{\small RANK}}$
is not continuous on
![]() $\overline{\Delta }$
. Donnelly and Joyce, [Reference Donnelly and Joyce13, Proposition 4], proved that
$\overline{\Delta }$
. Donnelly and Joyce, [Reference Donnelly and Joyce13, Proposition 4], proved that
![]() $\rm{{\small RANK}}$
is continuous on
$\rm{{\small RANK}}$
is continuous on
![]() $\Delta$
, observing that ‘…in parts of the literature some of these results seem already to have been assumed’.
$\Delta$
, observing that ‘…in parts of the literature some of these results seem already to have been assumed’.
By definition, a random
![]() $(X_1,X_2,\ldots\!) \in \Delta$
is the Poisson–Dirichlet process, or has the Poisson–Dirichlet distribution,Footnote
15
PD, if for each
$(X_1,X_2,\ldots\!) \in \Delta$
is the Poisson–Dirichlet process, or has the Poisson–Dirichlet distribution,Footnote
15
PD, if for each
![]() $k=1,2,\ldots$
, the joint density of the first
$k=1,2,\ldots$
, the joint density of the first
![]() $k$
coordinates is given by
$k$
coordinates is given by
on the region
![]() $x_1 \gt x_2 \gt \cdots \gt x_k \gt 0$
and
$x_1 \gt x_2 \gt \cdots \gt x_k \gt 0$
and
![]() $x_1+\cdots +x_k \lt 1$
, and zero elsewhere. The Poisson–Dirchlet process may be constructed from the GEM process, which appeared on the right side of (52), by sorting, with
$x_1+\cdots +x_k \lt 1$
, and zero elsewhere. The Poisson–Dirchlet process may be constructed from the GEM process, which appeared on the right side of (52), by sorting, with
For the process of largest cycle lengths in a random permutation, (48), the combination of the easy-to-see limit (52), and the continuity of RANK, and the characterisation (55) of the Poisson–Dirichlet distribution, proves that as
![]() $k \to \infty$
,
$k \to \infty$
,
Our goal is to derive a new tool for proving the same PD convergence as in (56), but for non uniform permutations, such as those arising from a random FSR. It might benefit the reader to jump ahead a little, and read the statement of Lemma 10, and then the more technical Lemma 9, which has the meat of the argument used to prove Lemma 10. We have stated Lemma 9 in a fairly general form, hoping that it may be useful in the context of other combinatorial structures, and perhaps with limits other than the Poisson–Dirichlet.
5.2. The partition sampling lemma
Lemma 9.
First, suppose that for each
![]() $N$
along a sequence of
$N$
along a sequence of
![]() $N$
tending to
$N$
tending to
![]() $\infty$
we have a random set partition
$\infty$
we have a random set partition
![]() $\pi$
on
$\pi$
on
![]() $[N] \;:\!=\;\{1,2,\ldots,N\}$
. Let
$[N] \;:\!=\;\{1,2,\ldots,N\}$
. Let
![]() $M_j \equiv M_j(N)$
be the size of the
$M_j \equiv M_j(N)$
be the size of the
![]() $j$
-th largest block of
$j$
-th largest block of
![]() $\pi$
, with
$\pi$
, with
![]() $M_j \;:\!=\;0$
for
$M_j \;:\!=\;0$
for
![]() $j$
greater than the number of blocks of
$j$
greater than the number of blocks of
![]() $\pi$
, so that
$\pi$
, so that
![]() $M_1+M_2+\cdots = N$
. Let
$M_1+M_2+\cdots = N$
. Let
![]() ${\boldsymbol{{M}}}(N)=(M_1(N),M_2(N),\ldots\!)$
and let
${\boldsymbol{{M}}}(N)=(M_1(N),M_2(N),\ldots\!)$
and let
![]() ${\overline{{\boldsymbol{{M}}}}}(N)=M(N)/N$
.
${\overline{{\boldsymbol{{M}}}}}(N)=M(N)/N$
.
Next, for each
![]() $k \ge 1$
, take an ordered sample of size
$k \ge 1$
, take an ordered sample of size
![]() $k$
, with replacement, from
$k$
, with replacement, from
![]() $[N]$
, with all
$[N]$
, with all
![]() $N^k$
possible outcomes equally likely. Such a sample picks out an ordered
$N^k$
possible outcomes equally likely. Such a sample picks out an ordered
![]() $($
by first appearance
$($
by first appearance
![]() $)$
list of blocks of
$)$
list of blocks of
![]() $\pi$
, say
$\pi$
, say
![]() $\beta _1,\dots,\beta _r$
, with
$\beta _1,\dots,\beta _r$
, with
![]() $r \le k$
. Let
$r \le k$
. Let
![]() $C_j \equiv C_j(N,k)$
be the number of elements of the
$C_j \equiv C_j(N,k)$
be the number of elements of the
![]() $k$
-sample landing in the block
$k$
-sample landing in the block
![]() $\beta _j$
, with
$\beta _j$
, with
![]() $C_j \;:\!=\; 0$
for
$C_j \;:\!=\; 0$
for
![]() $j\gt r$
, so that
$j\gt r$
, so that
![]() $C_1+C_2+\cdots = k$
. Let
$C_1+C_2+\cdots = k$
. Let
![]() ${\boldsymbol{{C}}} \equiv{\boldsymbol{{C}}}(N,k) = (C_1,C_2,\ldots\!)$
.
${\boldsymbol{{C}}} \equiv{\boldsymbol{{C}}}(N,k) = (C_1,C_2,\ldots\!)$
.
Finally, let
![]() ${\boldsymbol{{X}}} = (X_1,X_2,\ldots\!)$
be any random element of
${\boldsymbol{{X}}} = (X_1,X_2,\ldots\!)$
be any random element of
![]() $\Delta$
, with
$\Delta$
, with
![]() $X_1 \ge X_2 \cdots \ge 0$
, and let
$X_1 \ge X_2 \cdots \ge 0$
, and let
![]() ${\boldsymbol{{A}}}(k) \;:\!=\; (A_1(k),A_2(k),\cdots )$
be any random elements of
${\boldsymbol{{A}}}(k) \;:\!=\; (A_1(k),A_2(k),\cdots )$
be any random elements of
![]() $\mathbb{Z}_+^\infty$
for which
$\mathbb{Z}_+^\infty$
for which
![]() $A_1(k)+A_2(k)+\cdots =k$
, and such that
$A_1(k)+A_2(k)+\cdots =k$
, and such that
![]() ${\overline{{\boldsymbol{{A}}}}}(k) \;:\!=\;{\boldsymbol{{A}}}(k)/k$
has
${\overline{{\boldsymbol{{A}}}}}(k) \;:\!=\;{\boldsymbol{{A}}}(k)/k$
has
Then, if for each fixed
![]() $k$
, as
$k$
, as
![]() $N \to \infty$
, we have
$N \to \infty$
, we have
it follows that
Proof. Here is an outline of our proof. We begin with an analysis of ‘sampling using
![]() $k$
probes’, leading to (61), which gets coordinatewise nearness, with exceptional probability O(
$k$
probes’, leading to (61), which gets coordinatewise nearness, with exceptional probability O(
![]() $1/k)$
, uniformly over set partitions, which are indexed by
$1/k)$
, uniformly over set partitions, which are indexed by
![]() $N$
. This is the crux of our proof; the remainder is similar to Donnelly and Joyce, [Reference Donnelly and Joyce13, Proposition 4], on the continuity of RANK. For an overview, with
$N$
. This is the crux of our proof; the remainder is similar to Donnelly and Joyce, [Reference Donnelly and Joyce13, Proposition 4], on the continuity of RANK. For an overview, with
![]() $\overline{{\boldsymbol{{D}}}}$
defined in the following paragraph, and writing whp to mean ‘with high probability’, and
$\overline{{\boldsymbol{{D}}}}$
defined in the following paragraph, and writing whp to mean ‘with high probability’, and
![]() $\doteq$
to mean ‘approximately equals, in
$\doteq$
to mean ‘approximately equals, in
![]() $\ell _1$
’:
$\ell _1$
’:
Write the blocks of
![]() $\pi$
as
$\pi$
as
![]() $b_1,b_2,\ldots$
, listed in nonincreasing order of size, so that
$b_1,b_2,\ldots$
, listed in nonincreasing order of size, so that
![]() $M_i = |b_i|$
. Write
$M_i = |b_i|$
. Write
![]() $p_i \;:\!=\; M_i/N$
, so that
$p_i \;:\!=\; M_i/N$
, so that
![]() ${\boldsymbol{{p}}} \;:\!=\; (p_1,p_2,\ldots\!) \equiv{\overline{{\boldsymbol{{M}}}}}$
is a random probability distribution on the positive integers. Let
${\boldsymbol{{p}}} \;:\!=\; (p_1,p_2,\ldots\!) \equiv{\overline{{\boldsymbol{{M}}}}}$
is a random probability distribution on the positive integers. Let
![]() $D_j$
be the number of elements of the
$D_j$
be the number of elements of the
![]() $k$
-sample in
$k$
-sample in
![]() $b_j$
; the lists
$b_j$
; the lists
![]() $C_1,C_2,\ldots$
and
$C_1,C_2,\ldots$
and
![]() $D_1,D_2,\ldots$
represent the same multiset, apart from rearrangement, so that
$D_1,D_2,\ldots$
represent the same multiset, apart from rearrangement, so that
Write
![]() ${\boldsymbol{{D}}} \equiv{\boldsymbol{{D}}}(N,k) \;:\!=\; (D_1,D_2,\ldots\!)$
, and
${\boldsymbol{{D}}} \equiv{\boldsymbol{{D}}}(N,k) \;:\!=\; (D_1,D_2,\ldots\!)$
, and
![]() ${\overline{{\boldsymbol{{D}}}}} \equiv{\overline{{\boldsymbol{{D}}}}}(N,k) \;:\!=\;{\boldsymbol{{D}}}/k$
, so that
${\overline{{\boldsymbol{{D}}}}} \equiv{\overline{{\boldsymbol{{D}}}}}(N,k) \;:\!=\;{\boldsymbol{{D}}}/k$
, so that
![]() ${\overline{{\boldsymbol{{D}}}}}=({\overline{D}}_1,{\overline{D}}_2,\ldots\!)$
and
${\overline{{\boldsymbol{{D}}}}}=({\overline{D}}_1,{\overline{D}}_2,\ldots\!)$
and
![]() ${\overline{D}}_i = D_i/k$
.
${\overline{D}}_i = D_i/k$
.
Conditional on the value of
![]() $\boldsymbol{{p}}$
, the joint distribution of
$\boldsymbol{{p}}$
, the joint distribution of
![]() $(D_1,D_2,\ldots\!)$
is exactly Multinomial
$(D_1,D_2,\ldots\!)$
is exactly Multinomial
![]() $(k,{\boldsymbol{{p}}})$
. We want to establish a form of uniformity for the convergence of
$(k,{\boldsymbol{{p}}})$
. We want to establish a form of uniformity for the convergence of
![]() ${\overline{{\boldsymbol{{D}}}}}(k)$
to
${\overline{{\boldsymbol{{D}}}}}(k)$
to
![]() $\boldsymbol{{p}}$
. The first step is to recall the usual proof that for Binomial sampling, with a sample of size
$\boldsymbol{{p}}$
. The first step is to recall the usual proof that for Binomial sampling, with a sample of size
![]() $k$
and true parameter
$k$
and true parameter
![]() $p \in [0,1]$
, the sample mean
$p \in [0,1]$
, the sample mean
![]() $\hat{p}$
converges to the true parameter
$\hat{p}$
converges to the true parameter
![]() $p$
— because the proof provides a quantitative bound. Specifically, Chebyshev’s inequality gets used, with
$p$
— because the proof provides a quantitative bound. Specifically, Chebyshev’s inequality gets used, with
 \begin{align}{\mathbb{P}}( | \hat{p}-p | \ge \delta ) &={\mathbb{P}}( (\hat{p}-p)^2 \ge \delta ^2) \nonumber \\[5pt] & \le \frac{{\mathbb{E}\,} (\hat{p}-p)^2}{ \delta ^2} \nonumber \\[5pt] & = \frac{{\textrm{Var }} \hat{p}}{\delta ^2}\nonumber {}\\[5pt] & = \frac{p(1-p)}{k \delta ^2}\nonumber \\[5pt] & \le \frac{p}{k \delta ^2 }. \end{align}
\begin{align}{\mathbb{P}}( | \hat{p}-p | \ge \delta ) &={\mathbb{P}}( (\hat{p}-p)^2 \ge \delta ^2) \nonumber \\[5pt] & \le \frac{{\mathbb{E}\,} (\hat{p}-p)^2}{ \delta ^2} \nonumber \\[5pt] & = \frac{{\textrm{Var }} \hat{p}}{\delta ^2}\nonumber {}\\[5pt] & = \frac{p(1-p)}{k \delta ^2}\nonumber \\[5pt] & \le \frac{p}{k \delta ^2 }. \end{align}
In particular, conditional on any value for
![]() $\boldsymbol{{p}}$
, for
$\boldsymbol{{p}}$
, for
![]() $i=1,2,\ldots$
, with
$i=1,2,\ldots$
, with
![]() $p_i ={\overline{M}}_i = M_i(N)/N$
in the role of
$p_i ={\overline{M}}_i = M_i(N)/N$
in the role of
![]() $p$
for (60),
$p$
for (60),
Hence, taking expectation to remove the conditioning on
![]() $\boldsymbol{{p}}$
, and then using
$\boldsymbol{{p}}$
, and then using
![]() $\sum _i p_i=1$
to analyse the union bound, we have a good event
$\sum _i p_i=1$
to analyse the union bound, we have a good event
![]() $G$
(proximity in
$G$
(proximity in
![]() $\ell _\infty$
) whose complement
$\ell _\infty$
) whose complement
For
![]() ${\boldsymbol{{x}}} \in \Delta$
,
${\boldsymbol{{x}}} \in \Delta$
,
![]() $j \ge 1$
write
$j \ge 1$
write
![]() $S_j({\boldsymbol{{x}}})$
for the sum of the
$S_j({\boldsymbol{{x}}})$
for the sum of the
![]() $j$
largest coordinates of
$j$
largest coordinates of
![]() $\boldsymbol{{x}}$
. Obviously
$\boldsymbol{{x}}$
. Obviously
Let
![]() $\varepsilon \gt 0$
be given and fixed for the remainder of this proof.
$\varepsilon \gt 0$
be given and fixed for the remainder of this proof.
Let
the set of points in
![]() $\Delta$
where some set of
$\Delta$
where some set of
![]() $j$
coordinates sums to more than
$j$
coordinates sums to more than
![]() $1-\varepsilon$
. Note that
$1-\varepsilon$
. Note that
![]() $R(j,\varepsilon )$
is invariant under permutations of the coordinates, including
$R(j,\varepsilon )$
is invariant under permutations of the coordinates, including
![]() $\rm{{\small RANK}}$
. Since
$\rm{{\small RANK}}$
. Since
![]() $\Delta = \cup _j R(j,\varepsilon )$
, and
$\Delta = \cup _j R(j,\varepsilon )$
, and
![]() $\boldsymbol{{X}}$
from (57) is a random element of
$\boldsymbol{{X}}$
from (57) is a random element of
![]() $\Delta$
, there exists
$\Delta$
, there exists
![]() $j=j(\varepsilon ) \ge 1$
, depending on the distribution of
$j=j(\varepsilon ) \ge 1$
, depending on the distribution of
![]() $\boldsymbol{{X}}$
, such that
$\boldsymbol{{X}}$
, such that
fix such a value for
![]() $j$
. [When used in Lemma 10, where the distribution of
$j$
. [When used in Lemma 10, where the distribution of
![]() $\boldsymbol{{X}}$
is Poisson–Dirichlet, (55) can be used to show that the minimal such
$\boldsymbol{{X}}$
is Poisson–Dirichlet, (55) can be used to show that the minimal such
![]() $j$
is asympotically
$j$
is asympotically
![]() $\log (1/\varepsilon )$
.]
$\log (1/\varepsilon )$
.]
Using the hypothesis (57), and observing that
![]() $R(j,\varepsilon )$
is an open set, (the open set part of the Portmanteau Theorem on weak convergence implies that) we can pick and fix a finite
$R(j,\varepsilon )$
is an open set, (the open set part of the Portmanteau Theorem on weak convergence implies that) we can pick and fix a finite
![]() $k_0$
such that for all
$k_0$
such that for all
![]() $k \ge k_0$
,
$k \ge k_0$
,
Using the hypothesis (57) again, we can pick and fix a finite
![]() $k_1 \ge k_0$
such that for each
$k_1 \ge k_0$
such that for each
![]() $k \ge k_1$
, there exists a coupling (see Dudley [Reference Dudley14], Real Analysis and Probability, Corollary 11.6.4) such that the
$k \ge k_1$
, there exists a coupling (see Dudley [Reference Dudley14], Real Analysis and Probability, Corollary 11.6.4) such that the
![]() $\ell _1$
distance has
$\ell _1$
distance has
Next, intending to use (61) with
![]() $\varepsilon/j$
used in the role of
$\varepsilon/j$
used in the role of
![]() $\delta$
, the upper bound is
$\delta$
, the upper bound is
![]() $1/(k \delta ^2) = j^2/(k \varepsilon ^2)$
. To have this upper bound be at most
$1/(k \delta ^2) = j^2/(k \varepsilon ^2)$
. To have this upper bound be at most
![]() $\varepsilon$
, and also be able to apply (66), we take
$\varepsilon$
, and also be able to apply (66), we take
![]() $k$
to be the maximum of
$k$
to be the maximum of
![]() $k_1$
and the ceiling of
$k_1$
and the ceiling of
![]() $ j^2/ \varepsilon ^3$
.
$ j^2/ \varepsilon ^3$
.
The value
![]() $k$
has been fixed, in the previous paragraph. Now, the convergence in hypothesis (58) involves the topologically discrete space
$k$
has been fixed, in the previous paragraph. Now, the convergence in hypothesis (58) involves the topologically discrete space
![]() $\mathbb{Z}_+^k$
, so the distributional convergence can be metrized by the total variation distance, hence there exists a finite
$\mathbb{Z}_+^k$
, so the distributional convergence can be metrized by the total variation distance, hence there exists a finite
![]() $N_0(k)$
such that for all
$N_0(k)$
such that for all
![]() $N \ge N_0(k)$
, the total variation distance between distributions is at most
$N \ge N_0(k)$
, the total variation distance between distributions is at most
![]() $\varepsilon$
, and there exists a coupling with
$\varepsilon$
, and there exists a coupling with
Of course this same coupling and exceptional event yields
![]() ${\mathbb{P}}({\rm{{\small RANK}}}({\overline{{\boldsymbol{{C}}}}}) \ne{\rm{{\small RANK}}}({\overline{{\boldsymbol{{A}}}}}) ) \le \varepsilon$
, and using also (65),
${\mathbb{P}}({\rm{{\small RANK}}}({\overline{{\boldsymbol{{C}}}}}) \ne{\rm{{\small RANK}}}({\overline{{\boldsymbol{{A}}}}}) ) \le \varepsilon$
, and using also (65),
But then (59), and the permutation invariance of
![]() $R(j,\varepsilon )$
converts the above into
$R(j,\varepsilon )$
converts the above into
Next, observe that
![]() ${\overline{{\boldsymbol{{D}}}}}(N,k) \in R(j,\varepsilon )$
and
${\overline{{\boldsymbol{{D}}}}}(N,k) \in R(j,\varepsilon )$
and
![]() $G$
from (61) with
$G$
from (61) with
![]() $\delta = \varepsilon/j$
imply that, each of the
$\delta = \varepsilon/j$
imply that, each of the
![]() $j$
indices
$j$
indices
![]() $i$
for
$i$
for
![]() ${\overline{{\boldsymbol{{D}}}}}(N,k) \in R(j,\varepsilon )$
has
${\overline{{\boldsymbol{{D}}}}}(N,k) \in R(j,\varepsilon )$
has
![]() $|M_i - D_i| \lt \delta$
, so the sum of those
$|M_i - D_i| \lt \delta$
, so the sum of those
![]() $j$
coordinates of
$j$
coordinates of
![]() $\overline{{\boldsymbol{{M}}}}$
is at least
$\overline{{\boldsymbol{{M}}}}$
is at least
![]() $S_j({\overline{{\boldsymbol{{D}}}}}) - j \, \delta = S_j({\overline{{\boldsymbol{{D}}}}}) - \varepsilon \gt 1 - 2 \varepsilon$
(as observed in (62))), and the sum of the other (outside the chosen
$S_j({\overline{{\boldsymbol{{D}}}}}) - j \, \delta = S_j({\overline{{\boldsymbol{{D}}}}}) - \varepsilon \gt 1 - 2 \varepsilon$
(as observed in (62))), and the sum of the other (outside the chosen
![]() $j$
) coordinates of
$j$
) coordinates of
![]() $\overline{{\boldsymbol{{M}}}}$
is at most
$\overline{{\boldsymbol{{M}}}}$
is at most
![]() $2 \varepsilon$
, while the sum of the other (outside the chosen
$2 \varepsilon$
, while the sum of the other (outside the chosen
![]() $j$
) coordinates of
$j$
) coordinates of
![]() $\overline{{\boldsymbol{{D}}}}$
is at most
$\overline{{\boldsymbol{{D}}}}$
is at most
![]() $\varepsilon$
. Hence, the
$\varepsilon$
. Hence, the
![]() $\ell _1$
distance is at most
$\ell _1$
distance is at most
![]() $4 \varepsilon$
, accounted for by
$4 \varepsilon$
, accounted for by
![]() $j \delta = \varepsilon$
, from the
$j \delta = \varepsilon$
, from the
![]() $|M_i - D_i|$
with
$|M_i - D_i|$
with
![]() $i$
among the chosen
$i$
among the chosen
![]() $j$
, plus
$j$
, plus
![]() $2 \varepsilon + \varepsilon$
using
$2 \varepsilon + \varepsilon$
using
![]() $ |M_i - D_i| \le M_i + D_i$
on the other coordinates, outside the chosen
$ |M_i - D_i| \le M_i + D_i$
on the other coordinates, outside the chosen
![]() $j$
. This result was that
$j$
. This result was that
![]() $d({\overline{{\boldsymbol{{M}}}}},{\overline{{\boldsymbol{{D}}}}}) \lt 4 \varepsilon$
. Now
$d({\overline{{\boldsymbol{{M}}}}},{\overline{{\boldsymbol{{D}}}}}) \lt 4 \varepsilon$
. Now
![]() ${\overline{{\boldsymbol{{M}}}}} ={\rm{{\small RANK}}}({\overline{{\boldsymbol{{M}}}}})$
by construction, but due to sampling noise, maybe
${\overline{{\boldsymbol{{M}}}}} ={\rm{{\small RANK}}}({\overline{{\boldsymbol{{M}}}}})$
by construction, but due to sampling noise, maybe
![]() ${\overline{{\boldsymbol{{D}}}}} \ne{\rm{{\small RANK}}}({\overline{{\boldsymbol{{D}}}}})$
. However, since
${\overline{{\boldsymbol{{D}}}}} \ne{\rm{{\small RANK}}}({\overline{{\boldsymbol{{D}}}}})$
. However, since
![]() $\rm{{\small RANK}}$
is a contraction, we have
$\rm{{\small RANK}}$
is a contraction, we have
![]() $d({\overline{{\boldsymbol{{M}}}}},{\rm{{\small RANK}}}({\overline{{\boldsymbol{{D}}}}})) \lt 4 \varepsilon$
.
$d({\overline{{\boldsymbol{{M}}}}},{\rm{{\small RANK}}}({\overline{{\boldsymbol{{D}}}}})) \lt 4 \varepsilon$
.
Putting it all together, for any
![]() $N \ge N_0$
, the union of the exceptional events from (61) (
$N \ge N_0$
, the union of the exceptional events from (61) (
![]() $\overline{{\boldsymbol{{M}}}}$
near
$\overline{{\boldsymbol{{M}}}}$
near
![]() $\overline{{\boldsymbol{{D}}}}$
, coordinatewise, with
$\overline{{\boldsymbol{{D}}}}$
, coordinatewise, with
![]() ${\mathbb{P}}(G^c) \le \varepsilon$
), from (66) (
${\mathbb{P}}(G^c) \le \varepsilon$
), from (66) (
![]() ${\rm{{\small RANK}}}({\overline{{\boldsymbol{{A}}}}})$
near
${\rm{{\small RANK}}}({\overline{{\boldsymbol{{A}}}}})$
near
![]() $\boldsymbol{{X}}$
), and from (67) (
$\boldsymbol{{X}}$
), and from (67) (
![]() $\overline{{\boldsymbol{{D}}}}$
equals
$\overline{{\boldsymbol{{D}}}}$
equals
![]() ${\rm{{\small RANK}}}({\overline{{\boldsymbol{{A}}}}})$
, in
${\rm{{\small RANK}}}({\overline{{\boldsymbol{{A}}}}})$
, in
![]() $R(j,\varepsilon )$
) has probability at most
$R(j,\varepsilon )$
) has probability at most
![]() $4 \varepsilon$
, and outside this exceptional event,
$4 \varepsilon$
, and outside this exceptional event,
![]() $\overline{{\boldsymbol{{M}}}}$
is at most
$\overline{{\boldsymbol{{M}}}}$
is at most
![]() $4 \varepsilon$
away from
$4 \varepsilon$
away from
![]() ${\rm{{\small RANK}}}({\overline{{\boldsymbol{{D}}}}}) ={\rm{{\small RANK}}}({\overline{{\boldsymbol{{A}}}}})$
, which in turn is at most
${\rm{{\small RANK}}}({\overline{{\boldsymbol{{D}}}}}) ={\rm{{\small RANK}}}({\overline{{\boldsymbol{{A}}}}})$
, which in turn is at most
![]() $\varepsilon$
away from
$\varepsilon$
away from
![]() $\boldsymbol{{X}}$
. In summary, there are couplings so that
$\boldsymbol{{X}}$
. In summary, there are couplings so that
5.3. The permutation version of the sampling lemma
Lemma 10.
Suppose that for a sequence of
![]() $N$
tending to
$N$
tending to
![]() $\infty$
we have a random permutation
$\infty$
we have a random permutation
![]() $\pi$
on
$\pi$
on
![]() $[N] \;:\!=\;\{1,2,\ldots,N\}$
. Let
$[N] \;:\!=\;\{1,2,\ldots,N\}$
. Let
![]() $M_j \equiv M_j(N)$
be the size of the
$M_j \equiv M_j(N)$
be the size of the
![]() $j$
-th largest cycle of
$j$
-th largest cycle of
![]() $\pi$
, with
$\pi$
, with
![]() $M_j \;:\!=\;0$
for
$M_j \;:\!=\;0$
for
![]() $j$
greater than the number of cycles of
$j$
greater than the number of cycles of
![]() $\pi$
, so that
$\pi$
, so that
![]() $M_1+M_2+\cdots = N$
.
$M_1+M_2+\cdots = N$
.
Given
![]() $k \ge 1$
, take an ordered sample of size
$k \ge 1$
, take an ordered sample of size
![]() $k$
, with replacement, from
$k$
, with replacement, from
![]() $[N]$
, that is,
$[N]$
, that is,
![]() $e_1,\ldots,e_k$
with all
$e_1,\ldots,e_k$
with all
![]() $N^k$
possible outcomes equally likely. Let
$N^k$
possible outcomes equally likely. Let
![]() $\sigma$
be
$\sigma$
be
![]() $\pi$
relativised to
$\pi$
relativised to
![]() $e_1,\ldots,e_k$
, as defined at the start of Section 4.10.
$e_1,\ldots,e_k$
, as defined at the start of Section 4.10.
Now suppose that, for each fixed
![]() $k \ge 1$
,
$k \ge 1$
,
Then, as
![]() $N \to \infty$
,
$N \to \infty$
,
where
![]() $\boldsymbol{{X}}$
has the Poisson–Dirichlet distribution, as in (55) and (56).
$\boldsymbol{{X}}$
has the Poisson–Dirichlet distribution, as in (55) and (56).
Proof. Take the processes
![]() ${\boldsymbol{{A}}}(k)$
of cycle lengths, in age order, as given by (51), for uniform random permutations in
${\boldsymbol{{A}}}(k)$
of cycle lengths, in age order, as given by (51), for uniform random permutations in
![]() ${\mathcal{S}}_k$
, to serve as the random elements in the hypotheses (57) and (58) of Lemma 9. This requires using the Poisson–Dirichlet distribution, for
${\mathcal{S}}_k$
, to serve as the random elements in the hypotheses (57) and (58) of Lemma 9. This requires using the Poisson–Dirichlet distribution, for
![]() $\boldsymbol{{X}}$
in (57).
$\boldsymbol{{X}}$
in (57).
Fix
![]() $k$
. Then (68) holding for each
$k$
. Then (68) holding for each
![]() $\tau \in{\mathcal{S}}_k$
implies that the distribution of
$\tau \in{\mathcal{S}}_k$
implies that the distribution of
![]() $\sigma$
is close, in total variation distance, to the uniform distribution on
$\sigma$
is close, in total variation distance, to the uniform distribution on
![]() ${\mathcal{S}}_k$
. On the event, of probability
${\mathcal{S}}_k$
. On the event, of probability
![]() $\frac{N-1}{N} \cdots \frac{N-(k-1)}{N} \to 1$
, that the
$\frac{N-1}{N} \cdots \frac{N-(k-1)}{N} \to 1$
, that the
![]() $k$
-sample with replacement from the
$k$
-sample with replacement from the
![]() $N$
population has
$N$
population has
![]() $k$
distinct elements, the counts
$k$
distinct elements, the counts
![]() $C(N,k)$
from Lemma 9 agree exactly with the cycle lengths in
$C(N,k)$
from Lemma 9 agree exactly with the cycle lengths in
![]() $\sigma$
. Hence hypothesis (68) implies the hypothesis (58).
$\sigma$
. Hence hypothesis (68) implies the hypothesis (58).
6. Putting it all together: The Proof of Theorem 1
We now have established all the ingredients needed for our proof of Theorem 1. First, the conclusion (4) of Theorem 1 is exactly the conclusion (69) from Lemma 10.Footnote 16 To prove Theorem 1, it only remains to establish that the random FSR model (3) satisfies the hypothesis (68) of Lemma 10.
Fix
![]() $k$
for use in (68). The uniform choice of
$k$
for use in (68). The uniform choice of
![]() $(f,\boldsymbol{{e}}) \in S_{n,k}$
determines
$(f,\boldsymbol{{e}}) \in S_{n,k}$
determines
![]() $\pi _f$
and the random sample
$\pi _f$
and the random sample
![]() $e_1,\ldots,e_k$
— for convenience in Lemma 10 we labelled the set
$e_1,\ldots,e_k$
— for convenience in Lemma 10 we labelled the set
![]() $\mathbb{F}_2^n$
with the integers 1,2,
$\mathbb{F}_2^n$
with the integers 1,2,
![]() $\ldots,N$
. Let an arbitrary
$\ldots,N$
. Let an arbitrary
![]() $\varepsilon \gt 0$
be given. Fix
$\varepsilon \gt 0$
be given. Fix
![]() $m = m(k,\varepsilon )$
as per Lemma 7, so that with high probability, a random schedule of length
$m = m(k,\varepsilon )$
as per Lemma 7, so that with high probability, a random schedule of length
![]() $m$
over the alphabet of size
$m$
over the alphabet of size
![]() $\left(\substack{k \\[3pt] 2}\right)$
is
$\left(\substack{k \\[3pt] 2}\right)$
is
![]() $\varepsilon$
-good.
$\varepsilon$
-good.
We will take
![]() $t=N^{.6}$
, recalling that
$t=N^{.6}$
, recalling that
![]() $N=2^n$
. By Theorem 6, for sufficiently large
$N=2^n$
. By Theorem 6, for sufficiently large
![]() $n$
, on a good event
$n$
, on a good event
![]() $G_{(k,t)}$
of probability at least
$G_{(k,t)}$
of probability at least
![]() $1-\varepsilon$
, the two-dimensional process
$1-\varepsilon$
, the two-dimensional process
![]() ${\boldsymbol{{X}}}^{(v)}$
of indicators of vertex repeats, in
${\boldsymbol{{X}}}^{(v)}$
of indicators of vertex repeats, in
![]() ${\textrm{Seg}}(f,e_1,k(t+n))$
, agrees with the two-dimensional process
${\textrm{Seg}}(f,e_1,k(t+n))$
, agrees with the two-dimensional process
![]() $\boldsymbol{{X}}$
of indicators of leftmost
$\boldsymbol{{X}}$
of indicators of leftmost
![]() $(n-1)$
-tuple repeats for coin tossing; and cutting, to produce
$(n-1)$
-tuple repeats for coin tossing; and cutting, to produce
![]() $\boldsymbol{{e}}$
and
$\boldsymbol{{e}}$
and
![]() $k$
segments, causes no unwanted side effects. Then, by the Chen–Stein method as given by Theorem 3 of [Reference Arratia, Goldstein and Gordon6] (with a survey of applications to sequence repeats given by Section 5 of [Reference Arratia, Goldstein and Gordon7], and details for the sequence repeats problem given in (39)–(40) of [Reference Arratia, Martin, Reinert and Waterman8]), for sufficiently large
$k$
segments, causes no unwanted side effects. Then, by the Chen–Stein method as given by Theorem 3 of [Reference Arratia, Goldstein and Gordon6] (with a survey of applications to sequence repeats given by Section 5 of [Reference Arratia, Goldstein and Gordon7], and details for the sequence repeats problem given in (39)–(40) of [Reference Arratia, Martin, Reinert and Waterman8]), for sufficiently large
![]() $n$
the total variation distance between
$n$
the total variation distance between
![]() $\boldsymbol{{X}}$
and
$\boldsymbol{{X}}$
and
![]() ${\boldsymbol{{X}}}'$
is at most
${\boldsymbol{{X}}}'$
is at most
![]() $\varepsilon$
, where
$\varepsilon$
, where
![]() ${\boldsymbol{{X}}}'$
has the same marginals as
${\boldsymbol{{X}}}'$
has the same marginals as
![]() $\boldsymbol{{X}}$
, but all coordinates mutually independent. Combined, the total variation distance between
$\boldsymbol{{X}}$
, but all coordinates mutually independent. Combined, the total variation distance between
![]() ${\boldsymbol{{X}}}^{(v)}$
and
${\boldsymbol{{X}}}^{(v)}$
and
![]() ${\boldsymbol{{X}}}'$
is arbitrarily small, at most
${\boldsymbol{{X}}}'$
is arbitrarily small, at most
![]() $2 \varepsilon$
.
$2 \varepsilon$
.
The indicator of the happy event
![]() $H$
is a functional of the process
$H$
is a functional of the process
![]() ${\boldsymbol{{X}}}^{(v)}$
, so we can approximate
${\boldsymbol{{X}}}^{(v)}$
, so we can approximate
![]() ${\mathbb{P}}(H)$
, with an additive error of at most
${\mathbb{P}}(H)$
, with an additive error of at most
![]() $2 \varepsilon$
, by evaluating the same functional, applied to
$2 \varepsilon$
, by evaluating the same functional, applied to
![]() ${\boldsymbol{{X}}}'$
. The required estimates for this independent process are routine, via computations of the expected number of arrivals in various regions as in Section 4,Footnote
17
and we have already provided most of the details, in discussing (32) and (34). Additionally, one must check that the schedule resulting from use of (40) is close, in total variation distance, to the flat random choice in the hypothesis of Lemma 7; we omit the relatively easy details.
${\boldsymbol{{X}}}'$
. The required estimates for this independent process are routine, via computations of the expected number of arrivals in various regions as in Section 4,Footnote
17
and we have already provided most of the details, in discussing (32) and (34). Additionally, one must check that the schedule resulting from use of (40) is close, in total variation distance, to the flat random choice in the hypothesis of Lemma 7; we omit the relatively easy details.
To summarise, we picked
![]() $k$
for use in Lemma 10, then fixed an arbitrary
$k$
for use in Lemma 10, then fixed an arbitrary
![]() $\varepsilon \gt 0$
, then picked
$\varepsilon \gt 0$
, then picked
![]() $m$
via Lemma 7.Footnote
18
For large
$m$
via Lemma 7.Footnote
18
For large
![]() $n$
, the process of vertex repeats among the
$n$
, the process of vertex repeats among the
![]() $k$
segments of length
$k$
segments of length
![]() $t$
is controlled, via comparison of
$t$
is controlled, via comparison of
![]() ${{\boldsymbol{{X}}}^{(v)}},{\boldsymbol{{X}}},{{\boldsymbol{{X}}}'}$
, showing that most
${{\boldsymbol{{X}}}^{(v)}},{\boldsymbol{{X}}},{{\boldsymbol{{X}}}'}$
, showing that most
![]() $(f,\boldsymbol{{e}})$
lie in
$(f,\boldsymbol{{e}})$
lie in
![]() $H$
, and furthermore, the event
$H$
, and furthermore, the event
![]() $H^* \equiv H^*(\varepsilon ) \subset H$
, that the chosen potential toggle vertices
$H^* \equiv H^*(\varepsilon ) \subset H$
, that the chosen potential toggle vertices
![]() $v^{\#}_1,\ldots,v^{\#}_m$
pick out a
$v^{\#}_1,\ldots,v^{\#}_m$
pick out a
![]() $\varepsilon$
-good schedule, has
$\varepsilon$
-good schedule, has
![]() ${\mathbb{P}}(H^*)\gt 1-4 \varepsilon$
. (Attributing
${\mathbb{P}}(H^*)\gt 1-4 \varepsilon$
. (Attributing
![]() $2 \varepsilon$
to
$2 \varepsilon$
to
![]() ${d_{\textit{TV}}}({{\boldsymbol{{X}}}^{(v)}},{{\boldsymbol{{X}}}'})$
,
${d_{\textit{TV}}}({{\boldsymbol{{X}}}^{(v)}},{{\boldsymbol{{X}}}'})$
,
![]() $ \varepsilon$
to
$ \varepsilon$
to
![]() ${\mathbb{P}}(H^c)$
and
${\mathbb{P}}(H^c)$
and
![]() $ \varepsilon$
to
$ \varepsilon$
to
![]() ${\mathbb{P}}(H \setminus H^*)$
.) Section 4.9 shows that, on
${\mathbb{P}}(H \setminus H^*)$
.) Section 4.9 shows that, on
![]() $H^*$
, the settings of
$H^*$
, the settings of
![]() $f$
at its toggle vertices induce a nearly flat random matching between segment starts and ends, and (47) in Section 4.10 lifts this to show that
$f$
at its toggle vertices induce a nearly flat random matching between segment starts and ends, and (47) in Section 4.10 lifts this to show that
![]() $\pi _f$
relativised to
$\pi _f$
relativised to
![]() $e_1,\ldots,e_k$
is a nearly flat random permutation in
$e_1,\ldots,e_k$
is a nearly flat random permutation in
![]() ${\mathcal{S}}_k$
. Thus the combination of Section 4.9 and 4.10 shows that, on
${\mathcal{S}}_k$
. Thus the combination of Section 4.9 and 4.10 shows that, on
![]() $H^*$
, on each equivalence class
$H^*$
, on each equivalence class
![]() $[(f,\boldsymbol{{e}})] \in H^*$
, the total variation distance to the uniform distribution on
$[(f,\boldsymbol{{e}})] \in H^*$
, the total variation distance to the uniform distribution on
![]() ${\mathcal{S}}_k$
is at most
${\mathcal{S}}_k$
is at most
![]() $\varepsilon$
. Hence, averaging over the classes in
$\varepsilon$
. Hence, averaging over the classes in
![]() $H^*$
, and allowing distance 1 for the at most
$H^*$
, and allowing distance 1 for the at most
![]() $4 \varepsilon$
of probability mass outside of
$4 \varepsilon$
of probability mass outside of
![]() $H^*$
, we get that for our fixed
$H^*$
, we get that for our fixed
![]() $k$
, for arbitrary
$k$
, for arbitrary
![]() $\varepsilon$
, for all sufficiently large
$\varepsilon$
, for all sufficiently large
![]() $n$
,
$n$
,
![]() ${d_{\textit{TV}}}(\sigma,$
uniform
${d_{\textit{TV}}}(\sigma,$
uniform
![]() $({\mathcal{S}}_k)) = \frac{1}{2} \sum _{\tau \in{\mathcal{S}}_k} |{\mathbb{P}}(\sigma = \tau ) - \frac{1}{k!}| \lt 5 \varepsilon$
, which establishes (68). This completes the proof.
$({\mathcal{S}}_k)) = \frac{1}{2} \sum _{\tau \in{\mathcal{S}}_k} |{\mathbb{P}}(\sigma = \tau ) - \frac{1}{k!}| \lt 5 \varepsilon$
, which establishes (68). This completes the proof.
Acknowledgments
We would like to acknowledge numerous helpful discussions with Danny Goldstein, Max Hankins and Jay-C Reyes. We are grateful to an anonymous and diligent referee.