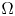1. Introduction
In this note we analyse some quantitative and qualitative results for the following partial differential inequalities (PDI in the sequel)
where $\Omega$![]() will be either a bounded open set in $\mathbb {R}^N$
will be either a bounded open set in $\mathbb {R}^N$![]() or the whole space itself, $N> 1$
or the whole space itself, $N> 1$![]() , $\mathcal {A}:\Omega \times \mathbb {R}\times \mathbb {R}^N\to \mathbb {R}^N$
, $\mathcal {A}:\Omega \times \mathbb {R}\times \mathbb {R}^N\to \mathbb {R}^N$![]() is a Carathéodory function (namely measurable in $x$
is a Carathéodory function (namely measurable in $x$![]() and continuous in the $u,\,\nabla u$
and continuous in the $u,\,\nabla u$![]() entries) such that
entries) such that
for every $(s,\,\xi )\in \mathbb {R}\times \mathbb {R}^N$![]() , a.e. $x\in \Omega$
, a.e. $x\in \Omega$![]() , and
, and
Here $\mathcal {B}_1:\Omega \times \mathbb {R}\times \mathbb {R}^N\to \mathbb {R}$![]() , $\mathcal {B}_2:\Omega \times \mathbb {R}\times \mathbb {R}^N\to \mathbb {R}$
, $\mathcal {B}_2:\Omega \times \mathbb {R}\times \mathbb {R}^N\to \mathbb {R}$![]() , $\lambda \geq 0$
, $\lambda \geq 0$![]() , $c_H>0$
, $c_H>0$![]() and $f$
and $f$![]() is a measurable source term belonging to $\mathcal {L}^{1,\frac {N}{q}}(\Omega )$
is a measurable source term belonging to $\mathcal {L}^{1,\frac {N}{q}}(\Omega )$![]() , the Morrey space of parameters $(1,\,N/q)$
, the Morrey space of parameters $(1,\,N/q)$![]() , $q\geq 1$
, $q\geq 1$![]() , $\gamma >p-1$
, $\gamma >p-1$![]() , $p>1$
, $p>1$![]() . A prototype equation satisfying the previous assumptions is the quasilinear Hamilton–Jacobi/Riccati equation driven by the $p$
. A prototype equation satisfying the previous assumptions is the quasilinear Hamilton–Jacobi/Riccati equation driven by the $p$![]() -Laplacian [Reference Bidaut-Véron, Garcia-Huidobro and Véron7, Reference Cirant and Goffi14, Reference Cirant and Goffi16, Reference Leonori and Porretta30, Reference Lions31]
-Laplacian [Reference Bidaut-Véron, Garcia-Huidobro and Véron7, Reference Cirant and Goffi14, Reference Cirant and Goffi16, Reference Leonori and Porretta30, Reference Lions31]
Our main results are the following. The first is a quantitative result for semi-solutions to PDIs, that is summarized in the next
Theorem 1.1 Let $\Omega$![]() be an open bounded and connected subset of $\mathbb {R}^N$
be an open bounded and connected subset of $\mathbb {R}^N$![]() having Lipschitz boundary and satisfying the uniform interior sphere condition. Assume (A) and (B1), $\gamma >p,$
having Lipschitz boundary and satisfying the uniform interior sphere condition. Assume (A) and (B1), $\gamma >p,$![]() $\lambda \geq 0$
$\lambda \geq 0$![]() and $f\in \mathcal {L}^{1,\frac {N}{q}}(\Omega )$
and $f\in \mathcal {L}^{1,\frac {N}{q}}(\Omega )$![]() for some $q>\frac {N}{\gamma }$
for some $q>\frac {N}{\gamma }$![]() . Let $u\in W^{1,\gamma }_{\mathrm {loc}}(\Omega )$
. Let $u\in W^{1,\gamma }_{\mathrm {loc}}(\Omega )$![]() be such that $\lambda u^-\in \mathcal {L}^{1,\frac {N}{q}}(\Omega )$
be such that $\lambda u^-\in \mathcal {L}^{1,\frac {N}{q}}(\Omega )$![]() satisfying, in the sense of distributions, the inequality
satisfying, in the sense of distributions, the inequality
Then $u$![]() is Hölder continuous up to the boundary (namely in the whole $\overline {\Omega }$
is Hölder continuous up to the boundary (namely in the whole $\overline {\Omega }$![]() ) and satisfies
) and satisfies
where
and $K$![]() depends on $c_H,\,p,\,q,\,\gamma,\,N,\,\nu,\,\Omega,\, \|f+\lambda u^-\|_{\mathcal {L}^{1,\frac {N}{q}}(\Omega )}$
depends on $c_H,\,p,\,q,\,\gamma,\,N,\,\nu,\,\Omega,\, \|f+\lambda u^-\|_{\mathcal {L}^{1,\frac {N}{q}}(\Omega )}$![]() . In particular, the estimate is satisfied when $f,\,\lambda u^-\in L^q(\Omega )$
. In particular, the estimate is satisfied when $f,\,\lambda u^-\in L^q(\Omega )$![]() , $q>\frac {N}{\gamma }$
, $q>\frac {N}{\gamma }$![]() .
.
The second is a Liouville/Bernstein-type result and states the nonexistence of nontrivial solutions to (1.2) for the corresponding homogeneous PDE/PDI without zero-th order terms on noncompact complete Riemannian manifolds $M$![]() in terms of the growth rate of the area of the geodesic spheres.
in terms of the growth rate of the area of the geodesic spheres.
Theorem 1.2 Let $(M,\,g)$![]() be a noncompact complete Riemannian manifold. If $p>1,$
be a noncompact complete Riemannian manifold. If $p>1,$![]() $\gamma >p-1$
$\gamma >p-1$![]() and
and

for some origin $o\in M$![]() , then any distributional solution of
, then any distributional solution of
where $\mathcal {A}$![]() satisfies (A), must be a.e. constant on $M$
satisfies (A), must be a.e. constant on $M$![]() . In particular, if (1.3) holds, any distributional solution to
. In particular, if (1.3) holds, any distributional solution to
with $\gamma >p-1$![]() must be a.e. constant on $M$
must be a.e. constant on $M$![]() .
.
The previous result leads to the following property when specialized to the Euclidean space $M=\mathbb {R}^N$![]() .
.
Corollary 1.3 Assume (A) and (B2). Any distributional solution to the inequality
must be a.e. constant in $\mathbb {R}^N$![]() provided that
provided that
Similarly, any distributional solution to
must be a.e. constant when $\gamma,\,p$![]() vary in the range (1.7).
vary in the range (1.7).
These results rely on interior integral gradient estimates of Morrey-type of the form
for some $\alpha \in \mathbb {R}$![]() , see lemma 2.3, remark 2.5 and lemma 4.4. Such bounds are obtained either by simple integral arguments that exploit test function methods or combine a weak version of the divergence theorem and the co-area formula.
, see lemma 2.3, remark 2.5 and lemma 4.4. Such bounds are obtained either by simple integral arguments that exploit test function methods or combine a weak version of the divergence theorem and the co-area formula.
Related properties to those in theorem 1.1 for problems with supernatural gradient growth, i.e. $\gamma >p$![]() , have been already analysed in the literature. The paper by I. Capuzzo-Dolcetta, F. Leoni and A. Porretta [Reference Capuzzo Dolcetta, Leoni and Porretta11] treated a large class of diffusion operators in non-divergence form (that also includes fully nonlinear uniformly elliptic operators and the $p$
, have been already analysed in the literature. The paper by I. Capuzzo-Dolcetta, F. Leoni and A. Porretta [Reference Capuzzo Dolcetta, Leoni and Porretta11] treated a large class of diffusion operators in non-divergence form (that also includes fully nonlinear uniformly elliptic operators and the $p$![]() -Laplacian) with bounded right-hand side $f$
-Laplacian) with bounded right-hand side $f$![]() (with estimates depending on $\|u\|_\infty$
(with estimates depending on $\|u\|_\infty$![]() ) in the realm of viscosity solutions. This was revisited with a shorter proof by G. Barles in [Reference Barles3], again in the framework of viscosity (semi-)solutions. This regularity problem has been much less investigated for unbounded data, where mostly optimal regularity at the level of Lebesgue spaces has been studied, see e.g. [Reference Grenon, Murat and Porretta24]. An analogue to our theorem 1.1 with unbounded source terms $f\in L^q$
) in the realm of viscosity solutions. This was revisited with a shorter proof by G. Barles in [Reference Barles3], again in the framework of viscosity (semi-)solutions. This regularity problem has been much less investigated for unbounded data, where mostly optimal regularity at the level of Lebesgue spaces has been studied, see e.g. [Reference Grenon, Murat and Porretta24]. An analogue to our theorem 1.1 with unbounded source terms $f\in L^q$![]() was proved by A. Dall'Aglio and A. Porretta in the case $p=2$
was proved by A. Dall'Aglio and A. Porretta in the case $p=2$![]() , and it has been the starting point of our work. At this stage, we stress that distributional solutions for these problems are not unique, cf § 3.2, and hence the quantitative result in theorem 1.1 takes on a stronger meaning.
, and it has been the starting point of our work. At this stage, we stress that distributional solutions for these problems are not unique, cf § 3.2, and hence the quantitative result in theorem 1.1 takes on a stronger meaning.
Recent advances on the Hölder regularity for problems driven by the Laplacian with coercive gradient terms and space-time $L^q$![]() right-hand side have been obtained for parabolic equations in [Reference Cirant and Goffi14] through quite different integral/duality methods, which, unfortunately, do not seem to extend to quasi-linear operators satisfying (A). We further mention that the Hölder regularity for solutions to these equations when $p=2$
right-hand side have been obtained for parabolic equations in [Reference Cirant and Goffi14] through quite different integral/duality methods, which, unfortunately, do not seem to extend to quasi-linear operators satisfying (A). We further mention that the Hölder regularity for solutions to these equations when $p=2$![]() has been also the focus of the recent work [Reference Cirant and Verzini17], but for solutions solving the PDE in strong sense, looking thus beyond the range of the Hölder bound stated in theorem 1.1 for source terms with better summability. Indeed, we also show that, as far as the Hölder regularity is concerned, the range found in theorem 1.1 is sharp for our class of functions, cf § 3.2. It is well-known that these regularity properties are the cornerstone for the analysis of many different problems ranging from those arising in ergodic control and homogenization to problems with state constraints, at least when $p=2$
has been also the focus of the recent work [Reference Cirant and Verzini17], but for solutions solving the PDE in strong sense, looking thus beyond the range of the Hölder bound stated in theorem 1.1 for source terms with better summability. Indeed, we also show that, as far as the Hölder regularity is concerned, the range found in theorem 1.1 is sharp for our class of functions, cf § 3.2. It is well-known that these regularity properties are the cornerstone for the analysis of many different problems ranging from those arising in ergodic control and homogenization to problems with state constraints, at least when $p=2$![]() , see [Reference Barles3, Reference Birindelli, Demengel and Leoni9]. Nonetheless, the case of quasilinear equations with terms having supernatural growth appears, to our knowledge, still an open line of research, cf [Reference Birindelli, Demengel and Leoni9, Reference Leonori and Porretta30, Reference Nguyen and Phuc34] for some recent contributions.
, see [Reference Barles3, Reference Birindelli, Demengel and Leoni9]. Nonetheless, the case of quasilinear equations with terms having supernatural growth appears, to our knowledge, still an open line of research, cf [Reference Birindelli, Demengel and Leoni9, Reference Leonori and Porretta30, Reference Nguyen and Phuc34] for some recent contributions.
Instead, statements like theorem 1.2, and its byproduct corollary 1.3, have been studied (almost) thoroughly and for many years through various different approaches, see e.g. Remark 3.7, § 3.3.1 and the general reference [Reference Bianchini, Mari, Pucci and Rigoli6]. Although the latter is a widely studied problem, we decided to propose a new unifying proof of the result, even in a more general context, due to its shortness, along with the treatment of some new endpoint cases (e.g. the borderline case $\gamma =\frac {N(p-1)}{N-1}$![]() in corollary 1.3). Here, our approach to tackle the Liouville property has been inspired by the works [Reference Lions31, Reference Pigola, Rigoli and Setti36, Reference Rigoli and Setti40]. At this point it is remarkable to emphasize that when $p=2$
in corollary 1.3). Here, our approach to tackle the Liouville property has been inspired by the works [Reference Lions31, Reference Pigola, Rigoli and Setti36, Reference Rigoli and Setti40]. At this point it is remarkable to emphasize that when $p=2$![]() the threshold $\gamma =\frac {N}{N-1}$
the threshold $\gamma =\frac {N}{N-1}$![]() is critical for the solvability and the regularity of solutions of the so-called viscous Hamilton–Jacobi equation, see e.g. [Reference Cirant and Goffi16, Reference Hansson, Maz'ya and Verbitsky27].
is critical for the solvability and the regularity of solutions of the so-called viscous Hamilton–Jacobi equation, see e.g. [Reference Cirant and Goffi16, Reference Hansson, Maz'ya and Verbitsky27].
Notably, the results in theorems 1.1, 1.2 and corollary 1.3 highlight a striking effect of the superlinear gradient term. Indeed, a simple zoom of the equation suggests that such a term is the dominating one at small scales in the supernatural regime $\gamma >p$![]() (i.e. in the regime of theorem 1.1), and it turns out to be the sole responsible of all the properties analysed throughout this manuscript, as one can realise by a careful inspection of the proofs of theorems 1.1 and 1.2. The link between the Liouville and the local regularity properties of nonlinear elliptic problems has been sometimes pointed out throughout some works, see e.g. [Reference Beck, Bulíček and Frehse4, Reference Meier33] among others, and our analysis underlines once more the bridge between nonexistence results and the Hölder regularity for semi-solutions of PDEs through the Morrey-type bounds in lemma 2.3 and remark 2.5.
(i.e. in the regime of theorem 1.1), and it turns out to be the sole responsible of all the properties analysed throughout this manuscript, as one can realise by a careful inspection of the proofs of theorems 1.1 and 1.2. The link between the Liouville and the local regularity properties of nonlinear elliptic problems has been sometimes pointed out throughout some works, see e.g. [Reference Beck, Bulíček and Frehse4, Reference Meier33] among others, and our analysis underlines once more the bridge between nonexistence results and the Hölder regularity for semi-solutions of PDEs through the Morrey-type bounds in lemma 2.3 and remark 2.5.
Some comments on the aforementioned results are now in order. On one hand, theorem 1.1 holds for merely distributional semi-solutions to PDEs with supernatural gradient growth and unbounded right-hand side. This is unusual for diffusive problems (e.g. of second order) with first-order terms above the natural growth imposed by the diffusion $\gamma =p$![]() , since such estimates hold, in general, for solutions of uniformly elliptic problems with subnatural gradient growth $\gamma < p$
, since such estimates hold, in general, for solutions of uniformly elliptic problems with subnatural gradient growth $\gamma < p$![]() and, usually, bounded data [Reference Bensoussan and Frehse5, Reference Ladyzhenskaya and Ural'tseva29]. Moreover, the estimate in theorem 1.1 holds up to the boundary of the domain and it is a universal estimate for positive solutions.
and, usually, bounded data [Reference Bensoussan and Frehse5, Reference Ladyzhenskaya and Ural'tseva29]. Moreover, the estimate in theorem 1.1 holds up to the boundary of the domain and it is a universal estimate for positive solutions.
On the other hand, the approach leading to theorem 1.2 does not require any one-side bound on the solution, being thus consistent with the companion results for solutions to the same kind of equations obtained through the Bernstein gradient estimates by L. Peletier-J. Serrin [Reference Peletier and Serrin35] and P.-L. Lions [Reference Lions31], and later in [Reference Bidaut-Véron, Garcia-Huidobro and Véron7] (see also [Reference Birindelli, Demengel and Leoni9, theorem 2.4] and [Reference Filippucci, Pucci and Souplet22, theorem 1.1] for recent refinements). Notably, in the context of Riemannian manifolds theorem 1.2 does not require curvature conditions on the background geometry. As a matter of fact, we emphasize that curvature bounds have been frequently imposed to derive the Liouville property for solutions to $-\Delta _pu+|\nabla u|^\gamma =0$![]() when the first-order term has ‘superlinear’ growth with respect to the diffusion (i.e. $\gamma >p-1$
when the first-order term has ‘superlinear’ growth with respect to the diffusion (i.e. $\gamma >p-1$![]() ) and the equation is posed on a noncompact manifold, see e.g. [Reference Bidaut-Véron, Garcia-Huidobro and Véron7, corollary 4.3]. This is a consequence of the use of Bernstein-type methods through the Böchner's identity. In this paper we adopt a different viewpoint, as in [Reference Pigola, Rigoli and Setti37, Reference Rigoli and Setti40]. Indeed, theorem 1.2 shows, in the case of distributional supersolutions to these homogeneous quasi-linear equations, that the Liouville property can be obtained under some area-growth conditions, at least for slowly increasing gradient terms, see § 4.2. It seems an open problem whether the Liouville result in [Reference Bidaut-Véron, Garcia-Huidobro and Véron7] holds for less regular solutions and with less restrictive bounds on the geometry in the general superlinear range $\gamma >p-1$
) and the equation is posed on a noncompact manifold, see e.g. [Reference Bidaut-Véron, Garcia-Huidobro and Véron7, corollary 4.3]. This is a consequence of the use of Bernstein-type methods through the Böchner's identity. In this paper we adopt a different viewpoint, as in [Reference Pigola, Rigoli and Setti37, Reference Rigoli and Setti40]. Indeed, theorem 1.2 shows, in the case of distributional supersolutions to these homogeneous quasi-linear equations, that the Liouville property can be obtained under some area-growth conditions, at least for slowly increasing gradient terms, see § 4.2. It seems an open problem whether the Liouville result in [Reference Bidaut-Véron, Garcia-Huidobro and Véron7] holds for less regular solutions and with less restrictive bounds on the geometry in the general superlinear range $\gamma >p-1$![]() . We further remark that the assumptions we impose in theorem 1.2 are closer to the ones used in [Reference Rigoli and Setti40, Reference Sun, Xiao and Xu43] rather than in [Reference Bidaut-Véron, Garcia-Huidobro and Véron7].
. We further remark that the assumptions we impose in theorem 1.2 are closer to the ones used in [Reference Rigoli and Setti40, Reference Sun, Xiao and Xu43] rather than in [Reference Bidaut-Véron, Garcia-Huidobro and Véron7].
Our results apply to general diffusion operators in divergence form. For instance $-\mathrm {div}(\mathcal {A}(x,\,u,\,\nabla u))$![]() can be one of the following:
can be one of the following:
• the (negative) Laplacian $-\Delta u=-\mathrm {div}(\nabla u)$
 or the mean-curvature operator $-\mathrm {div}(\frac {\nabla u}{\sqrt {1+|\nabla u|^2}})$
or the mean-curvature operator $-\mathrm {div}(\frac {\nabla u}{\sqrt {1+|\nabla u|^2}})$ when $p=2$
when $p=2$ ;
;• the $p$
 -Laplacian $-\Delta _pu=-\mathrm {div}(|\nabla u|^{p-2}\nabla u)$
-Laplacian $-\Delta _pu=-\mathrm {div}(|\nabla u|^{p-2}\nabla u)$ for $p>1$
for $p>1$ ;
;• the generalized mean-curvature operator $-\mathrm {div}(|\nabla u|^{k-2}\frac {\nabla u}{\sqrt {1+|\nabla u|^k}})$
 , $k\geq 2$
, $k\geq 2$ , for $p=\frac {k}{2}$
, for $p=\frac {k}{2}$ .
.
Moreover, the properties in theorem 1.1 also extend to the subelliptic framework when the standard derivatives in the aforementioned operators are replaced with derivatives along vector fields satisfying the Hörmander's rank condition, i.e. for the subelliptic inequality
where $\nabla _\mathcal {X}$![]() stands for the horizontal gradient built over the frame $\mathcal {X}$
stands for the horizontal gradient built over the frame $\mathcal {X}$![]() , see e.g. theorem 4.2 in § 4.1 for more details. This is the case, for instance, of problems structured over the fields generating a Carnot group of step 2, the main prototype being the Heisenberg group. The interior Hölder regularity for such subelliptic problems with power-like first-order terms on the horizontal gradient seems new to our knowledge.
, see e.g. theorem 4.2 in § 4.1 for more details. This is the case, for instance, of problems structured over the fields generating a Carnot group of step 2, the main prototype being the Heisenberg group. The interior Hölder regularity for such subelliptic problems with power-like first-order terms on the horizontal gradient seems new to our knowledge.
Moreover, the results in theorems 1.1 and 1.3 can be stated analogously for distributional supersolutions and subsolutions respectively by reversing the signs in the assumptions (B1) and (B2). For instance, the conclusions of theorem 1.1 hold for distributional solutions to the model PDI
under essentially the same regularity assumptions on the data, while the Liouville property in theorem 1.3 holds for the weak PDI
under the hypothesis (A). Indeed, the diffusion plays no role here, as in [Reference Capuzzo Dolcetta, Leoni and Porretta11, Reference Dall'Aglio and Porretta18], since the properties can be deduced from the sign of the gradient term in the equation, see remark 2.5. To convince the reader that such properties can be appropriately stated both for sub- and supersolutions to elliptic inequalities with power-growth gradient terms and compare the results with most of the literature on the subject, we decided to state theorem 1.1 for subsolutions and theorem 1.2 for supersolutions to elliptic inequalities.
We conclude by saying that our underlying aim here is also to lay the groundwork to investigate the problem of the optimal gradient regularity in Lebesgue spaces for equations with diffusion in divergence form as those modelled over the $p$![]() -Laplacian, as initiated in [Reference Cirant and Goffi14, Reference Cirant and Goffi16] for the viscous Hamilton–Jacobi equation, through blow-up arguments, see [Reference Beck, Bulíček and Frehse4, Reference Cirant and Verzini17].
-Laplacian, as initiated in [Reference Cirant and Goffi14, Reference Cirant and Goffi16] for the viscous Hamilton–Jacobi equation, through blow-up arguments, see [Reference Beck, Bulíček and Frehse4, Reference Cirant and Verzini17].
Plan of the paper. Section 2 introduces some preliminary definitions and contains the main integral bounds needed for the following sections. Section 3.1 studies the interior and global Hölder regularity for semi-solutions, while § 3.3 the Liouville property for homogeneous PDIs in the Euclidean space, that is corollary 1.3. Section 4.1 and 4.2 conclude the paper with the local Hölder regularity for solutions to quasi-linear subelliptic inequalities and the Liouville properties for inequalities posed on Riemannian manifolds.
2. Morrey-type inequalities
We begin with some preliminary definitions and notations. We set $u^+=\max \{u,\,0\}$![]() and $u^-=\max \{-u,\,0\}$
and $u^-=\max \{-u,\,0\}$![]() . If $r\in (1,\,\infty )$
. If $r\in (1,\,\infty )$![]() , we denote by $r'=\frac {r}{r-1}$
, we denote by $r'=\frac {r}{r-1}$![]() its Hölder conjugate exponent.
its Hölder conjugate exponent.
Definition 2.1 Let $\Omega$![]() be either a bounded open set or the whole Euclidean space $\mathbb {R}^N$
be either a bounded open set or the whole Euclidean space $\mathbb {R}^N$![]() . We say that $u\in W^{1,p}_{\text {loc}}(\Omega )$
. We say that $u\in W^{1,p}_{\text {loc}}(\Omega )$![]() is a distributional solution of (1.1) if $\mathcal {A}(\cdot,\,u,\,\nabla u)\in L^{p'}_{\mathrm {loc}}(\Omega )$
is a distributional solution of (1.1) if $\mathcal {A}(\cdot,\,u,\,\nabla u)\in L^{p'}_{\mathrm {loc}}(\Omega )$![]() , with $\mathcal {B}(\cdot,\,u,\,\nabla u)\in L^1_{\mathrm {loc}}(\Omega )$
, with $\mathcal {B}(\cdot,\,u,\,\nabla u)\in L^1_{\mathrm {loc}}(\Omega )$![]() and
and
Remark 2.2 When $\gamma >p$![]() as in theorem 1.1, it will be enough to consider distributional subsolutions belonging to $u\in W^{1,\gamma }_{\text {loc}}(\Omega )$
as in theorem 1.1, it will be enough to consider distributional subsolutions belonging to $u\in W^{1,\gamma }_{\text {loc}}(\Omega )$![]() in view of the inclusions of Lebesgue spaces.
in view of the inclusions of Lebesgue spaces.
Recall that for $s\geq 1$![]() and $\theta \in (0,\,N]$
and $\theta \in (0,\,N]$![]() , the Morrey space $\mathcal {L}^{s,\theta }(\Omega )$
, the Morrey space $\mathcal {L}^{s,\theta }(\Omega )$![]() comprises those functions $h\in L^s(\Omega )$
comprises those functions $h\in L^s(\Omega )$![]() such that
such that
for all $z\in \Omega$![]() , $r\in (0,\,\mathrm {diam}(\Omega )]$
, $r\in (0,\,\mathrm {diam}(\Omega )]$![]() and $C$
and $C$![]() independent of $z$
independent of $z$![]() and $r$
and $r$![]() . This space is equipped with the norm
. This space is equipped with the norm
Clearly, if $s=1$![]() and $\theta =N/q$
and $\theta =N/q$![]() , $q\geq 1$
, $q\geq 1$![]() , any function $h\in L^q(\Omega )$
, any function $h\in L^q(\Omega )$![]() satisfies the bound
satisfies the bound
by the Hölder's inequality. For the properties that will be stated in the Euclidean setting, $\mathcal {H}^{N-1}$![]() stands for the ($N-1$
stands for the ($N-1$![]() )-Hausdorff measure, $B_r(x)$
)-Hausdorff measure, $B_r(x)$![]() is the Euclidean ball with centre $x$
is the Euclidean ball with centre $x$![]() and radius $r$
and radius $r$![]() , hence $\mathrm {area}(\partial B_r(x))=N\omega _N r^{N-1}$
, hence $\mathrm {area}(\partial B_r(x))=N\omega _N r^{N-1}$![]() and $\mathrm {Vol}(B_r(x))=\omega _Nr^N$
and $\mathrm {Vol}(B_r(x))=\omega _Nr^N$![]() , where $\omega _N$
, where $\omega _N$![]() stands for the measure of the unit Euclidean ball.
stands for the measure of the unit Euclidean ball.
The main result of this section is the following Morrey estimate.
Lemma 2.3 Let $\gamma >p-1,$![]() $\lambda \geq 0,$
$\lambda \geq 0,$![]() $f\in \mathcal {L}^{1,\frac {N}{q}}(\Omega ),$
$f\in \mathcal {L}^{1,\frac {N}{q}}(\Omega ),$![]() $q\geq 1$
$q\geq 1$![]() . Assume that (A) and (B1) hold. Let $u$
. Assume that (A) and (B1) hold. Let $u$![]() be a distributional solution of (1.1) such that $\lambda u^-\in \mathcal {L}^{1,\frac {N}{q}}(\Omega )$
be a distributional solution of (1.1) such that $\lambda u^-\in \mathcal {L}^{1,\frac {N}{q}}(\Omega )$![]() . Then, for every pair of concentric balls $B_t\subset B_R\subset \Omega$
. Then, for every pair of concentric balls $B_t\subset B_R\subset \Omega$![]() we have
we have
where $s=\max \left \{\frac {N}{q},\,\frac {\gamma }{\gamma -(p-1)}\right \}$![]() and $K$
and $K$![]() is a constant depending on $\nu,\,p,\,\gamma,\,q,\,N,\,c_H$
is a constant depending on $\nu,\,p,\,\gamma,\,q,\,N,\,c_H$![]() and on $\|f+\lambda u^-\|_{\mathcal {L}^{1,\frac {N}{q}}(B_R)}$
and on $\|f+\lambda u^-\|_{\mathcal {L}^{1,\frac {N}{q}}(B_R)}$![]() .
.
Proof. Let $C$![]() be a generic constant depending on the data $\nu,\,p,\,\gamma,\,q,\,N,\,c_H$
be a generic constant depending on the data $\nu,\,p,\,\gamma,\,q,\,N,\,c_H$![]() . Let $\eta$
. Let $\eta$![]() be a $C^1$
be a $C^1$![]() cut-off function such that $0\leq \eta \leq 1$
cut-off function such that $0\leq \eta \leq 1$![]() , $\eta \equiv 1$
, $\eta \equiv 1$![]() on $B_t$
on $B_t$![]() , $\eta \equiv 0$
, $\eta \equiv 0$![]() outside $B_R$
outside $B_R$![]() , $|\nabla \eta |\leq \frac {C}{R-t}$
, $|\nabla \eta |\leq \frac {C}{R-t}$![]() . We use $\varphi =\eta ^\frac {\gamma }{\gamma -(p-1)}$
. We use $\varphi =\eta ^\frac {\gamma }{\gamma -(p-1)}$![]() as a test function in the distributional formulation of the inequality (1.1), together with (B1), to obtain
as a test function in the distributional formulation of the inequality (1.1), together with (B1), to obtain

Observe that by (A) and the weighted Young's inequality with exponents $(\frac {\gamma }{\gamma -(p-1)},\,\frac {\gamma }{p-1})$![]() we have
we have

We then get

where $s=\max \left \{\frac {N}{q},\,\frac {\gamma }{\gamma -(p-1)}\right \}$![]() and $K$
and $K$![]() depends on $N,\,c_H,\,\gamma,\,\nu,\,p,\,q$
depends on $N,\,c_H,\,\gamma,\,\nu,\,p,\,q$![]() and $\|f+\lambda u^-\|_{\mathcal {L}^{1,\frac {N}{q}}(B_R)}$
and $\|f+\lambda u^-\|_{\mathcal {L}^{1,\frac {N}{q}}(B_R)}$![]() .
.
Remark 2.4 The estimate in lemma 2.3 holds for any $\gamma >p-1$![]() , $p>1$
, $p>1$![]() , and hence slightly improves the one obtained in [Reference Dall'Aglio and Porretta18] for the case $p=2$
, and hence slightly improves the one obtained in [Reference Dall'Aglio and Porretta18] for the case $p=2$![]() , being new in the regime $1<\gamma \leq 2$
, being new in the regime $1<\gamma \leq 2$![]() . This will be important to derive the Liouville theorems for PDIs with nonlinearities having subnatural growth in the gradient in the next section.
. This will be important to derive the Liouville theorems for PDIs with nonlinearities having subnatural growth in the gradient in the next section.
Remark 2.5 As claimed in the introduction, the property in lemma 2.3 holds for supersolutions to equations of the form (1.9) having opposite signs, but estimates would now require $\lambda u^+\in \mathcal {L}^{1,\frac {N}{q}}(B_R)$![]() , while it holds for every pair of concentric balls $B_t\subset B_R\subset \Omega$
, while it holds for every pair of concentric balls $B_t\subset B_R\subset \Omega$![]() the estimate
the estimate
where $s=\max \left \{\frac {N}{q},\,\frac {\gamma }{\gamma -(p-1)}\right \}$![]() and $K$
and $K$![]() is a constant with the same dependence of that in lemma 2.3.
is a constant with the same dependence of that in lemma 2.3.
An alternative proof of the previous Morrey estimate for supersolutions in the simpler case $f=\lambda =0$![]() , i.e. for the inequality (1.2), can be performed using a different integral approach, inspired by [Reference Lions31, Reference Rigoli and Setti40]. This will be crucial to derive the Liouville results for supersolutions to homogeneous inequalities in the next section.
, i.e. for the inequality (1.2), can be performed using a different integral approach, inspired by [Reference Lions31, Reference Rigoli and Setti40]. This will be crucial to derive the Liouville results for supersolutions to homogeneous inequalities in the next section.
Suppose that $u$![]() is a nonconstant distributional solution to (1.2). We proceed formally integrating the PDI to highlight the main ingredients, although the argument can be made rigorous reasoning as in remark 2.6. In this way, we get
is a nonconstant distributional solution to (1.2). We proceed formally integrating the PDI to highlight the main ingredients, although the argument can be made rigorous reasoning as in remark 2.6. In this way, we get
to conclude after applying the Hölder's inequality

We set $\sigma (r)=\int _{B_r}|\nabla u|^\gamma$![]() . Note that since $u$
. Note that since $u$![]() is non-constant, there exists $\overline {R}$
is non-constant, there exists $\overline {R}$![]() such that for $r\geq \overline {R}$
such that for $r\geq \overline {R}$![]() it results $\sigma (r)>0$
it results $\sigma (r)>0$![]() . Moreover, by the co-area formula it follows that
. Moreover, by the co-area formula it follows that
Combining (2.1) and (2.2) we conclude
and so
We set
and integrate on $[R,\,r]$![]() , $R\geq \overline {R}$
, $R\geq \overline {R}$![]() . When $\alpha < 1$
. When $\alpha < 1$![]() , i.e. $\gamma <\frac {N(p-1)}{N-1}$
, i.e. $\gamma <\frac {N(p-1)}{N-1}$![]() , we obtain that
, we obtain that

which is essentially the same bound found in lemma 2.3 with $f=\lambda =0$![]() . Remarkably, when $\alpha =1$
. Remarkably, when $\alpha =1$![]() , i.e. $\gamma =\frac {N(p-1)}{N-1}$
, i.e. $\gamma =\frac {N(p-1)}{N-1}$![]() , we get the logarithmic bound
, we get the logarithmic bound

This procedure will be further generalized in lemma 4.4 in the context of Riemannian manifolds.
Remark 2.6 The computations in remark 2.5 can be made rigorous arguing as in [Reference Chen13, Reference Pigola, Rigoli and Setti37, Reference Pigola and Setti39, Reference Rigoli and Setti40]. We first recall that $u$![]() is a distributional solution of (1.2) if
is a distributional solution of (1.2) if
for all Lipschitz continuous functions $\varphi \geq 0$![]() with compact support. As already outlined in remark 2.5, the idea is to apply the divergence theorem to the vector field $\mathcal {A}$
with compact support. As already outlined in remark 2.5, the idea is to apply the divergence theorem to the vector field $\mathcal {A}$![]() . To this aim, we define the Lipschitz function $\psi _\varepsilon =\psi _{r,\varepsilon }$
. To this aim, we define the Lipschitz function $\psi _\varepsilon =\psi _{r,\varepsilon }$![]()

We then take a Lipschitz continuous function $\rho \geq 0$![]() with compact support to be defined later and use $\varphi =\rho \psi _\varepsilon$
with compact support to be defined later and use $\varphi =\rho \psi _\varepsilon$![]() as a test function, together with (A), to find
as a test function, together with (A), to find

We then choose $\rho$![]() such that $\rho =1$
such that $\rho =1$![]() on $\overline {B}_{r+\varepsilon }$
on $\overline {B}_{r+\varepsilon }$![]() and find
and find
Therefore, the leftmost side integral of the above inequality vanishes, so that we end up with the inequality
Then, owing to the co-area formula [Reference Evans and Gariepy20] we get

Letting $\varepsilon \to 0^+$![]() we finally obtain
we finally obtain
We can then proceed through the Hölder's inequality on the boundary integral as in remark 2.5 to conclude the statement.
Remark 2.7 One can also prove a similar property when the diffusion operator has the opposite sign, i.e. it is of the form $+\mathrm {div}(\mathcal {A}(x,\,u,\,\nabla u))$![]() , and when $|\mathcal {A}(x,\,u,\,\nabla u)|\leq h(x)+\nu |\xi |^{p-1}$
, and when $|\mathcal {A}(x,\,u,\,\nabla u)|\leq h(x)+\nu |\xi |^{p-1}$![]() with $h\in L^r(\Omega )$
with $h\in L^r(\Omega )$![]() (or in a suitable Morrey class) for some $r>1$
(or in a suitable Morrey class) for some $r>1$![]() with a (possibly) different Hölder exponent.
with a (possibly) different Hölder exponent.
Remark 2.8 A similar condition to (2.4) regarding the existence of solutions has been already pointed out in [Reference Hansson, Maz'ya and Verbitsky27, Reference Nguyen and Phuc34].
3. Some applications of the Morrey-type inequalities
3.1 Local and global Hölder regularity for semi-solutions
We now apply lemma 2.3 to prove the local Hölder continuity of semi-solutions to non-homogeneous PDEs with power-growth nonlinearities and unbounded right-hand side controlled in Morrey spaces. We will actually give a uniform estimate for the Hölder semi-norm on any ball $B\subset \Omega$![]() .
.
Theorem 3.1 Assume (A)–(B1) , $\gamma >p,$![]() $\lambda \geq 0,$
$\lambda \geq 0,$![]() with $f\in \mathcal {L}^{1,\frac {N}{q}}(\Omega )$
with $f\in \mathcal {L}^{1,\frac {N}{q}}(\Omega )$![]() for some $q>\frac {N}{\gamma }$
for some $q>\frac {N}{\gamma }$![]() . Let $u\in W^{1,\gamma }_{\mathrm {loc}}(\Omega )$
. Let $u\in W^{1,\gamma }_{\mathrm {loc}}(\Omega )$![]() such that $\lambda u^-\in \mathcal {L}^{1,\frac {N}{q}}(\Omega )$
such that $\lambda u^-\in \mathcal {L}^{1,\frac {N}{q}}(\Omega )$![]() which satisfies, in the sense of distributions, the inequality (1.1). Then $u$
which satisfies, in the sense of distributions, the inequality (1.1). Then $u$![]() is locally Hölder continuous and satisfies for every ball $B\subset \Omega$
is locally Hölder continuous and satisfies for every ball $B\subset \Omega$![]() the interior bound
the interior bound
where
and $K$![]() depends on $p,\,q,\,\gamma,\,N,\,\nu,\,\Omega,\,\|f\|_{\mathcal {L}^{1,\frac {N}{q}}(\Omega )}$
depends on $p,\,q,\,\gamma,\,N,\,\nu,\,\Omega,\,\|f\|_{\mathcal {L}^{1,\frac {N}{q}}(\Omega )}$![]() and $\lambda u^-\in \mathcal {L}^{1,\frac {N}{q}}(\Omega )$
and $\lambda u^-\in \mathcal {L}^{1,\frac {N}{q}}(\Omega )$![]() .
.
Proof. Step 1: Local Hölder regularity. Let $x_0\in \Omega$![]() and $B_r=B_r(x_0)$
and $B_r=B_r(x_0)$![]() be a ball such that the twice bigger ball $B_{2r}(x_0)\subset \Omega$
be a ball such that the twice bigger ball $B_{2r}(x_0)\subset \Omega$![]() . We apply lemma 2.3 and obtain the estimate
. We apply lemma 2.3 and obtain the estimate
where $s=\max \left \{\frac {N}{q},\,\frac {\gamma }{\gamma -(p-1)}\right \}$![]() and $K$
and $K$![]() depends on $\gamma,\,p,\,N,\,\nu,\,q,\,c_H$
depends on $\gamma,\,p,\,N,\,\nu,\,q,\,c_H$![]() and $\|f+\lambda u^-\|_{\mathcal {L}^{1,\frac {N}{q}}(\Omega )}$
and $\|f+\lambda u^-\|_{\mathcal {L}^{1,\frac {N}{q}}(\Omega )}$![]() . By the Hölder's inequality we can write
. By the Hölder's inequality we can write

and hence deduce that for a possibly different constant $\widetilde {K}$![]() we have
we have
If $B_R$![]() is any ball such that $B_{2R}\subset \Omega$
is any ball such that $B_{2R}\subset \Omega$![]() , the same property continues to hold for any smaller ball $B_r\subset B_R$
, the same property continues to hold for any smaller ball $B_r\subset B_R$![]() . We apply [Reference Gilbarg and Trudinger23, theorem 7.19] and conclude that $u$
. We apply [Reference Gilbarg and Trudinger23, theorem 7.19] and conclude that $u$![]() is Hölder continuous in $B_R$
is Hölder continuous in $B_R$![]() with the following explicit Hölder exponent
with the following explicit Hölder exponent
and
In particular, the last estimate holds for any couple of points $x,\,y$![]() belonging to some ball $B_R$
belonging to some ball $B_R$![]() such that $B_{2R}\subset \Omega$
such that $B_{2R}\subset \Omega$![]() .
.
Step 2: Uniform Hölder estimates. It is enough to argue through the same path outlined in step 2 of [Reference Dall'Aglio and Porretta18, theorem 3.1].
The previous result proves that $u$![]() is uniformly locally Hölder continuous in a domain $\Omega \subset \mathbb {R}^N$
is uniformly locally Hölder continuous in a domain $\Omega \subset \mathbb {R}^N$![]() . To prove the global Hölder regularity one needs some extra smoothness assumptions on the boundary of $\Omega$
. To prove the global Hölder regularity one needs some extra smoothness assumptions on the boundary of $\Omega$![]() . More precisely, we say that an open bounded subset $\Omega \subset \mathbb {R}^N$
. More precisely, we say that an open bounded subset $\Omega \subset \mathbb {R}^N$![]() has Lipschitz boundary if in a neighbourhood of each $x_0\in \partial \Omega$
has Lipschitz boundary if in a neighbourhood of each $x_0\in \partial \Omega$![]() the domain $\Omega$
the domain $\Omega$![]() can be represented as the subgraph of a Lipschitz function of $(N-1)$
can be represented as the subgraph of a Lipschitz function of $(N-1)$![]() -variables.
-variables.
Still, we need that $\Omega$![]() satisfies the uniform interior sphere condition with radius $r>0$
satisfies the uniform interior sphere condition with radius $r>0$![]() , i.e. for every $x_0\in \partial \Omega$
, i.e. for every $x_0\in \partial \Omega$![]() there exists a unit vector $\zeta (x_0)$
there exists a unit vector $\zeta (x_0)$![]() such that $B_r(x_0+r\zeta (x_0))\subset \Omega$
such that $B_r(x_0+r\zeta (x_0))\subset \Omega$![]() . Under these extra coupled conditions on the boundary of the domain, one has the following result taken from [Reference Capuzzo Dolcetta, Leoni and Porretta11, lemma 2.6], which is recalled here below for reader's convenience.
. Under these extra coupled conditions on the boundary of the domain, one has the following result taken from [Reference Capuzzo Dolcetta, Leoni and Porretta11, lemma 2.6], which is recalled here below for reader's convenience.
Lemma 3.2 Let $\Omega \subset \mathbb {R}^N$![]() be an open bounded domain with Lipschitz boundary and satisfying the uniform interior sphere condition. Let now $u:\Omega \to \mathbb {R}$
be an open bounded domain with Lipschitz boundary and satisfying the uniform interior sphere condition. Let now $u:\Omega \to \mathbb {R}$![]() be a continuous function such that there exist $K>0$
be a continuous function such that there exist $K>0$![]() and $\alpha \in (0,\,1)$
and $\alpha \in (0,\,1)$![]() such that
such that
Then, $u$![]() extends up to $\partial \Omega$
extends up to $\partial \Omega$![]() as a function verifying
as a function verifying
where $M\geq K$![]() depends on $\alpha,\,K$
depends on $\alpha,\,K$![]() and on $\partial \Omega$
and on $\partial \Omega$![]() .
.
We can then conclude the section with the proof of theorem 1.3.
Remark 3.3 Theorem 1.1 extends a result for semi-solutions to fully nonlinear equations with bounded right-hand side in the viscosity framework obtained in [Reference Capuzzo Dolcetta, Leoni and Porretta11, theorem 2.11], together with the one for the case $p=2$![]() obtained by A. Dall'Aglio and A. Porretta in [Reference Dall'Aglio and Porretta18] for subsolutions to equations with coercive Hamiltonians and $L^q$
obtained by A. Dall'Aglio and A. Porretta in [Reference Dall'Aglio and Porretta18] for subsolutions to equations with coercive Hamiltonians and $L^q$![]() source terms. We emphasize that the Hölder regularity we obtain here goes beyond the (continuous) viscosity solutions’ framework, and in particular we recover the same (optimal) exponent found in [Reference Capuzzo Dolcetta, Leoni and Porretta11] for $f\in L^\infty$
source terms. We emphasize that the Hölder regularity we obtain here goes beyond the (continuous) viscosity solutions’ framework, and in particular we recover the same (optimal) exponent found in [Reference Capuzzo Dolcetta, Leoni and Porretta11] for $f\in L^\infty$![]() .
.
Remark 3.4 The level of Hölder regularity obtained in theorem 1.1 is the starting point to derive more general quantitative (local) Calderón–Zygmund estimates for solutions to these classes of PDEs, as recently started in [Reference Cirant and Verzini17] for $p=2$![]() .
.
3.2 Sharpness of the Hölder regularity and further comments
We first observe that the exponents found in the Hölder regularity proved in theorem 1.1 are sharp. To do this, we first recall that if $u$![]() is radial, i.e. $u(x)=V(|x|)\equiv V(r)$
is radial, i.e. $u(x)=V(|x|)\equiv V(r)$![]() for some smooth function $V$
for some smooth function $V$![]() , if $x$
, if $x$![]() is such that $V'(|x|)\neq 0$
is such that $V'(|x|)\neq 0$![]() we have
we have
The result in theorem 1.1 shows that when $q>\frac {N(\gamma -(p-1))}{\gamma }$![]() the subsolutions to the PDI
the subsolutions to the PDI
belong to $C^\alpha$![]() with $\alpha =\frac {\gamma -p}{\gamma -(p-1)}$
with $\alpha =\frac {\gamma -p}{\gamma -(p-1)}$![]() . In this case, an example of the optimality concerning the Hölder exponent $\alpha =\frac {\gamma -p}{\gamma -(p-1)}$
. In this case, an example of the optimality concerning the Hölder exponent $\alpha =\frac {\gamma -p}{\gamma -(p-1)}$![]() can be obtained even in the class of (distributional) solutions to the equation
can be obtained even in the class of (distributional) solutions to the equation
i.e. for the equation with vanishing source term $f\equiv 0$![]() . It is sufficient to take $\Omega =B_1(0)$
. It is sufficient to take $\Omega =B_1(0)$![]() and the function $u(x)=c(|x|^{\frac {\gamma -p}{\gamma -(p-1)}}-1)$
and the function $u(x)=c(|x|^{\frac {\gamma -p}{\gamma -(p-1)}}-1)$![]() for $c=\frac {\gamma -(p-1)}{\gamma -p} (\frac {(N-1)\gamma -N(p-1)}{\gamma -(p-1)})^{\frac {1}{\gamma -(p-1)}}$
for $c=\frac {\gamma -(p-1)}{\gamma -p} (\frac {(N-1)\gamma -N(p-1)}{\gamma -(p-1)})^{\frac {1}{\gamma -(p-1)}}$![]() , $\gamma >p$
, $\gamma >p$![]() and $1< p< N$
and $1< p< N$![]() .
.
We observe that, though the method does not require any restriction on the order $p>1$![]() , the present analysis could have been restricted to the case $1< p< N$
, the present analysis could have been restricted to the case $1< p< N$![]() , since the weak solutions belonging to $W^{1,\gamma }$
, since the weak solutions belonging to $W^{1,\gamma }$![]() with $\gamma >p$
with $\gamma >p$![]() and $p>N$
and $p>N$![]() would have been automatically (locally) Hölder continuous by the Sobolev embeddings. This is completely in line with the way of proving the local Hölder regularity in the case of $p$
would have been automatically (locally) Hölder continuous by the Sobolev embeddings. This is completely in line with the way of proving the local Hölder regularity in the case of $p$![]() -harmonic functions (i.e. for weak solutions to $-\Delta _pu=0$
-harmonic functions (i.e. for weak solutions to $-\Delta _pu=0$![]() ). Indeed, the case $p>N$
). Indeed, the case $p>N$![]() is in general simpler than the cases $p=N$
is in general simpler than the cases $p=N$![]() and $p< N$
and $p< N$![]() , which in turn require finer arguments based on the Widman filling-the-hole technique and the Moser iteration respectively, cf [Reference Bensoussan and Frehse5]. We emphasize once more that in the case $1< p\leq N$
, which in turn require finer arguments based on the Widman filling-the-hole technique and the Moser iteration respectively, cf [Reference Bensoussan and Frehse5]. We emphasize once more that in the case $1< p\leq N$![]() , our result covers the case of semi-solutions and not only of solutions to such quasi-linear equations.
, our result covers the case of semi-solutions and not only of solutions to such quasi-linear equations.
Moreover, even the order of the Hölder class $\alpha =1-\frac {N}{q\gamma }$![]() cannot be improved when $\frac {N}{\gamma }< q<\frac {N(\gamma -(p-1))}{\gamma }$
cannot be improved when $\frac {N}{\gamma }< q<\frac {N(\gamma -(p-1))}{\gamma }$![]() , as shown in e.g. [Reference Dall'Aglio and Porretta18, remark 3.2] for the case $p=2$
, as shown in e.g. [Reference Dall'Aglio and Porretta18, remark 3.2] for the case $p=2$![]() . Finally, we stress again that when $\gamma >p$
. Finally, we stress again that when $\gamma >p$![]() , the gradient term dominates the diffusion at small scales, and hence the equation can be regarded as
, the gradient term dominates the diffusion at small scales, and hence the equation can be regarded as
so that the diffusion plays no role in the derivation of the Hölder regularity, as it can be seen by inspection throughout the proof of lemma 2.3. This result is thus consistent with the Lipschitz regularity for subsolutions of the first-order equation
as widely discussed in [Reference Barles3]. We conclude by recalling that the above example shows also that the uniqueness does not hold for these weak solutions, and hence this latter property really depends on the formulation of the problem, cf [Reference Dall'Aglio and Porretta18, remark 3.2].
3.3 Liouville theorems for homogeneous problems
A byproduct of the Morrey-type bounds obtained in remark 2.5 are the Liouville-type theorems for supersolutions to nonlinear homogeneous PDIs. Although the ideas behind the proofs contained in this section are not completely new, one remarkable observation is that the derivation of the Liouville property for PDIs with gradient terms does not need any a priori one-side bound on the solution, and it holds for merely distributional supersolutions to general PDI with measurable ingredients. This last feature is in line with the corresponding Liouville properties for solutions to the model equation $-\Delta _p u+|\nabla u|^\gamma =0$![]() obtained via the Bernstein method, cf [Reference Lions31, Reference Peletier and Serrin35] for $p=2$
obtained via the Bernstein method, cf [Reference Lions31, Reference Peletier and Serrin35] for $p=2$![]() and [Reference Bidaut-Véron, Garcia-Huidobro and Véron7] for $p>1$
and [Reference Bidaut-Véron, Garcia-Huidobro and Véron7] for $p>1$![]() .
.
In addition, we wish to emphasize that in the derivation of this kind of Liouville properties one usually needs to use different methods to handle the subcritical case for $\gamma$![]() (i.e. $p-1<\gamma <\frac {N(p-1)}{N-1}$
(i.e. $p-1<\gamma <\frac {N(p-1)}{N-1}$![]() ) and the critical regime ($\gamma =\frac {N(p-1)}{N-1}$
) and the critical regime ($\gamma =\frac {N(p-1)}{N-1}$![]() ). Here, our method of proof seems to unify the treatment of both regimes. To this aim, we consider the (distributional) inequality
). Here, our method of proof seems to unify the treatment of both regimes. To this aim, we consider the (distributional) inequality
with $\mathcal {B}_2$![]() satisfying (B2). For ease of presentation we decided to reverse the order of the proofs of theorem 1.2 and corollary 1.3. Thus, we first discuss how to derive corollary 1.3 in the Euclidean setting, then state some comments on the result. This will serve as a guideline to treat the more general case of Riemannian manifolds in § 4.2.
satisfying (B2). For ease of presentation we decided to reverse the order of the proofs of theorem 1.2 and corollary 1.3. Thus, we first discuss how to derive corollary 1.3 in the Euclidean setting, then state some comments on the result. This will serve as a guideline to treat the more general case of Riemannian manifolds in § 4.2.
Proof of corollary 1.3. Suppose by contradiction that $u$![]() were not constant on the ball $B_{\widetilde {R}}$
were not constant on the ball $B_{\widetilde {R}}$![]() for some $\widetilde {R}>0$
for some $\widetilde {R}>0$![]() . The required contradiction can be obtained exploiting (2.4) in remark 2.5 sending $r\to \infty$
. The required contradiction can be obtained exploiting (2.4) in remark 2.5 sending $r\to \infty$![]() or lemma 2.3 applied with $f=\lambda =0$
or lemma 2.3 applied with $f=\lambda =0$![]() and $t=0$
and $t=0$![]() , after letting $R\to \infty$
, after letting $R\to \infty$![]() , using that $\gamma <\frac {N(p-1)}{N-1}$
, using that $\gamma <\frac {N(p-1)}{N-1}$![]() . The Liouville property in the critical case $\gamma =\frac {N(p-1)}{N-1}$
. The Liouville property in the critical case $\gamma =\frac {N(p-1)}{N-1}$![]() readily follows through the same path using (2.5) after sending $r\to \infty$
readily follows through the same path using (2.5) after sending $r\to \infty$![]() .
.
Remark 3.5 Specializing corollary 1.3 to some well-known operators, we conclude that any distributional supersolution to
or

must be constant provided that $p-1<\gamma \leq \frac {N(p-1)}{N-1}$![]() , while any distributional supersolution to
, while any distributional supersolution to
or

satisfies the Liouville property provided that $1<\gamma \leq \frac {N}{N-1}$![]() .
.
Remark 3.6 Throughout this section we restricted to consider the case $1< p< N$![]() . Indeed, if one considers the inequality $-\Delta _pu\geq |\nabla u|^\gamma$
. Indeed, if one considers the inequality $-\Delta _pu\geq |\nabla u|^\gamma$![]() in $\mathbb {R}^N$
in $\mathbb {R}^N$![]() , we have that $u$
, we have that $u$![]() solves also $-\Delta _pu\geq 0$
solves also $-\Delta _pu\geq 0$![]() in $\mathbb {R}^N$
in $\mathbb {R}^N$![]() , and hence the Liouville property would have been trivial when $p\geq N$
, and hence the Liouville property would have been trivial when $p\geq N$![]() through classical results, see e.g. [Reference Serrin and Zou41] and the next § 3.3.1.
through classical results, see e.g. [Reference Serrin and Zou41] and the next § 3.3.1.
Remark 3.7 The results in corollary 1.3 have been deeply studied in the literature. When the PDI is driven by the Laplacian the result has been proved in e.g. [Reference Caristi and Mitidieri12] for classical solutions, i.e. when $u\in C^2(\mathbb {R}^N)$![]() , satisfying the inequality pointwisely, exploiting that the spherical mean preserves the PDI, reducing then the analysis to an ODE. Alternative test functions methods have been extensively used in various papers. For instance, R. Filippucci proved in [Reference Filippucci21, corollary 1] the Liouville property for nonnegative distributional solutions to $-\Delta _p u\geq u^m|\nabla u|^\gamma$
, satisfying the inequality pointwisely, exploiting that the spherical mean preserves the PDI, reducing then the analysis to an ODE. Alternative test functions methods have been extensively used in various papers. For instance, R. Filippucci proved in [Reference Filippucci21, corollary 1] the Liouville property for nonnegative distributional solutions to $-\Delta _p u\geq u^m|\nabla u|^\gamma$![]() in $\mathbb {R}^N$
in $\mathbb {R}^N$![]() under the following assumptions
under the following assumptions
and therefore the pure gradient nonlinearity case $m=0$![]() is excluded from that result. When $p=2$
is excluded from that result. When $p=2$![]() and $(N-1)\gamma \leq N(p-1)$
and $(N-1)\gamma \leq N(p-1)$![]() , $\gamma >0$
, $\gamma >0$![]() , the result was proved through a result similar to lemma 2.3 in [Reference D'Ambrosio and Mitidieri19] for distributional supersolutions. Different (recent) proofs have been obtained in [Reference Burgos-Pérez, García-Melián and Quaas10, corollary 3] and [Reference Bidaut-Véron, García-Huidobro and Véron8, theorem 2.1]. We emphasize once more that most of these proofs require to distinguish the treatment of the subcritical case (e.g. when $\gamma <\frac {N(p-1)}{N-1}$
, the result was proved through a result similar to lemma 2.3 in [Reference D'Ambrosio and Mitidieri19] for distributional supersolutions. Different (recent) proofs have been obtained in [Reference Burgos-Pérez, García-Melián and Quaas10, corollary 3] and [Reference Bidaut-Véron, García-Huidobro and Véron8, theorem 2.1]. We emphasize once more that most of these proofs require to distinguish the treatment of the subcritical case (e.g. when $\gamma <\frac {N(p-1)}{N-1}$![]() ) from the critical one (namely $\gamma =\frac {N(p-1)}{N-1}$
) from the critical one (namely $\gamma =\frac {N(p-1)}{N-1}$![]() ). More recent analyses for PDIs on noncompact complete manifolds, without curvature conditions and assuming suitable volume growths, have been carried out in [Reference Sun42, Reference Sun, Xiao and Xu43]. We remark in passing that our method differs from the ones proposed in the literature.
). More recent analyses for PDIs on noncompact complete manifolds, without curvature conditions and assuming suitable volume growths, have been carried out in [Reference Sun42, Reference Sun, Xiao and Xu43]. We remark in passing that our method differs from the ones proposed in the literature.
3.3.1 Further remarks and alternative approaches.
We conclude the section by observing that a different proof of the Liouville property given in e.g. [Reference Filippucci21, corollary 1], [Reference Burgos-Pérez, García-Melián and Quaas10, corollary 3] when a one-side bound on the solution is in force can be derived as follows. This method has been inspired by earlier results on the subject appeared in the context of Riemannian manifolds in [Reference Chen13] and [Reference Pigola, Rigoli and Setti36, Reference Rigoli and Setti40] (see also the lecture notes [Reference Pigola and Setti39]), although here we propose a variation of those schemes in view of the (superlinear) character of the gradient term. The basic idea relies on multiplying the inequality by $e^{-u}$![]() , use the chain rule and take the integration of the resulting inequality through the divergence theorem.
, use the chain rule and take the integration of the resulting inequality through the divergence theorem.
To simplify the presentation, consider diffusions driven by the $p$![]() -Laplacian. First, assume by contradiction that $u$
-Laplacian. First, assume by contradiction that $u$![]() is not constant on the ball $B_{R_0}$
is not constant on the ball $B_{R_0}$![]() for some $R_0>1$
for some $R_0>1$![]() . We proceed by considering the vector field $X=e^{-u}(-|\nabla u|^{p-2}\nabla u)$
. We proceed by considering the vector field $X=e^{-u}(-|\nabla u|^{p-2}\nabla u)$![]() and integrating its divergence. As before, the argument can be made more rigorous arguing as in remark 2.6 or [Reference Pigola, Rigoli and Setti37] through a test function argument. On one hand, expanding the divergence, after plugging back the equation $-\Delta _p u\geq c_H|\nabla u|^\gamma$
and integrating its divergence. As before, the argument can be made more rigorous arguing as in remark 2.6 or [Reference Pigola, Rigoli and Setti37] through a test function argument. On one hand, expanding the divergence, after plugging back the equation $-\Delta _p u\geq c_H|\nabla u|^\gamma$![]() we deduce
we deduce

Applying the divergence theorem we get
so that we end up with the inequality
We then use the Hölder's inequality with the conjugate pairs $(\frac {\gamma }{p-1},\,\frac {\gamma }{\gamma -(p-1)})$![]() , together with $u\geq 0$
, together with $u\geq 0$![]() , to conclude
, to conclude

We set
Applying the co-area formula [Reference Evans and Gariepy20] we deduce
therefore concluding

We then integrate on $[R,\,r]$![]() and get
and get

Therefore

We then let $r\to \infty$![]() and conclude $\mu (R)=0$
and conclude $\mu (R)=0$![]() , which then contradicts our initial hypothesis, implying that $u$
, which then contradicts our initial hypothesis, implying that $u$![]() must be constant a.e. on $\mathbb {R}^N$
must be constant a.e. on $\mathbb {R}^N$![]() .
.
When $\gamma =\frac {N(p-1)}{N-1}$![]() we instead get the inequality
we instead get the inequality

which leads again to a contradiction. Note that such an approach involving a vector field weighted with an exponential term allows to recover most of the well-known properties for linear and nonlinear problems without perturbative eikonal terms. For instance, one can deduce that every nonnegative superharmonic function in $\mathbb {R}^2$![]() must be constant, or the Liouville property for nonnegative classical solutions to $-\mathrm {div}(\nabla u/\sqrt {1+|\nabla u|^2})\geq 0$
must be constant, or the Liouville property for nonnegative classical solutions to $-\mathrm {div}(\nabla u/\sqrt {1+|\nabla u|^2})\geq 0$![]() in $\mathbb {R}^2$
in $\mathbb {R}^2$![]() , or even that any solution to the inequality $-\Delta _p u\geq 0$
, or even that any solution to the inequality $-\Delta _p u\geq 0$![]() in $\mathbb {R}^N$
in $\mathbb {R}^N$![]() is constant provided $p\geq N$
is constant provided $p\geq N$![]() . This can be done using inequality (3.3) and keeping the term $\int _{B_r}e^{-u}|\nabla u|^p\,{\rm d}x$
. This can be done using inequality (3.3) and keeping the term $\int _{B_r}e^{-u}|\nabla u|^p\,{\rm d}x$![]() instead of $\int _{B_r}e^{-u}|\nabla u|^\gamma \,{\rm d}x$
instead of $\int _{B_r}e^{-u}|\nabla u|^\gamma \,{\rm d}x$![]() . Actually, this approach can be applied even to deduce the Liouville property for nonnegative $p$
. Actually, this approach can be applied even to deduce the Liouville property for nonnegative $p$![]() -superharmonic functions on general noncompact Riemannian manifolds under the area-growth condition
-superharmonic functions on general noncompact Riemannian manifolds under the area-growth condition

see [Reference Pigola and Setti39] for further details. We recall that such results have been deduced through other different methods: maximum principle methods have been exploited in [Reference Bardi and Cesaroni1, Reference Bardi and Goffi2, Reference Pigola, Rigoli and Setti38], capacity methods have been used in [Reference Hansson, Maz'ya and Verbitsky27], and, finally, probabilistic approaches, through the recurrence properties of the Brownian motion, have been thoroughly discussed in [Reference Grigor'yan25].
Remark 3.8 The same integral argument can be repeated to show that any distributional solution to
must be constant when $p-1<\gamma \leq \frac {N(p-1)}{N-1}$![]() . On the other hand, if $\gamma >\frac {N(p-1)}{N-1}$
. On the other hand, if $\gamma >\frac {N(p-1)}{N-1}$![]() there exist global non-constant solutions belonging to $W^{1,\gamma }_{\text {loc}}(\mathbb {R}^N)$
there exist global non-constant solutions belonging to $W^{1,\gamma }_{\text {loc}}(\mathbb {R}^N)$![]() . Indeed, when $\frac {N(p-1)}{N-1}<\gamma < p$
. Indeed, when $\frac {N(p-1)}{N-1}<\gamma < p$![]() the function $u(x)=-c|x|^{\frac {p-\gamma }{\gamma -(p-1)}}$
the function $u(x)=-c|x|^{\frac {p-\gamma }{\gamma -(p-1)}}$![]() for an appropriate $c>0$
for an appropriate $c>0$![]() belongs to $W^{1,r}_{\mathrm {loc}}(\mathbb {R}^N)$
belongs to $W^{1,r}_{\mathrm {loc}}(\mathbb {R}^N)$![]() for $r< N[\gamma -(p-1)]$
for $r< N[\gamma -(p-1)]$![]() and solves the previous equation in distributional sense. When $\gamma >p$
and solves the previous equation in distributional sense. When $\gamma >p$![]() it is sufficient to consider $u(x)=c|x|^{\frac {\gamma -p}{\gamma -(p-1)}}$
it is sufficient to consider $u(x)=c|x|^{\frac {\gamma -p}{\gamma -(p-1)}}$![]() for a suitable constant $c>0$
for a suitable constant $c>0$![]() . When $\gamma =p$
. When $\gamma =p$![]() , one can construct a counterexample through logarithmic-type functions. Hence, the results proved in [Reference Bidaut-Véron, Garcia-Huidobro and Véron7, theorem A] entail that such distributional solutions cannot be more regular (i.e. of class $C^1$
, one can construct a counterexample through logarithmic-type functions. Hence, the results proved in [Reference Bidaut-Véron, Garcia-Huidobro and Véron7, theorem A] entail that such distributional solutions cannot be more regular (i.e. of class $C^1$![]() ). Actually, such a Liouville theorem has been proved for less regular solutions (continuous, in the viscosity sense) in [Reference Birindelli, Demengel and Leoni9, theorem 3.1] for a wider class of fully nonlinear second order equations avoiding any differentiation of the PDE as a consequence of gradient bounds via viscosity solutions methods initiated in [Reference Capuzzo Dolcetta, Leoni and Porretta11]. Therefore, this integral argument shows once more that such distributional solutions cannot be more regular (neither continuous). Therefore, as remarked in § 3.2 for the uniqueness of solutions, the formulation of the problem is really important even for the range of the validity of the Liouville theorem.
). Actually, such a Liouville theorem has been proved for less regular solutions (continuous, in the viscosity sense) in [Reference Birindelli, Demengel and Leoni9, theorem 3.1] for a wider class of fully nonlinear second order equations avoiding any differentiation of the PDE as a consequence of gradient bounds via viscosity solutions methods initiated in [Reference Capuzzo Dolcetta, Leoni and Porretta11]. Therefore, this integral argument shows once more that such distributional solutions cannot be more regular (neither continuous). Therefore, as remarked in § 3.2 for the uniqueness of solutions, the formulation of the problem is really important even for the range of the validity of the Liouville theorem.
Remark 3.9 The Liouville results of the previous sections transfer to some non-divergent and fully nonlinear elliptic equations. For instance, if the leading operator in divergence form in (1.2) is replaced with the so-called minimal Pucci's operator defined as
then
and hence the Liouville property follows from theorem 1.3 under the same range for $\gamma$![]() . We expect a similar property would hold for supersolutions to equations driven by linear non-divergent operators assuming suitable asymptotic conditions at infinity on the diffusion coefficients. Still, one expects the Liouville property to hold even for the maximal operator $\mathcal {P}^+_{\lambda,\Lambda }$
. We expect a similar property would hold for supersolutions to equations driven by linear non-divergent operators assuming suitable asymptotic conditions at infinity on the diffusion coefficients. Still, one expects the Liouville property to hold even for the maximal operator $\mathcal {P}^+_{\lambda,\Lambda }$![]() (which is defined replacing the $\inf$
(which is defined replacing the $\inf$![]() with the $\sup$
with the $\sup$![]() over the same class of matrices) and thus to second order fully nonlinear uniformly elliptic operators, as partly analysed in [Reference Cirant and Goffi15]. These properties in the non-divergence setting will be the matter of a future research, since these integral methods do not apply to such class of PDIs.
over the same class of matrices) and thus to second order fully nonlinear uniformly elliptic operators, as partly analysed in [Reference Cirant and Goffi15]. These properties in the non-divergence setting will be the matter of a future research, since these integral methods do not apply to such class of PDIs.
Remark 3.10 The results related to the Liouville property in theorem 1.3 are sharp with respect to the parameter range $p-1<\gamma \leq \frac {N(p-1)}{N-1}$![]() , as shown in e.g. [Reference D'Ambrosio and Mitidieri19, Reference Filippucci21]. Indeed, the function $u(x)=V(|x|)=c(1+|x|^2)^{-\frac {p-\gamma }{2(\gamma -(p-1))}}$
, as shown in e.g. [Reference D'Ambrosio and Mitidieri19, Reference Filippucci21]. Indeed, the function $u(x)=V(|x|)=c(1+|x|^2)^{-\frac {p-\gamma }{2(\gamma -(p-1))}}$![]() for a suitable $c>0$
for a suitable $c>0$![]() is a bounded non-constant solution to the inequality
is a bounded non-constant solution to the inequality
when $\gamma >\frac {N(p-1)}{N-1}$![]() . To see this, set $\delta :=\frac {p-\gamma }{\gamma -(p-1)}$
. To see this, set $\delta :=\frac {p-\gamma }{\gamma -(p-1)}$![]() . One can use (3.1) to show that
. One can use (3.1) to show that

The last inequality can be made greater than or equal to
provided that $c>0$![]() is a suitable small constant and $\gamma >\frac {N(p-1)}{N-1}$
is a suitable small constant and $\gamma >\frac {N(p-1)}{N-1}$![]() .
.
4. Generalizations to problems arising in sub-Riemannian and Riemannian geometry
4.1 Problems modelled on Hörmander's vector fields
In this section we briefly discuss some possible generalizations to problems modelled on a frame of vector fields of $\mathbb {R}^N$![]() . Consider a family of smooth, say $C^\infty$
. Consider a family of smooth, say $C^\infty$![]() , vector fields $\mathcal {X}=\{X_1,\,\ldots,\,X_m\}$
, vector fields $\mathcal {X}=\{X_1,\,\ldots,\,X_m\}$![]() , $m\leq N$
, $m\leq N$![]() , generating a Carnot groups, and thus satisfying the Hörmander's rank condition. We define the horizontal gradient as $\nabla _\mathcal {X} u=(X_1u,\,\ldots,\,X_mu)$
, generating a Carnot groups, and thus satisfying the Hörmander's rank condition. We define the horizontal gradient as $\nabla _\mathcal {X} u=(X_1u,\,\ldots,\,X_mu)$![]() and the symmetrized horizontal Hessian $(D^2_\mathcal {X} u)_{ij}=\frac {X_iX_ju+X_jX_iu}{2}$
and the symmetrized horizontal Hessian $(D^2_\mathcal {X} u)_{ij}=\frac {X_iX_ju+X_jX_iu}{2}$![]() , while the horizontal divergence is defined as $\mathrm {div}_\mathcal {X}(\Phi (x))=\sum _{i=1}^mX_i^*\Phi _i$
, while the horizontal divergence is defined as $\mathrm {div}_\mathcal {X}(\Phi (x))=\sum _{i=1}^mX_i^*\Phi _i$![]() , $X_i^*$
, $X_i^*$![]() being the formal adjoints of the $X_i$
being the formal adjoints of the $X_i$![]() 's. We also denote by $B_r^\mathcal {X}(x)=\{y\in \mathbb {R}^N:\rho < R\}$
's. We also denote by $B_r^\mathcal {X}(x)=\{y\in \mathbb {R}^N:\rho < R\}$![]() , where $\rho$
, where $\rho$![]() stands for a given homogeneous norm. In this case, it holds
stands for a given homogeneous norm. In this case, it holds
$\mathcal {Q}$![]() being the corresponding homogeneous dimension. We denote by $W^{1,r}_{\mathcal {X},\mathrm {loc}}(\Omega )=\{u\in L^r_{\mathrm {loc}}(\Omega ):X_iu\in L^r_{\mathrm {loc}}(\Omega )\ ,\,i=1,\,..,\,m\}$
being the corresponding homogeneous dimension. We denote by $W^{1,r}_{\mathcal {X},\mathrm {loc}}(\Omega )=\{u\in L^r_{\mathrm {loc}}(\Omega ):X_iu\in L^r_{\mathrm {loc}}(\Omega )\ ,\,i=1,\,..,\,m\}$![]() the standard (local) horizontal Sobolev space.
the standard (local) horizontal Sobolev space.
Let $\Omega$![]() be a bounded open set in $\mathbb {R}^N$
be a bounded open set in $\mathbb {R}^N$![]() , $N\geq 1$
, $N\geq 1$![]() . We consider the following degenerate PDI
. We consider the following degenerate PDI
where $\mathcal {A}:\Omega \times \mathbb {R}\times \mathbb {R}^N\to \mathbb {R}^N$![]() is a Carathéodory function such that (A) holds and
is a Carathéodory function such that (A) holds and
We first give the horizontal counterpart of lemma 2.3 (a similar result holds for inequalities with zero-th order terms of the form $\lambda u$![]() ).
).
Lemma 4.1 Let $\gamma >p-1$![]() , $f\in \mathcal {L}^{1,\frac {\mathcal {Q}}{q}}(\Omega )$
, $f\in \mathcal {L}^{1,\frac {\mathcal {Q}}{q}}(\Omega )$![]() , $q\geq 1$
, $q\geq 1$![]() . Assume that (A) and (B3) hold. Let $u$
. Assume that (A) and (B3) hold. Let $u$![]() be a distributional solution of (4.2). Then, for every pair of concentric balls $B_t^\mathcal {X}\subset B_R^\mathcal {X}\subset \Omega$
be a distributional solution of (4.2). Then, for every pair of concentric balls $B_t^\mathcal {X}\subset B_R^\mathcal {X}\subset \Omega$![]() we have
we have

where $s=\max \left \{\frac {\mathcal {Q}}{q},\,\frac {\gamma }{\gamma -(p-1)}\right \}$![]() and $K$
and $K$![]() is a constant depending on $\nu,\,\gamma,\,q,\,\mathcal {Q},\,c_H$
is a constant depending on $\nu,\,\gamma,\,q,\,\mathcal {Q},\,c_H$![]() and on $\|f\|_{\mathcal {L}^{1,\frac {\mathcal {Q}}{q}}(B_R^\mathcal {X})}$
and on $\|f\|_{\mathcal {L}^{1,\frac {\mathcal {Q}}{q}}(B_R^\mathcal {X})}$![]() . In particular, the result holds when $f\in L^q,$
. In particular, the result holds when $f\in L^q,$![]() $q>\frac {\mathcal {Q}}{\gamma }$
$q>\frac {\mathcal {Q}}{\gamma }$![]() .
.
Proof. The proof is the same as that in lemma 2.3, the only difference being the choice of a $C^1$![]() cut-off function $\eta$
cut-off function $\eta$![]() such that $0\leq \eta \leq 1$
such that $0\leq \eta \leq 1$![]() , $\eta \equiv 1$
, $\eta \equiv 1$![]() on $B_t^\mathcal {X}$
on $B_t^\mathcal {X}$![]() , $\eta \equiv 0$
, $\eta \equiv 0$![]() outside $B_R^\mathcal {X}$
outside $B_R^\mathcal {X}$![]() , $|\nabla _\mathcal {X} \eta |\leq \frac {C}{R-t}$
, $|\nabla _\mathcal {X} \eta |\leq \frac {C}{R-t}$![]() .
.
As in the Euclidean case, this leads to the corresponding local Hölder continuity for distributional subsolutions combining lemma 4.1 and applying [Reference Lu32, theorem 1.2], as stated in the next.
Theorem 4.2 Assume (A) and (B3) , $\gamma >p$![]() , and let $f\in \mathcal {L}^{1,\frac {\mathcal {Q}}{q}}(\Omega )$
, and let $f\in \mathcal {L}^{1,\frac {\mathcal {Q}}{q}}(\Omega )$![]() for some $q>\frac {\mathcal {Q}}{\gamma }$
for some $q>\frac {\mathcal {Q}}{\gamma }$![]() . Let $u\in W^{1,\gamma }_{\mathrm {loc}}(\Omega )$
. Let $u\in W^{1,\gamma }_{\mathrm {loc}}(\Omega )$![]() which satisfies, in the sense of distributions, the inequality
which satisfies, in the sense of distributions, the inequality
Then $u$![]() is locally Hölder continuous with exponent
is locally Hölder continuous with exponent
and $K$![]() depends on $p,\,q,\,N,\,\nu,\,\Omega,\,\|f\|_{\mathcal {L}^{1,\frac {\mathcal {Q}}{q}}(\Omega )}$
depends on $p,\,q,\,N,\,\nu,\,\Omega,\,\|f\|_{\mathcal {L}^{1,\frac {\mathcal {Q}}{q}}(\Omega )}$![]() .
.
Remark 4.3 Similarly to what obtained in corollary 1.3, lemma 4.1 leads to a Liouville property for distributional supersolutions (or solutions) when $\mathcal {B}(\nabla _\mathcal {X} u)=|\nabla _\mathcal {X} u|^\gamma$![]() and
and
These properties have been studied in detail in e.g. [Reference D'Ambrosio and Mitidieri19].
4.2 Problems posed on Riemannian manifolds
We end this section with some extensions of the Liouville property for supersolutions in the context of noncompact geodesically complete Riemannian manifolds. In what follows, $M$![]() will be a smooth connected, noncompact, complete $N$
will be a smooth connected, noncompact, complete $N$![]() -dimensional Riemannian manifold, while for a fixed origin $o\in M$
-dimensional Riemannian manifold, while for a fixed origin $o\in M$![]() , we denote by $r(x)$
, we denote by $r(x)$![]() the distance function from $o$
the distance function from $o$![]() and, as above, with $B_r$
and, as above, with $B_r$![]() , $\partial B_r$
, $\partial B_r$![]() the geodesic ball and the sphere of radius $r>0$
the geodesic ball and the sphere of radius $r>0$![]() centred at $o$
centred at $o$![]() . We will assume that $\partial B_r$
. We will assume that $\partial B_r$![]() is smooth for any $r>0$
is smooth for any $r>0$![]() . As discussed in the introduction of [Reference Rigoli and Setti40] (see also [Reference Pigola, Rigoli and Setti37, theorem 1.1]) this is not much restrictive. Moreover, $\mathrm {Vol}(B_r)$
. As discussed in the introduction of [Reference Rigoli and Setti40] (see also [Reference Pigola, Rigoli and Setti37, theorem 1.1]) this is not much restrictive. Moreover, $\mathrm {Vol}(B_r)$![]() stands for the Riemannian measure of $B_r$
stands for the Riemannian measure of $B_r$![]() , while $\mathrm {area}(\partial B_r)$
, while $\mathrm {area}(\partial B_r)$![]() the induced measure of $\partial B_r$
the induced measure of $\partial B_r$![]() . The volume growth of the manifold stands for the growth rate of the function $r\longmapsto \mathrm {Vol}(B_r)$
. The volume growth of the manifold stands for the growth rate of the function $r\longmapsto \mathrm {Vol}(B_r)$![]() , whilst the area growth of the manifold for the growth rate of $r\longmapsto \mathrm {area}(\partial B_r)$
, whilst the area growth of the manifold for the growth rate of $r\longmapsto \mathrm {area}(\partial B_r)$![]() . We will denote by $d\mathrm {vol}_N$
. We will denote by $d\mathrm {vol}_N$![]() the canonical Riemannian measure, and by $d\mathrm {vol}_{N-1}$
the canonical Riemannian measure, and by $d\mathrm {vol}_{N-1}$![]() the corresponding $(N-1)$
the corresponding $(N-1)$![]() -Hausdorff measure.
-Hausdorff measure.
We will consider inequalities like
where the divergence and the gradient are taken with respect to the Riemannian structure under the same growth assumptions of the previous sections. More precisely, $\mathcal {A}: TM\times _\Omega (M\times \mathbb {R})\to TM$![]() satisfies (A), where $TM$
satisfies (A), where $TM$![]() is the tangent bundle of $M$
is the tangent bundle of $M$![]() and $TM\times _\Omega (M\times \mathbb {R})$
and $TM\times _\Omega (M\times \mathbb {R})$![]() stands for the fibred product bundle of $TM$
stands for the fibred product bundle of $TM$![]() and $M\times \mathbb {R}$
and $M\times \mathbb {R}$![]() with $\mathcal {A}(x,\,s,\,\xi )\in T_xM$
with $\mathcal {A}(x,\,s,\,\xi )\in T_xM$![]() for all $x\in M$
for all $x\in M$![]() , $s\in \mathbb {R}$
, $s\in \mathbb {R}$![]() and $\xi \in T_xM$
and $\xi \in T_xM$![]() . Similarly, $\mathcal {B}_2:TM\times _\Omega (M\times \mathbb {R})\to \mathbb {R}$
. Similarly, $\mathcal {B}_2:TM\times _\Omega (M\times \mathbb {R})\to \mathbb {R}$![]() satisfies (B2). As in the Euclidean case, points of $TM\times _\Omega (M\times \mathbb {R})$
satisfies (B2). As in the Euclidean case, points of $TM\times _\Omega (M\times \mathbb {R})$![]() are denoted with $(x,\,s,\,\xi )$
are denoted with $(x,\,s,\,\xi )$![]() , with $(x,\,\xi )\in TM$
, with $(x,\,\xi )\in TM$![]() and $(x,\,s)\in M\times \mathbb {R}$
and $(x,\,s)\in M\times \mathbb {R}$![]() .
.
It is well-known that the Liouville property for subharmonic functions bounded from above, namely the parabolicity of the manifold, is strictly related with its volume growth, and it holds under the condition
see [Reference Grigor'yan25, theorem 7.5]. Moreover, these properties are tied up with the recurrence properties of the corresponding Brownian motion on $M$![]() and the existence of Green functions, cf [Reference Grigor'yan25, theorem 5.1]. This in particular implies that $M=\mathbb {R}^2$
and the existence of Green functions, cf [Reference Grigor'yan25, theorem 5.1]. This in particular implies that $M=\mathbb {R}^2$![]() is parabolic, i.e. the one-side Liouville property for subharmonic functions bounded from above holds in the plane.
is parabolic, i.e. the one-side Liouville property for subharmonic functions bounded from above holds in the plane.
Still, it is known, as discussed in [Reference Grigor'yan25], that the condition
is sufficient to derive the one-side property, but it is not necessary. Finally, we emphasize that (4.3) always follows from (4.4) by [Reference Rigoli and Setti40, proposition 1.3], but the converse does not hold in general. Therefore, in the study of the next properties we focus on conditions involving $\mathrm {area}(\partial B_r)$![]() rather than those in terms of $\mathrm {Vol}(B_r)$
rather than those in terms of $\mathrm {Vol}(B_r)$![]() or on the optimal parameters for the exponents $\gamma,\,p$
or on the optimal parameters for the exponents $\gamma,\,p$![]() appearing in the equation (which is the case when $M=\mathbb {R}^N$
appearing in the equation (which is the case when $M=\mathbb {R}^N$![]() ).
).
The next result provides a nonlinear version of (4.3) for quasi-linear equations with power-growth nonlinearities of Hamilton–Jacobi type. To prove theorem 1.2 we state the following useful result, which generalises remark 2.5.
Lemma 4.4 Let $u$![]() be a nonconstant distributional solution to the inequality
be a nonconstant distributional solution to the inequality
Then, there exists $\overline {R}>0$![]() and a constant $C$
and a constant $C$![]() depending on $\nu,\,p,\,\gamma,\,N,\,c_H$
depending on $\nu,\,p,\,\gamma,\,N,\,c_H$![]() such that for every $r>R\geq \overline {R}$
such that for every $r>R\geq \overline {R}$![]() we have
we have

Proof. Let $X$![]() be the vector field $X:=\mathcal {A}(x,\,u,\,\nabla u)$
be the vector field $X:=\mathcal {A}(x,\,u,\,\nabla u)$![]() . The proof follows the same steps of remark 2.5 integrating $\mathrm {div}(X)$
. The proof follows the same steps of remark 2.5 integrating $\mathrm {div}(X)$![]() and using the (weak) divergence theorem together with the co-area formula, cf remark 2.6, but we omit this step for brevity. We thus have
and using the (weak) divergence theorem together with the co-area formula, cf remark 2.6, but we omit this step for brevity. We thus have

We set $\sigma (r)=\int _{B_r}|\nabla u|^\gamma \,{\rm d}x$![]() . Hence, by the co-area formula it follows that
. Hence, by the co-area formula it follows that
We then get
which reads equivalently as
We now integrate on $[R,\,r]$![]() and obtain that
and obtain that

Proof of theorem 1.2 If $u$![]() were not constant on the ball $B_{\widetilde {R}}$
were not constant on the ball $B_{\widetilde {R}}$![]() , one can apply lemma 4.4 and find the desired contradiction using (1.3).
, one can apply lemma 4.4 and find the desired contradiction using (1.3).
Remark 4.5 The previous result is slightly different from the one in corollary 1.3 and must be understood in the following sense: for $\gamma,\,p$![]() fixed, (1.3) highlights how the area of the geodesic sphere can grow to ensure the validity of the Liouville property on a generic manifold without assuming any curvature restriction. This is in line with the recent analyses carried out in [Reference Grigor'yan and Sun26, Reference Sun, Xiao and Xu43] and the earlier works [Reference Pigola, Rigoli and Setti37, Reference Rigoli and Setti40], where the Liouville properties have been studied in terms of the volume (and not the area) growth of the geodesic balls. We emphasize that in view of [Reference Rigoli and Setti40, proposition 1.3] one has for any $\delta >0$
fixed, (1.3) highlights how the area of the geodesic sphere can grow to ensure the validity of the Liouville property on a generic manifold without assuming any curvature restriction. This is in line with the recent analyses carried out in [Reference Grigor'yan and Sun26, Reference Sun, Xiao and Xu43] and the earlier works [Reference Pigola, Rigoli and Setti37, Reference Rigoli and Setti40], where the Liouville properties have been studied in terms of the volume (and not the area) growth of the geodesic balls. We emphasize that in view of [Reference Rigoli and Setti40, proposition 1.3] one has for any $\delta >0$![]()

but the converse is not true in general, unless some curvature conditions are imposed on the manifold, see [Reference Rigoli and Setti40].
Remark 4.6 The same area-growth condition could have been obtained through the scheme outlined in § 3.3.1 for nonnegative solutions.
Remark 4.7 Although this result has been widely analysed in the literature in various different settings, we emphasize that the Liouville property under these area-growth conditions seem new. Moreover, though the approach to derive the Liouville property is mainly inspired by [Reference Lions31, Reference Rigoli and Setti40], the results of theorem 1.2 cannot be inferred from these works.
Remark 4.8 The previous result gives a critical condition in terms of the area of the geodesic spheres for the solvability of the equation in $M$![]() , and can be seen as a generalization of the condition found in [Reference Hansson, Maz'ya and Verbitsky27] in the context of Riemannian manfiolds. It is worth noting that when $M=\mathbb {R}^N$
, and can be seen as a generalization of the condition found in [Reference Hansson, Maz'ya and Verbitsky27] in the context of Riemannian manfiolds. It is worth noting that when $M=\mathbb {R}^N$![]() condition (4.3) leads to the restriction $p-1<\gamma \leq \frac {N(p-1)}{N-1}$
condition (4.3) leads to the restriction $p-1<\gamma \leq \frac {N(p-1)}{N-1}$![]() found in § 3.3.
found in § 3.3.
Remark 4.9 It is worth remarking that corollary 1.3 leads to the Liouville property for nonnegative solutions to an inequality involving powers of the unknown functions and its gradient of the form
when
cf [Reference Filippucci, Pucci and Souplet22, remark 1.1] for the case $p=2$![]() . This can be done through the transformation $v=u^b$
. This can be done through the transformation $v=u^b$![]() for a suitable $b>0$
for a suitable $b>0$![]() , which reduces the previous inequality to an inequality like $-\Delta _pv\geq c_H|\nabla v|^\gamma$
, which reduces the previous inequality to an inequality like $-\Delta _pv\geq c_H|\nabla v|^\gamma$![]() for $\gamma <\frac {N(p-1)}{N-1}$
for $\gamma <\frac {N(p-1)}{N-1}$![]() for some suitable $c_H>0$
for some suitable $c_H>0$![]() depending on $p,\,\gamma,\,m$
depending on $p,\,\gamma,\,m$![]() , and thus allows to exploit corollary 1.3, see e.g. [Reference Bidaut-Véron, García-Huidobro and Véron8, Reference Cirant and Goffi15].
, and thus allows to exploit corollary 1.3, see e.g. [Reference Bidaut-Véron, García-Huidobro and Véron8, Reference Cirant and Goffi15].
Remark 4.10 As remarked in [Reference Rigoli and Setti40, p.489] or in [Reference Impera, Pigola and Setti28, theorem 4.6 and remark 4.8], using the same techniques of the present paper one can obtain similar results for supersolutions to elliptic problems equipped with Neumann boundary conditions posed on manifolds with boundary.
Acknowledgements
The author is member of the Gruppo Nazionale per l'Analisi Matematica, la Probabilità e le loro Applicazioni (GNAMPA) of the Istituto Nazionale di Alta Matematica (INdAM). The author has been partially supported by the INdAM-GNAMPA Project 2022 ‘Proprietà quantitative e qualitative per EDP non lineari con termini di gradiente’ and by the King Abdullah University of Science and Technology (KAUST) project CRG2021-4674 ‘Mean-Field Games: models, theory and computational aspects’.