No CrossRef data available.
Published online by Cambridge University Press: 03 July 2023
Let G be a group that is either virtually soluble or virtually free, and let ω be a weight on G. We prove that if G is infinite, then there is some maximal left ideal of finite codimension in the Beurling algebra 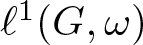 $\ell^1(G, \omega)$, which fails to be (algebraically) finitely generated. This implies that a conjecture of Dales and Żelazko holds for these Banach algebras. We then go on to give examples of weighted groups for which this property fails in a strong way. For instance, we describe a Beurling algebra on an infinite group in which every closed left ideal of finite codimension is finitely generated and which has many such ideals in the sense of being residually finite dimensional. These examples seem to be hard cases for proving Dales and Żelazko’s conjecture.
$\ell^1(G, \omega)$, which fails to be (algebraically) finitely generated. This implies that a conjecture of Dales and Żelazko holds for these Banach algebras. We then go on to give examples of weighted groups for which this property fails in a strong way. For instance, we describe a Beurling algebra on an infinite group in which every closed left ideal of finite codimension is finitely generated and which has many such ideals in the sense of being residually finite dimensional. These examples seem to be hard cases for proving Dales and Żelazko’s conjecture.