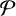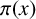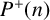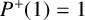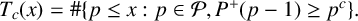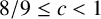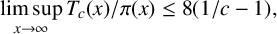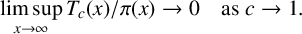1. Introduction
The investigation of shifted primes with large prime factors began in a brilliant article of Goldfeld [Reference Goldfeld12]. Historically, this topic had aroused great interest because of its unexpected connection with the first case of Fermat’s last theorem, thanks to the theorems of Fouvry [Reference Fouvry11] and Adleman and Heath-Brown [Reference Adleman and Heath-Brown1].
For any positive integer n, let
![]() $P^+(n)$
be the largest prime factor of n with the convention
$P^+(n)$
be the largest prime factor of n with the convention
![]() $P^+(1)=1$
. Let
$P^+(1)=1$
. Let
![]() $\mathcal {P}$
be the set of primes and
$\mathcal {P}$
be the set of primes and
![]() $\pi (x)$
the number of primes not exceeding x. For
$\pi (x)$
the number of primes not exceeding x. For
![]() $0<c<1$
, let
$0<c<1$
, let
![]() $T_c(x)=\#\{p\le x:p\in \mathcal {P},P^+(p-1)\ge p^c\}.$
As early as 1969, Goldfeld [Reference Goldfeld12] proved
$T_c(x)=\#\{p\le x:p\in \mathcal {P},P^+(p-1)\ge p^c\}.$
As early as 1969, Goldfeld [Reference Goldfeld12] proved
Goldfeld further remarked that his argument also leads to
provided that
![]() $c<{7}/{12}$
. It turns out that exploring large c which satisfy (1.1) is rather difficult and important. For improvements on the values of c, see Motohashi [Reference Motohashi21], Hooley [Reference Hooley15, Reference Hooley16], Deshouillers and Iwaniec [Reference Deshouillers, Iwaniec and Halász7], and Fouvry [Reference Fouvry11]. Up to now, the best numerical value of c satisfying (1.1), with a cost of replacing
$c<{7}/{12}$
. It turns out that exploring large c which satisfy (1.1) is rather difficult and important. For improvements on the values of c, see Motohashi [Reference Motohashi21], Hooley [Reference Hooley15, Reference Hooley16], Deshouillers and Iwaniec [Reference Deshouillers, Iwaniec and Halász7], and Fouvry [Reference Fouvry11]. Up to now, the best numerical value of c satisfying (1.1), with a cost of replacing
![]() $\pi (x)$
with
$\pi (x)$
with
![]() $\pi (x)/\log x$
, is 0.677, obtained by Baker and Harman [Reference Baker and Harman3].
$\pi (x)/\log x$
, is 0.677, obtained by Baker and Harman [Reference Baker and Harman3].
In an earlier note [Reference Ding8] on this topic, I showed that
holds for some absolute constant
![]() $c<1$
. As a corollary, I disproved a 2017 conjecture of Chen and Chen [Reference Chen and Chen6] that
$c<1$
. As a corollary, I disproved a 2017 conjecture of Chen and Chen [Reference Chen and Chen6] that
for any c with
![]() $1/2\le c<1$
. The proof in my earlier note is based on the following deep result which is a corollary of the Brun–Titchmarsh inequality.
$1/2\le c<1$
. The proof in my earlier note is based on the following deep result which is a corollary of the Brun–Titchmarsh inequality.
Proposition 1.1 [Reference Wu24, Lemma 2.2].
There exist two functions
![]() $K_2(\theta )>K_1(\theta )>0$
, defined on the interval
$K_2(\theta )>K_1(\theta )>0$
, defined on the interval
![]() $(0,17/32)$
such that for each fixed real
$(0,17/32)$
such that for each fixed real
![]() $A>0$
and all sufficiently large
$A>0$
and all sufficiently large
![]() $Q=x^\theta $
, the inequalities
$Q=x^\theta $
, the inequalities
 $$ \begin{align*}K_1(\theta)\frac{\pi(x)}{\varphi(m)}\le \pi(x;m,1)\le K_2(\theta)\frac{\pi(x)}{\varphi(m)}\end{align*} $$
$$ \begin{align*}K_1(\theta)\frac{\pi(x)}{\varphi(m)}\le \pi(x;m,1)\le K_2(\theta)\frac{\pi(x)}{\varphi(m)}\end{align*} $$
hold for all integers
![]() $m\in (Q,2Q]$
with at most
$m\in (Q,2Q]$
with at most
![]() $O(Q(\log Q)^{-A})$
exceptions, where the implied constant depends only on A and
$O(Q(\log Q)^{-A})$
exceptions, where the implied constant depends only on A and
![]() $\theta $
. Moreover, for any fixed
$\theta $
. Moreover, for any fixed
![]() $\varepsilon>0$
, these functions can be chosen to satisfy the following properties:
$\varepsilon>0$
, these functions can be chosen to satisfy the following properties:
-
•
 $K_1(\theta )$
is monotonic decreasing and
$K_1(\theta )$
is monotonic decreasing and
 $K_2(\theta )$
is monotonic increasing;
$K_2(\theta )$
is monotonic increasing; -
•
 $K_1(1/2)=1-\varepsilon $
and
$K_1(1/2)=1-\varepsilon $
and
 $K_2(1/2)=1+\varepsilon $
.
$K_2(1/2)=1+\varepsilon $
.
The constant c in (1.2) is not specified because of the indeterminate nature of
![]() $K_1(\theta )$
in Proposition 1.1. In fact,
$K_1(\theta )$
in Proposition 1.1. In fact,
![]() $K_1(\theta )$
(and hence c) can be explicitly given if one checks carefully the articles of Baker and Harman [Reference Baker, Harman, Berndt, Diamond and Hildebrand2] for
$K_1(\theta )$
(and hence c) can be explicitly given if one checks carefully the articles of Baker and Harman [Reference Baker, Harman, Berndt, Diamond and Hildebrand2] for
![]() $1/2\le \theta \le 13/25$
, and Mikawa [Reference Mikawa19] for
$1/2\le \theta \le 13/25$
, and Mikawa [Reference Mikawa19] for
![]() $13/25\le \theta \le 17/32$
. This gives
$13/25\le \theta \le 17/32$
. This gives
![]() $K_1(\theta )\ge 0.16$
for
$K_1(\theta )\ge 0.16$
for
![]() $1/2\le \theta \le 13/25$
[Reference Baker, Harman, Berndt, Diamond and Hildebrand2, Theorem 1] and
$1/2\le \theta \le 13/25$
[Reference Baker, Harman, Berndt, Diamond and Hildebrand2, Theorem 1] and
![]() $K_1(\theta )\ge 1/100$
for Mikawa’s range [Reference Mikawa19, (4)]. However, it seems that the constant c in (1.2) obtained in this way will be very close to
$K_1(\theta )\ge 1/100$
for Mikawa’s range [Reference Mikawa19, (4)]. However, it seems that the constant c in (1.2) obtained in this way will be very close to
![]() $1$
(see the proofs in [Reference Ding8]).
$1$
(see the proofs in [Reference Ding8]).
In [Reference Ding8], I also pointed out that Chen and Chen’s conjecture is already in contradiction with the Elliott–Halberstam conjecture (from Pomerance [Reference Pomerance22], Granville [Reference Granville, Buhler and Stevenhagen13], Wang [Reference Wang23] and Wu [Reference Wu24]). In fact,
under the assumption of the Elliott–Halberstam conjecture, where
![]() $\rho (u)$
is the Dickman function, defined as the unique continuous solution of the differential-difference equation
$\rho (u)$
is the Dickman function, defined as the unique continuous solution of the differential-difference equation
 $$ \begin{align*} \begin{cases} \rho(u)=1 & \mbox{for }0\le u\le 1, \\ u\rho'(u)=-\rho(u-1) & \mbox{for }u>1. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \rho(u)=1 & \mbox{for }0\le u\le 1, \\ u\rho'(u)=-\rho(u-1) & \mbox{for }u>1. \end{cases} \end{align*} $$
However, there are earlier results related to the conjecture of Chen and Chen, and my earlier result (1.2). In fact, as indicated by the proof of a result of Erdős [Reference Erdős9, Lemma 4], as early as 1935, one could already conclude from Erdős’ proof combined with Lemma 2.2 of Wu (see below) that (1.3) is true in part.
Theorem 1.2 (Erdős).
Unconditionally,
Essentially, Theorem 1.2 can be deduced from Erdős’ proof by adding Wu’s lemma (see Erdős’ argument in [Reference Erdős9, from page 212, line 6 to page 213, line 4]). Since Erdős’ conclusion is not clearly formulated, it is meaningful to restate it explicitly as Theorem 1.2. It is also of interest to pursue Erdős’ theorem a little further to reach the following quantitative form.
Theorem 1.3. For
![]() $8/9\le c<1$
,
$8/9\le c<1$
,
We note that the restriction on
![]() $c\ge 8/9$
in our theorem is natural since otherwise, the upper bound would exceed
$c\ge 8/9$
in our theorem is natural since otherwise, the upper bound would exceed
![]() $1$
which is certainly meaningless. Theorem 1.3 can also be compared with the results of Goldfeld [Reference Goldfeld12], Luca et al. [Reference Luca, Menares and Pizarro-Madariaga18], and Chen and Chen [Reference Chen and Chen6] which state that
$1$
which is certainly meaningless. Theorem 1.3 can also be compared with the results of Goldfeld [Reference Goldfeld12], Luca et al. [Reference Luca, Menares and Pizarro-Madariaga18], and Chen and Chen [Reference Chen and Chen6] which state that
for
![]() $0<c\le 1/2$
. These bounds were recently improved in part by Feng and Wu [Reference Feng and Wu10], and Liu, Wu and Xi [Reference Liu, Wu and Xi17]. From Theorem 1.3, we clearly have two corollaries, one of which is Erdős’ theorem (Theorem 1.2) while the other revisits the main result (1.2) of my earlier note in a quantitative form.
$0<c\le 1/2$
. These bounds were recently improved in part by Feng and Wu [Reference Feng and Wu10], and Liu, Wu and Xi [Reference Liu, Wu and Xi17]. From Theorem 1.3, we clearly have two corollaries, one of which is Erdős’ theorem (Theorem 1.2) while the other revisits the main result (1.2) of my earlier note in a quantitative form.
Corollary 1.4. For
![]() $c>16/17$
,
$c>16/17$
,
2. Proofs
From now on, p will always be a prime. The proof of Theorem 1.3 is based on the following lemma deduced from the sieve method (see, for example, [Reference Halberstam and Richert14, Theorem 5.7, page 172]).
Lemma 2.1. Let g be a natural number and let
![]() $a_i,b_i~(i=1,2,\ldots ,g)$
be integers satisfying
$a_i,b_i~(i=1,2,\ldots ,g)$
be integers satisfying
 $$ \begin{align*} E:=\prod_{i=1}^{g}a_i\prod_{1\le r<s\le g}(a_rb_s-a_sb_r)\neq0. \end{align*} $$
$$ \begin{align*} E:=\prod_{i=1}^{g}a_i\prod_{1\le r<s\le g}(a_rb_s-a_sb_r)\neq0. \end{align*} $$
Let
![]() $\rho (p)$
denote the number of solutions in n modulo p of
$\rho (p)$
denote the number of solutions in n modulo p of
 $$ \begin{align*} \prod_{i=1}^{g}(a_in+b_i)\equiv 0{\ (\mathrm{mod}\ p)}, \end{align*} $$
$$ \begin{align*} \prod_{i=1}^{g}(a_in+b_i)\equiv 0{\ (\mathrm{mod}\ p)}, \end{align*} $$
and suppose that
If the real numbers y and z satisfy
![]() $1<y\le z,$
then
$1<y\le z,$
then
 $$ \begin{align*} &\hspace{-13pt}|\{n:z-y<n\le z, a_in+b_i \text{ prime for } i=1,2,\ldots,g\}|\\ &\le 2^gg!\prod_{p}\bigg(1-\frac{\rho(p)-1}{p-1}\bigg)\bigg(1-\frac{1}{p}\bigg)^{-g+1}\frac{y}{\log ^gy} \bigg(1+O\bigg(\frac{\log\log3y+\log\log 3|E|}{\log y}\bigg)\bigg), \end{align*} $$
$$ \begin{align*} &\hspace{-13pt}|\{n:z-y<n\le z, a_in+b_i \text{ prime for } i=1,2,\ldots,g\}|\\ &\le 2^gg!\prod_{p}\bigg(1-\frac{\rho(p)-1}{p-1}\bigg)\bigg(1-\frac{1}{p}\bigg)^{-g+1}\frac{y}{\log ^gy} \bigg(1+O\bigg(\frac{\log\log3y+\log\log 3|E|}{\log y}\bigg)\bigg), \end{align*} $$
where the constant implied by the O-symbol depends at most on g.
We also need the following important relation established by Wu [Reference Wu24, Theorem 2].
Lemma 2.2. For
![]() $0<c<1$
, let
$0<c<1$
, let
Then for sufficiently large x,
 $$ \begin{align*} T_c(x)=T^{\prime}_c(x)+O\bigg(\frac{x\log\log x}{(\log x)^2}\bigg). \end{align*} $$
$$ \begin{align*} T_c(x)=T^{\prime}_c(x)+O\bigg(\frac{x\log\log x}{(\log x)^2}\bigg). \end{align*} $$
We now turn to the proof of Theorem 1.3.
Proof of Theorem 1.3.
Let x be a sufficiently large number throughout the proof. Instead of investigating
![]() $T_c(x)$
, we first deal with
$T_c(x)$
, we first deal with
![]() $T^{\prime }_c(x)$
. For
$T^{\prime }_c(x)$
. For
![]() $1/2\le c<1$
, it is easy to see that
$1/2\le c<1$
, it is easy to see that
 $$ \begin{align} T^{\prime}_c(x)= \sum_{\substack{x^c\le q<x\\ q\in \mathcal{P}}}\sum_{\substack{p\le x\\q|p-1}}1. \end{align} $$
$$ \begin{align} T^{\prime}_c(x)= \sum_{\substack{x^c\le q<x\\ q\in \mathcal{P}}}\sum_{\substack{p\le x\\q|p-1}}1. \end{align} $$
On putting
![]() $p-1=qh$
in the sum (2.1) and then exchanging the order of summation,
$p-1=qh$
in the sum (2.1) and then exchanging the order of summation,
 $$ \begin{align} T^{\prime}_c(x)=\sum_{\substack{x^c\le q<x \\ q\in \mathcal{P}}}\sum_{\substack{h< x/q\\qh+1\in \mathcal{P}}}1\le \sum_{\substack{h<x^{1-c}\\ 2|h}}\sum_{\substack{2<q<x/h \\ q,qh+1\in \mathcal{P}}}1. \end{align} $$
$$ \begin{align} T^{\prime}_c(x)=\sum_{\substack{x^c\le q<x \\ q\in \mathcal{P}}}\sum_{\substack{h< x/q\\qh+1\in \mathcal{P}}}1\le \sum_{\substack{h<x^{1-c}\\ 2|h}}\sum_{\substack{2<q<x/h \\ q,qh+1\in \mathcal{P}}}1. \end{align} $$
For any h with
![]() $2 \mid h$
and
$2 \mid h$
and
![]() $h<x^{1-c}$
, let
$h<x^{1-c}$
, let
![]() $\rho (p)$
denote the number of solutions of
$\rho (p)$
denote the number of solutions of
Then
 $$ \begin{align*} \rho(p)= \begin{cases} 1 & \text{if } p \mid h, \\ 2 & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} \rho(p)= \begin{cases} 1 & \text{if } p \mid h, \\ 2 & \text{otherwise.} \end{cases} \end{align*} $$
Now, by Lemma 2.1 with
![]() $g=2, a_1=1, b_1=0, a_2=h,b_2=1$
and
$g=2, a_1=1, b_1=0, a_2=h,b_2=1$
and
![]() $z=y=x/h$
,
$z=y=x/h$
,
from which it follows that
 $$ \begin{align} \sum_{\substack{2<q<x/h \\ q,qh+1\in \mathcal{P}}}1\le 16\mathfrak{S}\prod_{\substack{p|h\\ p>2}}\bigg(1+\frac{1}{p-2}\bigg) \frac{x/h}{\log^2(x/h)} \bigg(1+O\bigg(\frac{\log\log x}{\log x}\bigg)\bigg), \end{align} $$
$$ \begin{align} \sum_{\substack{2<q<x/h \\ q,qh+1\in \mathcal{P}}}1\le 16\mathfrak{S}\prod_{\substack{p|h\\ p>2}}\bigg(1+\frac{1}{p-2}\bigg) \frac{x/h}{\log^2(x/h)} \bigg(1+O\bigg(\frac{\log\log x}{\log x}\bigg)\bigg), \end{align} $$
where an empty product for
![]() $\prod _{p|h, p>2}$
above denotes
$\prod _{p|h, p>2}$
above denotes
![]() $1$
as usual and
$1$
as usual and
 $$ \begin{align*} \mathfrak{S}=\prod_{p>2}\bigg(1-\frac{1}{p-1}\bigg)\bigg(1-\frac{1}{p}\bigg)^{-1}= \prod_{p>2}\bigg(1-\frac{1}{(p-1)^2}\bigg). \end{align*} $$
$$ \begin{align*} \mathfrak{S}=\prod_{p>2}\bigg(1-\frac{1}{p-1}\bigg)\bigg(1-\frac{1}{p}\bigg)^{-1}= \prod_{p>2}\bigg(1-\frac{1}{(p-1)^2}\bigg). \end{align*} $$
Inserting (2.3) into (2.2) gives
 $$ \begin{align} T^{\prime}_c(x)&\le (1+o(1))16\mathfrak{S}\sum_{\substack{h<x^{1-c}\\ 2|h}}\prod_{\substack{p|h\\ p>2}}\bigg(1+\frac{1}{p-2}\bigg) \frac{x/h}{\log^2(x/h)}. \end{align} $$
$$ \begin{align} T^{\prime}_c(x)&\le (1+o(1))16\mathfrak{S}\sum_{\substack{h<x^{1-c}\\ 2|h}}\prod_{\substack{p|h\\ p>2}}\bigg(1+\frac{1}{p-2}\bigg) \frac{x/h}{\log^2(x/h)}. \end{align} $$
Note that
 $$ \begin{align} \prod_{\substack{p|h\\ p>2}}\bigg(1+\frac{1}{p-2}\bigg)\le 2\prod_{\substack{p|h\\ p>2}}\bigg(1+\frac{1}{p}\bigg) \end{align} $$
$$ \begin{align} \prod_{\substack{p|h\\ p>2}}\bigg(1+\frac{1}{p-2}\bigg)\le 2\prod_{\substack{p|h\\ p>2}}\bigg(1+\frac{1}{p}\bigg) \end{align} $$
since the gaps between odd primes are at least
![]() $2$
, from which we can already give a nontrivial upper bound of
$2$
, from which we can already give a nontrivial upper bound of
![]() $T^{\prime }_c(x)$
via partial summations. To make our bound more explicit than (2.5), we employ a nice result of Banks and Shparlinski [Reference Banks and Shparlinski4, Lemma 2.3] (on taking
$T^{\prime }_c(x)$
via partial summations. To make our bound more explicit than (2.5), we employ a nice result of Banks and Shparlinski [Reference Banks and Shparlinski4, Lemma 2.3] (on taking
![]() $a=1$
therein), which states that for
$a=1$
therein), which states that for
![]() $z\ge 2$
,
$z\ge 2$
,
 $$ \begin{align} S(z):=\sum_{\substack{h<z\\ 2|h}}\frac{1}{h}\prod_{\substack{p|h\\ p>2}}\bigg(1+\frac{1}{p-2}\bigg)=\frac{1+o(1)}{2\mathfrak{S}}\log z. \end{align} $$
$$ \begin{align} S(z):=\sum_{\substack{h<z\\ 2|h}}\frac{1}{h}\prod_{\substack{p|h\\ p>2}}\bigg(1+\frac{1}{p-2}\bigg)=\frac{1+o(1)}{2\mathfrak{S}}\log z. \end{align} $$
For
![]() $1\le z<2$
, we set
$1\le z<2$
, we set
![]() $S(z)=0$
. By partial summation,
$S(z)=0$
. By partial summation,
 $$ \begin{align} \sum_{\substack{h<x^{1-c}\\ 2|h}}\prod_{\substack{p|h\\ p>2}}\bigg(1+\frac{1}{p}\bigg)\frac{1/h}{\log^2(x/h)}=\frac{S(x^{1-c})}{(\log x^c)^2}-\int_{1}^{x^{1-c}}S(z)\,d\bigg(\log \frac{x}{z}\bigg)^{-2}. \end{align} $$
$$ \begin{align} \sum_{\substack{h<x^{1-c}\\ 2|h}}\prod_{\substack{p|h\\ p>2}}\bigg(1+\frac{1}{p}\bigg)\frac{1/h}{\log^2(x/h)}=\frac{S(x^{1-c})}{(\log x^c)^2}-\int_{1}^{x^{1-c}}S(z)\,d\bigg(\log \frac{x}{z}\bigg)^{-2}. \end{align} $$
Note also that for
![]() $z\ge 2$
,
$z\ge 2$
,
 $$ \begin{align*} S(z)\le \sum_{\substack{h<z}}\frac{1}{h}\prod_{\substack{p|h\\ p>2}}\bigg(1+\frac{1}{p-2}\bigg)\le \sum_{\substack{h<z}}\frac{1}{h}\prod_{\substack{p|h}}\bigg(1+\frac{3}{p}\bigg)=\sum_{\substack{h<z}}\frac{1}{h}\sum_{d|h} \frac{3^{\omega(d)}\mu^2(d)}{d}, \end{align*} $$
$$ \begin{align*} S(z)\le \sum_{\substack{h<z}}\frac{1}{h}\prod_{\substack{p|h\\ p>2}}\bigg(1+\frac{1}{p-2}\bigg)\le \sum_{\substack{h<z}}\frac{1}{h}\prod_{\substack{p|h}}\bigg(1+\frac{3}{p}\bigg)=\sum_{\substack{h<z}}\frac{1}{h}\sum_{d|h} \frac{3^{\omega(d)}\mu^2(d)}{d}, \end{align*} $$
where
![]() $\mu (d)$
is the Möbius function and
$\mu (d)$
is the Möbius function and
![]() $\omega (d)$
is the number of distinct prime factors of d. Exchanging the order of summation,
$\omega (d)$
is the number of distinct prime factors of d. Exchanging the order of summation,
 $$ \begin{align} S(z)\le \sum_{d<z}\frac{3^{\omega(d)}\mu^2(d)}{d}\sum_{\substack{h<z\\ d|h}}\frac{1}{h}\le 3\sum_{d<z}\frac{3^{\omega(d)}\mu^2(d)}{d^2}\log z<3K\log z, \end{align} $$
$$ \begin{align} S(z)\le \sum_{d<z}\frac{3^{\omega(d)}\mu^2(d)}{d}\sum_{\substack{h<z\\ d|h}}\frac{1}{h}\le 3\sum_{d<z}\frac{3^{\omega(d)}\mu^2(d)}{d^2}\log z<3K\log z, \end{align} $$
where
 $$ \begin{align*} K=3\sum_{d=1}^{\infty}\frac{3^{\omega(d)}\mu^2(d)}{d^2}. \end{align*} $$
$$ \begin{align*} K=3\sum_{d=1}^{\infty}\frac{3^{\omega(d)}\mu^2(d)}{d^2}. \end{align*} $$
From (2.8),
 $$ \begin{align} \int_{1}^{\log x}S(z)\,d\bigg(\log \frac{x}{z}\bigg)^{-2}\ll_K \frac{\log\log x}{(\log x)^2}=o((\log x)^{-1}). \end{align} $$
$$ \begin{align} \int_{1}^{\log x}S(z)\,d\bigg(\log \frac{x}{z}\bigg)^{-2}\ll_K \frac{\log\log x}{(\log x)^2}=o((\log x)^{-1}). \end{align} $$
Now, routine computations yield
 $$ \begin{align} \frac{S(x^{1-c})}{(\log x^c)^2}=\frac{1+o(1)}{\mathfrak{S}}\frac{(1-c)}{2c^2}(\log x)^{-1} \end{align} $$
$$ \begin{align} \frac{S(x^{1-c})}{(\log x^c)^2}=\frac{1+o(1)}{\mathfrak{S}}\frac{(1-c)}{2c^2}(\log x)^{-1} \end{align} $$
and
 $$ \begin{align} \int_{\log x}^{x^{1-c}}S(z)\,d\bigg(\log \frac{x}{z}\bigg)^{-2}&=\frac{1+o(1)}{\mathfrak{S}}\int_{\log x}^{x^{1-c}}\frac{\log z}{z}\bigg(\log \frac{x}{z}\bigg)^{-3}\,dz\nonumber\\ &= \frac{1+o(1)}{\mathfrak{S}}\int_{1}^{x^{1-c}}\frac{\log z}{z}\bigg(\log \frac{x}{z}\bigg)^{-3}\,dz+o((\log x)^{-1})\nonumber\\ &=\frac{1+o(1)}{\mathfrak{S}}\int_{x^c}^{x}\frac{\log x-\log u}{u}(\log u)^{-3}\,du+o((\log x)^{-1})\nonumber\\ &=\frac{1+o(1)}{\mathfrak{S}}\bigg(\frac{1-c}{2c^2}+\frac{1}{2}-\frac{1}{2c}\bigg)(\log x)^{-1}, \end{align} $$
$$ \begin{align} \int_{\log x}^{x^{1-c}}S(z)\,d\bigg(\log \frac{x}{z}\bigg)^{-2}&=\frac{1+o(1)}{\mathfrak{S}}\int_{\log x}^{x^{1-c}}\frac{\log z}{z}\bigg(\log \frac{x}{z}\bigg)^{-3}\,dz\nonumber\\ &= \frac{1+o(1)}{\mathfrak{S}}\int_{1}^{x^{1-c}}\frac{\log z}{z}\bigg(\log \frac{x}{z}\bigg)^{-3}\,dz+o((\log x)^{-1})\nonumber\\ &=\frac{1+o(1)}{\mathfrak{S}}\int_{x^c}^{x}\frac{\log x-\log u}{u}(\log u)^{-3}\,du+o((\log x)^{-1})\nonumber\\ &=\frac{1+o(1)}{\mathfrak{S}}\bigg(\frac{1-c}{2c^2}+\frac{1}{2}-\frac{1}{2c}\bigg)(\log x)^{-1}, \end{align} $$
thanks to the estimate (2.6). Combining (2.9), (2.10) and (2.11), one sees that the right-hand side of (2.7) equals
Taking (2.12) into (2.4), we immediately obtain
 $$ \begin{align*} T^{\prime}_c(x)&\le (1+o(1))8\bigg(\frac{1}{c}-1\bigg)\frac{x}{\log x}. \end{align*} $$
$$ \begin{align*} T^{\prime}_c(x)&\le (1+o(1))8\bigg(\frac{1}{c}-1\bigg)\frac{x}{\log x}. \end{align*} $$
Therefore, by Lemma 2.2,
 $$ \begin{align*} T_c(x)=T^{\prime}_c(x)+O\bigg(\frac{x\log\log x}{(\log x)^2}\bigg)\le (1+o(1))8\bigg(\frac{1}{c}-1\bigg)\frac{x}{\log x}. \end{align*} $$
$$ \begin{align*} T_c(x)=T^{\prime}_c(x)+O\bigg(\frac{x\log\log x}{(\log x)^2}\bigg)\le (1+o(1))8\bigg(\frac{1}{c}-1\bigg)\frac{x}{\log x}. \end{align*} $$
Our theorem now follows from the prime number theorem.
3. Remarks
Under the assumption of the Elliott–Halberstam conjecture, it is reasonable to predict that the exact value of c in Corollary 1.4 should be
![]() $e^{-1/2}=0.60653\ldots $
from (1.3) and the recursion formula (see, for example, [Reference Montgomery and Vaughan20, (7.6)]) for Dickman’s function:
$e^{-1/2}=0.60653\ldots $
from (1.3) and the recursion formula (see, for example, [Reference Montgomery and Vaughan20, (7.6)]) for Dickman’s function:
 $$ \begin{align*} \rho(v)=u-\int_{u}^{v}\frac{\rho(t-1)}{t}\,dt \quad (1\le u\le v). \end{align*} $$
$$ \begin{align*} \rho(v)=u-\int_{u}^{v}\frac{\rho(t-1)}{t}\,dt \quad (1\le u\le v). \end{align*} $$
It therefore seems to be of interest to improve, as far as possible, the numerical value of c in Corollary 1.4. We leave this as a challenge to readers.
Though we provided nontrivial upper bounds on
![]() $T_c(x)$
for
$T_c(x)$
for
![]() $8/9\le c<1$
in Theorem 1.3, the extension of these bounds to
$8/9\le c<1$
in Theorem 1.3, the extension of these bounds to
![]() $1/2\le c<1$
is an unsolved problem.
$1/2\le c<1$
is an unsolved problem.
Acknowledgments
The author would like to thank the anonymous referees for their very helpful comments. He is really grateful to the one who pointed out the facts involving Erdős’ article. Shortly after the manuscript of this note was put on the arXiv, Brad Rodgers informed the author that, joint with Bharadwaj, they independently obtained the same result of Theorem 1.2 with a general form in the probabilistic language (see [Reference Bharadwaj and Rodgers5, Theorem 8 and Corollary 9]). (At that time, all of us were unaware of Erdős’ article.)