1 Introduction
The growth rate of a continuous dynamical system
![]() $f:X \to X$
, where X is a compact topological space, is the exponential of the topological entropy of f,
$f:X \to X$
, where X is a compact topological space, is the exponential of the topological entropy of f,
![]() $e^{h_{\mathrm {top}}(f)}$
. When such a dynamical system admits a Markov partition—as is the case for continuous, multimodal, postcritically finite, self-maps of intervals, or pseudo-Anosov surface diffeomorphisms—a consequence of the Perron–Frobenius theorem is that the growth rate must be a weak Perron number, that is, a real, positive algebraic integer that is not less than the absolute value of any of its Galois conjugates. In [Reference Thurston, Bonifant, Lyubich and SutherlandThu14], Thurston proved that every weak Perron number arises as the growth rate of some continuous, multimodal, postcritically finite, self-maps of intervals. (The analogous question for pseudo-Anosov surface diffeomorphisms remains open.) By considering the set of all interval maps of any modality and any postcritical orbit portrait, Thurston stabilized the question; the question of characterizing the set of growth rates of all postcritically finite interval maps of any fixed modality
$e^{h_{\mathrm {top}}(f)}$
. When such a dynamical system admits a Markov partition—as is the case for continuous, multimodal, postcritically finite, self-maps of intervals, or pseudo-Anosov surface diffeomorphisms—a consequence of the Perron–Frobenius theorem is that the growth rate must be a weak Perron number, that is, a real, positive algebraic integer that is not less than the absolute value of any of its Galois conjugates. In [Reference Thurston, Bonifant, Lyubich and SutherlandThu14], Thurston proved that every weak Perron number arises as the growth rate of some continuous, multimodal, postcritically finite, self-maps of intervals. (The analogous question for pseudo-Anosov surface diffeomorphisms remains open.) By considering the set of all interval maps of any modality and any postcritical orbit portrait, Thurston stabilized the question; the question of characterizing the set of growth rates of all postcritically finite interval maps of any fixed modality
![]() $d \geq 2$
is more subtle, and remains open. This work investigates growth rates of the family of all continuous, unimodal, critically periodic interval self-maps, which we denote
$d \geq 2$
is more subtle, and remains open. This work investigates growth rates of the family of all continuous, unimodal, critically periodic interval self-maps, which we denote
![]() $\mathcal {F}^{cp}_2$
.
$\mathcal {F}^{cp}_2$
.
Since the growth rates of maps in
![]() $\mathcal {F}^{cp}_2$
are known to satisfy a condition involving their Galois conjugates (namely, they are weak Perron numbers), it is natural to consider, for any
$\mathcal {F}^{cp}_2$
are known to satisfy a condition involving their Galois conjugates (namely, they are weak Perron numbers), it is natural to consider, for any
![]() $f \in \mathcal {F}^{cp}_2$
, the set
$f \in \mathcal {F}^{cp}_2$
, the set
![]() $\{z \in \mathbb {C} : z \textrm { is a Galois conjugate of the growth rate, } e^{h_{\mathrm {top}}(f)} \textrm {, of } f\}$
. Another, related reason to consider the set of Galois conjugates of
$\{z \in \mathbb {C} : z \textrm { is a Galois conjugate of the growth rate, } e^{h_{\mathrm {top}}(f)} \textrm {, of } f\}$
. Another, related reason to consider the set of Galois conjugates of
![]() $e^{h_{\mathrm {top}}(f)}$
is that the Galois conjugates can be used to construct a ‘lift’ of this real, one-dimensional dynamical system defined by f to a dynamical system defined on
$e^{h_{\mathrm {top}}(f)}$
is that the Galois conjugates can be used to construct a ‘lift’ of this real, one-dimensional dynamical system defined by f to a dynamical system defined on
![]() $\mathbb {C}^s\times \mathbb {R}^d$
, where r is the number of real Galois conjugates of
$\mathbb {C}^s\times \mathbb {R}^d$
, where r is the number of real Galois conjugates of
![]() $e^{h_{\mathrm {top}}(f)}$
and s is the number of non-real complex-conjugate pairs of Galois conjugates (see, e.g., Theorem 2.1 of [Reference Thurston, Bonifant, Lyubich and SutherlandThu14]). The Master Teapot for the family
$e^{h_{\mathrm {top}}(f)}$
and s is the number of non-real complex-conjugate pairs of Galois conjugates (see, e.g., Theorem 2.1 of [Reference Thurston, Bonifant, Lyubich and SutherlandThu14]). The Master Teapot for the family
![]() $\mathcal {F}^{cp}_2$
is the set
$\mathcal {F}^{cp}_2$
is the set
Thurston coined the term ‘Master Teapot’ because plots of finite approximations of this set resemble a teapot, with a roughly cylindrical body over the unit circle, a ‘spout’ consisting of points of the form
![]() $\{\unicode{x3bb} ,\unicode{x3bb} \}$
, and a ‘handle’ protruding from the body opposite the spout. (See Figure 1.) Clearly, the geometry and topology of this set encode information about which growth rates are realized by maps in the family
$\{\unicode{x3bb} ,\unicode{x3bb} \}$
, and a ‘handle’ protruding from the body opposite the spout. (See Figure 1.) Clearly, the geometry and topology of this set encode information about which growth rates are realized by maps in the family
![]() $\mathcal {F}^{cp}_2$
. While the geometry of the Master Teapot retains information about which growth rate
$\mathcal {F}^{cp}_2$
. While the geometry of the Master Teapot retains information about which growth rate
![]() $\unicode{x3bb} $
corresponds to which Galois conjugate z, it is also interesting to consider the subset of
$\unicode{x3bb} $
corresponds to which Galois conjugate z, it is also interesting to consider the subset of
![]() $\mathbb {C}$
formed by plotting all the Galois conjugates (including the growth rate
$\mathbb {C}$
formed by plotting all the Galois conjugates (including the growth rate
![]() $\unicode{x3bb} $
) of all maps in
$\unicode{x3bb} $
) of all maps in
![]() $\mathcal {F}^{cp}_2$
in the same copy of
$\mathcal {F}^{cp}_2$
in the same copy of
![]() $\mathbb {C}$
, and taking the closure. The Thurston set is the set
$\mathbb {C}$
, and taking the closure. The Thurston set is the set
Equivalently, the Thurston set is the projection of the Master Teapot to the complex plane.

Figure 1 A plot of a finite approximation of
![]() ${\Upsilon _2^{cp}}$
, showing all points coming from maps in
${\Upsilon _2^{cp}}$
, showing all points coming from maps in
![]() $\mathcal {F}^{cp}$
whose critical orbits have periods at most 23. The two black circles are
$\mathcal {F}^{cp}$
whose critical orbits have periods at most 23. The two black circles are
![]() $S^1\times \{1\}$
and
$S^1\times \{1\}$
and
![]() $S^1\times \{2\}$
, where
$S^1\times \{2\}$
, where
![]() $S^1$
is the unit circle. The color gradients show the height of the plotted points. This figure is from [Reference Bray, Davis, Lindsey and WuBDLW19].
$S^1$
is the unit circle. The color gradients show the height of the plotted points. This figure is from [Reference Bray, Davis, Lindsey and WuBDLW19].
The Master Teapot and Thurston set have rich and mysterious geometrical and topological structures that have been investigated in several recent works, including [Reference Bray, Davis, Lindsey and WuBDLW19, Reference Calegari, Koch and WalkerCKW17, Reference ThompsonTho17, Reference Thurston, Bonifant, Lyubich and SutherlandThu14, Reference TiozzoTio15, Reference TiozzoTio18]. Describing the ‘shape’ of the Master Teapot
![]() $\Upsilon _2^{cp}$
or the Thurston set
$\Upsilon _2^{cp}$
or the Thurston set
![]() $\Omega _2^{cp}$
is a step toward refining Thurston’s result by characterizing which weak Perron numbers arise as the growth rates of which PCF interval maps. In particular, the ability to prove that a specific point z is not in the Master Teapot—which the algorithms we present in §8 accomplish—provides a necessary condition for a growth rate to be realized by a map in
$\Omega _2^{cp}$
is a step toward refining Thurston’s result by characterizing which weak Perron numbers arise as the growth rates of which PCF interval maps. In particular, the ability to prove that a specific point z is not in the Master Teapot—which the algorithms we present in §8 accomplish—provides a necessary condition for a growth rate to be realized by a map in
![]() $\mathcal {F}_2^{cp}$
.
$\mathcal {F}_2^{cp}$
.
In [Reference Bray, Davis, Lindsey and WuBDLW19], the authors prove that the Master Teapot
![]() $\Upsilon _2^{cp}$
is connected and contains the unit cylinder
$\Upsilon _2^{cp}$
is connected and contains the unit cylinder
![]() $S^1 \times [1,2]$
. Furthermore, the intersection of the height-
$S^1 \times [1,2]$
. Furthermore, the intersection of the height-
![]() $\unicode{x3bb} $
slice of the Master Teapot,
$\unicode{x3bb} $
slice of the Master Teapot,
with the closed unit disk
![]() $\overline {\mathbb {D}}$
grows monotonically with
$\overline {\mathbb {D}}$
grows monotonically with
![]() $\unicode{x3bb} $
[Reference Bray, Davis, Lindsey and WuBDLW19]. Consequently, the part of the top level slice of the Master Teapot that is inside the unit cylinder,
$\unicode{x3bb} $
[Reference Bray, Davis, Lindsey and WuBDLW19]. Consequently, the part of the top level slice of the Master Teapot that is inside the unit cylinder,
![]() $\Xi _2 \cap \overline {\mathbb {D}}$
, coincides with
$\Xi _2 \cap \overline {\mathbb {D}}$
, coincides with
![]() $\Omega _2^{cp} \cap \overline {\mathbb {D}}$
, the part of the Thurston set inside the unit disk.
$\Omega _2^{cp} \cap \overline {\mathbb {D}}$
, the part of the Thurston set inside the unit disk.
The growth rates of PCF self-maps of real intervals may be seen as a specific case of core entropy for PCF complex polynomials. Indeed, the filled Julia set of a PCF complex polynomial contains a forward invariant, finite topological tree, called the Hubbard tree, that contains the critical points of the polynomial; the core entropy of such a polynomial is the topological entropy of the restriction of the dynamics to the Hubbard tree. For a polynomial with real coefficients, the Hubbard tree is a real interval, and so the restriction of the map to the Hubbard tree is a PCF multimodal self-map of an interval. Although we confine our investigation here to self-maps of real polynomials, similar questions could be explored in the complex setting. The interested reader may read more about core entropy for complex polynomials in [Reference Gao and TiozzoGT21, Reference TiozzoTio16].
Another motivation for investigating PCF multimodal self-maps of real intervals is that these maps may also be seen as one-dimensional analogs of pseudo-Anosov surface diffeomorphisms. A uniform expander is a continuous, piecewise affine-linear (with finitely many pieces) self-map of an interval such that the derivative on each piece is
![]() $\pm \unicode{x3bb} $
for some expansion factor
$\pm \unicode{x3bb} $
for some expansion factor
![]() $\unicode{x3bb}> 1$
. Classical results in entropy theory imply that the growth rate of a uniform expander with expansion factor
$\unicode{x3bb}> 1$
. Classical results in entropy theory imply that the growth rate of a uniform expander with expansion factor
![]() $\unicode{x3bb} $
is
$\unicode{x3bb} $
is
![]() $\unicode{x3bb} $
. Milnor and Thurston proved that every continuous, self-map of an interval with finitely many critical points and positive topological entropy is semi-conjugate to a uniform expander with the same topological entropy [Reference Milnor and ThurstonMT88]. Both PCF uniform expanders and pseudo-Anosov surface diffeomorphisms are uniformly expanding maps except at finitely many points, admit Markov partitions, and their expansion factors (called the dilatation of a pseudo-Anosov surface diffeomorphism) coincide with their growth rates. Constructions of pseudo-Anosov surface diffeomorphisms from uniform expanders are explored in [Reference Baik, Rafiqi and WuBRW16, Reference FarberFar21]. Characterizing the set of dilatations realized by pseudo-Anosov surface diffeomorphisms remains an open question.
$\unicode{x3bb} $
. Milnor and Thurston proved that every continuous, self-map of an interval with finitely many critical points and positive topological entropy is semi-conjugate to a uniform expander with the same topological entropy [Reference Milnor and ThurstonMT88]. Both PCF uniform expanders and pseudo-Anosov surface diffeomorphisms are uniformly expanding maps except at finitely many points, admit Markov partitions, and their expansion factors (called the dilatation of a pseudo-Anosov surface diffeomorphism) coincide with their growth rates. Constructions of pseudo-Anosov surface diffeomorphisms from uniform expanders are explored in [Reference Baik, Rafiqi and WuBRW16, Reference FarberFar21]. Characterizing the set of dilatations realized by pseudo-Anosov surface diffeomorphisms remains an open question.
The Master Teapot and Thurston set are also closely related to the theory of
![]() $\beta $
- and generalized
$\beta $
- and generalized
![]() $\beta $
-expansions (cf. [Reference Dombek, Masáková and PelantováDMP11, Reference GóraǴ7, Reference Ito and SadahiroIS09, Reference Li, Sahlsten and SamuelLSS16, Reference SteinerSte13]), roots of Littlewood, Newman, and Borwein polynomials (cf. [Reference Borwein, Erdélyi and LittmannBEL08, Reference Hare and MossinghoffHM14, Reference KonyaginKon99, Reference MukundaMuk10, Reference Odlyzko and PoonenOP93, Reference Shmerkin and SolomyakSS06]), and dynamics of iterated function systems (cf. [Reference BandtBan02, Reference Barnsley and HarringtonBH85, Reference SolomyakSol04, Reference Solomyak and XuSX03]).
$\beta $
-expansions (cf. [Reference Dombek, Masáková and PelantováDMP11, Reference GóraǴ7, Reference Ito and SadahiroIS09, Reference Li, Sahlsten and SamuelLSS16, Reference SteinerSte13]), roots of Littlewood, Newman, and Borwein polynomials (cf. [Reference Borwein, Erdélyi and LittmannBEL08, Reference Hare and MossinghoffHM14, Reference KonyaginKon99, Reference MukundaMuk10, Reference Odlyzko and PoonenOP93, Reference Shmerkin and SolomyakSS06]), and dynamics of iterated function systems (cf. [Reference BandtBan02, Reference Barnsley and HarringtonBH85, Reference SolomyakSol04, Reference Solomyak and XuSX03]).
1.1 Overview of main results
The main contribution of this paper is an explicit characterization of the Master Teapot
![]() ${\Upsilon _2^{cp}}$
—necessary and sufficient conditions for a point to be in
${\Upsilon _2^{cp}}$
—necessary and sufficient conditions for a point to be in
![]() ${\Upsilon _2^{cp}}$
. (The part of the Master Teapot inside the unit cylinder
${\Upsilon _2^{cp}}$
. (The part of the Master Teapot inside the unit cylinder
![]() $\mathbb {D} \times [1,2]$
is described by Theorem 1.7 and the part outside the unit cylinder by Theorem 1.8.) Theorem 1.7 establishes a new connection between horizontal slices of the Master Teapot and iterated function systems. Specifically, the part in
$\mathbb {D} \times [1,2]$
is described by Theorem 1.7 and the part outside the unit cylinder by Theorem 1.8.) Theorem 1.7 establishes a new connection between horizontal slices of the Master Teapot and iterated function systems. Specifically, the part in
![]() $\mathbb {D}$
of each horizontal slice of the Teapot can be viewed as an analog of the Mandelbrot set for a family of ‘restricted iterated function systems’ (cf. Remark 1.15). From this characterization, we prove an algorithm (§8) for showing that certain weak Perron numbers cannot be the exponent of the topological entropy of a critically periodic unimodal interval map. As an application of this algorithm, we prove that the part of the Master Teapot inside the unit cylinder is not symmetrical with respect to reflection across the imaginary axis (Theorem 1.14). Conjecture 1.16 proposes that an analogy of the Mandelbrot–Julia set correspondence holds for horizontal slices and limit sets of restricted iterated function systems.
$\mathbb {D}$
of each horizontal slice of the Teapot can be viewed as an analog of the Mandelbrot set for a family of ‘restricted iterated function systems’ (cf. Remark 1.15). From this characterization, we prove an algorithm (§8) for showing that certain weak Perron numbers cannot be the exponent of the topological entropy of a critically periodic unimodal interval map. As an application of this algorithm, we prove that the part of the Master Teapot inside the unit cylinder is not symmetrical with respect to reflection across the imaginary axis (Theorem 1.14). Conjecture 1.16 proposes that an analogy of the Mandelbrot–Julia set correspondence holds for horizontal slices and limit sets of restricted iterated function systems.
1.2 Precise statement of results and commentary
To state the results precisely, we introduce some terminology and notation.
First, we define words and sequences in the alphabet
![]() $\{0, 1\}$
.
$\{0, 1\}$
.
Definition 1.1
-
(1) A sequence
 $w=w_1w_2\ldots $
is an element in
$w=w_1w_2\ldots $
is an element in
 $\{0, 1\}^{\mathbb {N}}$
. The shift map
$\{0, 1\}^{\mathbb {N}}$
. The shift map
 $\sigma : \{0,1\}^{\mathbb {N}} \to \{0,1\}^{\mathbb {N}}$
is defined by removing the first element of a sequence, that is,
$\sigma : \{0,1\}^{\mathbb {N}} \to \{0,1\}^{\mathbb {N}}$
is defined by removing the first element of a sequence, that is,
 $\sigma (w_1w_2w_3\ldots ) :=w_2w_3\ldots .$
$\sigma (w_1w_2w_3\ldots ) :=w_2w_3\ldots .$
-
(2) A word
 $w=w_1w_2\ldots w_n$
is an element in
$w=w_1w_2\ldots w_n$
is an element in
 $\{0, 1\}^n$
for some positive integer n. The number n is called the length of the word w and is denoted by
$\{0, 1\}^n$
for some positive integer n. The number n is called the length of the word w and is denoted by
 $|w|$
.
$|w|$
. -
(3) For
 $n \in \mathbb {N}$
, the reverse function
$n \in \mathbb {N}$
, the reverse function
 ${\textrm {Rev}} : \{0,1\}^n \to \{0,1\}^n$
is defined as
${\textrm {Rev}} : \{0,1\}^n \to \{0,1\}^n$
is defined as  $$ \begin{align*} {\textrm{Rev}}(w_1w_2\ldots w_n):=w_nw_{n-1}\ldots w_1.\end{align*} $$
$$ \begin{align*} {\textrm{Rev}}(w_1w_2\ldots w_n):=w_nw_{n-1}\ldots w_1.\end{align*} $$
-
(4) For
 $k \in \mathbb {N}$
, the k-prefix of a sequence
$k \in \mathbb {N}$
, the k-prefix of a sequence
 $w=w_1w_2\ldots $
is the word
$w=w_1w_2\ldots $
is the word  $$ \begin{align*}{\textrm{Pre}}_k(w):=w_1\ldots w_k.\end{align*} $$
$$ \begin{align*}{\textrm{Pre}}_k(w):=w_1\ldots w_k.\end{align*} $$
-
(5) For a word
 $w=w_1 \ldots w_n$
of length n and a natural number
$w=w_1 \ldots w_n$
of length n and a natural number
 $k \leq n$
, the k-prefix and k-suffix of w are the words
$k \leq n$
, the k-prefix and k-suffix of w are the words  $$ \begin{align*} {\textrm{Pre}}_k(w) & :=w_1\ldots w_k,\\ {\textrm{Suf}}_k(w) &:=w_{n-k+1}w_{n-k+2}\ldots w_n. \end{align*} $$
$$ \begin{align*} {\textrm{Pre}}_k(w) & :=w_1\ldots w_k,\\ {\textrm{Suf}}_k(w) &:=w_{n-k+1}w_{n-k+2}\ldots w_n. \end{align*} $$
Next, we relate words and sequences with dynamics on
![]() $\mathbb {C}$
via the following definitions.
$\mathbb {C}$
via the following definitions.
Definition 1.2
-
(1) For any
 $z\in \mathbb {C}$
, define maps
$z\in \mathbb {C}$
, define maps
 $f_{0,z},f_{1,z}: \mathbb {C} \to \mathbb {C}$
by
$f_{0,z},f_{1,z}: \mathbb {C} \to \mathbb {C}$
by  $$ \begin{align*}f_{0, z}(x):=zx, \quad f_{1, z}(x):=2-zx.\end{align*} $$
$$ \begin{align*}f_{0, z}(x):=zx, \quad f_{1, z}(x):=2-zx.\end{align*} $$
-
(2) For any
 $w=w_1\ldots w_n$
and
$w=w_1\ldots w_n$
and
 $z \in \mathbb {C}$
, set
$z \in \mathbb {C}$
, set  $$ \begin{align*}F(w,z):=f_{w_n,z}\circ \cdots \circ f_{w_1,z}(1).\end{align*} $$
$$ \begin{align*}F(w,z):=f_{w_n,z}\circ \cdots \circ f_{w_1,z}(1).\end{align*} $$
-
(3) For any sequence
 $w=w_1w_2\ldots $
and any
$w=w_1w_2\ldots $
and any
 $z \in \mathbb {C}$
with
$z \in \mathbb {C}$
with
 $|z|>1$
, set
$|z|>1$
, set  $$ \begin{align*} H(w, z) := & \lim_{n\rightarrow\infty}(-1)^{(\sum_{i=1}^nw_i)}z^{-n} F({\textrm{Pre}}_n(w), z) \\ = &\lim_{n\rightarrow\infty}(-1)^{(\sum_{i=1}^nw_i)}z^{-n}f_{w_n,z}\circ\cdots \circ f_{w_1, z}(1). \end{align*} $$
$$ \begin{align*} H(w, z) := & \lim_{n\rightarrow\infty}(-1)^{(\sum_{i=1}^nw_i)}z^{-n} F({\textrm{Pre}}_n(w), z) \\ = &\lim_{n\rightarrow\infty}(-1)^{(\sum_{i=1}^nw_i)}z^{-n}f_{w_n,z}\circ\cdots \circ f_{w_1, z}(1). \end{align*} $$
-
(4) For any sequence
 $w=w_1w_2\ldots $
and
$w=w_1w_2\ldots $
and
 $z \in \mathbb {C}$
with
$z \in \mathbb {C}$
with
 $|z|<1$
, set
$|z|<1$
, set  $$ \begin{align*} G(w, z):= & \lim_{n\rightarrow\infty}F({\textrm{Rev}}({\textrm{Pre}}_n(w)), z) \\ = &\lim_{n\rightarrow\infty}f_{w_1,z}\circ \cdots \circ f_{w_n, z}(1). \end{align*} $$
$$ \begin{align*} G(w, z):= & \lim_{n\rightarrow\infty}F({\textrm{Rev}}({\textrm{Pre}}_n(w)), z) \\ = &\lim_{n\rightarrow\infty}f_{w_1,z}\circ \cdots \circ f_{w_n, z}(1). \end{align*} $$
The following definition is partly from [Reference Milnor and ThurstonMT88].
Definition 1.3
-
(1) The cumulative sign of a word
 $w=w_1w_2\ldots w_n$
is defined as
$w=w_1w_2\ldots w_n$
is defined as
 $s(w):=(-1)^{\sum _iw_i}$
.
$s(w):=(-1)^{\sum _iw_i}$
. -
(2) The twisted lexicographic order
 $\le _E$
is a total ordering on the set of sequences, defined as follows:
$\le _E$
is a total ordering on the set of sequences, defined as follows:
 $w<_Ew'$
if and only if there is some
$w<_Ew'$
if and only if there is some
 $k\in \mathbb {N}$
such that
$k\in \mathbb {N}$
such that
 ${\textrm {Pre}}_{k-1}(w){\kern-1pt}={\kern-1pt}{\textrm {Pre}}_{k-1}(w')$
, and
${\textrm {Pre}}_{k-1}(w){\kern-1pt}={\kern-1pt}{\textrm {Pre}}_{k-1}(w')$
, and
 $s({\textrm {Pre}}_{k-1}(w))(w^{\prime }_{k}{\kern-1pt}-{\kern-1pt}w_{k})>{\kern-1pt}0$
. In other words,
$s({\textrm {Pre}}_{k-1}(w))(w^{\prime }_{k}{\kern-1pt}-{\kern-1pt}w_{k})>{\kern-1pt}0$
. In other words,
 $w {\kern-1pt}<_E w'$
if and only if, denoting by k the index of the first letter where w and
$w {\kern-1pt}<_E w'$
if and only if, denoting by k the index of the first letter where w and
 $w'$
differ, either
$w'$
differ, either
 $w^{\prime }_k>w_k$
and the common
$w^{\prime }_k>w_k$
and the common
 $(k-1)$
-prefix has positive cumulative sign, or
$(k-1)$
-prefix has positive cumulative sign, or
 $w^{\prime }_k<w_k$
and the common
$w^{\prime }_k<w_k$
and the common
 $(k-1)$
-prefix has negative cumulative sign.
$(k-1)$
-prefix has negative cumulative sign. -
(3) We define the total order
 $\le _E$
on the set of words of length n exactly the same way as above.
$\le _E$
on the set of words of length n exactly the same way as above.
Definition 1.4
-
(1) Let
 $\unicode{x3bb} \in (1, 2]$
. We call the map
$\unicode{x3bb} \in (1, 2]$
. We call the map
 $f_{\unicode{x3bb} }:[0,1] \to [0,1]$
given by the
$f_{\unicode{x3bb} }:[0,1] \to [0,1]$
given by the $$ \begin{align*}f_\unicode{x3bb}(x)=\begin{cases} \unicode{x3bb} x, & x\leq 1/\unicode{x3bb}, \\ 2-\unicode{x3bb} x, & x>1/\unicode{x3bb},\end{cases}\end{align*} $$
$$ \begin{align*}f_\unicode{x3bb}(x)=\begin{cases} \unicode{x3bb} x, & x\leq 1/\unicode{x3bb}, \\ 2-\unicode{x3bb} x, & x>1/\unicode{x3bb},\end{cases}\end{align*} $$
 $\unicode{x3bb} $
-tent map. Let
$\unicode{x3bb} $
-tent map. Let
 $I_{0, \unicode{x3bb} }=[0, 1/\unicode{x3bb} ]$
,
$I_{0, \unicode{x3bb} }=[0, 1/\unicode{x3bb} ]$
,
 $I_{1, \unicode{x3bb} }=[1/\unicode{x3bb} , 1]$
.
$I_{1, \unicode{x3bb} }=[1/\unicode{x3bb} , 1]$
.
-
(2) The
 $\unicode{x3bb} $
-itinerary, denoted as
$\unicode{x3bb} $
-itinerary, denoted as
 $\mathrm {{It}}_\unicode{x3bb} $
, is the minimum (with respect to
$\mathrm {{It}}_\unicode{x3bb} $
, is the minimum (with respect to
 $\leq _E$
) sequence w such that for any
$\leq _E$
) sequence w such that for any
 $k\geq 0$
,
$k\geq 0$
,
 $f_\unicode{x3bb} ^k(1)\in I_{w_{k+1},\unicode{x3bb} }$
.
$f_\unicode{x3bb} ^k(1)\in I_{w_{k+1},\unicode{x3bb} }$
.
One can easily check that
![]() $\mathrm {{It}}_{\unicode{x3bb} }$
is the itinerary of
$\mathrm {{It}}_{\unicode{x3bb} }$
is the itinerary of
![]() $1$
under
$1$
under
![]() $f_\unicode{x3bb} $
in the convention of the Milnor–Thurston kneading theory.
$f_\unicode{x3bb} $
in the convention of the Milnor–Thurston kneading theory.
Now we introduce a combinatorial condition on sequences.
Definition 1.5. For
![]() $\unicode{x3bb} \in (1,2]$
, a sequence w is called
$\unicode{x3bb} \in (1,2]$
, a sequence w is called
![]() $\unicode{x3bb} $
-suitable if for every
$\unicode{x3bb} $
-suitable if for every
![]() $\unicode{x3bb} '\in (\unicode{x3bb} , 2]$
, the following conditions hold:
$\unicode{x3bb} '\in (\unicode{x3bb} , 2]$
, the following conditions hold:
-
(1)
 ${\textrm {Rev}} ( {\textrm {Pre}}_n(w)) \leq _E {\textrm {Pre}}_n(\mathrm {{It}}_{\unicode{x3bb} '})$
for all
${\textrm {Rev}} ( {\textrm {Pre}}_n(w)) \leq _E {\textrm {Pre}}_n(\mathrm {{It}}_{\unicode{x3bb} '})$
for all
 $n \in \mathbb {N}$
;
$n \in \mathbb {N}$
; -
(2) if
 ${\textrm {Rev}}({\textrm {Pre}}_n(w)) = {\textrm {Pre}}_n(\mathrm {{It}}_{\unicode{x3bb} '})$
, then the cumulative sign
${\textrm {Rev}}({\textrm {Pre}}_n(w)) = {\textrm {Pre}}_n(\mathrm {{It}}_{\unicode{x3bb} '})$
, then the cumulative sign
 $s({\textrm {Pre}}_n(w)) = -1$
;
$s({\textrm {Pre}}_n(w)) = -1$
; -
(3) if
 $\mathrm {{It}}_{\unicode{x3bb} '} = 1 \cdot 0^k \cdot 1 \ldots , k \in \mathbb {N}$
, then w does not contain
$\mathrm {{It}}_{\unicode{x3bb} '} = 1 \cdot 0^k \cdot 1 \ldots , k \in \mathbb {N}$
, then w does not contain
 $k+1$
consecutive
$k+1$
consecutive
 $0$
s (that is, if
$0$
s (that is, if
 $\mathrm {{It}}_{\unicode{x3bb} '}$
starts with
$\mathrm {{It}}_{\unicode{x3bb} '}$
starts with
 $1$
followed by
$1$
followed by
 $k\ 0$
s and then
$k\ 0$
s and then
 $1$
, writing w as
$1$
, writing w as
 $w=w_1w_2\ldots ,$
there does not exist
$w=w_1w_2\ldots ,$
there does not exist
 $n \in \mathbb {N}$
such that
$n \in \mathbb {N}$
such that
 $w_i = 0$
for all
$w_i = 0$
for all
 $n \leq i \leq n+k$
);
$n \leq i \leq n+k$
); -
(4) if
 $k \in \mathbb {N}$
satisfies
$k \in \mathbb {N}$
satisfies
 $\sqrt {2}\leq \unicode{x3bb} ^{2^k}<2$
, then
$\sqrt {2}\leq \unicode{x3bb} ^{2^k}<2$
, then
 $w=\mathfrak {D'}^k(w')$
for some sequence
$w=\mathfrak {D'}^k(w')$
for some sequence
 $w'$
, where
$w'$
, where
 $\mathfrak {D'}$
is the map that replaces
$\mathfrak {D'}$
is the map that replaces
 $0$
with
$0$
with
 $11$
and
$11$
and
 $1$
with
$1$
with
 $01$
, such that for every
$01$
, such that for every
 $\unicode{x3bb} '>\unicode{x3bb} ^{2^k}$
, if
$\unicode{x3bb} '>\unicode{x3bb} ^{2^k}$
, if
 $\mathrm {{It}}_{\unicode{x3bb} '} = 1 \cdot 0^k \cdot 1 \ldots ,$
then
$\mathrm {{It}}_{\unicode{x3bb} '} = 1 \cdot 0^k \cdot 1 \ldots ,$
then
 $w'$
does not contain
$w'$
does not contain
 $k+1$
consecutive
$k+1$
consecutive
 $0$
s.
$0$
s.
Remark 1.6. Every sequence is (vacuously)
![]() $2$
-suitable.
$2$
-suitable.
For
![]() $\unicode{x3bb} \in (1, 2)$
, let
$\unicode{x3bb} \in (1, 2)$
, let
![]() ${\Xi }_\unicode{x3bb} $
be a height-
${\Xi }_\unicode{x3bb} $
be a height-
![]() $\unicode{x3bb} $
slice of the Master Teapot
$\unicode{x3bb} $
slice of the Master Teapot
![]() $\Upsilon _2$
:
$\Upsilon _2$
:
We will use the following notation:
 $$ \begin{align*} \mathbb{D} & := \{z \in \mathbb{C} : |z| <1\}\quad \textrm{the open unit disk}, \\ \overline{\mathbb{D}} & := \{z \in \mathbb{C} : |z| \leq 1\}\quad \textrm{the closed unit disk},\\ S^1 & := \{z \in \mathbb{C} : |z| = 1\}\quad \textrm{the unit circle} ,\\ \mathcal{C} & := \overline{\mathbb{D}} \times [1,2]\quad \textrm{the closed `unit cylinder'}. \end{align*} $$
$$ \begin{align*} \mathbb{D} & := \{z \in \mathbb{C} : |z| <1\}\quad \textrm{the open unit disk}, \\ \overline{\mathbb{D}} & := \{z \in \mathbb{C} : |z| \leq 1\}\quad \textrm{the closed unit disk},\\ S^1 & := \{z \in \mathbb{C} : |z| = 1\}\quad \textrm{the unit circle} ,\\ \mathcal{C} & := \overline{\mathbb{D}} \times [1,2]\quad \textrm{the closed `unit cylinder'}. \end{align*} $$
Our main theorem is the following.
Theorem 1.7. For any
![]() $\unicode{x3bb} \in (1,2]$
, the part of the slice
$\unicode{x3bb} \in (1,2]$
, the part of the slice
![]() ${\Xi }_\unicode{x3bb} $
inside the closed unit disk can be characterized as
${\Xi }_\unicode{x3bb} $
inside the closed unit disk can be characterized as
There is a similar characterization for outside the unit disc, which follows directly from results in [Reference TiozzoTio18].
Theorem 1.8. For any
![]() $\unicode{x3bb} \in (1,2)$
, the part of the slice
$\unicode{x3bb} \in (1,2)$
, the part of the slice
![]() ${\Xi }_\unicode{x3bb} $
outside the unit disk can be characterized as follows.
${\Xi }_\unicode{x3bb} $
outside the unit disk can be characterized as follows.
-
• If the
 $\unicode{x3bb} $
-tent map is not critically periodic, then
$\unicode{x3bb} $
-tent map is not critically periodic, then  $$ \begin{align*}{\Xi}_\unicode{x3bb} \setminus \overline{\mathbb{D}}= \{z \in \mathbb{C} \setminus \overline{\mathbb{D}}: H(\mathrm{{It}}_\unicode{x3bb}, z)=0 \}.\end{align*} $$
$$ \begin{align*}{\Xi}_\unicode{x3bb} \setminus \overline{\mathbb{D}}= \{z \in \mathbb{C} \setminus \overline{\mathbb{D}}: H(\mathrm{{It}}_\unicode{x3bb}, z)=0 \}.\end{align*} $$
-
• If the
 $\unicode{x3bb} $
-tent map is critically periodic with period p, then
$\unicode{x3bb} $
-tent map is critically periodic with period p, then  $$ \begin{align*}{\Xi}_\unicode{x3bb} \setminus \overline{\mathbb{D}}= \{z \in \mathbb{C} \setminus \overline{\mathbb{D}}: H(\mathrm{{It}}_\unicode{x3bb}, z)=0\text{ or }z^p=2 \}.\end{align*} $$
$$ \begin{align*}{\Xi}_\unicode{x3bb} \setminus \overline{\mathbb{D}}= \{z \in \mathbb{C} \setminus \overline{\mathbb{D}}: H(\mathrm{{It}}_\unicode{x3bb}, z)=0\text{ or }z^p=2 \}.\end{align*} $$
Remark 1.9. Theorems 1.7 and 1.8 both provide algorithms to certify that a point is in the complement of
![]() ${\Xi }_\unicode{x3bb} $
. This is useful since the definition of
${\Xi }_\unicode{x3bb} $
. This is useful since the definition of
![]() ${\Upsilon _2^{cp}}$
is not constructive, as it involves taking a closure. Section 8 describes these algorithms. Figure 4 is a finite approximation of
${\Upsilon _2^{cp}}$
is not constructive, as it involves taking a closure. Section 8 describes these algorithms. Figure 4 is a finite approximation of
![]() ${\Xi }_{1.8} \cap \overline {\mathbb {D}}$
using Theorem 1.7, and Figure 2 is a finite approximation of
${\Xi }_{1.8} \cap \overline {\mathbb {D}}$
using Theorem 1.7, and Figure 2 is a finite approximation of
![]() ${\Upsilon _2^{cp}}\backslash (\overline {\mathbb {D}}\times [1, 2])$
using Theorem 1.8.
${\Upsilon _2^{cp}}\backslash (\overline {\mathbb {D}}\times [1, 2])$
using Theorem 1.8.
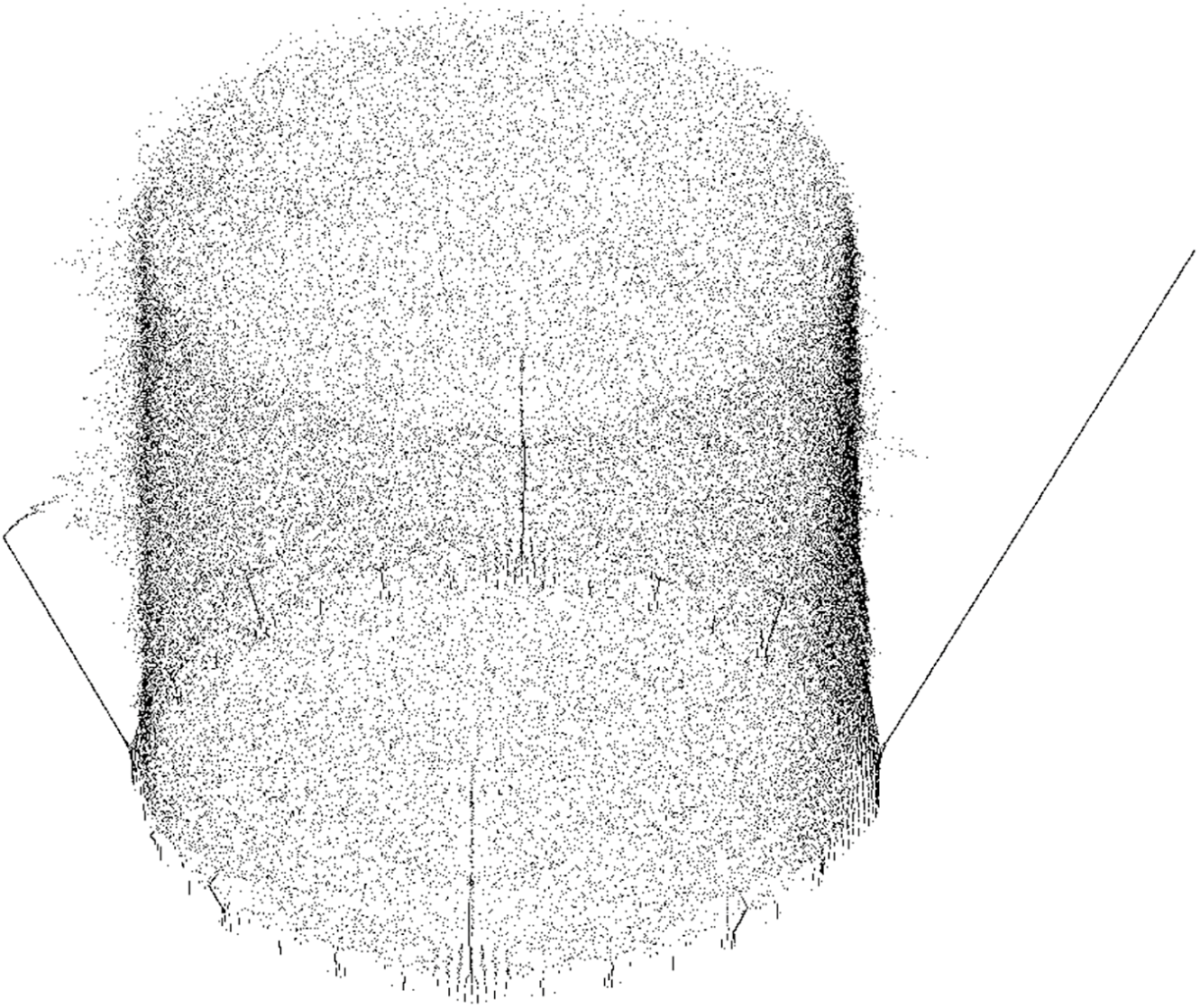
Figure 2 A constructive approximation of the part of
![]() ${\Upsilon _2^{cp}}$
outside the unit cylinder. This plot shows the 56 737 points outside the cylinder
${\Upsilon _2^{cp}}$
outside the unit cylinder. This plot shows the 56 737 points outside the cylinder
![]() $S^1 \times [1,2]$
that are roots of the degree 100 partial sums of the kneading power series for
$S^1 \times [1,2]$
that are roots of the degree 100 partial sums of the kneading power series for
![]() $1000$
different growth rates
$1000$
different growth rates
![]() $\unicode{x3bb} $
in
$\unicode{x3bb} $
in
![]() $[1,2]$
. The ‘spout’ on the right side of the image consists of points of the form
$[1,2]$
. The ‘spout’ on the right side of the image consists of points of the form
![]() $(\unicode{x3bb} ,\unicode{x3bb} )$
.
$(\unicode{x3bb} ,\unicode{x3bb} )$
.
Remark 1.10. Since the set of
![]() $\unicode{x3bb} $
-suitable sequences is semicontinuous with
$\unicode{x3bb} $
-suitable sequences is semicontinuous with
![]() $\unicode{x3bb} $
(Lemma 5.5), Theorem 1.7 implies that if
$\unicode{x3bb} $
(Lemma 5.5), Theorem 1.7 implies that if
![]() $1<\unicode{x3bb} <\unicode{x3bb} ' \leq 2$
, then
$1<\unicode{x3bb} <\unicode{x3bb} ' \leq 2$
, then
which is the ‘persistence theorem’ proved in [Reference Bray, Davis, Lindsey and WuBDLW19]. However, our proof of Theorem 1.7 depends on the persistence theorem in [Reference Bray, Davis, Lindsey and WuBDLW19].
Remark 1.11. Tiozzo showed in [Reference TiozzoTio18] that
and the persistence theorem [Reference Bray, Davis, Lindsey and WuBDLW19] shows that
![]() $\Omega _2 \cap \overline {\mathbb {D}} = {\Xi }_2 \cap \overline {\mathbb {D}}$
. It is also known that the unit cylinder is in the teapot, that is,
$\Omega _2 \cap \overline {\mathbb {D}} = {\Xi }_2 \cap \overline {\mathbb {D}}$
. It is also known that the unit cylinder is in the teapot, that is,
![]() $S^1 \times [1,2] \subset \Upsilon _2^{cp}$
[Reference Bray, Davis, Lindsey and WuBDLW19]. Since every sequence is
$S^1 \times [1,2] \subset \Upsilon _2^{cp}$
[Reference Bray, Davis, Lindsey and WuBDLW19]. Since every sequence is
![]() $2$
-suitable, this proves the conclusion of Theorem 1.7 for the top level of the teapot, the case
$2$
-suitable, this proves the conclusion of Theorem 1.7 for the top level of the teapot, the case
![]() $\unicode{x3bb} = 2$
.
$\unicode{x3bb} = 2$
.
Remark 1.12. Our first step towards proving Theorem 1.7 is proving Theorem 4.5, an alternative characterization of slices
![]() $\Xi _{\unicode{x3bb} } \cap \overline {\mathbb {D}}$
. A corollary of Theorem 4.5 is that all roots in
$\Xi _{\unicode{x3bb} } \cap \overline {\mathbb {D}}$
. A corollary of Theorem 4.5 is that all roots in
![]() $\overline {\mathbb {D}}$
of all Parry polynomials coming from admissible words—even reducible Parry polynomials—are in the Thurston set
$\overline {\mathbb {D}}$
of all Parry polynomials coming from admissible words—even reducible Parry polynomials—are in the Thurston set
![]() $\Omega _2^{cp}$
.
$\Omega _2^{cp}$
.
Corollary 1.13.
![]() $\Omega _2^{cp} \cap \overline {\mathbb {D}}$
is the closure of the set of all roots in
$\Omega _2^{cp} \cap \overline {\mathbb {D}}$
is the closure of the set of all roots in
![]() $\overline {\mathbb {D}}$
of all Parry polynomials associated to admissible words.
$\overline {\mathbb {D}}$
of all Parry polynomials associated to admissible words.
In particular, when using Parry polynomials to plot approximations of
![]() $\Omega _2^{cp}$
, it is not necessary to check whether the Parry polynomials are irreducible.
$\Omega _2^{cp}$
, it is not necessary to check whether the Parry polynomials are irreducible.
As an application of Theorem 1.7, we will show the following.
Theorem 1.14. The part of the Master Teapot inside the unit cylinder is not symmetrical with respect to reflection across the imaginary axis, that is,
![]() ${\Upsilon _2^{cp}} \cap \mathcal {C}$
is not invariant under the map
${\Upsilon _2^{cp}} \cap \mathcal {C}$
is not invariant under the map
![]() $(z,\unicode{x3bb} ) \mapsto (-z,\unicode{x3bb} )$
.
$(z,\unicode{x3bb} ) \mapsto (-z,\unicode{x3bb} )$
.
Since Galois conjugates occur in complex conjugate pairs, it is immediate that
![]() $(x+iy,\unicode{x3bb} ) \in {\Upsilon _2^{cp}}$
if and only if
$(x+iy,\unicode{x3bb} ) \in {\Upsilon _2^{cp}}$
if and only if
![]() $(x-iy,\unicode{x3bb} ) \in {\Upsilon _2^{cp}}$
.
$(x-iy,\unicode{x3bb} ) \in {\Upsilon _2^{cp}}$
.
Theorem 1.14 is surprising because the Thurston set,
![]() ${\Omega _2^{cp}}$
, which is the projection to
${\Omega _2^{cp}}$
, which is the projection to
![]() $\mathbb {C}$
of
$\mathbb {C}$
of
![]() ${\Upsilon _2^{cp}}$
, is symmetrical under the map
${\Upsilon _2^{cp}}$
, is symmetrical under the map
![]() $z \mapsto -z$
(Proposition 9.1). However, this asymmetry in the Master Teapot is confined to the slices of heights
$z \mapsto -z$
(Proposition 9.1). However, this asymmetry in the Master Teapot is confined to the slices of heights
![]() $\geq \sqrt {2}$
; one can prove, via the renormalization procedure described in §2.3, that the unit cylinder part of slices of height
$\geq \sqrt {2}$
; one can prove, via the renormalization procedure described in §2.3, that the unit cylinder part of slices of height
![]() $< \sqrt {2}$
is symmetrical under reflection across the imaginary axis.
$< \sqrt {2}$
is symmetrical under reflection across the imaginary axis.
Remark 1.15. Theorem 1.7 allow us to interpret each slice
![]() ${\Xi }_\unicode{x3bb} \cap \mathbb {D}$
as an analogy of the Mandelbrot set. The conclusion of Theorem 1.7 for the top slice (cf. Remark 1.11) allows one to characterize
${\Xi }_\unicode{x3bb} \cap \mathbb {D}$
as an analogy of the Mandelbrot set. The conclusion of Theorem 1.7 for the top slice (cf. Remark 1.11) allows one to characterize
![]() ${\Xi }_2$
as the union of
${\Xi }_2$
as the union of
![]() $S_1$
and the set of all parameters
$S_1$
and the set of all parameters
![]() $z \in \mathbb {D}$
such that the point
$z \in \mathbb {D}$
such that the point
![]() $1$
is an element of the limit set
$1$
is an element of the limit set
![]() $\Lambda _z$
associated to the iterated function system generated by
$\Lambda _z$
associated to the iterated function system generated by
![]() $f_{0,z}$
and
$f_{0,z}$
and
![]() $f_{1,z}$
. Theorem 1.7 suggests viewing
$f_{1,z}$
. Theorem 1.7 suggests viewing
![]() ${\Xi }_\unicode{x3bb} \cap \mathbb {D}$
as the set of parameters z for which the point
${\Xi }_\unicode{x3bb} \cap \mathbb {D}$
as the set of parameters z for which the point
![]() $1$
is an element of the ‘limit set’ associated to the ‘restricted iterated function system’ generated by
$1$
is an element of the ‘limit set’ associated to the ‘restricted iterated function system’ generated by
![]() $f_{0,z}$
and
$f_{0,z}$
and
![]() $f_{1,z}$
in which only the compositions represented by
$f_{1,z}$
in which only the compositions represented by
![]() $\unicode{x3bb} $
-suitable sequences are allowed.
$\unicode{x3bb} $
-suitable sequences are allowed.
Based on numerical experiments, we propose the following conjectured analogy of the Julia–Mandelbrot correspondence [Reference Douady and HubbardDH85, Reference LeiLei90].
Conjecture 1.16. For any complex number
![]() $|z|<1$
, any
$|z|<1$
, any
![]() $\unicode{x3bb} \kern1.2pt{\in}\kern1.2pt (1, 2]$
, the set
$\unicode{x3bb} \kern1.2pt{\in}\kern1.2pt (1, 2]$
, the set
![]() ${\{z'-z: z'\in {\Xi }_\unicode{x3bb} \}}$
is asymptotically similar to the set
${\{z'-z: z'\in {\Xi }_\unicode{x3bb} \}}$
is asymptotically similar to the set
By these two sets being asymptotically similar, we mean there exists a real number
![]() $r>0$
and sequences
$r>0$
and sequences
![]() $(t_n), (t^{\prime }_n) \in \mathbb {C}$
with
$(t_n), (t^{\prime }_n) \in \mathbb {C}$
with
![]() $t_n, t_n' \to \infty $
such that, denoting Hausdorff distance by
$t_n, t_n' \to \infty $
such that, denoting Hausdorff distance by
![]() $d_{\textrm {Haus}}$
,
$d_{\textrm {Haus}}$
,
If Conjecture 1.16 is true, or at least true for ‘enough’ points z, we would also be able to show the following.
Conjecture 1.17. There exists
![]() $\unicode{x3bb} \in (1, 2)$
such that
$\unicode{x3bb} \in (1, 2)$
such that
![]() ${\Xi }_\unicode{x3bb} \cap \overline {\mathbb {D}}$
has infinitely many connected components.
${\Xi }_\unicode{x3bb} \cap \overline {\mathbb {D}}$
has infinitely many connected components.
Figure 3 shows a constructive plot (in black) of the slice
![]() ${\Xi }_{1.8} \cap \overline {\mathbb {D}}$
, while Figure 4 shows (in white) points of
${\Xi }_{1.8} \cap \overline {\mathbb {D}}$
, while Figure 4 shows (in white) points of
![]() $\overline {\mathbb {D}} \setminus {\Xi }_{1.8}$
. Comparison of these images suggests the existence of multiple small connected components in the region
$\overline {\mathbb {D}} \setminus {\Xi }_{1.8}$
. Comparison of these images suggests the existence of multiple small connected components in the region
![]() $\textrm {Re}(z) < 0$
near the inner boundary of the ‘ring.’
$\textrm {Re}(z) < 0$
near the inner boundary of the ‘ring.’

Figure 3 A constructive plot of an approximation of the slice
![]() ${\Xi }_{1.8} \cap \mathbb {D}$
. The plotted black points are all the roots of modulus
${\Xi }_{1.8} \cap \mathbb {D}$
. The plotted black points are all the roots of modulus
![]() $\leq 1$
of all Parry polynomials for superattracting tent maps with growth rate
$\leq 1$
of all Parry polynomials for superattracting tent maps with growth rate
![]() $<1.8$
and critical length at most
$<1.8$
and critical length at most
![]() $29$
.
$29$
.
The Thurston set
![]() ${\Omega _2^{cp}}$
is known to be path-connected and locally connected [Reference TiozzoTio18, Theorem 1.3]. It follows from Theorem 1.8 that for many heights
${\Omega _2^{cp}}$
is known to be path-connected and locally connected [Reference TiozzoTio18, Theorem 1.3]. It follows from Theorem 1.8 that for many heights
![]() $\unicode{x3bb} \in (1,2]$
, the part of the slice of height
$\unicode{x3bb} \in (1,2]$
, the part of the slice of height
![]() $\unicode{x3bb} $
that is outside the unit cylinder consists of more than one connected component.
$\unicode{x3bb} $
that is outside the unit cylinder consists of more than one connected component.
Conjecture 1.17 could be potentially proven by computation via an effective version of Theorem 1.7 similar to Proposition 8.4. However, a tighter bound than that obtained in Proposition 8.4 would probably be needed for the computation to be feasible.
The structure of the paper is as follows.
Section 2 provides definitions and notation for Parry polynomials, admissible and dominant words and sequences, growth rates, and the renormalization/doubling operators.
Section 3 proves some elementary results about the doubling map which we will need in later sections to extend results about the top part of the teapot to the part with height
![]() $<\sqrt {2}$
.
$<\sqrt {2}$
.
Section 4 proves Theorem 4.5, which implies that all roots in the unit disk of all Parry polynomials associated to admissible words are in the teapot.
Section 5 discusses
![]() $\unicode{x3bb} $
-suitability and proves Lemma 5.7, which is the key combinatorial result we need to prove Theorem 1.7.
$\unicode{x3bb} $
-suitability and proves Lemma 5.7, which is the key combinatorial result we need to prove Theorem 1.7.
Section 6 uses Theorem 4.5 and Lemma 5.7 to prove Theorem 1.7.
Section 8 presents algorithms, derived from Theorems 1.7 and 1.8, which will detect if a point
![]() $(z,\unicode{x3bb} ) \in \mathbb {C} \times \mathbb {R}$
belongs to the complement of the height-
$(z,\unicode{x3bb} ) \in \mathbb {C} \times \mathbb {R}$
belongs to the complement of the height-
![]() $\unicode{x3bb} $
slice
$\unicode{x3bb} $
slice
![]() ${\Xi }_{\unicode{x3bb} }$
, and proves lemmas that justify the algorithms.
${\Xi }_{\unicode{x3bb} }$
, and proves lemmas that justify the algorithms.
Section 9 proves Theorem 1.14 by exhibiting a point
![]() $(z,\unicode{x3bb} )$
that is in the teapot and using the algorithm from §8 to prove that
$(z,\unicode{x3bb} )$
that is in the teapot and using the algorithm from §8 to prove that
![]() $(-\bar {z},\unicode{x3bb} )$
is in the complement of the slice
$(-\bar {z},\unicode{x3bb} )$
is in the complement of the slice
![]() ${\Xi }_{\unicode{x3bb} }$
.
${\Xi }_{\unicode{x3bb} }$
.
2 Preliminaries
2.1 Concatenation
We use
![]() $\cdot $
or just adjacency to denote concatenations, that is, for any word
$\cdot $
or just adjacency to denote concatenations, that is, for any word
![]() $w=w_1\ldots w_n$
and any word or sequence
$w=w_1\ldots w_n$
and any word or sequence
![]() $v=v_1v_2\ldots\, $
,
$v=v_1v_2\ldots\, $
,
We denote the concatenation of n copies of a word w by
![]() $w^n$
for
$w^n$
for
![]() $n \in \mathbb {N} \cup \{\infty \}$
.
$n \in \mathbb {N} \cup \{\infty \}$
.
2.2 Parry polynomials
Let w be a word with positive cumulative sign. The Parry polynomial of w,
![]() $P_w:\mathbb {C} \to \mathbb {C}$
, is defined as
$P_w:\mathbb {C} \to \mathbb {C}$
, is defined as
(cf. [Reference Bray, Davis, Lindsey and WuBDLW19, Definition 2.7]). It is evident that if
![]() $\mathrm {{It}}_\unicode{x3bb} =w^\infty $
, then
$\mathrm {{It}}_\unicode{x3bb} =w^\infty $
, then
![]() $\unicode{x3bb} $
is a root of
$\unicode{x3bb} $
is a root of
![]() $P_w$
, and hence all Galois conjugates of
$P_w$
, and hence all Galois conjugates of
![]() $\unicode{x3bb} $
must be roots of
$\unicode{x3bb} $
must be roots of
![]() $P_w$
.
$P_w$
.
One can check by simple bookkeeping that for any word w of positive cumulative sign,
![]() $P_w(z)$
,
$P_w(z)$
,
![]() $G({\textrm {Rev}}(w)^\infty , z)$
and
$G({\textrm {Rev}}(w)^\infty , z)$
and
![]() $H(w^\infty , z)$
satisfy the following relationship.
$H(w^\infty , z)$
satisfy the following relationship.
Lemma 2.1. If w is of length n and has positive cumulative sign, then
2.3 Admissibility, itineraries, and dominance
The shift map
![]() $\sigma $
is defined on sequences by
$\sigma $
is defined on sequences by
A sequence
![]() $w=w_1w_2\ldots $
is a generalized symbolic coding of
$w=w_1w_2\ldots $
is a generalized symbolic coding of
![]() $f_\unicode{x3bb} $
for some
$f_\unicode{x3bb} $
for some
![]() $\unicode{x3bb} \in (1,2]$
if and only if
$\unicode{x3bb} \in (1,2]$
if and only if
for every integer
![]() $k \geq 0$
. Because the point
$k \geq 0$
. Because the point
![]() $1/\unicode{x3bb} $
belongs to both intervals
$1/\unicode{x3bb} $
belongs to both intervals
![]() $I_{0,\unicode{x3bb} }$
and
$I_{0,\unicode{x3bb} }$
and
![]() $I_{1,\unicode{x3bb} }$
, there may exist more than one generalized symbolic coding for the itinerary of the point
$I_{1,\unicode{x3bb} }$
, there may exist more than one generalized symbolic coding for the itinerary of the point
![]() $1$
under
$1$
under
![]() $f_{\unicode{x3bb} }$
. The
$f_{\unicode{x3bb} }$
. The
![]() $\unicode{x3bb} $
-itinerary
$\unicode{x3bb} $
-itinerary
![]() $\mathrm {{It}}_{\unicode{x3bb} }$
is the least (with respect to
$\mathrm {{It}}_{\unicode{x3bb} }$
is the least (with respect to
![]() $\leq _E$
) such generalized symbolic coding.
$\leq _E$
) such generalized symbolic coding.
A sequence w starting with
![]() $10$
is called admissible if
$10$
is called admissible if
for all
![]() $k \in \mathbb {N}$
. A word w is called admissible if w has positive cumulative sign and
$k \in \mathbb {N}$
. A word w is called admissible if w has positive cumulative sign and
![]() $w^\infty $
is admissible.
$w^\infty $
is admissible.
We will use the following immediate consequence of Theorem 12.1 of [Reference Milnor and ThurstonMT88].
Theorem 2.2. For every
![]() $\unicode{x3bb} \in (1,2]$
,
$\unicode{x3bb} \in (1,2]$
,
![]() $\mathrm {{It}}_{\unicode{x3bb} }$
is admissible.
$\mathrm {{It}}_{\unicode{x3bb} }$
is admissible.
Proposition 2.3. [Reference Bray, Davis, Lindsey and WuBDLW19]
Let w be a word with positive cumulative sign. If w is admissible and the associated Parry polynomial,
![]() $P_w(z)$
, can be written as the product of
$P_w(z)$
, can be written as the product of
![]() $(z-1)$
and another irreducible factor, then
$(z-1)$
and another irreducible factor, then
![]() $w^{\infty } = \mathrm {{It}}_{\unicode{x3bb} }$
for some
$w^{\infty } = \mathrm {{It}}_{\unicode{x3bb} }$
for some
![]() $\unicode{x3bb} \in (1,2]$
.
$\unicode{x3bb} \in (1,2]$
.
The following is a straightforward corollary [Reference Milnor and ThurstonMT88, Theorem 13.1].
Corollary 2.4. If
![]() $1 < \unicode{x3bb} < \unicode{x3bb} ' \leq 2$
, then
$1 < \unicode{x3bb} < \unicode{x3bb} ' \leq 2$
, then
![]() $\mathrm {{It}}_{\unicode{x3bb} }<_E \mathrm {{It}}_{\unicode{x3bb} '}$
.
$\mathrm {{It}}_{\unicode{x3bb} }<_E \mathrm {{It}}_{\unicode{x3bb} '}$
.
A word w is called dominant (cf. [Reference Bray, Davis, Lindsey and WuBDLW19, Definition 4.1, Lemma 4.2]) if it has positive cumulative sign, and for any
![]() $1\leq k\leq |w|-1$
,
$1\leq k\leq |w|-1$
,
Every dominant word is admissible, but admissible words may not be dominant. A key property of the dominant words is the following, which is proved in [Reference TiozzoTio15] and reviewed in [Reference Bray, Davis, Lindsey and WuBDLW19, Proposition 4.4].
Proposition 2.5. If
![]() $\unicode{x3bb} \in (\sqrt {2}, 2)$
and
$\unicode{x3bb} \in (\sqrt {2}, 2)$
and
![]() $\mathrm {{It}}_\unicode{x3bb} =w^\infty $
, then for any
$\mathrm {{It}}_\unicode{x3bb} =w^\infty $
, then for any
![]() $n>0$
, there exists a word
$n>0$
, there exists a word
![]() $w'$
such that
$w'$
such that
![]() $w^nw'$
is dominant.
$w^nw'$
is dominant.
2.4 Growth rates and critically periodic tent maps
When a continuous self-map f of an interval is postcritically finite, the exponential of its topological entropy,
![]() $e^{h_{\mathrm {top}}(f)}$
, also called its growth rate, is a weak Perron number—a real positive algebraic integer whose modulus is greater than or equal to that of all of its Galois conjugates. This is because cutting the interval at the critical and postcritical sets yields a Markov partition; each of the resulting subintervals is mapped to a finite union of subintervals. The leading eigenvalue of the associated incidence matrix is
$e^{h_{\mathrm {top}}(f)}$
, also called its growth rate, is a weak Perron number—a real positive algebraic integer whose modulus is greater than or equal to that of all of its Galois conjugates. This is because cutting the interval at the critical and postcritical sets yields a Markov partition; each of the resulting subintervals is mapped to a finite union of subintervals. The leading eigenvalue of the associated incidence matrix is
![]() $e^{h_{\mathrm {top}}(f)}$
, which the Perron–Frobenius theorem implies is a weak Perron number.
$e^{h_{\mathrm {top}}(f)}$
, which the Perron–Frobenius theorem implies is a weak Perron number.
In the present work, we consider growth rates of critically periodic unimodal interval self-maps. A unimodal map f is said to be critically periodic if, denoting the critical point of f by c, there exists
![]() $n \in \mathbb {N}$
such that
$n \in \mathbb {N}$
such that
![]() $f^n(c) = c$
. A theorem of Milnor and Thurston [Reference Milnor and ThurstonMT88, Theorem 7.4] tells us that, from the point of view of entropy, instead of considering all critically periodic unimodal maps, we only need to consider critically periodic tent maps. For tent maps, it is easy to see that the growth rate is just the slope
$f^n(c) = c$
. A theorem of Milnor and Thurston [Reference Milnor and ThurstonMT88, Theorem 7.4] tells us that, from the point of view of entropy, instead of considering all critically periodic unimodal maps, we only need to consider critically periodic tent maps. For tent maps, it is easy to see that the growth rate is just the slope
![]() $\unicode{x3bb} $
.
$\unicode{x3bb} $
.
2.5 Renormalization and doubling
As shown in [Reference Bray, Davis, Lindsey and WuBDLW19, §3], for any
![]() $1< \unicode{x3bb} <\sqrt {2}$
, the tent map
$1< \unicode{x3bb} <\sqrt {2}$
, the tent map
![]() $f_\unicode{x3bb} $
is critically periodic if and only if the tent map
$f_\unicode{x3bb} $
is critically periodic if and only if the tent map
![]() $f_{\unicode{x3bb} ^2}$
is critically periodic. (This phenomenon is related to renormalization of the Mandelbrot set.) Furthermore, whenever
$f_{\unicode{x3bb} ^2}$
is critically periodic. (This phenomenon is related to renormalization of the Mandelbrot set.) Furthermore, whenever
![]() $1<\unicode{x3bb} <\sqrt {2}$
,
$1<\unicode{x3bb} <\sqrt {2}$
,
![]() $\mathrm {{It}}_{\unicode{x3bb} }$
can be obtained from
$\mathrm {{It}}_{\unicode{x3bb} }$
can be obtained from
![]() $\mathrm {{It}}_{\unicode{x3bb} ^2}$
by replacing each
$\mathrm {{It}}_{\unicode{x3bb} ^2}$
by replacing each
![]() $1$
in
$1$
in
![]() $\mathrm {{It}}_{\unicode{x3bb} }$
with
$\mathrm {{It}}_{\unicode{x3bb} }$
with
![]() $10$
and each
$10$
and each
![]() $0$
in
$0$
in
![]() $\mathrm {{It}}_{\unicode{x3bb} }$
with
$\mathrm {{It}}_{\unicode{x3bb} }$
with
![]() $11$
. That is, the doubling map
$11$
. That is, the doubling map
![]() $\mathfrak {D}:\{0,1\}^n \to \{0,1\}^{2n}$
,
$\mathfrak {D}:\{0,1\}^n \to \{0,1\}^{2n}$
,
![]() $n \in \mathbb {N} \cup \{\infty \}$
, defined by
$n \in \mathbb {N} \cup \{\infty \}$
, defined by
satisfies
![]() $\mathfrak {D}(\mathrm {{It}}_{\unicode{x3bb} ^2}) = \mathrm {{It}}_{\unicode{x3bb} }$
whenever
$\mathfrak {D}(\mathrm {{It}}_{\unicode{x3bb} ^2}) = \mathrm {{It}}_{\unicode{x3bb} }$
whenever
![]() $f_{\unicode{x3bb} }$
with
$f_{\unicode{x3bb} }$
with
![]() $1 < \unicode{x3bb} < 2$
is critically periodic. We say that a sequence w is renormalizable if there exists a sequence
$1 < \unicode{x3bb} < 2$
is critically periodic. We say that a sequence w is renormalizable if there exists a sequence
![]() $w'$
such that
$w'$
such that
![]() $w=\mathfrak {D}(w')$
; in this case, we say that w is the doubling of
$w=\mathfrak {D}(w')$
; in this case, we say that w is the doubling of
![]() $w'$
and call
$w'$
and call
![]() $w'$
the renormalization of w. We define renormalizable, doubling, and renormalization for words analogously.
$w'$
the renormalization of w. We define renormalizable, doubling, and renormalization for words analogously.
Remark 2.6. The ‘renormalization’ we are considering here is only the period-
![]() $2$
renormalization, that is, the inverse of tuning by the basilica. The reason is that higher order renormalization would create roots in the
$2$
renormalization, that is, the inverse of tuning by the basilica. The reason is that higher order renormalization would create roots in the
![]() $P_w$
that are Galois conjugate of the leading root.
$P_w$
that are Galois conjugate of the leading root.
3 Properties of the doubling map
The goal of this section is to prove some elementary properties of renormalizable words and sequences that we will use in later sections to extend the results about the part of the teapot above height
![]() $\sqrt {2}$
to the lower part.
$\sqrt {2}$
to the lower part.
Lemma 3.1. The doubling map
![]() $\mathfrak {D}$
preserves the twisted lexicographic ordering
$\mathfrak {D}$
preserves the twisted lexicographic ordering
![]() $\leq _E$
, cumulative signs, and hence also admissibility.
$\leq _E$
, cumulative signs, and hence also admissibility.
Proof. If the number of
![]() $1$
s in a word w equals n, then for any letter a, the number of
$1$
s in a word w equals n, then for any letter a, the number of
![]() $1$
s in
$1$
s in
![]() ${\textrm {Pre}}_{2|w|+1}(\mathfrak {D}(w\cdot a))$
equals
${\textrm {Pre}}_{2|w|+1}(\mathfrak {D}(w\cdot a))$
equals
![]() $2|w|+1-n$
. It follows that if n is odd,
$2|w|+1-n$
. It follows that if n is odd,
![]() $w\cdot 1 <_E w \cdot 0$
and
$w\cdot 1 <_E w \cdot 0$
and
![]() $\mathfrak {D}(w\cdot 1) <_E \mathfrak {D}(w\cdot 0)$
; if n is even,
$\mathfrak {D}(w\cdot 1) <_E \mathfrak {D}(w\cdot 0)$
; if n is even,
![]() $w\cdot 0 <_E w\cdot 1$
and
$w\cdot 0 <_E w\cdot 1$
and
![]() $\mathfrak {D}(w\cdot 0) <_E \mathfrak {D}(w\cdot 1)$
. Thus,
$\mathfrak {D}(w\cdot 0) <_E \mathfrak {D}(w\cdot 1)$
. Thus,
![]() $\mathfrak {D}$
preserves
$\mathfrak {D}$
preserves
![]() $\leq _E$
. Furthermore, if a word w has positive cumulative sign, then the number, n, of
$\leq _E$
. Furthermore, if a word w has positive cumulative sign, then the number, n, of
![]() $1$
s in w is even, implying that
$1$
s in w is even, implying that
![]() $\mathfrak {D}(w)$
, which contains
$\mathfrak {D}(w)$
, which contains
![]() $2w-n 1$
s, also has positive cumulative sign.
$2w-n 1$
s, also has positive cumulative sign.
Lemma 3.2. The doubling map
![]() $\mathfrak {D}$
takes itineraries to itineraries. That is, if
$\mathfrak {D}$
takes itineraries to itineraries. That is, if
![]() $\unicode{x3bb} ^{2^k} = \unicode{x3bb} '$
, then
$\unicode{x3bb} ^{2^k} = \unicode{x3bb} '$
, then
![]() $\mathfrak {D}^k(\mathrm {{It}}_{\unicode{x3bb} '}) = \mathrm {{It}}_{\unicode{x3bb} }$
.
$\mathfrak {D}^k(\mathrm {{It}}_{\unicode{x3bb} '}) = \mathrm {{It}}_{\unicode{x3bb} }$
.
Proof. By induction, it is easy to see that we only need to prove it for
![]() $k=1$
, that is,
$k=1$
, that is,
![]() $\mathfrak {D}(\mathrm {{It}}_{\unicode{x3bb} ^2})=\mathrm {{It}}_\unicode{x3bb} $
. For any
$\mathfrak {D}(\mathrm {{It}}_{\unicode{x3bb} ^2})=\mathrm {{It}}_\unicode{x3bb} $
. For any
![]() $\unicode{x3bb} \leq \sqrt {2}$
, the tent map
$\unicode{x3bb} \leq \sqrt {2}$
, the tent map
![]() $f_{\unicode{x3bb} }$
sends the interval
$f_{\unicode{x3bb} }$
sends the interval
![]() $[2/(\unicode{x3bb} +1), 1]$
to
$[2/(\unicode{x3bb} +1), 1]$
to
![]() $[2-\unicode{x3bb} , 2/(\unicode{x3bb} +1)]$
and vice versa. Hence,
$[2-\unicode{x3bb} , 2/(\unicode{x3bb} +1)]$
and vice versa. Hence,
![]() $f^2_{\unicode{x3bb} }$
is a tent map from
$f^2_{\unicode{x3bb} }$
is a tent map from
![]() $[2/(\unicode{x3bb} +1), 1]$
of slope
$[2/(\unicode{x3bb} +1), 1]$
of slope
![]() $\unicode{x3bb} ^2$
, and any
$\unicode{x3bb} ^2$
, and any
![]() $x=f^{2k}_{\unicode{x3bb} }(1)$
lies on the left-hand side of the critical point of
$x=f^{2k}_{\unicode{x3bb} }(1)$
lies on the left-hand side of the critical point of
![]() $f^2_{\unicode{x3bb} }$
if and only if x and
$f^2_{\unicode{x3bb} }$
if and only if x and
![]() $f_{\unicode{x3bb} }(x)$
are both to the right of
$f_{\unicode{x3bb} }(x)$
are both to the right of
![]() $1/\unicode{x3bb} $
, while
$1/\unicode{x3bb} $
, while
![]() $f^{2k}_{\unicode{x3bb} }(1)$
lies on the right-hand side of the critical point of
$f^{2k}_{\unicode{x3bb} }(1)$
lies on the right-hand side of the critical point of
![]() $f^2_{\unicode{x3bb} }$
if and only if x is to the right of
$f^2_{\unicode{x3bb} }$
if and only if x is to the right of
![]() $1/\unicode{x3bb} $
and
$1/\unicode{x3bb} $
and
![]() $f_{\unicode{x3bb} }(x)$
is to the left of
$f_{\unicode{x3bb} }(x)$
is to the left of
![]() $1/\unicode{x3bb} $
, and this finishes the proof for the case when
$1/\unicode{x3bb} $
, and this finishes the proof for the case when
![]() $\mathrm {{It}}_{\unicode{x3bb} ^2}$
is not periodic. The case when
$\mathrm {{It}}_{\unicode{x3bb} ^2}$
is not periodic. The case when
![]() $\mathrm {{It}}_{\unicode{x3bb} ^2}$
is periodic follows from this argument together with Lemma 3.1.
$\mathrm {{It}}_{\unicode{x3bb} ^2}$
is periodic follows from this argument together with Lemma 3.1.
Proposition 3.3. If w is a word with positive cumulative sign and
![]() $w'$
is the renormalization of w, then
$w'$
is the renormalization of w, then
Proof. Suppose w and
![]() $w'$
are words satisfying
$w'$
are words satisfying
![]() $\mathfrak {D}(w')=w$
. It is easy to see that if
$\mathfrak {D}(w')=w$
. It is easy to see that if
![]() $w=w_1w_2\ldots w_{2n}$
has a positive cumulative sign, then
$w=w_1w_2\ldots w_{2n}$
has a positive cumulative sign, then
![]() $w'=w^{\prime }_1w^{\prime }_2\ldots w^{\prime }_n$
also has a positive cumulative sign. So, the proposition follows from the following more general statement: if
$w'=w^{\prime }_1w^{\prime }_2\ldots w^{\prime }_n$
also has a positive cumulative sign. So, the proposition follows from the following more general statement: if
![]() $w'$
is any word, w is the doubling of
$w'$
is any word, w is the doubling of
![]() $w'$
, then
$w'$
, then
We will prove (3.1) using induction on
![]() $|w'|$
. In the base case,
$|w'|$
. In the base case,
![]() $|w'|=1$
,
$|w'|=1$
,
![]() $w'=1$
, or
$w'=1$
, or
![]() $w'=0$
, and the statement is true by calculation. Now assume the statement is true for all words
$w'=0$
, and the statement is true by calculation. Now assume the statement is true for all words
![]() $w'$
such that
$w'$
such that
![]() $|w'| \leq n-1$
. Let
$|w'| \leq n-1$
. Let
![]() $w'$
and w be words with
$w'$
and w be words with
![]() $|w'| =n$
and
$|w'| =n$
and
![]() $\mathfrak {D}(w')=w$
. Let
$\mathfrak {D}(w')=w$
. Let
![]() $w^{\prime }_0$
be
$w^{\prime }_0$
be
![]() $w'$
with the last letter removed, and let
$w'$
with the last letter removed, and let
![]() $w_0$
be w with the last two letters removed. Then, by the inductive hypothesis,
$w_0$
be w with the last two letters removed. Then, by the inductive hypothesis,
We divide the inductive step into two cases.
Case 1:
![]() $w^{\prime }_n=0$
. This implies
$w^{\prime }_n=0$
. This implies
![]() $w=w_0\cdot 11$
, so
$w=w_0\cdot 11$
, so
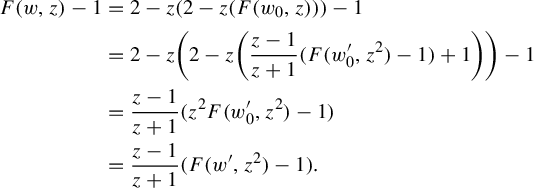 $$ \begin{align*} F(w, z)-1 &=2-z (2-z(F(w_0, z)))-1\\ &=2-z \bigg(2-z \bigg({z-1\over z+1}(F(w^{\prime}_0, z^2)-1)+1 \bigg)\bigg)-1\\ &={z-1\over z+1}(z^2F(w^{\prime}_0, z^2)-1)\\ &={z-1\over z+1}(F(w', z^2)-1). \end{align*} $$
$$ \begin{align*} F(w, z)-1 &=2-z (2-z(F(w_0, z)))-1\\ &=2-z \bigg(2-z \bigg({z-1\over z+1}(F(w^{\prime}_0, z^2)-1)+1 \bigg)\bigg)-1\\ &={z-1\over z+1}(z^2F(w^{\prime}_0, z^2)-1)\\ &={z-1\over z+1}(F(w', z^2)-1). \end{align*} $$
Case 2:
![]() $w^{\prime }_n=1$
. This implies
$w^{\prime }_n=1$
. This implies
![]() $w=w_0\cdot 10$
, so
$w=w_0\cdot 10$
, so
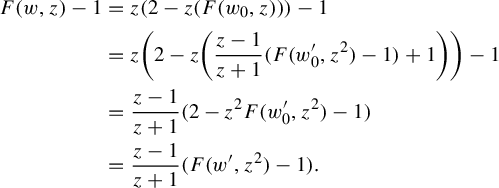 $$ \begin{align*} F(w, z)-1 &=z(2-z(F(w_0, z)) )-1\\ &=z \bigg(2-z \bigg({z-1\over z+1}(F(w^{\prime}_0, z^2)-1)+1\bigg)\bigg)-1\\ &={z-1\over z+1} (2-z^2F(w^{\prime}_0, z^2)-1)\\ &={z-1\over z+1}(F(w', z^2)-1).\\[-3.4pc] \end{align*} $$
$$ \begin{align*} F(w, z)-1 &=z(2-z(F(w_0, z)) )-1\\ &=z \bigg(2-z \bigg({z-1\over z+1}(F(w^{\prime}_0, z^2)-1)+1\bigg)\bigg)-1\\ &={z-1\over z+1} (2-z^2F(w^{\prime}_0, z^2)-1)\\ &={z-1\over z+1}(F(w', z^2)-1).\\[-3.4pc] \end{align*} $$
Proposition 3.4. Let w be an admissible word. Then
![]() $w^{\infty }$
renormalizable if only if
$w^{\infty }$
renormalizable if only if
Proof. First, it is easy to see that a sequence is renormalizable if and only if all its odd index letters are
![]() $1$
, and a word is renormalizable if and only if it has even length and all its odd indexed letters are
$1$
, and a word is renormalizable if and only if it has even length and all its odd indexed letters are
![]() $1$
. Because any admissible word starts with
$1$
. Because any admissible word starts with
![]() $10$
, an admissible word w is renormalizable if and only if
$10$
, an admissible word w is renormalizable if and only if
![]() $w^\infty $
is admissible and renormalizable.
$w^\infty $
is admissible and renormalizable.
Now suppose
![]() $w^\infty $
is admissible and renormalizable. Suppose the second
$w^\infty $
is admissible and renormalizable. Suppose the second
![]() $0$
in
$0$
in
![]() $w^\infty $
is at the
$w^\infty $
is at the
![]() $k\textrm {th}$
location. It suffices to show that
$k\textrm {th}$
location. It suffices to show that
![]() ${\textrm {Pre}}_{k-1}(w^\infty )$
has positive cumulative sign, which is equivalent to showing that k is even, because the
${\textrm {Pre}}_{k-1}(w^\infty )$
has positive cumulative sign, which is equivalent to showing that k is even, because the
![]() $(k-1)$
-prefix of
$(k-1)$
-prefix of
![]() $w^\infty $
and
$w^\infty $
and
![]() $10\cdot 1^\infty $
are the same. This is an immediate consequence of the admissibility of
$10\cdot 1^\infty $
are the same. This is an immediate consequence of the admissibility of
![]() $w^\infty $
.
$w^\infty $
.
Now we prove the other direction. The sequence
![]() $w^\infty $
being admissible implies that the first
$w^\infty $
being admissible implies that the first
![]() $0$
in
$0$
in
![]() $w^\infty $
is at the second location. If we can further prove that the distance between any two consecutive
$w^\infty $
is at the second location. If we can further prove that the distance between any two consecutive
![]() $0$
s is even, then all
$0$
s is even, then all
![]() $0$
s are at even locations, and hence
$0$
s are at even locations, and hence
![]() $w^\infty $
is admissible. Denote by
$w^\infty $
is admissible. Denote by
![]() $i_k$
the location of the
$i_k$
the location of the
![]() $k\textrm {th} 0$
. Let
$k\textrm {th} 0$
. Let
![]() $k_m$
be the smallest number such that
$k_m$
be the smallest number such that
![]() $i_{k_m}-i_{k_{m-1}}$
is odd. Then by definition of
$i_{k_m}-i_{k_{m-1}}$
is odd. Then by definition of
![]() $<_E$
,
$<_E$
,
Remark 3.5. By
![]() $k\textrm {th}$
renormalization or
$k\textrm {th}$
renormalization or
![]() $k\textrm {th}$
doubling, we mean carrying out the renormalization or doubling on a word or sequence k times. Proposition 3.3 above implies that if
$k\textrm {th}$
doubling, we mean carrying out the renormalization or doubling on a word or sequence k times. Proposition 3.3 above implies that if
![]() $w'$
is the
$w'$
is the
![]() $k\textrm {th}$
renormalization of w, then the roots of
$k\textrm {th}$
renormalization of w, then the roots of
![]() $P_w$
not on the unit circle are the
$P_w$
not on the unit circle are the
![]() $(2^k)\textrm {th}$
roots of the roots of
$(2^k)\textrm {th}$
roots of the roots of
![]() $P_{w'}$
that are not on the unit circle.
$P_{w'}$
that are not on the unit circle.
Furthermore, because renormalization of sequences preserves
![]() $<_E$
(Lemma 3.1), we can apply Proposition 3.4 above repeatedly to show that if the
$<_E$
(Lemma 3.1), we can apply Proposition 3.4 above repeatedly to show that if the
![]() $w_k$
is the
$w_k$
is the
![]() $k\textrm {th}$
doubling of
$k\textrm {th}$
doubling of
![]() $10\cdot 1^\infty $
, w is admissible, and
$10\cdot 1^\infty $
, w is admissible, and
![]() $w^\infty <_Ew_k$
, then w has a
$w^\infty <_Ew_k$
, then w has a
![]() $k\textrm {th}$
renormalization.
$k\textrm {th}$
renormalization.
4 Roots in
 $\mathbb {D}$
of reducible Parry polynomials
$\mathbb {D}$
of reducible Parry polynomials
The purpose of this section is to prove Theorem 4.5, an alternative characterization of sets
![]() ${\Xi }_\unicode{x3bb} \cap \overline {\mathbb {D}}$
, for
${\Xi }_\unicode{x3bb} \cap \overline {\mathbb {D}}$
, for
![]() $\unicode{x3bb} \in (1,2]$
, using the results in [Reference Bray, Davis, Lindsey and WuBDLW19]. An upshot of Theorem 4.5 is that we do not need to worry about extraneous roots in
$\unicode{x3bb} \in (1,2]$
, using the results in [Reference Bray, Davis, Lindsey and WuBDLW19]. An upshot of Theorem 4.5 is that we do not need to worry about extraneous roots in
![]() $\mathbb {D}$
from reducible Parry polynomials.
$\mathbb {D}$
from reducible Parry polynomials.
We will use the following four results from [Reference Bray, Davis, Lindsey and WuBDLW19].
Theorem 4.1. [Reference Bray, Davis, Lindsey and WuBDLW19, Theorem 1 (‘persistence theorem’), Theorem 2]
If
![]() $(z, \unicode{x3bb} )\in {\Upsilon _2^{cp}}$
,
$(z, \unicode{x3bb} )\in {\Upsilon _2^{cp}}$
,
![]() $|z|\leq 1$
, then so is
$|z|\leq 1$
, then so is
![]() $(z, y)$
for any
$(z, y)$
for any
![]() $y\in [\unicode{x3bb} , 2]$
.
$y\in [\unicode{x3bb} , 2]$
.
Proposition 4.2. [Reference Bray, Davis, Lindsey and WuBDLW19, Lemma 5.3]
Let
![]() $w_1$
be dominant,
$w_1$
be dominant,
![]() $w_1>_E10\cdot 1^{|w_1|-2}$
,
$w_1>_E10\cdot 1^{|w_1|-2}$
,
![]() $w_2$
be admissible,
$w_2$
be admissible,
![]() $w_1^\infty>_Ew_2^\infty $
, and assume that there is some m such that
$w_1^\infty>_Ew_2^\infty $
, and assume that there is some m such that
Then there is some
![]() $w'$
, some integer
$w'$
, some integer
![]() $m'\geq m$
, such that
$m'\geq m$
, such that
![]() $(w_1w'w_2^{m'})^\infty $
is admissible,
$(w_1w'w_2^{m'})^\infty $
is admissible,
and the Parry polynomial
![]() $P_{w_1w'w_2^{m'}}(z)$
can be written as the product of
$P_{w_1w'w_2^{m'}}(z)$
can be written as the product of
![]() $(z-1)$
and another polynomial
$(z-1)$
and another polynomial
![]() $Q(z)$
such that
$Q(z)$
such that
![]() $Q(z^{2^k})$
is irreducible for all integers
$Q(z^{2^k})$
is irreducible for all integers
![]() $k \geq 0$
.
$k \geq 0$
.
Proposition 4.3. [Reference Bray, Davis, Lindsey and WuBDLW19, Lemma 5.5]
If
![]() $w_2$
is an admissible word and
$w_2$
is an admissible word and
![]() $z\in \mathbb {D}$
is a root of
$z\in \mathbb {D}$
is a root of
![]() $P_{w_2}$
, then for any
$P_{w_2}$
, then for any
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $N\in \mathbb {N}$
such that for any word
$N\in \mathbb {N}$
such that for any word
![]() $w_1$
and any integer
$w_1$
and any integer
![]() $n\ge N$
,
$n\ge N$
,
![]() $P_{w_1w_2^n}$
has a root within distance
$P_{w_1w_2^n}$
has a root within distance
![]() $\epsilon $
of z.
$\epsilon $
of z.
Proposition 4.4. [Reference Bray, Davis, Lindsey and WuBDLW19, Lemma 5.7, Remark 5.8]
If
![]() $y\in [\sqrt {2}, 2]$
, for any
$y\in [\sqrt {2}, 2]$
, for any
![]() $\epsilon>0$
, there exists a dominant word
$\epsilon>0$
, there exists a dominant word
![]() $w_1$
such that for any word
$w_1$
such that for any word
![]() $w_2$
, the leading root of
$w_2$
, the leading root of
![]() $P_{w_1w_2}$
is within distance
$P_{w_1w_2}$
is within distance
![]() $\epsilon $
of y, and
$\epsilon $
of y, and
![]() $w_1>_E10\cdot 1^{|w_1|-2}$
.
$w_1>_E10\cdot 1^{|w_1|-2}$
.
We now use the above results to establish the following characterization of the sets
![]() ${\Xi }_\unicode{x3bb} \cap \overline {\mathbb {D}}$
, which will be the starting point of our proof of Theorem 1.7.
${\Xi }_\unicode{x3bb} \cap \overline {\mathbb {D}}$
, which will be the starting point of our proof of Theorem 1.7.
Theorem 4.5. Fix
![]() $1 < \unicode{x3bb} < 2$
. For each
$1 < \unicode{x3bb} < 2$
. For each
![]() $\unicode{x3bb} '> \unicode{x3bb} $
, define
$\unicode{x3bb} '> \unicode{x3bb} $
, define
![]() $Y_{\unicode{x3bb} '}$
to be the closure of the set of roots in
$Y_{\unicode{x3bb} '}$
to be the closure of the set of roots in
![]() $\overline {\mathbb {D}}$
of all Parry polynomials
$\overline {\mathbb {D}}$
of all Parry polynomials
![]() $P_w$
such that w is admissible and
$P_w$
such that w is admissible and
![]() $w^\infty \leq _E\mathrm {{It}}_{\unicode{x3bb} '}$
, union with
$w^\infty \leq _E\mathrm {{It}}_{\unicode{x3bb} '}$
, union with
![]() $S^1$
, that is,
$S^1$
, that is,
Then,
Remark 4.6. The condition ‘
![]() $w^\infty <_E\mathrm {{It}}_{\unicode{x3bb} '}$
for every
$w^\infty <_E\mathrm {{It}}_{\unicode{x3bb} '}$
for every
![]() $\unicode{x3bb} '>\unicode{x3bb} $
’ is different from ‘
$\unicode{x3bb} '>\unicode{x3bb} $
’ is different from ‘
![]() $w^{\infty } \leq \mathrm {{It}}_{\unicode{x3bb} }$
’ because there could exist a symbolic coding for the itinerary of
$w^{\infty } \leq \mathrm {{It}}_{\unicode{x3bb} }$
’ because there could exist a symbolic coding for the itinerary of
![]() $1$
under the tent map
$1$
under the tent map
![]() $f_{\unicode{x3bb} }$
that is
$f_{\unicode{x3bb} }$
that is
![]() $>_E \mathrm {{It}}_{\unicode{x3bb} }$
.
$>_E \mathrm {{It}}_{\unicode{x3bb} }$
.
Proof. For any
![]() $1 < \unicode{x3bb} < 2$
, let
$1 < \unicode{x3bb} < 2$
, let
We will first prove
![]() ${\Xi }_{\unicode{x3bb} } \subseteq {\Xi }_{\unicode{x3bb} }'$
. For any
${\Xi }_{\unicode{x3bb} } \subseteq {\Xi }_{\unicode{x3bb} }'$
. For any
![]() $\unicode{x3bb} '$
, define the set
$\unicode{x3bb} '$
, define the set
![]() $Z_{\unicode{x3bb} '}$
to be the closure of the set of Galois conjugates of critically periodic growth rates that are at most
$Z_{\unicode{x3bb} '}$
to be the closure of the set of Galois conjugates of critically periodic growth rates that are at most
![]() $\unicode{x3bb} '$
, union with
$\unicode{x3bb} '$
, union with
![]() $S^1$
. By the persistence theorem,
$S^1$
. By the persistence theorem,
![]() $\unicode{x3bb} _1 < \unicode{x3bb} _2$
implies
$\unicode{x3bb} _1 < \unicode{x3bb} _2$
implies
![]() $Z_{\unicode{x3bb} _1} \subseteq Z_{\unicode{x3bb} _2}$
. So if any point
$Z_{\unicode{x3bb} _1} \subseteq Z_{\unicode{x3bb} _2}$
. So if any point
![]() $x \in \bigcap _{\unicode{x3bb} '> \unicode{x3bb} } Z_{\unicode{x3bb} '}$
, then
$x \in \bigcap _{\unicode{x3bb} '> \unicode{x3bb} } Z_{\unicode{x3bb} '}$
, then
![]() $x \in {\Xi }_{\unicode{x3bb} }$
since
$x \in {\Xi }_{\unicode{x3bb} }$
since
![]() $\Upsilon _2^{cp}$
is closed; similarly, if
$\Upsilon _2^{cp}$
is closed; similarly, if
![]() $x \not \in \bigcap _{\unicode{x3bb} '> \unicode{x3bb} } Z_{\unicode{x3bb} '}$
, then
$x \not \in \bigcap _{\unicode{x3bb} '> \unicode{x3bb} } Z_{\unicode{x3bb} '}$
, then
![]() $x \not \in {\Xi }_{\unicode{x3bb} }$
. Hence,
$x \not \in {\Xi }_{\unicode{x3bb} }$
. Hence,
The conclusion will now follow from the statement that
![]() $Z_{\unicode{x3bb} '} \subseteq Y_{\unicode{x3bb} '}$
for all
$Z_{\unicode{x3bb} '} \subseteq Y_{\unicode{x3bb} '}$
for all
![]() $\unicode{x3bb} '$
. If z is a Galois conjugate of a critically periodic growth rate
$\unicode{x3bb} '$
. If z is a Galois conjugate of a critically periodic growth rate
![]() $\unicode{x3bb} "$
that is at most
$\unicode{x3bb} "$
that is at most
![]() $\unicode{x3bb} '$
, then z is a root of the Parry polynomial
$\unicode{x3bb} '$
, then z is a root of the Parry polynomial
![]() $P_w$
such that
$P_w$
such that
![]() $w^{\infty }=\mathrm {{It}}_{\unicode{x3bb} "}$
, and
$w^{\infty }=\mathrm {{It}}_{\unicode{x3bb} "}$
, and
![]() $\mathrm {{It}}_{\unicode{x3bb} "} \leq _E \mathrm {{It}}_{\unicode{x3bb} '}$
by Corollary 2.4. Thus,
$\mathrm {{It}}_{\unicode{x3bb} "} \leq _E \mathrm {{It}}_{\unicode{x3bb} '}$
by Corollary 2.4. Thus,
![]() $Z_{\unicode{x3bb} '} \subseteq Y_{\unicode{x3bb} '}$
for all
$Z_{\unicode{x3bb} '} \subseteq Y_{\unicode{x3bb} '}$
for all
![]() $\unicode{x3bb} '$
.
$\unicode{x3bb} '$
.
We will now prove
![]() ${\Xi }^{\prime }_\unicode{x3bb} \subseteq {\Xi }_\unicode{x3bb} $
. To do this, it suffices to show
${\Xi }^{\prime }_\unicode{x3bb} \subseteq {\Xi }_\unicode{x3bb} $
. To do this, it suffices to show
We first consider the case
![]() $\unicode{x3bb} '\geq \sqrt {2}$
. Suppose z is the root of some
$\unicode{x3bb} '\geq \sqrt {2}$
. Suppose z is the root of some
![]() $P_w$
, where w is admissible and the leading root of
$P_w$
, where w is admissible and the leading root of
![]() $P_w$
is no larger than
$P_w$
is no larger than
![]() $\unicode{x3bb} '$
. (
$\unicode{x3bb} '$
. (
![]() $Y_{\unicode{x3bb} '}$
is the closure of all such z terms.) For any
$Y_{\unicode{x3bb} '}$
is the closure of all such z terms.) For any
![]() $\epsilon>0$
, Proposition 4.4 guarantees the existence of a dominant word
$\epsilon>0$
, Proposition 4.4 guarantees the existence of a dominant word
![]() $w_1$
such that for any
$w_1$
such that for any
![]() $w_2$
, the leading root of
$w_2$
, the leading root of
![]() $P_{w_1w_2}$
is in
$P_{w_1w_2}$
is in
![]() $[\unicode{x3bb} ', \unicode{x3bb} '+\epsilon )$
and
$[\unicode{x3bb} ', \unicode{x3bb} '+\epsilon )$
and
![]() $w_1>_E10\cdot 1^{|w_1|-2}$
. By monotonicity (Corollary 2.4),
$w_1>_E10\cdot 1^{|w_1|-2}$
. By monotonicity (Corollary 2.4),
![]() $w_1^{\infty }>_E w^{\infty }$
. Without loss of generality, we may choose
$w_1^{\infty }>_E w^{\infty }$
. Without loss of generality, we may choose
![]() $w_1$
so that its length,
$w_1$
so that its length,
![]() $|w_1|$
, is arbitrarily big (this is because as we let
$|w_1|$
, is arbitrarily big (this is because as we let
![]() $\epsilon \to 0$
, we get arbitrarily many such dominant strings, and there are finitely many strings of at most any given length). Thus we may assume that
$\epsilon \to 0$
, we get arbitrarily many such dominant strings, and there are finitely many strings of at most any given length). Thus we may assume that
![]() $w_1$
and w satisfy the assumptions of Proposition 4.2 with the m of Proposition 4.2 being arbitrarily large, and in particular, m is
$w_1$
and w satisfy the assumptions of Proposition 4.2 with the m of Proposition 4.2 being arbitrarily large, and in particular, m is
![]() $\geq $
the N of Proposition 4.3 using w for
$\geq $
the N of Proposition 4.3 using w for
![]() $w_2$
. Let
$w_2$
. Let
![]() $w_3$
be the word constructed by Proposition 4.2. Because
$w_3$
be the word constructed by Proposition 4.2. Because
![]() $w_3$
is admissible, has positive cumulative sign, and
$w_3$
is admissible, has positive cumulative sign, and
![]() $P_{w_3}(z)/(z-1)$
is irreducible,
$P_{w_3}(z)/(z-1)$
is irreducible,
![]() $w_3^{\infty } = \mathrm {{It}}_{\unicode{x3bb} _3}$
for some
$w_3^{\infty } = \mathrm {{It}}_{\unicode{x3bb} _3}$
for some
![]() $\unicode{x3bb} _3$
by Proposition 2.3. We know
$\unicode{x3bb} _3$
by Proposition 2.3. We know
![]() $\unicode{x3bb} _3 \in [\unicode{x3bb} ', \unicode{x3bb} '+\epsilon ]$
because
$\unicode{x3bb} _3 \in [\unicode{x3bb} ', \unicode{x3bb} '+\epsilon ]$
because
![]() $w_3$
has the prefix
$w_3$
has the prefix
![]() $w_1$
. Also, any root of
$w_1$
. Also, any root of
![]() $P_{w_3}$
in
$P_{w_3}$
in
![]() $\mathbb {D}$
will be a Galois conjugate of
$\mathbb {D}$
will be a Galois conjugate of
![]() $\unicode{x3bb} _3$
, and by construction,
$\unicode{x3bb} _3$
, and by construction,
![]() $P_{w_3}$
has a root close to z. The containment now follows from letting
$P_{w_3}$
has a root close to z. The containment now follows from letting
![]() $\epsilon \rightarrow 0$
.
$\epsilon \rightarrow 0$
.
Now we deal with the case
![]() $1<\unicode{x3bb} '<\sqrt {2}$
. Let k be the unique natural number such that
$1<\unicode{x3bb} '<\sqrt {2}$
. Let k be the unique natural number such that
![]() $(\unicode{x3bb} ')^{2^k}\in [\sqrt {2}, 2)$
. Remark 3.5 implies that w has a
$(\unicode{x3bb} ')^{2^k}\in [\sqrt {2}, 2)$
. Remark 3.5 implies that w has a
![]() $k\textrm {th}$
renormalization
$k\textrm {th}$
renormalization
![]() $w_0$
, and
$w_0$
, and
![]() $z^{2^k}$
is a root of
$z^{2^k}$
is a root of
![]() $P_{w_0}$
. Using
$P_{w_0}$
. Using
![]() $w_0$
in place of w in the argument in the previous paragraph, we get a critically periodic growth rate
$w_0$
in place of w in the argument in the previous paragraph, we get a critically periodic growth rate
![]() $\unicode{x3bb} _4$
close to
$\unicode{x3bb} _4$
close to
![]() $(\unicode{x3bb} ')^{2^k}$
, such that one of its Galois conjugates
$(\unicode{x3bb} ')^{2^k}$
, such that one of its Galois conjugates
![]() $z_2$
is close to
$z_2$
is close to
![]() $z^{2^k}$
. The conclusion in Proposition 4.2 further implies that any
$z^{2^k}$
. The conclusion in Proposition 4.2 further implies that any
![]() $(2^k)\textrm {th}$
root of
$(2^k)\textrm {th}$
root of
![]() $z_2$
must be a Galois conjugate of the
$z_2$
must be a Galois conjugate of the
![]() $(2^k)\textrm {th}$
root of
$(2^k)\textrm {th}$
root of
![]() $\unicode{x3bb} _4$
as well, which implies that there is a Galois conjugate of
$\unicode{x3bb} _4$
as well, which implies that there is a Galois conjugate of
![]() $\unicode{x3bb} _4^{2^{-k}}$
which is close to z, which finishes the proof of the proposition.
$\unicode{x3bb} _4^{2^{-k}}$
which is close to z, which finishes the proof of the proposition.
The following corollary is not used to prove any further results in the present work.
Corollary 4.7. Let V denote the set of all real numbers
![]() $\unicode{x3bb} \in (1,2)$
such that:
$\unicode{x3bb} \in (1,2)$
such that:
-
(1) the tent map
 $f_{\unicode{x3bb} }$
is critically periodic;
$f_{\unicode{x3bb} }$
is critically periodic; -
(2) there exists a word w such that
 $\mathrm {{It}}_{\unicode{x3bb} } = w^{\infty }$
;
$\mathrm {{It}}_{\unicode{x3bb} } = w^{\infty }$
; -
(3) the Parry polynomial
 $P_w(z)$
can be written as the product of an irreducible polynomial (in
$P_w(z)$
can be written as the product of an irreducible polynomial (in
 $\mathbb {Z}[z]$
) and some cyclotomic polynomials.
$\mathbb {Z}[z]$
) and some cyclotomic polynomials.
Then V is dense in
![]() $[1,2]$
.
$[1,2]$
.
Proof. The growth rates
![]() $\unicode{x3bb} _3$
, as well as the growth rates
$\unicode{x3bb} _3$
, as well as the growth rates
![]() $\unicode{x3bb} _3^{2^{-k}}$
,
$\unicode{x3bb} _3^{2^{-k}}$
,
![]() $k \in \mathbb {N}$
, constructed in the proof of Theorem 4.5 all satisfy conditions (1)–(3).
$k \in \mathbb {N}$
, constructed in the proof of Theorem 4.5 all satisfy conditions (1)–(3).
5
 $\unicode{x3bb} $
-suitability
$\unicode{x3bb} $
-suitability
In this section, we establish some basic properties of
![]() $\unicode{x3bb} $
-suitability and prove the technical lemmas about
$\unicode{x3bb} $
-suitability and prove the technical lemmas about
![]() $\unicode{x3bb} $
-suitability that we will need in §6.
$\unicode{x3bb} $
-suitability that we will need in §6.
For convenience, we reproduce the definition of
![]() $\unicode{x3bb} $
-suitability here. For
$\unicode{x3bb} $
-suitability here. For
![]() $\unicode{x3bb} \in (1,2)$
, a sequence w is called
$\unicode{x3bb} \in (1,2)$
, a sequence w is called
![]() $\unicode{x3bb} $
-suitable if for every
$\unicode{x3bb} $
-suitable if for every
![]() $\unicode{x3bb} '\in (\unicode{x3bb} , 2]$
, the following conditions hold.
$\unicode{x3bb} '\in (\unicode{x3bb} , 2]$
, the following conditions hold.
-
(1)
 ${\textrm {Rev}} ( {\textrm {Pre}}_n(w)) \leq _E {\textrm {Pre}}_n(\mathrm {{It}}_{\unicode{x3bb} '})$
for all
${\textrm {Rev}} ( {\textrm {Pre}}_n(w)) \leq _E {\textrm {Pre}}_n(\mathrm {{It}}_{\unicode{x3bb} '})$
for all
 $n \in \mathbb {N}$
.
$n \in \mathbb {N}$
. -
(2) If
 ${\textrm {Rev}}({\textrm {Pre}}_n(w)) = {\textrm {Pre}}_n(\mathrm {{It}}_{\unicode{x3bb} '})$
, then the cumulative sign
${\textrm {Rev}}({\textrm {Pre}}_n(w)) = {\textrm {Pre}}_n(\mathrm {{It}}_{\unicode{x3bb} '})$
, then the cumulative sign
 $s({\textrm {Pre}}_n(w)) = -1$
.
$s({\textrm {Pre}}_n(w)) = -1$
. -
(3) If
 $\mathrm {{It}}_{\unicode{x3bb} '} = 1 \cdot 0^k \cdot 1 \ldots , k \in \mathbb {N}$
, then w does not contain
$\mathrm {{It}}_{\unicode{x3bb} '} = 1 \cdot 0^k \cdot 1 \ldots , k \in \mathbb {N}$
, then w does not contain
 $k+1$
consecutive
$k+1$
consecutive
 $0$
s (that is, if
$0$
s (that is, if
 $\mathrm {{It}}_{\unicode{x3bb} '}$
starts with
$\mathrm {{It}}_{\unicode{x3bb} '}$
starts with
 $1$
followed by
$1$
followed by
 $k 0$
s and then
$k 0$
s and then
 $1$
, writing w as
$1$
, writing w as
 $w=w_1w_2\ldots ,$
there does not exist
$w=w_1w_2\ldots ,$
there does not exist
 $n \in \mathbb {N}$
such that
$n \in \mathbb {N}$
such that
 $w_i = 0$
for all
$w_i = 0$
for all
 $n \leq i \leq n+k$
).
$n \leq i \leq n+k$
). -
(4) If
 $n \in \mathbb {N}$
satisfies
$n \in \mathbb {N}$
satisfies
 $\sqrt {2} \leq _E (\unicode{x3bb} ')^{2^n} < 2$
, then
$\sqrt {2} \leq _E (\unicode{x3bb} ')^{2^n} < 2$
, then
 $w = \mathfrak {D}^{\prime {n}}(w')$
for some sequence
$w = \mathfrak {D}^{\prime {n}}(w')$
for some sequence
 $w'$
, where
$w'$
, where
 $\mathfrak {D}'$
is the map that replaces
$\mathfrak {D}'$
is the map that replaces
 $0$
with
$0$
with
 $11$
and
$11$
and
 $1$
with
$1$
with
 $01$
. Furthermore, if then
$01$
. Furthermore, if then $$ \begin{align*}\mathrm{{It}}_{\unicode{x3bb}^{\prime2^n}} = 1\cdot 0^k \cdot1\ldots,\end{align*} $$
$$ \begin{align*}\mathrm{{It}}_{\unicode{x3bb}^{\prime2^n}} = 1\cdot 0^k \cdot1\ldots,\end{align*} $$
 $w'$
does not contain
$w'$
does not contain
 $k+1$
consecutive
$k+1$
consecutive
 $0$
s.
$0$
s.
The intuition behind the definition of
![]() $\unicode{x3bb} $
-suitability is that we need a condition on sequences w so that Lemma 5.7 works.
$\unicode{x3bb} $
-suitability is that we need a condition on sequences w so that Lemma 5.7 works.
Remark 5.1. An immediate consequence of monotonicity (Corollary 2.4) is that if
![]() $\unicode{x3bb} '$
satisfies conditions (1)–(4) of Definition 1.5 for a sequence w, then so does every
$\unicode{x3bb} '$
satisfies conditions (1)–(4) of Definition 1.5 for a sequence w, then so does every
![]() $\unicode{x3bb} "> \unicode{x3bb} '$
.
$\unicode{x3bb} "> \unicode{x3bb} '$
.
Remark 5.2. Every itinerary
![]() $\mathrm {{It}}_{\unicode{x3bb} '}$
is admissible (by Theorem 2.2), so the admissibility condition implies that if
$\mathrm {{It}}_{\unicode{x3bb} '}$
is admissible (by Theorem 2.2), so the admissibility condition implies that if
![]() $\mathrm {{It}}_{\unicode{x3bb} '} = 1 \cdot 0^k \cdot 1 \ldots $
, then
$\mathrm {{It}}_{\unicode{x3bb} '} = 1 \cdot 0^k \cdot 1 \ldots $
, then
![]() $\mathrm {{It}}_{\unicode{x3bb} }$
does not contain
$\mathrm {{It}}_{\unicode{x3bb} }$
does not contain
![]() $k+1$
consecutive
$k+1$
consecutive
![]() $0$
s.
$0$
s.
Remark 5.3. Note that the map
![]() $\frak {D}'$
defined in the definition of
$\frak {D}'$
defined in the definition of
![]() $\unicode{x3bb} $
-suitability is related to the doubling map
$\unicode{x3bb} $
-suitability is related to the doubling map
![]() $\frak {D}$
by
$\frak {D}$
by
for every sequence w and
![]() $n \in \mathbb {N}$
. (Recall that
$n \in \mathbb {N}$
. (Recall that
![]() $\frak {D}$
is replacing
$\frak {D}$
is replacing
![]() $0$
with
$0$
with
![]() $11$
,
$11$
,
![]() $1$
with
$1$
with
![]() $10$
, while
$10$
, while
![]() $\frak {D}'$
is replacing
$\frak {D}'$
is replacing
![]() $0$
with
$0$
with
![]() $11$
,
$11$
,
![]() $1$
with
$1$
with
![]() $01$
.)
$01$
.)
Lemma 5.4. The set of
![]() $\unicode{x3bb} $
-suitable sequences is closed.
$\unicode{x3bb} $
-suitable sequences is closed.
Proof. We will show that the set of all sequences that are not
![]() $\unicode{x3bb} $
-suitable is open. To do this, it suffices to show that given any sequence w which is not
$\unicode{x3bb} $
-suitable is open. To do this, it suffices to show that given any sequence w which is not
![]() $\unicode{x3bb} $
-suitable, we can find a prefix of w such that every sequence that shares this prefix is not
$\unicode{x3bb} $
-suitable, we can find a prefix of w such that every sequence that shares this prefix is not
![]() $\unicode{x3bb} $
-suitable. It is clear that conditions (1) and (2) are closed conditions. For condition (3), we choose the prefix to be one that contains the first
$\unicode{x3bb} $
-suitable. It is clear that conditions (1) and (2) are closed conditions. For condition (3), we choose the prefix to be one that contains the first
![]() $k+1$
consecutive
$k+1$
consecutive
![]() $0$
s. Condition (4) is similar.
$0$
s. Condition (4) is similar.
The following lemma is immediate because the definition of
![]() $\unicode{x3bb} $
-suitability is of the form ‘for all
$\unicode{x3bb} $
-suitability is of the form ‘for all
![]() $\unicode{x3bb} '> \unicode{x3bb} $
,
$\unicode{x3bb} '> \unicode{x3bb} $
,
![]() $P(w,\unicode{x3bb} ')$
,’ where P is a predicate.
$P(w,\unicode{x3bb} ')$
,’ where P is a predicate.
Lemma 5.5. Let
![]() $\mathcal {M}_\unicode{x3bb} $
denote the set of
$\mathcal {M}_\unicode{x3bb} $
denote the set of
![]() $\unicode{x3bb} $
-suitable sequences. Then,
$\unicode{x3bb} $
-suitable sequences. Then,
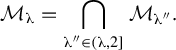 $$ \begin{align*}\mathcal{M}_\unicode{x3bb}=\bigcap_{\unicode{x3bb}" \in (\unicode{x3bb},2]}\mathcal{M}_{\unicode{x3bb}"}.\end{align*} $$
$$ \begin{align*}\mathcal{M}_\unicode{x3bb}=\bigcap_{\unicode{x3bb}" \in (\unicode{x3bb},2]}\mathcal{M}_{\unicode{x3bb}"}.\end{align*} $$
Lemma 5.6. If w is an admissible word that satisfies
![]() $w^{\infty } \leq _E \mathrm {{It}}_{\unicode{x3bb} }$
for
$w^{\infty } \leq _E \mathrm {{It}}_{\unicode{x3bb} }$
for
![]() $\unicode{x3bb} \in (1,2)$
, then
$\unicode{x3bb} \in (1,2)$
, then
![]() $(\mathrm {{Rev}}(w))^{\infty }$
is
$(\mathrm {{Rev}}(w))^{\infty }$
is
![]() $\unicode{x3bb} $
-suitable.
$\unicode{x3bb} $
-suitable.
Proof. Observe that for any
![]() $n \in \mathbb {N}$
, if we pick some
$n \in \mathbb {N}$
, if we pick some
![]() $k\in \mathbb {N}$
such that
$k\in \mathbb {N}$
such that
![]() $n+k$
is some multiple of
$n+k$
is some multiple of
![]() $|w|$
, then we have
$|w|$
, then we have
Since w is admissible,
![]() ${\textrm {Pre}}_n(\sigma ^k(w^{\infty })) \leq _E {\textrm {Pre}}_n(w^{\infty })$
for all
${\textrm {Pre}}_n(\sigma ^k(w^{\infty })) \leq _E {\textrm {Pre}}_n(w^{\infty })$
for all
![]() $k,n \in \mathbb {N}$
. By Corollary 2.4, for any
$k,n \in \mathbb {N}$
. By Corollary 2.4, for any
![]() $\unicode{x3bb} '> \unicode{x3bb} $
,
$\unicode{x3bb} '> \unicode{x3bb} $
,
We thus have that for any
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
which is condition (1) of the definition of
![]() $\unicode{x3bb} $
-suitability.
$\unicode{x3bb} $
-suitability.
Now suppose that for some
![]() $\unicode{x3bb} '> \unicode{x3bb} $
,
$\unicode{x3bb} '> \unicode{x3bb} $
,
and
![]() ${\textrm {Pre}}_n(\mathrm {{It}}_{\unicode{x3bb} '})$
has a positive cumulative sign. Then from (5.1), we have
${\textrm {Pre}}_n(\mathrm {{It}}_{\unicode{x3bb} '})$
has a positive cumulative sign. Then from (5.1), we have
Admissibility of w and (5.2) together imply that
Because
![]() ${\textrm {Pre}}_n(\mathrm {{It}}_{\unicode{x3bb} '})$
is the common prefix of
${\textrm {Pre}}_n(\mathrm {{It}}_{\unicode{x3bb} '})$
is the common prefix of
![]() $\sigma ^{k}(w^{\infty })$
and
$\sigma ^{k}(w^{\infty })$
and
![]() $\mathrm {{It}}_{\unicode{x3bb} '}$
, (5.3) implies it must also be a prefix of
$\mathrm {{It}}_{\unicode{x3bb} '}$
, (5.3) implies it must also be a prefix of
![]() $w^\infty $
. Removing this common n-prefix with positive cumulative sign from both sides of the inequality (by applying
$w^\infty $
. Removing this common n-prefix with positive cumulative sign from both sides of the inequality (by applying
![]() $\sigma ^n$
) yields
$\sigma ^n$
) yields
However, admissibility also implies that
![]() $\sigma ^{n}(w^\infty )\leq w^\infty $
, so in fact
$\sigma ^{n}(w^\infty )\leq w^\infty $
, so in fact
Therefore,
Let j be the index of the first place
![]() $w^{\infty }$
differs from
$w^{\infty }$
differs from
![]() $\mathrm {{It}}_{\unicode{x3bb} '}$
. Clearly,
$\mathrm {{It}}_{\unicode{x3bb} '}$
. Clearly,
![]() $j>n$
. Pick
$j>n$
. Pick
![]() $m \in \mathbb {N}$
such that
$m \in \mathbb {N}$
such that
![]() $mn<j\leq (m+1)n$
. Then, after removing the common prefix of length
$mn<j\leq (m+1)n$
. Then, after removing the common prefix of length
![]() $mn$
and positive cumulative sign from both
$mn$
and positive cumulative sign from both
![]() $w^{\infty }$
and
$w^{\infty }$
and
![]() $\mathrm {{It}}_{\unicode{x3bb} '}$
, we get from (5.4) and (5.2) that
$\mathrm {{It}}_{\unicode{x3bb} '}$
, we get from (5.4) and (5.2) that
and hence,
which contradicts with the fact that
![]() $\mathrm {{It}}_{\unicode{x3bb} '}$
is admissible (by Theorem 2.2). Thus, condition (2) of the definition of
$\mathrm {{It}}_{\unicode{x3bb} '}$
is admissible (by Theorem 2.2). Thus, condition (2) of the definition of
![]() $\unicode{x3bb} $
-suitability holds.
$\unicode{x3bb} $
-suitability holds.
Now condition (3) of the definition of
![]() $\unicode{x3bb} $
-suitability follows from the assumption that
$\unicode{x3bb} $
-suitability follows from the assumption that
![]() $w^{\infty } \leq _E \mathrm {{It}}_{\unicode{x3bb} }$
.
$w^{\infty } \leq _E \mathrm {{It}}_{\unicode{x3bb} }$
.
For condition (4), suppose for some
![]() $\unicode{x3bb} '>\unicode{x3bb} $
,
$\unicode{x3bb} '>\unicode{x3bb} $
,
![]() $\sqrt {2}\leq (\unicode{x3bb} ')^{2^n}<2$
. Then
$\sqrt {2}\leq (\unicode{x3bb} ')^{2^n}<2$
. Then
![]() $\unicode{x3bb} ^{2^n}<2$
, so by Lemma 3.4,
$\unicode{x3bb} ^{2^n}<2$
, so by Lemma 3.4,
![]() $w=\mathfrak {D}^n(w')$
for some
$w=\mathfrak {D}^n(w')$
for some
![]() $w'$
. Hence,
$w'$
. Hence,
Because
![]() $\mathfrak {D}$
preserves
$\mathfrak {D}$
preserves
![]() $\leq _E$
and sends itineraries to itineraries (Lemma 3.2), the number of consecutive
$\leq _E$
and sends itineraries to itineraries (Lemma 3.2), the number of consecutive
![]() $0$
s in
$0$
s in
![]() $({\textrm {Rev}}(w'))^\infty $
, which is the number of consecutive
$({\textrm {Rev}}(w'))^\infty $
, which is the number of consecutive
![]() $0$
s in
$0$
s in
![]() $w^{\prime \infty }$
, cannot be more than the number of consecutive
$w^{\prime \infty }$
, cannot be more than the number of consecutive
![]() $0$
s in
$0$
s in
![]() $\mathrm {{It}}_{\unicode{x3bb} ^{\prime 2^n}}$
.
$\mathrm {{It}}_{\unicode{x3bb} ^{\prime 2^n}}$
.
The key combinatorial result we need to prove Theorem 1.7 is the following.
Lemma 5.7. Fix
![]() $\unicode{x3bb} \in [1,2)$
and let
$\unicode{x3bb} \in [1,2)$
and let
![]() $w_0$
be a finite dominant word such that
$w_0$
be a finite dominant word such that
![]() $\mathrm {{It}}_{\unicode{x3bb} '}\leq _E w_0^\infty $
for some
$\mathrm {{It}}_{\unicode{x3bb} '}\leq _E w_0^\infty $
for some
![]() $\unicode{x3bb} '>\unicode{x3bb} $
. Let
$\unicode{x3bb} '>\unicode{x3bb} $
. Let
![]() $\alpha $
be a word such that
$\alpha $
be a word such that
![]() $\alpha $
:
$\alpha $
:
-
(1) ends with
 $1$
;
$1$
; -
(2) is a prefix of some
 $\unicode{x3bb} $
-suitable sequence;
$\unicode{x3bb} $
-suitable sequence; -
(3) has positive cumulative sign; and
-
(4)
 $|w_0|>|\alpha |$
.
$|w_0|>|\alpha |$
.
Then the word
![]() $w_0\cdot \mathrm {{Rev}}(\alpha )$
is admissible.
$w_0\cdot \mathrm {{Rev}}(\alpha )$
is admissible.
Proof. Let
![]() $\alpha '={\textrm {Rev}}(\alpha )$
. It suffices to show that the admissibility criterion
$\alpha '={\textrm {Rev}}(\alpha )$
. It suffices to show that the admissibility criterion
holds for all
![]() $1\leq k< |\alpha |+|w_0|$
.
$1\leq k< |\alpha |+|w_0|$
.
Case 1:
![]() $k<|w_0|$
. This implies that the comparison between
$k<|w_0|$
. This implies that the comparison between
![]() $\sigma ^k((w_0\alpha ')^\infty )$
and
$\sigma ^k((w_0\alpha ')^\infty )$
and
![]() $(w_0\alpha ')^\infty $
is equivalent to the comparison of a proper suffix of
$(w_0\alpha ')^\infty $
is equivalent to the comparison of a proper suffix of
![]() $w_0$
concatenated with
$w_0$
concatenated with
![]() $1$
with a prefix of
$1$
with a prefix of
![]() $w_0$
of the same length. Hence,
$w_0$
of the same length. Hence,
because
![]() $w_0$
is dominant.
$w_0$
is dominant.
Case 2:
![]() $|w_0|\leq k < |\alpha |+|w_0|$
. Suppose the first place
$|w_0|\leq k < |\alpha |+|w_0|$
. Suppose the first place
![]() $\sigma ^k((w_0\alpha ')^\infty )$
and
$\sigma ^k((w_0\alpha ')^\infty )$
and
![]() $(w_0\alpha ')^\infty $
differ is at the
$(w_0\alpha ')^\infty $
differ is at the
![]() $j\textrm {th}$
position. It is evident that
$j\textrm {th}$
position. It is evident that
![]() $1\leq j\leq |\alpha |+|w_0|$
. We divide this into two subcases.
$1\leq j\leq |\alpha |+|w_0|$
. We divide this into two subcases.
Case 2A:
![]() $j\leq |w_0|+|\alpha |-k$
. The fact that
$j\leq |w_0|+|\alpha |-k$
. The fact that
![]() $|w_0|>|\alpha |$
and
$|w_0|>|\alpha |$
and
![]() $k\geq |w_0|$
implies that
$k\geq |w_0|$
implies that
![]() $j\leq |w_0|$
. Hence, the comparison between
$j\leq |w_0|$
. Hence, the comparison between
![]() $\sigma ^k((w_0\alpha ')^\infty )$
and
$\sigma ^k((w_0\alpha ')^\infty )$
and
![]() $(w_0\alpha ')^\infty $
is equivalent to the comparison of a proper suffix of
$(w_0\alpha ')^\infty $
is equivalent to the comparison of a proper suffix of
![]() $\alpha '$
with a prefix of
$\alpha '$
with a prefix of
![]() $w_0$
. Hence, item (1) of Definition 1.5 gives us
$w_0$
. Hence, item (1) of Definition 1.5 gives us
Case 2B:
![]() $j>|w_0|+|\alpha |-k$
. The word
$j>|w_0|+|\alpha |-k$
. The word
![]() $\beta :={\textrm {Suf}}_{|w_0|+|\alpha |-k}(\alpha ')$
, which is a common prefix of
$\beta :={\textrm {Suf}}_{|w_0|+|\alpha |-k}(\alpha ')$
, which is a common prefix of
![]() $\sigma ^k((w_0\alpha ')^\infty )$
and
$\sigma ^k((w_0\alpha ')^\infty )$
and
![]() $(w_0\alpha ')^\infty $
, is identical to a prefix of
$(w_0\alpha ')^\infty $
, is identical to a prefix of
![]() $w_0$
, which is
$w_0$
, which is
![]() $\ge _E$
than a prefix of
$\ge _E$
than a prefix of
![]() $\mathrm {{It}}_{\unicode{x3bb} '}$
for some
$\mathrm {{It}}_{\unicode{x3bb} '}$
for some
![]() $\unicode{x3bb} '>\unicode{x3bb} $
. Hence, due to item (2) of Definition 1.5,
$\unicode{x3bb} '>\unicode{x3bb} $
. Hence, due to item (2) of Definition 1.5,
![]() $\beta $
has a negative cumulative sign. Now, using the conclusion of Case 1, we have
$\beta $
has a negative cumulative sign. Now, using the conclusion of Case 1, we have
Hence,
because
![]() $\beta $
has a negative cumulative sign.
$\beta $
has a negative cumulative sign.
Lemma 5.8. Let w and
![]() $w'$
be sequences, and let
$w'$
be sequences, and let
![]() $\unicode{x3bb} {\kern-1pt}\in{\kern-1pt} (1,2)$
and
$\unicode{x3bb} {\kern-1pt}\in{\kern-1pt} (1,2)$
and
![]() $k {\kern-1pt}\in{\kern-1pt} \mathbb {N}$
satisfy
$k {\kern-1pt}\in{\kern-1pt} \mathbb {N}$
satisfy
![]() $\sqrt {2}{\kern-1pt} \leq{\kern-1pt} \unicode{x3bb} ^{2^k} {\kern-2pt}<{\kern-1pt} 2$
. If w is
$\sqrt {2}{\kern-1pt} \leq{\kern-1pt} \unicode{x3bb} ^{2^k} {\kern-2pt}<{\kern-1pt} 2$
. If w is
![]() $\unicode{x3bb} $
-suitable and
$\unicode{x3bb} $
-suitable and
![]() $w = \mathfrak {D'}^k(w')$
, then
$w = \mathfrak {D'}^k(w')$
, then
![]() $w'$
is
$w'$
is
![]() $\unicode{x3bb} ^{2^k}$
-suitable.
$\unicode{x3bb} ^{2^k}$
-suitable.
Proof. By induction, we only need to prove it for
![]() $k=1$
. Assume
$k=1$
. Assume
![]() $w=\mathfrak {D'}(w')$
is
$w=\mathfrak {D'}(w')$
is
![]() $\unicode{x3bb} $
-suitable, we will now show that
$\unicode{x3bb} $
-suitable, we will now show that
![]() $w'$
satisfies conditions (1)–(4) of Definition 1.5. By definition,
$w'$
satisfies conditions (1)–(4) of Definition 1.5. By definition,
for any word v, so for any
![]() $\unicode{x3bb} '>\unicode{x3bb} $
,
$\unicode{x3bb} '>\unicode{x3bb} $
,
Hence condition (1) is true for
![]() $w'$
because of Lemmas 3.1 and 3.2. Condition (2) of Definition 1.5 can be verified similarly. It is easy to see that w satisfies condition (4) implies that
$w'$
because of Lemmas 3.1 and 3.2. Condition (2) of Definition 1.5 can be verified similarly. It is easy to see that w satisfies condition (4) implies that
![]() $w'$
satisfies condition (4). Lastly, we will now show that w satisfies condition (4) will imply
$w'$
satisfies condition (4). Lastly, we will now show that w satisfies condition (4) will imply
![]() $w'$
satisfies condition (3): if
$w'$
satisfies condition (3): if
![]() $\unicode{x3bb} ^2\geq \sqrt {2}$
, this follows from the statement of condition (4). If
$\unicode{x3bb} ^2\geq \sqrt {2}$
, this follows from the statement of condition (4). If
![]() $\unicode{x3bb} ^2<\sqrt {2}$
, condition (4) implies that
$\unicode{x3bb} ^2<\sqrt {2}$
, condition (4) implies that
![]() $w'=\mathfrak {D'}(w")$
for some
$w'=\mathfrak {D'}(w")$
for some
![]() $w"$
, which implies that
$w"$
, which implies that
![]() $w'$
can never have more than one consecutive 0, and hence it also satisfies condition (3).
$w'$
can never have more than one consecutive 0, and hence it also satisfies condition (3).
6 Characterization inside the unit cylinder
Lemma 6.1. Let
![]() $\mathcal {K}$
denote the space of compact subsets of
$\mathcal {K}$
denote the space of compact subsets of
![]() $\mathbb {R}^3$
with the Hausdorff metric topology. Given any compact subset K of
$\mathbb {R}^3$
with the Hausdorff metric topology. Given any compact subset K of
![]() $\mathcal {K}$
, the union of the elements of K is a compact subset of
$\mathcal {K}$
, the union of the elements of K is a compact subset of
![]() $\mathbb {R}^3$
.
$\mathbb {R}^3$
.
Proof. First, we claim there exists
![]() $R>0$
such that
$R>0$
such that
![]() $k \subset \overline {B_R(0)}$
for all
$k \subset \overline {B_R(0)}$
for all
![]() $k \in K$
. If this was not the case, then there exist
$k \in K$
. If this was not the case, then there exist
![]() $k_1$
and
$k_1$
and
![]() $k_2$
in K such that
$k_2$
in K such that
![]() $d_{\textrm {Haus}}(k_1,k_2)$
is arbitrarily large, contradicting the fact that K is compact. Thus the claim is true.
$d_{\textrm {Haus}}(k_1,k_2)$
is arbitrarily large, contradicting the fact that K is compact. Thus the claim is true.
Consider
![]() $K \times \overline {B_R(0)}$
. As a product of compact sets, it is compact. Consider the subset
$K \times \overline {B_R(0)}$
. As a product of compact sets, it is compact. Consider the subset
![]() $C \subseteq K$
such that C consists of all pairs
$C \subseteq K$
such that C consists of all pairs
![]() $(k,x)$
such that
$(k,x)$
such that
![]() $x \in k$
. We claim C is closed, and thus as a closed subset of a compact set, C is compact. To see this, we will show that C is sequentially closed, that is, if
$x \in k$
. We claim C is closed, and thus as a closed subset of a compact set, C is compact. To see this, we will show that C is sequentially closed, that is, if
![]() $(k_i,x_i)$
is a sequence in C converging to
$(k_i,x_i)$
is a sequence in C converging to
![]() $(k_{\infty },x_{\infty }) \in K \times \overline {B_R(0)}$
, then
$(k_{\infty },x_{\infty }) \in K \times \overline {B_R(0)}$
, then
![]() $(k_{\infty },x_{\infty }) \in C$
. We have that
$(k_{\infty },x_{\infty }) \in C$
. We have that
![]() $k_i \to k_{\infty }$
and
$k_i \to k_{\infty }$
and
![]() $x_i \to x_{\infty }$
, so suppose
$x_i \to x_{\infty }$
, so suppose
![]() $x_{\infty } \not \in k_{\infty }$
. Since
$x_{\infty } \not \in k_{\infty }$
. Since
![]() $k_{\infty }$
is a compact set,
$k_{\infty }$
is a compact set,
![]() $x \not \in k_{\infty }$
implies there exists
$x \not \in k_{\infty }$
implies there exists
![]() $\epsilon> 0$
such that
$\epsilon> 0$
such that
![]() $B_{\epsilon }(x)$
is contained in the complement of
$B_{\epsilon }(x)$
is contained in the complement of
![]() $k_{\infty }$
. This implies that
$k_{\infty }$
. This implies that
![]() $\liminf d_{\textrm {Haus}}(k_i,k_{\infty }) \geq \epsilon $
, contradicting the fact that
$\liminf d_{\textrm {Haus}}(k_i,k_{\infty }) \geq \epsilon $
, contradicting the fact that
![]() $k_i \to k_{\infty }$
in the Hausdorff metric. So we have a continuous map from C to
$k_i \to k_{\infty }$
in the Hausdorff metric. So we have a continuous map from C to
![]() $\mathbb {R}^3$
sending
$\mathbb {R}^3$
sending
![]() $(k,x)$
to x. The image under this map is compact.
$(k,x)$
to x. The image under this map is compact.
The following two lemmas, which we state without proof, are immediate consequences of Rouché’s theorem.
Lemma 6.2. Let
![]() $M>0$
be some fixed number. Let A be the set of power series with coefficients bounded by M equipped with the product topology. Let
$M>0$
be some fixed number. Let A be the set of power series with coefficients bounded by M equipped with the product topology. Let
![]() $\mathcal {C}$
be the set of compact subsets of
$\mathcal {C}$
be the set of compact subsets of
![]() $\mathbb {C}$
equipped with the Hausdorff topology. Then the map
$\mathbb {C}$
equipped with the Hausdorff topology. Then the map
![]() $\rho :A \to \mathcal {C}$
defined by
$\rho :A \to \mathcal {C}$
defined by
is continuous.
Lemma 6.3. Fix real numbers
![]() $M>0$
,
$M>0$
,
![]() $0<r<1$
,
$0<r<1$
,
![]() $\epsilon>0$
. Suppose
$\epsilon>0$
. Suppose
![]() $\alpha $
is a power series whose coefficients are all bounded in absolute value by M. Then there exists a real number
$\alpha $
is a power series whose coefficients are all bounded in absolute value by M. Then there exists a real number
![]() $N = N(\alpha ,r,\epsilon ,M)$
such that for every power series
$N = N(\alpha ,r,\epsilon ,M)$
such that for every power series
![]() $\beta $
, whose coefficients are all bounded in absolute value by M and whose first N terms equal the first N terms of
$\beta $
, whose coefficients are all bounded in absolute value by M and whose first N terms equal the first N terms of
![]() $\alpha $
, for each root z of
$\alpha $
, for each root z of
![]() $\alpha $
with
$\alpha $
with
![]() $|z|<r$
, there exists a root
$|z|<r$
, there exists a root
![]() $z'$
of
$z'$
of
![]() $\beta $
such that
$\beta $
such that
![]() $|z-z'|<\epsilon $
.
$|z-z'|<\epsilon $
.
Now we prove the first main theorem.
Proof of Theorem 1.7
For the reader’s convenience, we reproduce here the statement of Theorem 1.7. For any
![]() $\unicode{x3bb} \in (1,2]$
,
$\unicode{x3bb} \in (1,2]$
,
By Remark 1.11, the result holds for
![]() $\unicode{x3bb} =2$
. So fix
$\unicode{x3bb} =2$
. So fix
![]() $\unicode{x3bb} \in (1,2)$
. For brevity, let
$\unicode{x3bb} \in (1,2)$
. For brevity, let
First, we show that
![]() $S^1\cup Z_\unicode{x3bb} $
is compact. For each sequence w, the function from
$S^1\cup Z_\unicode{x3bb} $
is compact. For each sequence w, the function from
![]() $\mathbb {D}$
to
$\mathbb {D}$
to
![]() $\mathbb {C}$
given by
$\mathbb {C}$
given by
![]() $z \mapsto G(w, \cdot )-1$
is a power series with bounded coefficients. Furthermore, the map from the set of sequences w (with the product topology) to the set of power series (with the product topology on coefficients) given by
$z \mapsto G(w, \cdot )-1$
is a power series with bounded coefficients. Furthermore, the map from the set of sequences w (with the product topology) to the set of power series (with the product topology on coefficients) given by
![]() $w \mapsto G(w,\cdot )-1$
is continuous. Therefore, Lemma 6.2 implies that the map
$w \mapsto G(w,\cdot )-1$
is continuous. Therefore, Lemma 6.2 implies that the map
![]() $\rho $
from the set of sequences with the product topology to
$\rho $
from the set of sequences with the product topology to
![]() $\mathcal {C}$
, the set of compact subsets of
$\mathcal {C}$
, the set of compact subsets of
![]() $\mathbb {C}$
with the Hausdorff topology, given by
$\mathbb {C}$
with the Hausdorff topology, given by
is continuous. By Lemma 5.4, the set of all
![]() $\unicode{x3bb} $
-suitable sequences is closed (in the product topology on the set of sequences), and hence compact. Therefore, since
$\unicode{x3bb} $
-suitable sequences is closed (in the product topology on the set of sequences), and hence compact. Therefore, since
![]() $\rho $
is continuous,
$\rho $
is continuous,
is a compact subset of
![]() $\mathcal {C}$
. Hence, Lemma 6.1 implies that
$\mathcal {C}$
. Hence, Lemma 6.1 implies that
is compact. However, this set is precisely
![]() $S^1\cup Z_\unicode{x3bb} $
, so we have shown
$S^1\cup Z_\unicode{x3bb} $
, so we have shown
![]() $S^1\cup Z_\unicode{x3bb} $
is compact for any
$S^1\cup Z_\unicode{x3bb} $
is compact for any
![]() $\unicode{x3bb} \in [1,2]$
.
$\unicode{x3bb} \in [1,2]$
.
Next, we show that
Theorem 4.5 shows that
where
![]() $Y_{\unicode{x3bb} '}$
is defined to be the closure of the set of roots in
$Y_{\unicode{x3bb} '}$
is defined to be the closure of the set of roots in
![]() $\overline {\mathbb {D}}$
of all Parry polynomials
$\overline {\mathbb {D}}$
of all Parry polynomials
![]() $P_w$
such that w is admissible and
$P_w$
such that w is admissible and
![]() $w^\infty \leq _E\mathrm {{It}}_{\unicode{x3bb} '}$
, union with
$w^\infty \leq _E\mathrm {{It}}_{\unicode{x3bb} '}$
, union with
![]() $S^1$
. For each such w, let
$S^1$
. For each such w, let
![]() $w_r$
be the sequence
$w_r$
be the sequence
So fix
![]() $\unicode{x3bb} '> \unicode{x3bb} $
and consider any admissible word w such that
$\unicode{x3bb} '> \unicode{x3bb} $
and consider any admissible word w such that
![]() $w^{\infty } \leq _E \mathrm {{It}}_{\unicode{x3bb} '}$
. By Lemma 2.1,
$w^{\infty } \leq _E \mathrm {{It}}_{\unicode{x3bb} '}$
. By Lemma 2.1,
By Lemma 5.6,
![]() $w_r$
is
$w_r$
is
![]() $\unicode{x3bb} '$
-suitable. Hence, all roots in
$\unicode{x3bb} '$
-suitable. Hence, all roots in
![]() $\overline {\mathbb {D}}$
of
$\overline {\mathbb {D}}$
of
![]() $P_w$
are in
$P_w$
are in
![]() $S^1 \cup Z_{\unicode{x3bb} '}$
. Then, since
$S^1 \cup Z_{\unicode{x3bb} '}$
. Then, since
![]() $Z_{\unicode{x3bb} '}$
is closed, we have that
$Z_{\unicode{x3bb} '}$
is closed, we have that
Now, combining (6.1) and (6.2) shows that for any point
![]() $z\in {\Xi }_\unicode{x3bb} \cap \mathbb {D}$
, for each
$z\in {\Xi }_\unicode{x3bb} \cap \mathbb {D}$
, for each
![]() $n\in \mathbb {N}$
, there exists a
$n\in \mathbb {N}$
, there exists a
![]() $(\unicode{x3bb} +{1/n})$
-suitable sequence
$(\unicode{x3bb} +{1/n})$
-suitable sequence
![]() $v_n$
such that
$v_n$
such that
![]() $G(v_n, z)=1$
. Let
$G(v_n, z)=1$
. Let
![]() $v_\infty $
be an accumulation point of the set
$v_\infty $
be an accumulation point of the set
![]() $\{v_n : n \in \mathbb {N}\}$
. By Lemma 5.5, the sequence
$\{v_n : n \in \mathbb {N}\}$
. By Lemma 5.5, the sequence
![]() $v_\infty $
is
$v_\infty $
is
![]() $\unicode{x3bb} $
-suitable. The continuity of
$\unicode{x3bb} $
-suitable. The continuity of
![]() $w\mapsto G(w, \cdot )$
implies that
$w\mapsto G(w, \cdot )$
implies that
![]() $G(v_\infty , z)=1$
. Hence,
$G(v_\infty , z)=1$
. Hence,
![]() ${\Xi }_{\unicode{x3bb} }\cap \overline {\mathbb {D}}\subseteq S^1\cup Z_{\unicode{x3bb} }$
.
${\Xi }_{\unicode{x3bb} }\cap \overline {\mathbb {D}}\subseteq S^1\cup Z_{\unicode{x3bb} }$
.
Lastly, we show that
![]() $S^1\cup Z_\unicode{x3bb} \subseteq {\Xi }_\unicode{x3bb} \cap \overline {\mathbb {D}}.$
We know from [Reference Bray, Davis, Lindsey and WuBDLW19] that
$S^1\cup Z_\unicode{x3bb} \subseteq {\Xi }_\unicode{x3bb} \cap \overline {\mathbb {D}}.$
We know from [Reference Bray, Davis, Lindsey and WuBDLW19] that
![]() $S^1 \times [1,2] \subset \Upsilon _2^{cp}$
. Thus,
$S^1 \times [1,2] \subset \Upsilon _2^{cp}$
. Thus,
![]() $S^1\subset {\Xi }_\unicode{x3bb} $
, so it suffices to show that
$S^1\subset {\Xi }_\unicode{x3bb} $
, so it suffices to show that
![]() $Z_\unicode{x3bb} \subset {\Xi }_{\unicode{x3bb} }$
. Fix a point
$Z_\unicode{x3bb} \subset {\Xi }_{\unicode{x3bb} }$
. Fix a point
![]() $z\in Z_\unicode{x3bb} $
and let w be a
$z\in Z_\unicode{x3bb} $
and let w be a
![]() $\unicode{x3bb} $
-suitable sequence such that
$\unicode{x3bb} $
-suitable sequence such that
![]() $G(w, z)=1$
. By condition (4) of Definition 1.5, there exists a sequence
$G(w, z)=1$
. By condition (4) of Definition 1.5, there exists a sequence
![]() $w'$
such that
$w'$
such that
![]() $w=\mathfrak {D'}^k(w')$
, and by Lemma 5.8,
$w=\mathfrak {D'}^k(w')$
, and by Lemma 5.8,
![]() $w'$
is
$w'$
is
![]() $\unicode{x3bb} ^{2^k}$
-suitable and
$\unicode{x3bb} ^{2^k}$
-suitable and
![]() $\unicode{x3bb} ^{2^k}\geq \sqrt {2}$
. In particular, if
$\unicode{x3bb} ^{2^k}\geq \sqrt {2}$
. In particular, if
![]() $\unicode{x3bb} \geq \sqrt {2}$
, we can let
$\unicode{x3bb} \geq \sqrt {2}$
, we can let
![]() $k=0$
and
$k=0$
and
![]() $w'=w$
. As a consequence, there are infinitely many prefixes of
$w'=w$
. As a consequence, there are infinitely many prefixes of
![]() $w'$
that end with
$w'$
that end with
![]() $1$
and have a positive cumulative sign.
$1$
and have a positive cumulative sign.
For any
![]() $m \in \mathbb {N}$
such that
$m \in \mathbb {N}$
such that
![]() ${\textrm {Pre}}_m(w')$
has a positive cumulative sign and any word
${\textrm {Pre}}_m(w')$
has a positive cumulative sign and any word
![]() $w"$
with a positive cumulative sign, it follows immediately from the definitions of a Parry polynomial and of G that the first m terms of the power series
$w"$
with a positive cumulative sign, it follows immediately from the definitions of a Parry polynomial and of G that the first m terms of the power series
![]() $G(w', z)-1$
and
$G(w', z)-1$
and
![]() $P_{w" \cdot {\textrm {Rev}}({\textrm {Pre}}_m(w'))}(z)$
agree. Therefore, for any fixed
$P_{w" \cdot {\textrm {Rev}}({\textrm {Pre}}_m(w'))}(z)$
agree. Therefore, for any fixed
![]() $\epsilon _1>0$
, by Lemma 6.3, there exists
$\epsilon _1>0$
, by Lemma 6.3, there exists
![]() $N \in \mathbb {N}$
such that
$N \in \mathbb {N}$
such that
![]() ${\textrm {Pre}}_N(w')$
ends with
${\textrm {Pre}}_N(w')$
ends with
![]() $1$
and has a positive cumulative sign, and for any word
$1$
and has a positive cumulative sign, and for any word
![]() $w"$
with a positive cumulative sign, there exists a point
$w"$
with a positive cumulative sign, there exists a point
![]() $z' \in B_{\epsilon _1}(z^{2^k})$
such that
$z' \in B_{\epsilon _1}(z^{2^k})$
such that
For any fixed
![]() $\unicode{x3bb} '$
satisfying
$\unicode{x3bb} '$
satisfying
![]() $2> \unicode{x3bb} ' > \unicode{x3bb} ^{2^k}$
, pick a critically periodic growth rate
$2> \unicode{x3bb} ' > \unicode{x3bb} ^{2^k}$
, pick a critically periodic growth rate
![]() $\unicode{x3bb} " \in (\unicode{x3bb} ^{2^k},\unicode{x3bb} ')$
and word
$\unicode{x3bb} " \in (\unicode{x3bb} ^{2^k},\unicode{x3bb} ')$
and word
![]() $w_0$
with a positive cumulative sign such that
$w_0$
with a positive cumulative sign such that
![]() $\mathrm {{It}}_{\unicode{x3bb} "}=w_0^{\infty }$
. Since
$\mathrm {{It}}_{\unicode{x3bb} "}=w_0^{\infty }$
. Since
![]() $\unicode{x3bb} " < \unicode{x3bb} '$
, for sufficiently large n,
$\unicode{x3bb} " < \unicode{x3bb} '$
, for sufficiently large n,
Hence, by Proposition 2.5, there exists
![]() $n \in \mathbb {N}$
and a word
$n \in \mathbb {N}$
and a word
![]() $w_1'$
such that the word
$w_1'$
such that the word
is dominant,
![]() $|w_1|> |w'|$
, and
$|w_1|> |w'|$
, and
By Lemma 5.7,
is admissible. By (6.3),
has a root within distance
![]() $\epsilon _1$
of
$\epsilon _1$
of
![]() $z^{2^k}$
. By (6.4),
$z^{2^k}$
. By (6.4),
Hence, the
![]() $k\textrm {th}$
doubling of
$k\textrm {th}$
doubling of
![]() $w_1\cdot {\textrm {Rev}}({\textrm {Pre}}_N(w'))$
, denoted as
$w_1\cdot {\textrm {Rev}}({\textrm {Pre}}_N(w'))$
, denoted as
![]() $w_d$
, satisfies
$w_d$
, satisfies
and
![]() $P_{w_d}$
has leading root in
$P_{w_d}$
has leading root in
![]() $[\unicode{x3bb} , (\unicode{x3bb} ')^{1/2^k}]$
and a root in
$[\unicode{x3bb} , (\unicode{x3bb} ')^{1/2^k}]$
and a root in
![]() $B_{\epsilon ^{\prime }_1}(z)$
, where
$B_{\epsilon ^{\prime }_1}(z)$
, where
![]() $\epsilon ^{\prime }_1$
is the diameter of the preimage of
$\epsilon ^{\prime }_1$
is the diameter of the preimage of
![]() $B_{\epsilon '}(z^{2^k})$
under the map
$B_{\epsilon '}(z^{2^k})$
under the map
![]() $z\mapsto z^{2^k}$
.
$z\mapsto z^{2^k}$
.
Now, since
![]() $\epsilon _1>0$
and
$\epsilon _1>0$
and
![]() $\unicode{x3bb} '>\unicode{x3bb} $
were arbitrary, and since
$\unicode{x3bb} '>\unicode{x3bb} $
were arbitrary, and since
![]() ${\Upsilon _2^{cp}}$
is closed, we obtain that
${\Upsilon _2^{cp}}$
is closed, we obtain that
![]() $(z, \unicode{x3bb} )\in {\Upsilon _2^{cp}}$
, and hence
$(z, \unicode{x3bb} )\in {\Upsilon _2^{cp}}$
, and hence
![]() $z\in {\Xi }_\unicode{x3bb} $
.
$z\in {\Xi }_\unicode{x3bb} $
.
7 Characterization outside the unit cylinder
The goal of this section is to prove Theorem 1.8, a characterization of the part of the Master Teapot that is outside the unit cylinder.
Proof of Theorem 1.8
For any
![]() $\unicode{x3bb} \in (1, 2)$
, denote by
$\unicode{x3bb} \in (1, 2)$
, denote by
![]() $f_\unicode{x3bb} $
the
$f_\unicode{x3bb} $
the
![]() $\unicode{x3bb} $
-tent map, and define the set
$\unicode{x3bb} $
-tent map, and define the set
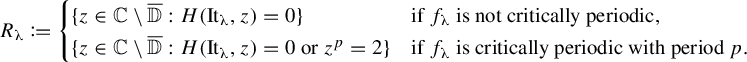
Next, define
We will show that
Our argument will almost immediately follow from results in [Reference TiozzoTio18], though these results must be translated from the context of the Mandelbrot set to the context of tent maps. The Milnor–Thurston kneading theory [Reference Milnor and ThurstonMT88] yields an entropy-preserving semiconjugacy from the set of real quadratic polynomials
![]() $f_c$
,
$f_c$
,
![]() $c \in [-2,1/4]$
, to the set of tent maps. If the quadratic
$c \in [-2,1/4]$
, to the set of tent maps. If the quadratic
![]() $f_c$
is sent by this semiconjugacy to a tent map
$f_c$
is sent by this semiconjugacy to a tent map
![]() $f_{\unicode{x3bb} }$
, then
$f_{\unicode{x3bb} }$
, then
![]() $(1-z^{-1})K_c(z^{-1}) = H(\mathrm {It}_{\unicode{x3bb} },z)$
, and hence the roots (in
$(1-z^{-1})K_c(z^{-1}) = H(\mathrm {It}_{\unicode{x3bb} },z)$
, and hence the roots (in
![]() $\mathbb {D}$
) of the kneading determinant
$\mathbb {D}$
) of the kneading determinant
![]() $K_c$
coincide with the reciprocals of the roots (in
$K_c$
coincide with the reciprocals of the roots (in
![]() $\mathbb {C} \setminus \overline {\mathbb {D}}$
) of
$\mathbb {C} \setminus \overline {\mathbb {D}}$
) of
![]() $H(\mathrm {It}_{\unicode{x3bb} },z)$
. By [Reference JungJun14, Theorem 4.7], on the real slice of the Mandelbrot set, core entropy of
$H(\mathrm {It}_{\unicode{x3bb} },z)$
. By [Reference JungJun14, Theorem 4.7], on the real slice of the Mandelbrot set, core entropy of
![]() $f_c:z \mapsto z^2+c$
is strictly increasing except on ‘small Mandelbrot sets,’ where the core entropy is constant. Consequently, the entropy-preserving semiconjugacy from real quadratics to tent maps is injective except for collapsing each small Mandelbrot set to a single tent map. Furthermore, the semiconjugacy induces a surjection from the set of critically periodic quadratics
$f_c:z \mapsto z^2+c$
is strictly increasing except on ‘small Mandelbrot sets,’ where the core entropy is constant. Consequently, the entropy-preserving semiconjugacy from real quadratics to tent maps is injective except for collapsing each small Mandelbrot set to a single tent map. Furthermore, the semiconjugacy induces a surjection from the set of critically periodic quadratics
![]() $f_c$
to the set of critically periodic tent maps, and each small Mandelbrot set contains a critically periodic quadratic.
$f_c$
to the set of critically periodic tent maps, and each small Mandelbrot set contains a critically periodic quadratic.
We will first show that R is a (relatively) closed subset of
![]() $\mathbb {C}\times (1, 2)$
. By Proposition 3.3 of [Reference TiozzoTio18], the set that is the union of
$\mathbb {C}\times (1, 2)$
. By Proposition 3.3 of [Reference TiozzoTio18], the set that is the union of
![]() $S^1$
and the roots of
$S^1$
and the roots of
![]() $K_c$
varies continuously in the Hausdorff topology with the parameter c. Consequently, when
$K_c$
varies continuously in the Hausdorff topology with the parameter c. Consequently, when
![]() $f_\unicode{x3bb} $
is not critically periodic, the function
$f_\unicode{x3bb} $
is not critically periodic, the function
![]() $s\mapsto R_s\cup S_1$
is continuous at
$s\mapsto R_s\cup S_1$
is continuous at
![]() $s=\unicode{x3bb} $
. As stated in the proof of Theorem 7.1 of [Reference TiozzoTio18], if
$s=\unicode{x3bb} $
. As stated in the proof of Theorem 7.1 of [Reference TiozzoTio18], if
![]() $(c_1,c_0)$
is the real section of a small Mandelbrot set of period p, then
$(c_1,c_0)$
is the real section of a small Mandelbrot set of period p, then
![]() $K_{c_0}(t) = P_{c_0}(t) / (1-t^p)$
and
$K_{c_0}(t) = P_{c_0}(t) / (1-t^p)$
and
![]() $K_{c_1}(t) = P_{c_0}(t)(1-2t^p) / (1-t^p)$
. Thus, in the Hausdorff topology,
$K_{c_1}(t) = P_{c_0}(t)(1-2t^p) / (1-t^p)$
. Thus, in the Hausdorff topology,
and so denoting by
![]() $\unicode{x3bb} $
the growth rate of
$\unicode{x3bb} $
the growth rate of
![]() $f_{c_0}$
, we have
$f_{c_0}$
, we have
Therefore, for any
![]() $\unicode{x3bb} $
for which the tent map
$\unicode{x3bb} $
for which the tent map
![]() $f_\unicode{x3bb} $
is critically periodic,
$f_\unicode{x3bb} $
is critically periodic,
Hence, R is a closed subset of
![]() $\mathbb {C}\times (1, 2)$
.
$\mathbb {C}\times (1, 2)$
.
When
![]() $f_\unicode{x3bb} $
is critically periodic,
$f_\unicode{x3bb} $
is critically periodic,
![]() $H(\mathrm {{It}}_\unicode{x3bb} , z)$
can be written as a rational function with integer coefficients; consequently,
$H(\mathrm {{It}}_\unicode{x3bb} , z)$
can be written as a rational function with integer coefficients; consequently,
![]() $R_{\unicode{x3bb} }$
contains all the Galois conjugates of
$R_{\unicode{x3bb} }$
contains all the Galois conjugates of
![]() $\unicode{x3bb} $
in
$\unicode{x3bb} $
in
![]() $\mathbb {C} \setminus \mathbb {D}$
. Therefore, for every
$\mathbb {C} \setminus \mathbb {D}$
. Therefore, for every
![]() $\unicode{x3bb} $
such that the tent map
$\unicode{x3bb} $
such that the tent map
![]() $f_{\unicode{x3bb} }$
is critically periodic,
$f_{\unicode{x3bb} }$
is critically periodic,
Since
![]() ${\Upsilon _2^{cp}} \cap \{z \mid |z| \geq 1\} \times (1,2)$
is formed by taking the closure of the union of all sets
${\Upsilon _2^{cp}} \cap \{z \mid |z| \geq 1\} \times (1,2)$
is formed by taking the closure of the union of all sets
![]() $({\Xi }_\unicode{x3bb} \backslash \mathbb {D})\cup S^1$
for
$({\Xi }_\unicode{x3bb} \backslash \mathbb {D})\cup S^1$
for
![]() $\unicode{x3bb} $
critically periodic, and since R is already closed, this implies
$\unicode{x3bb} $
critically periodic, and since R is already closed, this implies
To show containment in the other direction, Lemma 7.3 in [Reference TiozzoTio18] implies that when
![]() $f_\unicode{x3bb} $
is not critically periodic,
$f_\unicode{x3bb} $
is not critically periodic,
![]() $R_\unicode{x3bb} \times \{\unicode{x3bb} \}\subset {\Upsilon _2^{cp}}$
. However,
$R_\unicode{x3bb} \times \{\unicode{x3bb} \}\subset {\Upsilon _2^{cp}}$
. However,
 $$ \begin{align*}\bigcup_{f_\unicode{x3bb}\text{ is not critically periodic}}(R_\unicode{x3bb}\cup S^1)\times \{\unicode{x3bb}\}\end{align*} $$
$$ \begin{align*}\bigcup_{f_\unicode{x3bb}\text{ is not critically periodic}}(R_\unicode{x3bb}\cup S^1)\times \{\unicode{x3bb}\}\end{align*} $$
is dense in R, and hence
![]() $R\subset {\Upsilon _2^{cp}}$
.
$R\subset {\Upsilon _2^{cp}}$
.
8 Algorithms to test membership of
 ${\Xi }_\unicode{x3bb} $
${\Xi }_\unicode{x3bb} $
In this section, we will describe an algorithm to check if a point
![]() $z_0\in \mathbb {C}$
is in the complement of a slice
$z_0\in \mathbb {C}$
is in the complement of a slice
![]() ${\Xi }_\unicode{x3bb} $
for
${\Xi }_\unicode{x3bb} $
for
![]() $\unicode{x3bb} \in (1, 2)$
.
$\unicode{x3bb} \in (1, 2)$
.
First, if
![]() $\unicode{x3bb} <\sqrt {2}$
, Theorems 1.7 and 1.8 imply that
$\unicode{x3bb} <\sqrt {2}$
, Theorems 1.7 and 1.8 imply that
![]() $z\in {\Xi }_\unicode{x3bb} $
if and only if
$z\in {\Xi }_\unicode{x3bb} $
if and only if
![]() $z^2\in {\Xi }_{\unicode{x3bb} ^2}$
, so we can always reduce the question to the case
$z^2\in {\Xi }_{\unicode{x3bb} ^2}$
, so we can always reduce the question to the case
![]() $\unicode{x3bb} \in [\sqrt {2}, 2)$
.
$\unicode{x3bb} \in [\sqrt {2}, 2)$
.
8.1 Testing
 $z_0$
with
$z_0$
with
 $|z_0|> 1$
$|z_0|> 1$
When
![]() $|z_0|>1$
, Theorem 1.8 gives us a straightforward way to test if
$|z_0|>1$
, Theorem 1.8 gives us a straightforward way to test if
![]() $z_0\not \in {\Xi }_\unicode{x3bb} $
: calculating the first few terms of the power series
$z_0\not \in {\Xi }_\unicode{x3bb} $
: calculating the first few terms of the power series
![]() $H(\mathrm {{It}}_\unicode{x3bb} , z^{-1})$
, then checking if
$H(\mathrm {{It}}_\unicode{x3bb} , z^{-1})$
, then checking if
![]() $z_0^{-1}$
is a root of this power series. More precisely, we have the following algorithm.
$z_0^{-1}$
is a root of this power series. More precisely, we have the following algorithm.
Algorithm 1.

Remark 8.1. If instead of checking if
![]() $z_0\not \in {\Xi }_\unicode{x3bb} $
, we want to see if an
$z_0\not \in {\Xi }_\unicode{x3bb} $
, we want to see if an
![]() $\epsilon $
-neighborhood of
$\epsilon $
-neighborhood of
![]() $z_0$
is contained in the complement of
$z_0$
is contained in the complement of
![]() ${\Xi }_\unicode{x3bb} $
, we can change the last line of Algorithm 1 to make use of Rouché’s theorem.
${\Xi }_\unicode{x3bb} $
, we can change the last line of Algorithm 1 to make use of Rouché’s theorem.
8.2 Testing
 $z_0$
with
$z_0$
with
 $|z_0| < 1$
$|z_0| < 1$
If
![]() $|z_0|<1$
, a way to certify that
$|z_0|<1$
, a way to certify that
![]() $z_0\not \in {\Xi }_\unicode{x3bb} $
is by first finding the set of all words of length N that satisfy conditions (1)–(3) of Definition 1.5 (condition (4) is trivial because
$z_0\not \in {\Xi }_\unicode{x3bb} $
is by first finding the set of all words of length N that satisfy conditions (1)–(3) of Definition 1.5 (condition (4) is trivial because
![]() $\unicode{x3bb} \geq \sqrt {2}$
), denoted as
$\unicode{x3bb} \geq \sqrt {2}$
), denoted as
![]() $\mathcal {M}_{N, \unicode{x3bb} }$
, for each word
$\mathcal {M}_{N, \unicode{x3bb} }$
, for each word
![]() $w=(w_1\ldots w_N)\in \mathcal {M}_{N, \unicode{x3bb} }$
, evaluating
$w=(w_1\ldots w_N)\in \mathcal {M}_{N, \unicode{x3bb} }$
, evaluating
![]() $f_{w_N, z_0}^{-1}\circ f_{w_{N-1}, z_0}^{-1}\ldots f_{w_1, z_0}^{-1}(1)$
, and checking that they are all sufficiently large. More precisely, the algorithm can be described as follows.
$f_{w_N, z_0}^{-1}\circ f_{w_{N-1}, z_0}^{-1}\ldots f_{w_1, z_0}^{-1}(1)$
, and checking that they are all sufficiently large. More precisely, the algorithm can be described as follows.
Algorithm 2.

Remark 8.2. In the definition of
![]() $\mathcal {M}_{N, \unicode{x3bb} }$
above, one needs to check conditions (1)–(3) in Definition 1.5 for all the
$\mathcal {M}_{N, \unicode{x3bb} }$
above, one needs to check conditions (1)–(3) in Definition 1.5 for all the
![]() $\unicode{x3bb} '>\unicode{x3bb} $
. However, in practice, one does not really need to check these conditions for infinitely many
$\unicode{x3bb} '>\unicode{x3bb} $
. However, in practice, one does not really need to check these conditions for infinitely many
![]() $\unicode{x3bb} '$
: instead, one can pick a decreasing sequence
$\unicode{x3bb} '$
: instead, one can pick a decreasing sequence
![]() $\unicode{x3bb} ^{\prime }_j$
converging to
$\unicode{x3bb} ^{\prime }_j$
converging to
![]() $\unicode{x3bb} $
, then there must be some
$\unicode{x3bb} $
, then there must be some
![]() $j=j_0$
such that for any
$j=j_0$
such that for any
![]() $i\leq N$
, let
$i\leq N$
, let
![]() $f_s$
be the s-tent map, then
$f_s$
be the s-tent map, then
![]() $H_i(s)=f_s^{\circ i}(1)$
does not have any critical points in
$H_i(s)=f_s^{\circ i}(1)$
does not have any critical points in
![]() $(\unicode{x3bb} , \unicode{x3bb} ^{\prime }_{j_0})$
. One can show that the N-prefix of
$(\unicode{x3bb} , \unicode{x3bb} ^{\prime }_{j_0})$
. One can show that the N-prefix of
![]() $\mathrm {{It}}_{\unicode{x3bb} ^{\prime }_j}$
for
$\mathrm {{It}}_{\unicode{x3bb} ^{\prime }_j}$
for
![]() $j>j_0$
should be the same as the N-prefix of
$j>j_0$
should be the same as the N-prefix of
![]() $\mathrm {{It}}_{\unicode{x3bb} ^{\prime }_{j_0}}$
, and in Definition 1.5, the only thing we ever used for
$\mathrm {{It}}_{\unicode{x3bb} ^{\prime }_{j_0}}$
, and in Definition 1.5, the only thing we ever used for
![]() $\mathrm {{It}}_{\unicode{x3bb} '}$
is its N-prefix, so we can set
$\mathrm {{It}}_{\unicode{x3bb} '}$
is its N-prefix, so we can set
![]() $\unicode{x3bb} '=\unicode{x3bb} ^{\prime }_{j_0}$
and verify the three conditions in finite time.
$\unicode{x3bb} '=\unicode{x3bb} ^{\prime }_{j_0}$
and verify the three conditions in finite time.
The reason that Algorithm 2 is true is due to the following proposition.
Proposition 8.3. Let
![]() $\unicode{x3bb} \in [\sqrt {2}, 2)$
, and let
$\unicode{x3bb} \in [\sqrt {2}, 2)$
, and let
![]() $\mathcal {M}_{N, \unicode{x3bb} }$
be defined as in Algorithm 2. Suppose
$\mathcal {M}_{N, \unicode{x3bb} }$
be defined as in Algorithm 2. Suppose
![]() $|z|<1$
, then
$|z|<1$
, then
![]() $z\not \in {\Xi }_\unicode{x3bb} $
if and only if there exists
$z\not \in {\Xi }_\unicode{x3bb} $
if and only if there exists
![]() $N \in \mathbb {N}$
such that for every word
$N \in \mathbb {N}$
such that for every word
![]() $w=w_1\ldots w_N\in \mathcal {M}_{N, \unicode{x3bb} }$
,
$w=w_1\ldots w_N\in \mathcal {M}_{N, \unicode{x3bb} }$
,
Proof. First, we assume that there is some N such that for every word
![]() $w=w_1\ldots w_N\in \mathcal {M}_{N, \unicode{x3bb} }$
,
$w=w_1\ldots w_N\in \mathcal {M}_{N, \unicode{x3bb} }$
,
and prove that
![]() $z\not \in {\Xi }_\unicode{x3bb} $
. Suppose
$z\not \in {\Xi }_\unicode{x3bb} $
. Suppose
![]() $z\in {\Xi }_\unicode{x3bb} $
. Then by Theorem 1.7, there must be some
$z\in {\Xi }_\unicode{x3bb} $
. Then by Theorem 1.7, there must be some
![]() $\unicode{x3bb} $
-suitable sequence
$\unicode{x3bb} $
-suitable sequence
![]() $v=v_1v_2\ldots $
such that
$v=v_1v_2\ldots $
such that
In other words, for any
![]() $\delta>0$
, there is some
$\delta>0$
, there is some
![]() $n>N$
such that
$n>N$
such that
By the definition of
![]() $\mathcal {M}_{N, \unicode{x3bb} }$
, the word
$\mathcal {M}_{N, \unicode{x3bb} }$
, the word
![]() $v_1\ldots v_N\in \mathcal {M}_N$
. Let
$v_1\ldots v_N\in \mathcal {M}_N$
. Let
![]() $u=f_{v_1, z}\circ \cdots \circ f_{v_n, z}(1)$
. Then,
$u=f_{v_1, z}\circ \cdots \circ f_{v_n, z}(1)$
. Then,
![]() $|u-1|<\delta $
. Because
$|u-1|<\delta $
. Because
![]() $f_{v_N, z}^{-1} \circ \cdots \circ f_{v_1, z}^{-1}$
is continuous, we can pick
$f_{v_N, z}^{-1} \circ \cdots \circ f_{v_1, z}^{-1}$
is continuous, we can pick
![]() $\delta $
small enough such that
$\delta $
small enough such that
However,
By calculation, it is easy to verify that
![]() $1$
is in the disc
$1$
is in the disc
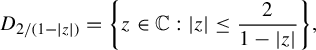 $$ \begin{align*}D_{2/ ({1-|z|})}= \bigg\{z\in\mathbb{C}:|z|\leq {2\over {1-|z|}} \bigg\},\end{align*} $$
$$ \begin{align*}D_{2/ ({1-|z|})}= \bigg\{z\in\mathbb{C}:|z|\leq {2\over {1-|z|}} \bigg\},\end{align*} $$
and both
![]() $f_{0, z}$
and
$f_{0, z}$
and
![]() $f_{1, z}$
send
$f_{1, z}$
send
![]() $D_{2/ ({1-|z|})}$
to itself. Hence,
$D_{2/ ({1-|z|})}$
to itself. Hence,
which is a contradiction.
Now, for the other direction, we assume that for any
![]() $N \in \mathbb {N}$
, there is some word
$N \in \mathbb {N}$
, there is some word
![]() $w=w_1\ldots w_N\in \mathcal {M}_{N, \unicode{x3bb} }$
such that
$w=w_1\ldots w_N\in \mathcal {M}_{N, \unicode{x3bb} }$
such that
and prove that
![]() $z\not \in {\Xi }_\unicode{x3bb} $
. Let
$z\not \in {\Xi }_\unicode{x3bb} $
. Let
![]() $C_N$
be the set of sequences such that an N-prefix of it is in
$C_N$
be the set of sequences such that an N-prefix of it is in
![]() $\mathcal {M}_{N, \unicode{x3bb} }$
, and this N prefix is of the form
$\mathcal {M}_{N, \unicode{x3bb} }$
, and this N prefix is of the form
![]() $w_1\ldots w_N$
such that
$w_1\ldots w_N$
such that
The fact that
![]() $f_{0, z}$
and
$f_{0, z}$
and
![]() $f_{1, z}$
both send
$f_{1, z}$
both send
![]() $D_{2/({1-|z|})}$
to itself implies that
$D_{2/({1-|z|})}$
to itself implies that
![]() $C_{N+1}\subset C_{N}$
, and all these sets are non-empty and compact under the product topology, and hence their intersection is non-empty. Let
$C_{N+1}\subset C_{N}$
, and all these sets are non-empty and compact under the product topology, and hence their intersection is non-empty. Let
![]() $w\in \bigcap _NC_N$
, then w is
$w\in \bigcap _NC_N$
, then w is
![]() $\unicode{x3bb} $
-suitable and it is easy to see that
$\unicode{x3bb} $
-suitable and it is easy to see that
![]() $G(w, z)=1$
.
$G(w, z)=1$
.
Furthermore, we have an effective version of the Proposition 8.3 above.
Proposition 8.4. Let
![]() $\unicode{x3bb} $
, z, N, and
$\unicode{x3bb} $
, z, N, and
![]() $\epsilon $
be as in Proposition 8.3 above,
$\epsilon $
be as in Proposition 8.3 above,
![]() ${1\over 2}<|z|<1$
. Then for any
${1\over 2}<|z|<1$
. Then for any
![]() $y\in \mathbb {C}$
, if
$y\in \mathbb {C}$
, if
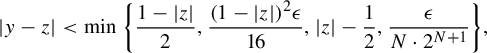 $$ \begin{align*}|y-z|<\min \bigg\{{1-|z|\over 2}, {(1-|z|)^2\epsilon\over 16}, |z|-{1\over 2}, {\epsilon\over N\cdot 2^{N+1}} \bigg\},\end{align*} $$
$$ \begin{align*}|y-z|<\min \bigg\{{1-|z|\over 2}, {(1-|z|)^2\epsilon\over 16}, |z|-{1\over 2}, {\epsilon\over N\cdot 2^{N+1}} \bigg\},\end{align*} $$
then
![]() $y\not \in {\Xi }_\unicode{x3bb} $
.
$y\not \in {\Xi }_\unicode{x3bb} $
.
Remark 8.5. The assumption
![]() $|z|>{1\over 2}$
is a reasonable one because it is well known (cf. [Reference TiozzoTio18]) that if
$|z|>{1\over 2}$
is a reasonable one because it is well known (cf. [Reference TiozzoTio18]) that if
![]() $|z|<{1\over 2}$
, then
$|z|<{1\over 2}$
, then
![]() $z\not \in {\Xi }_\unicode{x3bb} $
for any
$z\not \in {\Xi }_\unicode{x3bb} $
for any
![]() $\unicode{x3bb} \in (1, 2)$
.
$\unicode{x3bb} \in (1, 2)$
.
Proof. It is easy to see that as long as
![]() $|y|<1$
,
$|y|<1$
,
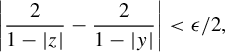 $$ \begin{align*}\bigg|{2\over 1-|z|}-{2\over 1-|y|}\bigg|<\epsilon/2,\end{align*} $$
$$ \begin{align*}\bigg|{2\over 1-|z|}-{2\over 1-|y|}\bigg|<\epsilon/2,\end{align*} $$
and for any
![]() $w=w_1\ldots w_N\in \mathcal {M}_{N, \unicode{x3bb} }$
,
$w=w_1\ldots w_N\in \mathcal {M}_{N, \unicode{x3bb} }$
,
then y also satisfies the assumption in Proposition 8.3. The first condition,
![]() $|y|<1$
, holds because
$|y|<1$
, holds because
![]() $|y-z|<{(1-|z|)/ 2}$
, which implies
$|y-z|<{(1-|z|)/ 2}$
, which implies
![]() $|y|<{(1+|z|)/ 2}<1$
. The second condition,
$|y|<{(1+|z|)/ 2}<1$
. The second condition,
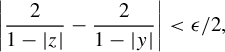 $$ \begin{align*}\bigg|{2\over 1-|z|}-{2\over 1-|y|}\bigg|<\epsilon/2,\end{align*} $$
$$ \begin{align*}\bigg|{2\over 1-|z|}-{2\over 1-|y|}\bigg|<\epsilon/2,\end{align*} $$
holds because
![]() $|y|<{(1+|z|)/ 2}$
and
$|y|<{(1+|z|)/ 2}$
and
![]() $|y-z|<{(1-|z|)^2\epsilon / 16}$
. The third condition,
$|y-z|<{(1-|z|)^2\epsilon / 16}$
. The third condition,
holds because of the following argument. As a polynomial of
![]() ${1/ z}$
,
${1/ z}$
,
has degree N and coefficients bounded between
![]() $-2$
and
$-2$
and
![]() $2$
, and hence has its derivative bounded by
$2$
, and hence has its derivative bounded by
![]() $N2^{N-1}\cdot 2=N\cdot 2^N$
on the annulus
$N2^{N-1}\cdot 2=N\cdot 2^N$
on the annulus
![]() $\{y\in \mathbb {C}:1\leq |y|\leq 2\}$
. Because
$\{y\in \mathbb {C}:1\leq |y|\leq 2\}$
. Because
![]() $|y-z|<|z|-{1\over 2}$
, y is inside this annulus, so this third condition follows from the assumption that
$|y-z|<|z|-{1\over 2}$
, y is inside this annulus, so this third condition follows from the assumption that
![]() $|y-z|<{\epsilon / N\cdot 2^{N+1}}$
and the mean value theorem.
$|y-z|<{\epsilon / N\cdot 2^{N+1}}$
and the mean value theorem.
9 Asymmetry of
 ${\Xi }_{\unicode{x3bb} }$
${\Xi }_{\unicode{x3bb} }$
The following proposition is likely well known to experts; we include the proof for completeness.
Proposition 9.1.
![]() $\Omega _2^{cp} \cap \mathbb {D}$
is invariant under reflection across the real axis and across the imaginary axis.
$\Omega _2^{cp} \cap \mathbb {D}$
is invariant under reflection across the real axis and across the imaginary axis.
Proof. The set
![]() $\Omega _2^{cp} \cap \mathbb {D}$
is invariant under reflection across the real axis because Galois conjugates come in complex conjugate pairs. Tiozzo [Reference TiozzoTio18] showed that
$\Omega _2^{cp} \cap \mathbb {D}$
is invariant under reflection across the real axis because Galois conjugates come in complex conjugate pairs. Tiozzo [Reference TiozzoTio18] showed that
![]() $\Omega _2^{cp} \cap \mathbb {D}\backslash S^1$
is the set of all the roots in
$\Omega _2^{cp} \cap \mathbb {D}\backslash S^1$
is the set of all the roots in
![]() $\mathbb {D}$
of all power series with all coefficients in
$\mathbb {D}$
of all power series with all coefficients in
![]() $\{\pm 1\}$
. So if
$\{\pm 1\}$
. So if
![]() $z \in \mathbb {D}$
is a root of a power series S with coefficients in
$z \in \mathbb {D}$
is a root of a power series S with coefficients in
![]() $\{\pm 1\}$
, then
$\{\pm 1\}$
, then
![]() $-z$
is a root of the power series formed from S by flipping the sign of the coefficients on all terms of odd degree. Therefore, the complex conjugate,
$-z$
is a root of the power series formed from S by flipping the sign of the coefficients on all terms of odd degree. Therefore, the complex conjugate,
![]() $\overline {-z}$
, is in
$\overline {-z}$
, is in
![]() $\Omega _2^{cp}$
.
$\Omega _2^{cp}$
.
However, our Algorithm 2 in the previous section can be used to show that
![]() ${\Xi }_\unicode{x3bb} \cap \mathbb {D}$
does not necessarily have such symmetry, which proves Theorem 1.14.
${\Xi }_\unicode{x3bb} \cap \mathbb {D}$
does not necessarily have such symmetry, which proves Theorem 1.14.
Proof of Theorem 1.14
We only need to show that there is some
![]() $z\in {\Xi }_{1.82}\cap \mathbb {D}$
such that
$z\in {\Xi }_{1.82}\cap \mathbb {D}$
such that
![]() $-z\not \in {\Xi }_{1.82}\cap \mathbb {D}$
. Consider the tent map with growth rate being the leading root of
$-z\not \in {\Xi }_{1.82}\cap \mathbb {D}$
. Consider the tent map with growth rate being the leading root of
which is approximately
![]() $1.8149185987640513$
and is smaller than
$1.8149185987640513$
and is smaller than
![]() $1.82$
, and hence any Galois conjugate of this leading root must be in
$1.82$
, and hence any Galois conjugate of this leading root must be in
![]() ${\Xi }_{1.82}$
. Let z be the Galois conjugate near the point
${\Xi }_{1.82}$
. Let z be the Galois conjugate near the point
![]() $-0.5840341196392905+0.4820600149798202 i$
. Applying Algorithm 2 to
$-0.5840341196392905+0.4820600149798202 i$
. Applying Algorithm 2 to
![]() $-z$
for
$-z$
for
![]() $N=20$
shows that
$N=20$
shows that
![]() $-z\not \in {\Xi }_{1.82}$
.
$-z\not \in {\Xi }_{1.82}$
.
Acknowledgements
The authors thank Diana Davis for many helpful conversations. K.L. was supported by the National Science Foundation under grant DMS-1901247.