Hostname: page-component-76c49bb84f-lvrpm Total loading time: 0 Render date: 2025-07-03T00:32:53.093Z Has data issue: false hasContentIssue false
  • English
  • Français

A rigid analytic proof that the Abel–Jacobi map extends to compact-type models

Part of: Arithmetic problems. Diophantine geometry Abelian varieties and schemes

Published online by Cambridge University Press:  09 January 2024

Taylor Dupuy  and
Joseph Rabinoff
Taylor Dupuy*
Affiliation:
Department of Mathematics and Statistics, University of Vermont, 82 University Place, Innovation Hall E220, Burlington, VT 05405, United States
Joseph Rabinoff
Affiliation:
Department of Mathematics, Duke University, 120 Science Drive, Durham, NC 27708- 0320, United States e-mail: jdr@math.duke.edu
*
e-mail: taylor.dupuy@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let K be a non-Archimedean valued field with valuation ring R. Let $C_\eta $ be a K-curve with compact-type reduction, so its Jacobian 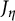$J_\eta $ extends to an abelian R-scheme J. We prove that an Abel–Jacobi map 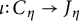$\iota \colon C_\eta \to J_\eta $ extends to a morphism 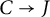$C\to J$, where C is a compact-type R-model of J, and we show this is a closed immersion when the special fiber of C has no rational components. To do so, we apply a rigid-analytic “fiberwise” criterion for a morphism to extend to integral models, and geometric results of Bosch and Lütkebohmert on the analytic structure of 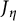$J_\eta $.

Keywords

Abel–jacobibad reductiontropicalnon-Archimedean

MSC classification

Primary: 14G22: Rigid analytic geometry 14K99: None of the above, but in this section

Information

Type
Article
Information
Canadian Mathematical Bulletin , Volume 67 , Issue 3 , September 2024 , pp. 648 - 654
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Dupuy was supported by the European Research Council under the European Union’s Seventh Framework Program (FP7/2007-2013)/ERC Grant agreement no. 291111/MODAG. Rabinoff was supported by NSF DMS-1601842.

References

Bosch, S., Güntzer, U., and Remmert, R., Non-Archimedean analysis, Grundlehren der Mathematischen Wissenschaften, 261, Springer, Berlin, 1984. MR 746961 (86b:32031)CrossRefGoogle Scholar
Bosch, S. and Lütkebohmert, W., Stable reduction and uniformization of abelian varieties. II . Invent. Math. 78(1984), no. 2, 257–297. MR 767194 (86j:14040b)CrossRefGoogle Scholar
Bosch, S. and Lütkebohmert, W., Stable reduction and uniformization of abelian varieties. I . Math. Ann. 270(1985), no. 3, 349–379. MR 774362 (86j:14040a)CrossRefGoogle Scholar
Bosch, S. and Lütkebohmert, W., Formal and rigid geometry. I. Rigid spaces . Math. Ann. 295(1993), no. 2, 291–317. MR 1202394 (94a:11090)CrossRefGoogle Scholar
Bosch, S., Lütkebohmert, W., and Raynaud, M., Néron models, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], 21, Springer, Berlin, 1990. MR 1045822 (91i:14034)CrossRefGoogle Scholar
Caporaso, L., Naturality of Abel maps . Manuscripta Math. 123(2007), no. 1, 53–71. MR 2300059CrossRefGoogle Scholar
Caporaso, L. and Esteves, E., On Abel maps of stable curves . Michigan Math. J. 55(2007), no. 3, 575–607. MR 2372617CrossRefGoogle Scholar
Caporaso, L. and Harris, J., Counting plane curves of any genus . Invent. Math. 131(1998), no. 2, 345–392. MR 1608583 (99i:14064)CrossRefGoogle Scholar
Conrad, B., Irreducible components of rigid spaces . Ann. Inst. Fourier (Grenoble) 49(1999), no. 2, 473–541. MR 1697371 (2001c:14045)CrossRefGoogle Scholar
Edixhoven, B, On Néron models, divisors and modular curves . J. Ramanujan Math. Soc. 13(1998), no. 2, 157–194. MR 1666374Google Scholar
Grothendieck, A., Éléments de géométrie algébrique. III. Étude cohomologique des faisceaux cohérents. I. Inst. Hautes Études Sci. Publ. Math. 11(1961), no. 11, 5–167. MR 0163910 (29 #1209)Google Scholar
Fujiwara, K. and Kato, F., Foundations of rigid geometry I. EMS Monographs in Mathematics, European Mathematical Society (EMS), Zürich (2018), xxxiv+829 MR 3752648.Google Scholar