There is considerable interest in the causes and consequences of associations between cognitive ability and fertility. A recent meta-analysis found that these two variables have typically been negatively correlated in the United States in the 20th and 21st centuries, with some (albeit far more limited) evidence of such a negative relationship in a small number of other areas of the world for which data were available (Reeve et al., Reference Reeve, Heeney and Woodley of Menie2018). The identification of genetic variants that predict cognitive ability and educational attainment (in the form of polygenic scores, PGSs) has enabled analyses that indicate that these variants are under direct negative directional selection in contemporary populations (Beauchamp, Reference Beauchamp2016; Conley et al., Reference Conley, Laidley, Belsky, Fletcher, Boardman and Domingue2016; Kong et al., Reference Kong, Banks, Poplin, Garimella, Maguire and Stefansson2017), effectively confirming predictions made by Galton 140 years ago (Galton, Reference Galton1869).
Studies utilizing PGSs have found negative genetic correlations between cognitive ability measures and fertility (Kong et al., Reference Kong, Banks, Poplin, Garimella, Maguire and Stefansson2017), indicating that at least some genetic variants that tend to raise cognitive ability also tend to depress fertility. However, the causal basis of this negative correlation is unclear. There are indications of historical positive directional selection favoring higher frequencies of variants predictive of cognitive ability when ancient (Bronze and early Iron Age) and ancestrally matched modern genomes are compared (Woodley of Menie et al., Reference Woodley of Menie, Younuskunju, Balan and Piffer2017b). This suggests that in Western populations the negative association only arose relatively recently, most likely during the period of industrialization, when increasing ecological mildness lifted reproductive constraints on those with lower cognitive ability and the development of innovations such as contraception created opportunities for those with high cognitive ability to limit their fertility (Lynn, Reference Lynn1996; Woodley of Menie et al., Reference Woodley of Menie, Figueredo, Sarraf, Hertler, Fernandes and Peñaherrera-Aguirre2017a).
A major factor associated with modernization that may have played a pivotal role in reversing the genetic correlation between cognitive ability and fertility (from positive to negative) is the rise of universal education. Education causes fertility delay, which reduces opportunity for fertility, more so in the case of females than males. This is because the female fertility window is narrower than the male window. Consistent with this observation, fertility by educational attainment correlations are of consistently higher magnitude among females compared to males across cultures (Meisenberg, Reference Meisenberg2008).
Phenotype-only analyses involving path modeling have offered evidence for the predicted role of educational attainment as a mediator of the association between IQ and fertility. A study by Retherford and Sewell (Reference Retherford and Sewell1989) found that educational attainment completely mediated the associations between IQ and (largely completed) fertility in the Wisconsin Longitudinal Study (WLS). A study by Meisenberg (Reference Meisenberg2010) also found indications of mediation when additional predictors were used (sex, liberal gender attitudes, and income) in the National Longitudinal Study of Youth ’79 cohort (which was also in mostly completed fertility). A more recent study by Mededović (Reference Mededović2017) employed a small sample (N = 191) of the Serbian population at completed fertility (aged in their 50s, fertility is typically complete at >45 years of age among Western populations; Fieder & Huber, Reference Fieder and Huber2007; Martin et al., Reference Martin, Hamilton, Ventura, Osterman and Mathews2013), finding positive associations between cognitive performance (evaluated using the Advanced Progressive Matrices test) and number of children, but negative associations between cognitive performance and numbers of grandchildren. It also considered the role of age at first birth, finding no significant direct effect of cognitive ability on this measure, but negative associations between age at first birth and number of grandchildren. The study also found strong indications that educational attainment mediated the effect of cognitive performance on the sample’s reproductive characteristics.
Finally, a study utilizing PGSs in a sample at approximately 50% completed fertility sourced from the US AddHealth dataset found substantial evidence of mediation, with the direct effect of the cognitive ability PGS on fertility being reduced to effectively zero after the indirect paths via cognitive ability and educational attainment were modeled (Woodley of Menie et al., Reference Woodley of Menie, Schwartz and Beaver2016). This latter study discussed the need for genetically informed studies involving samples at completed fertility in order to replicate this mediation. It also highlighted the need for consideration of a larger number of covariates, including age at first birth, which likely increases the fitness of those with lower cognitive ability by allowing them earlier and thus fuller participation in reproduction (Kong et al., Reference Kong, Banks, Poplin, Garimella, Maguire and Stefansson2017).
A genetically informed study using the same variables in Mededović’s (Reference Mededović2017) study will be attempted here. We analyze new data released from the WLS, including number of grand children and a PGS predictive of cognitive ability and educational attainment. Revisiting this issue is appropriate as it has been 30 years since Retherford and Sewell (Reference Retherford and Sewell1988, Reference Retherford and Sewell1989) conducted their own seminal analyses of the fertility × cognitive ability association in the WLS, which did much to revive interest in the association after nearly 40 years of neglect. With the additional variables, the robustness of their findings can furthermore be ascertained.
Methods
Data
Wisconsin Longitudinal Study
The data were drawn from the WLS, a longitudinal, mixed-sex sample of 10,317 almost exclusively European-American individuals sourced from the graduate population of the Wisconsin High School system. This sample was first surveyed in 1957, with the most recent wave sampled in 2011. The WLS tracks the development of a considerable number of measures, including those relevant to the current study (for further sample details, see Herd et al., Reference Herd, Carr and Roan2014). For the total set of variables (described below), data were available for a combined sample of 5629 individuals (male n = 2617, female n = 3012)
Variables
EA3 genome wide association study polygenic score
A total of 9012 WLS study participants were genotyped on the Illumina HumanOmniExpress array as part of a recent genome wide association study (GWAS) for IQ, educational attainment, and self-reported mathematical ability (Lee et al., Reference Lee, Wedow, Okbay, Kong, Maghzian and Cesarini2018). The genetic samples came from saliva collected first in 2007–08 by mail, then during the course of home interviews conducted initially in March 2010. In this study, the educational attainment polygenic score (Educational Attainment 3 [EA3] PGS) was estimated using a GWAS approach for a reduced sample of 8527 individuals, employing genotype probabilities obtained from the haplotype reference consortium imputation and linkage disequilibrium (LD)-adjusted weights. The educational attainment ‘phenotype’ was defined based on the ISCED 1997 UNESCO classification, which incorporates seven internationally comparable categories of educational attainment, rescaled as US years-of-schooling equivalents (Lee et al., Reference Lee, Wedow, Okbay, Kong, Maghzian and Cesarini2018). The PGS, which is only available for this sample as a standardized single-indicator variable, includes a total of 1,170,820 single nucleotide polymorphisms (SNPs). In computing this PGS, Lee et al. (Reference Lee, Wedow, Okbay, Kong, Maghzian and Cesarini2018) excluded long-range LD regions on chromosomes 5 (44–51.5 Mb), 6 (25–33.5 Mb), 8 (8–12 Mb), and 11 (45–57 Mb). They also LD pruned the remaining SNPs (R 2 < .1 on a 1000-kb window). The extremely high ethnic homogeneity of the WLS sample (Herd et al., Reference Herd, Carr and Roan2014) negates the need for population stratification controls. For full information on the sampling and genotyping procedures used in constructing this PGS, see www.ssc.wisc.edu/wlsresearch/documentation/GWAS/Herd_QC_report.pdf.
Intelligence
In WLS, the respondents’ IQ was measured in 1957 using the Henmon–Nelson test, a 30-minute test consisting of 90 items of increasing difficulty, sampling across the domains of spatial, verbal, and mathematical ability. In 1957, during the first wave of data collection, the test administration was standardized across the state of Wisconsin. The test exhibits high reliability (α ≍ .95; e.g., Hansen, Reference Hansen1968), and scores on the test are strongly associated with full-scale IQ scores obtained using other psychometric batteries, such as the WAIS (r ≍ .80 - .85; e.g., Klett et al., Reference Klett, Watson and Hoffman1986). The variable employed in this analysis is labeled ‘preferred measure of IQ’ in the WLS data file.
Educational attainment
Educational attainment, measured as educational level, was obtained from the participants in 1975 when they were in their mid-30s. The level of education was estimated using a 9-point scale, the lowest level of which was associated with ‘High school graduate or less, less than one year of college’ and the highest level with ‘PhD, MD, other doctorates not previously included, and post-doctorate education’.
Sex
Respondent sex in WLS was measured during the first wave of data collection in 1957 and is scaled 1 for male and 2 for female.
Number of children
Respondent number of children was obtained for both sexes in two waves. The first wave was collected in 1975 when the participants were in their mid-30s, the second wave was collected in 2011, updating the previous wave with fertility values collected for the cohort in its early 70s. At this age, fertility among US Whites is >99% complete for females (Martin et al., Reference Martin, Hamilton, Ventura, Osterman and Mathews2013).
Number of grandchildren
Number of grandchildren was measured in 2011 when the respondents were in their early 70s.
Age at first birth
Age at first birth was collected in 1975 when the respondents were in their mid-30s.
Analysis
Both correlational and path analyses were used to examine the associations among the variables for both the combined sample and the male and female subsamples, respectively. The path analyses were implemented in Mplus v.5.21. To examine sex differences, multi-group path models were constructed (using the Mplus option ‘grouping’; Geiser, Reference Geiser2013). An additional analysis was conducted using a less restricted sample to determine the decadal decline in IQ predicted using the strength of genetic selection on the PGS employing formulas from Kong et al. (Reference Kong, Banks, Poplin, Garimella, Maguire and Stefansson2017), which account for the joint impact of both the quantum (number) and timing of fertility on the rate of trait change.
Results
Analysis 1: Mixed Sex Sample
Table 1 presents the results of the correlation analysis involving all variables for the combined sex sample (N = 5629).
Table 1. Correlation matrix for the entire sample (N = 5629)
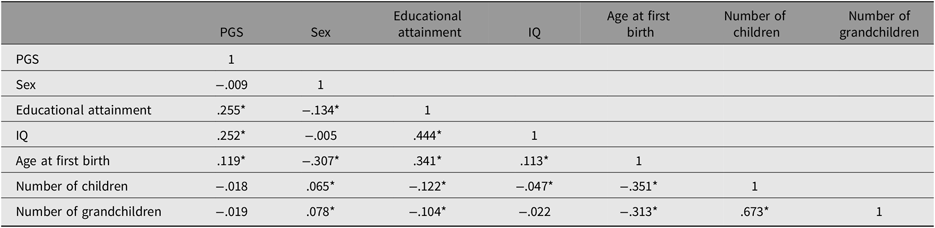
Note: *p < .05, N = 5629.
PGS indicates polygenic score.
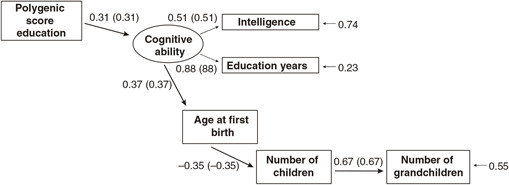
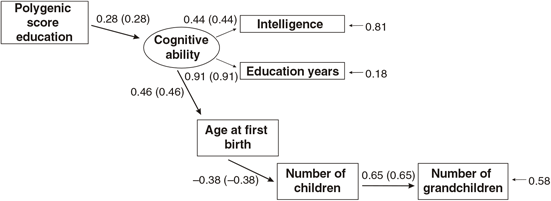
Figures 1 and 2 report the results of two alternative path models, one in which the PGS is modeled as having joint effects on the intelligence (IQ) and years of education (educational attainment) measures, with the latter predicting age at first birth, and a second model in which a latent cognitive ability variable is constructed using the common variance between both intelligence and educational attainment, which has direct effects on age at first birth. In both models, age at first birth is modeled as having a direct effect on the number of children. Number of children is modeled as having a direct effect on number of grandchildren.
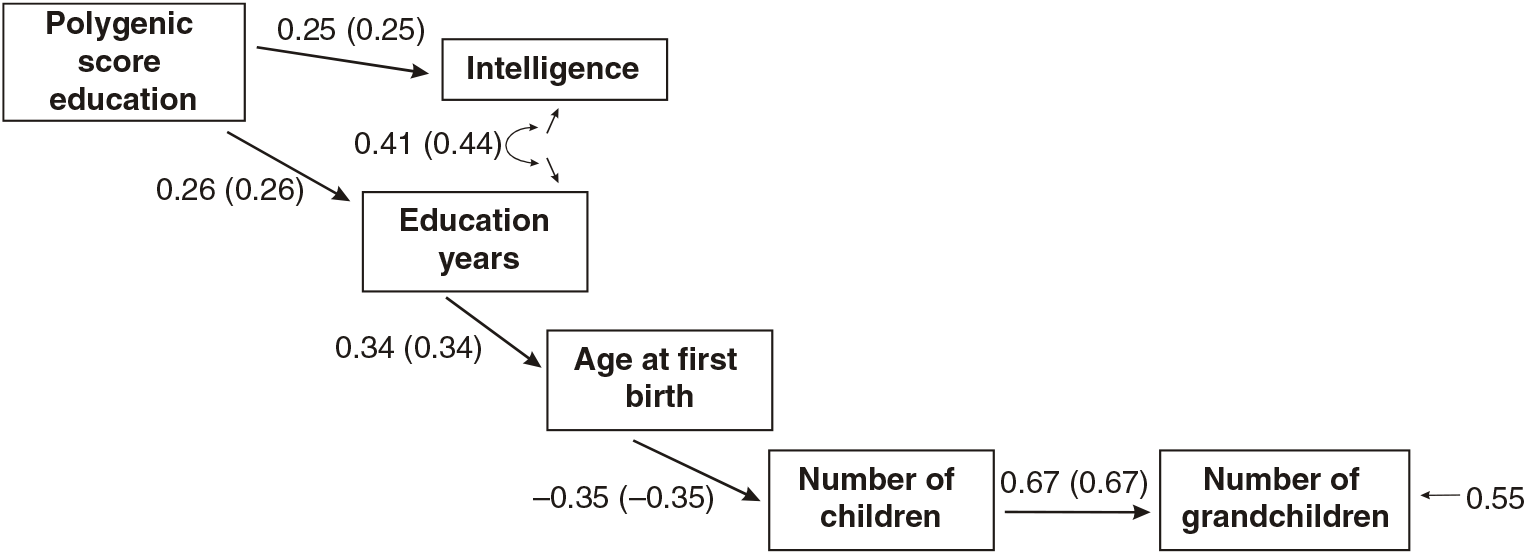
Fig. 1. Path model predicting number of children by age at first birth, education and the polygenic score (standardized beta-coefficients, correlations in parentheses, confirmatory fit index = .99, Standardized Root Mean Square Residual (SRMR) = .02), N = 5629, entire sample.

Fig 2. Path model predicting number of children by age at first birth, a latent cognitive ability factor and the EA3 polygenic score (standardized beta-coefficients, correlations in parentheses, confirmatory fit index = .97, SRMR = .03), N = 5629, entire sample.
The two models exhibit approximately equal goodness-of-fit. The model in which a latent cognitive ability factor is modeled benefits from parsimony (fewer paths). In examining the associations for each sex separately and determining the presence of sex differences, the second (latent variable) model will be used.
Analysis 2: Sex Differences
Table 2 reports the results of the correlations among the variables broken out by sex.
Table 2. Correlation matrix for the male (n = 2617; below the diagonal) and female (n = 3012; above the diagonal) subsamples

Note: *p < .05.
PGS indicates polygenic score.
Figures 3 and 4 present the results of multi-group path models run for each sex separately.

Fig. 3. Multigroup path model predicting number of children with age at first birth, education and the polygenic score (standardized beta-coefficients, correlations in parentheses, confirmatory fit index = .96, SRMR = .04), N = 2617, males only.
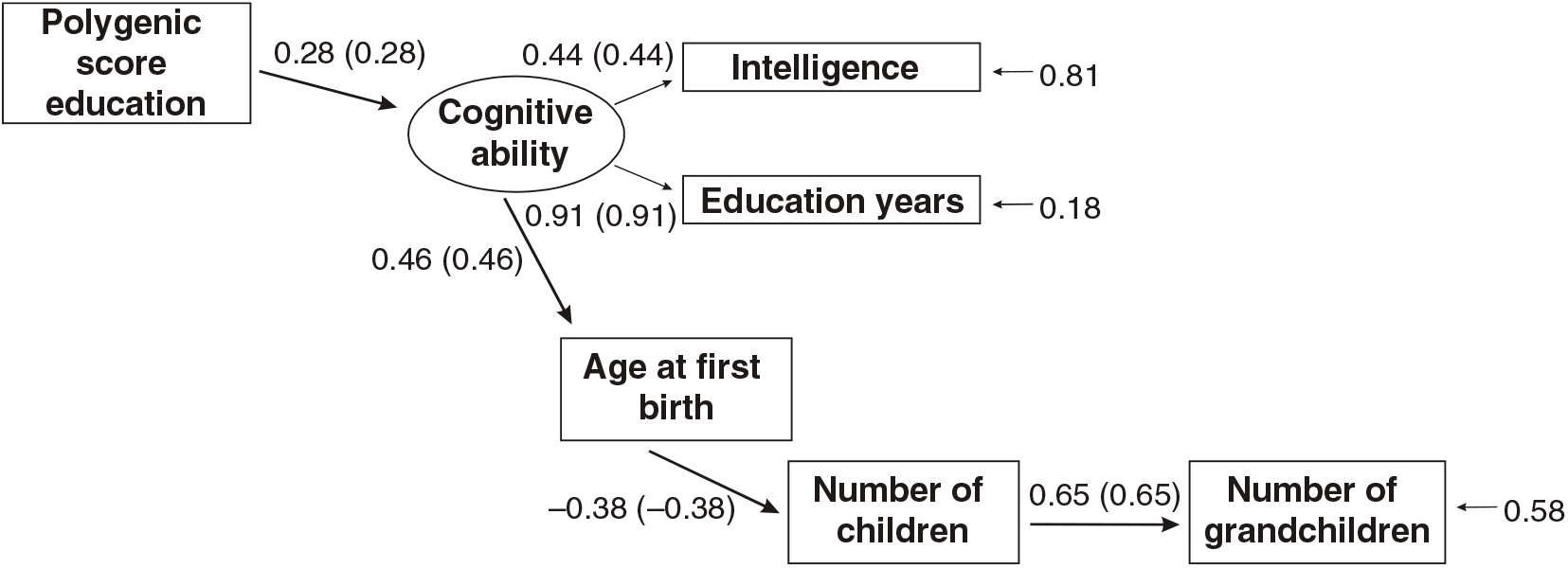
Fig 4. Multigroup path model predicting number of children with age at first birth, education and the polygenic score (standardized beta-coefficients, correlations in parentheses, confirmatory fit index = .96, SRMR = .04), N = 3012, females only.
As shown in Figures 3 and 4, all paths are similar for males and females except for the path from the latent cognitive ability factor to age at first birth. While for males the effect is βCA→A1B = .25, for females it is much larger: βCA→A1B = .46.
The difference was tested for significance by comparing a model with free paths (as shown in Figures 3 and 4) with a model where the path from cognitive ability to age at first birth was restricted (i.e., it was assumed that they were identical for each sex). While the first model (unconstrained paths) had a χ2 of 284.16 (df = 20), the model with one constrained path had a χ2 of 348.63 (df = 21). The fit of the second more restricted model to the data was much lower. A significance test of the χ2 difference (64.47, df = 1) using a calculator for social science statistics (available from: www.socscistatistics.com, p value from chi-square calculator) found a highly significant result (p < .00001) meaning that the fit of the second model is worse.
This means that the impact of cognitive ability on delay of age at first birth is much less severe for men than for women.
Analysis 3. Estimating the Decadal IQ Loss Using the Polygenic Scores
Given the availability of PGSs in the WLS database, along with data on IQ and both the quantum and timing of fertility, it should be possible to utilize the same formula employed by Kong et al. (Reference Kong, Banks, Poplin, Garimella, Maguire and Stefansson2017) to estimate the IQ decline due to the action of genetic selection.
The formula utilized by Kong et al. (Reference Kong, Banks, Poplin, Garimella, Maguire and Stefansson2017) combines both the quantum and the timing of fertility to estimate the yearly impact of selection on PGS level, as follows:
Regression 1:
Regression 2:
The mean parental age at birth of children was obtained from the 1975 interviews. A subset of the individuals who participated in the interview in 2011 have updated information on the ages at birth. However, these were not used because (1) at the time of the original interview the participants were 35–36, which, based on the 2011 census data for US Whites, equates to a completed fertility percentage for women of approximately 97% (for the 35–39 age range; Martin et al., Reference Martin, Hamilton, Ventura, Osterman and Mathews2013); (2) the later estimates may be inflated via the inclusion of birth ages of children who are not biologically theirs. For example, it is observed that some individuals jump from reporting a relatively low to a relatively high (i.e., 4–10) number of children, which might in part be driven by adoptions; and (3) the 2011 data are only available for a small subset of participants. Further derestricting the sample by dropping number of grandchildren enhances the size of the sample that can be employed for this analysis. The correlations among the variables for the larger sample used in this calculation, along with sample sizes, are presented in Table 3.
Table 3. Correlations among all of the variables used in calculating the IQ decline, along with sample sizes

Note: All correlations p < .05.
PGS indicates polygenic score.
Based on these calculations, the PGS can be expected to decline at a rate of −.001 Haldanes (standard deviation units) per year (95% CI [−.000 (1), −.002 Haldanes]). In order to calculate the decline in IQ expected, based on the predicted change in the PGS, first the yearly change in PGS derived from the equations is multiplied by 10, yielding a decadal decline of d = −.011 Haldanes per decade (95% CI [−.001, −.02 Haldanes]). Next, the IQ change per standard deviation change in PGS is calculated yielding 4.71 IQ points per Haldane. This can be used to convert the predicted change in PGS (per Haldane) into an equivalent change in IQ, yielding an IQ decline of −.052 IQ points per decade (95% CI [−.005, −.094 IQ points per decade]).
It is important to note that this estimated IQ loss is a substantial underestimate of the actual IQ loss, owing to the fact that the PGS yields an imperfect measure of the actual heritability of IQ — thus, to recover the actual loss, which will be considerably larger, a correction is needed for ‘missing’ heritability. This is achieved by taking the change in IQ per Haldane of PGS, and multiplying it by the quotient of the ‘missing’ heritability of IQ, and the actual variance in IQ explained by the PGS. There is debate about the actual heritability of IQ in the literature, with studies employing genome-wide complex trait analysis (GCTA), genome-based restricted maximum likelihood (GREML)-based approaches (where the additive heritability is estimated based on the use of a restricted maximum likelihood estimate of the aggregate influence of large numbers of variants) tending to be lower than those computed on the basis of classical behavior genetic studies employing twins. GCTA-GREML estimates of IQ heritability in adults are around .40 (Plomin & Deary, Reference Plomin and Deary2015); however, such estimates also suffer from a ‘missing’ GCTA heritability issue, as this technique likely underestimates the heritability of a trait related to the action of rare variants that are effectively additive in their responsiveness to selection (Plomin & Deary, Reference Plomin and Deary2015). Classical behavior genetic estimates of the additive heritability of IQ are considerably higher in adults (h 2 ≈ .80; Bouchard Jr., Reference Bouchard2004), reflecting the use of phenotypic convergence that necessarily captures all salient additive and near-additive influences on trait variance. Based on the GCTA-GREML IQ additive heritability estimate (i.e., .40), IQ in the WLS sample would be expected to decline at a rate of −.208 points per decade (95% CI [−.020, −.383 points per decade]). Based on classical behavior genetic estimates of additive IQ heritability (i.e., .80), the decline is −.424 points per decade (95% CI [−.041, −.766 points per decade]).
Discussion
The availability of a PGS for cognitive ability (and educational attainment) in the WLS permits the presence of genetic selection for lower IQ to be directly established in this dataset, which confirms predictions made by Retherford and Sewell (Reference Retherford and Sewell1988, Reference Retherford and Sewell1989). This is demonstrated with path modeling, which indicates that the effect of cognitive ability on fertility is primarily mediated by age at first birth. These models also indicate the presence of mediated positive effects on age at first birth of the PGS, stemming from a latent cognitive ability factor, composed of both educational attainment and IQ. An alternative model allowed for reciprocal effects on educational attainment and IQ, modeled as separate variables, and found that educational attainment rather than IQ mediated the positive association between the PGS and age at first birth.
The availability of data on grandchildren furthermore permitted the effect of the PGS and cognitive variables on number of grandchildren to be modeled. It was found that number of children mediated the effect of age at first birth on the number of grand-children. These results are consistent with the findings of Woodley of Menie et al. (Reference Woodley of Menie, Schwartz and Beaver2016), in that the impact of the PGS can be modeled as having mediated effects on the sample’s fitness characteristics, via the cognitive phenotype, and in particular educational attainment (when this is modeled separately). This is consistent with the ‘tradeoff’ model (Lynn, Reference Lynn1996), whereby high-IQ individuals select for higher levels of educational attainment, which causes delayed fertility, and consequently lower numbers of both children and grandchildren.
Furthermore, consistent with the results of a recent large-scale meta-analysis of the phenotypic association between IQ and fertility (Reeve et al., Reference Reeve, Heeney and Woodley of Menie2018), the use of restricted multi-group path models indicates the presence of a sex difference, characterized by a significantly larger impact of cognitive ability on fertility characteristics among the female relative to male subsample. The finding that age at first birth mediates the impact of cognitive ability on number of children, which in turn predicts number of grand-children, in addition to the presence of negative correlations between educational attainment, IQ, and number of children, is also inconsistent with the findings of Mededović’s (Reference Mededović2017) study of a Serbian population, which failed to find effects of IQ on age at first birth, but identified direct effects of IQ on number of children and grandchildren, with the effect of the former being positive and the effect on the latter being negative. Mededović’s analysis also identified direct positive effects of educational attainment on age at first birth and on the number of children, but no significant effect on number of grandchildren. The small sample size (N = 191) employed by Mededović (Reference Mededović2017), coupled with the use of a population that may have undergone the transition into selection for lower IQ more recently than the US and the use of a ‘narrow’ measure of g (the APM; see Gignac, Reference Gignac2015), limits the scope for comparing the two sets of results; however, it should be noted that Mededović (Reference Mededović2017) is the only study other than the present effort to attempt to directly estimate the effect of IQ on number of grandchildren. Future research should try to ascertain the multigenerational persistence of selection effects on cognitive ability using grandchildren in addition to children.
The apparent lack of a direct effect of the PGS on the sample’s fertility characteristics in the path models results from the fact that the present sample is very likely underpowered to detect the direct effect net of covariates, the sample size being relatively modest compared to very high-power samples that have detected the direct effect (e.g., Kong et al., Reference Kong, Banks, Poplin, Garimella, Maguire and Stefansson2017; N = 129,808). That there likely exist weak but direct negative genetic correlations between the two is nevertheless suggestive of a relatively strong regime of selection acting against cognitive ability — which appears to have been present in the West since the industrial revolution of the early to mid-19th century (Skirbekk, Reference Skirbekk2008; Woodley of Menie et al., Reference Woodley of Menie, Figueredo, Sarraf, Hertler, Fernandes and Peñaherrera-Aguirre2017a).
Consistent with this inference, utilizing a formula from Kong et al. Reference Kong, Banks, Poplin, Garimella, Maguire and Stefansson(2017) to estimate the joint effect of both the timing and quantum of fertility on cognitive ability (scaled as IQ) based on the strength of polygenic selection, we find evidence that the genetic variance component of IQ should be declining anywhere between dec = −.208 and −.424 of an IQ point in this sample, depending on whether GCTA-GREML or classical behavior genetic estimates of additive IQ heritability are used to correct for ‘missing’ heritability in the equation.
In an earlier analysis of selection on IQ in WLS, Retherford and Sewell (Reference Retherford and Sewell1988) estimated a decline of -.81 IQ points per generation, assuming an IQ heritability of .40 (based on parent–offspring resemblance, which is in line with the contemporary GCTA GREML estimates), which translates in a decline of dec = -.23, IQ points assuming a generation length approximately equal to the mean age of their sample (which was in the mid-30s). Thus, the present estimates based on actual polygenic selection are similar — assuming an equivalently low value for IQ heritability.
Some might find it puzzling that there is apparent selection against intelligence alongside massive increases in IQ test performance, that is, the Flynn effect. The apparent discrepancy between these observations is known as Cattell’s paradox, named after psychologist Raymond B. Cattell, one of the first observers of what is now known as the Flynn effect, which he noted in a study that he expected to yield evidence of phenotypic declines in intelligence resulting from selection (Higgins et al., Reference Higgins, Reed and Reed1962). The most popular approach to resolving Cattell’s paradox has been called the attenuation model, which posits that despite decreases in genotypic IQ, phenotypic IQ has risen nonetheless following industrialization as a function of environmental improvements (e.g., better nutrition; Lynn, Reference Lynn1996). A more promising approach has recently emerged, however: the co-occurrence model (Woodley & Figueredo, Reference Woodley and Figueredo2013). The co-occurrence model posits that the Flynn effect is driven by environmental enhancements that augment specialized and minimally heritable cognitive abilities. These improvements occur together in time with phenotypic decreases in the highly heritable general cognitive ability factor; further, these phenotypic declines in g are explained as a function of genetic selection against g (Woodley & Figuerdo, Reference Woodley and Figueredo2013). A number of studies have found compelling evidence supporting the co-occurrence model, specifically indications of long-term declines in certain endophenotypes that likely track g over time, such as working memory (Wongupparaj et al., Reference Wongupparaj, Wongupparaj, Kumari and Morris2017; Woodley of Menie et al., Reference Woodley of Menie, Figueredo, Sarraf, Hertler, Fernandes and Peñaherrera-Aguirre2017a, Reference Woodley of Menie, Sarraf, Peñaherrera-Aguirre, Fernandes and Becker2018).
Finally, estimates of the strength of selection acting directly on the genetic variants associated with cognitive ability, such as the current effort, will shed much light on the determinants of the contemporary evolutionary dynamics of this trait. Such research furthermore has great potential to help in evaluating the magnitude of any existential risk (Bostrom, Reference Bostrom2002) to civilization that trends in g pose.