Hostname: page-component-6766d58669-zlvph Total loading time: 0 Render date: 2026-05-19T00:31:03.086Z Has data issue: false hasContentIssue false
  • English
  • Français

CHOQUET INTEGRALS, HAUSDORFF CONTENT AND FRACTIONAL OPERATORS

Part of: Harmonic analysis in several variables

Published online by Cambridge University Press:  19 March 2024

NAOYA HATANO ,
RYOTA KAWASUMI ,
HIROKI SAITO  and
HITOSHI TANAKA
NAOYA HATANO*
Affiliation:
Department of Mathematics, Chuo University, 1-13-27, Kasuga, Bunkyo-ku, Tokyo 112-8551, Japan
RYOTA KAWASUMI
Affiliation:
Graduate School of Economics, Hitotsubashi University, 2-1 Naka, Kunitachi, Tokyo 186-8601, Japan e-mail: a241010y@r.hit-u.ac.jp
HIROKI SAITO
Affiliation:
College of Science and Technology, Nihon University, Narashinodai 7-24-1, Funabashi City, Chiba 274-8501, Japan e-mail: saitou.hiroki@nihon-u.ac.jp
HITOSHI TANAKA
Affiliation:
Research and Support Center on Higher Education for the Hearing and Visually Impaired, National University Corporation Tsukuba University of Technology, Kasuga 4-12-7, Tsukuba City, Ibaraki 305-8521, Japan e-mail: htanaka@k.tsukuba-tech.ac.jp
*
e-mail: n.hatano.chuo@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that the fractional integral operator 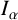$I_{\alpha }$, 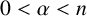$0<\alpha <n$, and the fractional maximal operator 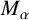$M_{\alpha }$, 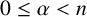$0\le \alpha <n$, are bounded on weak Choquet spaces with respect to Hausdorff content. We also investigate these operators on Choquet–Morrey spaces. The results for the fractional maximal operator 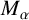$M_\alpha $ are extensions of the work of Tang [‘Choquet integrals, weighted Hausdorff content and maximal operators’, Georgian Math. J. 18(3) (2011), 587–596] and earlier work of Adams and Orobitg and Verdera. The results for the fractional integral operator 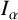$I_{\alpha }$ are essentially new.

Keywords

Choquet–Morrey spacesfractional integral operatorfractional maximal operatorHausdorff contentweak Choquet spaces

MSC classification

Primary: 42B25: Maximal functions, Littlewood-Paley theory
Secondary: 42B35: Function spaces arising in harmonic analysis

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 110 , Issue 2 , October 2024 , pp. 355 - 366
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

N.H. is financially supported by a Foundation of Research Fellows, The Mathematical Society of Japan. H.S. is supported by Grant-in-Aid for Young Scientists (19K14577), the Japan Society for the Promotion of Science. H.T. is supported by Grant-in-Aid for Scientific Research (C) (15K04918 and 19K03510), the Japan Society for the Promotion of Science.

References

Adams, D. R., ‘A note on Riesz potentials’, Duke Math. J. 42(4) (1975), 765–778.10.1215/S0012-7094-75-04265-9CrossRefGoogle Scholar
Adams, D. R., ‘Choquet integrals in potential theory’, Publ. Mat. 42 (1998), 3–66.10.5565/PUBLMAT_42198_01CrossRefGoogle Scholar
Chiarenza, F. and Frasca, M., ‘Morrey spaces and Hardy–Littlewood maximal function’, Rend. Mat. Appl. (7) 7 (1987), 273–279.Google Scholar
Gunawan, H., Hakim, D. I., Limanta, K. M. and Masta, A. A., ‘Inclusion properties of generalized Morrey spaces’, Math. Nachr. 290(2–3) (2017), 332–340.10.1002/mana.201500425CrossRefGoogle Scholar
Hedberg, L. I., ‘On certain convolution inequalities’, Proc. Amer. Math. Soc. 36 (1972), 505–510.10.1090/S0002-9939-1972-0312232-4CrossRefGoogle Scholar
Orobitg, J. and Verdera, J., ‘Choquet integrals, Hausdorff content and the Hardy–Littlewood maximal operator’, Bull. Lond. Math. Soc. 30(2) (1998), 145–150.10.1112/S0024609397003688CrossRefGoogle Scholar
Peetre, J., ‘On the theory of $\mathcal{L}_{p,\lambda}$ spaces’, J. Funct. Anal. 4 (1969), 71–87.10.1016/0022-1236(69)90022-6CrossRefGoogle Scholar
Saito, H., Tanaka, H. and Watanabe, T., ‘Block decomposition and weighted Hausdorff content’, Canad. Math. Bull. 63(1) (2020), 141–156.10.4153/S000843951900033XCrossRefGoogle Scholar
Sawano, Y., Di Fazio, G. and Hakim, D. I., Morrey Spaces: Introduction and Applications to Integral Operators and PDE’s, Volume I, CRC Monographs and Research Notes in Mathematics (Chapman and Hall, London, 2020).Google Scholar
Tang, L., ‘Choquet integrals, weighted Hausdorff content and maximal operators’, Georgian Math. J. 18(3) (2011), 587–596.10.1515/gmj.2011.0036CrossRefGoogle Scholar