Since its introduction in 2010 by Lyubashevsky, Peikert and Regev, the ring learning with errors problem (ring-LWE) has become a popular building block for cryptographic primitives, due to its great versatility and its hardness proof consisting of a (quantum) reduction from ideal lattice problems. But, for a given modulus 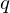$q$ and degree 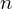$n$ number field 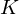$K$, generating ring-LWE samples can be perceived as cumbersome, because the secret keys have to be taken from the reduction mod 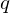$q$ of a certain fractional ideal 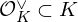${\mathcal{O}}_{K}^{\vee }\subset K$ called the codifferent or ‘dual’, rather than from the ring of integers 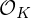${\mathcal{O}}_{K}$ itself. This has led to various non-dual variants of ring-LWE, in which one compensates for the non-duality by scaling up the errors. We give a comparison of these versions, and revisit some unfortunate choices that have been made in the recent literature, one of which is scaling up by 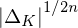${|\unicode[STIX]{x1D6E5}_{K}|}^{1/2n}$ with 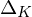$\unicode[STIX]{x1D6E5}_{K}$ the discriminant of 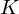$K$. As a main result, we provide, for any 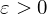$\unicode[STIX]{x1D700}>0$, a family of number fields 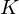$K$ for which this variant of ring-LWE can be broken easily as soon as the errors are scaled up by 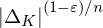${|\unicode[STIX]{x1D6E5}_{K}|}^{(1-\unicode[STIX]{x1D700})/n}$.