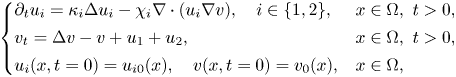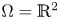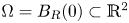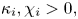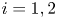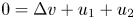1. Introduction
Chemotaxis is a common phenomenon in mathematical biology. Since Keller and Segel [Reference Keller and Segel14] suggested a mathematical chemotaxis model for chemotactic aggregation of the cellular slime mold Dictyostelium discoideum in the early 1970s, a large number of theoretical (mathematical) models, including the chemotactic movement of multi populations along with multiple stimuli in the environment, have been proposed by many researchers (see [Reference Horstmann12]). In this paper, a chemotaxis system for two populations interaction via the same chemical signal will be considered as follows:

where $u_i$![]() denotes the population density for the $i$
denotes the population density for the $i$![]() -th population, and $v$
-th population, and $v$![]() represents the chemical signal concentration. $\kappa _i>0$
represents the chemical signal concentration. $\kappa _i>0$![]() is the diffusion coefficient for the $i$
is the diffusion coefficient for the $i$![]() -th population and the chemotactic coefficient $\chi _i>0$
-th population and the chemotactic coefficient $\chi _i>0$![]() measures the strength of the chemical signal with respect to $u_i$
measures the strength of the chemical signal with respect to $u_i$![]() . Here the domain $\Omega$
. Here the domain $\Omega$![]() is
is
When $\Omega$![]() is the above bounded domain, the system (1.1) is supplemented with homogenous Neumann boundary condition
is the above bounded domain, the system (1.1) is supplemented with homogenous Neumann boundary condition
For a two-dimensional domain, one of the most interesting and important question for the chemotaxis system in both biological and mathematical contexts is to determine critical mass phenomenon, namely, the behaviour of the solutions is only dependent on the initial mass of the system. This mass threshold phenomenon was exactly confirmed in the well-known Keller–Segel chemotaxis model for one population:

Let $m_1(u_{10};D)=\|u_{10}\|_1=\int _{D}u_{10}(x)\,{\rm d}x$![]() for $D\subset \mathbb {R}^2$
for $D\subset \mathbb {R}^2$![]() . Consider (1.4) with boundary condition (1.3) in a bounded domain $\Omega \subset \mathbb {R}^2$
. Consider (1.4) with boundary condition (1.3) in a bounded domain $\Omega \subset \mathbb {R}^2$![]() . An application of the Moser–Trudinger inequality to (1.4) ensures that the solution exists globally in time provided $m_1(u_{10};\Omega )<4\pi \kappa _1/\chi _1$
. An application of the Moser–Trudinger inequality to (1.4) ensures that the solution exists globally in time provided $m_1(u_{10};\Omega )<4\pi \kappa _1/\chi _1$![]() for arbitrary smooth domain or $m_1(u_{10};\Omega )<8\pi \kappa _1/\chi _1$
for arbitrary smooth domain or $m_1(u_{10};\Omega )<8\pi \kappa _1/\chi _1$![]() for radial domain [Reference Nagai, Senba and Yoshida21]. Conversely, if $m_1(u_{10};\Omega )>8\pi \kappa _1/\chi _1$
for radial domain [Reference Nagai, Senba and Yoshida21]. Conversely, if $m_1(u_{10};\Omega )>8\pi \kappa _1/\chi _1$![]() , then there exists a blow-up solution in finite time [Reference Herrero and Velázquez10]. Similar to [Reference Herrero and Velázquez10], there also exists a blow-up solution for (1.4) for $\Omega =\mathbb {R}^2$
, then there exists a blow-up solution in finite time [Reference Herrero and Velázquez10]. Similar to [Reference Herrero and Velázquez10], there also exists a blow-up solution for (1.4) for $\Omega =\mathbb {R}^2$![]() when $m_1(u_{10};\mathbb {R}^2)>8\pi \kappa _1/\chi _1$
when $m_1(u_{10};\mathbb {R}^2)>8\pi \kappa _1/\chi _1$![]() . However, it was shown in [Reference Calvez and Corrias3] that the solution with $m_1(u_{10};\mathbb {R}^2)<8\pi \kappa _1/\chi _1$
. However, it was shown in [Reference Calvez and Corrias3] that the solution with $m_1(u_{10};\mathbb {R}^2)<8\pi \kappa _1/\chi _1$![]() exists globally over time under the following conditions $u_{10}\log (1 + |x|^2)\in L^1(\mathbb {R}^2)$
exists globally over time under the following conditions $u_{10}\log (1 + |x|^2)\in L^1(\mathbb {R}^2)$![]() and $u_{10}\log u_{10}\in L^1(\mathbb {R}^2)$
and $u_{10}\log u_{10}\in L^1(\mathbb {R}^2)$![]() . While these additional initial data conditions have been completely removed in [Reference Mizoguchi15] by terms of the Moser–Trudinger inequality. Moreover, the critical case $m_1(u_{10};\mathbb {R}^2)=8\pi \kappa _1/\chi _1$
. While these additional initial data conditions have been completely removed in [Reference Mizoguchi15] by terms of the Moser–Trudinger inequality. Moreover, the critical case $m_1(u_{10};\mathbb {R}^2)=8\pi \kappa _1/\chi _1$![]() was also studied in [Reference Mizoguchi15], the solutions exist globally or the blow-up set of solutions equals $\mathbb {R}^2$
was also studied in [Reference Mizoguchi15], the solutions exist globally or the blow-up set of solutions equals $\mathbb {R}^2$![]() . Because chemicals diffuse much faster than population then it is feasible to study a simple parabolic-elliptic version of (1.4), i.e., the second parabolic equation is replaced with an elliptic form
. Because chemicals diffuse much faster than population then it is feasible to study a simple parabolic-elliptic version of (1.4), i.e., the second parabolic equation is replaced with an elliptic form
or
where $\mu :=\|u_{10}\|_1/|\Omega |$![]() . We refer the readers to the papers [Reference Biler2, Reference Horstmann11, Reference Jäger and Luckhaus13, Reference Nagai17–Reference Nagai19] for a similar and satisfactory analytical description about the critical mass for these situations in two dimensions. The above results show that $8\pi \kappa _1/\chi _1$
. We refer the readers to the papers [Reference Biler2, Reference Horstmann11, Reference Jäger and Luckhaus13, Reference Nagai17–Reference Nagai19] for a similar and satisfactory analytical description about the critical mass for these situations in two dimensions. The above results show that $8\pi \kappa _1/\chi _1$![]() is the critical mass for (1.4), and determines that the solutions exist globally or blow up if $\Omega$
is the critical mass for (1.4), and determines that the solutions exist globally or blow up if $\Omega$![]() satisfies (1.2).
satisfies (1.2).
For multi-population chemotaxis system, a natural question arises: do there exist critical numbers such that whenever the initial masses for populations are smaller than them then the solution will exist globally, whereas the masses are larger then the solution will blow up? Espejo et al. [Reference Conca, Espejo and Vilches5, Reference Espejo, Stevens and Velzquez7–Reference Espejo, Vilches and Conca9] consider a simplified parabolic-elliptic version of two-population system likes

where $\mu ':=(\|u_{10}\|_1+\|u_{20}\|_1)/|\Omega |$![]() . The proof of blow-up solutions is based on a suitable adaptation of the moments technique [Reference Conca, Espejo and Vilches5, Reference Espejo, Stevens and Velzquez7]. To see the known results for the global existence, based on the expression for $v$
. The proof of blow-up solutions is based on a suitable adaptation of the moments technique [Reference Conca, Espejo and Vilches5, Reference Espejo, Stevens and Velzquez7]. To see the known results for the global existence, based on the expression for $v$![]() in terms of $u_1$
in terms of $u_1$![]() and $u_2$
and $u_2$![]() through the fundamental solution or the Green function associated to the Laplace operator, the main tool used in the paper by Espejo et al. is the logarithmic Hardy–Littlewood–Sobolev (HLS) inequality for system (see [Reference Chipot, Shafrir and Wolansky4, Reference Shafrir and Wolansky22, Reference Shafrir and Wolansky23]): the function
through the fundamental solution or the Green function associated to the Laplace operator, the main tool used in the paper by Espejo et al. is the logarithmic Hardy–Littlewood–Sobolev (HLS) inequality for system (see [Reference Chipot, Shafrir and Wolansky4, Reference Shafrir and Wolansky22, Reference Shafrir and Wolansky23]): the function

over the class

is bounded from below if and only if $\Lambda _{\mathcal {I}}(\boldsymbol {M})= 0$![]() and
and

where $\mathcal {I}:=\{1,2,\dots,n\}$![]() , $\boldsymbol {M}:=\{M_1,\dots,M_n\}\in (\mathbb {R}_+)^n$
, $\boldsymbol {M}:=\{M_1,\dots,M_n\}\in (\mathbb {R}_+)^n$![]() , $A:=(a_{i,j})_{n\times n}$
, $A:=(a_{i,j})_{n\times n}$![]() is a $n\times n$
is a $n\times n$![]() symmetric matrix with nonnegative elements, i.e., $a_{i,j}\geq 0$
symmetric matrix with nonnegative elements, i.e., $a_{i,j}\geq 0$![]() , $i,j\in \mathcal {I},$
, $i,j\in \mathcal {I},$![]() and the quadratic polynomial is given by
and the quadratic polynomial is given by
While replacing the $-({1}/{2\pi })\log |x-y|$![]() in (1.6) by the Green function $G_{\Omega }(x,y)$
in (1.6) by the Green function $G_{\Omega }(x,y)$![]() for the Laplace operator, then another version of the HLS inequality for system is given when $\Omega$
for the Laplace operator, then another version of the HLS inequality for system is given when $\Omega$![]() is a bounded domain (see [Reference Shafrir and Wolansky23, theorem 5]). Here we summarize the main results for (1.5) obtained by Espejo et al. through above methods for convenience (see [Reference Conca, Espejo and Vilches5, Reference Espejo, Vilches and Conca8]): the system admits a globally bounded solution if
is a bounded domain (see [Reference Shafrir and Wolansky23, theorem 5]). Here we summarize the main results for (1.5) obtained by Espejo et al. through above methods for convenience (see [Reference Conca, Espejo and Vilches5, Reference Espejo, Vilches and Conca8]): the system admits a globally bounded solution if
on the other hand, the solution blows up if $m_1,m_2$![]() satisfy any of the inequalities
satisfy any of the inequalities
where $m_i=m_i(u_{i0};\mathbb {R}^2)=\|u_{i0}\|_1$![]() , $i=1,2$
, $i=1,2$![]() . Similar results for Dirichlet boundary problem (1.5) was obtained in [Reference Wolansky25] by Wolansky. Hence in the plane, the critical curve of initial masses for (1.5) had been achieved.
. Similar results for Dirichlet boundary problem (1.5) was obtained in [Reference Wolansky25] by Wolansky. Hence in the plane, the critical curve of initial masses for (1.5) had been achieved.
However, there is still no available result for the parabolic-parabolic chemotaxis system (1.1) as far as the authors know. In this work, we will show that any solution of the system (1.1) exists globally in time under the sub-criticality condition (1.8). The main tool for the analysis is a version of the Moser–Trudinger inequality for system in a bounded domain $\Omega \subset \mathbb {R}^2$![]() [Reference Chipot, Shafrir and Wolansky4, Reference Shafrir and Wolansky22], that is, for $\forall \ \rho _i\in H^1_0(\Omega ),\ i\in \mathcal {I}$
[Reference Chipot, Shafrir and Wolansky4, Reference Shafrir and Wolansky22], that is, for $\forall \ \rho _i\in H^1_0(\Omega ),\ i\in \mathcal {I}$![]() ,
,

is bounded from below if and only if (1.7) holds, where the matrix $A=(a_{i,j})_{n\times n}$![]() is a positive definite matrix with nonnegative elements, see [Reference Shafrir and Wolansky23, theorem 5$(i)$
is a positive definite matrix with nonnegative elements, see [Reference Shafrir and Wolansky23, theorem 5$(i)$![]() ].
].
We list two basic facts about the solution of (1.1). In the case that $\Omega$![]() is a bounded domain, the boundary condition (1.3) should be added. The first one is the formal conservation of the total mass:
is a bounded domain, the boundary condition (1.3) should be added. The first one is the formal conservation of the total mass:
due to the integration (1.1) $_1$![]() and (1.1) $_2$
and (1.1) $_2$![]() over the domain, respectively. For $v$
over the domain, respectively. For $v$![]() , integrating over the domain yields that
, integrating over the domain yields that
Secondly, the system (1.1) always admits a unique nonnegative (local) solution under some mild assumptions on the nonnegative initial data if $\Omega =\mathbb {R}^2$![]() or $\Omega \subset \mathbb {R}^2$
or $\Omega \subset \mathbb {R}^2$![]() is a bounded domain with smooth boundary. This fact can be proved by using some similar arguments as in one-population chemotaxis model [Reference Diaz, Nagai and Rakotoson6, Reference Nagai, Senba and Yoshida21]. However we omit the proof for simplicity since our main interest is to find optimal conditions on the initial data, which guarantee the local solution to be global one. Through this paper, we assume that the initial data satisfies
is a bounded domain with smooth boundary. This fact can be proved by using some similar arguments as in one-population chemotaxis model [Reference Diaz, Nagai and Rakotoson6, Reference Nagai, Senba and Yoshida21]. However we omit the proof for simplicity since our main interest is to find optimal conditions on the initial data, which guarantee the local solution to be global one. Through this paper, we assume that the initial data satisfies
or
Let $T_{\max }>0$![]() be a maximal existence time of $(u_1,u_2,v)$
be a maximal existence time of $(u_1,u_2,v)$![]() to (1.1). The first result states that
to (1.1). The first result states that
Theorem 1.1 Let $\Omega =B_R(0)\subset \mathbb {R}^2$![]() with $R>0$
with $R>0$![]() . Assume that nonnegative functions $u_{i0}(x),$
. Assume that nonnegative functions $u_{i0}(x),$![]() $i=1,2,$
$i=1,2,$![]() and $v_0(x)$
and $v_0(x)$![]() satisfy (1.8) and (1.12). Then there exists a unique triple $(u_1,u_2,v)$
satisfy (1.8) and (1.12). Then there exists a unique triple $(u_1,u_2,v)$![]() of non-negative bounded function which solves (1.1) with boundary condition (1.3) globally, i.e., $T_{\max }=\infty$
of non-negative bounded function which solves (1.1) with boundary condition (1.3) globally, i.e., $T_{\max }=\infty$![]() .
.
Now, we would like to extend the global result of bounded domain to the whole space. More precisely,
Theorem 1.2 Let $\Omega =\mathbb {R}^2$![]() . Assume that nonnegative functions $u_{i0}(x),$
. Assume that nonnegative functions $u_{i0}(x),$![]() $i=1,2,$
$i=1,2,$![]() and $v_0(x)$
and $v_0(x)$![]() satisfy (1.8) and (1.11). Then $T_{\max }=\infty$
satisfy (1.8) and (1.11). Then $T_{\max }=\infty$![]() .
.
The paper is organized as follows. In § 2, compared with (1.9), we give another version of the Moser–Trudinger inequality for system if $\rho _i\in H^1(\Omega )$![]() , $i\in \mathcal {I}$
, $i\in \mathcal {I}$![]() . The third section is dedicated to the global existence in bounded domain. Section 4 is contributed to show the solution exists globally in the whole space.
. The third section is dedicated to the global existence in bounded domain. Section 4 is contributed to show the solution exists globally in the whole space.
2. Preliminaries
In this section, let us recall the following well-known Moser's inequality given by [Reference Moser16] as
where $\Omega \subset \mathbb {R}^2$![]() is a domain with finite Lebesgue measure. In [Reference Shafrir and Wolansky22, theorem 3] or [Reference Shafrir and Wolansky23, theorem 5$(i)$
is a domain with finite Lebesgue measure. In [Reference Shafrir and Wolansky22, theorem 3] or [Reference Shafrir and Wolansky23, theorem 5$(i)$![]() ], there exists an analogous inequality for system defined on a bounded domain of $\mathbb {R}^2$
], there exists an analogous inequality for system defined on a bounded domain of $\mathbb {R}^2$![]() .
.
Lemma 2.1 Let $\mathcal {I}=\{1,\ldots,n\}$![]() , and let $\boldsymbol{M}=(M_1,\dots,M_n)\in (\mathbb {R}_+)^n$
, and let $\boldsymbol{M}=(M_1,\dots,M_n)\in (\mathbb {R}_+)^n$![]() . Assume that $A=(a_{i,j})_{n\times n}$
. Assume that $A=(a_{i,j})_{n\times n}$![]() is a positive definite matrix with nonnegative elements. Then for any $\boldsymbol {\rho }=(\rho _1,\dots,\rho _n)\in (H^1_0(\Omega ))^n$
is a positive definite matrix with nonnegative elements. Then for any $\boldsymbol {\rho }=(\rho _1,\dots,\rho _n)\in (H^1_0(\Omega ))^n$![]() ,
,

is bounded from below if and only if

Inspired by [Reference Nagai, Senba and Yoshida21, theorem 2.1], for radially symmetric functions we extend the Moser–Trudinger inequality for system to the Sobolev space $H^1(\Omega )$![]() with trace boundary.
with trace boundary.
Lemma 2.2 Let $\Omega =B_R(0)\subset \mathbb {R}^2$![]() with $R>0$
with $R>0$![]() , and let $A=(a_{i,j})_{n\times n}$
, and let $A=(a_{i,j})_{n\times n}$![]() be a positive definite matrix with nonnegative elements. Then for nonnegative $\boldsymbol{w}=(w_1,\dots,w_n)\in (H^1(\Omega ))^n$
be a positive definite matrix with nonnegative elements. Then for nonnegative $\boldsymbol{w}=(w_1,\dots,w_n)\in (H^1(\Omega ))^n$![]() and $\eta >0$
and $\eta >0$![]() , then there exists a constant $C(\eta )$
, then there exists a constant $C(\eta )$![]() such that
such that

if and only if

Proof. We only consider nonnegative $\boldsymbol {w}\in (C^1(\bar {\Omega }))^n$![]() because $C^1(\bar {\Omega })$
because $C^1(\bar {\Omega })$![]() is dense in $H^1(\Omega )$
is dense in $H^1(\Omega )$![]() . Define
. Define
Thanks to $\boldsymbol{z}=(z_1,\dots,z_n)\in (H^1_0(\Omega ))^n$![]() , lemma 2.1 implies that
, lemma 2.1 implies that

holds if and only if

It is clear that

Then

Now we proceed to estimate the boundary value $w_j(R)$![]() . Fixed $r_0\in (R/2,R)$
. Fixed $r_0\in (R/2,R)$![]() such that
such that

then from
applying Hölder's inequality and Young's inequality with $\eta >0$![]() , then it yields that
, then it yields that

By (2.3), we have

Observing that

it implies that

After a simple arrangement, we finally have

As a consequence of lemma 2.2, we have
Lemma 2.3 Let $\mathcal {I}=\{1,2\}$![]() , $\Omega =B_R(0)\subset \mathbb {R}^2$
, $\Omega =B_R(0)\subset \mathbb {R}^2$![]() with $R>0$
with $R>0$![]() , and let $A=(a_{i,j})_{2\times 2}$
, and let $A=(a_{i,j})_{2\times 2}$![]() be a positive definite matrix with nonnegative elements. Then for nonnegative $\boldsymbol{w}=(w,w)\in (H^1(\Omega ))^2$
be a positive definite matrix with nonnegative elements. Then for nonnegative $\boldsymbol{w}=(w,w)\in (H^1(\Omega ))^2$![]() and $\eta >0$
and $\eta >0$![]() , then there exists a constant $C(\eta )$
, then there exists a constant $C(\eta )$![]() such that
such that

if and only if

3. The bounded domain
The global existence of solution to (1.1) in a bounded domain $\Omega =B_R(0)\subset \mathbb {R}^2$![]() will be considered in this section. The proof of theorem 1.1 will be divided into several lemmas.
will be considered in this section. The proof of theorem 1.1 will be divided into several lemmas.
3.1 Free energy functional
The free energy functional

plays an important role in the analysis of the global existence.
Lemma 3.1 Consider the local smooth solution $(u_1,u_2,v)$![]() to (1.1), subject to initial data $(u_{10},u_{20},v_0)$
to (1.1), subject to initial data $(u_{10},u_{20},v_0)$![]() . Then
. Then

Proof. Multiplying (1.1) $_i$![]() by $\kappa _i\log u_i-\chi _iv,i\in \{1,2\},$
by $\kappa _i\log u_i-\chi _iv,i\in \{1,2\},$![]() respectively, we see that
respectively, we see that
and
Testing (3.1) by $1/\chi _1$![]() and (3.2) by $1/\chi _2$
and (3.2) by $1/\chi _2$![]() , respectively, it is easy to obtain that
, respectively, it is easy to obtain that

where we have used the fact that $({{\rm d}}/{{\rm d}t})\int _{\Omega }u_i\,{\rm d}x=0$![]() . Notice that
. Notice that

Hence

which implies that we have finished the proof of this lemma.
A simple fact from lemma 3.1 yields an upper bound for $\mathcal {F}$![]() .
.
3.2 An upper bound for the entropy
In two-dimensional case, the natural way to prove the global existence of solutions to chemotaxis system is to give a bound for the entropy $\|u_i\log u_i\|_{L^1(\Omega )}$![]() , $i=1,2$
, $i=1,2$![]() . From lemma 3.2, this can be actually achieved if the term
. From lemma 3.2, this can be actually achieved if the term
can be controlled by the entropy. To see this, we derive a general form as follows.
Lemma 3.3 Let $\alpha _i,\kappa _i,\chi _i>0$![]() , $i=1,2$
, $i=1,2$![]() . For any nonnegative functions $\phi _i\in L^1(\Omega )\cap L\log L(\Omega ),\psi \in L^{\infty }(\Omega )$
. For any nonnegative functions $\phi _i\in L^1(\Omega )\cap L\log L(\Omega ),\psi \in L^{\infty }(\Omega )$![]() satisfying $m_i=\int _{\Omega }\phi _{i}\,{\rm d}x>0$
satisfying $m_i=\int _{\Omega }\phi _{i}\,{\rm d}x>0$![]() , $i=1,2$
, $i=1,2$![]() , it holds that
, it holds that

Proof. It follows from the Jensen's inequality that

where we have used the fact that $m_1=\int _{\Omega }\phi _1\,{\rm d}x$![]() , and $x\log x>-1/e$
, and $x\log x>-1/e$![]() for all $x>0$
for all $x>0$![]() . Similarly, given any $\alpha _2>0$
. Similarly, given any $\alpha _2>0$![]() we also have
we also have
Putting the above inequalities together, it yields (3.4).
Lemma 3.4 Let $(u_1,u_2,v)$![]() be the local smooth solution to (1.1), subject to initial data $(u_{10},u_{20},v_0)$
be the local smooth solution to (1.1), subject to initial data $(u_{10},u_{20},v_0)$![]() satisfying (1.12). Assume that $\kappa _i>0$
satisfying (1.12). Assume that $\kappa _i>0$![]() , $\chi _i>0$
, $\chi _i>0$![]() and $m_i=\int _{\Omega }u_{i0}\,{\rm d}x,i=1,2,$
and $m_i=\int _{\Omega }u_{i0}\,{\rm d}x,i=1,2,$![]() fulfill
fulfill
Then there exists $\alpha _1>1$![]() and $\alpha _2>1$
and $\alpha _2>1$![]() such that
such that

for some $C>0$![]() .
.
Proof. In view of (3.6), we can choose small $\epsilon >0$![]() such that
such that

and
Choose $\alpha _1>0$![]() and $\alpha _2>0$
and $\alpha _2>0$![]() in lemma 3.3 as
in lemma 3.3 as
Denote

then it is clear that $a_{11}+a_{12}=\chi _1\alpha _1/\kappa _1$![]() , $a_{21}+a_{22}=\chi _2\alpha _2/\kappa _2$
, $a_{21}+a_{22}=\chi _2\alpha _2/\kappa _2$![]() and
and
is a positive definite matrix. Fixed a positive constant $\eta >0$![]() small enough such that
small enough such that

Since we have



by (3.7) and (3.8), applying lemma 2.3, then there exists a positive constant $C>0$![]() such that
such that

which together with (3.10) implies that

Then lemma 3.3 tells that

which proves the lemma by (1.10).
Lemma 3.5 Under the same assumptions in lemma 3.4, then there exists $C>0$![]() such that
such that
Proof. Lemma 3.1 asserts that
in the sense that

According to the choices of $\alpha _1>1$![]() and $\alpha _2>1$
and $\alpha _2>1$![]() in lemma 3.4, we may find $C>0$
in lemma 3.4, we may find $C>0$![]() such that
such that

which yields that
by (1.10) and (3.11). From (3.11), this in turn shows that there exists $C>0$![]() such that
such that
Proof of theorem 1.1 Assume that $(u_1,u_2,v)$![]() is a local classical solution of (1.1) over $(0,T_{\max })$
is a local classical solution of (1.1) over $(0,T_{\max })$![]() with the following blow-up criterion: either $T_{\max }=\infty$
with the following blow-up criterion: either $T_{\max }=\infty$![]() , or if $T_{\max }<\infty$
, or if $T_{\max }<\infty$![]() , it should satisfy:
, it should satisfy:
A version of the Gagliardo–Nirenberg inequality in two-dimensional bounded domain shows that for each $\epsilon >0$![]() , there exists a positive constant $C_{\epsilon }>0$
, there exists a positive constant $C_{\epsilon }>0$![]() such that (see [Reference Nagai, Senba and Yoshida21, lemma 3.5], [Reference Tao and Winkler24, lemma A.5])
such that (see [Reference Nagai, Senba and Yoshida21, lemma 3.5], [Reference Tao and Winkler24, lemma A.5])
By means of (3.12) and lemma 3.5, we follow a similar argument in [Reference Nagai, Senba and Yoshida21, lemma 3.6] to find $C>0$![]() such that
such that
By the well-known Moser–Alikakos iteration procedure [Reference Alikakos1], the solutions of (1.1) must be uniformly bounded for all $t\in (0,T_{\max })$![]() , that is, $T_{\max }=\infty$
, that is, $T_{\max }=\infty$![]() .
.
4. The whole space
The proof of global existence for the whole space $\mathbb {R}^2$![]() also relies on the Moser–Trudinger inequality for system given in lemma 2.1. Similar to the bounded domain case, it is possible to control (3.3) by the entropy. For this purpose, we have
also relies on the Moser–Trudinger inequality for system given in lemma 2.1. Similar to the bounded domain case, it is possible to control (3.3) by the entropy. For this purpose, we have
Lemma 4.1 Consider a local solution $(u_1,u_2,v)$![]() to (1.1) in $\mathbb {R}^2\times (0,T)$
to (1.1) in $\mathbb {R}^2\times (0,T)$![]() with $T>0$
with $T>0$![]() , subject to initial data $(u_{10},u_{20},v_0)$
, subject to initial data $(u_{10},u_{20},v_0)$![]() satisfying (1.11). Suppose that $m_i=\int _{\Omega }u_{i0}\,{\rm d}x$
satisfying (1.11). Suppose that $m_i=\int _{\Omega }u_{i0}\,{\rm d}x$![]() , $i=1,2$
, $i=1,2$![]() , fulfills
, fulfills
Then there exists $\epsilon >0$![]() such that
such that

for some $C>0$![]() .
.
Proof. Inspired by lemma from [Reference Mizoguchi15, lemma 2.1] for a single-species chemotaxis system, we use the similar argument to deal with multi-species scenario on the base of the Moser–Trudinger inequality for system. For any initial data $(u_{10},u_{20},v_0)$![]() satisfying (1.11), we
satisfying (1.11), we
Choose $\epsilon >0$![]() small enough and $s>0$
small enough and $s>0$![]() large enough, then the assumption (4.1) ensures that
large enough, then the assumption (4.1) ensures that

and

Let
and
Note that the Lebesgue measure of $\Omega (t)$![]() denoted by $|\Omega (t)|$
denoted by $|\Omega (t)|$![]() is finite, because (1.10) and
is finite, because (1.10) and
imply that
Moreover, we see that

A similar computation as (3.5) and utilizing (4.4), we obtain that

where $\alpha _i>1$![]() , $m_i(t)=\int _{\Omega (t)}u_i\,{\rm d}x\leq m_i$
, $m_i(t)=\int _{\Omega (t)}u_i\,{\rm d}x\leq m_i$![]() , $i=1,2$
, $i=1,2$![]() , and
, and
Without loss of generality, we assume that $|\Omega (t)|>1$![]() , otherwise we may take $\widetilde {\Omega }(t)$
, otherwise we may take $\widetilde {\Omega }(t)$![]() such that $|\widetilde {\Omega }(t)|>1$
such that $|\widetilde {\Omega }(t)|>1$![]() and $\Omega (t)\subset \widetilde {\Omega }(t)$
and $\Omega (t)\subset \widetilde {\Omega }(t)$![]() . Define $M_1,M_2>0$
. Define $M_1,M_2>0$![]() as
as

Let $A=(a_{i,j})_{2\times 2}$![]() be a positive definite matrix with elements from (3.9) and $\alpha _1=\alpha _2=1+\epsilon$
be a positive definite matrix with elements from (3.9) and $\alpha _1=\alpha _2=1+\epsilon$![]() . According to (4.2)–(4.3), we have
. According to (4.2)–(4.3), we have
then applying lemma 2.1 to see that

Then we have the following inequality

Inserting the above into (4.5) yields that

for all $t\in (0,T)$![]() , so we have
, so we have

This lemma is complete.
The following proposition could be regarded as an analogue of the result for one-single Keller–Segel chemotaxis model (see [Reference Nagai and Ogawa20, proposition 4.1]).
Lemma 4.2 Consider a local solution $(u_1,u_2,v)$![]() to (1.1), subject to initial data $(u_{10},u_{20},v_0)$
to (1.1), subject to initial data $(u_{10},u_{20},v_0)$![]() satisfying (1.11). Then
satisfying (1.11). Then

where

Proof. We adopt the similar arguments as lemma 3.1 to prove this lemma. Multiplying (1.1) $_i$![]() by $\kappa _i/\chi _i\log (u_i+1),$
by $\kappa _i/\chi _i\log (u_i+1),$![]() $i=1,2,$
$i=1,2,$![]() and integrating over $\mathbb {R}^2$
and integrating over $\mathbb {R}^2$![]() , it induces that
, it induces that

Moreover, we have

where we use the fact that $({{\rm d}}/{{\rm d}t})\int _{\mathbb {R}^2}(u_i+1)\,{\rm d}x=0$![]() , $i=1,2$
, $i=1,2$![]() . Since
. Since

and

hold out, then it is obvious that

Therefore, we have finished the proof of this lemma.
Lemma 4.3 Consider a local solution $(u_1,u_2,v)$![]() to (1.1) in $\mathbb {R}^2\times (0,T)$
to (1.1) in $\mathbb {R}^2\times (0,T)$![]() , subject to initial data $(u_{10},u_{20},v_0)$
, subject to initial data $(u_{10},u_{20},v_0)$![]() satisfying (1.11). Under the same assumptions in lemma 4.1, then there exists a positive constant $C>0$
satisfying (1.11). Under the same assumptions in lemma 4.1, then there exists a positive constant $C>0$![]() such that
such that
and
Proof. Invoking the definition of $\mathcal {G}$![]() and lemma 4.1, we firstly obtain
and lemma 4.1, we firstly obtain

Moreover, lemma 4.1 ensures that there exist $\epsilon >0$![]() and $C>0$
and $C>0$![]() such that
such that

Reversely, it implies that

Hence, one can see that
Combining it with (4.6) yields that

Using Gronwall's inequality to above inequality, it means that
Proof of theorem 1.2 Prove by contradiction. Under the assumptions in theorem 1.2, suppose that there exists a solution $(u_1,u_2,v)$![]() of (1.1) which blows up at finite time $T<\infty$
of (1.1) which blows up at finite time $T<\infty$![]() . Lemma 4.3 tells us that there exists $C>0$
. Lemma 4.3 tells us that there exists $C>0$![]() such that
such that
Based on the following inequality in two-dimensional domain
we have
by a similar argument in [Reference Nagai and Ogawa20, proposition 5.1]. However, through the standard theory of the parabolic regularity, it is straightforward to show that the solution $(u_1,u_2,v)$![]() remains in $L^{\infty }(\mathbb {R}^2)$
remains in $L^{\infty }(\mathbb {R}^2)$![]() for all $t\in (0,T]$
for all $t\in (0,T]$![]() . It is a contradiction with the blow-up criteria, which implies the solution $(u_1,u_2,v)$
. It is a contradiction with the blow-up criteria, which implies the solution $(u_1,u_2,v)$![]() exists globally in time.
exists globally in time.
Acknowledgements
The author thanks the anonymous referee very much for carefully reading our manuscript and giving positive and valuable comments, which further helped them to improve the exposition of this work. K. Lin is supported by the NSF of China (No. 11801461), Natural Science Foundation of Sichuan, China (No. 2022NSFSC1837), and Guanghua Talent Project of Southwestern University of Finance and Economics.