A) Latent factor model – conventional MF framework

Latent factor models are constructed under the belief that a handful of factors affect a user's like/dislike for an item. As an example consider a movie recommendation system. Any movie can be described in terms of its genre, language, cast, director, and few other related features. Users exhibit varying degree of affinity toward each of these traits. Under this scenario, a user can be modeled as a vector (L _u) describing his affinity to the latent factors and items cast as a vector (L _m) defining the degree to which they possess the corresponding latent factors. A user's choice of an item is governed by these few (latent) factors only; via interaction between their individual latent factor vectors.

However, the actual (explicit) ratings given by users also include a bias component (baseline estimate) apart from the interaction part. Certain users tend to be generous in their ratings (all items rated on a higher side); they tend to possess positive (user) bias(b _u). Also, more popular items (such as award winning movies) are rated above average by almost all users; they tend to possess positive (item) bias (b _m). The net (actual) rating (R _{u, m}) can be modeled as a summation of bias and interaction component (2) [Reference Koren, Bell and Volinsky14], where μ_g is the mean of the entire dataset.

(2)$$R_{u\comma m} =\underbrace{\langle L_u\comma \; L_m \rangle}_{Interaction}+\underbrace{\mu_g +b_u +b_m}_{Baseline}. $$

The baseline can be easily estimated using stochastic gradient descent (SGD) algorithm to solve (3). The regularization parameter (γ) is used to prevent over fitting to available data and compensate for interaction component.

(3)$$\mathop{\min}\limits_{b_\ast} \sum_{u\comma m\in \Theta} \lpar R_{u\comma m} -b_u -b_m -\mu_g\rpar ^2 +\gamma \lpar \Vert b_u\Vert_2^2 +\Vert b_m \Vert_2^2 \rpar . $$

The most popular method for recovering the interaction component is MF [Reference Koren, Bell and Volinsky14] which recovers the rating matrix as a product of two matrices (4) – one consisting of user's latent factor vectors (U) and other of items (M) stacked together.

(4)$$\mathop{\min}\limits_{U\comma M} \Vert Y-A\lpar UM\rpar \Vert _F^2 +\lambda \lpar \Vert U \Vert_F^2 +\Vert M \Vert_F^2 \rpar \comma \; $$

where A is the (binary) sub-sampling operator that has 1's in place of available data and 0's for missing values; Y is the interaction component of available ratings (Y _u,m = R _u,m − b _u − b _m − μ_g); λ is the regularization parameter; and use of Frobenius norm regularization terms promote recovery of dense user and item latent factor matrices.

B) Blind compressive sensing

Compressive sensing (CS) paradigm [Reference Donoho21,Reference Candès and Wakin22] focuses on recovery of sparse or compressible signals from a given set of observations, obtained at sub-Nyquist rates. A sparse signal, x can be uniquely and exactly recovered by minimizing the l ₁ norm (convex surrogate of l ₀ norm) of the vector to be recovered under the constraint that recovery is consistent with the observations.

Real-world signals are rarely sparse in spatial/time domain; however, most have a sparse/compressible transform domain representation. In such a case, we can modify recover x as follows:

(5)$$\mathop{\min}\limits_c \Vert c \Vert _1 \hbox{subject to } y=A \Psi c\comma \; $$

where Ψ is the sparsifying transform; x = Ψ c. The above equation can be used to recover c and hence x accurately, if the sensing and sparsifying matrices are mutually incoherent [Reference Natarajan23].

In practice, the measurement process is corrupted by noise; therefore one needs to solve a noisy under-determined system, y = Ax + η= AΨx + η, where the noise η is assumed to be normally distributed. For such a system, the equality constrained problem (5) is relaxed and the following is solved instead:

(6)$$\mathop{\min}\limits_c \Vert c \Vert _1 \hbox{subject to } \Vert y-A\Psi c\Vert _2^2 \le \varepsilon \comma \; \quad \hbox{where}\quad \varepsilon =n\sigma^2\comma \; $$

Usually the unconstrained counterpart (7) of (6) is solved [Reference Candes and Romberg24], where λ is the regularization parameter.

(7)$$\mathop{\min}\limits_c \Vert y-A\Psi c \Vert _2^2 +\lambda \Vert c \Vert _1. $$

According to previously explained theory of CS, we need to know the sparsifying transform/domain in advance in order to sense as well as recover the original signal. The concept of BCS introduced in [Reference Gleichman, Eldar, Vigneron, Zarzoso, Moreau, Gribonval and Emmanuel17] eliminates the necessity to have prior knowledge of the sparsifying basis. It essentially is an amalgamation of concepts of CS and dictionary learning (DL). The authors proposed a framework and gave theoretical guarantees to recover the signal as solution to

(8)$$\mathop{\min}\limits_{\hat{\Psi}\comma c} \Vert y-A\hat{\Psi}c \Vert _2^2\; \hbox{subject to }\; \Vert c \Vert _0 \le k\comma \; $$

where ${\hat{\Psi}}$ is the unknown basis under which signal $x={\hat{\Psi}} c $ has a sparse representation. The unique solution for the above problem is guaranteed if apart from the above constraints, some additional constraints (such as dictionary being selected from a finite predefined set, and dictionary having orthogonal block diagonal structure, etc.) are imposed on the dictionary.

BCS framework has recently been applied to domains such as dynamic magnetic resonance imaging (MRI) [Reference Lingala and Jacob25]. They solve the problem of form as in (9) to simultaneously solve for the dictionary and sparse coefficient set.

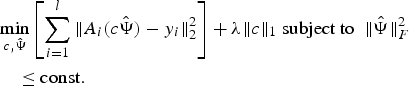(9)$$\eqalign{& \mathop{\min}\limits_{c\comma \hat{\Psi}} \left[\sum_{i=1}^l \Vert A_i \lpar c\hat{\Psi}\rpar -y_i\Vert_2^2\right]+\lambda \Vert c \Vert _1 \; \hbox{subject to }\; \Vert \hat{\Psi} \Vert _F^2 \cr & \quad \le \hbox{const}.} $$

Here a constraint on Frobenius norm of the dictionary is imposed to recover a unique solution.

C) Incorporating metadata in the CF framework

The sparsity of available rating information is the major bottleneck in achieving high prediction accuracy in RS. To overcome this sparsity challenge several works have been proposed that utilize data from secondary sources to augment rating data. In this section, we review some of the works incorporating the same in neighborhood or model-based approaches.

Authors in [Reference Vozalis and Margaritis18] proposed to use user's demographic information in neighborhood-based setup via a modified similarity measure (similarity _modified) (10).

(10)$$\eqalign{similarity_{modified} & =similarity_{demographic} \cr & \quad \times similarity_{rating}+similarity_{rating}\comma \; } $$

where similarity _demographic is computed based on the demographic profile of users and similarity _racing is computed using the explicit rating data.

Neighborhood-based design is augmented with geospatial information for photograph recommendation in [Reference Ostrikov, Rokach and Shapira26]. They used geographical tagging of photos to group items into clusters and propagate ratings among the members of the clusters. Thus, a dense rating matrix is obtained which is used as input to the K-nearest neighbor (KNN)-based technique.

Gu et al. [Reference Gu, Zhou and Ding20] constructed graphs for users and items with edges being weighted by corresponding similarity measures computed using user's social profile and demographic data, and item genres. They used this graphical modeling to augment the basic MF model as follows:

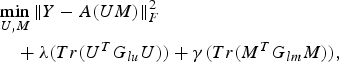(11)$$\eqalign{& \mathop{\min}\limits_{U\comma M} \Vert Y-A\lpar UM\rpar \Vert _F^2 \cr & \quad +\lambda \lpar Tr\lpar U^TG_{lu} U\rpar \rpar +\gamma \lpar Tr\lpar M^TG_{lm} M\rpar \rpar \comma \; } $$

where G _lu and G _lm are the graph Laplacians for the user and item graphs, respectively. The resulting optimization problem is formulated as low-rank semi-definite program.

In [Reference Jamali and Ester27,Reference Zhou, Shan, Banerjee and Sapiro28], social network information is integrated into a Matrix factorization framework. Authors in [Reference Zhou, Shan, Banerjee and Sapiro28] constructed a probabilistic matrix factorization (PMF) framework by modelling latent factor vectors as Gaussian distributed priors whose correlation function captures interdependencies between latent factor vectors. They utilized user's social network information to construct kernels capturing the social/trust relations. SGD was employed for solving the proposed formulation.

Existing works, including those discussed above, build up on the conventional MF framework (4). In this work, we incorporate secondary data in our proposed BCS framework. We make use of user and item metadata to encourage recovery of similar latent factor vectors for similar users (based on demographic data) and items (based on genre information).

A) Problem formulation

In this section, we present our proposed formulation for modified MF framework and scheme to incorporate user and item metadata into the same.

1) Novel MF model – BCS framework

As discussed above, the explicit ratings can be modeled as a sum of interaction and baseline components (2). In this work, we estimate the baseline component offline using (3). Offline computation of baseline makes the prediction process faster without impacting the prediction accuracy. Once, the baseline is estimated, we obtain the interaction portion of the available ratings; which is used in our proposed model. After the complete interaction matrix (Z) is recovered baseline estimates are added back to obtain the predicted rating values.

Traditionally, Z is completely recovered from its sub-sampled observation using MF approach outlined in (4). Equation (4) aims to recover the rating (interaction) matrix assuming that both user and item latent factor matrices have a dense structure or none of the terms in the latent factor vectors are zero for either users or items.

However, such an assumption is not entirely correct. Consider an RS which recommends movies to users. Each user can be described as a vector of values indicating his preference for a particular trait such as violence, musical, rom-com, etc. Usually all users will have a certain affinity either for or against each of these traits. Thus, the latent factor vector for any user will be dense, having non-zero values throughout. However, the same reasoning cannot be applied to the items. Each item, say a movie in the above scenario will either possess a trait or not. For example, a movie with a comic storyline or a children movie will not have any presence of violence in it. Each item will thus be profiled by a latent factor vector which is sparse. There will be zeros in positions corresponding to traits which an item does not possess altogether. Thus, the item matrix (M) will have sparse structure with several zeros in each column unlike the assumption made in previous models.

Carrying forward this logic, we put forth a new formulation for MF model using the BCS framework described in Section II. We aim to predict the missing ratings by formulating an optimization problem which promotes recovery of a dense user factor matrix (U) and a sparse item factor matrix (M). Our formulation can be mathematically stated as follows:

(12)$$\mathop{\min}\limits_{U\comma M} \Vert Y-A\lpar UM\rpar \Vert _F^2 +\lambda_u \Vert U \Vert _F^2 +\lambda_m \Vert vec\lpar M\rpar \Vert _1\comma \; $$

where λ_u and λ_m are the regularization parameters and A is the (binary) sub-sampling operator (zeros in positions corresponding to missing ratings), and Y is the matrix having the given ratings and missing ratings being replaced by zeros. The use of regularization terms promote recovery of a dense user factor matrix (penalty term being Frobenius norm) and a sparse item factor matrix (penalty term being l ₁ norm).

Our formulation follows the BCS framework and is similar to unconstrained form of (9) with the sparse coefficient set (c) equivalent to (M) and the dictionary being equivalent to (U). The added constraint on (U) required for the unique solution, is that it should have a dense structure incorporated as Frobenius norm penalty term.

We will briefly justify the choice of BCS for solving our problem. According to the CS convention, A is the sensing matrix and U is the sparsifying basis/dictionary. For our problem A is a Dirac/sampling operator; A is the canonical basis. In order to satisfy the incoherence criterion demanded by CS the dictionary U should be incoherent with A, i.e. it should be incoherent with the canonical basis. In other words, the elements in U should be of small magnitude in order to ensure the coherence to be small. As the columns of A are sparse (canonical basis), the rows of U should be dense, i.e. should have small valued coefficients throughout. The Frobenius norm penalty on the dictionary (U) enforces a minimum energy solution; it is well known that the minimum energy solution is dense with small values everywhere. This guarantees that the dictionary is incoherent with the sensing matrix A. Therefore, by design the BCS formulation yields a theoretically sound recovery framework for our problem.

2) Incorporating user metadata in BCS framework

The standard (latent factor) model-based methods rely on explicit ratings and hence suffer from the challenge of extreme data sparsity. With <10% of ratings available, the problem is highly underdetermined. In such a scenario, use of additional information from secondary sources can greatly mitigate the problem and help achieve greater prediction accuracy. In this work, we use user's demographic profile – age, gender, and occupational information – to support the rating database and improve prediction quality. Such information is generally acquired at the time of user's registration/sign-up on the portal and thus is available at no extra cost.

Our model is based on the belief that users who have the similar demographic profile, display similar affinities toward items (or features defining the items). Thus, the latent factor vectors of such similar users will also be similar. We group together users based on some demographic trait (say age). To model our notion of similar latent factor vectors, we impose the constraint of minimizing the variance among latent factor vectors of users belonging to a common group. This constraint is included in the proposed BCS formulation (13) as an additional penalty term representing intra-group variance (13).

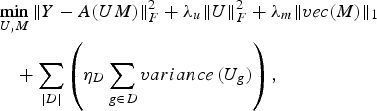(13)$$\eqalign{ & \mathop{\min}\limits_{U\comma M} \Vert Y-A\lpar UM\rpar \Vert _F^2 +\lambda_u \Vert U \Vert _F^2 +\lambda_m \Vert vec\lpar M\rpar \Vert _1 \cr & \quad +\sum\limits_{\vert D \vert } \left(\eta_D \sum\limits_{g\in D} variance\, \lpar U_g\rpar \right)\comma \; } $$

where D defines the groups formed using a particular demographic trait (occupation); | D| is the cardinality of D, i.e. number of different demographic features considered; g is the group of similar (clubbed) users; U _g is the set of latent factor vectors of users belonging to group g and η_D is the regularization parameter for each group structure D. Variance amongst user's latent factor vectors within a group (g) can be defined as $\sum\nolimits_{u\in g} \Vert L_{u} -\hbox{mean}\lpar U_{g}\rpar \Vert _{2}^{2}$, where L _u is the latent factor vector for user u belonging to group g.

Term representing the summation of all intra-group variances among latent factor vectors can be recast as a matrix operation (15)

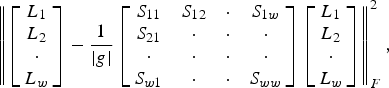(14)$$\left\Vert \left[{ \matrix{L_1 \cr L_2 \cr \cdot \cr L_w \cr}}\right]-\displaystyle{{1} \over {\vert g \vert }}\left[{ \matrix{ S_{11} & S_{12} &\cdot & S_{1w} \cr S_{21} &\cdot &\cdot &\cdot \cr \cdot &\cdot &\cdot &\cdot \cr S_{w1} & \cdot & \cdot & S_{ww} \cr }}\right]\left[{\matrix{ L_1 \cr L_2 \cr \cdot \cr L_w \cr }}\right]\right\Vert _F^2\comma \; $$

where L _* is the row vector defining the latent factor vector of users; w is the number of users; S is the similarity matrix constructed such that S _{i, j} = 1 if users i and j belong to same group and 0 otherwise.

Using (14) we can rewrite (13) as

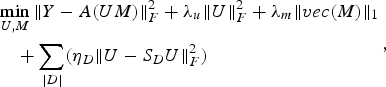(15)$$\eqalign{& \mathop{\min}\limits_{U\comma M} \Vert Y-A\lpar UM\rpar \Vert _F^2 +\lambda_u \Vert U \Vert _F^2 +\lambda_m \Vert vec\lpar M\rpar \Vert _1 \cr & \quad +\sum_{\vert D \vert } \lpar \eta_D \Vert U-S_D U \Vert_F^2\rpar }\comma \; $$

where S _D is the similarity matrix for group structure D constructed as discussed above.

With I _w − S _D = G _D; I _w:w × w identity matrix, we can rewrite (16) as

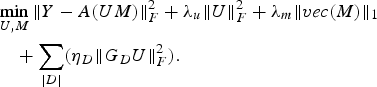(16)$$\eqalign{ &\mathop{\min}\limits_{U\comma M} \Vert Y-A\lpar UM\rpar \Vert _F^2 +\lambda_u \Vert U \Vert _F^2 +\lambda_m \Vert vec\lpar M\rpar \Vert _1 \cr & \quad +\sum_{\vert D \vert } \lpar \eta_D \Vert G_D U \Vert_F^2\rpar .} $$

Equation (16) is our generalized formulation for including user metadata into the BCS framework. The model enables inclusion of grouping using multiple demographic features and hence can be expanded as per available information. It models our notion that users sharing a demographic trait can be characterized by similar latent factor vectors. Use of additional information, augmenting the rating data, helps improve the robustness and accuracy of our design.

In this work, we define user groups based on age–gender combination (user having same gender and falling in same age bracket clubbed together) and as per user's occupational data. Thus, our net formulation can be written as a special case of (16) as follows (17) representing two group structures – one for age–gender combination and other for occupation.

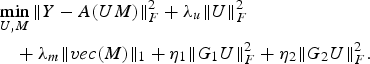(17)$$\eqalign{ &\mathop{\min}\limits_{U\comma M} \Vert Y-A\lpar UM\rpar \Vert _F^2+\lambda_u \Vert U \Vert _F^2 \cr & \quad +\lambda_m \Vert vec\lpar M\rpar \Vert _1 +\eta_1 \Vert G_1 U\Vert _F^2 +\eta_2 \Vert G_2 U\Vert _F^2.} $$

3) Incorporating item metadata in the BCS framework

In the previous section, we discussed formulation for utilizing user metadata to alleviate the problem of data sparsity. Similarly, item metadata can also be used to augment the model utilizing only the available rating values. This provides additional information about items and thus makes the task of recovery of item's latent factor vector less underdetermined.

In this work, we use information about item genre as the additional data source. Most portals maintain a database of such information, like a movie-renting portals or an online book website have information about the categories to which the items belong. However, we can do not extend the scheme used for incorporating user's metadata to items. This is because each item might belong to multiple genres, for example, a movie may belong to two genres – drama and romance. In such a case, each item is part of multiple groups making the intra-group variance-based formulation highly complex.

It was argued in preceding sections that item's latent factor vector is sparse, i.e. only a few latent factors have non-zero values – corresponding to traits possessed by it. Building up on this notion, we exploit the belief that items that share a genre (category) tend to display the similar sparsity pattern. To understand this better consider two books authored by Arthor C. Doyle. They will have suspense or action but highly unlikely to possess features such as comedy. Thus, the latent factor vectors defining the two books will rate highly on factors corresponding to suspense, action, and adventure, but will have zeros for those corresponding to comedy. Hence, they will display the similar sparsity pattern. To capture this belief, we augment the basic BCS framework by replacing the sparsity constraint (l ₁ norm) by a group sparsity penalty term (l ₂₁ norm) as in (18).

(18)$$\mathop{\min}\limits_{U\comma M} \Vert Y-A\lpar UM\rpar \Vert _F^2 +\lambda_u \Vert U \Vert _F^2 +\lambda_m \sum_{\vert C \vert } \Vert M_C\Vert _{2\comma 1}\comma \; $$

where C defines the group formed for each item category; |C| is the cardinality of C, i.e. number of different genres; M _C is the set of latent factor vectors of items belonging to genre C. M _C is of the form [L ₁L ₂·L _Z], where L _* is the column vector defining the latent factor vector of each item and Z is the total number of items falling in genre defined by C. Thus, we devise a formulation which minimizes the l ₂₁ norm across latent factor vectors of items belonging to each (same) genre. Use of group sparsity constraint promotes recovery of latent factor vectors having similar sparsity pattern.

We also combine the models for user and item metadata-based design strategies to devise a joint formulation (19).

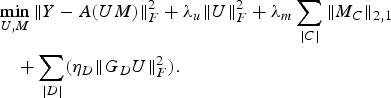(19)$$\eqalign{ &\mathop{\min}\limits_{U\comma M} \Vert Y-A\lpar UM\rpar \Vert _F^2 +\lambda_u \Vert U \Vert _F^2 +\lambda_m \sum_{\vert C \vert } \Vert M_C \Vert _{2\comma 1} \cr & \quad +\sum_{\vert D \vert } \lpar \eta_D \Vert G_D U\Vert_F^2\rpar .} $$

B) Algorithm design

We design efficient algorithms using MM technique [Reference Figueiredo, Bioucas-Dias and Nowak29] for our two formulations – one using user metadata and other exploiting item metadata.

1) Algorithm – user metadata in the BCS framework

We discuss our algorithm using the MM technique for our formulation proposed in (19) repeated here for convenience. The use of MM approach enables us to break complex optimization problem into simpler and more efficiently solvable steps.

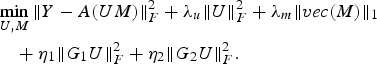(20)$$\eqalign{& \mathop{\min}\limits_{U\comma M} \Vert Y-A\lpar UM\rpar \Vert _F^2 +\lambda_u \Vert U \Vert _F^2 +\lambda_m \Vert vec\lpar M\rpar \Vert _1 \cr & \quad + \eta_1 \Vert G_1 U \Vert _F^2 +\eta_2 \Vert G_2 U \Vert _F^2.} $$

First, we briefly discuss the MM approach to depict its advantage in reducing computational complexity. Consider an underdetermined system of equation, y = Ax, where A ∈ R ^l×p, where p > l is a fat matrix. As A is not full rank, we can compute x by least-squares minimization as x = (A ^TA)⁻¹A ^Ty which involves computation of inverse of large matrices.

For cases where the variables to be recovered are very large, such as in RSs, the size of A ^TA becomes prohibitively large to efficiently compute its inverse within reasonable resource requirements. Use of the MM approach eliminates the need to compute such inverses and reduces the computational burden significantly.

The MM approach essentially involves replacing the minimization of an existing function, F(x), by minimization of another function, G(x), which is easier to minimize. G(x) should be majorizer of F(x), i.e. G(x) ≥ F(x) ∀x and G(x) = F(x) at x = x _k.

For the function F(x) = ||y − Ax||₂Reference Liu, Chen, Xiong, Ge, Li and Wu², we can take G(x) s.t. at kth iteration it is given by (21)

(21)$$G_k \lpar x\rpar =\Vert y-Ax\Vert _2^2 +\lpar x-x_k \rpar ^T\lpar \beta I-A^TA\rpar \lpar x-x_k\rpar \comma \; $$

where β ≥ max eig(A ^TA) to ensure the second term in (21) is always a positive quantity. After some mathematical manipulation it can be shown that G(x) can be minimized iteratively using the following steps.

(22a)$$v = x_k +\displaystyle{{1} \over {\beta}}A^T\lpar y-Ax_k\rpar \comma \; $$

(22b)$$\mathop{\min}\limits_x \Vert v-x\Vert _2^2. $$

The above steps of (22) are computationally much simpler and faster than the original solution.

Now, returning to our problem formulation (20), we firstly use Alternate Direction Method of Multipliers (ADMM), to split it into two simpler sub-problems (minimizing over a single variable)

Sub-problem 1

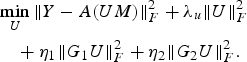(23)$$\eqalign{ & \mathop{\min}\limits_U \Vert Y-A\lpar UM\rpar \Vert _F^2 +\lambda_u \Vert U \Vert _F^2 \cr & \quad +\eta _1 \Vert G_1 U\Vert _F^2 +\eta_2 \Vert G_2 U \Vert _F^2.} $$

Sub-problem 2

(24)$$\mathop{\min}\limits_{U\comma M} \Vert Y-A\lpar UM\rpar \Vert _F^2 +\lambda_m \Vert vec\lpar M\rpar \Vert _1. $$

Considering sub-problem 1 (23), we use MM scheme to break it into two simpler steps:

(25)$$\eqalign{& V=U_k M_k +\displaystyle{{1} \over {\beta}}A^T\lpar Y-A\lpar U_k M_k \rpar \rpar \cr & \mathop{\min}\limits_U \Vert V-UM \Vert _F^2 +\lambda_u \Vert U \Vert _F^2 +\eta_1 \Vert G_1 U\Vert _F^2 \cr & \quad \quad + \eta_2 \Vert G_2 U \Vert _F^2.} $$

The minimization problem in (25) can be recast as

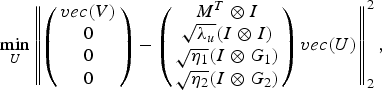(26)$$\mathop{\min}\limits_U \left\Vert \left({\matrix{vec\lpar V\rpar \cr 0 \cr 0 \cr 0 \cr }} \right)-\left({\matrix{ M^T \otimes I \cr \sqrt{\lambda_u} \lpar I \otimes I\rpar \cr \sqrt{\eta_1} \lpar I \otimes G_1\rpar \cr \sqrt{\eta_2} \lpar I \otimes G_2\rpar \cr } }\right)vec\lpar U\rpar \right\Vert _2^2\comma \; $$

which is a simple least-squares formulation having a closed-form solution.

Now, Considering sub-problem 2 (24), we use MM scheme to break it into simpler steps

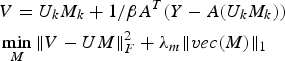(27)$$\eqalign {& V=U_k M_k + 1/\beta A^T\lpar Y-A\lpar U_k M_k\rpar \rpar \cr & \mathop{\min}\limits_M \Vert V-UM\Vert _F^2 +\lambda _m \Vert vec\lpar M\rpar \Vert _1} $$

The minimization step in (27) can be solved using iterative soft thresholding [Reference Daubechies, Defrise and Mol30] as follows:

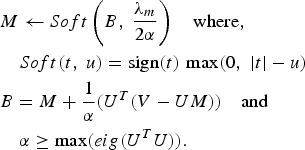(28)$$\eqalign{ & M \leftarrow Soft \left(B\comma \; \displaystyle{{\lambda_m} \over {2\alpha}}\right)\quad \hbox{where}\comma \; \cr & \quad Soft\lpar t\comma \; u\rpar =\hbox{sign}\lpar t\rpar \, \max \lpar 0\comma \; \vert t \vert -u\rpar \cr & B=M+\displaystyle{{1} \over {\alpha}}\lpar U^T\lpar V-UM\rpar \rpar \quad \hbox{and} \cr & \quad \alpha \ge \max \lpar eig\lpar U^TU\rpar \rpar .} $$

Both the sub-problems are alternately solved until convergence, i.e. either the maximum number of iterations reached or reduction in objective function falls below the threshold over consecutive iterations. The complete algorithm (BCS-User-Metadata) is given in Fig. 1.

Fig. 1.

Algorithm for BCS-User-Metadata.

2) Algorithm – item metadata in the BCS framework

In this section, we discuss our algorithm using MM for our formulation proposed in (18) repeated here for convenience involving item metadata.

(29)$$\mathop{\min}\limits_{U\comma M} \Vert Y-A\lpar UM\rpar \Vert _F^2 +\lambda_u \Vert U \Vert _F^2 +\lambda_m \sum_{\vert C \vert } \Vert M_C\Vert _{2\comma 1} $$

Similar to the procedure followed above, we use ADMM to split the problem into simpler sub-problems

(30)$$\mathop{\min}\limits_U \Vert Y-A\lpar UM\rpar \Vert _F^2 +\lambda_u \Vert U \Vert _F^2. $$

Sub-problem 2

(31)$$\mathop{\min}\limits_{U\comma M} \Vert Y-A\lpar UM\rpar \Vert _F^2 +\lambda_m \sum_{\vert C \vert } \Vert M_C\Vert _{2\comma 1}. $$

First, considering sub-problem 1, using MM we can write it as iterative steps

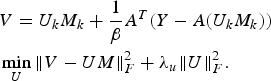(32)$$\eqalign{ & V=U_k M_k +\displaystyle{{1} \over {\beta}} A^T\lpar Y-A\lpar U_k M_k\rpar \rpar \cr & \mathop{\min}\limits_U \Vert V-UM\Vert _F^2 +\lambda_u \Vert U \Vert _F^2.} $$

Equation (32) can be recast into simple least-squares form (33) having the closed-form solution

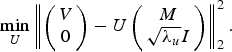(33)$$\mathop{\min}\limits_U \left\Vert \left({\matrix{ V \cr 0 \cr}}\right)-U\left({\matrix{ M \cr \sqrt{\lambda_u} I \cr }} \right)\right\Vert _2^2. $$

Now, moving to sub-problem 2, we consider each group separately, i.e. one group at a time. Applying the MM technique we can rewrite the same (for say group 1) as

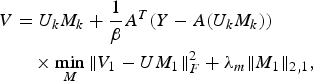(34)$$\eqalign{ V & = U_k M_k +\displaystyle{{1} \over {\beta}}A^T\lpar Y-A\lpar U_k M_k \rpar \rpar \cr & \quad \times \mathop{\min}\limits_M \Vert V_1 -UM_1 \Vert _F^2 +\lambda_m \Vert M_1\Vert _{2\comma 1}\comma \; } $$

where V ₁ is the set of columns of V having correspondence in M ₁.

Solution to minimization problem in (34) is given by [Reference Chartrand and Wohlberg31]

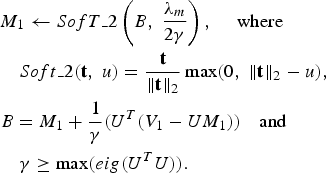(35)$$\eqalign{ & M_1 \leftarrow SofT\_2\left(B\comma \; \displaystyle{{\lambda_m} \over {2\gamma}}\right)\comma \; \quad \hbox{where} \cr & \quad Soft\_2 \lpar {\bf t}\comma \; u\rpar =\displaystyle{{\bf t} \over {\Vert {\bf t}\Vert _2}} \max\lpar 0\comma \; \Vert {\bf t} \Vert_2 -u\rpar \comma \; \cr & B=M_1 +\displaystyle{{1} \over {\gamma }}\lpar U^T\lpar V_1 -UM_1 \rpar \rpar \quad \hbox{and} \cr & \quad \gamma \ge \max\lpar eig\lpar U^TU\rpar \rpar .} $$

Similar procedure is repeated for all groups (formed as per genre data). The overall item's latent factor vector is computed as an average of latent factor vectors obtained from each group data. The two sub-problems are alternately solved until convergence. The complete algorithm (BCS-Item-Metadata) is given in Fig. 2.

Fig. 2.

Algorithm for BCS-Item-Metadata.

A) Description of dataset

The 100 K dataset consists of 100 000 ratings (on a scale of 1–5) given by 943 users on a total of 1682 movies. The 1 M dataset has about 3900 movie ids, 6040 users, and 1 million ratings. Both the datasets are extremely sparse (<5% of ratings available) and hence an optimum candidate for illustrating the benefits of adding metadata toward improving prediction accuracy.

For incorporating user metadata (for both datasets) we consider their age–gender combination and occupational profiles. For 100 K dataset, the groups formed are Male and Female in age brackets of 1–10, 11–20, 21–30, 31–40, 41–50, 51–60, 61–70, and 71–80. Thus, we have a total of 18 groups of similar users as per their age–gender combination. We also grouped users on the basis of their occupation, wherein there are 21 different occupations and equal number of groups. In case of 1 M dataset, there are seven different age groups: 1–17, 18–24, 25–34, 35–44, 45–49, 50–55, and 56+. So, a total of 14 groups are made with age–gender (M/F) information. Similar to 100 K dataset, users are divided into 21 groups based on their occupation.

Item metadata is exploited by forming 19 groups as per the available genre information in case of both the datasets. Each movie can belong to more than one genre and hence the groups are overlapping.

B) Parameter selection and evaluation criteria

We performed fivefold cross-validation on both the datasets with 80% data forming the train set and remaining 20% used as test data. For each algorithm–test set combinations, 100 independent simulations were carried out and the results show are the mean values and standard deviation for all 100 runs. The simulations are carried out on system with i7–3770S CPU at 3.10 | GHz with 8 | GB RAM.

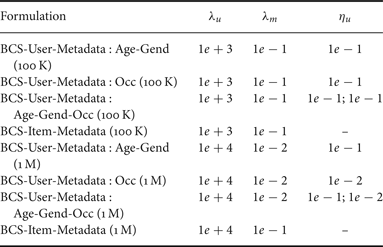
We computed the baseline offline using (3) with regularization parameter kept at 1e–3. For BCS algorithm we used the code provided by authors of [Reference Lingala and Jacob25]. The parameter selection for our formulations was done using L-curve technique [Reference Lawson and Hanson32]. The values for all the formulations namely, BCS-User-Metadata (16) for cases using only age–gender information, only occupational data and both combined together and BCS-Item-Metadata (18) are given in Table 1.

Table 1.

Regularization parameter values.

The performance of the proposed approach viz-a-viz other methods is evaluated on the basis of two error measures – mean absolute error (MAE) (37) and root-mean-square error (RMSE) (38), where R contains the actual rating values, $\hat{R}$ consists of predicted ratings, and | R| is the cardinality of the rating matrix.

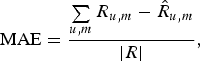(36)$$\hbox{MAE} = \displaystyle{{\sum\limits_{u\comma m} R_{u\comma m}-\hat{R}_{u\comma m}} \over {\vert R \vert }}\comma \; $$

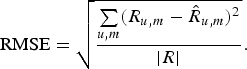(37)$$\hbox{RMSE} = \sqrt{\displaystyle{{\sum\limits_{u\comma m} \lpar R_{u\comma m} -\hat{R}_{u\comma m}\rpar ^2} \over {\vert R \vert }}}. $$

In addition to these error measures, we also evaluate the performance of algorithms in terms of top-N recommendation accuracy via precision (38) and recall (39) [Reference Shani, Gunawardana, Ricci, Rokach, Shapira and Kantor33].

(38)$$\hbox{Precision}=\displaystyle{{\# t_p } \over {\# t_p +\# f_p }}\comma \; $$

(39)$$\hbox{Recall}=\displaystyle{{\# t_p } \over {\# t_p +\# f_n }}\comma \; $$

where t _p denotes the true positive (item relevant and recommended), f _p denotes the false positive (item irrelevant and recommended), and f _n denotes the false negative (item relevant and not recommended). To differentiate the relevant and irrelevant items, we binarize the available ratings; marking the items rated as 4 or 5 as irrelevant, and those rated below (1–3) as irrelevant to the user. We plot the precision and recall curves for varying number of recommendations (N) for all algorithms.

C) Performance evaluation of novel MF (BCS) formulation

In this section, we highlight the improvement in prediction accuracy achieved by use of our modified MF model, i.e. BCS framework (12). We compare the performance of our formulation – BCS algorithm – against the state-of-the-art MF algorithms, namely, SGD [Reference Koren, Bell and Volinsky14], PMF [Reference Mnih, Salakhutdinov, Platt, Koller, Singer and Roweis15] and Block co-ordinate descent algorithm for non-negative matrix factorization (BCD-NMF) [Reference Xu and Yin16]. SGD algorithm involves online baseline estimation, whereas the other two work with raw (non-negative) rating data. For our formulation, BCS, baseline correction is carried out offline.

Table 2 lists the MAE and RMSE values for all the algorithms for 100 K dataset. The error values for our formulation and SGD is about 2% better than those for the other two algorithm (PMF and BCD-NMF), highlighting the importance of baseline estimation. Despite the online baseline estimation carried out in the SGD algorithm, our formulation gives an improvement of over 1% in the MAE value as compared with the former. Table 3 gives similar values for the 1 M dataset. Here also, it can be observed that the methods involving baseline estimation give superior results. For 1M dataset also, our algorithm gives the highest prediction accuracy among the algorithms compared.

Table 2.

Error measures (100 K dataset).

Table 3.

Error measures (1 M dataset).

Table 4 gives the run time comparison for various algorithms compared above for 100 K dataset. It can be seen from values in the table that our novel BCS formulation performs comparable in terms of run time to existing state-of-the-art methods while providing substantial gain in terms of recovery accuracy.

Table 4.

Run time comparison (100 K dataset).

Figures 3 and 4 give the precision and recall values as a function of number of recommendations for all the algorithms compared above for the 100 K dataset. Corresponding graph for 1M dataset are shown in Figs 5 and 6. Our formulation (BCS) performs better (especially for 1M dataset) or comparable with other state-of-the-art methods on this measure as well.

Fig. 3.

Precision (100 K).

Fig. 4.

Recall (100 K).

Fig. 5.

Precision (1 M).

Fig. 6.

Recall (1 M).

The above results validate our claim that our formulation promoting recovery of a dense user and sparse item latent factor matrix better models the rating data.

D) Effect of incorporating user and item metadata

In this section, we demonstrate the impact of incorporating user and item metadata to our BCS formulation. We study the impact of user metadata (age–gender, occupation, and both combined) and item metadata (genre information) on prediction accuracy. We compare the result of our formulations incorporating metadata – BCS-User-Metadata (16) and BCS-Item-Metadata (18) with those obtained using the base BCS framework.

Tables 5 and 6 list the MAE and RMSE values for all the formulations for 100 K and 1 M datasets, respectively. Use of metadata to supplement the rating data using our formulation is able to bring an improvement of over 2% in prediction accuracy (in terms of MAE values) over the BCS formulation using only rating data, which is a substantial gain. Among the metadata information, grouping using user demographic data give slightly better results than the item category information. Further, age–gender-based grouping is able to capture the user similarity better and additional use of occupational profile does not introduce any substantial improvement. For the 1 M dataset, the improvement is around even more pronounced (>2.5%). This is because the rating matrix for 1 M dataset is ever sparser and hence better benefits from use of secondary data.

Table 5.

Error measures (100 K dataset).

Table 6.

Error measures (1 M dataset).

Figures 7 and 8 give the precision and recall values all the algorithms for 100 K dataset and Figs 9 and 10 gives similar graphs for 1M dataset. It can be observed from the figure that inclusion of metadata in the model helps improve both precision and recall considerably. For each item or user metadata, the values are almost comparable.

Fig. 7.

Precision (100 K).

Fig. 8.

Recall (100 K).

Fig. 9.

Precision (1 M).

Fig. 10.

Recall (1 M).

E) Comparison with existing methods

This section contains the comparison of our proposed formulations (BCS-User-Metadata and BCS-Item-Metadata) with existing works exploiting user/item metadata. We also show the results for combine formulation using both item and user metadata (BCS-User-Item-Metadata) (19). We compare our work with graph-regularized matrix factorization (Graph-Reg NMF) formulation proposed in [Reference Gu, Zhou and Ding20] and the neighborhood method (KNN-based) proposed in [Reference Vozalis and Margaritis18], both utilizing user's auxiliary (demographic) information. These two works are representative of the existing state-of-the-art formulation incorporating metadata information; others rely on social profiling and network information.

Tables 7 and 8 give the MAE and RMSE values for 100 K and 1 M datasets, respectively. The values clearly indicate the superiority of our design over the neighborhood based as well as latent factor model. The prediction accuracy is lowest for neighborhood-based methods showing the advantage of latent factor models in better modeling the rating data. Our algorithm is able to achieve about 5% better MAE than the graph-Reg NMF algorithm for the 100 K dataset.

Table 7.

Error measures (100 K dataset).

Table 8.

Error measures (1 M dataset).

The improvement for 1 M dataset is even higher about 7.5% for MAE values. Use of user's demographic data gives slightly better results than item category information. However, combining item information with user data does not increase the prediction accuracy further.

As can be observed from the values in Tables 5–8, that use of user or item metadata with the rating information provide considerable improvement in prediction accuracy. However, a combination of user and item metadata together with rating information is unable to surpass the performance of algorithms using either of the metadata. This observation can be explained by going back to latent factor model's assumption of interaction between users and items. As per the latent factor model, only a few factors determine a user's choice of an item. Thus, there exists correlation among users and items which is reflected in the low-rank nature of the rating matrix. The rating data is highly sparse and thus unable to capture the interaction between users and items completely. Use of either user or item metadata helps provide additional data to establish this correlation further. However, there is a practical limit to which such metadata or item–user correlation can be exploited to improve accuracy. Sufficient information is captured by rating and user or item metadata to provide further benefit of additional metadata. Also, the formulation suffer from practical implementation constraint in terms of selecting optimal regulation parameters and others which hinders further improvement in accuracy.

Table 9 gives the run time comparison of our formulation using user metadata and item genre information with existing works. Here also, our formulation utilizing item metadata has run times comparable with state-of-the-art methods while achieving a significant reduction in error measures. Even though our user metadata-based formulation has higher run times than the Graph-Reg method, it is still reasonable and far lesser than neighborhood-based scheme. Also, the improvement in prediction accuracy compensates for run time increase.

Table 9.

Run time comparison (100 K dataset).

Figures 11 and 12 give the precision and recall values for 100 K dataset. Our algorithm outperforms the other two approaches by a wide margin on this measure. Figures 13 and 14 show the same data curves for 1 M dataset. Here also, our algorithm performs better or comparably to others. The item and user metadata based formulations based on BCS, both perform comparably.

Fig. 11.

Precision (100 K).

Fig. 12.

Recall (100 K).

Fig. 13.

Precision (1 M).

Fig. 14.

Recall (1 M).