1. Introduction
Real-time strategy (RTS) (Ontañón et al., Reference Ontañón, Synnaeve, Uriarte, Richoux, Churchill and Preuss2013) games belong to the genre of 2-player strategy games where a player’s goal is to build sufficient economic and military might to destroy the opponent. A wide array of actions are available to a player, ranging from gathering resources, to building bases that train and churn out soldiers, to attacking opponent’s units and bases to ultimately destroy them. For over two decades, RTS games have provided a rich substrate for AI research as they feature many of its key challenges, viz., complex dynamic environments with incomplete information and partial observability (fog-of-war), simultaneous and durative actions with potentially nondeterministic effects, real-time response, and unfathomably large strategy spaces. Consequently, research focused on RTS games can have significant potential impact in many real-world domains (e.g., business, finance, and governance) as they share many of the same challenges (Ontañón et al., Reference Ontañón, Synnaeve, Uriarte, Richoux, Churchill and Preuss2013).
Reinforcement learning (RL) has been a popular technique for training AI agents for computer games, including RTS games. Decades of research in this field boosted by the deep learning revolution have culminated in spectacular successes recently, where trained agents have matched and surpassed human expertise in domains where humans were once considered invulnerable to AI (Mnih et al., Reference Mnih, Kavukcuoglu, Silver, Rusu, Veness, Bellemare, Graves, Riedmiller, Fidjeland, Ostrovski, Petersen, Beattie, Sadik, Antonoglou, King, Kumaran, Wierstra, Legg and Hassabis2015; Vinyals et al., Reference Vinyals, Babuschkin, Czarnecki, Mathieu, Dudzik, Chung, Choi, Powell, Ewalds, Georgiev, Oh, Horgan, Kroiss, Danihelka, Huang, Sifre, Cai, Agapiou, Jaderberg and Silver2019). However, RL remains a data-hungry approach that requires the agent to conduct a large number of simulations in order to comparatively evaluate a vast space of strategic alternatives. This is often measured as sample complexity. Despite decades worth of significant effort devoted toward reducing sample complexity, it still takes hundreds of millions of samples/simulations to train an RL agent in complex domains such as RTS games. This problem is compounded in partially observable settings (a.k.a fog-of-war in RTS games) where parts of the state are hidden from the agent.
In this paper, we focus on a sample complexity reduction technique called reinforcement learning as a rehearsal (RLaR), and on the RTS game of MicroRTS to formulate and evaluate it. As argued in Kraemer and Banerjee (Reference Kraemer and Banerjee2016), RLaR is most suited in partially observable environments where the hidden/unobservable part of the state can be made available to an RL agent during training (training phase), but not when the learned policies are to be executed in the task (execution phase). While partial observability makes RL more challenging, RLaR is only relevant in such settings, reducing to regular RL in fully observable settings. RLaR has been formulated in the context of action-value function based RL before (Kraemer & Banerjee Reference Kraemer and Banerjee2016). However, a major drawback of action-value based RL is that exploration and discovery can be extremely slow and difficult when the action space is very large. This is indeed the case in many RTS games such as MicroRTS and StarCraft, where policy search methods (e.g., actor-critic RL) remain the only practical option. As we argue in Section 3.3, value-function based methods are impractical in MicroRTS. Hence in this paper we formulate RLaR for actor-critic RL as our first contribution. We show that on the one hand the actor-critic framework allows RLaR to be much simpler, but on the other hand it leaves room for a key component of RLaR—a prediction function that relates a learner’s observations with that of its opponent. This function, when leveraged for exploration, accelerates RL compared to a variant that does not utilize this prediction function, as our experiments in MicroRTS show. This is a second major contribution of this paper. Further experiments provide evidence that RLaR may reduce actor noise compared to a variant that does not utilize RLaR’s exploration—a third contribution of this paper.
The rest of this paper is organized as follows: We present literature review centered on RTS game research in Section 2. In Section 3, we present key concepts that this paper builds on, viz., RL, the actor-critic framework, and RL as a rehearsal (RLaR). We also present a brief description of MicroRTS, along with estimations of its spaces relevant to RL. In Section 4, we present our formulation for RL and RLaR in MicroRTS with the detailed neural network architectures. We conduct an experimental study in a few MicroRTS maps, and discuss the results in Section 5. Finally, we present our conclusions in Section 6.
2. Related work
One of the earliest works that called for attention to RTS games as a challenging domain for AI research was by Buro (Reference Buro2003). In that work, Buro identified a broad mix of AI challenges, including resource management, opponent modeling and learning, real-time adversarial planning, spatial and temporal reasoning, and decision making under uncertainty. Another definitive account of task decomposition for RTS-playing AIs can be found in Weber et al. (Reference Weber, Mateas and Jhala2011 a). Our evaluation domain of MicroRTS features all of these challenges. Due to the sheer size of the strategy space as well as the availability of human play data, some of the earliest AI approaches considered case-based reasoning (CBR) and planning, for example, Sharma et al. (Reference Sharma, Holmes, Santamara and Irani2007), Ontañón et al. (Reference Ontañón, Mishra, Sugandh and Ram2008) among many others. These approaches match a current situation with situations stored in a knowledgbase of cases (from past/human play) to trigger the corresponding response, leading to fast and real-time response despite the vastness of the strategy space. Sharma et al. (Reference Sharma, Holmes, Santamara and Irani2007) combined CBR with RL in a transfer learning context to facilitate the reuse of tactical plan components. Ontañón et al. (Reference Ontañón, Mishra, Sugandh and Ram2008) demonstrated the utility of case based planning for real-time decision making in the game of Wargus–a Warcraft II clone. Rapid progress in RL over the past decade has brought us to a point where we can now take a purely RL approach despite the size of the strategy space, and do not need to maintain a database for case matching.
Standard AI techniques for search, planning, state estimation, etc. have also long been adapted to RTS and strategy games. For instance, Forbus et al. (Reference Forbus, Mahoney and Dill2002) applied qualitative spatial information acquired from geometric and path-finding analyses to wargames. Weber et al. (Reference Weber, Mateas and Jhala2011
b) used a particle model with state estimation to track opponent units under fog-of-war. Perkins (Reference Perkins2010) applied Voronoi tesselation followed by search space pruning to identify regions and choke points in RTS maps. Churchill and Buro (Reference Churchill and Buro2011) used AI planning to optimize build orders in StarCraft, taking into account timing and scheduling constraints. Churchill et al. (Reference Churchill, Saffidine and Buro2012) also adapted the
$\alpha-\beta$
pruning technique for durative actions for fast heuristic search in RTS combat. Chung et al. (Reference Chung, Buro and Schaeffer2005) applied Monte Carlo planning to a version of Open RTS (ORTS). Balla and Fern (Reference Balla and Fern2009) applied the well-known Monte Carlo Tree Search algorithm based on upper confidence bounds, called UCT, to tactical assault planning in Wargus. More recently, Critch and Churchill (Reference Critch and Churchill2020) used influence maps to plan navigation that maintains safe distance from enemy units and scouts. To reduce the search space to a manageable size, most of these techniques rely on abstraction in state and action spaces. Our RL-based approach performs many of these tasks differently, and does not rely on additional abstractions than what is provided by the game. For instance, spatial reasoning and planning are accommodated via convolutional neural network (CNN) and recurrence in our actor model. While state estimation is obviated by the observation of hidden state during training, our specialized exploration of RLaR also favors policies that minimize state ambiguity during the execution of trained policies when the hidden state is no longer available.
Learning techniques, specifically supervised learning and RL, have also been applied to RTS games in the past. Synnaeve and Bessiere (Reference Synnaeve and Bessiere2011) presented a Bayesian learning framework to predict the opponent’s build tree based on replays, applied to StarCraft. Wender and Watson (Reference Wender and Watson2012) evaluated a range of major RL algorithms for decentralized micromanagement in Broodwar (StarCraft). Marthi et al. (Reference Marthi, Russell, Latham and Guestrin2005) view an RTS player’s control of a set of units as a robot with multiple effectors, and applied concurrent hierarchical Q-learning to efficiently control units. However, all units are afforded Q-functions at the bottom level. By contrast, Jaidee and Muñoz-Avila (Reference Jaidee and Muñoz-Avila2012) use a single Q-function for each unit type, thus significantly reducing learning complexity. Since the spectacular success of (deep-) RL reported in Mnih et al.’s Reference Mnih, Kavukcuoglu, Silver, Rusu, Veness, Bellemare, Graves, Riedmiller, Fidjeland, Ostrovski, Petersen, Beattie, Sadik, Antonoglou, King, Kumaran, Wierstra, Legg and Hassabis2015 Nature article (Mnih et al., Reference Mnih, Kavukcuoglu, Silver, Rusu, Veness, Bellemare, Graves, Riedmiller, Fidjeland, Ostrovski, Petersen, Beattie, Sadik, Antonoglou, King, Kumaran, Wierstra, Legg and Hassabis2015) where AI matched and even surpassed human level play in a range of Atari games, deep-RL has become a staple for computer games, including RTS games. Recently, (multi-agent) RL has achieved grandmaster-level sophistication in StarCraft II (Vinyals et al., Reference Vinyals, Babuschkin, Czarnecki, Mathieu, Dudzik, Chung, Choi, Powell, Ewalds, Georgiev, Oh, Horgan, Kroiss, Danihelka, Huang, Sifre, Cai, Agapiou, Jaderberg and Silver2019). It is called AlphaStar. We pick a component of AlphaStar that also exploits the idea of rehearsal—i.e., that the learner can be allowed to see more than its observation during training but not during the execution of trained policies—as a baseline in this paper that we call RLAlpha. Among other work that leverage abstractions, Niel et al. (Reference Niel, Krebbers, Drugan and Wiering2018) evaluate hierarchical RL in conjunction with unit-wise reward decomposition, while Barriga et al. (Reference Barriga, Stanescu, Besoain and Buro2019) use RL with CNNs (with data labeled by Puppet Search) to select among (fewer) abstract actions to save computation budget for game tree search to improve lower level tactics. More recently, Ray and Sturtevant (Reference Ray and Sturtevant2023) propose adversarial navigation planning with RL and PRA* to delegate micromanagement to autonomous agents, and show that this approach is not only effective at dynamic replanning but also adaptive to unseen environments.
In this paper, we focus on MicroRTS (a.k.a
$\mu$
RTS) (Ontañón Reference Ontañón2013)—a gridworld RTS game developed by Santiago Ontañón for AI research and competition. It contains much of the same components of an RTS game, but with less complex graphics. It has been the substrate of RTS competitions held in conjunction with the IEEE Conference on Games (COG) since 2017. Other relevant competitions include the Open RTS (ORTS) game AI competition (held from 2006-2009), AIIDE StarCraft AI competition and CIG/COG StarCraft RTS AI competition, both held annually since 2010. The annual MicroRTS competitions feature two tracks: the fully observable ‘Classic Track’, and the ‘Partial Observability’ track that simulates fog-of-war. We focus on the latter. The top two entries in the latest 2021 competition were MentalSealPO and MicroPhantom. Since MicroPhantom follows a published methodology based on constraint programming and decision theory (Richoux Reference Richoux2020), we have chosen this bot as the opponent against which we train our learning agents.
Summary of common notations used with variations in the paper
3. Background
3.1. Reinforcement learning
RL problems are modeled as Markov Decision Processes or MDPs (Sutton & Barto Reference Sutton and Barto1998). An MDP is given by the tuple
$\langle S,A,R,P\rangle$
, where S is the set of environmental states that an agent can occupy at any given time, A is the set of actions from which it can select one at a given state,
$R\,:\,S\times A \mapsto \mathbb{R}$
is the reward function, that is, R(s, a) specifies the reward from the environment that the agent gets for executing action
$a\in A$
in state
$s\in S$
;
$P\,:\,S\times A\times S\mapsto [0,1]$
is the state transition probability function, that is, P(s, a, s’) specifies the probability of the next state in the Markov chain being s’ following the agent’s selection of action a in state s. The agent’s goal is to learn a policy
$\pi\,:\,S\mapsto A$
that maximizes the sum of current and future rewards from any state s, given by,
\begin{align}V^{\pi}(s^{0})=\mathbb{E}_{P}\biggl[R(s^0,\pi(s^0))+\gamma R(s^1,\pi(s^1))+\gamma^2R(s^2,\pi(s^2))+\gamma^3R(s^3,\pi(s^3))+\ldots\biggr]\end{align}
where
$s^0,s^1,s^2,\ldots$
are successive samplings from the distribution P following the Markov chain with policy
$\pi$
, and
$\gamma\in(0,1)$
is a discount factor.
In this paper we consider policy search methods (Sutton et al., Reference Sutton, McAllester, Singh and Mansour2000) that explicitly maintain a policy
$\pi_\theta(a|s)$
denoting the probability of taking action a in state s, with the distribution being parametrized by
$\theta$
. In this paper, we use a policy gradient method—belonging to the class of policy search methods—where
$\pi_\theta(a|s)$
is differentiable w.r.t
$\theta$
.
One popular policy gradient technique, called Advantage Actor-Critic (A2C), uses two function approximations. One function approximation represents the actor, viz.
$\pi_\theta(a|s)$
responsible for selecting an action given a state, as stated above. The other function approximation represents the critic, viz.,
$V^\pi_\phi(s)$
which gives the value of the state s under the actor policy
$\pi$
(in essence it critiques the actor’s performance), and is parametrized by
$\phi$
. Normally
$\theta$
is improved by policy gradient, optimizing
\begin{equation} J(\theta) =\mathbb{E}_{s\sim d^{\pi_\theta},a\sim\pi_\theta}A(s,a)\end{equation}
where
$d^{\pi_\theta}(s)=\sum_{t=0}^{\infty}\gamma^tPr(s_t=s|s_o,\pi_\theta)$
is the discounted state distribution that results from following policy
$\pi_\theta$
, and A(s, a) is called the advantage function that represents how much better (or worse) the value of taking action a in state s is compared to the average value from state s. A simple yet good estimate of the advantage function is the temporal difference (TD) error (Sutton et al., Reference Sutton, McAllester, Singh and Mansour2000) given by
\begin{equation} A_{TD}(s,a)=r_{sa}+\gamma V^\pi_\phi(s')-V^\pi_\phi(s) \end{equation}
where
$r_{sa}\sim R(s,a)$
and
$s'\sim P(s,a,.)$
. This estimate only depends on the reward and states from the actual trajectories and the critic itself. While the mean squared TD errors (from Equation 3) is used as the loss function for updating the parameters
$\phi$
of the critic network, the actor network’s parameters
$\theta$
are updated using the gradient (Williams, Reference Williams1992)
\begin{equation} \nabla_\theta J(\theta)=\mathbb{E}_{s\sim d^{\pi_\theta},a\sim\pi_\theta}\nabla_\theta\log\pi_\theta(a|s)A_{TD}(s,a). \end{equation}
In order to encourage exploration, an exploration bonus is added to the objective
$J(\theta)$
whereby the entropy of the policy
$\pi_\theta$
is also maximized, precluding the policy from settling into deterministic actions that could foreclose exploration. This gives a more complete expression for
$\theta$
update:
\begin{align} \nabla_\theta J(\theta)=\mathbb{E}_{s\sim d^{\pi_\theta}}\biggl[\mathbb{E}_{a\sim\pi_\theta}\nabla_\theta\log\pi_\theta(a|s)A_{TD}(s,a) - \beta\nabla_\theta \sum_a\pi_\theta(a|s)\log(\pi_\theta(a|s))\biggr] \end{align}
where
$\beta$
is the entropy bonus (regularization) weight.
When the MDP is partially observable (POMDP), the state is not directly observed. Instead, the agent receives an observation,
$\omega$
, that is (perhaps noisily) correlated with the hidden state. A common technique is to simply replace the states in the above equations with observations, or a history of past observations, as a sufficient statistic for the hidden state. In training neural networks
$\pi_\theta$
and
$V^\pi_\phi$
, history is accommodated via recurrence, for example, using LSTM (Hochreiter & Schmidhuber, Reference Hochreiter and Schmidhuber1997). A summary of common notations is provided in Table 1, along with the variations used in Section 3.2.
In this paper, we use a variation of A2C, called A2C with self-imitation learning (A2C+SIL) (Oh et al., Reference Oh, Guo, Singh and Lee2018), where apart from the A2C loss functions a SIL loss function is added where advantages corresponding only to positive experiences are used. In other words, states where advantages are negative are zeroed out, thus simulating a learner’s desire to recreate positive experiences from its past. This approach has been shown to be effective for hard exploration tasks.
3.2. Reinforcement Learning as a Rehearsal (RLaR)
RLaR (Kraemer & Banerjee, Reference Kraemer and Banerjee2016) was designed for partially observable settings where a training stage could be distinguished from an execution stage where the learned policy is applied/evaluated. In partially observable settings, the state s can be decomposed into a hidden part (say
$s_h$
) and an observable part (say
$s_o$
), such that
$s=s_h\cup s_o$
. Furthermore, RLaR was formulated in the context of Q-learning (Watkins & Dayan, Reference Watkins and Dayan1992), where an action-value function called Q-function is learned. This function is typically predicated on only the observable part of the state,
$s_o$
, that is, expressed as
$Q(s_o,a)$
. Similarly
$V^\pi(s_o)$
. These two functions are related as follows:
\begin{equation}V^\pi(s_o) = \max_a Q^\pi(s_o,a).\end{equation}
$Q^\pi(s_o,a)$
represents the long term value from following action a upon receiving observation
$s_o$
, and the policy
$\pi$
thereafter. A Q-learning agent learns the optimal Q-values,
$Q^\ast(s_o,a)\ \forall s_o,a$
, and then constructs the optimal policy
$\pi^\ast(s_o)=\arg\max_aQ^\ast(s_o,a)$
. RLaR allows a learner to observe the hidden part of the state (
$s_h$
that includes system state as well as opponent’s observations and actions) in addition to its observation (
$s_o$
), but only during the training stage as if to practice/rehearse. A RLaR agent learns an augmented Q-function,
$Q^\ast(s=s_o\cup s_h,a)$
, as well as an auxiliary predictor function (essentially a conditional probability distribution)
$P(s_h|s_o)$
, during the training/rehearsal stage. During the execution stage, the agent can construct a policy that no longer relies on hidden features, as
\begin{equation} \pi^\ast(s_o)=\arg\max_a\sum_{s_h}Q^\ast(s_h\cup s_o,a)P(s_h|s_o).\end{equation}
This approach has been shown to expedite RL in simple 2-agent tasks (Kraemer & Banerjee, Reference Kraemer and Banerjee2016), as well as in a larger swarm foraging task (Nguyen & Banerjee, Reference Nguyen and Banerjee2021) more recently. In this paper, we formulate RLaR within the actor-critic framework instead of Q-learning, and evaluate its effectiveness in a game with a large strategy space viz., MicroRTS.
3.3. MicroRTS
The components present in MicroRTS are bases, resources, barracks, worker units, and soldier units. A game is played between two players (learning agent controls the blue team), and the winner is determined when a player destroys all its opponent’s units, including base, barracks and soldiers/units. If neither of the players is able to destroy it opponent’s units within a given number of steps (3000 for this paper), then it is a draw. Both the players are given a worker unit, a base and 5 number of resources initially. Their locations, as well as the locations of unowned mineable resources, are symmetric to prevent either player from having an initial advantage. Worker units can harvest resources and build bases and barracks. Barracks produce soldier units of three types: light, heavy and ranged. Light units have less hitpoints whereas heavy units have high hitpoints, but both can only attack immediately neighboring cells. By contrast, ranged units can attack from 3 grid cells away.
In this paper, the learning agent is allowed to create up to
$N_E=70$
units–a number determined from game traces between MicroPhantom and MentalSealPO. We also limit the map sizes to
$16\times 16$
in order to restrict training time. Actions available to a unit include ‘noop’, ‘attack’, and 4 directions each of ‘move’, ‘harvest’, ‘return’, and ‘produce’, leading to
$N_A=18$
action types. Actions ‘attack’ and ‘produce’ are further qualified by which location to attack and what type of unit to produce. Considering
$N_T=7$
types of units and up to 10 hitpoints, these choices lead to a state space of maximum size
$(7\times 10)^{70+70}*\binom{256}{70+70}\approx 10^{333}$
, assuming both players are allowed up to 70 units. The learner’s observation space is of maximum size
$(7\times 10)^{70}*\binom{128}{70}\approx 10^{166}$
, assuming about half of the grid space is available to locate its units. Its action space is of maximum size
$18^{70}\approx 10^{87}$
, conservatively assuming only one attack location and one produce type per unit. This leads to a strategy (mapping from observations to actions) space that is truly unfathomable. Unless other assumptions are made (e.g., factored or composable value function; see Kelly and Churchill (Reference Kelly and Churchill2020) for an example), Q-learning would need to output the values of
$10^{87}$
actions, which makes action-value based methods impractical here. This is our main motivation for extending RLaR to the actor-critic method.
4. RL and RLaR for MicroRTS
We apply actor-critic learning to MicroRTS using deep neural networks. The architectures of these networks are described next. Despite the existence of an OpenAI Gym framework (Huang et al., Reference Huang, Ontañón, Bamford and Grela2021) for RL in MicroRTS, we develop our own framework to gain the ability to (a) pass the hidden state to the RLaR agent, and (b) select an opponent of our choice (MicroPhantom for this paper).
4.1. Actor network
The architecture of the actor network,
$\pi_\theta$
, is shown in Figure 1, and is used for all versions of RL studied here. Its input is the learner’s observation at step t,
$\omega_t$
, consisting of the following components
-
Scalar Features: Binary encoding of scalar features, for example, time, score, resources;
-
Own Entities: Sparse encoding of its own units (their types, locations, health and resource);
-
Other Entities: Similar sparse encoding of other visible units either owned by the opponent, or unowned (e.g., harvestable resources);
-
Map: A grid encoding of all visible units with their types.
The actor’s output specifies the learner’s action at step t,
$a_t$
. This is sampled from 3 softmax probability distributions to yield the following:
-
Action Index: For each of up to
$N_E$
(=70 in our experiments) units that the learner owns, one of (
$N_A$
=) 18 indices that encode noop, attack, and 4 directions each of move, harvest, return, and produce; -
Produce Type Index: If the produce action is selected for any of up to
$N_E$
units, the type index (from a set of
$N_T=7$
possible types) of what that unit will produce; -
Attack Location Index: If the attack action is selected for any of up to
$N_E$
units, the target location of the attack from a set of
$N_L\ (=256)$
possible locations.
The softmax layers are also provided with masks that reduce the support of the distributions, by deactivating elements that are invalid. Examples include movement directions that are blocked, harvest directions that do not contain resources, return directions that do not contain any self-base, produce types that are disallowed or require more resources than the agent/unit possesses, attack locations that are invisible or do not contain opponent units, etc. These masks allow the distributions to be learned rapidly despite the large strategy space and are computable from
$\omega_t$
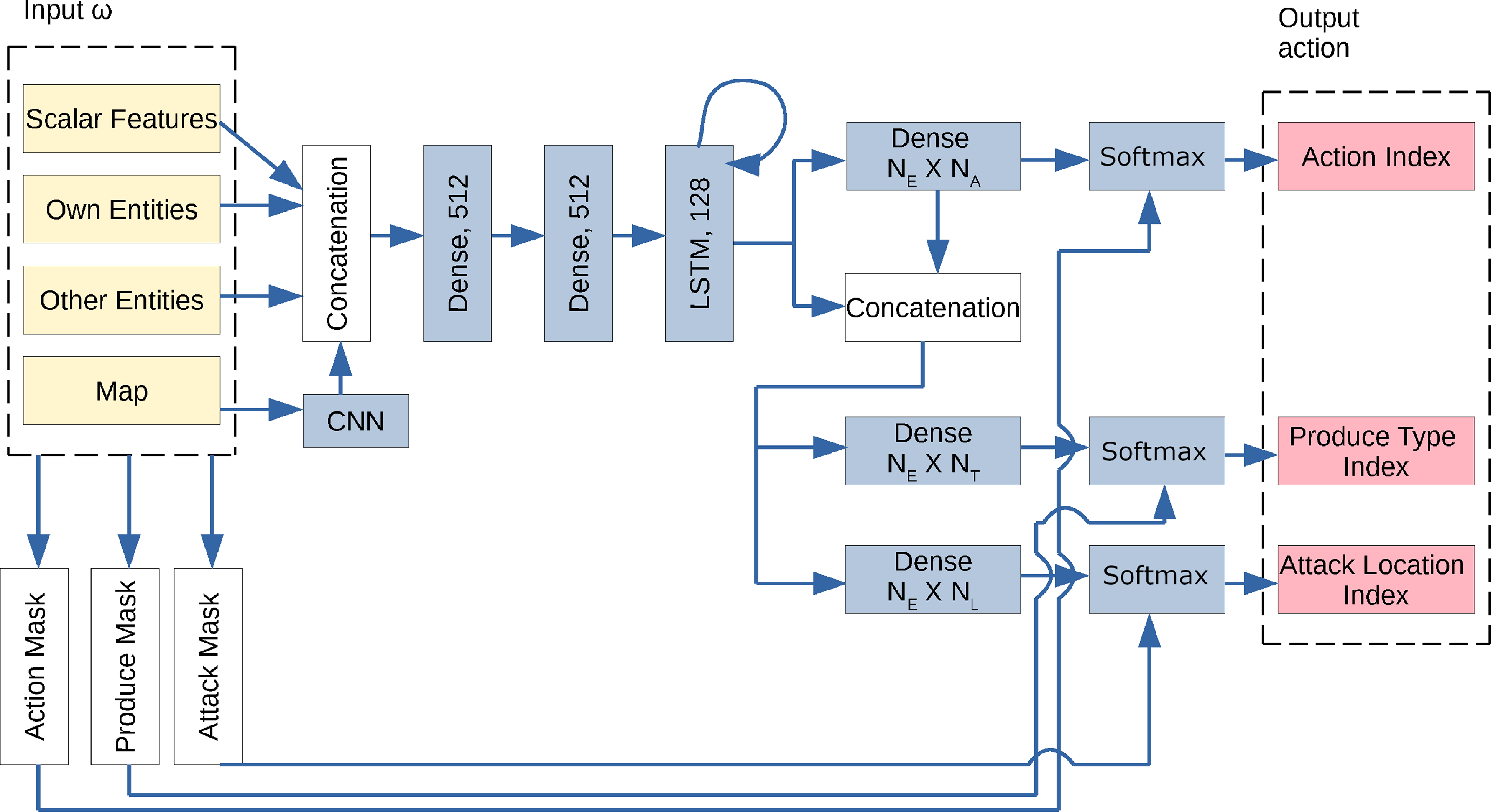
and the information available from the unit_type_table provided at the beginning of the game. Similar invalid action masks are also used in Huang et al., (Reference Huang, Ontañón, Bamford and Grela2021).
The actor network used for all three agent types. Neural network layers are shaded in blue. Inputs (
$\omega$
) are shaded in yellow, and outputs (samplings from softmax layers) are shaded in pink. Here,
$N_E$
is the number of entities owned by any player,
$N_A$
is the number of actions allowed,
$N_T$
is the number of entity-types that can be produced, and
$N_L$
is the number of locations that can be attacked. Masks are computed from inputs to suppress, and thus reduce, the support of softmax distributions. For instance, only the visible locations that contain opponent entities are allowed to be activated for sampling ‘Attack Location Index’.
4.2. Critic network
Let
$s_t=(\omega_{1\,:\,t}, a_{1\,:\,t-1})$
be the observation-action history of the learner, and
$s_t^-=(\omega_{1\,:\,t}^-, a_{1\,:\,t-1}^-)$
be that of the opponent. Normally the opponent’s observations are not available to a learner, hence for baseline RL the critic network learns the function
$V_\phi(s_t)$
as described in Section 3.1. A distinct feature of RLaR is that both the learner and opponent’s observations are available to the learner during the training stage, and accommodated in its critic,
$V^\pi_\phi(s_t, s^-_{t})$
. Following Kraemer and Banerjee (Reference Kraemer and Banerjee2016),
$s^-_t$
can be marginalized out to compute a policy as
\begin{equation}\pi^\ast=\arg\max_{\pi}\sum_{s^-_t}P(s^-_t|s_t,\pi)V^\pi(s_t,s^-_t),\end{equation}
using the learned auxiliary distribution
$P(s^-_t|s_t,\pi)$
. However, the actor-critic framework’s clean separation of the policy from the value function makes this unnecessary. Since only the actor is needed after the training stage, and the critic is discarded, the accommodation of
$s^-_t$
in V is immaterial as long as the actor network is independent of
$s^-_t$
. Thus, for actor-critic training a simpler strategy is to exclude
$s^-_t$
altogether from the actor network, that is,
$\pi_\theta(a|s_t)$
instead of
$\pi_\theta(a|s_t,s^-_t)$
. This obviates the need for marginalization in the actor, and allows us to use the actor network from Section 4.1 for all methods. Notice that
$s^-_t$
still impacts the actor updates since V is needed in Equation (4) via Equation (3). This strategy is followed in AlphaStar (Vinyals et al., Reference Vinyals, Babuschkin, Czarnecki, Mathieu, Dudzik, Chung, Choi, Powell, Ewalds, Georgiev, Oh, Horgan, Kroiss, Danihelka, Huang, Sifre, Cai, Agapiou, Jaderberg and Silver2019), hence we call this approach RLAlpha and include it as a baseline in our experimental study. Both RLAlpha and RLaR use the same critic network architecture, in addition to the same actor network architecture as mentioned in Section 4.1. The main difference between RLaR and RLAlpha is that the former uses a prediction network (explained in Section 4.3) while the latter does not.
The common critic architecture of RLaR and RLAlpha is shown in Figure 2. While the action and produce type indices are converted to one-hot representation as
$N_A,N_T$
are small,
$N_L$
is large and therefore the attack location index is embedded. The critic for baseline RL simply omits
$\omega^-_t$
and
$a^-_t$
in its input, and is not shown separately. In contrast with the standard practice of combining the actor and critic networks to enable shared layers, we separate these networks such that the critics of the RL variants can be built incrementally without touching the actor.
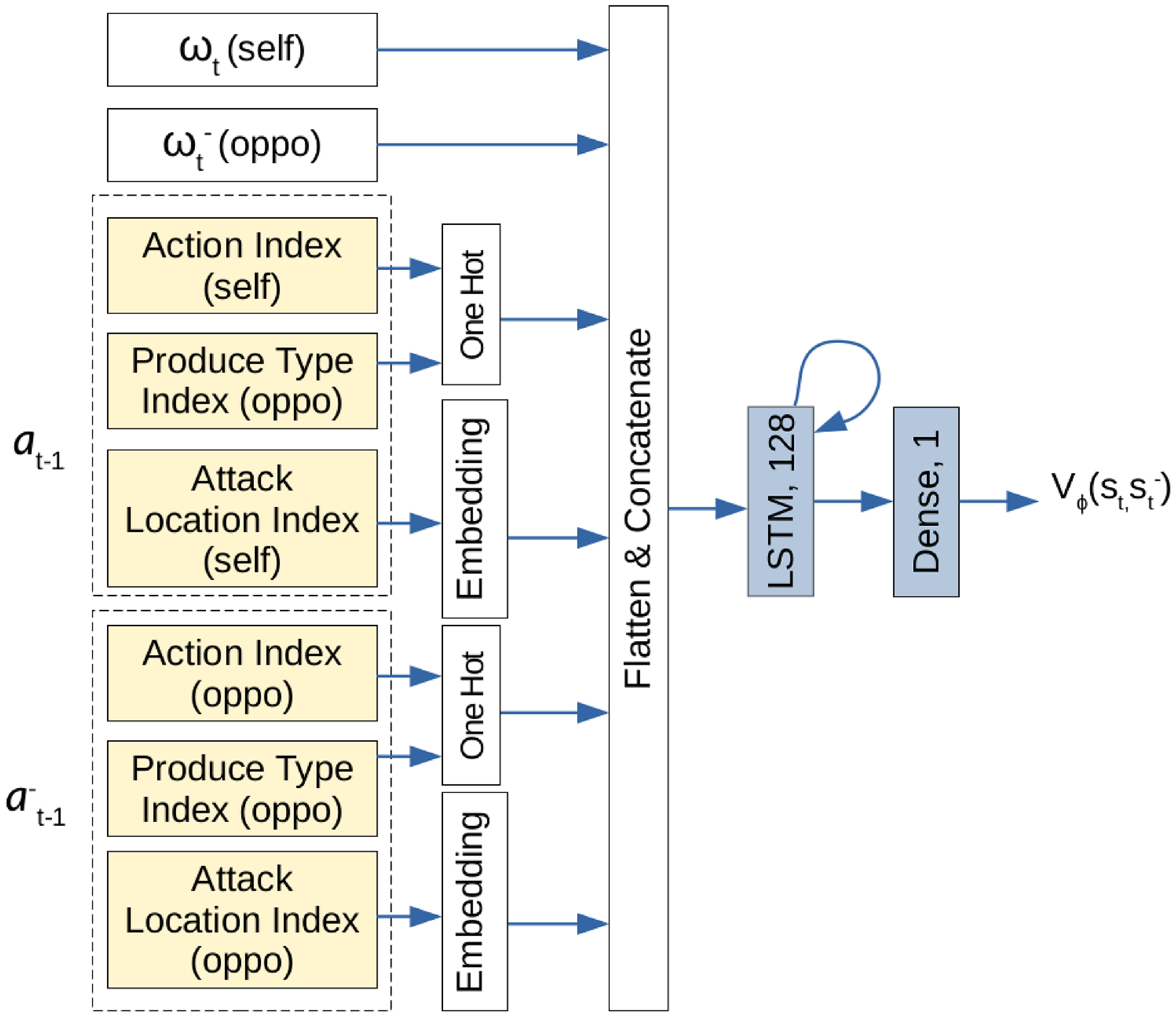
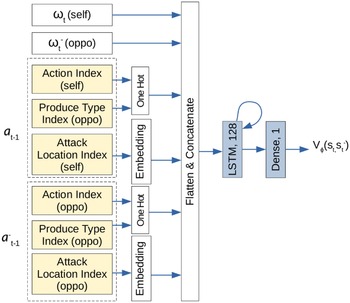
The critic network used for RLAlpha and RLaR agents. Neural network layers are shaded in blue. Inputs are shaded in yellow.
$\omega_t$
and
$\omega^-_t$
contain the same components (from the perspectives of the player and its opponent, respectively) as shown in Figure 1’s input.
4.3. Prediction network for RLaR
Although the auxiliary distribution
$P(s^-_t|s_t,\pi)$
was shown to be unnecessary for actor-critic in Section 4.2, there are still good reasons to learn it. An important feature of RLaR (as explained in Kraemer & Banerjee, Reference Kraemer and Banerjee2016) is a principled incentive for exploration,
\begin{equation}\pi_{explore}=\arg\min_{\pi}-\sum_{s^-_t}P(s^-_t|s_t,\pi)\log P(s^-_t|s_t,\pi),\end{equation}
that seeks to reduce the entropy of the prediction
$P(s^-_t|s_t,\pi)$
. Ideally, if
$P(s^-_t|s_t,\pi)$
is 1 then
$s_t$
is perfectly predictive of
$s^-_t$
under the current policy
$\pi$
, and the RLaR agent is truly independent of
$s^-_t$
. While RLAlpha does not have any incentive for this exploration, we can still endow RLaR with this capability for the following potential benefits:
-
•
$\pi_{explore}$
may reduce noise in actor updates. Consider two situations where the learner observes
$s_t$
in both, but the opponent observes
$s^-_{t,1}$
in one, and
$s^-_{t,2}$
in another. While the critic can distinguish these situations being privy to
$s^-_{t,1}$
and
$s^-_{t,2}$
, the actor cannot. If
$V^\pi_\phi(s_t, s^-_{t,1})\neq V^\pi_\phi(s_t, s^-_{t,2})$
, then the resulting updates will appear as noise to the actor. However, if
$P(s^-_t|s_t,\pi)=1$
then
$(s_t,s^-_t)\equiv s_t$
under
$\pi$
, and the above situation will not materialize. Thus
$\pi_{explore}$
may push the actor toward generating situations where the updates are more stable. From this perspective, another distinction from RLAlpha is that the latter may experience noisier actor updates compared to RLaR. -
• In the context of MicroRTS (and RTS games in general),
$\pi_{explore}$
may encourage the usage of scouts. In the partially observable setting of MicroRTS, a player can observe the set union of what its units can observe depending on their locations. Therefore, with strategically located units (a.k.a scouts), a learner could make
$\omega^-_t\subset\omega_t$
, which would also minimize the entropy of
$P(\omega^-_t|\omega_t,\pi)$
. While scouting may not be a worthwhile goal in and of itself, choosing actions with the knowledge of the opponent’s configuration may be more desirable than without. Specifically, the success of the learned policy may be less dependent on the opponent’s strategy, and more robust against other strategies. Thus, compared to RLAlpha, RLaR will visit states where the learner’s observations are more predictive of the opponent’s state.
Consequently, we seek to minimize the entropy of the distribution
$P(\omega^-_t|\omega_{1\,:\,t},\pi_{1\,:\,t-1})$
, which reflects the objective of Equation (9) more closely than
$P(s^-_t|s_t,\pi)$
in the context of MicroRTS. In particular, the condition
$(\omega_{1\,:\,t},\pi_{1\,:\,t-1})$
subsumes
$(s_t,\pi)$
as the action history embedded in
$s_t$
is sampled from the policy history
$\pi_{1\,:\,t-1}$
. Although MicroRTS allows the opponent’s actions
$a^-_{t-1}$
to be observed partly/wholly as a part of
$\omega_t$
with sufficient proximity, we focus on the prediction of
$\omega^-_t$
alone, rather than
$s^-_t$
in order to restrict the size of the prediction network.
To capture the conditional distribution
$P(\omega^-_t|\omega_{1\,:\,t},\pi_{1\,:\,t-1})$
, we use a probabilistic auto-encoder (shown in Figure 3) similar to Sohn et al. (Reference Sohn, Lee and Yan2015), albeit with an additional objective. In particular, an encoder network learns a latent representation of
$\omega^-_t$
notated by latent variable Z, thus capturing the distribution
$P(Z|\omega^-_t,\omega_{1\,:\,t},\pi_{1\,:\,t-1})$
. A decoder network is then tasked with reconstructing
$\omega^-_t$
given inputs Z and
$\omega_{1\,:\,t},\pi_{1\,:\,t-1}$
, thus inferring the distribution
$P(\omega^-_t|Z,\omega_{1\,:\,t},\pi_{1\,:\,t-1})$
. Unlike Sohn et al. (Reference Sohn, Lee and Yan2015), we do not use this auto-encoder as a generative model; yet we perform standard optimization of the variational evidence lower bound (ELBO) by minimizing the latent and reconstruction losses to update the predictor network, since it allows the latent variables to be distributed as
$P(Z|\omega_{1\,:\,t},\pi_{1\,:\,t-1})$
. Our objective, in addition to the ELBO, is to minimize the entropy of this distribution. In order to serve as the exploration component (Equation 9), the gradients resulting from this entropy loss are only used to update the actor network, not the predictor network itself. The predictor update is solely based on the ELBO.
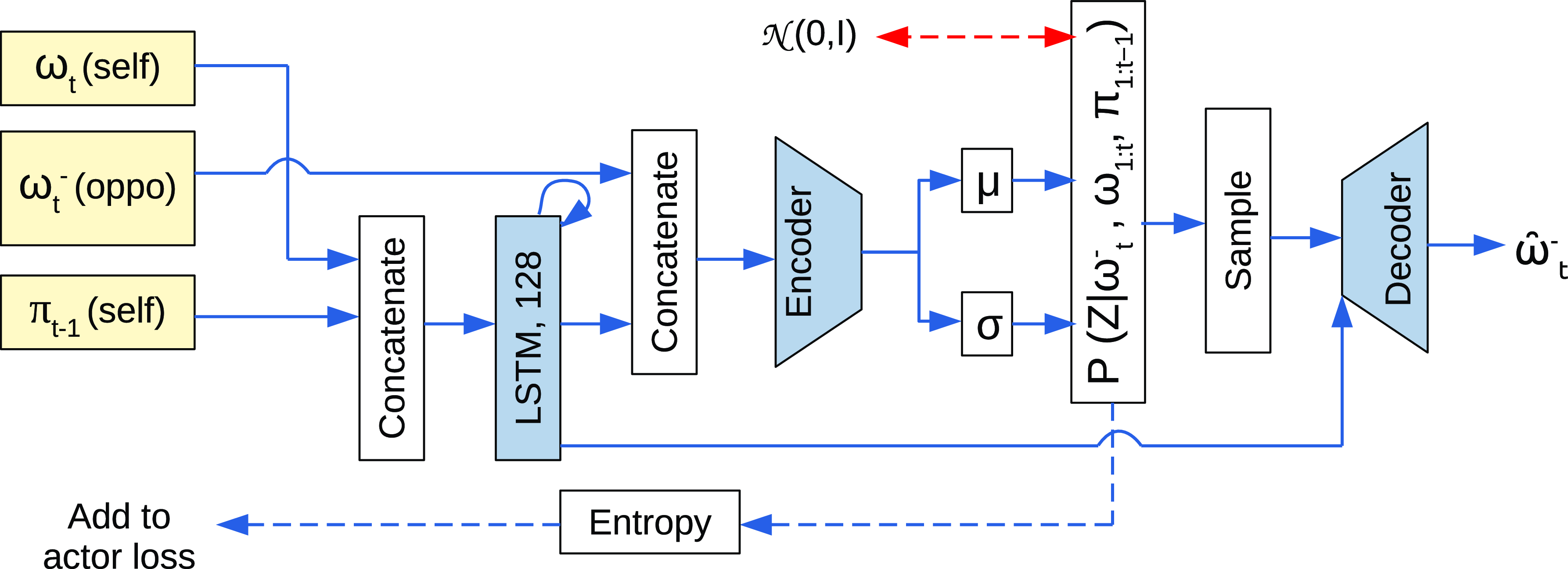
The prediction network used for the RLaR agent. Neural network layers are shaded in blue. Inputs are shaded in yellow. One of the inputs is from the output layer of the policy/actor network (
$\pi_{t-1}$
) shown in Figure 1. This network minimizes 2 standard loss components: latent loss (KL divergence between the captured distribution and standard Gaussians (
${\mathcal{N}}(0,I)$
), shown in red double-headed arrow), and a reconstruction loss measured by the cross entropy between the input
$\omega^-_t$
and predicted
$\hat{\omega}^-_t$
. A third loss function (entropy of the captured conditional distribution) is added to the actor network’s loss and does not participate in training this network.
5. Experimental results
We experiment with the three methods discussed in Section 4, viz., baseline RL, RLAlpha, and RLaR. For baseline RL, we use the advantage actor-critic (A2C) algorithm described in Section 3.1, modified with self-imitation learning (Oh et al., Reference Oh, Guo, Singh and Lee2018), A2C+SIL. Both RLAlpha and RLaR are built on top of A2C+SIL, thus sharing this common baseline. We train each variant in four different maps, shown in Figure 4. We selected these maps to incorporate variety of difficulty. For instance, the map ‘basesWorkers12x12F’ (Figure 4(a)) has the resources (bright green cells) in (relatively) opposite and non-corner locations, compared to other maps. The map ‘FourBasesWorkers12x12’ (Figure 4(c)) contains more initial bases and resources than other maps. Finally, the map ‘LetMeOut’ (Figure 4(d)) has a very different layout than other maps, where the players are walled (dark green cells) off, with doorways initially blocked by resources (although the blue agent had cleared one doorway by the time the screenshot was taken).
The 4 maps used in our experiments. White cells are unobserved, purple cells are observed by both blue and red teams. The learning agents always assume the role of the blue team, but there is no advantage to either role due to initial symmetry. The red team is MicroPhantom.
Games are capped at a maximum of 3000 steps. We use a sparse reward scheme, with 0 reward for any intermediate step, and non-zero rewards only for terminal steps:
$+1000$
Footnote
1
for a win,
$-1000$
for a loss,
$50+score$
for a draw (i.e., when a game does not complete within 3000 steps), where score is the learner’s MicroRTS assigned terminal score that reflects the strength/weakness of its final position in the absence of a clear winner. 50 bonus points are added for drawn games in order avoid 0 returns for the entire trajectory when
$score=0$
. The rest of the parameters are set as follows:
-
•
$\gamma=0.999$
-
•
$\beta=0.005$
-
• Actor learning rate =
$5\times10^{-5}$
-
• Critic learning rate =
$5\times10^{-4}$
The learning curves corresponding to the 4 maps are shown in Figure 5, over a series of 5500 games. Each curve is averaged over 6 independent trials, with half standard deviation bands shown in corresponding colors. The initial policy/actor for all versions were trained by supervised learning from a set of games played between MicroPhantom and MentalSeal. This results in positive initial performance of all variants, as seen in Figures 5(b–d), although the trained initial policy was practically useless in (a). The learning curves demonstrate a superior learning rate for RLaR, and also serve as an ablation for the predictor network as that is the only difference between RLAlpha and RLaR. Also note that a total reward approaching +1000 indicates that the agent has learned to almost always defeat MicroPhantom. Videos of trained RLaR policy against MicroPhantom are posted at https://tinyurl.com/y3xhb9nt.
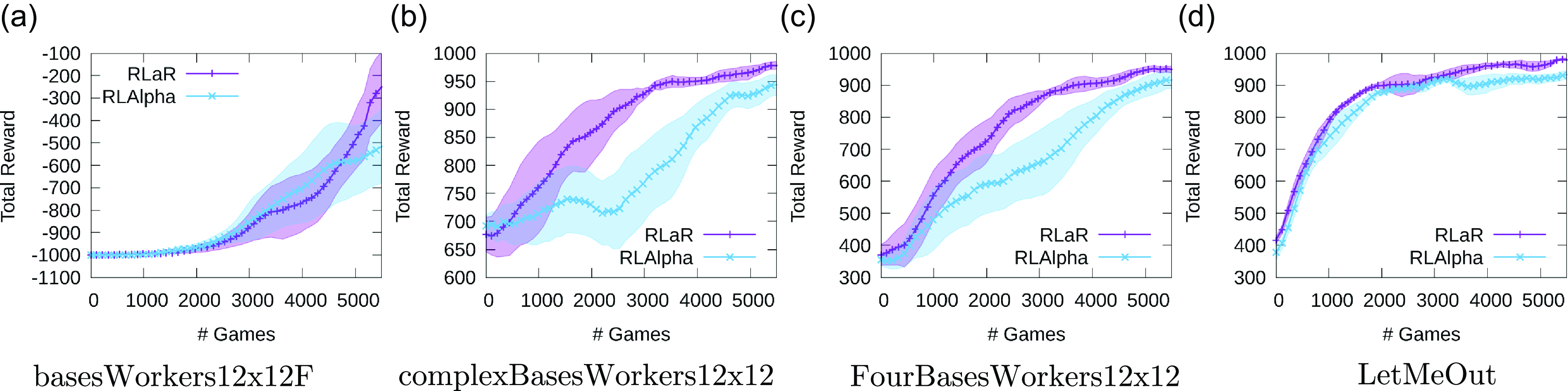
Learning curves of RLAlpha (RLAlpha+A2C+SIL) and RLaR (RLaR+A2C+SIL) against MicroPhantom in 4 maps. Baseline RL (A2C+SIL) is excluded due to poor performance. The terminal reward for win/loss/draw are +1000/–1000/+50. The initial policy/actor was trained by supervised learning from games between MentalSeal and MicroPhantom on large set of maps, but performs poorly in (a).
Baseline RL is not shown in Figure 5 as its performance is poor in comparison with RLAlpha and RLaR. In particular, starting with the trained initial policy, baseline RL essentially unlearns it, dropping the total reward to –1000 (even in maps (b–d)) before improving it again. Essentially, baseline RL is unable to leverage the initial policy at all, requiring more time to learn.
We also evaluate the learning performance using a second measure. We save the learned policies during training at intervals of 100 games, and later run each policy against MicroPhantom for 100 independent trials/games. We show the percentage of wins for the learned policies, averaged over 100 evaluation trials and 6 learning trials in Figure 6. Note that while Figure 5 uses data from every training game and exponential moving averages to achieve smoothness, data is sparse (only available every 100 games) for Figure 6. Due to this lack of data between plot points, the curves in Figure 6 are noticeably less smooth, but they follow roughly the same trends as Figure 5. However, a closer comparison of the trends in the two figures reveals that the difference between RLaR and RLAlpha is less accentuated in Figure 6 not because of the overperformance of RLAlpha but because of the underperformance of RLaR by this measure. This leads us to the following conclusion: in the games that are drawn and discounted in Figure 6, RLaR must be achieving terminal positional advantages relative to MicroPhantom—something that is, in fact, rewarded by the native game score and included in Figure 5—because score can be a large negative number for an inferior terminal position. This observation appears to especially hold in the maps complexBasesWorkers12x12 and FourBasesWorkers12x12.
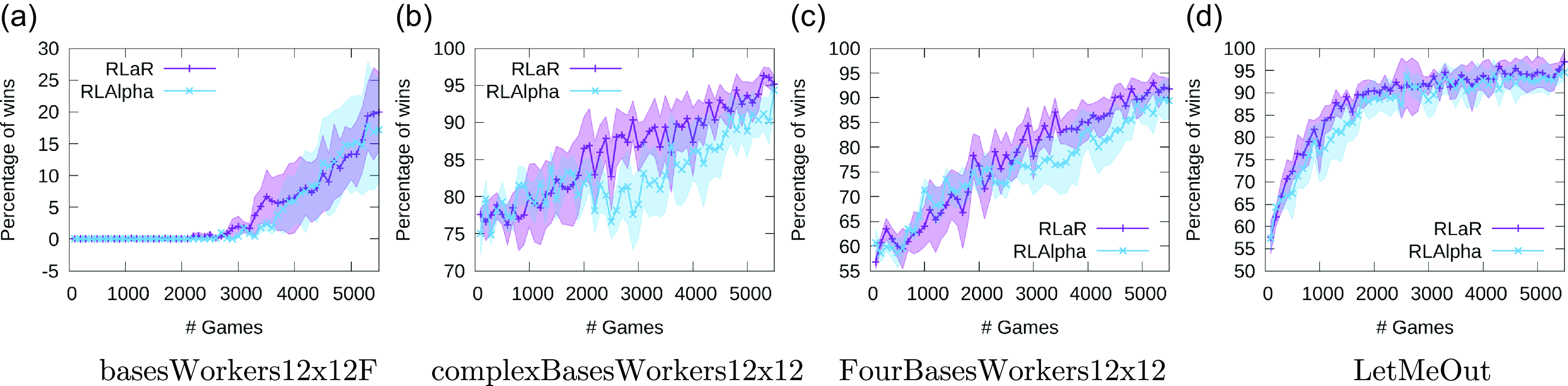
Win percentages of intermediate policies in 4 maps. Policies were saved at intervals of 100 games during training, and evaluated against MicroPhantom later.
As a final part of this experiment, we also show the performance of the learned policy at the end of 5500 games for all three variants in Tables 2, 3 in terms of the two measures used above.
Performance of final/trained policies for 3 variants in 4 maps, in terms of the rewards against MicroPhantom averaged over 100 games and over 6 trials.
Win percentages of final/trained policies for 3 variants in 4 maps, in terms of the percentages of wins (no loss/draw) against MicroPhantom averaged over 100 games and over 6 trials.
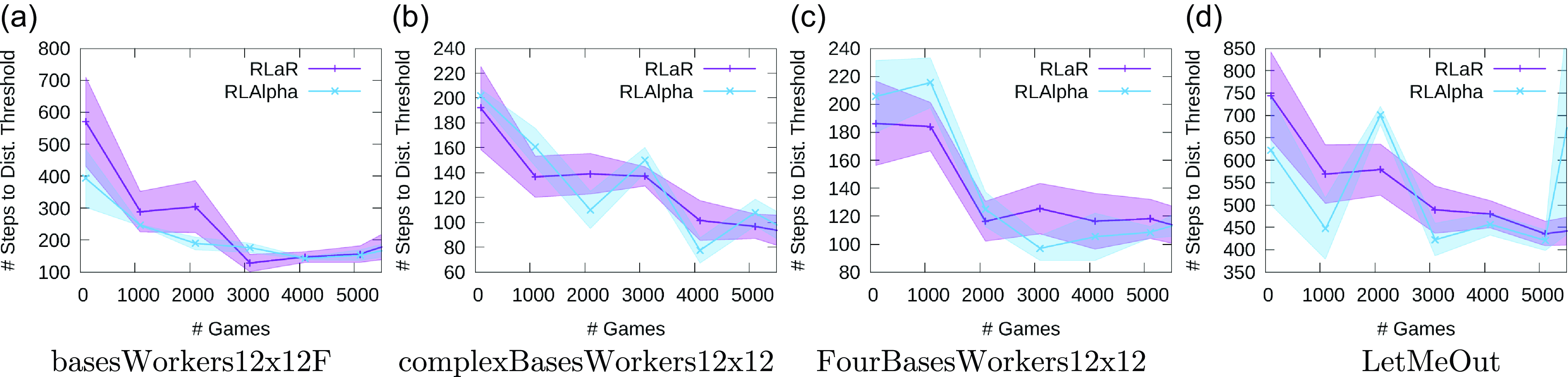
Plots showing the number of steps that the learner needs before at least one of its units gets within a distance threshold of 4.0 of the opponent’s base, thereby bringing it within the radius of the learner’s visibility.
Tables 2, 3 clearly demonstrate the futility of single agent (baseline A2C+SIL) RL in the face of a large strategy space. Although the centralized (i.e., joint) critic of RLAlpha brings it closer to RLaR, Table 2 also demonstrates the scope for further improvement in terms of a principled exploration component that is unique to RLaR.
In order to further evaluate the impact of RLaR’s characteristic exploration, we conduct a second experiment. In this experiment, we note the number of steps in a game that it takes the learner to get close enough to the opponent’s base, that is, for any of its units to get within a distance threshold of the opponent’s base. When there are multiple opponent bases, we take the centroid of their locations. This can be viewed as a rough measure of how quickly the learner deploys spies. The results are shown in Figure 7 for a distance threshold of 4.0–sufficient to bring it within the observable radius. The first observation is that this measure does not correlate accurately with learning performance (Figure 5), as early spying can end in failure while late spying can still end in victory. Neither is it a measure of the effectiveness of spying, as observing the opponent’s base does not mean all of the opponent’s units are also visible. However, another observation from Figure 7 is that while the trend is expected to be decreasing with continued learning, this does not occur reliably with RLAlpha. Particularly in Figure 7(b) and (d), we notice spikes where the learner appears to be regressing in terms of this measure. RLaR, by contrast, achieves a steadier acceleration toward proximity. As proximity is a reliable predictor of the opponent’s observation in MicroRTS, we speculate that this is a direct result of RLaR’s use of predictor-based exploration.
5.1. Robustness
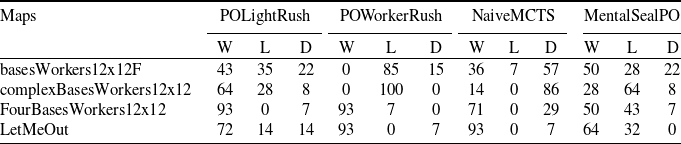
We also evaluate the robustness of the learned policies to other opponents that RLaR was not trained against. Specifically, MicroRTS contains built-in handcoded opponents such as POLightRush, POWorkerRush and NaiceMCTS. As RLaR was not trained directly against MentalSealPO, we select this as the 4th opponent. We select the best of the RLaR policies and pit it against each of these 4 opponents and record the win/loss/draw rates over 100 games, each limited to 3000 steps similar to the training setup. The results are shown in Table 4. We find that RLaR wins more often than it loses against all but POWorkerRush (in basesWorkers12x12F and complexBasesWorkers12x12) and MentalSealPO (in complexBasesWorkers12x12). Especially in FourBasesWorkers12x12 and LetMeOut, RLaR wins by significant margins against POLightRush, POWorkerRush and NaiveMCTS, albeit the margins are much lower against MentalSealPO. The severe losses against POWorkerRush in two environments is consistent with the findings of Huang et al. (Reference Huang, Ontañón, Bamford and Grela2021) who also report their agent struggling most against Droplet bot (based on WorkerRush strategy) even in fully observable setting.
Win(W)/Loss(L)/Draw(D) percentages of the best RLaR policy against 4 scripted opponents in 4 maps over 100 games
6. Conclusion
We have presented a principled formulation of RL as a rehearsal (RLaR) for the first time within the actor-critic framework. We have shown how a key component of RLaR, a prediction function that correlates the opponent’s observations to the learner’s own observations, can be constructed within a deep learning pipeline. Although the formulation is in the context of MicroRTS, it can be easily extended to other RTS games, for example, StarCraft. We have experimentally validated two of the benefits of RLaR compared to a variant that has all the same features as RLaR except the prediction function. Consistent with previous findings on RLaR in smaller strategy spaces, we have shown that RLaR improves learning speed even in a domain with a large strategy space such as MicroRTS. A second experiment has shown that RLaR achieves visibility of the opponent’s base more predictably as learning progresses. We speculate that this might be indirect evidence of noise reduction in actor updates–a second benefit of our approach–and at least partly responsible for improved learning rate of RLaR.
One limitation of this study is that the initial policies were sophisticated to begin with, having been trained on games played between leaderboard programs. Our preliminary experiments (not reported here) suggested a very slow rate of training when starting from randomized initial policies, further compounded by the slowness of MicroRTS games even when run without the GUI. For this reason, in order to conduct RL in a reasonable time frame, we have adopted competent initial policies. Since they were the same for all RL variants studied here, this appears adequate for assessing the relative efficacies of the RL variants. However, it remains unclear how sensitive the performances of RLaR and RLAlpha might be to the quality of the initial policies. A study of such sensitivity could be undertaken in the future. A second limitation is that we have limited the maximum map size (
$16\times 16$
) and number of units produced (
$N_E=70$
) to pre-define the shapes of neural network layers. These limits were set to restrict both the memory footprint of the networks and the training times. It is important to note that these limits do not entail any limitation on the technique of RLaR itself; rather they are limitations on the use of neural networks for RL in general. Huang et al. (Reference Huang, Ontañón, Bamford and Grela2021) discuss ways to accommodate a variable number of units, but these techniques have other limitations—one technique (called ‘unit action simulation’) requires the actor network to be run iteratively over the units thus requiring an internal simulator that slows down training, and the other technique (‘gridnet’) issues potentially many invalid actions. Importantly, they also do not offer any way to accommodate variable map sizes. A third limitation is that we have excluded the opponent’s actions from the prediction network in order to restrict its size. However, this exclusion also means that the predictive power of the opponent’s past actions on its future observations is not leveraged. Once actions are taken into account, the prediction network may explore states where the learner not only observes its opponent’s observations but also its actions, leading to more effective spycraft. This intuition could also be verified in the future.
Reward shaping (Ng et al., Reference Ng, Harada and Russell1999) is a well-established technique in RL where domain/prior knowledge is often used to supplement the reward function, in order to shape and accelerate learning. It is conceivable that a shaping function that rewards a learner for observing more of the opponent’s units and penalizes it for observing less, could achieve similar learning speedup as RLaR in this paper, because that is a known effect of reward shaping. Additionally, it might also achieve similar noise reduction, since the effect of such shaping on the actor in terms of the generated trajectories is likely to be similar. Further experiments can be conducted in the future to evaluate these intuitions. In contrast with this potentially alternative approach, we have relied on a simple (sparse) reward scheme in this paper, and avoided explicit domain-specific reward engineering. More importantly, our approach is more general than reward shaping, as shaping functions can vary from domain to domain, but entropy minimization of the prediction function is a general principle that does not need domain-specific engineering, and can benefit domains well beyond RTS games.
Acknowledgment
We gratefully acknowledge constructive feedback from anonymous reviewers on previous drafts of this manuscript. This work was supported in part by Air Force Research Lab grant FA8750-20-1-0105.
Competing interests
The author(s) declare none.
Open access
