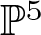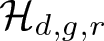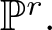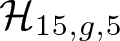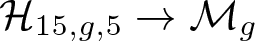1. Introduction
In this article, we study the Hilbert scheme of smooth and non-degenerate curves ![]() $X\subset {\mathbb{P}}^5$ of degree 15.
$X\subset {\mathbb{P}}^5$ of degree 15.
Let ![]() $\mathcal{H}_{d,g,r}$ denote the Hilbert scheme of smooth curves of degree d and genus g in
$\mathcal{H}_{d,g,r}$ denote the Hilbert scheme of smooth curves of degree d and genus g in ![]() ${\mathbb{P}}^r$. We determine the number of irreducible components, their dimensions and study the properties of
${\mathbb{P}}^r$. We determine the number of irreducible components, their dimensions and study the properties of ![]() $\mathcal{H}_{15,g,5}$ such as the gonality of a general element in each component
$\mathcal{H}_{15,g,5}$ such as the gonality of a general element in each component ![]() $\mathcal{H}\subset \mathcal{H}_{15,g,5}$. We also study the natural functorial map
$\mathcal{H}\subset \mathcal{H}_{15,g,5}$. We also study the natural functorial map ![]() $\mu : \mathcal{H} \rightarrow\mathcal{M}_g$.
$\mu : \mathcal{H} \rightarrow\mathcal{M}_g$.
Severi [Reference Severi33] asserted that the Hilbert scheme ![]() $\mathcal{H}_{d,g,r}$ is irreducible for triples
$\mathcal{H}_{d,g,r}$ is irreducible for triples ![]() $(d,g,r)$ in the range
$(d,g,r)$ in the range
(i) ![]() $d\ge g+r~~~~$
$d\ge g+r~~~~$
or in the much wider Brill–Noether range
(ii) ![]() $\rho(d,g,r):=g-(r+1)(g-d+r)\ge 0$.
$\rho(d,g,r):=g-(r+1)(g-d+r)\ge 0$.
In general, determining the irreducibility of a Hilbert scheme is a non-trivial task. The assertion of Severi turns out to be true for ![]() $r=3, 4$ under the condition (i); cf. [Reference Ein16, Reference Ein17]. However, our overall knowledge on
$r=3, 4$ under the condition (i); cf. [Reference Ein16, Reference Ein17]. However, our overall knowledge on ![]() $\mathcal{H}_{d,g,5}$ is not as extensive as those on
$\mathcal{H}_{d,g,5}$ is not as extensive as those on ![]() $\mathcal{H}_{d,g,3}$ or
$\mathcal{H}_{d,g,3}$ or ![]() $\mathcal{H}_{d,g,4}$.
$\mathcal{H}_{d,g,4}$.
In this article, we would like to concentrate on ![]() $\mathcal{H}_{d,g,5}$ when the degree d of the curve in
$\mathcal{H}_{d,g,5}$ when the degree d of the curve in ![]() ${\mathbb{P}}^5$ is relatively low. Specifically, we focus our attention on curves in
${\mathbb{P}}^5$ is relatively low. Specifically, we focus our attention on curves in ![]() ${\mathbb{P}}^5$ of degree d = 15 and determine when
${\mathbb{P}}^5$ of degree d = 15 and determine when ![]() $\mathcal{H}_{15,g,5}$ is irreducible for every possible genus
$\mathcal{H}_{15,g,5}$ is irreducible for every possible genus ![]() $g\le \pi(15,5)=18$. Our results include:
$g\le \pi(15,5)=18$. Our results include:
1.1. Main results
(i)
 $\mathcal{H}_{15,g,5}$ is irreducible unless
$\mathcal{H}_{15,g,5}$ is irreducible unless  $g=13, 14, 16$; propositions 3.2, 3.4, 3.5, 3.6, 6.2 and theorems 4.1, 5.1, and [Reference Ballico and Keem7, theorem 1.1].
$g=13, 14, 16$; propositions 3.2, 3.4, 3.5, 3.6, 6.2 and theorems 4.1, 5.1, and [Reference Ballico and Keem7, theorem 1.1].(ii)
 $\mathcal{H}_{15,g,5}=\emptyset$ for g = 17; proposition 6.1.
$\mathcal{H}_{15,g,5}=\emptyset$ for g = 17; proposition 6.1.(iii) An estimate of the dimension of the image of the forgetful map
 $\mathcal{H}\rightarrow\mathcal{M}_g$ and the gonality of curves in each component
$\mathcal{H}\rightarrow\mathcal{M}_g$ and the gonality of curves in each component  $\mathcal{H}\subset\mathcal{H}_{15,g,5}$.
$\mathcal{H}\subset\mathcal{H}_{15,g,5}$.(iv) A general
 $X \in \mathcal{H}_{15,15,5}$ has exactly one
$X \in \mathcal{H}_{15,15,5}$ has exactly one  $g^2_8$, one base-point-free
$g^2_8$, one base-point-free  $g^1_5$, and three base-point-free
$g^1_5$, and three base-point-free  $g^1_6$’s; theorem 4.5.
$g^1_6$’s; theorem 4.5.
The reducibility of ![]() ${\mathcal{H}}_{15,14,5}$ is a result of another article [Reference Ballico and Keem7], which we listed in §1.1 for a more comprehensive list of results concerning
${\mathcal{H}}_{15,14,5}$ is a result of another article [Reference Ballico and Keem7], which we listed in §1.1 for a more comprehensive list of results concerning ![]() ${\mathcal{H}}_{15,g,5}$. Our main reason for aiming at an extensive study of curves of degree d = 15 in
${\mathcal{H}}_{15,g,5}$. Our main reason for aiming at an extensive study of curves of degree d = 15 in ![]() ${\mathbb{P}}^5$ can be addressed as follows. The case g = 14, which we studied in [Reference Ballico and Keem7], was hard enough requiring several new techniques. If we shift our attention to curves of higher genus, e.g.
${\mathbb{P}}^5$ can be addressed as follows. The case g = 14, which we studied in [Reference Ballico and Keem7], was hard enough requiring several new techniques. If we shift our attention to curves of higher genus, e.g. ![]() $15\le g\le 18=\pi(15,5)$, there appear more interesting cases and components containing fruitful information on the geometry of projective algebraic curves.
$15\le g\le 18=\pi(15,5)$, there appear more interesting cases and components containing fruitful information on the geometry of projective algebraic curves.
Besides using classical methods in analysing curves on smooth and singular rational surfaces, we use the irreducibility of Severi varieties of nodal curves on Hirzebruch surfaces [Reference Tyomkin34] in a key step in theorem 4.1. We also use and prove seemingly well-known facts stating that curves on singular surfaces of low degrees such as singular del Pezzo or cone over an elliptic curve are flat limits of curves on smooth surfaces when we need to rule out the possibility for a family of curves on such singular surfaces constituting a full component; proposition 2.1 and lemma 5.12. We also use the notion of residual schemes in one of our main results; cf. remark 4.3 and theorem 4.5.
Unless the genus g of a smooth curve ![]() $X\subset{\mathbb{P}}^r$ is fairly high with respect to
$X\subset{\mathbb{P}}^r$ is fairly high with respect to ![]() $\deg X$, a curve in a component of
$\deg X$, a curve in a component of ![]() $\mathcal{H}_{d,g,r}$ with the very ample
$\mathcal{H}_{d,g,r}$ with the very ample ![]() $|{\mathcal{O}}_X(1)|$ is by no means contained in a surface of low degrees. However, the residual series
$|{\mathcal{O}}_X(1)|$ is by no means contained in a surface of low degrees. However, the residual series ![]() $|K_X(-1)|$ may induce possibly singular curves of lower degrees which may sit on surfaces of small degrees with better classifications in lower dimensional projective spaces. If this occurs, studying (extrinsic) projective curves defined by the residual series may become easier than directly handling the original curve
$|K_X(-1)|$ may induce possibly singular curves of lower degrees which may sit on surfaces of small degrees with better classifications in lower dimensional projective spaces. If this occurs, studying (extrinsic) projective curves defined by the residual series may become easier than directly handling the original curve ![]() $X\subset{\mathbb{P}}^r$. We use this simple idea several times throughout the article.
$X\subset{\mathbb{P}}^r$. We use this simple idea several times throughout the article.
The organization of this article is as follows. In the next section, we prepare some preliminaries. In §3, we treat curves of genus ![]() $g\le 13$. In §4 and §5, we study curves of genus 15 and 16 and in the final section we finish off by considering curves of genus 17 and 18 and making a small observation regarding larger-than-expected components of Hilbert schemes.
$g\le 13$. In §4 and §5, we study curves of genus 15 and 16 and in the final section we finish off by considering curves of genus 17 and 18 and making a small observation regarding larger-than-expected components of Hilbert schemes.
1.2. Notation and conventions
For notation and conventions, we follow those in [Reference Arbarello, Cornalba, Griffiths and Harris4] and [Reference Arbarello, Cornalba and Griffiths3]; e.g. ![]() $\pi (d,r)$ is the maximal possible arithmetic genus of an irreducible, non-degenerate, and reduced curve of degree d in
$\pi (d,r)$ is the maximal possible arithmetic genus of an irreducible, non-degenerate, and reduced curve of degree d in ![]() ${\mathbb{P}}^r$ which is usually referred to the first Castelnuovo genus bound. We shall refer to irreducible curves
${\mathbb{P}}^r$ which is usually referred to the first Castelnuovo genus bound. We shall refer to irreducible curves ![]() $X\subset {\mathbb{P}}^r$ with the maximal possible genus
$X\subset {\mathbb{P}}^r$ with the maximal possible genus ![]() $g=\pi (d,r)$ as extremal curves.
$g=\pi (d,r)$ as extremal curves. ![]() $\pi_1(d,r)$ is the so-called second Castelnuovo genus bound which is the maximal possible arithmetic genus of an irreducible, non-degenerate, and reduced curve of degree d in
$\pi_1(d,r)$ is the so-called second Castelnuovo genus bound which is the maximal possible arithmetic genus of an irreducible, non-degenerate, and reduced curve of degree d in ![]() ${\mathbb{P}}^r$ not lying on a surface of minimal degree r − 1; cf. [Reference Harris19, p. 99], [Reference Arbarello, Cornalba, Griffiths and Harris4, p. 123].
${\mathbb{P}}^r$ not lying on a surface of minimal degree r − 1; cf. [Reference Harris19, p. 99], [Reference Arbarello, Cornalba, Griffiths and Harris4, p. 123].
Following classical terminology, a linear series of degree d and dimension r on a smooth curve X is denoted by ![]() $g^r_d$. A base-point-free linear series
$g^r_d$. A base-point-free linear series ![]() $g^r_d$ (
$g^r_d$ (![]() $r\ge 2$) on X is called birationally very ample when the morphism
$r\ge 2$) on X is called birationally very ample when the morphism ![]() $X \rightarrow \mathbb{P}^r$ induced by the
$X \rightarrow \mathbb{P}^r$ induced by the ![]() $g^r_d$ is generically one-to-one onto (or is birational to) its image curve. A base-point-free linear series
$g^r_d$ is generically one-to-one onto (or is birational to) its image curve. A base-point-free linear series ![]() $g^r_d$ on X is said to be compounded of an involution (compounded for short) if the morphism induced by the linear series gives rise to a non-trivial covering map
$g^r_d$ on X is said to be compounded of an involution (compounded for short) if the morphism induced by the linear series gives rise to a non-trivial covering map ![]() $X\rightarrow C^{\prime}$ of degree
$X\rightarrow C^{\prime}$ of degree ![]() $k\ge 2$.
$k\ge 2$.
We also recall the following standard set up and notation; cf. [Reference Arbarello, Cornalba and Griffiths3, Ch. 21, § 3, 5, 6, 11, 12] or [Reference Arbarello and Cornalba2, § 1 and § 2]. Let ![]() $\mathcal{M}_g$ be the moduli space of smooth curves of genus g. Given an isomorphism class
$\mathcal{M}_g$ be the moduli space of smooth curves of genus g. Given an isomorphism class ![]() $[C] \in \mathcal{M}_g$ corresponding to a smooth irreducible curve C, there exist a neighbourhood
$[C] \in \mathcal{M}_g$ corresponding to a smooth irreducible curve C, there exist a neighbourhood ![]() $U\subset \mathcal{M}_g$ of
$U\subset \mathcal{M}_g$ of ![]() $[C]$ and a smooth connected variety
$[C]$ and a smooth connected variety ![]() $\mathcal{M}$ which is a finite ramified covering
$\mathcal{M}$ which is a finite ramified covering ![]() $h:\mathcal{M} \rightarrow U$, as well as varieties
$h:\mathcal{M} \rightarrow U$, as well as varieties ![]() $\mathcal{C}$ and
$\mathcal{C}$ and ![]() $\mathcal{G}^r_d$ proper over
$\mathcal{G}^r_d$ proper over ![]() $\mathcal{M}$ with the following properties:
$\mathcal{M}$ with the following properties:
(1)
 $\xi:\mathcal{C}\rightarrow{\mathcal{M}}$ is a universal curve, i.e. for every
$\xi:\mathcal{C}\rightarrow{\mathcal{M}}$ is a universal curve, i.e. for every  $p\in \mathcal{M}$,
$p\in \mathcal{M}$,  $\xi^{-1}(p)$ is a smooth curve of genus g whose isomorphism class is h(p).
$\xi^{-1}(p)$ is a smooth curve of genus g whose isomorphism class is h(p).(2)
 $\mathcal{G}^r_d$ parametrizes the pairs
$\mathcal{G}^r_d$ parametrizes the pairs  $(p, \mathcal{D})$, where
$(p, \mathcal{D})$, where  $\mathcal{D}$ is possibly an incomplete linear series of degree d and dimension r on
$\mathcal{D}$ is possibly an incomplete linear series of degree d and dimension r on  $\xi^{-1}(p)$.
$\xi^{-1}(p)$.(3) For any component
 ${\mathcal{G}}\subset\mathcal{G}^{r}_{d}$,
${\mathcal{G}}\subset\mathcal{G}^{r}_{d}$,
 \begin{equation*}\dim{\mathcal{G}}\ge\lambda(d,g,r):=3g-3+\rho(d,g,r)\end{equation*}
\begin{equation*}\dim{\mathcal{G}}\ge\lambda(d,g,r):=3g-3+\rho(d,g,r)\end{equation*}and for any component
 ${\mathcal{H}}\subset\mathcal{H}_{d,g,r}$,
${\mathcal{H}}\subset\mathcal{H}_{d,g,r}$,
 \begin{equation*}\dim{\mathcal{H}}\ge\mathcal{X}(d,g,r):=\lambda (d,g,r)+\dim{\operatorname{Aut}}({\mathbb{P}}^r).\end{equation*}
\begin{equation*}\dim{\mathcal{H}}\ge\mathcal{X}(d,g,r):=\lambda (d,g,r)+\dim{\operatorname{Aut}}({\mathbb{P}}^r).\end{equation*}
Throughout, we work over an algebraically closed field ![]() ${\mathbb{K}}$ of characteristic zero.
${\mathbb{K}}$ of characteristic zero.
2. Preliminaries and several related results
2.1. Curves on rational surfaces and curves on a cone
We collect results on curves contained in low degree surfaces. We need the following proposition in the final part of the proof of theorem 4.1.
Proposition 2.1. Let ![]() $S\subset {\mathbb{P}}^r$,
$S\subset {\mathbb{P}}^r$, ![]() $3\le r \le 9$, be a normal rational del Pezzo surface of degree r. Fix an integral curve
$3\le r \le 9$, be a normal rational del Pezzo surface of degree r. Fix an integral curve ![]() $C\subset S$. Then C is a flat limit of a family of curves, contained in smooth del Pezzo surfaces of degree r.
$C\subset S$. Then C is a flat limit of a family of curves, contained in smooth del Pezzo surfaces of degree r.
Proof. For ![]() $7\le r\le 9$, the proposition is trivial because S is smooth. The case r = 3 is the main result of [Reference Brevik9]. Assume r > 3. Fix a general
$7\le r\le 9$, the proposition is trivial because S is smooth. The case r = 3 is the main result of [Reference Brevik9]. Assume r > 3. Fix a general ![]() $A\subset S$ such that
$A\subset S$ such that ![]() $\#A=r-3$ and let S ʹ be the blowing-up of S at all points of A. Let
$\#A=r-3$ and let S ʹ be the blowing-up of S at all points of A. Let ![]() $M\subset {\mathbb{P}}^r$ be the
$M\subset {\mathbb{P}}^r$ be the ![]() $(r-4)$-dimensional linear space spanned by A. For a general A, the surface S ʹ has the same number of singularities as S and it is isomorphic to the cubic surface
$(r-4)$-dimensional linear space spanned by A. For a general A, the surface S ʹ has the same number of singularities as S and it is isomorphic to the cubic surface ![]() $S^{\prime\prime}\subset {\mathbb{P}}^3$ which is the closure in
$S^{\prime\prime}\subset {\mathbb{P}}^3$ which is the closure in ![]() ${\mathbb{P}}^3$ of the image of
${\mathbb{P}}^3$ of the image of ![]() $S\setminus A$ by the linear projection
$S\setminus A$ by the linear projection ![]() ${\ell} : {\mathbb{P}}^r\setminus M\rightarrow {\mathbb{P}}^3$; [Reference Dolgachev15, p. 389]. Since A is general we know
${\ell} : {\mathbb{P}}^r\setminus M\rightarrow {\mathbb{P}}^3$; [Reference Dolgachev15, p. 389]. Since A is general we know ![]() $C\cap A=\emptyset$. Since the linear projection
$C\cap A=\emptyset$. Since the linear projection ![]() $\ell$ restricted to C is an embedding,
$\ell$ restricted to C is an embedding, ![]() $C\cong \ell(C)$ and
$C\cong \ell(C)$ and ![]() $\deg(\ell(C)) =\deg (C)$. By [Reference Brevik9], there is a smoothing family of Sʹʹ on which the curve
$\deg(\ell(C)) =\deg (C)$. By [Reference Brevik9], there is a smoothing family of Sʹʹ on which the curve ![]() $\ell(C)$ is a flat limit of a family of curves on nearby smooth cubic surface St;
$\ell(C)$ is a flat limit of a family of curves on nearby smooth cubic surface St; ![]() $t\in T\setminus \{0\}$, T an integral quasi-projective curve,
$t\in T\setminus \{0\}$, T an integral quasi-projective curve, ![]() $0\in T$,
$0\in T$, ![]() $S_0= S^{\prime\prime}$, and St smooth for all
$S_0= S^{\prime\prime}$, and St smooth for all ![]() $t\in T\setminus \{0\}$. Obviously,
$t\in T\setminus \{0\}$. Obviously, ![]() $\ell(C)\cap \ell_i=\emptyset$ for all r − 3 exceptional divisors
$\ell(C)\cap \ell_i=\emptyset$ for all r − 3 exceptional divisors ![]() $\ell _i$ of Sʹʹ associated with the exceptional divisors of the blowing up of the r − 3 points of A. By [Reference Brevik9, proposition 4.7], we may assume that the curve
$\ell _i$ of Sʹʹ associated with the exceptional divisors of the blowing up of the r − 3 points of A. By [Reference Brevik9, proposition 4.7], we may assume that the curve ![]() $\ell (C)$ is a limit of curves
$\ell (C)$ is a limit of curves ![]() $C_t\subset S_t$,
$C_t\subset S_t$, ![]() $t\in T\setminus \{0\}$, which have empty intersection with the r − 3 exceptional divisors
$t\in T\setminus \{0\}$, which have empty intersection with the r − 3 exceptional divisors ![]() $\ell_i(t)$ of St,
$\ell_i(t)$ of St, ![]() $t\in T\setminus \{0\}$ specializing to the r − 3 exceptional divisors
$t\in T\setminus \{0\}$ specializing to the r − 3 exceptional divisors ![]() $\ell _i$ of Sʹʹ. For
$\ell _i$ of Sʹʹ. For ![]() $t\in T\setminus \{0\}$, let
$t\in T\setminus \{0\}$, let ![]() $\tilde{S}_t$ the surface obtained from St by blowing down the r − 3 divisors
$\tilde{S}_t$ the surface obtained from St by blowing down the r − 3 divisors ![]() $\ell_i(t)$. Each surface
$\ell_i(t)$. Each surface ![]() $\tilde{S}_t$ is a smooth del Pezzo surface in
$\tilde{S}_t$ is a smooth del Pezzo surface in ![]() ${\mathbb{P}}^r$. Since
${\mathbb{P}}^r$. Since ![]() $C_t\cap \ell_i(t)=\emptyset$, each curve Ct is isomorphic to a curve
$C_t\cap \ell_i(t)=\emptyset$, each curve Ct is isomorphic to a curve ![]() $\tilde{C}_t\subset \tilde{S}_t$. The flat family over T gives rise to a flat family of smooth del Pezzo surfaces
$\tilde{C}_t\subset \tilde{S}_t$. The flat family over T gives rise to a flat family of smooth del Pezzo surfaces ![]() $\tilde{S}_t$,
$\tilde{S}_t$, ![]() $t\in T\setminus \{0\}$ with S as its flat limit together with a flat family curves
$t\in T\setminus \{0\}$ with S as its flat limit together with a flat family curves ![]() $\tilde{C}_t$,
$\tilde{C}_t$, ![]() $t\in T\setminus \{0\}$ with C as its flat limit.
$t\in T\setminus \{0\}$ with C as its flat limit.
When we deal with curves on a cone in ![]() ${\mathbb{P}}^r$ (usually
${\mathbb{P}}^r$ (usually ![]() $r=4,5$) over a rational normal curve, we use the following elementary facts in several places of this article; in the proofs of proposition 3.2, theorems 4.1, 5.1, and Proposition 6.2. We include these facts mainly for fixing notation.
$r=4,5$) over a rational normal curve, we use the following elementary facts in several places of this article; in the proofs of proposition 3.2, theorems 4.1, 5.1, and Proposition 6.2. We include these facts mainly for fixing notation.
(a) Let
 $S\subset{\mathbb{P}}^r$ (
$S\subset{\mathbb{P}}^r$ ( $r\ge 3$) be a cone over a rational normal curve
$r\ge 3$) be a cone over a rational normal curve  $R\subset H\cong{\mathbb{P}}^{r-1}$ with vertex outside H. Recall that S is the image of the birational morphism
$R\subset H\cong{\mathbb{P}}^{r-1}$ with vertex outside H. Recall that S is the image of the birational morphism  ${\mathbb{F}}_{r-1}=\mathbb{P}(\mathcal{O}_{{\mathbb{P}}^1}\oplus\mathcal{O}_{{\mathbb{P}}^1}(r-1))\rightarrow S\subset{\mathbb{P}}^r$ induced by
${\mathbb{F}}_{r-1}=\mathbb{P}(\mathcal{O}_{{\mathbb{P}}^1}\oplus\mathcal{O}_{{\mathbb{P}}^1}(r-1))\rightarrow S\subset{\mathbb{P}}^r$ induced by  $|h+(r-1)f|$, where
$|h+(r-1)f|$, where  $h^2=-(r-1)$ and f is a fibre of
$h^2=-(r-1)$ and f is a fibre of  ${\mathbb{F}}_{r-1}\rightarrow{\mathbb{P}}^1$. Let
${\mathbb{F}}_{r-1}\rightarrow{\mathbb{P}}^1$. Let  $C\subset S$ be an integral curve of degree d, with the strict transformation
$C\subset S$ be an integral curve of degree d, with the strict transformation  $\widetilde{C}$ of C under
$\widetilde{C}$ of C under  $\mathbb{F}_{r-1}\rightarrow S$. Setting
$\mathbb{F}_{r-1}\rightarrow S$. Setting  $k=\widetilde{C}\cdot f$, we have
$k=\widetilde{C}\cdot f$, we have  $\widetilde{C}\equiv kh+df$ and
(1)
$\widetilde{C}\equiv kh+df$ and
(1) \begin{equation}
0\le \widetilde{C}\cdot h=(kh+df)\cdot h=d-(r-1)k=m
\end{equation}
\begin{equation}
0\le \widetilde{C}\cdot h=(kh+df)\cdot h=d-(r-1)k=m
\end{equation}where m is the multiplicity of C at the vertex of S.
(b) In the case (a), there is no smooth
 $C\subset S\subset{\mathbb{P}}^5$ with
$C\subset S\subset{\mathbb{P}}^5$ with  $\deg C=15$ by (1); i.e. there is no integer k such that
$\deg C=15$ by (1); i.e. there is no integer k such that  $d=15=m+4k$ with
$d=15=m+4k$ with  $m\in\{0,1\}$. If
$m\in\{0,1\}$. If  $S\subset{\mathbb{P}}^5$ is a Veronese surface, there is no irreducible
$S\subset{\mathbb{P}}^5$ is a Veronese surface, there is no irreducible  $C\subset S$ with odd
$C\subset S$ with odd  $\deg C$.
$\deg C$.(c) Therefore, we may assume that a quartic surface
 $S\subset{\mathbb{P}}^5$ containing a smooth curve of degree d = 15 is a rational normal scroll.
$S\subset{\mathbb{P}}^5$ containing a smooth curve of degree d = 15 is a rational normal scroll.(d) Let
 $S\subset{\mathbb{P}}^r$ be a rational normal surface scroll. For
$S\subset{\mathbb{P}}^r$ be a rational normal surface scroll. For  $X\in|aH+bL|$—where H (resp. L) is the class of a hyperplane section (resp. the class a line of the ruling)—we have
(2)
$X\in|aH+bL|$—where H (resp. L) is the class of a hyperplane section (resp. the class a line of the ruling)—we have
(2) \begin{equation}
\deg X=(r-1)a+b, ~
p_a(X)=\tbinom{a-1}{2}(r-1)+(r-2+b)(a-1)
\end{equation}(3)
\begin{equation}
\deg X=(r-1)a+b, ~
p_a(X)=\tbinom{a-1}{2}(r-1)+(r-2+b)(a-1)
\end{equation}(3) \begin{equation}
\dim|aH+bL|=\frac{a \left(a +1\right) (r-1)}{2}+\left(a +1\right) \left(b +1\right)-1
\end{equation}(4)
\begin{equation}
\dim|aH+bL|=\frac{a \left(a +1\right) (r-1)}{2}+\left(a +1\right) \left(b +1\right)-1
\end{equation}(4) \begin{equation}\dim\mathcal{S}(r)= (r+3)(r-1)-3 \end{equation}
\begin{equation}\dim\mathcal{S}(r)= (r+3)(r-1)-3 \end{equation}where
 $\mathcal{S}(r)$ is the irreducible family of rational normal surface scrolls in
$\mathcal{S}(r)$ is the irreducible family of rational normal surface scrolls in  ${\mathbb{P}}^r$; [Reference Harris19, p. 91].
${\mathbb{P}}^r$; [Reference Harris19, p. 91].
2.2. Some remarks on moduli maps
Let ![]() $\mu: \mathcal{H}_{15,g,5}\rightarrow {\mathcal{M}}_g$ denote the natural functorial map—which we call the moduli map—sending
$\mu: \mathcal{H}_{15,g,5}\rightarrow {\mathcal{M}}_g$ denote the natural functorial map—which we call the moduli map—sending ![]() $X\in\mathcal{H}_{15,g,5}$ to its isomorphism class
$X\in\mathcal{H}_{15,g,5}$ to its isomorphism class ![]() $\mu (X)\in\mathcal{M}_g$. In the last two sections, we study
$\mu (X)\in\mathcal{M}_g$. In the last two sections, we study ![]() $\mathcal{H}_{15,g,5}$ in some detail. For example, we use the following for the dimension estimate of the image of the moduli map
$\mathcal{H}_{15,g,5}$ in some detail. For example, we use the following for the dimension estimate of the image of the moduli map ![]() $\mathcal{H}_{15,18,5}\rightarrow \mathcal{M}_{18}$; proposition 6.5.
$\mathcal{H}_{15,18,5}\rightarrow \mathcal{M}_{18}$; proposition 6.5.
Proposition 2.3. Let ![]() $Q\subset{\mathbb{P}}^3$ be a smooth quadric surface. Fix integers
$Q\subset{\mathbb{P}}^3$ be a smooth quadric surface. Fix integers ![]() $3\le a \lt b\le 2a-1$ and a smooth
$3\le a \lt b\le 2a-1$ and a smooth ![]() $X\in |{\mathcal{O}}_Q(a,b)|$. Then X is a-gonal with a unique
$X\in |{\mathcal{O}}_Q(a,b)|$. Then X is a-gonal with a unique ![]() $g^1_a$, no base-point-free
$g^1_a$, no base-point-free ![]() $g^1_c$ for
$g^1_c$ for ![]() $a \lt c \lt b$ and a unique base-point-free
$a \lt c \lt b$ and a unique base-point-free ![]() $g^1_b$, the pencil induced by
$g^1_b$, the pencil induced by ![]() $|{\mathcal{O}}_Q(1,0)|$.
$|{\mathcal{O}}_Q(1,0)|$.
Proof. By [Reference Martens28, corollary 1], X is a-gonal with a unique pencil ![]() $g^1_a$ induced by the pencil
$g^1_a$ induced by the pencil ![]() $|{\mathcal{O}}_Q(0,1)|$. By [Reference Paxia, Raciti and Ragusa32, theorem 2.1], there is no base-point-free
$|{\mathcal{O}}_Q(0,1)|$. By [Reference Paxia, Raciti and Ragusa32, theorem 2.1], there is no base-point-free ![]() $g^1_c$ with
$g^1_c$ with ![]() $a \lt c \lt b$. Take any
$a \lt c \lt b$. Take any ![]() $g^1_b$ and take a general
$g^1_b$ and take a general ![]() $A\in g^1_b$. Since X has no base-point-free
$A\in g^1_b$. Since X has no base-point-free ![]() $g^1_{b-1}$ (or if
$g^1_{b-1}$ (or if ![]() $b=a+1$ a unique
$b=a+1$ a unique ![]() $g^1_a$), the linear series
$g^1_a$), the linear series ![]() $g^1_b$ is complete. By adjunction, we have
$g^1_b$ is complete. By adjunction, we have ![]() $h^1(Q,{\mathcal{I}}_A(a-2,b-2)) \gt 0$. To prove the lemma, it is sufficient to find
$h^1(Q,{\mathcal{I}}_A(a-2,b-2)) \gt 0$. To prove the lemma, it is sufficient to find ![]() $R\in |{\mathcal{O}}_Q(1,0)|$ containing A.
$R\in |{\mathcal{O}}_Q(1,0)|$ containing A.
Set ![]() $A_0:= A$. Take any
$A_0:= A$. Take any ![]() $L_1\in |{\mathcal{O}}_Q(0,1)|$ such that
$L_1\in |{\mathcal{O}}_Q(0,1)|$ such that ![]() $e_1:= \#(L_1\cap A_0)$ is maximal and set
$e_1:= \#(L_1\cap A_0)$ is maximal and set ![]() $A_1:= A_0\setminus A_0\cap L_1$. Take any
$A_1:= A_0\setminus A_0\cap L_1$. Take any ![]() $L_2\in |{\mathcal{O}}_Q(0,1)|$ such that
$L_2\in |{\mathcal{O}}_Q(0,1)|$ such that ![]() $e_2:= \#(L_2\cap A_1)$ is maximal and set
$e_2:= \#(L_2\cap A_1)$ is maximal and set ![]() $A_2:= A_1\setminus A_1\cap L_2$. We define recursively the sets
$A_2:= A_1\setminus A_1\cap L_2$. We define recursively the sets ![]() $A_3,\ldots,A_b$, the elements
$A_3,\ldots,A_b$, the elements ![]() $L_3,\ldots ,L_b\in |{\mathcal{O}}_Q(0,1)|$, and the integers
$L_3,\ldots ,L_b\in |{\mathcal{O}}_Q(0,1)|$, and the integers ![]() $e_3,\ldots ,e_b$ with
$e_3,\ldots ,e_b$ with ![]() $e_i:= \#(A_{i-1}\cap L_i)$ maximal and
$e_i:= \#(A_{i-1}\cap L_i)$ maximal and ![]() $A_i:= A_{i-1}\setminus A_{i-1}\cap L_i$. Since at each step we require the maximality of the integer i and
$A_i:= A_{i-1}\setminus A_{i-1}\cap L_i$. Since at each step we require the maximality of the integer i and ![]() $A_{i-1}\supseteq A_i$, we have
$A_{i-1}\supseteq A_i$, we have ![]() $e_i\ge e_{i+1}$ for all
$e_i\ge e_{i+1}$ for all ![]() $1\le i\le b-1$. Note that if
$1\le i\le b-1$. Note that if ![]() $e_i=0$, then
$e_i=0$, then ![]() $A_{i-1}=\emptyset$ and
$A_{i-1}=\emptyset$ and ![]() $A_j=\emptyset$ for all
$A_j=\emptyset$ for all ![]() $j \gt i-1$ with
$j \gt i-1$ with ![]() $j\le b$. Thus
$j\le b$. Thus ![]() $A_b=\emptyset$.
$A_b=\emptyset$.
Let c be the first integer such that ![]() $\#A_c\le 2$. We saw that
$\#A_c\le 2$. We saw that ![]() $c\le b-2$ and
$c\le b-2$ and ![]() $c=b-2$ if and only if
$c=b-2$ if and only if ![]() $e_1=1$. Set
$e_1=1$. Set ![]() $T:= L_1\cup \cdots \cup L_c\in |{\mathcal{O}}_Q(0,c)|$. Consider the exact sequence
$T:= L_1\cup \cdots \cup L_c\in |{\mathcal{O}}_Q(0,c)|$. Consider the exact sequence
First assume ![]() $e_1\ge 2$ and hence
$e_1\ge 2$ and hence ![]() $c\le b-3$. Since
$c\le b-3$. Since ![]() ${\mathcal{O}}_Q(a-2,b-2-c)$ is very ample and
${\mathcal{O}}_Q(a-2,b-2-c)$ is very ample and ![]() $\#A_c\le 2$, we have
$\#A_c\le 2$, we have ![]() $h^1(Q,{\mathcal{I}}_{A_c}(a-2,b-2-c))=0$. Thus, the long cohomology exact sequence of (5) gives
$h^1(Q,{\mathcal{I}}_{A_c}(a-2,b-2-c))=0$. Thus, the long cohomology exact sequence of (5) gives ![]() $h^1(T,{\mathcal{I}}_{A\cap T}(a-2,b-2)) \gt 0$. The set T has c connected components,
$h^1(T,{\mathcal{I}}_{A\cap T}(a-2,b-2)) \gt 0$. The set T has c connected components, ![]() $L_1,\dots ,L_c$, with
$L_1,\dots ,L_c$, with ![]() $L_i\cong {\mathbb{P}}^1$. Since
$L_i\cong {\mathbb{P}}^1$. Since  $
\displaystyle{h^1(T,{\mathcal{I}}_{A\cap T,T}(a-2,b-2))= \sum_{i=1}^{c} h^1(L_i,{\mathcal{I}}_{A\cap T,T}(a-2,b-2)_{|L_i}) \gt 0,}
$ we get
$
\displaystyle{h^1(T,{\mathcal{I}}_{A\cap T,T}(a-2,b-2))= \sum_{i=1}^{c} h^1(L_i,{\mathcal{I}}_{A\cap T,T}(a-2,b-2)_{|L_i}) \gt 0,}
$ we get  $h^1(L_i,{\mathcal{I}}_{A\cap T,T}(a-2,b-2)_{|L_i}) \gt 0$ and
$h^1(L_i,{\mathcal{I}}_{A\cap T,T}(a-2,b-2)_{|L_i}) \gt 0$ and ![]() $e_i\ge a$ for some i; by
$e_i\ge a$ for some i; by ![]() $\deg {\mathcal{O}}_{L_i}(a-2,b-2) =a-2$ for all i, we have
$\deg {\mathcal{O}}_{L_i}(a-2,b-2) =a-2$ for all i, we have  $h^1(L_i,{\mathcal{I}}_{A\cap T,T}(a-2,b-2)_{|L_i})=0$ if
$h^1(L_i,{\mathcal{I}}_{A\cap T,T}(a-2,b-2)_{|L_i})=0$ if ![]() $e_i\le a-1$ for all i. But then A contains a subset A ʹ such that
$e_i\le a-1$ for all i. But then A contains a subset A ʹ such that ![]() $\#A^{\prime}=a$,
$\#A^{\prime}=a$, ![]() $A^{\prime}\subset L_i$ and
$A^{\prime}\subset L_i$ and ![]() $|A^{\prime}|$ is the
$|A^{\prime}|$ is the ![]() $g^1_a$ on X. Since the
$g^1_a$ on X. Since the ![]() $g^1_b$ is base-point-free and complete, we get a contradiction.
$g^1_b$ is base-point-free and complete, we get a contradiction.
Now assume ![]() $e_1=1$. Thus
$e_1=1$. Thus ![]() $c=b-2$ and
$c=b-2$ and ![]() $\#(A\cap L)\le 1$ for all
$\#(A\cap L)\le 1$ for all ![]() $L\in |{\mathcal{O}}_Q(0,1)|$. Thus
$L\in |{\mathcal{O}}_Q(0,1)|$. Thus ![]() $h^1(T,{\mathcal{I}}_{T\cap A, T}(a-2,b-2)) =0$. Hence the long cohomology exact sequence of (5) gives
$h^1(T,{\mathcal{I}}_{T\cap A, T}(a-2,b-2)) =0$. Hence the long cohomology exact sequence of (5) gives ![]() $h^1(Q,{\mathcal{I}}_{A_c}(a-2,0)) \gt 0$, i.e. two points in
$h^1(Q,{\mathcal{I}}_{A_c}(a-2,0)) \gt 0$, i.e. two points in ![]() $A_c=\{p,s\}$ fail to impose independent conditions on
$A_c=\{p,s\}$ fail to impose independent conditions on ![]() $|{\mathcal{O}}_Q(a-2,0)|$. Therefore, there is
$|{\mathcal{O}}_Q(a-2,0)|$. Therefore, there is ![]() $R\in |{\mathcal{O}}_Q(1,0)|$ such that
$R\in |{\mathcal{O}}_Q(1,0)|$ such that ![]() $A_c\subset R$. Fix any
$A_c\subset R$. Fix any ![]() $q\in A\setminus A_c$. Since
$q\in A\setminus A_c$. Since ![]() $\#(A\cap L)\le 1$ for all
$\#(A\cap L)\le 1$ for all ![]() $L\in |{\mathcal{O}}_Q(0,1)|$, there are
$L\in |{\mathcal{O}}_Q(0,1)|$, there are ![]() $D_1,\ldots,D_{b-2}\in |{\mathcal{O}}_Q(0,1)|$ such that
$D_1,\ldots,D_{b-2}\in |{\mathcal{O}}_Q(0,1)|$ such that ![]() $T^{\prime}:= D_1\cup \cdots \cup D_{b-2}$ contains
$T^{\prime}:= D_1\cup \cdots \cup D_{b-2}$ contains ![]() $A\setminus \{p,q\}$. Using T ʹ instead of T, we get the existence of
$A\setminus \{p,q\}$. Using T ʹ instead of T, we get the existence of ![]() $R^{\prime}\in |{\mathcal{O}}_Q(1,0)|$ such that
$R^{\prime}\in |{\mathcal{O}}_Q(1,0)|$ such that ![]() $\{p,q\}\subset R^{\prime}$. Since R is the unique element of
$\{p,q\}\subset R^{\prime}$. Since R is the unique element of ![]() $|{\mathcal{O}}_Q(1,0)|$ containing p,
$|{\mathcal{O}}_Q(1,0)|$ containing p, ![]() $R^{\prime}=R$. Thus
$R^{\prime}=R$. Thus ![]() $A\subset R$.
$A\subset R$.
The following is a consequence of proposition 2.3 which we use in §6.1; proposition 6.5.
Corollary 2.4 Fix integers ![]() $2a-1\ge b \gt a\ge 3$ and smooth
$2a-1\ge b \gt a\ge 3$ and smooth  $X,\tilde{X}\in |{\mathcal{O}}_Q(a,b)|$. If
$X,\tilde{X}\in |{\mathcal{O}}_Q(a,b)|$. If ![]() $\tilde{X}\cong X$ as abstract curves, then there is
$\tilde{X}\cong X$ as abstract curves, then there is ![]() $v\in {\operatorname{Aut}}({\mathbb{P}}^1)\times {\operatorname{Aut}}({\mathbb{P}}^1)$ such that
$v\in {\operatorname{Aut}}({\mathbb{P}}^1)\times {\operatorname{Aut}}({\mathbb{P}}^1)$ such that ![]() $v({X})={\tilde{X}}$.
$v({X})={\tilde{X}}$.
Proof. Take any isomorphism ![]() $\tilde{X}\stackrel{u}{\cong}{X}$. The line bundles
$\tilde{X}\stackrel{u}{\cong}{X}$. The line bundles ![]() $R_1:= u^\ast ({\mathcal{O}}_X(0,1))$ and
$R_1:= u^\ast ({\mathcal{O}}_X(0,1))$ and ![]() $R_2:= u^\ast ({\mathcal{O}}_X(1,0))$ are the unique base-point-free line bundles on
$R_2:= u^\ast ({\mathcal{O}}_X(1,0))$ are the unique base-point-free line bundles on ![]() $\tilde{X}$ of degrees a and b, respectively by proposition 2.3, and hence
$\tilde{X}$ of degrees a and b, respectively by proposition 2.3, and hence ![]() $R_1= {\mathcal{O}}_{\tilde{X}}(0,1)$ and
$R_1= {\mathcal{O}}_{\tilde{X}}(0,1)$ and ![]() $R_2 ={\mathcal{O}}_{\tilde{X}}(1,0)$. Thus, u induces isomorphisms
$R_2 ={\mathcal{O}}_{\tilde{X}}(1,0)$. Thus, u induces isomorphisms ![]() $|{\mathcal{O}}_{{X}}(1,0)|={\mathbb{P}}^1\rightarrow {\mathbb{P}}^1=|{\mathcal{O}}_{\tilde{X}}(1,0)|$ and
$|{\mathcal{O}}_{{X}}(1,0)|={\mathbb{P}}^1\rightarrow {\mathbb{P}}^1=|{\mathcal{O}}_{\tilde{X}}(1,0)|$ and ![]() $|{\mathcal{O}}_{{X}}(0,1)| \rightarrow |{\mathcal{O}}_{\tilde{X}}(0,1)|$ and the corresponding pair in
$|{\mathcal{O}}_{{X}}(0,1)| \rightarrow |{\mathcal{O}}_{\tilde{X}}(0,1)|$ and the corresponding pair in ![]() ${\operatorname{Aut}}({\mathbb{P}}^1)\times {\operatorname{Aut}}({\mathbb{P}}^1)$ induces v.
${\operatorname{Aut}}({\mathbb{P}}^1)\times {\operatorname{Aut}}({\mathbb{P}}^1)$ induces v.
We use the following remark, similar to corollary 2.4, for the study of the moduli map ![]() $\mu: \mathcal{H}_{15,16,5}\rightarrow {\mathcal{M}}_{16}$ in §5.2; propositions 5.17 and 5.18.
$\mu: \mathcal{H}_{15,16,5}\rightarrow {\mathcal{M}}_{16}$ in §5.2; propositions 5.17 and 5.18.
Remark 2.5. Let S and ![]() $\tilde{S}$ be rational normal surface scrolls in
$\tilde{S}$ be rational normal surface scrolls in ![]() ${\mathbb{P}}^5$. If
${\mathbb{P}}^5$. If ![]() ${S}\stackrel{u}{\cong} \tilde{S}$ as abstract varieties, then they are projectively equivalent. To see this, assume
${S}\stackrel{u}{\cong} \tilde{S}$ as abstract varieties, then they are projectively equivalent. To see this, assume ![]() $S\cong\widetilde{S}\cong {\mathbb{F}}_2$. Note that the only very ample line bundle on
$S\cong\widetilde{S}\cong {\mathbb{F}}_2$. Note that the only very ample line bundle on ![]() ${\mathbb{F}}_2$ inducing an embedding onto a surface of minimal degree
${\mathbb{F}}_2$ inducing an embedding onto a surface of minimal degree ![]() $S\cong\tilde{S}\subset{\mathbb{P}}^5$ is
$S\cong\tilde{S}\subset{\mathbb{P}}^5$ is ![]() ${\mathcal{O}}_{{\mathbb{F}}_2}({h+3f})$. Hence there is
${\mathcal{O}}_{{\mathbb{F}}_2}({h+3f})$. Hence there is  $v\in {\operatorname{Aut}}( {\mathbb{P}} H^0({\mathbb{F}}_2, {\mathcal{O}}_{{\mathbb{F}}_2}({h+3f})))={\operatorname{Aut}}({\mathbb{P}}^5)$ such that
$v\in {\operatorname{Aut}}( {\mathbb{P}} H^0({\mathbb{F}}_2, {\mathcal{O}}_{{\mathbb{F}}_2}({h+3f})))={\operatorname{Aut}}({\mathbb{P}}^5)$ such that ![]() $v(S)=\tilde{S}$ and
$v(S)=\tilde{S}$ and ![]() $v_{|S} =u$. Let
$v_{|S} =u$. Let ![]() $S\cong\tilde{S}\cong{\mathbb{F}}_0\cong{\mathbb{P}}^1\times{\mathbb{P}}^1$. Assume that
$S\cong\tilde{S}\cong{\mathbb{F}}_0\cong{\mathbb{P}}^1\times{\mathbb{P}}^1$. Assume that ![]() $u\in {\operatorname{Aut}}({\mathbb{P}}^1)\times {\operatorname{Aut}}({\mathbb{P}}^1)$. The only very ample line bundle on
$u\in {\operatorname{Aut}}({\mathbb{P}}^1)\times {\operatorname{Aut}}({\mathbb{P}}^1)$. The only very ample line bundle on ![]() ${\mathbb{F}}_0$ inducing an embedding onto a minimal degree surface in
${\mathbb{F}}_0$ inducing an embedding onto a minimal degree surface in ![]() ${\mathbb{P}}^5$ is
${\mathbb{P}}^5$ is ![]() ${\mathcal{O}}_{{\mathbb{P}}^1\times{\mathbb{P}}^1}(1,2)$, hence the conclusion follows.
${\mathcal{O}}_{{\mathbb{P}}^1\times{\mathbb{P}}^1}(1,2)$, hence the conclusion follows.
3. Curves of genus  $g\le 13$ and degree d = 15 in
$g\le 13$ and degree d = 15 in  ${\mathbb{P}}^5$
${\mathbb{P}}^5$
We denote by  $\mathcal{H}^\mathcal{L}_{d,g,r}$ the subscheme of
$\mathcal{H}^\mathcal{L}_{d,g,r}$ the subscheme of ![]() $\mathcal{H}_{d,g,r}$ consisting of components of
$\mathcal{H}_{d,g,r}$ consisting of components of ![]() $\mathcal{H}_{d,g,r}$ whose general element is linearly normal. We set
$\mathcal{H}_{d,g,r}$ whose general element is linearly normal. We set ![]() $\alpha :=g-d+r=g-10$ for
$\alpha :=g-d+r=g-10$ for ![]() $(d,r)=(15,5)$. For a general element X in a component of
$(d,r)=(15,5)$. For a general element X in a component of  $\mathcal{H}^\mathcal{L}_{15,g,5}$, α is the index of speciality of
$\mathcal{H}^\mathcal{L}_{15,g,5}$, α is the index of speciality of ![]() $|{\mathcal{O}}_X(1)|$, the complete hyperplane series
$|{\mathcal{O}}_X(1)|$, the complete hyperplane series ![]() $\mathcal{D}$ of
$\mathcal{D}$ of ![]() $X\subset{\mathbb{P}}^5$. For a possible component
$X\subset{\mathbb{P}}^5$. For a possible component ![]() $\mathcal{H}\subset\mathcal{H}_{15,g,5}$ which may not be a component of
$\mathcal{H}\subset\mathcal{H}_{15,g,5}$ which may not be a component of  $\mathcal{H}^\mathcal{L}_{15,g,5}$, we set
$\mathcal{H}^\mathcal{L}_{15,g,5}$, we set ![]() $\beta:=g-15+\dim |\mathcal{D}| \gt g-10=\alpha$, where
$\beta:=g-15+\dim |\mathcal{D}| \gt g-10=\alpha$, where ![]() $\mathcal{D}$ is the (incomplete) hyperplane series of a general
$\mathcal{D}$ is the (incomplete) hyperplane series of a general ![]() $X\in\mathcal{H}$.
$X\in\mathcal{H}$.
In this section, we study ![]() $\mathcal{H}_{15,g,5}$ for genus
$\mathcal{H}_{15,g,5}$ for genus ![]() $g\le 13$, which is relatively simple to handle. We recall the following concerning an upper bound of the dimension of a birationally very ample linear series on curves, which enables us to simplify some of our computation.
$g\le 13$, which is relatively simple to handle. We recall the following concerning an upper bound of the dimension of a birationally very ample linear series on curves, which enables us to simplify some of our computation.
Remark 3.1. By [Reference Harris19, p. 75], the largest possible dimension of a birationally very ample linear series of degree ![]() $d\ge g$ on a curve of genus g is
$d\ge g$ on a curve of genus g is  $\frac{2d-g+1}{3}$.
$\frac{2d-g+1}{3}$.
Proposition 3.2. ![]() $\mathcal{H}_{15,13,5}$ is reducible with two components
$\mathcal{H}_{15,13,5}$ is reducible with two components ![]() $\mathcal{H}_1$ and
$\mathcal{H}_1$ and ![]() $\mathcal{H}_2$.
$\mathcal{H}_2$.
(i)
 $\mathcal{H}_1=\mathcal{H}^\mathcal{L}_{15,13,5}$ and
$\mathcal{H}_1=\mathcal{H}^\mathcal{L}_{15,13,5}$ and  $\dim \mathcal{H}^\mathcal{L}_{15,13,5}=\mathcal{X}(d,g,r)=66$ with a 7-gonal general element.
$\dim \mathcal{H}^\mathcal{L}_{15,13,5}=\mathcal{X}(d,g,r)=66$ with a 7-gonal general element.(ii)
 $\dim \mathcal{H}_2=68 \gt \mathcal{X}(d,g,r),$ a general
$\dim \mathcal{H}_2=68 \gt \mathcal{X}(d,g,r),$ a general  $X\in\mathcal{H}_2$ is trigonal consisting of the image of external projection of extremal curves of degree 15 in
$X\in\mathcal{H}_2$ is trigonal consisting of the image of external projection of extremal curves of degree 15 in  ${\mathbb{P}}^6$.
${\mathbb{P}}^6$.
Proof. We denote by ![]() $\Sigma_{d,g}$ the irreducible Severi variety of plane curves of degree d and genus g; cf. [Reference Harris20]. By [Reference Keem26, theorem 3.7] and [Reference Ballico, Fontanari and Keem6, theorem 2.5],
$\Sigma_{d,g}$ the irreducible Severi variety of plane curves of degree d and genus g; cf. [Reference Harris20]. By [Reference Keem26, theorem 3.7] and [Reference Ballico, Fontanari and Keem6, theorem 2.5],  $\mathcal{H}^\mathcal{L}_{15,13,5}\neq\emptyset$ and is irreducible of dimension
$\mathcal{H}^\mathcal{L}_{15,13,5}\neq\emptyset$ and is irreducible of dimension ![]() ${\mathcal{X}}(15,13,5)$. For a general
${\mathcal{X}}(15,13,5)$. For a general  $X\in\mathcal{H}^\mathcal{L}_{15,13,5}$,
$X\in\mathcal{H}^\mathcal{L}_{15,13,5}$, ![]() $|K_X(-1)|=g^2_9$ is birationally very ample, base-point-free and hence X has a plane model of degree 9 which follows from the proof of [Reference Ballico, Fontanari and Keem6, theorem 2.5]. Therefore,
$|K_X(-1)|=g^2_9$ is birationally very ample, base-point-free and hence X has a plane model of degree 9 which follows from the proof of [Reference Ballico, Fontanari and Keem6, theorem 2.5]. Therefore,  $X\in\mathcal{H}^\mathcal{L}_{15,13,5}$ corresponds to an element of
$X\in\mathcal{H}^\mathcal{L}_{15,13,5}$ corresponds to an element of ![]() $\Sigma_{9,13}$.
$\Sigma_{9,13}$.
Conversely, the residual series of the series cut out by lines in ![]() ${\mathbb{P}}^2$ on (the non-singular model of) a general member in
${\mathbb{P}}^2$ on (the non-singular model of) a general member in ![]() $\Sigma_{9,13}$ is a very ample
$\Sigma_{9,13}$ is a very ample ![]() $g^5_{15}$ by a result of d’Almeida and Hirschowitz [Reference Coppens13, theorem 0]; cf. [Reference Keem26, pp. 13–15] for details in a similar situation. Therefore, we have a generically one-to-one correspondence
$g^5_{15}$ by a result of d’Almeida and Hirschowitz [Reference Coppens13, theorem 0]; cf. [Reference Keem26, pp. 13–15] for details in a similar situation. Therefore, we have a generically one-to-one correspondence
 \begin{equation*}\mathcal{H}^\mathcal{L}_{15,13,5}/{\operatorname{Aut}}({\mathbb{P}}^5)\stackrel{bir}{\cong} \Sigma_{9,13}/{\operatorname{Aut}}({\mathbb{P}}^2)\end{equation*}
\begin{equation*}\mathcal{H}^\mathcal{L}_{15,13,5}/{\operatorname{Aut}}({\mathbb{P}}^5)\stackrel{bir}{\cong} \Sigma_{9,13}/{\operatorname{Aut}}({\mathbb{P}}^2)\end{equation*} via residualization. Recall that a general member in ![]() $\Sigma_{9,13}$ is a plane curve of degree 9 with δ = 15 nodes as its only singularities. By a theorem of Coppens [Reference Coppens12, theorem], X is 7-gonal with gonality pencils cut out by lines through a node on the plane model of degree 9.
$\Sigma_{9,13}$ is a plane curve of degree 9 with δ = 15 nodes as its only singularities. By a theorem of Coppens [Reference Coppens12, theorem], X is 7-gonal with gonality pencils cut out by lines through a node on the plane model of degree 9.
Suppose there is a component ![]() $\mathcal{H}$ other than
$\mathcal{H}$ other than  $\mathcal{H}^\mathcal{L}_{15,14,5}$. A general
$\mathcal{H}^\mathcal{L}_{15,14,5}$. A general ![]() $X\in\mathcal{H}$ is not linearly normal, β = 4 by remark 3.1 and we have
$X\in\mathcal{H}$ is not linearly normal, β = 4 by remark 3.1 and we have ![]() $|\mathcal{D}|=g^6_{15}$ where
$|\mathcal{D}|=g^6_{15}$ where ![]() ${\mathcal{D}}$ is the incomplete hyperplane series of
${\mathcal{D}}$ is the incomplete hyperplane series of ![]() $X\subset{\mathbb{P}}^5$. Since
$X\subset{\mathbb{P}}^5$. Since ![]() $\pi (15,6)=13=g$, the curve
$\pi (15,6)=13=g$, the curve ![]() $\widetilde{X}\subset{\mathbb{P}}^6$ induced by the complete
$\widetilde{X}\subset{\mathbb{P}}^6$ induced by the complete ![]() $|\mathcal{D}|=g^6_{15}$ is an extremal curve lying on a quintic surface
$|\mathcal{D}|=g^6_{15}$ is an extremal curve lying on a quintic surface ![]() $S\subset{\mathbb{P}}^6$. If S is a smooth rational normal scroll, by solving (2), we get
$S\subset{\mathbb{P}}^6$. If S is a smooth rational normal scroll, by solving (2), we get  $\widetilde{X}\in |3H|$,
$\widetilde{X}\in |3H|$,  $|K_S+\widetilde{X}-H|=|3L|$ and
$|K_S+\widetilde{X}-H|=|3L|$ and ![]() $X\cong\widetilde{X}$ is trigonal with the trigonal pencil cut out by the ruling
$X\cong\widetilde{X}$ is trigonal with the trigonal pencil cut out by the ruling ![]() $|L|$. If S is a cone over a rational normal curve in
$|L|$. If S is a cone over a rational normal curve in ![]() ${\mathbb{P}}^5$, by (1) in remark 2.2 (a), we again may conclude that X is trigonal. Conversely, on a trigonal curve X of genus g = 13,
${\mathbb{P}}^5$, by (1) in remark 2.2 (a), we again may conclude that X is trigonal. Conversely, on a trigonal curve X of genus g = 13, ![]() $|K_X-3g^1_3|=g^6_{15}$ is very ample, hence the moduli map
$|K_X-3g^1_3|=g^6_{15}$ is very ample, hence the moduli map  $\mathcal{H} \rightarrow \mathcal{M}^1_{g,3}$ is dominant. The incomplete very ample linear series
$\mathcal{H} \rightarrow \mathcal{M}^1_{g,3}$ is dominant. The incomplete very ample linear series ![]() $g^5_{15}$ which is a codimension one subspace of the complete
$g^5_{15}$ which is a codimension one subspace of the complete ![]() $|K_X-3g^1_3|$ over the family of trigonal curves
$|K_X-3g^1_3|$ over the family of trigonal curves  $\mathcal{M}^1_{g,3}$ forms an irreducible family
$\mathcal{M}^1_{g,3}$ forms an irreducible family ![]() $\mathcal{F}\subset{\mathcal{G}}^5_{15}$ of dimension
$\mathcal{F}\subset{\mathcal{G}}^5_{15}$ of dimension
 \begin{equation*}\dim\mathcal{M}^1_{g,3}+\dim\mathbb{G}(5,6)=33 \gt 3g-3+\rho(d,g,r)=31.\end{equation*}
\begin{equation*}\dim\mathcal{M}^1_{g,3}+\dim\mathbb{G}(5,6)=33 \gt 3g-3+\rho(d,g,r)=31.\end{equation*} Therefore, the ![]() ${\operatorname{Aut}}({\mathbb{P}}^5)$-bundle over
${\operatorname{Aut}}({\mathbb{P}}^5)$-bundle over ![]() $\mathcal{F}$ may contribute to an extra component
$\mathcal{F}$ may contribute to an extra component ![]() $\mathcal{H}_2$ other than
$\mathcal{H}_2$ other than  $\mathcal{H}^\mathcal{L}_{d,g,r}$. By lower semicontinuity of gonality,
$\mathcal{H}^\mathcal{L}_{d,g,r}$. By lower semicontinuity of gonality, ![]() $\mathcal{H}_1$ is not in the boundary of
$\mathcal{H}_1$ is not in the boundary of ![]() $\mathcal{H}_2$. Hence
$\mathcal{H}_2$. Hence ![]() $\mathcal{H}_1$ and
$\mathcal{H}_1$ and ![]() $\mathcal{H}_2$ are the only two distinct components of
$\mathcal{H}_2$ are the only two distinct components of ![]() $\mathcal{H}_{15,13,5}$ by exhaustion.
$\mathcal{H}_{15,13,5}$ by exhaustion.
The following lemma is easy to prove and useful when we deal with double coverings of curves of small genus which may be induced by the compounded residual series ![]() $|K_X(-1)|$,
$|K_X(-1)|$, ![]() $X\in \mathcal{H}_{d,g,r}$; proposition 3.4 and theorem 4.1.
$X\in \mathcal{H}_{d,g,r}$; proposition 3.4 and theorem 4.1.
Lemma 3.3. Let ![]() $X\stackrel{\eta}{\rightarrow} E$ be a double covering of a curve E of genus
$X\stackrel{\eta}{\rightarrow} E$ be a double covering of a curve E of genus ![]() $h\ge 1$. Let
$h\ge 1$. Let ![]() $\mathcal{E}=g^s_{e}$ be a non-special linear series on E. Assume that
$\mathcal{E}=g^s_{e}$ be a non-special linear series on E. Assume that ![]() $|\eta^*(g^s_{e})|=g^s_{2e}$. Then the base-point-free part of the complete
$|\eta^*(g^s_{e})|=g^s_{2e}$. Then the base-point-free part of the complete ![]() $|K_X(-\eta^*(g^s_{e}))|$ is compounded.
$|K_X(-\eta^*(g^s_{e}))|$ is compounded.
Proof. Note that for any ![]() $p\in E$,
$p\in E$,  $|g^s_{e}+p|=g^{s+1}_{e+1}$ since
$|g^s_{e}+p|=g^{s+1}_{e+1}$ since ![]() $g^s_{e}$ is non-special and
$g^s_{e}$ is non-special and
 \begin{equation*}\dim|\eta^*(g^s_{e})+\eta^*(p))|=\dim|\eta^*(g^s_{e}+p)|=\dim|\eta^*(g^{s+1}_{e+1})|\ge \dim\mathcal{E} +1.\end{equation*}
\begin{equation*}\dim|\eta^*(g^s_{e})+\eta^*(p))|=\dim|\eta^*(g^s_{e}+p)|=\dim|\eta^*(g^{s+1}_{e+1})|\ge \dim\mathcal{E} +1.\end{equation*} Hence ![]() $|K_X(-\eta^*(g^s_{e}))|$ is compounded.
$|K_X(-\eta^*(g^s_{e}))|$ is compounded.
Proposition 3.4.  $\mathcal{H}_{15,12,5}=\mathcal{H}^\mathcal{L}_{15,12,5}$ is irreducible of the expected dimension and a general
$\mathcal{H}_{15,12,5}=\mathcal{H}^\mathcal{L}_{15,12,5}$ is irreducible of the expected dimension and a general ![]() $X\in\mathcal{H}_{15,12,5}$ is 7-gonal.
$X\in\mathcal{H}_{15,12,5}$ is 7-gonal.
Proof. By [Reference Ballico, Fontanari and Keem6, theorem 2.3],  $\mathcal{H}^\mathcal{L}_{15,12,5}$ is irreducible. Suppose there is a component
$\mathcal{H}^\mathcal{L}_{15,12,5}$ is irreducible. Suppose there is a component  $\mathcal{H}\neq\mathcal{H}^\mathcal{L}_{15,12,5}$. For a general
$\mathcal{H}\neq\mathcal{H}^\mathcal{L}_{15,12,5}$. For a general ![]() $X\in\mathcal{H}$ with an incomplete hyperplane series
$X\in\mathcal{H}$ with an incomplete hyperplane series ![]() $\mathcal{D}$,
$\mathcal{D}$, ![]() $\beta=g-15+\dim |\mathcal{D}|\ge 3$ and hence β = 3 by remark 3.1.
$\beta=g-15+\dim |\mathcal{D}|\ge 3$ and hence β = 3 by remark 3.1.
If  $\mathcal{E}=|K_X-\mathcal{D}|=g^{\beta-1}_7=g^2_7$ is compounded,
$\mathcal{E}=|K_X-\mathcal{D}|=g^{\beta-1}_7=g^2_7$ is compounded, ![]() $\mathcal{E}$ has non-empty base locus Δ with
$\mathcal{E}$ has non-empty base locus Δ with ![]() $\deg\Delta=1$. Therefore, X is bielliptic which is impossible by lemma 3.3.
$\deg\Delta=1$. Therefore, X is bielliptic which is impossible by lemma 3.3.
If ![]() $\mathcal{E}$ is birationally very ample,
$\mathcal{E}$ is birationally very ample, ![]() $\mathcal{E}$ is base-point-free since
$\mathcal{E}$ is base-point-free since  $g=12 \gt \binom{6-1}{2}$ and hence X has a plane model of degree 7. Consider the Severi variety
$g=12 \gt \binom{6-1}{2}$ and hence X has a plane model of degree 7. Consider the Severi variety ![]() $\Sigma_{7,12}$ of plane septics of genus g = 12 whose general member is a curve with δ = 3 nodes. Since
$\Sigma_{7,12}$ of plane septics of genus g = 12 whose general member is a curve with δ = 3 nodes. Since
the family ![]() $\mathcal{F}\subset\mathcal{G}^2_7$ consisting of base-point-free birationally very ample nets of degree 7 on moving curves has dimension
$\mathcal{F}\subset\mathcal{G}^2_7$ consisting of base-point-free birationally very ample nets of degree 7 on moving curves has dimension
Hence the residual family ![]() $\mathcal{F}^\vee:=\{|K_X-\mathcal{E}|; \mathcal{E}\in\mathcal{F}\}\subset\mathcal{G}^6_{15}$ has dimension 24 and the family
$\mathcal{F}^\vee:=\{|K_X-\mathcal{E}|; \mathcal{E}\in\mathcal{F}\}\subset\mathcal{G}^6_{15}$ has dimension 24 and the family ![]() $\widetilde{\mathcal{F}}$ consisting of incomplete very ample
$\widetilde{\mathcal{F}}$ consisting of incomplete very ample ![]() $g^5_{15}$’s arising this way has dimension
$g^5_{15}$’s arising this way has dimension
Thus ![]() $\widetilde{\mathcal{F}}$ does not constitute a full component.
$\widetilde{\mathcal{F}}$ does not constitute a full component.
Note that α = 2, ![]() $\rho (d,g,5)=g-6\alpha=0$ and hence there is a unique component of
$\rho (d,g,5)=g-6\alpha=0$ and hence there is a unique component of ![]() $\mathcal{H}_{d,g,r}$ dominating
$\mathcal{H}_{d,g,r}$ dominating ![]() $\mathcal{M}_g$ [Reference Harris19, theorem, pp. 69–70], which is
$\mathcal{M}_g$ [Reference Harris19, theorem, pp. 69–70], which is  $\mathcal{H}^\mathcal{L}_{d,g,r}.$ A general curve of genus g = 12 is 7-gonal by the Brill–Noether theorem.
$\mathcal{H}^\mathcal{L}_{d,g,r}.$ A general curve of genus g = 12 is 7-gonal by the Brill–Noether theorem.
Proposition 3.5.  $\mathcal{H}_{15,11,5}=\mathcal{H}^\mathcal{L}_{15,11,5}$ is irreducible of the expected dimension and a general X is 7-gonal.
$\mathcal{H}_{15,11,5}=\mathcal{H}^\mathcal{L}_{15,11,5}$ is irreducible of the expected dimension and a general X is 7-gonal.
Proof. We have α = 1. By [Reference Ballico, Fontanari and Keem6, theorem 2.2],  $\mathcal{H}^\mathcal{L}_{15,11,5}$ is irreducible of the expected dimension. Suppose there is a component
$\mathcal{H}^\mathcal{L}_{15,11,5}$ is irreducible of the expected dimension. Suppose there is a component ![]() $\mathcal{H}$ other than
$\mathcal{H}$ other than  $\mathcal{H}^\mathcal{L}_{15,11,5}$. A general
$\mathcal{H}^\mathcal{L}_{15,11,5}$. A general ![]() $X\in\mathcal{H}$ is not linearly normal,
$X\in\mathcal{H}$ is not linearly normal, ![]() $\beta\ge 2$ and hence β = 2 by remark 3.1. Thus, we have
$\beta\ge 2$ and hence β = 2 by remark 3.1. Thus, we have ![]() $|K_X-\mathcal{D}|=g^1_5$ and
$|K_X-\mathcal{D}|=g^1_5$ and ![]() $|\mathcal{D}|=g^6_{15}$. A general element of
$|\mathcal{D}|=g^6_{15}$. A general element of ![]() $\mathcal{H}$ is induced by
$\mathcal{H}$ is induced by ![]() $6=\dim\mathbb{G}(5,6)$ dimensional subseries of a complete
$6=\dim\mathbb{G}(5,6)$ dimensional subseries of a complete ![]() $g^6_{15}=|K_X-g^1_5|$. Such family of incomplete
$g^6_{15}=|K_X-g^1_5|$. Such family of incomplete ![]() $g^5_{15}$’s forms an irreducible family of dimension at most
$g^5_{15}$’s forms an irreducible family of dimension at most
 \begin{equation*}\dim\mathcal{M}^1_{g,5}+\dim\mathbb{G}(5,6)=33 \lt 3g-3+\rho(15,11,5)=35, \end{equation*}
\begin{equation*}\dim\mathcal{M}^1_{g,5}+\dim\mathbb{G}(5,6)=33 \lt 3g-3+\rho(15,11,5)=35, \end{equation*} hence such family does not contribute to a full component of ![]() $\mathcal{H}_{15,11,5}$.
$\mathcal{H}_{15,11,5}$.
Since ![]() $\rho (d,g,5) \gt 0$, the unique component
$\rho (d,g,5) \gt 0$, the unique component  $\mathcal{H}^\mathcal{L}_{d,g,r}$ of
$\mathcal{H}^\mathcal{L}_{d,g,r}$ of ![]() $\mathcal{H}_{d,g,r}$ dominates
$\mathcal{H}_{d,g,r}$ dominates ![]() ${\mathcal{M}}_g$ whose general curve member is
${\mathcal{M}}_g$ whose general curve member is  $7=[\frac{g+3}{2}]$-gonal.
$7=[\frac{g+3}{2}]$-gonal.
Proposition 3.6. For ![]() $g\le 10$,
$g\le 10$, ![]() $\mathcal{H}_{15,g,5}$ is irreducible of the expected dimension and a general element X is
$\mathcal{H}_{15,g,5}$ is irreducible of the expected dimension and a general element X is  $[\frac{g+3}{2}]$-gonal.
$[\frac{g+3}{2}]$-gonal.
Proof. This follows from [Reference Harris19, p. 75] for ![]() $g\le 9$ and [Reference Keem25, theorem] for g = 10.
$g\le 9$ and [Reference Keem25, theorem] for g = 10.
4. Curves of genus g = 15
This section is devoted to the family of curves of genus g = 15. The following subsection contains the main result of this section.
4.1. Irreducibility of  $\mathcal{H}_{15,15,5}$
$\mathcal{H}_{15,15,5}$
Theorem 4.1  $\mathcal{H}^\mathcal{L}_{15,15,5}=\mathcal{H}_{15,15,5}$ is irreducible whose general element is a 5-gonal curve lying on a smooth del Pezzo surface in
$\mathcal{H}^\mathcal{L}_{15,15,5}=\mathcal{H}_{15,15,5}$ is irreducible whose general element is a 5-gonal curve lying on a smooth del Pezzo surface in ![]() ${\mathbb{P}}^5$ and
${\mathbb{P}}^5$ and ![]() $\dim\mathcal{H}_{15,15,5}=64$.
$\dim\mathcal{H}_{15,15,5}=64$.
Proof. Note that a general element in any component of ![]() $\mathcal{H}_{15,15,5}$ is linearly normal since
$\mathcal{H}_{15,15,5}$ is linearly normal since ![]() $\pi (15,6)=13 \lt g=15$ and hence
$\pi (15,6)=13 \lt g=15$ and hence  $\mathcal{H}_{15,15,5}=\mathcal{H}^\mathcal{L}_{15,15,5}$.
$\mathcal{H}_{15,15,5}=\mathcal{H}^\mathcal{L}_{15,15,5}$.
Since ![]() $\pi_1(15,5)=16 \gt g$, X is not extremal or nearly extremal—a curve with
$\pi_1(15,5)=16 \gt g$, X is not extremal or nearly extremal—a curve with ![]() $p_a(X) \gt \pi_1(d,r)$—and hence
$p_a(X) \gt \pi_1(d,r)$—and hence ![]() $X\subset{\mathbb{P}}^5$ may not sit on a surface of small degree. Instead, we look at the residual series
$X\subset{\mathbb{P}}^5$ may not sit on a surface of small degree. Instead, we look at the residual series ![]() $|K_X(-1)|$ and study the curve induced by it. This technique—if one may call this ‘a technique’—is not new and has been used before, e.g. in [Reference Keem26] or possibly in works by other authors.
$|K_X(-1)|$ and study the curve induced by it. This technique—if one may call this ‘a technique’—is not new and has been used before, e.g. in [Reference Keem26] or possibly in works by other authors.
For a general ![]() $X\in\mathcal{H}_{15,15,5}$, set
$X\in\mathcal{H}_{15,15,5}$, set ![]() $\mathcal{E}:=g^4_{13}=|K_X(-1)|$ and let
$\mathcal{E}:=g^4_{13}=|K_X(-1)|$ and let ![]() $C_{\mathcal{E}}\subset{\mathbb{P}}^4$ be the dual curve of X, which is by definition the image curve induced by the base-point-free part of
$C_{\mathcal{E}}\subset{\mathbb{P}}^4$ be the dual curve of X, which is by definition the image curve induced by the base-point-free part of ![]() $\mathcal{E}$. We first claim that
$\mathcal{E}$. We first claim that ![]() $\mathcal{E}$ is birationally very ample, possibly with non-empty base locus.
$\mathcal{E}$ is birationally very ample, possibly with non-empty base locus.
Claim 1: ![]() $|K_X(-1)|$ is birationally very ample.
$|K_X(-1)|$ is birationally very ample.
Suppose ![]() $|K_X(-1)|$ is compounded. Since
$|K_X(-1)|$ is compounded. Since ![]() $\deg |K_X(-1)|=13$ is prime,
$\deg |K_X(-1)|=13$ is prime, ![]() $|K_X(-1)|$ has non-empty base locus Δ and we have the following four possibilities:
$|K_X(-1)|$ has non-empty base locus Δ and we have the following four possibilities:
(i)
 $|K_X(-1)|=g^4_{12}+\Delta$,
$|K_X(-1)|=g^4_{12}+\Delta$,  $\deg\Delta=1$,
$\deg\Delta=1$,(ii)
 $|K_X(-1)|=g^4_{10}+\Delta$,
$|K_X(-1)|=g^4_{10}+\Delta$,  $\deg\Delta=3$,
$\deg\Delta=3$,(iii)
 $|K_X(-1)|=g^4_{9}+\Delta$,
$|K_X(-1)|=g^4_{9}+\Delta$,  $\deg\Delta=4$; this can be excluded since the dual curve
$\deg\Delta=4$; this can be excluded since the dual curve  $C_{\mathcal{E}}\subset{\mathbb{P}}^4$ induced by the compounded
$C_{\mathcal{E}}\subset{\mathbb{P}}^4$ induced by the compounded  $g^4_{9}$ is non-degenerate.
$g^4_{9}$ is non-degenerate.(iv)
 $|K_X(-1)|=g^4_{8}+\Delta$,
$|K_X(-1)|=g^4_{8}+\Delta$,  $\deg\Delta=5$; in this case, X is hyperelliptic and does not carry a very ample special linear series.
$\deg\Delta=5$; in this case, X is hyperelliptic and does not carry a very ample special linear series.
(i) Suppose ![]() $|K_X(-1)|=g^4_{12}+\Delta$,
$|K_X(-1)|=g^4_{12}+\Delta$, ![]() $\deg\Delta=1$, then one of the following holds;
$\deg\Delta=1$, then one of the following holds;
 \begin{equation*}
\begin{cases}
\mathrm{(ia)} ~X \mathrm{~is ~~trigonal ~~with~} |K_X(-1)(-\Delta)|=g^4_{12}=4g^1_3 \mathrm{~or~~ }
\\
\mathrm{(ib)} ~\exists ~~X\stackrel{\varphi}{\rightarrow}C_{\mathcal{E}}\subset{\mathbb{P}}^4, \deg\varphi=2,
\mathrm{~~genus}(C_{\mathcal{E}})=2, g^4_{12}=
\varphi^*(g^4_6).
\end{cases}
\end{equation*}
\begin{equation*}
\begin{cases}
\mathrm{(ia)} ~X \mathrm{~is ~~trigonal ~~with~} |K_X(-1)(-\Delta)|=g^4_{12}=4g^1_3 \mathrm{~or~~ }
\\
\mathrm{(ib)} ~\exists ~~X\stackrel{\varphi}{\rightarrow}C_{\mathcal{E}}\subset{\mathbb{P}}^4, \deg\varphi=2,
\mathrm{~~genus}(C_{\mathcal{E}})=2, g^4_{12}=
\varphi^*(g^4_6).
\end{cases}
\end{equation*} (ia) Set ![]() $\Delta=p$ and let
$\Delta=p$ and let ![]() $p+q+r\in g^1_3$. We have
$p+q+r\in g^1_3$. We have
and hence
 \begin{align*}
|\mathcal{O}_X(1)-q-r|&=|K_X-K_X(-1)-q-r|\\ &=|K_X-(4g^1_3+p)-q-r|=|K_X-5g^1_3|=g^{s}_{13}, s\ge 4
\end{align*}
\begin{align*}
|\mathcal{O}_X(1)-q-r|&=|K_X-K_X(-1)-q-r|\\ &=|K_X-(4g^1_3+p)-q-r|=|K_X-5g^1_3|=g^{s}_{13}, s\ge 4
\end{align*} from which it follows that ![]() $|\mathcal{O}_X(1)|$ is not very ample.
$|\mathcal{O}_X(1)|$ is not very ample.
(ib) Since ![]() $\deg \varphi=2$,
$\deg \varphi=2$, ![]() $\deg \varphi (X)=\deg C_{\mathcal{E}}=6$ and
$\deg \varphi (X)=\deg C_{\mathcal{E}}=6$ and ![]() $g(C_{\mathcal{E}})\le\pi(6,4)\le 2$ by Castelnuovo genus bound. Since
$g(C_{\mathcal{E}})\le\pi(6,4)\le 2$ by Castelnuovo genus bound. Since ![]() $|K_X(-1)(-\Delta)|$ is complete,
$|K_X(-1)(-\Delta)|$ is complete, ![]() $g^4_6$ on the normalization of
$g^4_6$ on the normalization of ![]() $C_{\mathcal{E}}$ such that
$C_{\mathcal{E}}$ such that ![]() $g^4_{12}=|K_X(-1)(-\Delta)|=
\varphi^*(g^4_6)$ is also complete. Hence
$g^4_{12}=|K_X(-1)(-\Delta)|=
\varphi^*(g^4_6)$ is also complete. Hence ![]() $C_{\mathcal{E}}$ has geometric genus
$C_{\mathcal{E}}$ has geometric genus ![]() $g(C_{\mathcal{E}})=2$, smooth and
$g(C_{\mathcal{E}})=2$, smooth and  $|\mathcal{O}_{C_{\mathcal{E}}}(1)|=g^4_6$ is non-special. However, we may exclude this case by lemma 3.3.
$|\mathcal{O}_{C_{\mathcal{E}}}(1)|=g^4_6$ is non-special. However, we may exclude this case by lemma 3.3.
(ii) Suppose ![]() $|K_X(-1)|=g^4_{10}+\Delta$,
$|K_X(-1)|=g^4_{10}+\Delta$, ![]() $\deg\Delta=3$. Since
$\deg\Delta=3$. Since ![]() $C_{\mathcal{E}}\subset{\mathbb{P}}^4$ is non-degenerate and X is non-hyperelliptic, we have
$C_{\mathcal{E}}\subset{\mathbb{P}}^4$ is non-degenerate and X is non-hyperelliptic, we have ![]() $g^4_{10}=\varphi^*(g^4_5)$ where
$g^4_{10}=\varphi^*(g^4_5)$ where ![]() $\varphi :X\rightarrow C_{\mathcal{E}}$ is a double cover of an elliptic curve
$\varphi :X\rightarrow C_{\mathcal{E}}$ is a double cover of an elliptic curve ![]() $C_{\mathcal{E}}$ with complete, non-special
$C_{\mathcal{E}}$ with complete, non-special ![]() $g^4_5$. Again by lemma 3.3, we may exclude this case, finishing the proof of Claim 1.
$g^4_5$. Again by lemma 3.3, we may exclude this case, finishing the proof of Claim 1.
Claim 2: No smooth ![]() $X\in\mathcal{H}_{15,15,5}$ is trigonal: Suppose there is a trigonal
$X\in\mathcal{H}_{15,15,5}$ is trigonal: Suppose there is a trigonal ![]() $X\in\mathcal{H}_{15,15,5}$. Recall that on a trigonal curve X of genus
$X\in\mathcal{H}_{15,15,5}$. Recall that on a trigonal curve X of genus ![]() $g\ge 5$ with a
$g\ge 5$ with a ![]() $g^r_d, ~ d\le g-1$, either
$g^r_d, ~ d\le g-1$, either ![]() $g^r_d$ is compounded with the unique
$g^r_d$ is compounded with the unique ![]() $g^1_3$ or
$g^1_3$ or ![]() $|K_X-g^r_d|$ is compounded with
$|K_X-g^r_d|$ is compounded with ![]() $g^1_3$ by Maroni theory; cf. [Reference Martens and Schreyer29, proposition 1]. Since
$g^1_3$ by Maroni theory; cf. [Reference Martens and Schreyer29, proposition 1]. Since ![]() $\mathcal{E}$ is birationally very ample by Claim 1,
$\mathcal{E}$ is birationally very ample by Claim 1, ![]() $|K_X-\mathcal{E}|=|{\mathcal{O}}_X(1)|$ is compounded with
$|K_X-\mathcal{E}|=|{\mathcal{O}}_X(1)|$ is compounded with ![]() $g^1_3$, a contradiction. This finishes the proof of Claim 2.
$g^1_3$, a contradiction. This finishes the proof of Claim 2.
Claim 3: ![]() $|K_X(-1)|$ is base-point-free.
$|K_X(-1)|$ is base-point-free.
For the birationally very ample ![]() ${\mathcal{E}}=|K_X(-1)|$, suppose
${\mathcal{E}}=|K_X(-1)|$, suppose ![]() $\Delta=\mathrm{Bs}(\mathcal{E})\neq\emptyset$ and set
$\Delta=\mathrm{Bs}(\mathcal{E})\neq\emptyset$ and set ![]() $\mathcal{E}=\widetilde{\mathcal{E}}+\Delta$. Note that
$\mathcal{E}=\widetilde{\mathcal{E}}+\Delta$. Note that ![]() $\deg\Delta=1$ otherwise
$\deg\Delta=1$ otherwise ![]() $\pi(e,4)\le 12 \lt g$ if
$\pi(e,4)\le 12 \lt g$ if ![]() $e\le 11$. Put
$e\le 11$. Put ![]() $\Delta=p$ and let
$\Delta=p$ and let ![]() $C_{\widetilde{\mathcal{E}}}\subset{\mathbb{P}}^4$ be the image of the morphism induced by the moving part
$C_{\widetilde{\mathcal{E}}}\subset{\mathbb{P}}^4$ be the image of the morphism induced by the moving part ![]() $\widetilde{\mathcal{E}}$. Since
$\widetilde{\mathcal{E}}$. Since ![]() $\deg C_{\widetilde{\mathcal{E}}}=12$ and
$\deg C_{\widetilde{\mathcal{E}}}=12$ and ![]() $\pi(12,4)=15=g$,
$\pi(12,4)=15=g$, ![]() $C_{\widetilde{\mathcal{E}}}$ is an (smooth) extremal curve lying on a cubic surface
$C_{\widetilde{\mathcal{E}}}$ is an (smooth) extremal curve lying on a cubic surface ![]() $S\subset{\mathbb{P}}^4$.
$S\subset{\mathbb{P}}^4$.
(i) Suppose S is a smooth cubic scroll in ![]() ${\mathbb{P}}^4$ and let
${\mathbb{P}}^4$ and let ![]() $C_{\widetilde{\mathcal{E}}}\in|aH+bL|$. We solve the degree and genus formula (2) for r = 4 to get
$C_{\widetilde{\mathcal{E}}}\in|aH+bL|$. We solve the degree and genus formula (2) for r = 4 to get ![]() $a=4, b=0$. Since
$a=4, b=0$. Since ![]() $X\cong C_{\widetilde{\mathcal{E}}}$ and
$X\cong C_{\widetilde{\mathcal{E}}}$ and  $|K_X(-1)|=\mathcal{E}=\widetilde{\mathcal{E}}+\Delta$, we have
$|K_X(-1)|=\mathcal{E}=\widetilde{\mathcal{E}}+\Delta$, we have
 \begin{equation*}|K_S+C_{\widetilde{\mathcal{E}}}-H|_{|X}=|H+L|_{|X}=|K_X-\widetilde{\mathcal{E}}|,\end{equation*}
\begin{equation*}|K_S+C_{\widetilde{\mathcal{E}}}-H|_{|X}=|H+L|_{|X}=|K_X-\widetilde{\mathcal{E}}|,\end{equation*}which is birationally very ample. From the standard exact sequence
 \begin{equation*}0\rightarrow \mathcal{I}_{C_{\widetilde{\mathcal{E}}}}(H+L)\rightarrow \mathcal{O}(H+L)\rightarrow\mathcal{O}(H+L)\otimes\mathcal{O}_{C_{\widetilde{\mathcal{E}}}}\rightarrow 0\end{equation*}
\begin{equation*}0\rightarrow \mathcal{I}_{C_{\widetilde{\mathcal{E}}}}(H+L)\rightarrow \mathcal{O}(H+L)\rightarrow\mathcal{O}(H+L)\otimes\mathcal{O}_{C_{\widetilde{\mathcal{E}}}}\rightarrow 0\end{equation*} the restriction map  $H^0(S, \mathcal{O}(H+L))\stackrel{\rho}{\longrightarrow} H^0(C_{\widetilde{\mathcal{E}}},\mathcal{O}(H+L)\otimes\mathcal{O}_{C_{\widetilde{\mathcal{E}}}})$ is injective since
$H^0(S, \mathcal{O}(H+L))\stackrel{\rho}{\longrightarrow} H^0(C_{\widetilde{\mathcal{E}}},\mathcal{O}(H+L)\otimes\mathcal{O}_{C_{\widetilde{\mathcal{E}}}})$ is injective since  $H^0(S, \mathcal{I}_{C_{{\widetilde{\mathcal{E}}}}}(H+L))=H^0(S, \mathcal{O}(-3H+L))=0$. ρ is surjective as well by Castelnuovo genus bound; if ρ is not surjective then
$H^0(S, \mathcal{I}_{C_{{\widetilde{\mathcal{E}}}}}(H+L))=H^0(S, \mathcal{O}(-3H+L))=0$. ρ is surjective as well by Castelnuovo genus bound; if ρ is not surjective then
 \begin{equation*}\mathbb{C}^7\cong H^0(S, \mathcal{O}(H+L))\subsetneq
H^0(C_{\widetilde{\mathcal{E}}},\mathcal{O}(H+L)\otimes\mathcal{O}_{C_{\widetilde{\mathcal{E}}}}),\end{equation*}
\begin{equation*}\mathbb{C}^7\cong H^0(S, \mathcal{O}(H+L))\subsetneq
H^0(C_{\widetilde{\mathcal{E}}},\mathcal{O}(H+L)\otimes\mathcal{O}_{C_{\widetilde{\mathcal{E}}}}),\end{equation*} which would imply that the birationally very ample  $|\mathcal{O}(H+L)\otimes\mathcal{O}_{C_{\widetilde{\mathcal{E}}}}|=|K_X-\widetilde{\mathcal{E}}|$ on
$|\mathcal{O}(H+L)\otimes\mathcal{O}_{C_{\widetilde{\mathcal{E}}}}|=|K_X-\widetilde{\mathcal{E}}|$ on ![]() $C_{\widetilde{\mathcal{E}}}\cong X$ induces a morphism
$C_{\widetilde{\mathcal{E}}}\cong X$ induces a morphism ![]() $X\rightarrow{\mathbb{P}}^s, s\ge 7$, a contradiction by
$X\rightarrow{\mathbb{P}}^s, s\ge 7$, a contradiction by ![]() $\pi(16,7)=12 \lt g$.
$\pi(16,7)=12 \lt g$.
By the surjectivity of the restriction map ρ and by the very ampleness of ![]() $|H+L|$ on the cubic scroll S,
$|H+L|$ on the cubic scroll S,  $|K_X-\widetilde{\mathcal{E}}|$ is very ample. Note that
$|K_X-\widetilde{\mathcal{E}}|$ is very ample. Note that  $|\mathcal{O}_X(1)|=|K_X-\mathcal{E}|=|K_X-\widetilde{\mathcal{E}}-\Delta|$ gives rise to the morphism which is the composition of the embedding
$|\mathcal{O}_X(1)|=|K_X-\mathcal{E}|=|K_X-\widetilde{\mathcal{E}}-\Delta|$ gives rise to the morphism which is the composition of the embedding ![]() $X\stackrel{\varphi}{\longrightarrow}{\mathbb{P}}^6$ given by the very ample
$X\stackrel{\varphi}{\longrightarrow}{\mathbb{P}}^6$ given by the very ample  $|K_X-\widetilde{\mathcal{E}}|$ followed by the projection τ with centre at p;
$|K_X-\widetilde{\mathcal{E}}|$ followed by the projection τ with centre at p;

However, the four-secant line through Δ, i.e. the line though Δ in the ruling ![]() $|L|$, produces a singularity and hence
$|L|$, produces a singularity and hence ![]() $|\mathcal{O}_X(1)|$ is not very ample if
$|\mathcal{O}_X(1)|$ is not very ample if ![]() $\Delta\neq \emptyset$.
$\Delta\neq \emptyset$.
(ii) Suppose ![]() $S\subset{\mathbb{P}}^4$ is a cone over a twisted cubic in
$S\subset{\mathbb{P}}^4$ is a cone over a twisted cubic in ![]() ${\mathbb{P}}^3$. Let
${\mathbb{P}}^3$. Let  $\widetilde{C_{\widetilde{\mathcal{E}}}}\subset \mathbb{F}_3$ be the strict transformation of
$\widetilde{C_{\widetilde{\mathcal{E}}}}\subset \mathbb{F}_3$ be the strict transformation of ![]() $C_{\widetilde{\mathcal{E}}}\subset{\mathbb{P}}^4$ under
$C_{\widetilde{\mathcal{E}}}\subset{\mathbb{P}}^4$ under  $\mathbb{F}_{3}\stackrel{|h+3f|}{\longrightarrow} S$ and set
$\mathbb{F}_{3}\stackrel{|h+3f|}{\longrightarrow} S$ and set  $\widetilde{C_{\widetilde{\mathcal{E}}}}\in |ah+bf|$. Recall that
$\widetilde{C_{\widetilde{\mathcal{E}}}}\in |ah+bf|$. Recall that ![]() $C_{\widetilde{\mathcal{E}}}$ is smooth (extremal) and so is
$C_{\widetilde{\mathcal{E}}}$ is smooth (extremal) and so is  $\widetilde{C_{\widetilde{\mathcal{E}}}}\cong X$. From
$\widetilde{C_{\widetilde{\mathcal{E}}}}\cong X$. From
 \begin{equation*}\widetilde{C_{\widetilde{\mathcal{E}}}}\cdot (h+3f)=(ah+bf)\cdot (h+3f)=b=\deg\widetilde{{\mathcal{E}}}=12\end{equation*}
\begin{equation*}\widetilde{C_{\widetilde{\mathcal{E}}}}\cdot (h+3f)=(ah+bf)\cdot (h+3f)=b=\deg\widetilde{{\mathcal{E}}}=12\end{equation*} \begin{equation*}\widetilde{C_{\widetilde{\mathcal{E}}}}\cdot(\widetilde{C_{\widetilde{\mathcal{E}}}}+K_{\mathbb{F}_3})=(ah+bf)\cdot((a-2)h+(b-5)f)=2g-2=28\end{equation*}
\begin{equation*}\widetilde{C_{\widetilde{\mathcal{E}}}}\cdot(\widetilde{C_{\widetilde{\mathcal{E}}}}+K_{\mathbb{F}_3})=(ah+bf)\cdot((a-2)h+(b-5)f)=2g-2=28\end{equation*} we get a = 4 and  $\widetilde{C_{\widetilde{\mathcal{E}}}}\in |4h+12f|$. Note that
$\widetilde{C_{\widetilde{\mathcal{E}}}}\in |4h+12f|$. Note that
 \begin{equation*}
|K_{\mathbb{F}_3}+\widetilde{C_{\widetilde{\mathcal{E}}}}-(h+3f)|=|h+4f|
\end{equation*}
\begin{equation*}
|K_{\mathbb{F}_3}+\widetilde{C_{\widetilde{\mathcal{E}}}}-(h+3f)|=|h+4f|
\end{equation*} is very ample by [Reference Hartshorne22, V.Cor. 2.18, p. 380]. We consider the restriction map  $H^0(\mathbb{F}_3, \mathcal{O}(h+4f))\stackrel{\rho}{\longrightarrow} H^0(\widetilde{C_{\widetilde{\mathcal{E}}}}, \mathcal{O}(h+4f)\otimes\mathcal{O}_{\widetilde{C_{\widetilde{\mathcal{E}}}}})=H^0(\widetilde{C_{\widetilde{\mathcal{E}}}}, |K_X-\widetilde{\mathcal{E}}|).$ By the same routine as we did for the previous case (smooth cubic scroll case), we may claim that the restriction map ρ is surjective.
$H^0(\mathbb{F}_3, \mathcal{O}(h+4f))\stackrel{\rho}{\longrightarrow} H^0(\widetilde{C_{\widetilde{\mathcal{E}}}}, \mathcal{O}(h+4f)\otimes\mathcal{O}_{\widetilde{C_{\widetilde{\mathcal{E}}}}})=H^0(\widetilde{C_{\widetilde{\mathcal{E}}}}, |K_X-\widetilde{\mathcal{E}}|).$ By the same routine as we did for the previous case (smooth cubic scroll case), we may claim that the restriction map ρ is surjective.
By the surjectivity of the restriction map ρ and the very ampleness of ![]() $|h+4f|$ on
$|h+4f|$ on ![]() ${\mathbb{F}}_3$, we see that
${\mathbb{F}}_3$, we see that  $|K_X-\widetilde{\mathcal{E}}|$ is very ample.
$|K_X-\widetilde{\mathcal{E}}|$ is very ample.  $|\mathcal{O}_X(1)|=|K_X-\widetilde{\mathcal{E}}-\Delta|$ induces the composition of two maps
$|\mathcal{O}_X(1)|=|K_X-\widetilde{\mathcal{E}}-\Delta|$ induces the composition of two maps  $X\stackrel{|h+4f|_{|X}}{\longrightarrow}{\mathbb{P}}^6\stackrel{\pi_p}{\longrightarrow}{\mathbb{P}}^5$ and the projection map πp is not an embedding; since
$X\stackrel{|h+4f|_{|X}}{\longrightarrow}{\mathbb{P}}^6\stackrel{\pi_p}{\longrightarrow}{\mathbb{P}}^5$ and the projection map πp is not an embedding; since  $f\cdot (h+4f)=1, f\cdot \widetilde{C_{\widetilde{\mathcal{E}}}}=4$, the image of f under
$f\cdot (h+4f)=1, f\cdot \widetilde{C_{\widetilde{\mathcal{E}}}}=4$, the image of f under ![]() $|h+4f|$ in
$|h+4f|$ in ![]() ${\mathbb{P}}^6$ is a four-secant line to the smooth image of
${\mathbb{P}}^6$ is a four-secant line to the smooth image of  $X\cong\widetilde{C_{\widetilde{\mathcal{E}}}}$. Therefore,
$X\cong\widetilde{C_{\widetilde{\mathcal{E}}}}$. Therefore, ![]() $|\mathcal{O}_X(1)|$ is not very ample, finishing the proof of Claim 3.
$|\mathcal{O}_X(1)|$ is not very ample, finishing the proof of Claim 3.
Since ![]() $\mathcal{E}=|K_X(-1)|$ is base-point-free and birationally very ample, we have
$\mathcal{E}=|K_X(-1)|$ is base-point-free and birationally very ample, we have
Thus, ![]() $C_{\mathcal{E}}\subset{\mathbb{P}}^4$ lies on a surface S,
$C_{\mathcal{E}}\subset{\mathbb{P}}^4$ lies on a surface S, ![]() $3\le\deg S\le4$; cf. [Reference Harris19, theorem 3.15, p. 99].
$3\le\deg S\le4$; cf. [Reference Harris19, theorem 3.15, p. 99].
(A) Suppose ![]() $\deg S=3$ and S is smooth. Let
$\deg S=3$ and S is smooth. Let ![]() $C_{\mathcal{E}}\in|aH+bL|$. Solving (2), i.e.
$C_{\mathcal{E}}\in|aH+bL|$. Solving (2), i.e.  $13=C_{\mathcal{E}}\cdot H=3a+b, ~p_a(C_{\mathcal{E}})=\frac{3(a-1)(a-2)}{2}+(2+b)(a-1),$ the following pairs
$13=C_{\mathcal{E}}\cdot H=3a+b, ~p_a(C_{\mathcal{E}})=\frac{3(a-1)(a-2)}{2}+(2+b)(a-1),$ the following pairs ![]() $(a,b)\in\mathbb{Z}\times\mathbb{Z}$ are possible for
$(a,b)\in\mathbb{Z}\times\mathbb{Z}$ are possible for ![]() $15\le p_a(C_{\mathcal{E}})\le 18$:
$15\le p_a(C_{\mathcal{E}})\le 18$:
 \begin{equation*}
\begin{cases}
p_a(C_{\mathcal{E}})=18: (5,-2), (4,1), \textrm{cases (A1), (A2) below} \\
p_a(C_{\mathcal{E}})=17, 16: \mathrm{no ~~ solution }\\
p_a(C_{\mathcal{E}})=15: (3,4), (6-5), \textrm{cases (A3), (A4) below}. \
\end{cases}
\end{equation*}
\begin{equation*}
\begin{cases}
p_a(C_{\mathcal{E}})=18: (5,-2), (4,1), \textrm{cases (A1), (A2) below} \\
p_a(C_{\mathcal{E}})=17, 16: \mathrm{no ~~ solution }\\
p_a(C_{\mathcal{E}})=15: (3,4), (6-5), \textrm{cases (A3), (A4) below}. \
\end{cases}
\end{equation*} Before proceeding, we recall some standard notation concerning linear systems and divisors on a blown up projective plane. Let ![]() ${\mathbb{P}}^2_s$ be the rational surface
${\mathbb{P}}^2_s$ be the rational surface ![]() ${\mathbb{P}}^2$ blown up at s general points. Let ei be the class of the exceptional divisor Ei and l be the class of a line L in
${\mathbb{P}}^2$ blown up at s general points. Let ei be the class of the exceptional divisor Ei and l be the class of a line L in ![]() ${\mathbb{P}}^2$. For integers
${\mathbb{P}}^2$. For integers ![]() $b_1\ge b_2\ge\cdots\ge b_s$, let
$b_1\ge b_2\ge\cdots\ge b_s$, let ![]() $(a;b_1,\cdots, b_i, \cdots,b_s)$ denote class of the linear system
$(a;b_1,\cdots, b_i, \cdots,b_s)$ denote class of the linear system ![]() $|aL-\sum b_i E_i|$ on
$|aL-\sum b_i E_i|$ on ![]() ${\mathbb{P}}^2_s$. By abuse of notation, we use the expression
${\mathbb{P}}^2_s$. By abuse of notation, we use the expression ![]() $(a;b_1,\cdots, b_i, \cdots,b_s)$ for the divisor
$(a;b_1,\cdots, b_i, \cdots,b_s)$ for the divisor ![]() $aL-\sum b_i E_i$ and
$aL-\sum b_i E_i$ and ![]() $|(a;b_1,\cdots, b_i, \cdots,b_s)|$ for the linear system
$|(a;b_1,\cdots, b_i, \cdots,b_s)|$ for the linear system ![]() $|aL-\sum b_i E_i|$. We use the convention
$|aL-\sum b_i E_i|$. We use the convention
 \begin{equation*}(a;b_1^{s_1},\cdots,b_j^{s_j},\cdots,b_t^{s_t}), ~ \sum s_j=s\end{equation*}
\begin{equation*}(a;b_1^{s_1},\cdots,b_j^{s_j},\cdots,b_t^{s_t}), ~ \sum s_j=s\end{equation*} when bj appears sj times consecutively in the linear system ![]() $|aL-\sum b_i E_i|$.
$|aL-\sum b_i E_i|$.
For computational reasons, we sometimes identify a smooth rational normal surface scroll ![]() $S\subset {\mathbb{P}}^4$ with the Hirzebruch surface
$S\subset {\mathbb{P}}^4$ with the Hirzebruch surface ![]() $\mathbb{F}_1$ embedded by the very ample linear system
$\mathbb{F}_1$ embedded by the very ample linear system ![]() $|e+2f|$ on
$|e+2f|$ on ![]() ${\mathbb{P}}^2_1$. We also make obvious identifications among divisor classes such as
${\mathbb{P}}^2_1$. We also make obvious identifications among divisor classes such as
where e is the class of the minimal degree self-intersection curve and f is class of the fibre on ![]() $\mathbb{F}_1$ (l is the class of a line, e 1 the exceptional divisor on
$\mathbb{F}_1$ (l is the class of a line, e 1 the exceptional divisor on ![]() ${\mathbb{P}}^1_1$, and f 1 is the proper transformation of the line through the blown up point). By abusing notation, we make no distinction between f and f 1 (e and e 1) and use the same letters.
${\mathbb{P}}^1_1$, and f 1 is the proper transformation of the line through the blown up point). By abusing notation, we make no distinction between f and f 1 (e and e 1) and use the same letters.
(A1) ![]() $C_{\mathcal{E}}\in |5H-2L|$,
$C_{\mathcal{E}}\in |5H-2L|$, ![]() $p_a(C_{\mathcal{E}})=18$: Note that
$p_a(C_{\mathcal{E}})=18$: Note that
and hence ![]() $C_{\mathcal{E}}$ has a plane model of degree 8. On a fixed
$C_{\mathcal{E}}$ has a plane model of degree 8. On a fixed ![]() $S\cong{\mathbb{F}}_1$, we consider the Severi variety
$S\cong{\mathbb{F}}_1$, we consider the Severi variety ![]() $\Sigma_{{15},\mathcal{M}}$ of curves of genus g = 15 in the linear system
$\Sigma_{{15},\mathcal{M}}$ of curves of genus g = 15 in the linear system ![]() $\mathcal{M}=|5H-2L|$. It is known that
$\mathcal{M}=|5H-2L|$. It is known that ![]() $\Sigma_{{15},\mathcal{M}}$ is irreducible,
$\Sigma_{{15},\mathcal{M}}$ is irreducible,
and a general element of ![]() $\Sigma_{{15},\mathcal{M}}$ is a nodal curve with δ = 3 nodes as its only singularities; cf. [Reference Tyomkin34]. We now take a general
$\Sigma_{{15},\mathcal{M}}$ is a nodal curve with δ = 3 nodes as its only singularities; cf. [Reference Tyomkin34]. We now take a general ![]() $C\in \Sigma_{{15},\mathcal{M}}$, i.e. a curve with three nodes in
$C\in \Sigma_{{15},\mathcal{M}}$, i.e. a curve with three nodes in ![]() $|5H-2L|$ on S or equivalently a curve with a plane model of degree 8 with an ordinary triple point and three nodes. Let
$|5H-2L|$ on S or equivalently a curve with a plane model of degree 8 with an ordinary triple point and three nodes. Let  $\widetilde{C}\subset{\mathbb{P}}^2_4$ be the strict transformation of C under the blowing up
$\widetilde{C}\subset{\mathbb{P}}^2_4$ be the strict transformation of C under the blowing up ![]() ${\mathbb{P}}^2_4
\stackrel{\varphi}{\longrightarrow}
S\cong{\mathbb{P}}^2_1$ at three nodal singularities. By abusing notation, we set
${\mathbb{P}}^2_4
\stackrel{\varphi}{\longrightarrow}
S\cong{\mathbb{P}}^2_1$ at three nodal singularities. By abusing notation, we set ![]() $H:=\varphi^*({\mathcal{O}}_S(1))$. We have
$H:=\varphi^*({\mathcal{O}}_S(1))$. We have  $\widetilde{C}\in |(8;3,2^3)|$ and
$\widetilde{C}\in |(8;3,2^3)|$ and
 \begin{equation}
|K_{{\mathbb{P}}^2_4}+\widetilde{C}-(2l-e_1)|=|-(3;1^4)+(8;3,2^3)-(2;1,0^3)|=|(3;1^4)|.
\end{equation}
\begin{equation}
|K_{{\mathbb{P}}^2_4}+\widetilde{C}-(2l-e_1)|=|-(3;1^4)+(8;3,2^3)-(2;1,0^3)|=|(3;1^4)|.
\end{equation}On the other hand, the restriction map
 \begin{equation*}H^0({\mathbb{P}}^2_4,\mathcal{O}(K_{{\mathbb{P}}^2_4}+\widetilde{C}-H)\longrightarrow H^0(\widetilde{C}, \mathcal{O}(K_{{\mathbb{P}}^2_4}+\widetilde{C}-H)\otimes\mathcal{O}_{\widetilde{C}})\end{equation*}
\begin{equation*}H^0({\mathbb{P}}^2_4,\mathcal{O}(K_{{\mathbb{P}}^2_4}+\widetilde{C}-H)\longrightarrow H^0(\widetilde{C}, \mathcal{O}(K_{{\mathbb{P}}^2_4}+\widetilde{C}-H)\otimes\mathcal{O}_{\widetilde{C}})\end{equation*} is an isomorphism; injective by  $H^0({\mathbb{P}}^2_4, \mathcal{O}(K_{{\mathbb{P}}^2_4}-H))=0$ and surjective by the Castelnuovo genus bound
$H^0({\mathbb{P}}^2_4, \mathcal{O}(K_{{\mathbb{P}}^2_4}-H))=0$ and surjective by the Castelnuovo genus bound ![]() $\pi(15,6)=13 \lt g$, as we did in the proof of Claim 3. Therefore, the residual series
$\pi(15,6)=13 \lt g$, as we did in the proof of Claim 3. Therefore, the residual series
 \begin{equation*}|K_{{\mathbb{P}}^2_4}+\widetilde{C}-\varphi^*{\mathcal{O}}_S(1)|_{|\widetilde{C}}=|K_{\widetilde{C}}-\varphi^*{\mathcal{O}}_S(1)_{|\widetilde{C}}|\end{equation*}
\begin{equation*}|K_{{\mathbb{P}}^2_4}+\widetilde{C}-\varphi^*{\mathcal{O}}_S(1)|_{|\widetilde{C}}=|K_{\widetilde{C}}-\varphi^*{\mathcal{O}}_S(1)_{|\widetilde{C}}|\end{equation*} of  $|\varphi^*{\mathcal{O}}_S(1)|_{|\widetilde{C}}$ is completely cut out by the very ample linear system
$|\varphi^*{\mathcal{O}}_S(1)|_{|\widetilde{C}}$ is completely cut out by the very ample linear system ![]() $|(3;1^4)|$ on
$|(3;1^4)|$ on ![]() ${\mathbb{P}}^2_4$ which induces an embedding
${\mathbb{P}}^2_4$ which induces an embedding ![]() $\widetilde{C}\rightarrow{\mathbb{P}}^5$ as a smooth curve of degree
$\widetilde{C}\rightarrow{\mathbb{P}}^5$ as a smooth curve of degree
 \begin{equation*}(3;1^4)\cdot \widetilde{C}=(3;1^4)\cdot (8;3,2^3)=24-3-6=15.\end{equation*}
\begin{equation*}(3;1^4)\cdot \widetilde{C}=(3;1^4)\cdot (8;3,2^3)=24-3-6=15.\end{equation*} Let ![]() $\mathcal{F}\subset\mathcal{G}^4_{13}$ be the family of such
$\mathcal{F}\subset\mathcal{G}^4_{13}$ be the family of such ![]() $\mathcal{E}=g^4_{13}$’s arising this way; i.e. the family of complete linear series
$\mathcal{E}=g^4_{13}$’s arising this way; i.e. the family of complete linear series ![]() $\mathcal{E}=g^4_{13}$’s such that
$\mathcal{E}=g^4_{13}$’s such that ![]() $C_{\mathcal{E}}\in \Sigma_{15,\mathcal{M}}$ on a rational normal scroll
$C_{\mathcal{E}}\in \Sigma_{15,\mathcal{M}}$ on a rational normal scroll ![]() $S\subset{\mathbb{P}}^4$,
$S\subset{\mathbb{P}}^4$, ![]() $\mathcal{M}=|5H-2L|$ and
$\mathcal{M}=|5H-2L|$ and  $\mathcal{E}=|\varphi^*{\mathcal{O}}_S(1)|_{|\widetilde{C_{\mathcal{E}}}}$.
$\mathcal{E}=|\varphi^*{\mathcal{O}}_S(1)|_{|\widetilde{C_{\mathcal{E}}}}$. ![]() $\mathcal{F}$ is irreducible since
$\mathcal{F}$ is irreducible since ![]() $\Sigma_{15,\mathcal{M}}$ is irreducible. By an easy dimension count,
$\Sigma_{15,\mathcal{M}}$ is irreducible. By an easy dimension count,
 \begin{align*}
\dim\mathcal{F}&=\dim\Sigma_{{15},\mathcal{M}}-\dim\mathrm{Aut}(S)\\ &=\dim|5H-2L|-\delta-\dim\mathrm{Aut}(S)=\dim|(8;3)|-3-6=29\\ & \gt 3g-3+\rho(13,15,4)=3g-3+\rho(15,15,5)=27,
\end{align*}
\begin{align*}
\dim\mathcal{F}&=\dim\Sigma_{{15},\mathcal{M}}-\dim\mathrm{Aut}(S)\\ &=\dim|5H-2L|-\delta-\dim\mathrm{Aut}(S)=\dim|(8;3)|-3-6=29\\ & \gt 3g-3+\rho(13,15,4)=3g-3+\rho(15,15,5)=27,
\end{align*} hence the family ![]() $\mathcal{F}$ is our first candidate which may contribute to a full component of
$\mathcal{F}$ is our first candidate which may contribute to a full component of ![]() $\mathcal{H}_{15,15,5}$. Explicitly, we have the natural map
$\mathcal{H}_{15,15,5}$. Explicitly, we have the natural map ![]() $\mathcal{F}\stackrel{\psi}{\rightarrow} \mathcal{F}^\vee$ sending
$\mathcal{F}\stackrel{\psi}{\rightarrow} \mathcal{F}^\vee$ sending ![]() $\mathcal{E}=g^4_{13}$ to its residual series
$\mathcal{E}=g^4_{13}$ to its residual series ![]() $|K-\mathcal{E}|=g^5_{15}$ such that
$|K-\mathcal{E}|=g^5_{15}$ such that ![]() $\psi(\mathcal{E})$ is very ample for a general
$\psi(\mathcal{E})$ is very ample for a general ![]() $\mathcal{E}\in\mathcal{F}$. Thus, there exists an irreducible family of smooth curves of degree d = 15 and g = 15 in
$\mathcal{E}\in\mathcal{F}$. Thus, there exists an irreducible family of smooth curves of degree d = 15 and g = 15 in ![]() ${\mathbb{P}}^5$ which is an
${\mathbb{P}}^5$ which is an ![]() ${\operatorname{Aut}}({\mathbb{P}}^5)$-bundle over the family
${\operatorname{Aut}}({\mathbb{P}}^5)$-bundle over the family ![]() $\mathcal{F}^\vee\subset\mathcal{G}^5_{15}$.
$\mathcal{F}^\vee\subset\mathcal{G}^5_{15}$.
(A2) ![]() $C_{\mathcal{E}}\in |4H+L|$,
$C_{\mathcal{E}}\in |4H+L|$, ![]() $p_a(C_{\mathcal{E}})=18$: We have
$p_a(C_{\mathcal{E}})=18$: We have ![]() $C_{\mathcal{E}}\in|4H+L|=|4(2l-e_1)+l-e_1|=|9l-5e_1|$. Set
$C_{\mathcal{E}}\in|4H+L|=|4(2l-e_1)+l-e_1|=|9l-5e_1|$. Set ![]() $\mathcal{L}=|4H+L|$ and let
$\mathcal{L}=|4H+L|$ and let ![]() $\Sigma_{{15},\mathcal{L}}$ be the Severi variety
$\Sigma_{{15},\mathcal{L}}$ be the Severi variety ![]() $\Sigma_{{15},\mathcal{L}}$ of curves of genus g = 15 in the linear system
$\Sigma_{{15},\mathcal{L}}$ of curves of genus g = 15 in the linear system ![]() $\mathcal{L}$. A general element of
$\mathcal{L}$. A general element of ![]() $\Sigma_{{15},\mathcal{L}}$ is a nodal curve with δ = 3 nodes as its only singularities. We take a general
$\Sigma_{{15},\mathcal{L}}$ is a nodal curve with δ = 3 nodes as its only singularities. We take a general ![]() $C\in \Sigma_{{15},\mathcal{L}}$. Let
$C\in \Sigma_{{15},\mathcal{L}}$. Let  $\widetilde{C}\subset{\mathbb{P}}^2_4$ be the strict transformation of C under the blow up of
$\widetilde{C}\subset{\mathbb{P}}^2_4$ be the strict transformation of C under the blow up of ![]() $S\cong{\mathbb{P}}^2_1$ at three nodal singularities. Hence
$S\cong{\mathbb{P}}^2_1$ at three nodal singularities. Hence  $\widetilde{C}\in|(9;5,2^3)|$ and
$\widetilde{C}\in|(9;5,2^3)|$ and
 \begin{equation*}|K_{{\mathbb{P}}^2_4}+\widetilde{C}-(2l-e_1)|=|-(3;1^4)+(9;5,2^3)-(2;1,0^3)|=|(4;3,1^3)|.\end{equation*}
\begin{equation*}|K_{{\mathbb{P}}^2_4}+\widetilde{C}-(2l-e_1)|=|-(3;1^4)+(9;5,2^3)-(2;1,0^3)|=|(4;3,1^3)|.\end{equation*}The restriction map
 \begin{equation*}H^0({\mathbb{P}}^2_4,\mathcal{O}(K_{{\mathbb{P}}^2_4}+\widetilde{C}-H)\longrightarrow H^0(\widetilde{C}, \mathcal{O}(K_{{\mathbb{P}}^2_4}+\widetilde{C}-H)\otimes\mathcal{O}_{\widetilde{C}})\end{equation*}
\begin{equation*}H^0({\mathbb{P}}^2_4,\mathcal{O}(K_{{\mathbb{P}}^2_4}+\widetilde{C}-H)\longrightarrow H^0(\widetilde{C}, \mathcal{O}(K_{{\mathbb{P}}^2_4}+\widetilde{C}-H)\otimes\mathcal{O}_{\widetilde{C}})\end{equation*} is an isomorphism; injective by  $H^0({\mathbb{P}}^2_4, \mathcal{O}(K_{{\mathbb{P}}^2_4}-H))=0$ and surjective by the Castelnuovo genus bound
$H^0({\mathbb{P}}^2_4, \mathcal{O}(K_{{\mathbb{P}}^2_4}-H))=0$ and surjective by the Castelnuovo genus bound ![]() $\pi(15,6)=13 \lt g$ by the same routine as we did in (i) in the proof of Claim 3. Therefore the residual series of
$\pi(15,6)=13 \lt g$ by the same routine as we did in (i) in the proof of Claim 3. Therefore the residual series of  $|\varphi^*{\mathcal{O}}_S(1)|_{|\widetilde{C}}$ is completely cut out by the linear system
$|\varphi^*{\mathcal{O}}_S(1)|_{|\widetilde{C}}$ is completely cut out by the linear system ![]() $|(4;3,1^3)|$ on
$|(4;3,1^3)|$ on ![]() ${\mathbb{P}}^2_4$. Note that
${\mathbb{P}}^2_4$. Note that ![]() $|(4;3,1^3)|$ is not very ample by [Reference Di Rocco14]. Furthermore, we have
$|(4;3,1^3)|$ is not very ample by [Reference Di Rocco14]. Furthermore, we have ![]() $(9;5,2^3)\cdot (2,1,1,0^2)=2$ whereas
$(9;5,2^3)\cdot (2,1,1,0^2)=2$ whereas ![]() $(4;3,1^3)\cdot (2;1,1,0^2)=0$ contracting the
$(4;3,1^3)\cdot (2;1,1,0^2)=0$ contracting the ![]() $(-1)$ curve
$(-1)$ curve ![]() $l-e_1-e_2$ to a point. Hence, the image curve under the morphism induced by
$l-e_1-e_2$ to a point. Hence, the image curve under the morphism induced by ![]() $|K_{\widetilde{C}}-\mathcal{E}|$ has a singularity. Therefore, the family of linear series arising from
$|K_{\widetilde{C}}-\mathcal{E}|$ has a singularity. Therefore, the family of linear series arising from ![]() $\mathcal{L}=|4H+L|$ does not contribute to a component of
$\mathcal{L}=|4H+L|$ does not contribute to a component of ![]() $\mathcal{H}_{15,15,5}$.
$\mathcal{H}_{15,15,5}$.
(A3) ![]() $C_{\mathcal{E}}\in |3H+4L|$,
$C_{\mathcal{E}}\in |3H+4L|$, ![]() $p_a(C_{\mathcal{E}})=15$: In this case,
$p_a(C_{\mathcal{E}})=15$: In this case, ![]() $C_{\mathcal{E}}$ is trigonal and by Claim 2, this case does not occur.
$C_{\mathcal{E}}$ is trigonal and by Claim 2, this case does not occur.
(A4) ![]() $C_{\mathcal{E}}\in |6H-5L|$,
$C_{\mathcal{E}}\in |6H-5L|$, ![]() $p_a(C_{\mathcal{E}})=15$: In this case,
$p_a(C_{\mathcal{E}})=15$: In this case, ![]() $C_{\mathcal{E}}\subset{\mathbb{P}}^4$ is smooth. For
$C_{\mathcal{E}}\subset{\mathbb{P}}^4$ is smooth. For ![]() $C_\mathcal{E}\in |6H-5L|$, we have
$C_\mathcal{E}\in |6H-5L|$, we have ![]() $|K_S+C_{\mathcal{E}}-H|=|3H-4L|.$ We may argue as in the two previous cases (A1) and (A2) to see that the restriction map
$|K_S+C_{\mathcal{E}}-H|=|3H-4L|.$ We may argue as in the two previous cases (A1) and (A2) to see that the restriction map
 \begin{equation*}H^0(S,\mathcal{O}(3H-4L))\rightarrow H^0(C_{\mathcal{E}},\mathcal{O}(3H-4L)\otimes\mathcal{O}_{C_{\mathcal{E}}})\end{equation*}
\begin{equation*}H^0(S,\mathcal{O}(3H-4L))\rightarrow H^0(C_{\mathcal{E}},\mathcal{O}(3H-4L)\otimes\mathcal{O}_{C_{\mathcal{E}}})\end{equation*} is an isomorphism; by ![]() $H^0(S,\mathcal{O}(3H-4L-C_{\mathcal{E}}))=H^0(S,\mathcal{O}(-3H+L))=0$ and by Castelnuovo genus bound.
$H^0(S,\mathcal{O}(3H-4L-C_{\mathcal{E}}))=H^0(S,\mathcal{O}(-3H+L))=0$ and by Castelnuovo genus bound.
We also remark that the linear system ![]() $|3H-4L|=|2(H-L)+(H-2L)|$ has the fixed part
$|3H-4L|=|2(H-L)+(H-2L)|$ has the fixed part ![]() $|H-2L|$;
$|H-2L|$;
Hence the linear series ![]() $|K_{C_{\mathcal{E}}}-\mathcal{E}|$ cut out by the linear system
$|K_{C_{\mathcal{E}}}-\mathcal{E}|$ cut out by the linear system ![]() $|3H-4L|$ has non-empty base locus B,
$|3H-4L|$ has non-empty base locus B, ![]() $\deg B= (H-2L)\cdot C_{\mathcal{E}}=(H-2L)\cdot(6H-5L)=1$ and hence
$\deg B= (H-2L)\cdot C_{\mathcal{E}}=(H-2L)\cdot(6H-5L)=1$ and hence ![]() $C_{\mathcal{E}}\cdot 2(H-L)=14\neq 15$. This shows that curves in
$C_{\mathcal{E}}\cdot 2(H-L)=14\neq 15$. This shows that curves in ![]() $|6H-5L|$ does not contribute to a component of
$|6H-5L|$ does not contribute to a component of ![]() $\mathcal{H}_{15,15,5}$.
$\mathcal{H}_{15,15,5}$.
(B) ![]() $\deg S=3$ and S is a cone over a twisted cubic in
$\deg S=3$ and S is a cone over a twisted cubic in ![]() ${\mathbb{P}}^3$;
${\mathbb{P}}^3$; ![]() $C_{\mathcal{E}}\subset S\subset{\mathbb{P}}^4$.
$C_{\mathcal{E}}\subset S\subset{\mathbb{P}}^4$.
Let  $\mathbb{F}_3\stackrel{|h+3f|}{\longrightarrow} S\subset{\mathbb{P}}^4$ be the minimal desingularization, which contracts h to the vertex
$\mathbb{F}_3\stackrel{|h+3f|}{\longrightarrow} S\subset{\mathbb{P}}^4$ be the minimal desingularization, which contracts h to the vertex ![]() $q\in S$;
$q\in S$; ![]() $h^2=-3, h\cdot f=0, f^2=0$. Let
$h^2=-3, h\cdot f=0, f^2=0$. Let ![]() $\widetilde{C_{{\mathcal{E}}}}\subset \mathbb{F}_3$ be the strict transformation of
$\widetilde{C_{{\mathcal{E}}}}\subset \mathbb{F}_3$ be the strict transformation of ![]() $C_{{\mathcal{E}}}\subset{\mathbb{P}}^4$ and set
$C_{{\mathcal{E}}}\subset{\mathbb{P}}^4$ and set  $\widetilde{C_{{\mathcal{E}}}}\in |ah+bf|$. We have
$\widetilde{C_{{\mathcal{E}}}}\in |ah+bf|$. We have
 \begin{equation*}\widetilde{C_{{\mathcal{E}}}}\cdot (h+3f)=(ah+bf)\cdot (h+3f)=b=13.\end{equation*}
\begin{equation*}\widetilde{C_{{\mathcal{E}}}}\cdot (h+3f)=(ah+bf)\cdot (h+3f)=b=13.\end{equation*} By (1),  $m:=h\cdot\widetilde{C_{\mathcal{E}}}=h\cdot (ah+13f)=-3a+13\ge 0,$ thus
$m:=h\cdot\widetilde{C_{\mathcal{E}}}=h\cdot (ah+13f)=-3a+13\ge 0,$ thus ![]() $a\le 4$ and hence a = 4 by Claim 2. Thus
$a\le 4$ and hence a = 4 by Claim 2. Thus  $\widetilde{C_{\mathcal{E}}}\in|4h+13f|$, m = 1,
$\widetilde{C_{\mathcal{E}}}\in|4h+13f|$, m = 1,  $p_a(\widetilde{C_{\mathcal{E}}})=18$ by adjunction formula,
$p_a(\widetilde{C_{\mathcal{E}}})=18$ by adjunction formula, ![]() $C_{\mathcal{E}}$ passes through the vertex q of S and
$C_{\mathcal{E}}$ passes through the vertex q of S and ![]() $C_{\mathcal{E}}$ is smooth at q.
$C_{\mathcal{E}}$ is smooth at q.
Set ![]() $\mathcal{N}=|4h+13f|$ and let
$\mathcal{N}=|4h+13f|$ and let ![]() $\Sigma_{15,\mathcal{N}}$ be the Severi variety
$\Sigma_{15,\mathcal{N}}$ be the Severi variety ![]() $\Sigma_{15,\mathcal{N}}$ consisting of curves of genus g = 15 in the linear system
$\Sigma_{15,\mathcal{N}}$ consisting of curves of genus g = 15 in the linear system ![]() $\mathcal{N}$ on
$\mathcal{N}$ on ![]() $\mathbb{F}_3$. Since a general element of
$\mathbb{F}_3$. Since a general element of ![]() $\Sigma_{15,\mathcal{N}}$ is a nodal curve, we may assume that
$\Sigma_{15,\mathcal{N}}$ is a nodal curve, we may assume that ![]() $\widetilde{C_{\mathcal{E}}}$ has three nodes. Let
$\widetilde{C_{\mathcal{E}}}$ has three nodes. Let ![]() $\mathbb{F}_{3,3}$ be the blow up of
$\mathbb{F}_{3,3}$ be the blow up of ![]() $\mathbb{F}_3$ at three nodes. Let
$\mathbb{F}_3$ at three nodes. Let ![]() $e_i~ (i=1,\ldots, 3)$ be exceptional divisors of the blow up and let
$e_i~ (i=1,\ldots, 3)$ be exceptional divisors of the blow up and let ![]() $f_i~ (i=1,\ldots, 3)$ be three typical fibres containing the three nodal points of
$f_i~ (i=1,\ldots, 3)$ be three typical fibres containing the three nodal points of ![]() $\widetilde{C_{\mathcal{E}}}$. After resolving the three nodal singularities of
$\widetilde{C_{\mathcal{E}}}$. After resolving the three nodal singularities of ![]() $\widetilde{C_{\mathcal{E}}}$, we get a smooth curve
$\widetilde{C_{\mathcal{E}}}$, we get a smooth curve  ${\widehat{C_{\mathcal{E}}}}\subset\mathbb{F}_{3,3}$. We have
${\widehat{C_{\mathcal{E}}}}\subset\mathbb{F}_{3,3}$. We have
 \begin{equation*}\widehat{C_{\mathcal{E}}}\in|4h+13f-\sum2e_i|, \mathrm{~~ and ~set}\end{equation*}
\begin{equation*}\widehat{C_{\mathcal{E}}}\in|4h+13f-\sum2e_i|, \mathrm{~~ and ~set}\end{equation*} \begin{align*}
\mathcal{M}:&=|\widehat{C_{\mathcal{E}}}+K_{\mathbb{F}_{3,3}}-(h+3f)|\\ &=|(4h+13f-\sum2e_i)+(-2h-5f+\sum e_i)-(h+3f)|\\ &=|h+5f-\sum e_i|.
\end{align*}
\begin{align*}
\mathcal{M}:&=|\widehat{C_{\mathcal{E}}}+K_{\mathbb{F}_{3,3}}-(h+3f)|\\ &=|(4h+13f-\sum2e_i)+(-2h-5f+\sum e_i)-(h+3f)|\\ &=|h+5f-\sum e_i|.
\end{align*} Since  $\mathcal{O}_{\mathbb{F}_{3,3}}(\mathcal{M}-\widehat{C_{\mathcal{E}}})=\mathcal{O}_{\mathbb{F}_{3,3}}(-(3h+8f-\sum e_i))$ and
$\mathcal{O}_{\mathbb{F}_{3,3}}(\mathcal{M}-\widehat{C_{\mathcal{E}}})=\mathcal{O}_{\mathbb{F}_{3,3}}(-(3h+8f-\sum e_i))$ and  $f\cdot (\mathcal{M}-\widetilde{C_{\mathcal{E}}}) \lt 0$, we have
$f\cdot (\mathcal{M}-\widetilde{C_{\mathcal{E}}}) \lt 0$, we have  $h^0({\mathbb{F}_{3,3}},\mathcal{O}(\mathcal{M}-\widehat{C_{\mathcal{E}}}))=0$ implying that the restriction map
$h^0({\mathbb{F}_{3,3}},\mathcal{O}(\mathcal{M}-\widehat{C_{\mathcal{E}}}))=0$ implying that the restriction map
 \begin{equation*}\rho: H^0({\mathbb{F}_{3,3}},\mathcal{O}(\mathcal{M}))\longrightarrow H^0(\widehat{C_{\mathcal{E}}},\mathcal{O}(\mathcal{M})\otimes\mathcal{O}_{\widehat{C_{\mathcal{E}}}})\end{equation*}
\begin{equation*}\rho: H^0({\mathbb{F}_{3,3}},\mathcal{O}(\mathcal{M}))\longrightarrow H^0(\widehat{C_{\mathcal{E}}},\mathcal{O}(\mathcal{M})\otimes\mathcal{O}_{\widehat{C_{\mathcal{E}}}})\end{equation*} is injective. Note that ![]() $h^0({\mathbb{F}_{3,3}},\mathcal{O}(\mathcal{M}))=
h^0(\mathbb{F}_3,\mathcal{O}(h+5f))-3=6$. Set
$h^0({\mathbb{F}_{3,3}},\mathcal{O}(\mathcal{M}))=
h^0(\mathbb{F}_3,\mathcal{O}(h+5f))-3=6$. Set  $\mathcal{D}:={\mathbb{P}}(H^0(\widehat{C_{\mathcal{E}}},\mathcal{O}(\mathcal{M})\otimes\mathcal{O}_{\widehat{C_{\mathcal{E}}}}))$. Since
$\mathcal{D}:={\mathbb{P}}(H^0(\widehat{C_{\mathcal{E}}},\mathcal{O}(\mathcal{M})\otimes\mathcal{O}_{\widehat{C_{\mathcal{E}}}}))$. Since  $X\stackrel{iso}{\cong}\widehat{C_{\mathcal{E}}}\stackrel{bir}{\cong}{\widetilde{C_{\mathcal{E}}}}\stackrel{bir}{\cong}{C_{\mathcal{E}}}$,
$X\stackrel{iso}{\cong}\widehat{C_{\mathcal{E}}}\stackrel{bir}{\cong}{\widetilde{C_{\mathcal{E}}}}\stackrel{bir}{\cong}{C_{\mathcal{E}}}$,  ${\mathcal{D}}=|K_{\widehat{C_{\mathcal{E}}}}-{\mathcal{E}}|$ is birationally very ample. If ρ is not surjective, we have
${\mathcal{D}}=|K_{\widehat{C_{\mathcal{E}}}}-{\mathcal{E}}|$ is birationally very ample. If ρ is not surjective, we have ![]() $\dim{\mathcal{D}}\ge 6$ and
$\dim{\mathcal{D}}\ge 6$ and ![]() $\pi(15,6)=13 \lt g=15$, which is a contradiction. Therefore, we have
$\pi(15,6)=13 \lt g=15$, which is a contradiction. Therefore, we have
 \begin{equation*}\mathrm{Im}(\rho)= H^0(\widehat{C_{\mathcal{E}}},\mathcal{O}(\mathcal{M})\otimes\mathcal{O}_{\widehat{C_{\mathcal{E}}}})\end{equation*}
\begin{equation*}\mathrm{Im}(\rho)= H^0(\widehat{C_{\mathcal{E}}},\mathcal{O}(\mathcal{M})\otimes\mathcal{O}_{\widehat{C_{\mathcal{E}}}})\end{equation*} and the restriction map ρ is surjective. Denoting by ![]() $\widetilde{f}_i$ the proper transformation of three typical fibres of fi under the blow up
$\widetilde{f}_i$ the proper transformation of three typical fibres of fi under the blow up ![]() ${\mathbb{F}}_{3,3}\rightarrow{\mathbb{F}}_3$, we have
${\mathbb{F}}_{3,3}\rightarrow{\mathbb{F}}_3$, we have
 \begin{equation*}\tilde{f}_i^2=-1, \tilde{f}_i\cdot e_i=1, h\cdot\tilde{f}_i=1, \widehat{C_{\mathcal{E}}}\cdot \tilde{f}_i=2,
(h+5f-\Sigma e_i)\cdot \tilde{f}_i=0.\end{equation*}
\begin{equation*}\tilde{f}_i^2=-1, \tilde{f}_i\cdot e_i=1, h\cdot\tilde{f}_i=1, \widehat{C_{\mathcal{E}}}\cdot \tilde{f}_i=2,
(h+5f-\Sigma e_i)\cdot \tilde{f}_i=0.\end{equation*} Hence the morphism ψ induced by  $\mathcal{M}=|\widehat{C_{\mathcal{E}}}+K_{\mathbb{F}_{3,3}}-(h+3f)|$ contracts
$\mathcal{M}=|\widehat{C_{\mathcal{E}}}+K_{\mathbb{F}_{3,3}}-(h+3f)|$ contracts ![]() $(-1)$ curves
$(-1)$ curves ![]() $\tilde{f}_i$ and the image curve
$\tilde{f}_i$ and the image curve  $\psi (\widehat{C_{\mathcal{E}}})\subset{\mathbb{P}}^5$ acquires singularities. It then follows that
$\psi (\widehat{C_{\mathcal{E}}})\subset{\mathbb{P}}^5$ acquires singularities. It then follows that  $\mathcal{M}\otimes\mathcal{O}_{\widehat{C_{\mathcal{E}}}}=|K_{\widehat{C_{\mathcal{E}}}}(-1)|={\mathcal{D}}$ is not very ample.
$\mathcal{M}\otimes\mathcal{O}_{\widehat{C_{\mathcal{E}}}}=|K_{\widehat{C_{\mathcal{E}}}}(-1)|={\mathcal{D}}$ is not very ample.
(C) ![]() $\deg S=4$ and S is smooth.
$\deg S=4$ and S is smooth.
Note that ![]() $S\cong{\mathbb{P}}^2_5$ and
$S\cong{\mathbb{P}}^2_5$ and ![]() $C_{\mathcal{E}}$ is smooth; if not, we have
$C_{\mathcal{E}}$ is smooth; if not, we have ![]() $15=g=\pi_1(13,4)\lneq p_a(C_{\mathcal{E}})\le \pi(13,4)=18$ and hence
$15=g=\pi_1(13,4)\lneq p_a(C_{\mathcal{E}})\le \pi(13,4)=18$ and hence ![]() $C_{\mathcal{E}}$ is a nearly extremal curve lying on a cubic surface, which has been treated already in the steps (A) and (B). Setting
$C_{\mathcal{E}}$ is a nearly extremal curve lying on a cubic surface, which has been treated already in the steps (A) and (B). Setting ![]() $C_{\mathcal{E}}\in |(a;b_1,\ldots ,b_5)|$, we have
$C_{\mathcal{E}}\in |(a;b_1,\ldots ,b_5)|$, we have
 \begin{equation*}\deg C_{\mathcal{E}} =3a-\sum b_i=13, C_{\mathcal{E}}^2=a^2-\sum b_i^2=2g-2-K_S\cdot C=41.\end{equation*}
\begin{equation*}\deg C_{\mathcal{E}} =3a-\sum b_i=13, C_{\mathcal{E}}^2=a^2-\sum b_i^2=2g-2-K_S\cdot C=41.\end{equation*}By Schwartz’s inequality, we have
 \begin{equation*}(\sum b_i)^2\le 5(\sum b_i^2)\end{equation*}
\begin{equation*}(\sum b_i)^2\le 5(\sum b_i^2)\end{equation*} and substituting ![]() $\sum b_i=3a-13$ and
$\sum b_i=3a-13$ and ![]() $\sum b_i^2=a^2-41$ we obtain
$\sum b_i^2=a^2-41$ we obtain
 \begin{equation*}5\,({a}^{2}-41)- \left( 13-3\,a \right) ^{2}\ge 0 \Leftrightarrow a=9, 10, 11\end{equation*}
\begin{equation*}5\,({a}^{2}-41)- \left( 13-3\,a \right) ^{2}\ge 0 \Leftrightarrow a=9, 10, 11\end{equation*}and therefore we have the following three cases:
 \begin{equation*} (a;b_1,\cdots, b_5)=
\begin{cases}
(9;3^4,2)\\
(10;4^2,3^3)\\
(11;4^5).
\end{cases}
\end{equation*}
\begin{equation*} (a;b_1,\cdots, b_5)=
\begin{cases}
(9;3^4,2)\\
(10;4^2,3^3)\\
(11;4^5).
\end{cases}
\end{equation*} We need to check if ![]() $|K_{C_{\mathcal{E}}}-\mathcal{E}|=|K_S+C_{\mathcal{E}}-H|_{|C_{\mathcal{E}}}=|C_{\mathcal{E}}+2K_S|_{|C_{\mathcal{E}}}$ is very ample. The restriction map
$|K_{C_{\mathcal{E}}}-\mathcal{E}|=|K_S+C_{\mathcal{E}}-H|_{|C_{\mathcal{E}}}=|C_{\mathcal{E}}+2K_S|_{|C_{\mathcal{E}}}$ is very ample. The restriction map  $\rho: H^0(S,\mathcal{O}(C_{\mathcal{E}}+2K_S)\rightarrow H^0(C_{\mathcal{E}},\mathcal{O}(C_{\mathcal{E}}+2K_S)\otimes\mathcal{O}_{C_{\mathcal{E}}})$ is an isomorphism;
$\rho: H^0(S,\mathcal{O}(C_{\mathcal{E}}+2K_S)\rightarrow H^0(C_{\mathcal{E}},\mathcal{O}(C_{\mathcal{E}}+2K_S)\otimes\mathcal{O}_{C_{\mathcal{E}}})$ is an isomorphism; ![]() $\ker(\rho)=H^0(S, 2K_S)=0$,
$\ker(\rho)=H^0(S, 2K_S)=0$, ![]() $h^0(S,\mathcal{O}(C_{\mathcal{E}}+2K_S))=6$ and by the Castelnuovo genus bound
$h^0(S,\mathcal{O}(C_{\mathcal{E}}+2K_S))=6$ and by the Castelnuovo genus bound ![]() $\pi (15,6)=13 \lt g$ if ρ is not surjective. Assume the last case among three in the above list;
$\pi (15,6)=13 \lt g$ if ρ is not surjective. Assume the last case among three in the above list; ![]() $C_{\mathcal{E}}\in |(11;4^5)|$. We have
$C_{\mathcal{E}}\in |(11;4^5)|$. We have
whose restriction on ![]() $C_{\mathcal{E}}$ does not induce an isomorphism onto its image. To see this, the
$C_{\mathcal{E}}$ does not induce an isomorphism onto its image. To see this, the ![]() $(-1)$ curve
$(-1)$ curve ![]() $(2;1^5)$ on S is contracted to a point;
$(2;1^5)$ on S is contracted to a point; ![]() $(2;1^5)\cdot (5;2^5)=0$ whereas
$(2;1^5)\cdot (5;2^5)=0$ whereas ![]() $(11;4^5)\cdot (2;1^5)=2$ and hence the image curve in
$(11;4^5)\cdot (2;1^5)=2$ and hence the image curve in ![]() ${\mathbb{P}}^5$ is singular. The verification for the other two cases
${\mathbb{P}}^5$ is singular. The verification for the other two cases ![]() $(9;3^4,2),
(10;4^2,3^3)$ are similar which we omit. Hence we conclude that
$(9;3^4,2),
(10;4^2,3^3)$ are similar which we omit. Hence we conclude that ![]() $|K_{C_{\mathcal{E}}}-\mathcal{E}|$ is not very ample.
$|K_{C_{\mathcal{E}}}-\mathcal{E}|$ is not very ample.
(D) ![]() $\deg S=4$ and S is a cone over an elliptic curve
$\deg S=4$ and S is a cone over an elliptic curve ![]() $E\subset{\mathbb{P}}^3$:
$E\subset{\mathbb{P}}^3$:
Recall that a cone ![]() $S\subset{\mathbb{P}}^r$ over an elliptic curve
$S\subset{\mathbb{P}}^r$ over an elliptic curve ![]() $E\subset H\cong{\mathbb{P}}^{r-1}$ with vertex outside H is the image of the birational morphism
$E\subset H\cong{\mathbb{P}}^{r-1}$ with vertex outside H is the image of the birational morphism ![]() $\mathbb{E}_{r}:=\mathbb{P}(\mathcal{O}_{E}\oplus\mathcal{O}_{E}(r))\rightarrow S\subset{\mathbb{P}}^r$ induced by
$\mathbb{E}_{r}:=\mathbb{P}(\mathcal{O}_{E}\oplus\mathcal{O}_{E}(r))\rightarrow S\subset{\mathbb{P}}^r$ induced by ![]() $|\overline{h}|:=|h+rf|$, where
$|\overline{h}|:=|h+rf|$, where ![]() $h^2=-r$ and f is the fibre of
$h^2=-r$ and f is the fibre of ![]() $\mathbb{E}_{r}\stackrel{\eta}{\rightarrow} E$. Let
$\mathbb{E}_{r}\stackrel{\eta}{\rightarrow} E$. Let ![]() $C\subset S$ be an integral curve of degree d with the strict transformation
$C\subset S$ be an integral curve of degree d with the strict transformation ![]() $\widetilde{C}$ under
$\widetilde{C}$ under ![]() $\mathbb{E}_{r}\rightarrow S$. Setting
$\mathbb{E}_{r}\rightarrow S$. Setting ![]() $k=\widetilde{C}\cdot f$, we have
$k=\widetilde{C}\cdot f$, we have ![]() $\widetilde{C}\equiv kh+df$,
$\widetilde{C}\equiv kh+df$,  $\deg\eta_{|\widetilde{C}}= \widetilde{C}\cdot f=k$ and
$\deg\eta_{|\widetilde{C}}= \widetilde{C}\cdot f=k$ and
 \begin{equation}
p_a(\widetilde{C})=
(k-1)(d-\frac{kr}{2})+1,~~
0\le \widetilde{C}\cdot h=d-rk=m
\end{equation}
\begin{equation}
p_a(\widetilde{C})=
(k-1)(d-\frac{kr}{2})+1,~~
0\le \widetilde{C}\cdot h=d-rk=m
\end{equation}where m is the multiplicity of C at the vertex.
For ![]() $C=C_{\mathcal{E}}$, d = 13, and r = 4, we get
$C=C_{\mathcal{E}}$, d = 13, and r = 4, we get  $(k,m,p_a(\widetilde{C_{\mathcal{E}}}))\in\{(3,1,15), (2,5,10)\}$ by (8). In the first case, since
$(k,m,p_a(\widetilde{C_{\mathcal{E}}}))\in\{(3,1,15), (2,5,10)\}$ by (8). In the first case, since  $g=15=p_a(\widetilde{C_{\mathcal{E}}})$,
$g=15=p_a(\widetilde{C_{\mathcal{E}}})$,  $\widetilde{C_{\mathcal{E}}}\in |3h+13f|=|3\overline{h}+f|$ is smooth and is a triple covering of an elliptic curve. The second case is not possible since
$\widetilde{C_{\mathcal{E}}}\in |3h+13f|=|3\overline{h}+f|$ is smooth and is a triple covering of an elliptic curve. The second case is not possible since  $p_a(\widetilde{C_{\mathcal{E}}}) \lt g$. We now check if
$p_a(\widetilde{C_{\mathcal{E}}}) \lt g$. We now check if
 \begin{equation*}|K_{\mathbb{E}_4}+\widetilde{C_{\mathcal{E}}}-\overline{h}|_{|\widetilde{C_{\mathcal{E}}}}=|(-2\overline{h}+4f+(k\overline{h}+(d-4k)f)-\overline{h}|_{|\widetilde{C_{\mathcal{E}}}}=|5f|_{|\widetilde{C_{\mathcal{E}}}}\end{equation*}
\begin{equation*}|K_{\mathbb{E}_4}+\widetilde{C_{\mathcal{E}}}-\overline{h}|_{|\widetilde{C_{\mathcal{E}}}}=|(-2\overline{h}+4f+(k\overline{h}+(d-4k)f)-\overline{h}|_{|\widetilde{C_{\mathcal{E}}}}=|5f|_{|\widetilde{C_{\mathcal{E}}}}\end{equation*}is very ample.
Claim: The restriction map
 \begin{equation*}\rho: H^0(\mathbb{E}_4,|K_{\mathbb{E}_4}+\widetilde{C_{\mathcal{E}}}-\overline{h}|)\rightarrow H^0(\widetilde{C_{\mathcal{E}}},K_{\widetilde{C_{\mathcal{E}}}}((-1)))\end{equation*}
\begin{equation*}\rho: H^0(\mathbb{E}_4,|K_{\mathbb{E}_4}+\widetilde{C_{\mathcal{E}}}-\overline{h}|)\rightarrow H^0(\widetilde{C_{\mathcal{E}}},K_{\widetilde{C_{\mathcal{E}}}}((-1)))\end{equation*}fails to be surjective: We consider the exact sequence
 \begin{equation*}0\rightarrow\mathcal{I}_{\widetilde{C_{\mathcal{E}}}}(5f)=\mathcal{O}_{{\mathbb{E}}_4}(-3\overline{h}+4f)\rightarrow\mathcal{O}_{{\mathbb{E}}_4}(5f)\rightarrow\mathcal{O}(5f)_{|\widetilde{C_{\mathcal{E}}}}\rightarrow 0.\end{equation*}
\begin{equation*}0\rightarrow\mathcal{I}_{\widetilde{C_{\mathcal{E}}}}(5f)=\mathcal{O}_{{\mathbb{E}}_4}(-3\overline{h}+4f)\rightarrow\mathcal{O}_{{\mathbb{E}}_4}(5f)\rightarrow\mathcal{O}(5f)_{|\widetilde{C_{\mathcal{E}}}}\rightarrow 0.\end{equation*} We have  $h^0({\mathbb{E}}_4,\mathcal{O}_{{\mathbb{E}}_4}(-3\overline{h}+4f))=0$,
$h^0({\mathbb{E}}_4,\mathcal{O}_{{\mathbb{E}}_4}(-3\overline{h}+4f))=0$,  $h^0({{\mathbb{E}}_4},\mathcal{O}_{{\mathbb{E}}_4}(5f))=5$,
$h^0({{\mathbb{E}}_4},\mathcal{O}_{{\mathbb{E}}_4}(5f))=5$,  $h^1({{\mathbb{E}}_4},\mathcal{O}_{{\mathbb{E}}_4}(5f))=0$ and by Serre’s duality
$h^1({{\mathbb{E}}_4},\mathcal{O}_{{\mathbb{E}}_4}(5f))=0$ and by Serre’s duality
 \begin{equation*}h^1({\mathbb{E}}_4,\mathcal{O}_{{\mathbb{E}}_4}(-3\overline{h}+4f))=h^1(\mathcal{O}_{{\mathbb{E}}_4}(\overline{h}))=1.\end{equation*}
\begin{equation*}h^1({\mathbb{E}}_4,\mathcal{O}_{{\mathbb{E}}_4}(-3\overline{h}+4f))=h^1(\mathcal{O}_{{\mathbb{E}}_4}(\overline{h}))=1.\end{equation*} Thus ρ is not surjective and  $h^0(\widetilde{C_{\mathcal{E}}}, \mathcal{O}(5f)_{|\widetilde{C_{\mathcal{E}}}})=6$.
$h^0(\widetilde{C_{\mathcal{E}}}, \mathcal{O}(5f)_{|\widetilde{C_{\mathcal{E}}}})=6$.
Claim:  $|K_{\widetilde{C_{\mathcal{E}}}}(-1)|=|K_{\mathbb{E}_4}+\widetilde{C_{\mathcal{E}}}-\overline{h}|_{|\widetilde{C_{\mathcal{E}}}}$ is not very ample.
$|K_{\widetilde{C_{\mathcal{E}}}}(-1)|=|K_{\mathbb{E}_4}+\widetilde{C_{\mathcal{E}}}-\overline{h}|_{|\widetilde{C_{\mathcal{E}}}}$ is not very ample.
Let  $V:=\mathrm{Im}(\rho)\subset H^0(\widetilde{C_{\mathcal{E}}},\mathcal{O}(5f)_{|\widetilde{C_{\mathcal{E}}}})$ and we assume
$V:=\mathrm{Im}(\rho)\subset H^0(\widetilde{C_{\mathcal{E}}},\mathcal{O}(5f)_{|\widetilde{C_{\mathcal{E}}}})$ and we assume  $|K_{\widetilde{C_{\mathcal{E}}}}(-1)|$ is very ample inducing an isomorphism φ onto X 1. Since
$|K_{\widetilde{C_{\mathcal{E}}}}(-1)|$ is very ample inducing an isomorphism φ onto X 1. Since  ${\mathbb{P}}(V)\subsetneq |K_{\widetilde{C_{\mathcal{E}}}}(-1)|$ and
${\mathbb{P}}(V)\subsetneq |K_{\widetilde{C_{\mathcal{E}}}}(-1)|$ and ![]() $\dim V=5$, we have the following commutative diagram:
$\dim V=5$, we have the following commutative diagram:

(a) ψ is the morphism on ![]() ${\mathbb{E}}_4$ induced by the base-point-free
${\mathbb{E}}_4$ induced by the base-point-free ![]() ${\mathbb{P}}(V)=|5f|$,
${\mathbb{P}}(V)=|5f|$, ![]() $\deg E_1=\overline{h}\cdot 5f=5$,
$\deg E_1=\overline{h}\cdot 5f=5$,  $\deg\psi_{|\widetilde C_{\mathcal{E}}}=\widetilde{C_{\mathcal{E}}}\cdot f=(3\overline{h}+f)\cdot f =3$. E 1 is elliptic by Claim 2.
$\deg\psi_{|\widetilde C_{\mathcal{E}}}=\widetilde{C_{\mathcal{E}}}\cdot f=(3\overline{h}+f)\cdot f =3$. E 1 is elliptic by Claim 2.
(b) τ is the projection map with centre of projection ![]() $p_1\in{\mathbb{P}}^5$ corresponding to
$p_1\in{\mathbb{P}}^5$ corresponding to ![]() ${\mathbb{P}}(V)$, i.e. the intersection of all hyperplanes corresponding to divisors in
${\mathbb{P}}(V)$, i.e. the intersection of all hyperplanes corresponding to divisors in ![]() ${\mathbb{P}}(V)$, inducing a morphism
${\mathbb{P}}(V)$, inducing a morphism  $X_1\stackrel{\tau}{\rightarrow{E}}_1$,
$X_1\stackrel{\tau}{\rightarrow{E}}_1$, ![]() $\deg\psi=\deg\tau =3$,
$\deg\psi=\deg\tau =3$, ![]() $\tau\circ\varphi=\psi$, and
$\tau\circ\varphi=\psi$, and ![]() $p_1\notin X_1$ since
$p_1\notin X_1$ since ![]() ${\mathbb{P}}(V)$ is base-point-free.
${\mathbb{P}}(V)$ is base-point-free.
Let ![]() $T_1\subset{\mathbb{P}}^5$ be a cone over E 1 with vertex p 1. T 1 is the image of the morphism on
$T_1\subset{\mathbb{P}}^5$ be a cone over E 1 with vertex p 1. T 1 is the image of the morphism on ![]() $\mathbb{E}_5:=\mathbb{P}(\mathcal{O}_{E_1}\oplus\mathcal{O}_{E_1}(5))$ induced by
$\mathbb{E}_5:=\mathbb{P}(\mathcal{O}_{E_1}\oplus\mathcal{O}_{E_1}(5))$ induced by  $|\widetilde{h}|:=|h+5f|$ and we have
$|\widetilde{h}|:=|h+5f|$ and we have ![]() $X_1\subset T_1$. Let
$X_1\subset T_1$. Let ![]() $\widetilde{X}_1$ be the strict transformation of X 1 via
$\widetilde{X}_1$ be the strict transformation of X 1 via ![]() ${\mathbb{E}}_5\rightarrow T_1$. Setting
${\mathbb{E}}_5\rightarrow T_1$. Setting ![]() $k=\widetilde{X}_1\cdot f$, we have
$k=\widetilde{X}_1\cdot f$, we have  $\widetilde{X}_1\equiv k\widetilde{h}+(d-5k)f$. By (8) (for d = 15, r = 5), we get
$\widetilde{X}_1\equiv k\widetilde{h}+(d-5k)f$. By (8) (for d = 15, r = 5), we get  $(k,m,p_a({\widetilde{X}_1}))\in\{(3,0,16), (2,5,11)\}$. In the first case
$(k,m,p_a({\widetilde{X}_1}))\in\{(3,0,16), (2,5,11)\}$. In the first case  $p_a(\widetilde{X})=p_a(X)=16 \gt g=15$, a contradiction since X 1 and
$p_a(\widetilde{X})=p_a(X)=16 \gt g=15$, a contradiction since X 1 and ![]() $\widetilde{X}_1$ are smooth. The second case is not possible since
$\widetilde{X}_1$ are smooth. The second case is not possible since  $p_a(\widetilde{X}) \lt g$. Thus we deduce that
$p_a(\widetilde{X}) \lt g$. Thus we deduce that  $|K_{\widetilde{C_{\mathcal{E}}}}(-1)|$ is not very ample.
$|K_{\widetilde{C_{\mathcal{E}}}}(-1)|$ is not very ample.
(E) ![]() $\deg S=4$ and S is singular with isolated singularities;
$\deg S=4$ and S is singular with isolated singularities; ![]() $C_{\mathcal{E}}\subset S\subset{\mathbb{P}}^4$. We see that
$C_{\mathcal{E}}\subset S\subset{\mathbb{P}}^4$. We see that ![]() $C_{\mathcal{E}}$ is smooth; otherwise, we have
$C_{\mathcal{E}}$ is smooth; otherwise, we have ![]() $15=g=\pi_1(13,4)\lneq p_a(C_{\mathcal{E}})\le \pi(13,4)=18$, hence
$15=g=\pi_1(13,4)\lneq p_a(C_{\mathcal{E}})\le \pi(13,4)=18$, hence ![]() $C_{\mathcal{E}}$ is a nearly extremal curve lying on a cubic surface which has been treated already in the steps (A) and (B). We assume that there is a smooth curve C—which we may take as
$C_{\mathcal{E}}$ is a nearly extremal curve lying on a cubic surface which has been treated already in the steps (A) and (B). We assume that there is a smooth curve C—which we may take as ![]() $C_{\mathcal{E}}\subset{\mathbb{P}}^4$ under our current situation—of degree d = 13 and genus g = 15 on a singular del-Pezzo surface S with isolated singularities. We also assume that the dual curve of
$C_{\mathcal{E}}\subset{\mathbb{P}}^4$ under our current situation—of degree d = 13 and genus g = 15 on a singular del-Pezzo surface S with isolated singularities. We also assume that the dual curve of ![]() $C_{\mathcal{E}}$ is a smooth curve
$C_{\mathcal{E}}$ is a smooth curve ![]() $X\subset{\mathbb{P}}^5$. By proposition 2.1, we let
$X\subset{\mathbb{P}}^5$. By proposition 2.1, we let ![]() $\{C_t\}$ be a one parameter flat family of (smooth) curves with
$\{C_t\}$ be a one parameter flat family of (smooth) curves with ![]() $C_0=C=C_{\mathcal{E}}$ lying on a singular del Pezzo
$C_0=C=C_{\mathcal{E}}$ lying on a singular del Pezzo ![]() $S\subset{\mathbb{P}}^4$ and
$S\subset{\mathbb{P}}^4$ and ![]() $\{C_t; t\neq 0 \},$ lying on smooth del Pezzo surfaces. If the dual curve
$\{C_t; t\neq 0 \},$ lying on smooth del Pezzo surfaces. If the dual curve ![]() $X=C_0^\vee\subset{\mathbb{P}}^5$ is smooth, dual curves
$X=C_0^\vee\subset{\mathbb{P}}^5$ is smooth, dual curves ![]() $\{C_t^\vee; t\neq 0\}$ are also smooth since singular curves cannot specialize to a smooth curve
$\{C_t^\vee; t\neq 0\}$ are also smooth since singular curves cannot specialize to a smooth curve ![]() $X=C_0^\vee$. However, this is contradictory to what we have verified in (C), i.e. every smooth curve
$X=C_0^\vee$. However, this is contradictory to what we have verified in (C), i.e. every smooth curve ![]() $C_t\subset {\mathbb{P}}^4$ with
$C_t\subset {\mathbb{P}}^4$ with ![]() $(d,g)=(13,15)$ lying on a smooth del Pezzo has its dual curve in
$(d,g)=(13,15)$ lying on a smooth del Pezzo has its dual curve in ![]() ${\mathbb{P}}^5$ which is always singular.
${\mathbb{P}}^5$ which is always singular.
Conclusion: We have exhausted all the possibilities for the surfaces ![]() $S\subset {\mathbb{P}}^4$ on which dual curves
$S\subset {\mathbb{P}}^4$ on which dual curves ![]() $C_{\mathcal{E}}$ of
$C_{\mathcal{E}}$ of ![]() $X\in\mathcal{H}_{15,15,5}$ may sit. Our lengthy discussion in parts (A)–(E) shows that the only case such that the residual series of the hyperplane series of
$X\in\mathcal{H}_{15,15,5}$ may sit. Our lengthy discussion in parts (A)–(E) shows that the only case such that the residual series of the hyperplane series of ![]() $C_{\mathcal{E}}\subset{\mathbb{P}}^4$ is very ample—among all the possibilities for the surface S—is the case (A1);
$C_{\mathcal{E}}\subset{\mathbb{P}}^4$ is very ample—among all the possibilities for the surface S—is the case (A1); ![]() $C_{\mathcal{E}}\subset S\subset{\mathbb{P}}^4$ lies a smooth cubic surface S,
$C_{\mathcal{E}}\subset S\subset{\mathbb{P}}^4$ lies a smooth cubic surface S, ![]() $p_a(C_{\mathcal{E}})=18$,
$p_a(C_{\mathcal{E}})=18$, ![]() $C_{\mathcal{E}}\in \Sigma_{15,\mathcal{M}}$ where
$C_{\mathcal{E}}\in \Sigma_{15,\mathcal{M}}$ where ![]() $\mathcal{M}=|5H-2L|$. Part (A1) also shows that the curve X corresponding to a general element in the Severi variety
$\mathcal{M}=|5H-2L|$. Part (A1) also shows that the curve X corresponding to a general element in the Severi variety ![]() $\Sigma_{15,\mathcal{M}}$ lies on a smooth del Pezzo surface in
$\Sigma_{15,\mathcal{M}}$ lies on a smooth del Pezzo surface in ![]() ${\mathbb{P}}^5$; cf. (7). From (6), we see that a general
${\mathbb{P}}^5$; cf. (7). From (6), we see that a general ![]() $X\in\mathcal{H}_{15,15,5}$ has a plane model of degree 8 with an ordinary triple point and lines through the triple point cut out a base-point-free
$X\in\mathcal{H}_{15,15,5}$ has a plane model of degree 8 with an ordinary triple point and lines through the triple point cut out a base-point-free ![]() $g^1_5$. X does not have
$g^1_5$. X does not have ![]() $g^1_4$ by Castelnuvo–Severi inequality.
$g^1_4$ by Castelnuvo–Severi inequality.
4.2. Moduli map  $\mu: \mathcal{H}_{15,15,5}\rightarrow {\mathcal{M}}_{15}$
$\mu: \mathcal{H}_{15,15,5}\rightarrow {\mathcal{M}}_{15}$
In this subsection, we show that two smooth curves in ![]() $\mathcal{H}_{15,15,5}$ are isomorphic as abstract curves if and only if they are projectively equivalent. In order to prove this seemingly plausible assertion, we need several preparatory results which occupy a major part of this subsection.
$\mathcal{H}_{15,15,5}$ are isomorphic as abstract curves if and only if they are projectively equivalent. In order to prove this seemingly plausible assertion, we need several preparatory results which occupy a major part of this subsection.
Let ![]() $X\subset {\mathbb{P}}^r$,
$X\subset {\mathbb{P}}^r$, ![]() $r\ge 2$, be a smooth curve of genus
$r\ge 2$, be a smooth curve of genus ![]() $g\ge 2$. Since X has only finitely many automorphisms, the set
$g\ge 2$. Since X has only finitely many automorphisms, the set ![]() $G:=\{h\in {\operatorname{Aut}}({\mathbb{P}}^r)| h(X)=X\}$ is a finite group. Hence the set
$G:=\{h\in {\operatorname{Aut}}({\mathbb{P}}^r)| h(X)=X\}$ is a finite group. Hence the set
consisting of all curves ![]() $Y\subset {\mathbb{P}}^r$ projectively equivalent to X is an irreducible quasi-projective variety isomorphic to
$Y\subset {\mathbb{P}}^r$ projectively equivalent to X is an irreducible quasi-projective variety isomorphic to ![]() ${\operatorname{Aut}}({\mathbb{P}}^r)/G$.
${\operatorname{Aut}}({\mathbb{P}}^r)/G$.
Theorem 4.2 Let ![]() $\mu: \mathcal{H}_{15,15,5}\rightarrow {\mathcal{M}}_{15}$ denote the moduli map. Then we have
$\mu: \mathcal{H}_{15,15,5}\rightarrow {\mathcal{M}}_{15}$ denote the moduli map. Then we have ![]() $\mu^{-1}(\mu(X)) =\mathrm{Aut}({\mathbb{P}}^5)X$ for a general
$\mu^{-1}(\mu(X)) =\mathrm{Aut}({\mathbb{P}}^5)X$ for a general ![]() $X\in \mathcal{H}_{15,15,5}$.
$X\in \mathcal{H}_{15,15,5}$.
We review a few basic facts about residual schemes which we use in theorem 4.5, an essential step towards the proof of theorem 4.2.
Remark 4.3. Let S be a projective variety, D an effective Cartier divisor of S and ![]() $Z\subset S$ a zero-dimensional scheme. The residual scheme
$Z\subset S$ a zero-dimensional scheme. The residual scheme ![]() $\operatorname{Res}_D(Z)$ of Z is by definition the closed subscheme of S with
$\operatorname{Res}_D(Z)$ of Z is by definition the closed subscheme of S with ![]() ${\mathcal{I}}_Z:{\mathcal{I}}_D$ as its ideal sheaf. We have
${\mathcal{I}}_Z:{\mathcal{I}}_D$ as its ideal sheaf. We have ![]() $\operatorname{Res}_D(Z)\subseteq Z$ and
$\operatorname{Res}_D(Z)\subseteq Z$ and
We also have
•
 $\operatorname{Res}_D(Z)=Z$ if and only if
$\operatorname{Res}_D(Z)=Z$ if and only if  $Z\cap D=\emptyset$.
$Z\cap D=\emptyset$.•
 $\operatorname{Res}_D(Z)=\emptyset$ if and only if
$\operatorname{Res}_D(Z)=\emptyset$ if and only if  $Z\subset D$.
$Z\subset D$.• If Z is a finite set then
 $\operatorname{Res}_D(Z) =Z\setminus Z\cap D$.
$\operatorname{Res}_D(Z) =Z\setminus Z\cap D$.• If
 $Z =Z_1\cup Z_2$ with
$Z =Z_1\cup Z_2$ with  $Z_1\cap Z_2=\emptyset$ then
$Z_1\cap Z_2=\emptyset$ then  $\operatorname{Res}_D(Z) =\operatorname{Res}_D(Z_1)\cup \operatorname{Res}_D(Z_2)$. Hence to compute
$\operatorname{Res}_D(Z) =\operatorname{Res}_D(Z_1)\cup \operatorname{Res}_D(Z_2)$. Hence to compute  $\operatorname{Res}_D(Z)$ we may look separately at the connected components of Z.
$\operatorname{Res}_D(Z)$ we may look separately at the connected components of Z.• Let D 1 and D 2 be effective Cartier divisors of S. Call
 $D_1+D_2$ the sum of effective divisors. We have
$D_1+D_2$ the sum of effective divisors. We have⋄
 $D_1+D_2=D_1\cup D_2$ if and only if D 1 and D 2 have no common irreducible component.
$D_1+D_2=D_1\cup D_2$ if and only if D 1 and D 2 have no common irreducible component.⋄
 $\operatorname{Res}_{D_1+D_2}(Z) =\operatorname{Res}_{D_1}(\operatorname{Res}_{D_2}(Z))$.
$\operatorname{Res}_{D_1+D_2}(Z) =\operatorname{Res}_{D_1}(\operatorname{Res}_{D_2}(Z))$.⋄ If
 $Z\subset D_1+D_2$, then
$Z\subset D_1+D_2$, then  $\operatorname{Res}_{D_1}(Z)\subset D_2$ and
$\operatorname{Res}_{D_1}(Z)\subset D_2$ and  $\operatorname{Res}_{D_2}(Z)\subset D_1$.
$\operatorname{Res}_{D_2}(Z)\subset D_1$.
• Take a smooth point p of S and call 2p (resp. 3p) the closed subscheme of S with
 $({\mathcal{I}}_p)^2$ (resp.
$({\mathcal{I}}_p)^2$ (resp.  $({\mathcal{I}}_p)^3)$ as its ideal sheaf. We have
$({\mathcal{I}}_p)^3)$ as its ideal sheaf. We have⋄
 $(2p)_{\mathrm{red}} =(3p)_{\mathrm{red}} =\{p\}$,
$(2p)_{\mathrm{red}} =(3p)_{\mathrm{red}} =\{p\}$,  $\deg (2p) =1+\dim S$,
$\deg (2p) =1+\dim S$,  $\deg (3p) =\binom{\dim S +2}{2}$.
$\deg (3p) =\binom{\dim S +2}{2}$.⋄ For a smooth point p of D,
 $\operatorname{Res}_D(2p) = p$ and
$\operatorname{Res}_D(2p) = p$ and  $\operatorname{Res}_D(3p) =2p$.
$\operatorname{Res}_D(3p) =2p$.⋄ For a singular point p of D, we have
 $2p\subset D$ and
$2p\subset D$ and  $\operatorname{Res}_D(2p) =\emptyset$.
$\operatorname{Res}_D(2p) =\emptyset$.
• Let
 ${\mathcal{R}}$ be a line bundle on S. We have the following exact sequence, usually called the residual exact sequence of Z with respect to D:
(10)
${\mathcal{R}}$ be a line bundle on S. We have the following exact sequence, usually called the residual exact sequence of Z with respect to D:
(10) \begin{equation}
0 \rightarrow {\mathcal{I}}_{\operatorname{Res}_D(Z)} \otimes {\mathcal{R}}(-D) \rightarrow {\mathcal{I}}_Z\otimes {\mathcal{R}} \rightarrow {\mathcal{I}}_{Z\cap D,D}\otimes {\mathcal{R}}_{|D}\rightarrow 0.
\end{equation}
\begin{equation}
0 \rightarrow {\mathcal{I}}_{\operatorname{Res}_D(Z)} \otimes {\mathcal{R}}(-D) \rightarrow {\mathcal{I}}_Z\otimes {\mathcal{R}} \rightarrow {\mathcal{I}}_{Z\cap D,D}\otimes {\mathcal{R}}_{|D}\rightarrow 0.
\end{equation}
For further details on residual schemes, readers are advised to consult [Reference Ballico5, Section 2] and references therein.
Remark 4.4 (a) Let ![]() $g^r_d$,
$g^r_d$, ![]() $r\ge 2$, be a base-point-free linear series on a smooth curve X which is not compounded. Then its monodromy is the full symmetric group Sd ([Reference Arbarello, Cornalba, Griffiths and Harris4, p. 111] or [Reference Harris19, pp. 85–86]). Later in this section, this will be used in the following way. Let Li (
$r\ge 2$, be a base-point-free linear series on a smooth curve X which is not compounded. Then its monodromy is the full symmetric group Sd ([Reference Arbarello, Cornalba, Griffiths and Harris4, p. 111] or [Reference Harris19, pp. 85–86]). Later in this section, this will be used in the following way. Let Li (![]() $1\le i\le s$) be linear series on X, possibly incomplete. Since the monodromy group of the
$1\le i\le s$) be linear series on X, possibly incomplete. Since the monodromy group of the ![]() $g^r_d$ is the full symmetric group, there is a non-empty open subset Ui of
$g^r_d$ is the full symmetric group, there is a non-empty open subset Ui of ![]() $g^r_d$ such that for each
$g^r_d$ such that for each ![]() $V\in U_i$ all subsets of V with the same cardinality impose the same number of conditions on Li. Every element of
$V\in U_i$ all subsets of V with the same cardinality impose the same number of conditions on Li. Every element of ![]() $U_1\cap \cdots \cap U_s$ has the same property for all Li,
$U_1\cap \cdots \cap U_s$ has the same property for all Li, ![]() $1\le i\le s$.
$1\le i\le s$.
(b) In the next theorem, we use a well-known and strong tool known as Horace method. Let ![]() $Y\subset {\mathbb{P}}^2$ be an integral curve of degree d and
$Y\subset {\mathbb{P}}^2$ be an integral curve of degree d and ![]() $v: X\rightarrow Y$ the normalization map. Let
$v: X\rightarrow Y$ the normalization map. Let ![]() $Z\subset {\mathbb{P}}^2$ be the zero-dimensional scheme associated with v, i.e. the scheme such that
$Z\subset {\mathbb{P}}^2$ be the zero-dimensional scheme associated with v, i.e. the scheme such that ![]() $H^0({\mathbb{P}}^2,{\mathcal{I}}_Z(d-3)) \cong H^0(X,K_X)$. Take a base point free linear system
$H^0({\mathbb{P}}^2,{\mathcal{I}}_Z(d-3)) \cong H^0(X,K_X)$. Take a base point free linear system ![]() ${\mathcal{T}}$ on X and take a general
${\mathcal{T}}$ on X and take a general ![]() $E\in {\mathcal{T}}$. Set
$E\in {\mathcal{T}}$. Set ![]() $m:=\deg(E)$ and
$m:=\deg(E)$ and ![]() $B:=v(E)$. Since
$B:=v(E)$. Since ![]() ${\mathcal{T}}$ is base point free E is formed by m distinct points,
${\mathcal{T}}$ is base point free E is formed by m distinct points, ![]() $\#B=m$ and
$\#B=m$ and ![]() $B\cap Z=\emptyset$. Set
$B\cap Z=\emptyset$. Set ![]() $W:= B\cup Z$. Knowing the integer
$W:= B\cup Z$. Knowing the integer ![]() $h^1({\mathbb{P}}^2,{\mathcal{I}}_W(d-3))$ provides a key information on
$h^1({\mathbb{P}}^2,{\mathcal{I}}_W(d-3))$ provides a key information on ![]() ${\mathcal{T}}$. For instance, if we take
${\mathcal{T}}$. For instance, if we take ![]() ${\mathcal{L}}:= v^\ast ({\mathcal{O}}_Y(1))$ and
${\mathcal{L}}:= v^\ast ({\mathcal{O}}_Y(1))$ and ![]() ${\mathcal{T}} =|{\mathcal{L}}|$ and take as B the union of d collinear smooth points of Y we get that
${\mathcal{T}} =|{\mathcal{L}}|$ and take as B the union of d collinear smooth points of Y we get that ![]() $h^0(X,{\mathcal{L}})=3$ if and only if
$h^0(X,{\mathcal{L}})=3$ if and only if ![]() $h^1({\mathbb{P}}^2,{\mathcal{I}}_W(d-3)) =h^1({\mathbb{P}}^2,{\mathcal{I}}_Z(d-4)) =0$. To say something about the Brill–Noether theory on X, e.g. in the next theorem, given a plane curve Y with
$h^1({\mathbb{P}}^2,{\mathcal{I}}_W(d-3)) =h^1({\mathbb{P}}^2,{\mathcal{I}}_Z(d-4)) =0$. To say something about the Brill–Noether theory on X, e.g. in the next theorem, given a plane curve Y with ![]() $\deg Y=d=8$ having certain prescribed singularity types (one ordinary triple point and three nodes or cusps), we want to show that there is a unique
$\deg Y=d=8$ having certain prescribed singularity types (one ordinary triple point and three nodes or cusps), we want to show that there is a unique ![]() $g^1_5$ evincing the gonality of X, exactly three base-point-free
$g^1_5$ evincing the gonality of X, exactly three base-point-free ![]() $g^1_6$’s and that Y has a unique degree d plane model. For this, we need to give upper bounds on
$g^1_6$’s and that Y has a unique degree d plane model. For this, we need to give upper bounds on ![]() $h^1({\mathbb{P}}^2,{\mathcal{I}}_{B\cup Z}(d-3))$ only from the information
$h^1({\mathbb{P}}^2,{\mathcal{I}}_{B\cup Z}(d-3))$ only from the information ![]() $\#B=m$. Specifically, to show that X has a unique
$\#B=m$. Specifically, to show that X has a unique ![]() $g^1_5$ and exactly three
$g^1_5$ and exactly three ![]() $g^1_6$, we take B with
$g^1_6$, we take B with ![]() $\#B \in \{5,6\}$ and assume
$\#B \in \{5,6\}$ and assume ![]() $h^1({\mathbb{P}}^2,{\mathcal{I}}_{B\cup Z}(5)) \gt 0$. By [Reference Bernardi, Gimigliano and Idà8, lemma 34], there is a line L such that
$h^1({\mathbb{P}}^2,{\mathcal{I}}_{B\cup Z}(5)) \gt 0$. By [Reference Bernardi, Gimigliano and Idà8, lemma 34], there is a line L such that ![]() $\deg(L\cap (Z\cup B)) \ge 7$ and then use a residual exact sequence and the explicit form of scheme Z to conclude the proof of the characterization (or description) of the base-point-free
$\deg(L\cap (Z\cup B)) \ge 7$ and then use a residual exact sequence and the explicit form of scheme Z to conclude the proof of the characterization (or description) of the base-point-free ![]() $g^1_t$’s,
$g^1_t$’s, ![]() $t\le 6$, on X. This part is a key step to prove that X has a unique
$t\le 6$, on X. This part is a key step to prove that X has a unique ![]() $g^2_8$, an essential step towards the proof of the description of the general fiber of the moduli map in genus 15; theorem 4.2. This approach, the study of the cohomology group of a certain zero-dimensional scheme
$g^2_8$, an essential step towards the proof of the description of the general fiber of the moduli map in genus 15; theorem 4.2. This approach, the study of the cohomology group of a certain zero-dimensional scheme ![]() $W\subset {\mathbb{P}}^2$ using low degree curves, say a line L, with
$W\subset {\mathbb{P}}^2$ using low degree curves, say a line L, with ![]() $\deg(L\cap W)$ very high is usually called the ‘Horace Method’; cf. [Reference Hirschowitz23].
$\deg(L\cap W)$ very high is usually called the ‘Horace Method’; cf. [Reference Hirschowitz23].
Theorem 4.5 Fix a set ![]() $A\subset {\mathbb{P}}^2$ such that
$A\subset {\mathbb{P}}^2$ such that ![]() $\#A=3$ and A is not collinear. Fix
$\#A=3$ and A is not collinear. Fix ![]() $p\in {\mathbb{P}}^2\setminus A$ such that p is not contained in a line spanned by two points in A. Let
$p\in {\mathbb{P}}^2\setminus A$ such that p is not contained in a line spanned by two points in A. Let ![]() $Y\subset {\mathbb{P}}^2$ be an integral degree 8 curve whose only singularities are either an ordinary node or an ordinary cusp at each point of A with an ordinary triple point at p. Let
$Y\subset {\mathbb{P}}^2$ be an integral degree 8 curve whose only singularities are either an ordinary node or an ordinary cusp at each point of A with an ordinary triple point at p. Let ![]() $v: X\rightarrow Y$ denote the normalization map. Then X has genus 15. Moreover
$v: X\rightarrow Y$ denote the normalization map. Then X has genus 15. Moreover
(a) X is 5-gonal and the only
 $g^1_5$ on X is induced by the pencil of lines through the ordinary triple point p.
$g^1_5$ on X is induced by the pencil of lines through the ordinary triple point p.(b) X has exactly three base-point-free
 $g^1_6$, which are induced by the pencils of lines through one of the points of A.
$g^1_6$, which are induced by the pencils of lines through one of the points of A.(c) Set
 ${\mathcal{L}}:= v^\ast ({\mathcal{O}}_Y(1))$. Then
${\mathcal{L}}:= v^\ast ({\mathcal{O}}_Y(1))$. Then  $h^0(X,{\mathcal{L}})=3$ and
$h^0(X,{\mathcal{L}})=3$ and  $|{\mathcal{L}}|$ is the unique
$|{\mathcal{L}}|$ is the unique  $g^2_8$ on X.
$g^2_8$ on X.
Proof. X has genus g = 15 by the assumption that Y has three ordinary nodes or ordinary cusps at points in A and an ordinary triple point at p. Let 2p the closed subscheme of ![]() ${\mathbb{P}}^2$ with
${\mathbb{P}}^2$ with ![]() $({\mathcal{I}}_p)^2$ as its ideal sheaf. We have
$({\mathcal{I}}_p)^2$ as its ideal sheaf. We have ![]() $\deg (2p)=3$ and
$\deg (2p)=3$ and ![]() $(2p)_{\mathrm{red}} =\{p\}$. Set and fix
$(2p)_{\mathrm{red}} =\{p\}$. Set and fix ![]() $Z:=A \cup 2p$ once and for all;
$Z:=A \cup 2p$ once and for all; ![]() $\deg (Z)=6$. We note that Z is the conductor of the normalization map, i.e. the complete linear system
$\deg (Z)=6$. We note that Z is the conductor of the normalization map, i.e. the complete linear system ![]() $|K_X|$ is induced by
$|K_X|$ is induced by ![]() $|{\mathcal{I}}_Z(5)|$. Thus to prove that
$|{\mathcal{I}}_Z(5)|$. Thus to prove that ![]() $h^0(X,{\mathcal{L}})=3$, it is sufficient to show that Z imposes six independent conditions on
$h^0(X,{\mathcal{L}})=3$, it is sufficient to show that Z imposes six independent conditions on ![]() $|{\mathcal{O}}_{{\mathbb{P}}^2}(4)|$, i.e.
$|{\mathcal{O}}_{{\mathbb{P}}^2}(4)|$, i.e. ![]() $h^1({\mathbb{P}}^2,{\mathcal{I}}_Z(4)) =0$. Recall that for a degree 6 zero-dimensional scheme
$h^1({\mathbb{P}}^2,{\mathcal{I}}_Z(4)) =0$. Recall that for a degree 6 zero-dimensional scheme ![]() $F\subset {\mathbb{P}}^2$,
$F\subset {\mathbb{P}}^2$, ![]() $h^1({\mathbb{P}}^2,{\mathcal{I}}_F(4))=0$ if and only if F is not contained in a line; cf. [Reference Bernardi, Gimigliano and Idà8, lemma 34]. Therefore, we have
$h^1({\mathbb{P}}^2,{\mathcal{I}}_F(4))=0$ if and only if F is not contained in a line; cf. [Reference Bernardi, Gimigliano and Idà8, lemma 34]. Therefore, we have ![]() $h^1({\mathbb{P}}^2,{\mathcal{I}}_Z(4)) =0$ by the assumption on Z and hence
$h^1({\mathbb{P}}^2,{\mathcal{I}}_Z(4)) =0$ by the assumption on Z and hence ![]() $h^0(X, {\mathcal{L}})=3$. We can also deduce easily that the line bundle
$h^0(X, {\mathcal{L}})=3$. We can also deduce easily that the line bundle ![]() ${\mathcal{R}}$ described in (a) and the three line bundles
${\mathcal{R}}$ described in (a) and the three line bundles ![]() ${\mathcal{L}}_1,{\mathcal{L}}_2,{\mathcal{L}}_3$ described in (b) are complete pencils. After the characterization of the (unique)
${\mathcal{L}}_1,{\mathcal{L}}_2,{\mathcal{L}}_3$ described in (b) are complete pencils. After the characterization of the (unique) ![]() $g^1_5$ and the (only) three
$g^1_5$ and the (only) three ![]() $g^1_6$’s in the following part (a) and (b), the uniqueness of the
$g^1_6$’s in the following part (a) and (b), the uniqueness of the ![]() $g^2_8$ is shown in (c).
$g^2_8$ is shown in (c).
For a line ![]() $L\subset {\mathbb{P}}^2$,
$L\subset {\mathbb{P}}^2$, ![]() $\deg (L\cap Z)\le 3$ by our assumptions on
$\deg (L\cap Z)\le 3$ by our assumptions on ![]() $A\cup \{p\}$. Note that
$A\cup \{p\}$. Note that
(i)
 $\deg (L\cap Z)=3$ if and only if L is one of the three lines, say
$\deg (L\cap Z)=3$ if and only if L is one of the three lines, say  $R_1,R_2,R_3$, containing p and one of the points of A.
$R_1,R_2,R_3$, containing p and one of the points of A.(ii)
 $\deg (L\cap Z)=2$ if and only if either L is one of the lines,
$\deg (L\cap Z)=2$ if and only if either L is one of the lines,  $L_1,L_2,L_3$, containing two of the points of A or
$L_1,L_2,L_3$, containing two of the points of A or  $p\in L$ and
$p\in L$ and  $L\notin \{R_1,R_2,R_3\}$.
$L\notin \{R_1,R_2,R_3\}$.
Recall that a conic ![]() $D\subset {\mathbb{P}}^2$ contains 2p if and only D is singular at p if and only if D is a union of two lines intersecting at p or a double line through p. Thus
$D\subset {\mathbb{P}}^2$ contains 2p if and only D is singular at p if and only if D is a union of two lines intersecting at p or a double line through p. Thus
 \begin{equation}
\begin{cases}
h^0({\mathbb{P}}^2,{\mathcal{I}}_Z(2)) =0,\\
h^1({\mathbb{P}}^2,{\mathcal{I}}_Z(2)) =0 \mathrm{~since ~} \deg (Z)=6 \mathrm{~and
~therefore }\\
h^1({\mathbb{P}}^2,{\mathcal{I}}_Z(t)) =0 \,\textrm{for all } t\ge 3.
\end{cases}
\end{equation}
\begin{equation}
\begin{cases}
h^0({\mathbb{P}}^2,{\mathcal{I}}_Z(2)) =0,\\
h^1({\mathbb{P}}^2,{\mathcal{I}}_Z(2)) =0 \mathrm{~since ~} \deg (Z)=6 \mathrm{~and
~therefore }\\
h^1({\mathbb{P}}^2,{\mathcal{I}}_Z(t)) =0 \,\textrm{for all } t\ge 3.
\end{cases}
\end{equation} (a) X has no pencil of degree four or less by the Castelnuovo–Severi inequality [Reference Accola1, theorem 3.5] and hence X is 5-gonal with a ![]() $g^1_5$ cut out by lines through p. Take a complete base-point-free pencil
$g^1_5$ cut out by lines through p. Take a complete base-point-free pencil ![]() ${\mathcal{R}}$ on X such that
${\mathcal{R}}$ on X such that ![]() $\deg ({\mathcal{R}}) = 5$. Fix a general
$\deg ({\mathcal{R}}) = 5$. Fix a general ![]() $E\in {\mathcal{R}}$ and set
$E\in {\mathcal{R}}$ and set ![]() $B:= v(E)$. We note that
$B:= v(E)$. We note that
(ai)
 $B\cap Z=\emptyset$ since
$B\cap Z=\emptyset$ since  ${\mathcal{R}}$ is base-point-free and E is general,
${\mathcal{R}}$ is base-point-free and E is general,(aii)
 $h^1({\mathbb{P}}^2,{\mathcal{I}}_{Z\cup B}(5)) \gt 0$ since
$h^1({\mathbb{P}}^2,{\mathcal{I}}_{Z\cup B}(5)) \gt 0$ since  $|K_X|$ is induced by
$|K_X|$ is induced by  $|{\mathcal{I}}_Z(5)|$ and
$|{\mathcal{I}}_Z(5)|$ and  ${\mathcal{R}}$ is a pencil,
${\mathcal{R}}$ is a pencil,(aiii)
 $h^1({\mathbb{P}}^2,{\mathcal{I}}_{Z\cup B^{\prime}}(5)) =0$ for all
$h^1({\mathbb{P}}^2,{\mathcal{I}}_{Z\cup B^{\prime}}(5)) =0$ for all  $B^{\prime}\subsetneq B$ since
$B^{\prime}\subsetneq B$ since  ${\mathcal{R}}$ is complete and base-point-free,
${\mathcal{R}}$ is complete and base-point-free,(aiv)
 $|{\mathcal{I}}_B(2)|\ne \emptyset$ since
$|{\mathcal{I}}_B(2)|\ne \emptyset$ since  $\#B=5$.
$\#B=5$.
Fix a general ![]() $C\in |{\mathcal{I}}_B(2)|$. Set
$C\in |{\mathcal{I}}_B(2)|$. Set ![]() $M:= C\cap (Z\cup B)$. Since
$M:= C\cap (Z\cup B)$. Since ![]() $B\subset C$, we have
$B\subset C$, we have ![]() $\operatorname{Res}_C(Z\cup B) =\operatorname{Res}_C(Z)$. We consider the residual exact sequence
$\operatorname{Res}_C(Z\cup B) =\operatorname{Res}_C(Z)$. We consider the residual exact sequence
of ![]() $Z\cup B$ with respect to C. Since
$Z\cup B$ with respect to C. Since ![]() $\operatorname{Res}_C(Z)\subseteq Z$ and
$\operatorname{Res}_C(Z)\subseteq Z$ and ![]() $h^1({\mathbb{P}}^2,{\mathcal{I}}_Z(2)) =0$ by (11), we have
$h^1({\mathbb{P}}^2,{\mathcal{I}}_Z(2)) =0$ by (11), we have  $h^1({\mathbb{P}}^2,{\mathcal{I}}_{\operatorname{Res}_C(Z)}(3)) =0$. Hence by (aii), the long cohomology sequence of (12) yields
$h^1({\mathbb{P}}^2,{\mathcal{I}}_{\operatorname{Res}_C(Z)}(3)) =0$. Hence by (aii), the long cohomology sequence of (12) yields
 \begin{equation*}h^1(C,{\mathcal{I}}_{M,C}(5)) \gt 0.\end{equation*}
\begin{equation*}h^1(C,{\mathcal{I}}_{M,C}(5)) \gt 0.\end{equation*} We first assume that C is smooth. Since ![]() $\deg M\le\deg (Z\cup B) =11$,
$\deg M\le\deg (Z\cup B) =11$, ![]() $\deg ({\mathcal{O}}_C(5)) =10$ and
$\deg ({\mathcal{O}}_C(5)) =10$ and ![]() $C\cong {\mathbb{P}}^1$, we have
$C\cong {\mathbb{P}}^1$, we have ![]() $h^1(C,{\mathcal{I}}_{M,C}(5))=0$, a contradiction.
$h^1(C,{\mathcal{I}}_{M,C}(5))=0$, a contradiction.
We next assume that C is singular (a priori even a double line), say ![]() $C=C_1+C_2$ with
$C=C_1+C_2$ with ![]() $\deg (C_1\cap (Z\cup B)) \ge \deg (C_2\cap (Z\cup B))$ if
$\deg (C_1\cap (Z\cup B)) \ge \deg (C_2\cap (Z\cup B))$ if ![]() $C_1\ne C_2$.
$C_1\ne C_2$.
Since ![]() $M\subset C_1+C_2$, we have
$M\subset C_1+C_2$, we have ![]() $\operatorname{Res}_{C_1+C_2}(M) =\emptyset$,
$\operatorname{Res}_{C_1+C_2}(M) =\emptyset$, ![]() $\operatorname{Res}_{C_2}(\operatorname{Res}_{C_1}(M)) =\emptyset$ and hence
$\operatorname{Res}_{C_2}(\operatorname{Res}_{C_1}(M)) =\emptyset$ and hence ![]() $\operatorname{Res}_{C_1}(M)\subset C_2$. By the basic property (9) on residual schemes in remark 4.3,
$\operatorname{Res}_{C_1}(M)\subset C_2$. By the basic property (9) on residual schemes in remark 4.3, ![]() $\deg (\mathrm{Res}_{C_1}(M))
=\deg (M) -\deg (M\cap C_1)$. Since
$\deg (\mathrm{Res}_{C_1}(M))
=\deg (M) -\deg (M\cap C_1)$. Since ![]() $\deg (M)\le 11$ and
$\deg (M)\le 11$ and ![]() $\deg (M\cap C_1)\ge \deg(M\cap C_2)$ by assumption, we have
$\deg (M\cap C_1)\ge \deg(M\cap C_2)$ by assumption, we have ![]() $\deg (M\cap C_2)\le 5$. Since
$\deg (M\cap C_2)\le 5$. Since ![]() $\operatorname{Res}_{C_1}(M)\subset C_2$ and
$\operatorname{Res}_{C_1}(M)\subset C_2$ and ![]() $\operatorname{Res}_{C_1}(M)\subseteq M$, we have
$\operatorname{Res}_{C_1}(M)\subseteq M$, we have
Since ![]() $h^1(C,{\mathcal{I}}_{M,C}(5)) \gt 0$, we have
$h^1(C,{\mathcal{I}}_{M,C}(5)) \gt 0$, we have ![]() $h^1({\mathbb{P}}^2,{\mathcal{I}}_M(5)) \gt 0$ by usual cohomology computation of the sequence
$h^1({\mathbb{P}}^2,{\mathcal{I}}_M(5)) \gt 0$ by usual cohomology computation of the sequence ![]() $0\rightarrow {\mathcal{I}}_C(5)\rightarrow {\mathcal{I}}_M(5) \rightarrow{\mathcal{I}}_{M,C}(5)\rightarrow 0$. Consider the residual exact sequence of M with respect to the line C 1;
$0\rightarrow {\mathcal{I}}_C(5)\rightarrow {\mathcal{I}}_M(5) \rightarrow{\mathcal{I}}_{M,C}(5)\rightarrow 0$. Consider the residual exact sequence of M with respect to the line C 1;
 \begin{equation}
0 \rightarrow {\mathcal{I}}_{\mathrm{Res}_{C_1}(M)}(4)\rightarrow {\mathcal{I}}_M(5) \rightarrow {\mathcal{I}}_{C_1\cap M,C_1}(5)\rightarrow 0.
\end{equation}
\begin{equation}
0 \rightarrow {\mathcal{I}}_{\mathrm{Res}_{C_1}(M)}(4)\rightarrow {\mathcal{I}}_M(5) \rightarrow {\mathcal{I}}_{C_1\cap M,C_1}(5)\rightarrow 0.
\end{equation} Since ![]() $\deg (\operatorname{Res}_{C_1}(M)) \le 5$, we have
$\deg (\operatorname{Res}_{C_1}(M)) \le 5$, we have  $h^1({\mathbb{P}}^2,{\mathcal{I}}_{\operatorname{Res}_{C_1}(M)}(4)) =0$ [Reference Bernardi, Gimigliano and Idà8, lemma 34]. Thus, the long cohomology exact sequence of (13) and
$h^1({\mathbb{P}}^2,{\mathcal{I}}_{\operatorname{Res}_{C_1}(M)}(4)) =0$ [Reference Bernardi, Gimigliano and Idà8, lemma 34]. Thus, the long cohomology exact sequence of (13) and ![]() $h^1({\mathbb{P}}^2,{\mathcal{I}}_M(5)) \gt 0$ yield
$h^1({\mathbb{P}}^2,{\mathcal{I}}_M(5)) \gt 0$ yield
 \begin{equation*}h^1(C_1,{\mathcal{I}}_{C_1\cap M}(5)) \gt 0 ~ \textrm{implying} ~\deg (C_1\cap M)\ge 7.\end{equation*}
\begin{equation*}h^1(C_1,{\mathcal{I}}_{C_1\cap M}(5)) \gt 0 ~ \textrm{implying} ~\deg (C_1\cap M)\ge 7.\end{equation*}From this, we have the following two cases:
 \begin{equation*}
\begin{cases} B\subset C_1 \mathrm{~and ~}\deg (Z\cap C_1)\ge 2 \mathrm{~ or ~} \\
\#(B\cap C_1)=4 \mathrm{~and~ } \deg (Z\cap C_1)=3.
\end{cases}
\end{equation*}
\begin{equation*}
\begin{cases} B\subset C_1 \mathrm{~and ~}\deg (Z\cap C_1)\ge 2 \mathrm{~ or ~} \\
\#(B\cap C_1)=4 \mathrm{~and~ } \deg (Z\cap C_1)=3.
\end{cases}
\end{equation*} The latter possibility is excluded for a general ![]() $E\in |{\mathcal{R}}|$, because only three lines,
$E\in |{\mathcal{R}}|$, because only three lines, ![]() $R_1,R_2,R_3$, intersect Z in a degree 3 schemes. Thus
$R_1,R_2,R_3$, intersect Z in a degree 3 schemes. Thus ![]() $B\subset C_1$ and
$B\subset C_1$ and ![]() $\deg (Z\cap C_1)=2$. Since there are only three lines,
$\deg (Z\cap C_1)=2$. Since there are only three lines, ![]() $L_1,L_2,L_3$, intersecting Z in a degree 2 scheme and not containing p, we get
$L_1,L_2,L_3$, intersecting Z in a degree 2 scheme and not containing p, we get ![]() $p\in C_1$, concluding the proof of (a).
$p\in C_1$, concluding the proof of (a).
(b) Fix a base-point-free line bundle ![]() ${\mathcal{M}}$ on X such that
${\mathcal{M}}$ on X such that ![]() $\deg ({\mathcal{M}})=6$. Since X has a unique
$\deg ({\mathcal{M}})=6$. Since X has a unique ![]() $g^1_5$ by part (a), we have
$g^1_5$ by part (a), we have ![]() $h^0(X,{\mathcal{M}})=2$. To see this, X has no birationally very ample
$h^0(X,{\mathcal{M}})=2$. To see this, X has no birationally very ample ![]() $g^2_6$ by the uniqueness of
$g^2_6$ by the uniqueness of ![]() $g^1_5$ or by genus reason. X does carry a compounded
$g^1_5$ or by genus reason. X does carry a compounded ![]() $g^2_6$ either since C is neither trigonal nor bi-elliptic.
$g^2_6$ either since C is neither trigonal nor bi-elliptic.
Fix a general ![]() $G\in |{\mathcal{M}}|$ and set
$G\in |{\mathcal{M}}|$ and set ![]() $F:= v(G)$. Since
$F:= v(G)$. Since ![]() ${\mathcal{M}}=g^1_6$ is base-point-free and complete, we have
${\mathcal{M}}=g^1_6$ is base-point-free and complete, we have ![]() $h^1({\mathbb{P}}^2,{\mathcal{I}}_{Z\cup F}(5)) \gt 0$ and
$h^1({\mathbb{P}}^2,{\mathcal{I}}_{Z\cup F}(5)) \gt 0$ and ![]() $h^1({\mathbb{P}}^2,{\mathcal{I}}_{Z\cup F^{\prime}}(5)) =0$ for all
$h^1({\mathbb{P}}^2,{\mathcal{I}}_{Z\cup F^{\prime}}(5)) =0$ for all ![]() $F^{\prime}\subsetneq F$. Choose any
$F^{\prime}\subsetneq F$. Choose any ![]() $F^{\prime}\subset F$ formed by five points and take
$F^{\prime}\subset F$ formed by five points and take ![]() $D\in |{\mathcal{I}}_{F^{\prime}}(2)|\neq\emptyset$. Set
$D\in |{\mathcal{I}}_{F^{\prime}}(2)|\neq\emptyset$. Set ![]() $N:= D\cap (Z\cup F)$. Assume D is smooth thus no 3 among F ʹ is collinear. Consider the residual exact sequence of
$N:= D\cap (Z\cup F)$. Assume D is smooth thus no 3 among F ʹ is collinear. Consider the residual exact sequence of ![]() $Z\cup F$ with respect to D;
$Z\cup F$ with respect to D;
Since ![]() $\#(F\setminus F\cap D)\le 1$,
$\#(F\setminus F\cap D)\le 1$, ![]() $\deg{\mathrm{Res}_D(Z\cup F)}\le 7$. Since no 5 among
$\deg{\mathrm{Res}_D(Z\cup F)}\le 7$. Since no 5 among ![]() $\mathrm{Res}_D(Z\cup F)$ is collinear,
$\mathrm{Res}_D(Z\cup F)$ is collinear,  $h^1({\mathbb{P}}^2,{\mathcal{I}}_{\mathrm{Res}_D(Z\cup F)}(3))=0$ by [Reference Bernardi, Gimigliano and Idà8, lemma 34]. Thus, the long cohomology sequence from (14) gives
$h^1({\mathbb{P}}^2,{\mathcal{I}}_{\mathrm{Res}_D(Z\cup F)}(3))=0$ by [Reference Bernardi, Gimigliano and Idà8, lemma 34]. Thus, the long cohomology sequence from (14) gives ![]() $h^1(D,{\mathcal{I}}_{N,D}(5)) \gt 0$. Since
$h^1(D,{\mathcal{I}}_{N,D}(5)) \gt 0$. Since ![]() $D\cong {\mathbb{P}}^1$,
$D\cong {\mathbb{P}}^1$, ![]() $\deg({\mathcal{O}}_D(5)) =10$, and
$\deg({\mathcal{O}}_D(5)) =10$, and ![]() $h^1(D,{\mathcal{I}}_{N,D}(5)) \gt 0$, we get
$h^1(D,{\mathcal{I}}_{N,D}(5)) \gt 0$, we get
On the other hand, we have ![]() $\deg (D\cap Z)\le 5$. To see this, we assume
$\deg (D\cap Z)\le 5$. To see this, we assume ![]() $\deg (D\cap Z)\ge 6$ and hence D is smooth. From the exact sequence
$\deg (D\cap Z)\ge 6$ and hence D is smooth. From the exact sequence ![]() $0\rightarrow{\mathcal{I}}_{D\cap Z, D}(2)\rightarrow{\mathcal{O}}_D(2)\rightarrow{\mathcal{O}}_{D\cap Z}(2)\rightarrow 0$, we have
$0\rightarrow{\mathcal{I}}_{D\cap Z, D}(2)\rightarrow{\mathcal{O}}_D(2)\rightarrow{\mathcal{O}}_{D\cap Z}(2)\rightarrow 0$, we have ![]() $h^1(D,{\mathcal{I}}_{D\cap Z,D}(2)) \gt 0$ following from
$h^1(D,{\mathcal{I}}_{D\cap Z,D}(2)) \gt 0$ following from ![]() $h^0(D,{\mathcal{O}}_D(2))=5$ and
$h^0(D,{\mathcal{O}}_D(2))=5$ and ![]() $h^0({\mathcal{O}}_{D\cap Z})=\deg (D\cap Z)\ge 6$. From the exact sequence
$h^0({\mathcal{O}}_{D\cap Z})=\deg (D\cap Z)\ge 6$. From the exact sequence ![]() $0\rightarrow{\mathcal{I}}_{D}(2)\rightarrow {\mathcal{I}}_{D\cap Z}(2)\rightarrow{\mathcal{I}}_{D\cap Z,D}(2)\rightarrow 0$ and by
$0\rightarrow{\mathcal{I}}_{D}(2)\rightarrow {\mathcal{I}}_{D\cap Z}(2)\rightarrow{\mathcal{I}}_{D\cap Z,D}(2)\rightarrow 0$ and by ![]() $h^i({\mathbb{P}}^2,{\mathcal{I}}_D(2))= h^i({\mathbb{P}}^2,{\mathcal{O}}_{{\mathbb{P}}^2}) =0~ (i\ge 1)$, we get
$h^i({\mathbb{P}}^2,{\mathcal{I}}_D(2))= h^i({\mathbb{P}}^2,{\mathcal{O}}_{{\mathbb{P}}^2}) =0~ (i\ge 1)$, we get ![]() $h^1({\mathbb{P}}^2,{\mathcal{I}}_{D\cap Z}(2)) \gt 0$. Since
$h^1({\mathbb{P}}^2,{\mathcal{I}}_{D\cap Z}(2)) \gt 0$. Since ![]() $D\cap Z\subseteq Z$, we get
$D\cap Z\subseteq Z$, we get ![]() $h^1({\mathbb{P}}^2,{\mathcal{I}}_Z(2)) \gt 0$ contrary to (11) concluding
$h^1({\mathbb{P}}^2,{\mathcal{I}}_Z(2)) \gt 0$ contrary to (11) concluding ![]() $\deg (D\cap Z)\le 5$, thus
$\deg (D\cap Z)\le 5$, thus
This contradiction shows that D is not smooth. Set ![]() $D=D_1+D_2$. Exactly as in step (a), we may prove the existence of a line D 1 with
$D=D_1+D_2$. Exactly as in step (a), we may prove the existence of a line D 1 with ![]() $\deg (D_1\cap N)\ge 7$. Since
$\deg (D_1\cap N)\ge 7$. Since ![]() ${\mathcal{M}}$ is not induced by the pencil of lines through p,
${\mathcal{M}}$ is not induced by the pencil of lines through p, ![]() $p\notin D_1$. For a general
$p\notin D_1$. For a general ![]() $G\in|{\mathcal{M}}|$, we have
$G\in|{\mathcal{M}}|$, we have ![]() $D_1\notin \{L_1,L_2,L_3\}$. Thus
$D_1\notin \{L_1,L_2,L_3\}$. Thus ![]() $F\subset D_1$ and D 1 contains one of the points of A, concluding the proof of (b).
$F\subset D_1$ and D 1 contains one of the points of A, concluding the proof of (b).
(c) We only need to prove the uniqueness part. Take a line bundle ![]() ${\mathcal{N}}$ on X such that
${\mathcal{N}}$ on X such that ![]() $h^0({\mathcal{N}})\ge 3$ and
$h^0({\mathcal{N}})\ge 3$ and ![]() $\deg ({\mathcal{N}})\le 8$. Since X has only finitely many base-point-free
$\deg ({\mathcal{N}})\le 8$. Since X has only finitely many base-point-free ![]() $g^1_6$’s by part (b),
$g^1_6$’s by part (b), ![]() $\deg({\mathcal{N}})=8, h^0(X,{\mathcal{N}})=3$ and
$\deg({\mathcal{N}})=8, h^0(X,{\mathcal{N}})=3$ and ![]() ${\mathcal{N}}$ is base-point-free. Part (a) implies that
${\mathcal{N}}$ is base-point-free. Part (a) implies that ![]() $|{\mathcal{N}}|$ is not compounded; if it were then either X is 4-gonal or a double covering of a smooth plane curve of degree 3, which may be excluded by the Castelnuovo–Severi inequality. We want to apply remark 4.4(a) to the linear series
$|{\mathcal{N}}|$ is not compounded; if it were then either X is 4-gonal or a double covering of a smooth plane curve of degree 3, which may be excluded by the Castelnuovo–Severi inequality. We want to apply remark 4.4(a) to the linear series ![]() $|{\mathcal{N}}|$.
$|{\mathcal{N}}|$.
Fix a general ![]() $V\in |{\mathcal{N}}|$ and set
$V\in |{\mathcal{N}}|$ and set ![]() $U:= {v}(V)$. To conclude the proof we need to prove that U is formed by eight collinear points. For a general V, we have
$U:= {v}(V)$. To conclude the proof we need to prove that U is formed by eight collinear points. For a general V, we have ![]() $Z\cap {v}(V) =\emptyset$. Since
$Z\cap {v}(V) =\emptyset$. Since ![]() $h^0(X,{\mathcal{N}})=3$, we have
$h^0(X,{\mathcal{N}})=3$, we have
Observation 1:
(0) Since V is general, remark 4.4(a) implies that if
 $\#(U\cap L)\ge 3$ for some line L, then
$\#(U\cap L)\ge 3$ for some line L, then  $U\subset L$, concluding the proof.
$U\subset L$, concluding the proof.(i) Thus from now on we may assume that no 3 points among U are collinear.
(ii) Suppose
 $\#(U\cap D)\ge 6$ for some conic D, i.e.
$\#(U\cap D)\ge 6$ for some conic D, i.e.  $U\cap D$ fails to impose independent conditions on
$U\cap D$ fails to impose independent conditions on  $|{\mathcal{O}}_{{\mathbb{P}}^2}(2)|$. Hence by remark 4.4(a), we have
$|{\mathcal{O}}_{{\mathbb{P}}^2}(2)|$. Hence by remark 4.4(a), we have  $U\subset D$.
$U\subset D$.
Observation 2:
(0) The zero-dimensional scheme
 $Z =2p\cup A$ has degree 6 and is not contained in a conic; just because A is not formed by three collinear points and any conic containing Z is singular at p.
$Z =2p\cup A$ has degree 6 and is not contained in a conic; just because A is not formed by three collinear points and any conic containing Z is singular at p.(i) We set
 ${\mathcal{Z}}:=\{D\in |{\mathcal{O}}_{{\mathbb{P}}^2}(2)| | \deg Z\cap D=5\}, {\mathcal{Z}}_1:=\{D\in {\mathcal{Z}} | 2p\subset D\},$
${\mathcal{Z}}:=\{D\in |{\mathcal{O}}_{{\mathbb{P}}^2}(2)| | \deg Z\cap D=5\}, {\mathcal{Z}}_1:=\{D\in {\mathcal{Z}} | 2p\subset D\},$  ${\mathcal{Z}}_2:= {\mathcal{Z}}\setminus {\mathcal{Z}}_1.$ Each
${\mathcal{Z}}_2:= {\mathcal{Z}}\setminus {\mathcal{Z}}_1.$ Each  $D\in {\mathcal{Z}}_1$ is singular at p and hence
$D\in {\mathcal{Z}}_1$ is singular at p and hence  $\#{\mathcal{Z}}_1=3$; each
$\#{\mathcal{Z}}_1=3$; each  $D\in {\mathcal{Z}}_1$ is the union of two lines through p containing one of the points of A. For
$D\in {\mathcal{Z}}_1$ is the union of two lines through p containing one of the points of A. For  $D\in {\mathcal{Z}}_2$,
$D\in {\mathcal{Z}}_2$,  $D\cap Z=A\cup w$, where w is degree 2 connected zero-dimensional subscheme with p as its reduction. Since no conic contains Z,
$D\cap Z=A\cup w$, where w is degree 2 connected zero-dimensional subscheme with p as its reduction. Since no conic contains Z,  $A\cup w$ uniquely determines D. Thus
$A\cup w$ uniquely determines D. Thus  ${\mathcal{Z}}_2$ is a one-dimensional family and
${\mathcal{Z}}_2$ is a one-dimensional family and  ${\mathcal{Z}}$ is an algebraic family of dimension 1.
${\mathcal{Z}}$ is an algebraic family of dimension 1.
Given ![]() $U={v}(V)$, let
$U={v}(V)$, let ![]() $D_U\in |{\mathcal{O}}_{{\mathbb{P}}^2}(2)|$ be such that
$D_U\in |{\mathcal{O}}_{{\mathbb{P}}^2}(2)|$ be such that ![]() $\#(D_U\cap U)$ is maximal. Note that
$\#(D_U\cap U)$ is maximal. Note that ![]() $\#(U\cap D_U)\ge 5$ since
$\#(U\cap D_U)\ge 5$ since ![]() $\dim |{\mathcal{O}}_{{\mathbb{P}}^2}(2)| =5$. By Observation 1(i), DU is a smooth conic. Bezout gives
$\dim |{\mathcal{O}}_{{\mathbb{P}}^2}(2)| =5$. By Observation 1(i), DU is a smooth conic. Bezout gives ![]() $\#(D_U\cap v(X)) \le 16$. Thus DU contains at most one other set U ʹ with
$\#(D_U\cap v(X)) \le 16$. Thus DU contains at most one other set U ʹ with ![]() $\#U^{\prime} =8$ with
$\#U^{\prime} =8$ with ![]() $U^{\prime}=\#v(V^{\prime}) =8$ for some
$U^{\prime}=\#v(V^{\prime}) =8$ for some ![]() $V^{\prime}\in |{\mathcal{N}}|$ and
$V^{\prime}\in |{\mathcal{N}}|$ and ![]() $U^{\prime}\cap U=\emptyset$
$U^{\prime}\cap U=\emptyset$
 \begin{equation*}
\begin{cases}
\#(D_U\cap U) =5 \,\textrm{or }
\\ U\subset D_U.
\end{cases}
\end{equation*}
\begin{equation*}
\begin{cases}
\#(D_U\cap U) =5 \,\textrm{or }
\\ U\subset D_U.
\end{cases}
\end{equation*}Now we know that there are two-dimensional family of conics
On the other hand, the family of conics
moves only in one-dimensional family by Observation 2(i). Hence for general ![]() $D_U\in{\mathcal{U}}$, we have
$D_U\in{\mathcal{U}}$, we have
(c1) Assume ![]() $\#(D_U\cap U)=5$ for general
$\#(D_U\cap U)=5$ for general ![]() $D_U\in{\mathcal{U}}$. Recall that by Observation 1(i), DU is a smooth conic and we set
$D_U\in{\mathcal{U}}$. Recall that by Observation 1(i), DU is a smooth conic and we set ![]() $W:= U\setminus D_U\cap U$ consisting of three non-collinear points. Note that
$W:= U\setminus D_U\cap U$ consisting of three non-collinear points. Note that
and hence ![]() $\deg{\mathcal{I}}_{D_U\cap (Z\cup U),D_U}(5)\ge 1$ implying
$\deg{\mathcal{I}}_{D_U\cap (Z\cup U),D_U}(5)\ge 1$ implying  $h^1(D_U,{\mathcal{I}}_{D_U\cap (Z\cup U),D_U}(5)) =0$. Consider the residual exact sequence of
$h^1(D_U,{\mathcal{I}}_{D_U\cap (Z\cup U),D_U}(5)) =0$. Consider the residual exact sequence of ![]() $Z\cup U$ with respect to D:
$Z\cup U$ with respect to D:
From the long cohomology exact sequence of (17) and (15), we have
 \begin{equation*}h^1({\mathbb{P}}^2,{\mathcal{I}}_{\mathrm{Res}_D(Z\cup U)}(3))\ge 2\end{equation*}
\begin{equation*}h^1({\mathbb{P}}^2,{\mathcal{I}}_{\mathrm{Res}_D(Z\cup U)}(3))\ge 2\end{equation*}and hence
 \begin{equation}
h^1({\mathbb{P}}^2,{\mathcal{I}}_{Z\cup W}(3))\ge h^1({\mathbb{P}}^2,{\mathcal{I}}_{\mathrm{Res}_D(Z\cup U)}(3))\ge 2.
\end{equation}
\begin{equation}
h^1({\mathbb{P}}^2,{\mathcal{I}}_{Z\cup W}(3))\ge h^1({\mathbb{P}}^2,{\mathcal{I}}_{\mathrm{Res}_D(Z\cup U)}(3))\ge 2.
\end{equation} Take a line L containing two points of W and set ![]() $\{o\}:= W\setminus W\cap L$. We consider the residual exact sequence of
$\{o\}:= W\setminus W\cap L$. We consider the residual exact sequence of ![]() $Z\cup W$ with respect to L; note that
$Z\cup W$ with respect to L; note that ![]() $\operatorname{Res}_L(Z\cup W)=\operatorname{Res}_L(Z)\cup\{o\}$. Hence we have the exact sequence
$\operatorname{Res}_L(Z\cup W)=\operatorname{Res}_L(Z)\cup\{o\}$. Hence we have the exact sequence
Since ![]() $\operatorname{Res}_L(Z)\subseteq Z$ and
$\operatorname{Res}_L(Z)\subseteq Z$ and ![]() $h^1({\mathbb{P}}^2, {\mathcal{I}} _Z(2)) =0$ (by (11)), we have
$h^1({\mathbb{P}}^2, {\mathcal{I}} _Z(2)) =0$ (by (11)), we have
 \begin{equation*}h^1({\mathcal{I}}_{\operatorname{Res}_L(Z)\cup \{o\}}(2))\le 1.\end{equation*}
\begin{equation*}h^1({\mathcal{I}}_{\operatorname{Res}_L(Z)\cup \{o\}}(2))\le 1.\end{equation*} From the long cohomology exact sequence of (19) together with (18), we have  $h^1(L,{\mathcal{I}}_{(Z\cup W)\cap L,L}(3))\ge 1$. Thus
$h^1(L,{\mathcal{I}}_{(Z\cup W)\cap L,L}(3))\ge 1$. Thus ![]() $\deg ((Z\cup W)\cap L)) \ge 5$. Since
$\deg ((Z\cup W)\cap L)) \ge 5$. Since ![]() $\deg (W\cap L) =2$, we obtain
$\deg (W\cap L) =2$, we obtain ![]() $\deg (Z\cap L)\ge 3$. Thus L is one of the three lines spanned by p and one of the points of A, say
$\deg (Z\cap L)\ge 3$. Thus L is one of the three lines spanned by p and one of the points of A, say ![]() $L=R_1$; remember that the three lines
$L=R_1$; remember that the three lines ![]() $R_i, i=1,2,3$ do not depend on the choice of
$R_i, i=1,2,3$ do not depend on the choice of ![]() $V\in|{\mathcal{N}}|$ and
$V\in|{\mathcal{N}}|$ and ![]() $U=v(V)$. On the other hand, since
$U=v(V)$. On the other hand, since ![]() $R_1\cap v(X)$ is a finite set, for a general
$R_1\cap v(X)$ is a finite set, for a general ![]() $V\in |{\mathcal{N}}|$, we have
$V\in |{\mathcal{N}}|$, we have ![]() $v(V)\cap R_1=U\cap R_1=\emptyset$. However, we took the line L containing two of the points of
$v(V)\cap R_1=U\cap R_1=\emptyset$. However, we took the line L containing two of the points of ![]() $W\subset U$, a contradiction.
$W\subset U$, a contradiction.
(c2) Assume ![]() $U\subset D_U$. In this case, we have
$U\subset D_U$. In this case, we have ![]() $\mathrm{Res}_{D_U}(Z\cup U)\subseteq Z$ and hence
$\mathrm{Res}_{D_U}(Z\cup U)\subseteq Z$ and hence  $h^1({\mathbb{P}}^2,{\mathcal{I}}_{\mathrm{Res}_{D_U}(Z\cup U)}(3)) =0$ since
$h^1({\mathbb{P}}^2,{\mathcal{I}}_{\mathrm{Res}_{D_U}(Z\cup U)}(3)) =0$ since ![]() $h^1({\mathbb{P}}^2, {\mathcal{I}}_Z(3))=0$ by (11). The long cohomology exact sequence of (17) together with (15), i.e.
$h^1({\mathbb{P}}^2, {\mathcal{I}}_Z(3))=0$ by (11). The long cohomology exact sequence of (17) together with (15), i.e. ![]() $h^1({\mathbb{P}}^2,{\mathcal{I}} _{Z\cup U}(5))\ge 2$ yields
$h^1({\mathbb{P}}^2,{\mathcal{I}} _{Z\cup U}(5))\ge 2$ yields
 \begin{equation*}h^1({D_U},{\mathcal{I}}_{{D_U}\cap (Z\cup U),{D_U}}(5)) \ge 2.\end{equation*}
\begin{equation*}h^1({D_U},{\mathcal{I}}_{{D_U}\cap (Z\cup U),{D_U}}(5)) \ge 2.\end{equation*} Recalling ![]() $\deg (Z\cap {D_U})\le 4$, on a smooth conic
$\deg (Z\cap {D_U})\le 4$, on a smooth conic ![]() ${D_U}$, we have
${D_U}$, we have ![]() $\deg ({D_U}\cap (Z\cup U)) \le 12$,
$\deg ({D_U}\cap (Z\cup U)) \le 12$, ![]() $\deg{\mathcal{I}}_{{D_U}\cap (Z\cup U),{D_U}}(5)\ge -2$ and hence
$\deg{\mathcal{I}}_{{D_U}\cap (Z\cup U),{D_U}}(5)\ge -2$ and hence  $h^1({D_U},{\mathcal{I}}_{{D_U}\cap (Z\cup U), {D_U}}(5))\le 1,$ a contradiction.
$h^1({D_U},{\mathcal{I}}_{{D_U}\cap (Z\cup U), {D_U}}(5))\le 1,$ a contradiction.
Conclusion: (c1) and (c2) show that there is a subset ![]() $B\subset U$ with
$B\subset U$ with ![]() $\#B=3$ and B is collinear, i.e.
$\#B=3$ and B is collinear, i.e. ![]() $v^{-1}(B)$ fails to impose independent conditions on
$v^{-1}(B)$ fails to impose independent conditions on ![]() ${\mathcal{L}}=v^*({\mathcal{O}}_{{\mathbb{P}}^2}(1))$, hence any subset
${\mathcal{L}}=v^*({\mathcal{O}}_{{\mathbb{P}}^2}(1))$, hence any subset ![]() $B^{\prime}\subset U$ with
$B^{\prime}\subset U$ with ![]() $\#B^{\prime}=3$ is collinear by remark 4.4 and we are done.
$\#B^{\prime}=3$ is collinear by remark 4.4 and we are done.
Proof of theorem 4.2
Recall that a general element of ![]() $X\in\mathcal{H}_{15,15,5}$ has a plane model of degree 8 with one ordinary triple point and three nodes as its only singularities; cf. part (A1) in the proof of theorem 4.1. We also recall that a curve with a plane model C of degree 8 with such prescribed singularities is embedded into
$X\in\mathcal{H}_{15,15,5}$ has a plane model of degree 8 with one ordinary triple point and three nodes as its only singularities; cf. part (A1) in the proof of theorem 4.1. We also recall that a curve with a plane model C of degree 8 with such prescribed singularities is embedded into ![]() ${\mathbb{P}}^5$ as a smooth curve of degree 15 and genus g = 15 in the following way:
${\mathbb{P}}^5$ as a smooth curve of degree 15 and genus g = 15 in the following way:
(i) Blowing up ![]() ${\mathbb{P}}^2$ at four (singular) points in general position in
${\mathbb{P}}^2$ at four (singular) points in general position in ![]() ${\mathbb{P}}^2$ and then take the strict transformation
${\mathbb{P}}^2$ and then take the strict transformation ![]() $\widetilde{C}$ of C in
$\widetilde{C}$ of C in ![]() ${\mathbb{P}}^2_4$ under this blow up.
${\mathbb{P}}^2_4$ under this blow up.
(ii) We then embed ![]() ${\mathbb{P}}^2_4$ and
${\mathbb{P}}^2_4$ and ![]() $\widetilde{C}$ by the anticanonical system
$\widetilde{C}$ by the anticanonical system  $|-K_{{\mathbb{P}}^2_4}|=|(3;1^4)|$ to get a smooth del Pezzo
$|-K_{{\mathbb{P}}^2_4}|=|(3;1^4)|$ to get a smooth del Pezzo ![]() $S\subset{\mathbb{P}}^5$ and smooth
$S\subset{\mathbb{P}}^5$ and smooth ![]() $\widetilde{C}\cong X\subset{\mathbb{P}}^5$.
$\widetilde{C}\cong X\subset{\mathbb{P}}^5$.
Now we fix four points ![]() $A\subset{\mathbb{P}}^2$ in general linear position. Let
$A\subset{\mathbb{P}}^2$ in general linear position. Let ![]() $C_i,~ 1\le i\le2$ be two plane curves of degree 8 with one triple point and three nodes with
$C_i,~ 1\le i\le2$ be two plane curves of degree 8 with one triple point and three nodes with ![]() $\mathrm{Sing}(C_i)=A$. By theorem 4.5, we have the following equivalent conditions:
$\mathrm{Sing}(C_i)=A$. By theorem 4.5, we have the following equivalent conditions:
(a) Two curves
 $X_i\subset{\mathbb{P}}^5, i=1,2$ such that
$X_i\subset{\mathbb{P}}^5, i=1,2$ such that  $X_i\cong\widetilde{C}_i$ are isomorphic.
$X_i\cong\widetilde{C}_i$ are isomorphic.(b) Two singular plane models Ci of Xi are projectively equivalent under a projective motion of
 ${\mathbb{P}}^2$ inducing a permutation on the set
${\mathbb{P}}^2$ inducing a permutation on the set  $A\subset{\mathbb{P}}^2$.
$A\subset{\mathbb{P}}^2$.(c) Xi lies on a same smooth del Pezzo surface
 $S\subset{\mathbb{P}}^5$.
$S\subset{\mathbb{P}}^5$.(d) There exists
 $\tau\in{\operatorname{Aut}}(S)$ such that
$\tau\in{\operatorname{Aut}}(S)$ such that  $X_1=\tau(X_2)$.
$X_1=\tau(X_2)$.
Note that for a smooth del Pezzo ![]() $S\subset{\mathbb{P}}^5$ and
$S\subset{\mathbb{P}}^5$ and ![]() $\tau\in{\operatorname{Aut}}(S)$, there is
$\tau\in{\operatorname{Aut}}(S)$, there is ![]() $\beta\in {\operatorname{Aut}}({\mathbb{P}}^5)$ such that
$\beta\in {\operatorname{Aut}}({\mathbb{P}}^5)$ such that ![]() $\beta_{|S} =\tau$ since S is anticanonically embedded in
$\beta_{|S} =\tau$ since S is anticanonically embedded in ![]() ${\mathbb{P}}^5$. Hence we have
${\mathbb{P}}^5$. Hence we have ![]() $\beta(X_2)=\tau(X_2)=X_1$.
$\beta(X_2)=\tau(X_2)=X_1$.
5. Curves of genus g = 16
5.1. Reducibility of  $\mathcal{H}_{15,16,5}$
$\mathcal{H}_{15,16,5}$
The aim of this subsection is to prove the following reducibility result for ![]() $\mathcal{H}_{15,16,5}$.
$\mathcal{H}_{15,16,5}$.
Theorem 5.1 ![]() $\mathcal{H}_{15,16,5}$ has three irreducible components, Γ1, Γ2 and Γ3, described as follows:
$\mathcal{H}_{15,16,5}$ has three irreducible components, Γ1, Γ2 and Γ3, described as follows:
(1)
 $\dim \Gamma _1=68$, every
$\dim \Gamma _1=68$, every  $X\in \Gamma _1$ lies on a smooth quartic surface and is trigonal.
$X\in \Gamma _1$ lies on a smooth quartic surface and is trigonal.(2)
 $\dim \Gamma_2=64$, every
$\dim \Gamma_2=64$, every  $X\in \Gamma _2$ lies on a smooth quartic surface and is pentagonal.
$X\in \Gamma _2$ lies on a smooth quartic surface and is pentagonal.(3)
 $\dim \Gamma_3=65$, every
$\dim \Gamma_3=65$, every  $X\in \Gamma_3$ is ACM, lies on a quintic surface, is 6-gonal and
$X\in \Gamma_3$ is ACM, lies on a quintic surface, is 6-gonal and  $K_X\cong {\mathcal{O}}_X(2)$.
$K_X\cong {\mathcal{O}}_X(2)$.
Take ![]() $X\in \mathcal{H}_{15,16,5}$. By the Castelnuovo’s genus bound,
$X\in \mathcal{H}_{15,16,5}$. By the Castelnuovo’s genus bound, ![]() $\pi(15,6)=13$ and
$\pi(15,6)=13$ and ![]() $\pi(15,5)=18$, hence X is linearly normal. Since
$\pi(15,5)=18$, hence X is linearly normal. Since ![]() $\pi_1(15,5)=16=g \lt \pi (15,5)$,
$\pi_1(15,5)=16=g \lt \pi (15,5)$, ![]() $X\subset S\subset{\mathbb{P}}^5$ where S an irreducible surface with
$X\subset S\subset{\mathbb{P}}^5$ where S an irreducible surface with ![]() $4\le \deg S\le 5$ by [Reference Harris19, theorem 3.15]. We start making observations for the case
$4\le \deg S\le 5$ by [Reference Harris19, theorem 3.15]. We start making observations for the case ![]() $\deg S=4$.
$\deg S=4$.
(A) ![]() $\deg S=4$ case:
$\deg S=4$ case:
We may assume that S is a smooth rational normal scroll by remark 2.2 (c). Let ![]() $X\in |aH+bL|$ on S. By solving (2)—the degree and genus formula for d = 15 and
$X\in |aH+bL|$ on S. By solving (2)—the degree and genus formula for d = 15 and ![]() $p_a(X)=16$—we get
$p_a(X)=16$—we get ![]() $(a,b)\in \{(3,3), (5,-5)\}$. Thus we have an irreducible family
$(a,b)\in \{(3,3), (5,-5)\}$. Thus we have an irreducible family ![]() $\Gamma(a,b)$ of smooth curves in
$\Gamma(a,b)$ of smooth curves in ![]() ${\mathbb{P}}^5$ lying on smooth quartic surface scrolls for each
${\mathbb{P}}^5$ lying on smooth quartic surface scrolls for each ![]() $(a,b)\in \{(3,3), (5,-5)\}$ with
$(a,b)\in \{(3,3), (5,-5)\}$ with
 \begin{align*}
\dim\Gamma(a,b)&=\dim|aH+bL|+\dim\mathcal{S}(r)\\ &=\frac{a \left(a +1\right) (r-1)}{2}+\left(a +1\right) \left(b +1\right)-1+(r+3)(r-1)-3
\end{align*}
\begin{align*}
\dim\Gamma(a,b)&=\dim|aH+bL|+\dim\mathcal{S}(r)\\ &=\frac{a \left(a +1\right) (r-1)}{2}+\left(a +1\right) \left(b +1\right)-1+(r+3)(r-1)-3
\end{align*}For simpler notation, we set
Remark 5.2. ![]() $X\in \Gamma _1$ has a unique
$X\in \Gamma _1$ has a unique ![]() $g^1_3$ by the Castelnuovo–Severi inequality. By the same reason, X has no complete base-point-free
$g^1_3$ by the Castelnuovo–Severi inequality. By the same reason, X has no complete base-point-free ![]() $g^1_x$ for
$g^1_x$ for ![]() $x=4,5, 6,7$ and is not a double covering or a triple covering of an elliptic curve.
$x=4,5, 6,7$ and is not a double covering or a triple covering of an elliptic curve.
Remark 5.3. We recall that the smooth rational normal surface scrolls in ![]() ${\mathbb{P}}^5$ are either an image of an embedding of
${\mathbb{P}}^5$ are either an image of an embedding of ![]() ${\mathbb{F}}_0$ or an image of an embedding of
${\mathbb{F}}_0$ or an image of an embedding of ![]() ${\mathbb{F}}_2$. The image of
${\mathbb{F}}_2$. The image of ![]() ${\mathbb{F}}_2$ is limits of the image of
${\mathbb{F}}_2$ is limits of the image of ![]() ${\mathbb{F}}_0$ and this phenomenon is carried over to the curves lying on them.
${\mathbb{F}}_0$ and this phenomenon is carried over to the curves lying on them. ![]() ${\mathbb{F}}_0$ is isomorphic to a smooth quadric surface
${\mathbb{F}}_0$ is isomorphic to a smooth quadric surface ![]() $Q\subset{\mathbb{P}}^3$ and with this isomorphism
$Q\subset{\mathbb{P}}^3$ and with this isomorphism ![]() ${\mathcal{O}}_{{\mathbb{F}}_0}(1) \cong {\mathcal{O}}_Q(1,2)$.
${\mathcal{O}}_{{\mathbb{F}}_0}(1) \cong {\mathcal{O}}_Q(1,2)$.
(i) Take ![]() $X\in \Gamma_1$. If
$X\in \Gamma_1$. If ![]() $S\cong {\mathbb{F}}_0$,
$S\cong {\mathbb{F}}_0$, ![]() ${\mathcal{O}}_S(H)\cong{\mathcal{O}}_Q(1,2)$,
${\mathcal{O}}_S(H)\cong{\mathcal{O}}_Q(1,2)$, ![]() ${\mathcal{O}}_S(L)\cong{\mathcal{O}}_Q(0,1)$ hence
${\mathcal{O}}_S(L)\cong{\mathcal{O}}_Q(0,1)$ hence ![]() $X\in |3H+3L|=|{\mathcal{O}}_Q(1,2)^{\otimes 3}\otimes{\mathcal{O}}_Q(0,1)^{\otimes 3}|=|{\mathcal{O}}_Q(3,9)|$.
$X\in |3H+3L|=|{\mathcal{O}}_Q(1,2)^{\otimes 3}\otimes{\mathcal{O}}_Q(0,1)^{\otimes 3}|=|{\mathcal{O}}_Q(3,9)|$.
(ii) If ![]() $X\in \Gamma_1$ and
$X\in \Gamma_1$ and ![]() $S\cong {\mathbb{F}}_2$,
$S\cong {\mathbb{F}}_2$, ![]() $X\in |3H+3L|=|{\mathcal{O}}_{{\mathbb{F}}_2}(3h+12f)|$.
$X\in |3H+3L|=|{\mathcal{O}}_{{\mathbb{F}}_2}(3h+12f)|$.
(iii) For ![]() $X\in \Gamma_2$ with
$X\in \Gamma_2$ with ![]() $S\cong {\mathbb{F}}_0$,
$S\cong {\mathbb{F}}_0$, ![]() $X\in |5H-5L|=|{\mathcal{O}}_Q(5,5)|$. Thus X has exactly two
$X\in |5H-5L|=|{\mathcal{O}}_Q(5,5)|$. Thus X has exactly two ![]() $g^1_5$’s; cf. [Reference Martens28, corollary 1].
$g^1_5$’s; cf. [Reference Martens28, corollary 1].
(iv) For ![]() $X\in \Gamma _2$ with
$X\in \Gamma _2$ with ![]() $S\cong {\mathbb{F}}_2$,
$S\cong {\mathbb{F}}_2$, ![]() $X\in |5H-5L|=|{\mathcal{O}}_{{\mathbb{F}}_2}(5h+10f)|$. Thus X has only one
$X\in |5H-5L|=|{\mathcal{O}}_{{\mathbb{F}}_2}(5h+10f)|$. Thus X has only one ![]() $g^1_5$ by [Reference Martens28, corollary 1].
$g^1_5$ by [Reference Martens28, corollary 1].
Lemma 5.4. We have ![]() $h^1({\mathcal{O}}_X(2)) =0$ for all
$h^1({\mathcal{O}}_X(2)) =0$ for all ![]() $X\in \Gamma_1$.
$X\in \Gamma_1$.
Proof. Note that ![]() $\deg ({\mathcal{O}}_X(2)) =\deg (K_X)$ for
$\deg ({\mathcal{O}}_X(2)) =\deg (K_X)$ for ![]() $X\in \Gamma_1$. Suppose
$X\in \Gamma_1$. Suppose ![]() $S\cong{\mathbb{F}}_0$. By remark 5.3 (i),
$S\cong{\mathbb{F}}_0$. By remark 5.3 (i), ![]() $X\in |{\mathcal{O}}_Q(3,9)|$. From the standard exact sequence
$X\in |{\mathcal{O}}_Q(3,9)|$. From the standard exact sequence
and by ![]() $h^0({\mathcal{O}}_Q(-1,-5))=h^1({\mathcal{O}}_Q(-1,-5))=0$, we have
$h^0({\mathcal{O}}_Q(-1,-5))=h^1({\mathcal{O}}_Q(-1,-5))=0$, we have ![]() $h^0(X, {\mathcal{O}}_X(2))= h^0(X,{\mathcal{O}}_X(2,4))
=h^0( {\mathcal{O}}_Q(2,4))=15\neq g$. The case
$h^0(X, {\mathcal{O}}_X(2))= h^0(X,{\mathcal{O}}_X(2,4))
=h^0( {\mathcal{O}}_Q(2,4))=15\neq g$. The case ![]() $S\cong{\mathbb{F}}_2$ is similar.
$S\cong{\mathbb{F}}_2$ is similar.
Lemma 5.5 Let ![]() $X\in \Gamma_2$.
$X\in \Gamma_2$.
(i) If
 $X\subset S\cong{\mathbb{F}}_0$,
$X\subset S\cong{\mathbb{F}}_0$,  $h^1({\mathcal{O}}_X(2)) =0$.
$h^1({\mathcal{O}}_X(2)) =0$.(ii) If
 $X\subset S\cong{\mathbb{F}}_2$,
$X\subset S\cong{\mathbb{F}}_2$,  $h^1({\mathcal{O}}_X(2)) =1$ and
$h^1({\mathcal{O}}_X(2)) =1$ and  $K_X\cong{\mathcal{O}}_X(2)$.
$K_X\cong{\mathcal{O}}_X(2)$.
Proof. (i) If ![]() $S\cong{\mathbb{F}}_0$,
$S\cong{\mathbb{F}}_0$, ![]() $h^1({\mathcal{O}}_X(2))=0$ follows from the same computation as in lemma 5.4.
$h^1({\mathcal{O}}_X(2))=0$ follows from the same computation as in lemma 5.4.
(ii) For the case ![]() $S\cong{\mathbb{F}}_2$, we have
$S\cong{\mathbb{F}}_2$, we have ![]() $X\in |{\mathcal{O}}_{{\mathbb{F}}_2}(5h+10f)|$; remark 5.3 (iii). The exact sequence
$X\in |{\mathcal{O}}_{{\mathbb{F}}_2}(5h+10f)|$; remark 5.3 (iii). The exact sequence ![]() $0\rightarrow{\mathcal{O}}_{{\mathbb{F}}_2}(-3h-4f)\rightarrow {\mathcal{O}}_{{\mathbb{F}}_2}(2h+6f)\rightarrow {\mathcal{O}}_X(2h+6f)\rightarrow 0$ and the cohomology of line bundles on
$0\rightarrow{\mathcal{O}}_{{\mathbb{F}}_2}(-3h-4f)\rightarrow {\mathcal{O}}_{{\mathbb{F}}_2}(2h+6f)\rightarrow {\mathcal{O}}_X(2h+6f)\rightarrow 0$ and the cohomology of line bundles on ![]() ${\mathbb{F}}_2$ [Reference Laface27, proposition 2.3] yield
${\mathbb{F}}_2$ [Reference Laface27, proposition 2.3] yield
 \begin{align*}h^0(X, {\mathcal{O}}_X(2))&=h^0({\mathbb{F}}_2, {\mathcal{O}}_{{\mathbb{F}}_2}(2h+6f))+h^1({\mathbb{F}}_2,{\mathcal{O}}_{{\mathbb{F}}_2}(-3h-4f))\\ &=h^0({\mathbb{F}}_2, {\mathcal{O}}_{{\mathbb{F}}_2}(2h+6f))+h^1({\mathbb{F}}_2,{\mathcal{O}}_{{\mathbb{F}}_2}(h))=15+1=16.
\end{align*}
\begin{align*}h^0(X, {\mathcal{O}}_X(2))&=h^0({\mathbb{F}}_2, {\mathcal{O}}_{{\mathbb{F}}_2}(2h+6f))+h^1({\mathbb{F}}_2,{\mathcal{O}}_{{\mathbb{F}}_2}(-3h-4f))\\ &=h^0({\mathbb{F}}_2, {\mathcal{O}}_{{\mathbb{F}}_2}(2h+6f))+h^1({\mathbb{F}}_2,{\mathcal{O}}_{{\mathbb{F}}_2}(h))=15+1=16.
\end{align*} Therefore ![]() $h^1({\mathcal{O}}_X(2)) =1$ by Riemann–Roch.
$h^1({\mathcal{O}}_X(2)) =1$ by Riemann–Roch.
Lemma 5.6. For ![]() $X\in \Gamma_1\cup\Gamma_2$,
$X\in \Gamma_1\cup\Gamma_2$, ![]() $h^1({\mathbb{P}}^5,{\mathcal{I}}_X(3)) =2$ and
$h^1({\mathbb{P}}^5,{\mathcal{I}}_X(3)) =2$ and ![]() $h^1({\mathbb{P}}^5,{\mathcal{I}}_X(t))=0$ for all
$h^1({\mathbb{P}}^5,{\mathcal{I}}_X(t))=0$ for all ![]() $t\ge 4$.
$t\ge 4$.
Proof. Since S is ACM, ![]() $h^1({\mathbb{P}}^5,{\mathcal{I}}_X(t)) =h^1(S,{\mathcal{I}}_{X,S}(t))$ for all
$h^1({\mathbb{P}}^5,{\mathcal{I}}_X(t)) =h^1(S,{\mathcal{I}}_{X,S}(t))$ for all ![]() $t\in {\mathbb{N}}$.
$t\in {\mathbb{N}}$.
(a) Take ![]() $X\in \Gamma_1$:
$X\in \Gamma_1$:
(a-1) Assume
 $S\cong Q$. Since
$S\cong Q$. Since  $X\in |{\mathcal{O}}_Q(3,9)|$,
$X\in |{\mathcal{O}}_Q(3,9)|$,  $h^1(Q,{\mathcal{I}}_{X,Q}(t)) = h^1(Q,{\mathcal{O}}_Q(t-3,2t-9))$. We have
$h^1(Q,{\mathcal{I}}_{X,Q}(t)) = h^1(Q,{\mathcal{O}}_Q(t-3,2t-9))$. We have  $h^1(Q,{\mathcal{O}}_Q(0,-3)) =2$ and
$h^1(Q,{\mathcal{O}}_Q(0,-3)) =2$ and  $h^1(Q,{\mathcal{O}}_Q(t-3,2t-9)) =0$ for all
$h^1(Q,{\mathcal{O}}_Q(t-3,2t-9)) =0$ for all  $t\ge 4$ by the Künneth formula.
$t\ge 4$ by the Künneth formula.(a-2) Assume
 $S\cong {\mathbb{F}}_2$. We have
$S\cong {\mathbb{F}}_2$. We have  ${\mathcal{O}}_S(1) \cong {\mathcal{O}}_{{\mathbb{F}}_2}(h+3f)$,
${\mathcal{O}}_S(1) \cong {\mathcal{O}}_{{\mathbb{F}}_2}(h+3f)$,  $X\in |{\mathcal{O}}_{{\mathbb{F}}_2}(3h+ 12f)|$ and
$X\in |{\mathcal{O}}_{{\mathbb{F}}_2}(3h+ 12f)|$ and  ${\mathcal{I}}_{X,S}(t) \cong {\mathcal{O}}_{{\mathbb{F}}_2}((t-3)h+(3t-12)f)$. For t = 3,
${\mathcal{I}}_{X,S}(t) \cong {\mathcal{O}}_{{\mathbb{F}}_2}((t-3)h+(3t-12)f)$. For t = 3,  $h^1({\mathbb{P}}^5,{\mathcal{I}}_X(3)) =h^1({\mathbb{F}}_2,{\mathcal{O}}_{{\mathbb{F}}_2}(-3f)) = 2$. For
$h^1({\mathbb{P}}^5,{\mathcal{I}}_X(3)) =h^1({\mathbb{F}}_2,{\mathcal{O}}_{{\mathbb{F}}_2}(-3f)) = 2$. For  $t\ge 4$,
$t\ge 4$,  $h^1({\mathbb{P}}^5,{\mathcal{I}}_X(t))=h^1({\mathbb{F}}_2, {\mathcal{O}}_{{\mathbb{F}}_2}((t-3)h+(3t-12)f)) = 0$; cf. [Reference Laface27, proposition 2.3].
$h^1({\mathbb{P}}^5,{\mathcal{I}}_X(t))=h^1({\mathbb{F}}_2, {\mathcal{O}}_{{\mathbb{F}}_2}((t-3)h+(3t-12)f)) = 0$; cf. [Reference Laface27, proposition 2.3].
(b) Take ![]() $X\in \Gamma_2$:
$X\in \Gamma_2$:
(b-1) If
 $S\cong Q$, we have
$S\cong Q$, we have  $X\in |{\mathcal{O}}_Q(5,5)|$ and
$X\in |{\mathcal{O}}_Q(5,5)|$ and  ${\mathcal{I}}_{X,S}(t) \cong {\mathcal{O}}_Q(t-5,2t-5)$.
${\mathcal{I}}_{X,S}(t) \cong {\mathcal{O}}_Q(t-5,2t-5)$.(b-2) If
 $S\cong {\mathbb{F}}_2$, we have
$S\cong {\mathbb{F}}_2$, we have  $X\in |{\mathcal{O}}_{{\mathbb{F}}_2}(5h+ 10f)|$ and
$X\in |{\mathcal{O}}_{{\mathbb{F}}_2}(5h+ 10f)|$ and  ${\mathcal{I}}_{X,S}(t)\cong {\mathcal{O}}_{{\mathbb{F}}_2}((t-5)h+(3t-10)f)$.
${\mathcal{I}}_{X,S}(t)\cong {\mathcal{O}}_{{\mathbb{F}}_2}((t-5)h+(3t-10)f)$.
The verification for this case (b) is similar and we omit the routine.
(B) ![]() $\deg S=5$ case: We set
$\deg S=5$ case: We set
We recall the following well-known fact regarding surfaces of degree 5 in ![]() ${\mathbb{P}}^5$.
${\mathbb{P}}^5$.
Remark 5.7. Let ![]() $S\subset{\mathbb{P}}^5$ be a quintic surface. By the classification of quintic surfaces in
$S\subset{\mathbb{P}}^5$ be a quintic surface. By the classification of quintic surfaces in ![]() ${\mathbb{P}}^5$, S is one of the following:
${\mathbb{P}}^5$, S is one of the following:
(i) a del Pezzo surface possibly with finitely many isolated double points
(ii) a cone over a smooth quintic elliptic curve in
 ${\mathbb{P}}^4$
${\mathbb{P}}^4$(iii) a cone over a rational quintic curve (either smooth or singular) in
 ${\mathbb{P}}^4$
${\mathbb{P}}^4$(iv) an image of a projection into
 ${\mathbb{P}}^5$ of a surface
${\mathbb{P}}^5$ of a surface  $\widetilde{S}\subset{\mathbb{P}}^6$ of minimal degree 5 with centre of projection
$\widetilde{S}\subset{\mathbb{P}}^6$ of minimal degree 5 with centre of projection  $p\notin\widetilde{S}$.
$p\notin\widetilde{S}$.
We now assume that there is a smooth curve ![]() $X\subset S$ with
$X\subset S$ with ![]() $\deg X=15$ and genus g = 16. We remark that the last case (iv) is not possible under this assumption; X is linearly normal since
$\deg X=15$ and genus g = 16. We remark that the last case (iv) is not possible under this assumption; X is linearly normal since ![]() $\pi(15,6)=13$. For the case (iii), we have either
$\pi(15,6)=13$. For the case (iii), we have either ![]() $\dim\mathrm{Sing}(S)=0$ or S has a double line. In both cases, S is the image of a linear projection of a cone
$\dim\mathrm{Sing}(S)=0$ or S has a double line. In both cases, S is the image of a linear projection of a cone ![]() $\widetilde{S}\subset{\mathbb{P}}^6$ over a rational normal curve
$\widetilde{S}\subset{\mathbb{P}}^6$ over a rational normal curve ![]() $\widetilde{C}\subset\widetilde{H}\cong{\mathbb{P}}^5$ with centre of projection
$\widetilde{C}\subset\widetilde{H}\cong{\mathbb{P}}^5$ with centre of projection  $p\in\widetilde{H}\setminus\widetilde{C}$. This is not possible under the existence of a linearly normal
$p\in\widetilde{H}\setminus\widetilde{C}$. This is not possible under the existence of a linearly normal ![]() $X\subset S$.
$X\subset S$.
Remark 5.8. (i) By the preceding discussion, the assumption of the following lemma 5.10—S is a quintic surface containing ![]() $X\in\mathcal{H}_{15,16,5}$—implies that either S is a possibly singular del Pezzo surface or it is a cone over a linearly normal elliptic curve of
$X\in\mathcal{H}_{15,16,5}$—implies that either S is a possibly singular del Pezzo surface or it is a cone over a linearly normal elliptic curve of ![]() ${\mathbb{P}}^4$. Singular del Pezzo surface of degree 5 is described in [Reference Dolgachev15, § 8.5.1]. They form an irreducible family.
${\mathbb{P}}^4$. Singular del Pezzo surface of degree 5 is described in [Reference Dolgachev15, § 8.5.1]. They form an irreducible family.
(ii) From proposition 2.1, we recall that the set of all ![]() $X\in \mathcal{H}_{15,16,5}$ contained in a singular del Pezzo surface are limits of curves lying on a smooth del Pezzo surface. Therefore in order to identify possible irreducible components of
$X\in \mathcal{H}_{15,16,5}$ contained in a singular del Pezzo surface are limits of curves lying on a smooth del Pezzo surface. Therefore in order to identify possible irreducible components of ![]() $\mathcal{H}_{15,16,5}$ whose general element lies on a smooth quintic surface, it is sufficient to study the general ones, i.e. the ones contained in a blowing-up of
$\mathcal{H}_{15,16,5}$ whose general element lies on a smooth quintic surface, it is sufficient to study the general ones, i.e. the ones contained in a blowing-up of ![]() ${\mathbb{P}}^2$ at four distinct points in general position.
${\mathbb{P}}^2$ at four distinct points in general position.
We use the following simple observation several times.
Remark 5.9. Fix any surface ![]() $S\supset X$ such that
$S\supset X$ such that ![]() $\deg (S) \le 5$. Let
$\deg (S) \le 5$. Let ![]() $M\subset {\mathbb{P}}^5$ be a quadric hypersurface containing X. If
$M\subset {\mathbb{P}}^5$ be a quadric hypersurface containing X. If ![]() $S\nsubseteq M$ then
$S\nsubseteq M$ then ![]() $\deg (M\cap S)\le 10 \lt \deg X$ and it follows that
$\deg (M\cap S)\le 10 \lt \deg X$ and it follows that ![]() $|{\mathcal{I}}_X(2)| =|{\mathcal{I}}_S(2)|$ if
$|{\mathcal{I}}_X(2)| =|{\mathcal{I}}_S(2)|$ if ![]() $\deg X \gt 10$.
$\deg X \gt 10$.
Lemma 5.10. We choose a smooth ![]() $X\in\mathcal{H}_{15,16,5}$ and assume that X lies on an irreducible quintic surface
$X\in\mathcal{H}_{15,16,5}$ and assume that X lies on an irreducible quintic surface ![]() $S\subset{\mathbb{P}}^5$. Then
$S\subset{\mathbb{P}}^5$. Then
(i) X is the complete intersection of S and a cubic hypersurface and
(ii)
 $K_X \cong {\mathcal{O}}_X(2)$, X is ACM,
$K_X \cong {\mathcal{O}}_X(2)$, X is ACM,  $h^0({\mathbb{P}}^5,{\mathcal{I}}_X(2))=5$ and
$h^0({\mathbb{P}}^5,{\mathcal{I}}_X(2))=5$ and  $h^0({\mathbb{P}}^5,{\mathcal{I}}_S(t)) =\binom{t+5}{5} -15t+15$ for all
$h^0({\mathbb{P}}^5,{\mathcal{I}}_S(t)) =\binom{t+5}{5} -15t+15$ for all  $t\ge 3$.
$t\ge 3$.
Proof. By remark 5.8, we may assume that S is either smooth or with finitely many singular points such that the general hyperplane section of S is a smooth linearly normal elliptic curve in ![]() ${\mathbb{P}}^4$. Fix a general hyperplane
${\mathbb{P}}^4$. Fix a general hyperplane ![]() $H\subset {\mathbb{P}}^5$. By the assumption,
$H\subset {\mathbb{P}}^5$. By the assumption, ![]() $E:= S\cap H$ is a smooth linearly normal quintic elliptic curve in H. Since
$E:= S\cap H$ is a smooth linearly normal quintic elliptic curve in H. Since ![]() $p_a(E)=1=\pi(5,4)$, E is ACM, i.e.
$p_a(E)=1=\pi(5,4)$, E is ACM, i.e. ![]() $h^1(H,{\mathcal{I}}_{E,H}(t)) =0$ for all
$h^1(H,{\mathcal{I}}_{E,H}(t)) =0$ for all ![]() $t\in {\mathbb{Z}}$; cf. [Reference Harris19, theorem 3.7, p. 87]. For an integer t, we consider the exact sequence
$t\in {\mathbb{Z}}$; cf. [Reference Harris19, theorem 3.7, p. 87]. For an integer t, we consider the exact sequence
Note that S is ACM [Reference Migliore31, theorem 1.3.3], i.e. ![]() $h^1({\mathbb{P}}^5,{\mathcal{I}}_S(x))=0$ for all
$h^1({\mathbb{P}}^5,{\mathcal{I}}_S(x))=0$ for all ![]() $x\in {\mathbb{Z}}$. Since
$x\in {\mathbb{Z}}$. Since ![]() $h^1(H,{\mathcal{I}}_{E,H}(t)) =0$, we have
$h^1(H,{\mathcal{I}}_{E,H}(t)) =0$, we have  $h^0(H,{\mathcal{I}}_{E}(t)) = \binom{4+t}{4}-5t$ for all
$h^0(H,{\mathcal{I}}_{E}(t)) = \binom{4+t}{4}-5t$ for all ![]() $t\ge 0$ by Riemann–Roch. Since
$t\ge 0$ by Riemann–Roch. Since ![]() $h^1({\mathbb{P}}^5, {\mathcal{I}}_S(t-1)) =0$ for all
$h^1({\mathbb{P}}^5, {\mathcal{I}}_S(t-1)) =0$ for all ![]() $t\ge 0$ and
$t\ge 0$ and ![]() $h^0({\mathbb{P}}^5, {\mathcal{I}}_S(1))=0$, the long cohomology exact sequence of (21) gives
$h^0({\mathbb{P}}^5, {\mathcal{I}}_S(1))=0$, the long cohomology exact sequence of (21) gives ![]() $h^0({\mathbb{P}}^5,{\mathcal{I}}_S(2)) =5$ and then
$h^0({\mathbb{P}}^5,{\mathcal{I}}_S(2)) =5$ and then
Since ![]() $\deg ({\mathcal{O}}_X(3)) =45 \gt 30 =\deg K_X$,
$\deg ({\mathcal{O}}_X(3)) =45 \gt 30 =\deg K_X$, ![]() $h^0(X, {\mathcal{O}}_X(3))=30$ and therefore
$h^0(X, {\mathcal{O}}_X(3))=30$ and therefore
 \begin{equation*}h^0({\mathbb{P}}^5,{\mathcal{I}}_X(3))\ge h^0({\mathbb{P}}^5,{\mathcal{O}}_{{\mathbb{P}}^5}(3))-h^0(X,{\mathcal{O}}_X(3))=\tbinom{8}{3} -h^0(X,{\mathcal{O}}_X(3))=26.\end{equation*}
\begin{equation*}h^0({\mathbb{P}}^5,{\mathcal{I}}_X(3))\ge h^0({\mathbb{P}}^5,{\mathcal{O}}_{{\mathbb{P}}^5}(3))-h^0(X,{\mathcal{O}}_X(3))=\tbinom{8}{3} -h^0(X,{\mathcal{O}}_X(3))=26.\end{equation*} By (22), ![]() $h^0({\mathbb{P}}^5,{\mathcal{I}}_S(3)) \lt h^0({\mathbb{P}}^5,{\mathcal{I}}_X(3))$ and there is a cubic hypersurface
$h^0({\mathbb{P}}^5,{\mathcal{I}}_S(3)) \lt h^0({\mathbb{P}}^5,{\mathcal{I}}_X(3))$ and there is a cubic hypersurface ![]() $W\subset{\mathbb{P}}^5$ containing X such that
$W\subset{\mathbb{P}}^5$ containing X such that ![]() $W\nsupseteq S$, the curve
$W\nsupseteq S$, the curve ![]() $S\cap W$ has
$S\cap W$ has ![]() $\deg S\cap W=\deg S\cdot\deg W=15$.
$\deg S\cap W=\deg S\cdot\deg W=15$.
We want to prove that X is the scheme-theoretic intersection of S and W, i.e. ![]() $S\cap W$ is not the union of X and some zero-dimensional scheme. First of all, the scheme-theoretic intersection
$S\cap W$ is not the union of X and some zero-dimensional scheme. First of all, the scheme-theoretic intersection ![]() $S\cap W$ is ACM since S is ACM, W is given by a single equation and
$S\cap W$ is ACM since S is ACM, W is given by a single equation and ![]() $\dim S\cap W \lt \dim S$ ([Reference Bruns and Herzog10, th. 2.1.3], [Reference Eisenbud18, prop. 18.13], [Reference Matsumura30, ex. 17.4 with ν = 1 and n = 1]). Since
$\dim S\cap W \lt \dim S$ ([Reference Bruns and Herzog10, th. 2.1.3], [Reference Eisenbud18, prop. 18.13], [Reference Matsumura30, ex. 17.4 with ν = 1 and n = 1]). Since ![]() $S\cap W$ is ACM, it has no embedded component ([Reference Bruns and Herzog10, th. 2.1.2(a)], [Reference Eisenbud18, cor. 18.10], [Reference Kaplansky24, th. 141]), i.e.
$S\cap W$ is ACM, it has no embedded component ([Reference Bruns and Herzog10, th. 2.1.2(a)], [Reference Eisenbud18, cor. 18.10], [Reference Kaplansky24, th. 141]), i.e. ![]() $S\cap W =X$ scheme-theoretically.
$S\cap W =X$ scheme-theoretically.
By remark 5.9, ![]() $h^0({\mathbb{P}}^5,{\mathcal{I}}_X(2)) =h^0({\mathbb{P}}^5,{\mathcal{I}}_S(2)) =5$. Since X is ACM,
$h^0({\mathbb{P}}^5,{\mathcal{I}}_X(2)) =h^0({\mathbb{P}}^5,{\mathcal{I}}_S(2)) =5$. Since X is ACM,
 \begin{align*}
h^0({\mathcal{O}}_X(2))&= h^0({\mathbb{P}}^5,{\mathcal{O}}(2))-h^0({\mathbb{P}}^5,{\mathcal{I}}_X(2))+h^1({\mathbb{P}}^5,{\mathcal{I}}_X(2))\\
&=h^0({\mathbb{P}}^5,{\mathcal{O}}(2))-h^0({\mathbb{P}}^5,{\mathcal{I}}_S(2))=16.
\end{align*}
\begin{align*}
h^0({\mathcal{O}}_X(2))&= h^0({\mathbb{P}}^5,{\mathcal{O}}(2))-h^0({\mathbb{P}}^5,{\mathcal{I}}_X(2))+h^1({\mathbb{P}}^5,{\mathcal{I}}_X(2))\\
&=h^0({\mathbb{P}}^5,{\mathcal{O}}(2))-h^0({\mathbb{P}}^5,{\mathcal{I}}_S(2))=16.
\end{align*} Since ![]() $\deg ({\mathcal{O}}_X(2)) =\deg (K_X)$, Riemann–Roch gives
$\deg ({\mathcal{O}}_X(2)) =\deg (K_X)$, Riemann–Roch gives ![]() ${\mathcal{O}}_X(2)\cong K_X$. For
${\mathcal{O}}_X(2)\cong K_X$. For ![]() $t\ge 3$, we have
$t\ge 3$, we have ![]() $h^1({\mathcal{O}}_X(t)) =0$ and by
$h^1({\mathcal{O}}_X(t)) =0$ and by ![]() $h^1({\mathbb{P}}^5,{\mathcal{I}}_X(t))=0$
$h^1({\mathbb{P}}^5,{\mathcal{I}}_X(t))=0$
 \begin{align*}
h^0({\mathbb{P}}^5,{\mathcal{I}}_X(t)) &=h^0({\mathbb{P}}^5,{\mathcal{O}}_{{\mathbb{P}}^5}(t))-h^0(X,{\mathcal{O}}_X(t))+h^1({\mathbb{P}}^5,{\mathcal{I}}_X(t))\\ &=\tbinom{t+5}{5} -15t+15.
\end{align*}
\begin{align*}
h^0({\mathbb{P}}^5,{\mathcal{I}}_X(t)) &=h^0({\mathbb{P}}^5,{\mathcal{O}}_{{\mathbb{P}}^5}(t))-h^0(X,{\mathcal{O}}_X(t))+h^1({\mathbb{P}}^5,{\mathcal{I}}_X(t))\\ &=\tbinom{t+5}{5} -15t+15.
\end{align*} We consider the family Δ consisting of curves ![]() $X\in \mathcal{H}_{15,16,5}$ contained in an elliptic cone. The following lemma asserts that Δ is an irreducible family of dimension 60.
$X\in \mathcal{H}_{15,16,5}$ contained in an elliptic cone. The following lemma asserts that Δ is an irreducible family of dimension 60.
(i) Δ is an irreducible family of dimension 60.
(ii) For each
 $X\in \Delta$, there is a unique degree 3 morphism
$X\in \Delta$, there is a unique degree 3 morphism  $u: X\rightarrow E$ with E an elliptic curve, X is 6-gonal and the
$u: X\rightarrow E$ with E an elliptic curve, X is 6-gonal and the  $g^1_6$’s on X are the pull-backs of the
$g^1_6$’s on X are the pull-backs of the  $g^1_2$’s on E which are parametrized by the points of E.
$g^1_2$’s on E which are parametrized by the points of E.
Proof. (i) Let Δ1 denote the family of all degree 5 elliptic cones in ![]() ${\mathbb{P}}^5$. The family
${\mathbb{P}}^5$. The family ![]() $\mathcal{H}_{5,1,4}$ of linearly normal elliptic curves in
$\mathcal{H}_{5,1,4}$ of linearly normal elliptic curves in ![]() ${\mathbb{P}}^4$ forms an irreducible family of the expected dimension 25; cf. [Reference Ein16]. Hence
${\mathbb{P}}^4$ forms an irreducible family of the expected dimension 25; cf. [Reference Ein16]. Hence ![]() $\dim\Delta_1=\dim{\mathbb{P}}^5+\dim\mathcal{H}_{5,1,4}=30$ and Δ1 is irreducible; note that there is a natural dominant rational map
$\dim\Delta_1=\dim{\mathbb{P}}^5+\dim\mathcal{H}_{5,1,4}=30$ and Δ1 is irreducible; note that there is a natural dominant rational map ![]() $\Delta_1\rightarrow {{\mathbb{P}}^{5}}^*$ whose fibre over
$\Delta_1\rightarrow {{\mathbb{P}}^{5}}^*$ whose fibre over ![]() $H\in {{\mathbb{P}}^{5}}^*$ is the irreducible Hilbert scheme
$H\in {{\mathbb{P}}^{5}}^*$ is the irreducible Hilbert scheme ![]() $\mathcal{H}_{5,1,4}$ of the same dimension. We note that the proof of lemma 5.10 (i) only requires the assumption
$\mathcal{H}_{5,1,4}$ of the same dimension. We note that the proof of lemma 5.10 (i) only requires the assumption ![]() $X\in\mathcal{H}_{15,16,5}$ lying on surface of degree 5 with isolated singularities. Therefore, each element
$X\in\mathcal{H}_{15,16,5}$ lying on surface of degree 5 with isolated singularities. Therefore, each element ![]() $X\in \Delta$ is a smooth complete intersections of an element of Δ1 and a cubic hypersurface. Consider the locus
$X\in \Delta$ is a smooth complete intersections of an element of Δ1 and a cubic hypersurface. Consider the locus
 \begin{equation*}\Psi := \{(S,T)|S\nsubseteq T\} \subset \Delta_1\times{\mathbb{P}}(H^0({\mathbb{P}}^5,{\mathcal{O}}_{{\mathbb{P}}^5}(3))).\end{equation*}
\begin{equation*}\Psi := \{(S,T)|S\nsubseteq T\} \subset \Delta_1\times{\mathbb{P}}(H^0({\mathbb{P}}^5,{\mathcal{O}}_{{\mathbb{P}}^5}(3))).\end{equation*} The projection ![]() $\pi_1:\Psi \rightarrow \Delta_1$ is surjective with the fiber
$\pi_1:\Psi \rightarrow \Delta_1$ is surjective with the fiber
 \begin{equation*}\pi^{-1}(S)\cong
{\mathbb{P}}(H^0({\mathbb{P}}^5,{\mathcal{O}}_{{\mathbb{P}}^5}(3))/H^0({\mathbb{P}}^5,{\mathcal{I}}_S(3))).\end{equation*}
\begin{equation*}\pi^{-1}(S)\cong
{\mathbb{P}}(H^0({\mathbb{P}}^5,{\mathcal{O}}_{{\mathbb{P}}^5}(3))/H^0({\mathbb{P}}^5,{\mathcal{I}}_S(3))).\end{equation*}By the same computation as (22), we get
By (23), we conclude that Ψ is irreducible and
 \begin{equation*}\dim\Psi=\dim\Delta_1+\dim{\mathbb{P}}(H^0({\mathbb{P}}^5,{\mathcal{O}}_{{\mathbb{P}}^5}(3))/H^0({\mathbb{P}}^5,{\mathcal{I}}_S(3)))=60.\end{equation*}
\begin{equation*}\dim\Psi=\dim\Delta_1+\dim{\mathbb{P}}(H^0({\mathbb{P}}^5,{\mathcal{O}}_{{\mathbb{P}}^5}(3))/H^0({\mathbb{P}}^5,{\mathcal{I}}_S(3)))=60.\end{equation*} We note that every smooth curve ![]() $X\in\mathcal{H}_{15,16,5}$ is contained in a unique elliptic cone
$X\in\mathcal{H}_{15,16,5}$ is contained in a unique elliptic cone ![]() $S\in\Delta_1$ if any. This follows from the following argument. By remark 5.9,
$S\in\Delta_1$ if any. This follows from the following argument. By remark 5.9, ![]() $|{\mathcal{I}}_X(2))| =|{\mathcal{I}}_S(2))|$ if
$|{\mathcal{I}}_X(2))| =|{\mathcal{I}}_S(2))|$ if ![]() $X\subset S$. In particular, S is the base locus of
$X\subset S$. In particular, S is the base locus of ![]() $|{\mathcal{I}}_X(2)|$ and therefore X is contained in a unique
$|{\mathcal{I}}_X(2)|$ and therefore X is contained in a unique ![]() $S\in\Delta_1$. From this, we may deduce that the natural map
$S\in\Delta_1$. From this, we may deduce that the natural map ![]() $\Psi \stackrel{\psi}{\rightarrow} \Delta$ where
$\Psi \stackrel{\psi}{\rightarrow} \Delta$ where ![]() $\psi(S,T)=S\cap T$ is injective and surjective, hence
$\psi(S,T)=S\cap T$ is injective and surjective, hence ![]() $\dim\Delta=\dim\Psi=60$.
$\dim\Delta=\dim\Psi=60$.
(ii) By (8) (with ![]() $d=15, r=5$), for each
$d=15, r=5$), for each ![]() $X\in \Delta$, there is a degree 3 morphism
$X\in \Delta$, there is a degree 3 morphism ![]() $u: X\rightarrow E$ onto an elliptic curve induced by
$u: X\rightarrow E$ onto an elliptic curve induced by ![]() ${\mathbb{E}}_5\rightarrow E$; the uniqueness of the triple covering follows from the Castelnuovo-Severi inequality. X is 6-gonal and the
${\mathbb{E}}_5\rightarrow E$; the uniqueness of the triple covering follows from the Castelnuovo-Severi inequality. X is 6-gonal and the ![]() $g^1_6$’s on X are the pull-backs of
$g^1_6$’s on X are the pull-backs of ![]() $g^1_2\in W^1_2(E)\cong W_1(E)\cong\mathrm{Jac}(E)\cong E$ by the Castelnuovo–Severi inequality.
$g^1_2\in W^1_2(E)\cong W_1(E)\cong\mathrm{Jac}(E)\cong E$ by the Castelnuovo–Severi inequality.
Since ![]() $\dim\Delta =60=\mathcal{X}(15,16,5)$ by lemma 5.11, we cannot exclude the possibility that Δ may constitute a full component of
$\dim\Delta =60=\mathcal{X}(15,16,5)$ by lemma 5.11, we cannot exclude the possibility that Δ may constitute a full component of ![]() $\mathcal{H}_{15,16,5}$. The following two lemmas show that Δ is in the boundary of the component Γ3.
$\mathcal{H}_{15,16,5}$. The following two lemmas show that Δ is in the boundary of the component Γ3.
Lemma 5.12. Every degree 5 elliptic cone T is a flat limit of a family of smooth del Pezzo. More precisely, there is a flat family ![]() $\{S_t\}_{t\in {\mathbb{K}}}$ of degree 5 surfaces of
$\{S_t\}_{t\in {\mathbb{K}}}$ of degree 5 surfaces of ![]() ${\mathbb{P}}^5$ such that
${\mathbb{P}}^5$ such that ![]() $S_0=T$ and St is a smooth del Pezzo for all
$S_0=T$ and St is a smooth del Pezzo for all ![]() $t\ne 0$.
$t\ne 0$.
Proof. From lemma 5.10 (ii), ![]() $h^0({\mathbb{P}}^5,{\mathcal{I}}_T(2)) =5$ for all degree 5 surface T containing an element of
$h^0({\mathbb{P}}^5,{\mathcal{I}}_T(2)) =5$ for all degree 5 surface T containing an element of ![]() $\mathcal{H}_{15,16,5}$. Given
$\mathcal{H}_{15,16,5}$. Given ![]() $X\in\mathcal{H}_{15,16,5}$, we fix an elliptic cone T with the vertex p. We fix a hyperplane
$X\in\mathcal{H}_{15,16,5}$, we fix an elliptic cone T with the vertex p. We fix a hyperplane ![]() $H\subset {\mathbb{P}}^5$ such that
$H\subset {\mathbb{P}}^5$ such that ![]() $p\notin H$ and set
$p\notin H$ and set ![]() $E:= S\cap H$. The linearly normal elliptic curve E and p uniquely determine T. We take a set of four points
$E:= S\cap H$. The linearly normal elliptic curve E and p uniquely determine T. We take a set of four points ![]() $\{p_1,p_2,p_3,p_4\}\subset{\mathbb{P}}^2$ such that no 3 of them is collinear. We take a smooth plane cubic
$\{p_1,p_2,p_3,p_4\}\subset{\mathbb{P}}^2$ such that no 3 of them is collinear. We take a smooth plane cubic ![]() $E^{\prime}\subset {\mathbb{P}}^2$ containing
$E^{\prime}\subset {\mathbb{P}}^2$ containing ![]() $\{p_1,p_2,p_3,p_4\}$,
$\{p_1,p_2,p_3,p_4\}$, ![]() $E^{\prime}\stackrel{u}{\cong} E$ such that
$E^{\prime}\stackrel{u}{\cong} E$ such that ![]() ${\mathcal{O}}_{E^{\prime}}(3)(-p_1-p_2-p_3-p_4)\cong u^\ast({\mathcal{O}}_E(1))$. This can be done by taking an isomorphism
${\mathcal{O}}_{E^{\prime}}(3)(-p_1-p_2-p_3-p_4)\cong u^\ast({\mathcal{O}}_E(1))$. This can be done by taking an isomorphism ![]() $u: E^{\prime}\rightarrow E$ first, where u −1 is an arbitrary embedding of E as a plane cubic, taking 3 general
$u: E^{\prime}\rightarrow E$ first, where u −1 is an arbitrary embedding of E as a plane cubic, taking 3 general ![]() $o_1,o_2,o_3\in E^{\prime}$, then taking as o 4 the unique point of E ʹ such that
$o_1,o_2,o_3\in E^{\prime}$, then taking as o 4 the unique point of E ʹ such that ![]() ${\mathcal{O}}_{E^{\prime}}(3)(-o_1-o_2-o_3-o_4)\cong u^\ast({\mathcal{O}}_E(1))$. Blowing up
${\mathcal{O}}_{E^{\prime}}(3)(-o_1-o_2-o_3-o_4)\cong u^\ast({\mathcal{O}}_E(1))$. Blowing up ![]() ${\mathbb{P}}^2$ at
${\mathbb{P}}^2$ at ![]() $\{o_1,o_2,o_3,o_4\}$, we get a smooth del Pezzo
$\{o_1,o_2,o_3,o_4\}$, we get a smooth del Pezzo ![]() $S\subset {\mathbb{P}}^5$ such that
$S\subset {\mathbb{P}}^5$ such that ![]() $S\cap H =E =T\cap H$. We take homogeneous coordinates
$S\cap H =E =T\cap H$. We take homogeneous coordinates ![]() $x_0,x_1,\ldots,x_5$ such that
$x_0,x_1,\ldots,x_5$ such that ![]() $H =\{x_0=0\}$ and
$H =\{x_0=0\}$ and ![]() $p =(1:0:0:0:0:0)$. We take a bases
$p =(1:0:0:0:0:0)$. We take a bases
For any ![]() $t\in {\mathbb{K}}$ (the base field) and
$t\in {\mathbb{K}}$ (the base field) and ![]() $i=1,2,3,4,5$ we set
$i=1,2,3,4,5$ we set
For t = 1, these five quadratic forms generate ![]() $H^0({\mathbb{P}}^5,{\mathcal{I}}_S(2))$, while for t = 0, they span
$H^0({\mathbb{P}}^5,{\mathcal{I}}_S(2))$, while for t = 0, they span ![]() $H^0({\mathbb{P}}^5,{\mathcal{I}}_T(2))$. For any
$H^0({\mathbb{P}}^5,{\mathcal{I}}_T(2))$. For any ![]() $t\in {\mathbb{K}}\setminus \{0\}$ consider the automorphism of
$t\in {\mathbb{K}}\setminus \{0\}$ consider the automorphism of ![]() ${\mathbb{P}}^5$ sending
${\mathbb{P}}^5$ sending ![]() $x_0\mapsto tx_0$ and
$x_0\mapsto tx_0$ and ![]() $x_i\mapsto x_i$ for
$x_i\mapsto x_i$ for ![]() $i=1,\ldots,5$. For each
$i=1,\ldots,5$. For each ![]() $t\ne 0$, the common zero locus the forms
$t\ne 0$, the common zero locus the forms ![]() $q_{i,t}(x_0,\ldots,x_5)$,
$q_{i,t}(x_0,\ldots,x_5)$, ![]() $i=1,\ldots,5$, is a surface St projectively equivalent to
$i=1,\ldots,5$, is a surface St projectively equivalent to ![]() $S_1=S$ while
$S_1=S$ while ![]() $S_0=T$. The family
$S_0=T$. The family ![]() $\{S_t\}_{t\in {\mathbb{K}}}$ is flat, because all St have the same Hilbert polynomial [Reference Hartshorne22, Theorem III.9.9]. Thus,
$\{S_t\}_{t\in {\mathbb{K}}}$ is flat, because all St have the same Hilbert polynomial [Reference Hartshorne22, Theorem III.9.9]. Thus, ![]() $T=S_0$ is a flat limit of del Pezzo surfaces St.
$T=S_0$ is a flat limit of del Pezzo surfaces St.
Lemma 5.13. Δ is in the closure of ![]() $\Gamma_3\setminus \Delta$, Γ3 is irreducible and
$\Gamma_3\setminus \Delta$, Γ3 is irreducible and ![]() $\dim\Gamma_3=65$.
$\dim\Gamma_3=65$.
Proof. Fix ![]() $X\in \Delta$ and let T denote the degree 5 elliptic cone containing X. By lemma 5.12, there is a flat family
$X\in \Delta$ and let T denote the degree 5 elliptic cone containing X. By lemma 5.12, there is a flat family ![]() $\{S_t\}_{t\in {\mathbb{K}}}$ of degree 5 surfaces of
$\{S_t\}_{t\in {\mathbb{K}}}$ of degree 5 surfaces of ![]() ${\mathbb{P}}^5$ such that
${\mathbb{P}}^5$ such that ![]() $S_0=T$ and St is a smooth del Pezzo for all
$S_0=T$ and St is a smooth del Pezzo for all ![]() $t\ne 0$. Lemma 5.10 shows that
$t\ne 0$. Lemma 5.10 shows that ![]() $X = T\cap W$ for some cubic hypersurface W. Since X is smooth, W is transversal to T. Since smoothness is an open condition, there is an open neighbourhood
$X = T\cap W$ for some cubic hypersurface W. Since X is smooth, W is transversal to T. Since smoothness is an open condition, there is an open neighbourhood ![]() $U\subset {\mathbb{K}}$ containing 0 such that W is transversal to St for all
$U\subset {\mathbb{K}}$ containing 0 such that W is transversal to St for all ![]() $t\in U$. For each
$t\in U$. For each ![]() $t\in U\setminus \{0\}$, we have
$t\in U\setminus \{0\}$, we have ![]() $S_t\cap W \in \Gamma _3\setminus \{S_0\}$. Therefore,
$S_t\cap W \in \Gamma _3\setminus \{S_0\}$. Therefore, ![]() $X\subset T$ is a flat limit of the curves
$X\subset T$ is a flat limit of the curves ![]() $S_t\cap W$,
$S_t\cap W$, ![]() $t\in U\setminus \{0\}$.
$t\in U\setminus \{0\}$.
A standard computation in the proof of theorem 4.1 (B-iii) shows that ![]() $X\in\Gamma_3\setminus\Delta$ contained in a fixed smooth del Pezzo surface
$X\in\Gamma_3\setminus\Delta$ contained in a fixed smooth del Pezzo surface  ${\mathbb{P}}^2_4\stackrel{|(3:1^4)|}{\hookrightarrow}S\subset{\mathbb{P}}^5$ is in
${\mathbb{P}}^2_4\stackrel{|(3:1^4)|}{\hookrightarrow}S\subset{\mathbb{P}}^5$ is in ![]() $|(9;3^4)|=|3(3:1^4)|$. Since no non-trivial automorphism of
$|(9;3^4)|=|3(3:1^4)|$. Since no non-trivial automorphism of ![]() ${\mathbb{P}}^2$ fixes a set of four points in general position, the open subset of Γ3 formed by curves lying on a smooth del Pezzo is irreducible and
${\mathbb{P}}^2$ fixes a set of four points in general position, the open subset of Γ3 formed by curves lying on a smooth del Pezzo is irreducible and
 \begin{equation*}\dim\Gamma_3=\dim \mathrm{Aut}({\mathbb{P}}^5)+\dim|(9;3^4)|=35+\tbinom{9+2}{2}-1 -4\tbinom{3+1}{2}=65.\end{equation*}
\begin{equation*}\dim\Gamma_3=\dim \mathrm{Aut}({\mathbb{P}}^5)+\dim|(9;3^4)|=35+\tbinom{9+2}{2}-1 -4\tbinom{3+1}{2}=65.\end{equation*}Proposition 5.14. A general ![]() $X\in \Gamma_3$ is 6-gonal.
$X\in \Gamma_3$ is 6-gonal.
Proof. Take ![]() $Y\in \Gamma_3$ contained in a smooth del Pezzo surface, i.e. assume that Y is a normalization of a degree 9 plane curve having ordinary triple points at the four general points
$Y\in \Gamma_3$ contained in a smooth del Pezzo surface, i.e. assume that Y is a normalization of a degree 9 plane curve having ordinary triple points at the four general points ![]() $p_1,p_2,p_3,p_4$ as its only singularities. The pencil of lines through each pi induces a base-point-free
$p_1,p_2,p_3,p_4$ as its only singularities. The pencil of lines through each pi induces a base-point-free ![]() $g^1_6$. A fifth base-point-free
$g^1_6$. A fifth base-point-free ![]() $g^1_6$ on Y is induced by the pencil of conics containing
$g^1_6$ on Y is induced by the pencil of conics containing ![]() $\{p_1,p_2,p_3,p_4\}$. Hence lemma 5.13 gives that a general element of Γ3 has a base-point-free
$\{p_1,p_2,p_3,p_4\}$. Hence lemma 5.13 gives that a general element of Γ3 has a base-point-free ![]() $g^1_6$. By lemma 5.11 (ii),
$g^1_6$. By lemma 5.11 (ii), ![]() $X\in\Delta\subset\Gamma_3$ is 6-gonal. By lower semi continuity of gonality, a general element of Γ3 has gonality at least 6 and we are done.
$X\in\Delta\subset\Gamma_3$ is 6-gonal. By lower semi continuity of gonality, a general element of Γ3 has gonality at least 6 and we are done.
Proof of theorem 5.1
We saw that ![]() $\mathcal{H}_{15,16,5}$ is the union of three pairwise disjoint irreducible families Γ1, Γ2, and Γ3. Dimensions of
$\mathcal{H}_{15,16,5}$ is the union of three pairwise disjoint irreducible families Γ1, Γ2, and Γ3. Dimensions of ![]() $\Gamma_i$ are computed and the gonality of elements in each
$\Gamma_i$ are computed and the gonality of elements in each ![]() $\Gamma_i$ has been determined; cf. dimension count (20), lemma 5.13, remarks 5.2 & 5.3, and Proposition 5.14.
$\Gamma_i$ has been determined; cf. dimension count (20), lemma 5.13, remarks 5.2 & 5.3, and Proposition 5.14.
Recall that each element of Γ3 is ACM by lemma 5.10, while no element of ![]() $\Gamma _1\cup \Gamma_2$ is ACM by lemma 5.6. Hence by upper semicontinuity for cohomology, no element of Γ3 is a limit of elements of
$\Gamma _1\cup \Gamma_2$ is ACM by lemma 5.6. Hence by upper semicontinuity for cohomology, no element of Γ3 is a limit of elements of ![]() $\Gamma_1\cup \Gamma _2$.
$\Gamma_1\cup \Gamma _2$.
On the other hand, by lemma 5.4 and lemma 5.5, ![]() $h^1(X,{\mathcal{O}}_X(2)) =0$ for all
$h^1(X,{\mathcal{O}}_X(2)) =0$ for all ![]() $X\in \Gamma _1$, while
$X\in \Gamma _1$, while ![]() $h^1(X,{\mathcal{O}}_X(2))=1$ for all
$h^1(X,{\mathcal{O}}_X(2))=1$ for all ![]() $X\in \Gamma_3$ by lemma 5.10. Again, semicontinuity for cohomology tells that no element of Γ1 is a limit of a family of elements of Γ3.
$X\in \Gamma_3$ by lemma 5.10. Again, semicontinuity for cohomology tells that no element of Γ1 is a limit of a family of elements of Γ3.
Likewise, we can deduce that a general element of Γ2 is not a limit of a family of elements of Γ3. Note that we have ![]() $\dim \Gamma_1 \gt \dim \Gamma_2$ and each element of Γ1 is trigonal and each element of Γ2 is 5-gonal.
$\dim \Gamma_1 \gt \dim \Gamma_2$ and each element of Γ1 is trigonal and each element of Γ2 is 5-gonal.
By (lower) semicontinuity of gonality, no element of Γ2 is a limit of elements of Γ1. Therefore, ![]() $\mathcal{H}_{15,16,5}$ has exactly three distinct irreducible components, Γ1, Γ2, and Γ3.
$\mathcal{H}_{15,16,5}$ has exactly three distinct irreducible components, Γ1, Γ2, and Γ3.
5.2. The moduli map  $\mu: \mathcal{H}_{15,16,5}\rightarrow {\mathcal{M}}_{16}$
$\mu: \mathcal{H}_{15,16,5}\rightarrow {\mathcal{M}}_{16}$
Let ![]() $\mu: \mathcal{H}_{15,16,5}\rightarrow {\mathcal{M}}_{16}$ denote the moduli map. Since elements of Γ1, Γ2, and Γ3 have different gonalities, for each
$\mu: \mathcal{H}_{15,16,5}\rightarrow {\mathcal{M}}_{16}$ denote the moduli map. Since elements of Γ1, Γ2, and Γ3 have different gonalities, for each ![]() $X\in \Gamma _i$, we have
$X\in \Gamma _i$, we have ![]() $\mu^{-1}(\mu(X)) \subset \Gamma_i$. For
$\mu^{-1}(\mu(X)) \subset \Gamma_i$. For ![]() $i=1,2$ let
$i=1,2$ let ![]() $\Gamma _{i,0}$ denote the non-empty open subset of
$\Gamma _{i,0}$ denote the non-empty open subset of ![]() $\Gamma _i$ formed by all
$\Gamma _i$ formed by all ![]() $X\in \Gamma_i$ contained in a minimal degree surface isomorphic to
$X\in \Gamma_i$ contained in a minimal degree surface isomorphic to ![]() ${\mathbb{F}}_0$. For
${\mathbb{F}}_0$. For ![]() $i=1,2$ set
$i=1,2$ set ![]() $\Gamma_{i,2}:= \Gamma_i\setminus \Gamma_{i,0}$, i.e.
$\Gamma_{i,2}:= \Gamma_i\setminus \Gamma_{i,0}$, i.e. ![]() $\Gamma_{i,2}$ is the set of all
$\Gamma_{i,2}$ is the set of all ![]() $X\in \Gamma_i$ contained in a minimal degree surface isomorphic to
$X\in \Gamma_i$ contained in a minimal degree surface isomorphic to ![]() ${\mathbb{F}}_2$.
${\mathbb{F}}_2$.
Remark 5.15. For each ![]() $X\in \Gamma _{2,0}$ (resp.
$X\in \Gamma _{2,0}$ (resp. ![]() $X\in \Gamma _{2,2}$) we have
$X\in \Gamma _{2,2}$) we have ![]() $\mu^{-1}(\mu(X)) \subset \Gamma_{2,0}$ (resp.
$\mu^{-1}(\mu(X)) \subset \Gamma_{2,0}$ (resp. ![]() $\mu^{-1}(\mu(X)) \subset \Gamma_{2,2}$); elements of
$\mu^{-1}(\mu(X)) \subset \Gamma_{2,2}$); elements of ![]() $\Gamma_{2,0}$ have exactly two
$\Gamma_{2,0}$ have exactly two ![]() $g^1_5$ and elements of
$g^1_5$ and elements of ![]() $\Gamma_{i,2}$ have only one
$\Gamma_{i,2}$ have only one ![]() $g^1_5$; cf. remark 5.3.
$g^1_5$; cf. remark 5.3.
Let C be a trigonal curve of genus ![]() $g\ge 5$. By the Castelnuovo–Severi inequality, C has a unique
$g\ge 5$. By the Castelnuovo–Severi inequality, C has a unique ![]() $g^1_3$. Let R be the trigonal line bundle on C. Let m(C) be the Maroni invariant of C, i.e. let
$g^1_3$. Let R be the trigonal line bundle on C. Let m(C) be the Maroni invariant of C, i.e. let ![]() $m(C)+2$ be the first integer t such that
$m(C)+2$ be the first integer t such that ![]() $h^0(R^{\otimes t}) \ge t+2$ [Reference Martens and Schreyer29, eq. 1.2]. We always have
$h^0(R^{\otimes t}) \ge t+2$ [Reference Martens and Schreyer29, eq. 1.2]. We always have ![]() $(g-4)/3 \le m(C)\le (g-2)/2$ and the canonical model of C sits in a surface of degree g − 2 in
$(g-4)/3 \le m(C)\le (g-2)/2$ and the canonical model of C sits in a surface of degree g − 2 in ![]() ${\mathbb{P}}^{g-1}$ isomorphic to the Hirzebruch surface
${\mathbb{P}}^{g-1}$ isomorphic to the Hirzebruch surface ![]() ${\mathbb{F}}_e$ where
${\mathbb{F}}_e$ where ![]() $e:=g-2-2m(C)\ge 0$; cf. [Reference Martens and Schreyer29, p. 172].
$e:=g-2-2m(C)\ge 0$; cf. [Reference Martens and Schreyer29, p. 172].
Lemma 5.16. If ![]() $X\in \Gamma_{1,e}$,
$X\in \Gamma_{1,e}$, ![]() $e\in \{0,2\}$, then
$e\in \{0,2\}$, then ![]() $e =14-2m(X)$.
$e =14-2m(X)$.
Proof. We use notation in remark 5.3. For e = 0, we have ![]() $X\in |{\mathcal{O}}_Q(3,9)|$ and
$X\in |{\mathcal{O}}_Q(3,9)|$ and ![]() $\omega _X \cong {\mathcal{O}}_X(1,7)$. For e = 2, we have
$\omega _X \cong {\mathcal{O}}_X(1,7)$. For e = 2, we have ![]() $X\in |{\mathcal{O}}_{{\mathbb{F}}_2}(3h+12f)|$ and
$X\in |{\mathcal{O}}_{{\mathbb{F}}_2}(3h+12f)|$ and ![]() $\omega _X \cong {\mathcal{O}}_X(h+8f)$. Hence the canonical model of X sits inside the image of
$\omega _X \cong {\mathcal{O}}_X(h+8f)$. Hence the canonical model of X sits inside the image of ![]() ${\mathbb{F}}_0$ (resp.
${\mathbb{F}}_0$ (resp. ![]() ${\mathbb{F}}_2$) under the morphism induced by the linear system
${\mathbb{F}}_2$) under the morphism induced by the linear system ![]() $|{\mathcal{O}}_Q(1,7)|$ (resp.
$|{\mathcal{O}}_Q(1,7)|$ (resp. ![]() $|{\mathcal{O}}_{{\mathbb{F}}_2}(h+8f)|$).
$|{\mathcal{O}}_{{\mathbb{F}}_2}(h+8f)|$).
Let ![]() $\sigma: Q\rightarrow Q$ be the automorphism which shifts the two factors of
$\sigma: Q\rightarrow Q$ be the automorphism which shifts the two factors of ![]() $Q={\mathbb{P}}^1\times{\mathbb{P}}^1$.
$Q={\mathbb{P}}^1\times{\mathbb{P}}^1$.
Proposition 5.17. For ![]() $X\in \Gamma _{2,0}$, we have
$X\in \Gamma _{2,0}$, we have
 \begin{equation*}\mu^{-1}(\mu(X)) =\mathrm{Aut}({\mathbb{P}}^5)X\cup \mathrm{Aut}({\mathbb{P}}^5)\sigma(X) \mathrm{~~and ~~}\dim \mu(\Gamma_{2,0}) = 29.\end{equation*}
\begin{equation*}\mu^{-1}(\mu(X)) =\mathrm{Aut}({\mathbb{P}}^5)X\cup \mathrm{Aut}({\mathbb{P}}^5)\sigma(X) \mathrm{~~and ~~}\dim \mu(\Gamma_{2,0}) = 29.\end{equation*}Proof. For the first assertion, we observe that ![]() $\mu^{-1}(\mu(X))\subset \Gamma_{2,0}$; remark 5.15. We use corollary 2.4 and remark 2.5 to conclude that
$\mu^{-1}(\mu(X))\subset \Gamma_{2,0}$; remark 5.15. We use corollary 2.4 and remark 2.5 to conclude that
Therefore ![]() $\dim\mu(\Gamma_{2,0})=\dim\Gamma_2-\dim{\operatorname{Aut}} ({\mathbb{P}}^5)=29.$
$\dim\mu(\Gamma_{2,0})=\dim\Gamma_2-\dim{\operatorname{Aut}} ({\mathbb{P}}^5)=29.$
Proposition 5.18. Fix ![]() $X\in \Gamma _{1,0}$ and
$X\in \Gamma _{1,0}$ and ![]() $X_1\in \Gamma_{1,2}$. Then we have
$X_1\in \Gamma_{1,2}$. Then we have
Proof. Lemma 5.16 implies ![]() $\mu(\Gamma_{1,0})\cap \mu(\Gamma_{1,2}) =\emptyset$. Any isomorphism between two non-hyperelliptic curves
$\mu(\Gamma_{1,0})\cap \mu(\Gamma_{1,2}) =\emptyset$. Any isomorphism between two non-hyperelliptic curves ![]() $C_1, C_2$ of genus
$C_1, C_2$ of genus ![]() $g\ge 5$ induces a projective automorphism
$g\ge 5$ induces a projective automorphism ![]() $\varphi\in{\operatorname{Aut}}({\mathbb{P}}^{g-1})$ such that
$\varphi\in{\operatorname{Aut}}({\mathbb{P}}^{g-1})$ such that ![]() $\varphi(C_1^\kappa)=C_2^\kappa$ where
$\varphi(C_1^\kappa)=C_2^\kappa$ where ![]() $C_i^\kappa\subset{\mathbb{P}}^{g-1}$ is the canonical model of Ci. Now assume that C 1 (and hence C 2) is trigonal and call
$C_i^\kappa\subset{\mathbb{P}}^{g-1}$ is the canonical model of Ci. Now assume that C 1 (and hence C 2) is trigonal and call ![]() $T_i\subset {\mathbb{P}}^{g-1}$ (
$T_i\subset {\mathbb{P}}^{g-1}$ (![]() $i=1,2$), the base locus of
$i=1,2$), the base locus of  $|{\mathcal{I}}_{C_i^\kappa}(2)|$. Obviously
$|{\mathcal{I}}_{C_i^\kappa}(2)|$. Obviously ![]() $\varphi(T_1)=T_2$. Up to
$\varphi(T_1)=T_2$. Up to ![]() ${\operatorname{Aut}}({\mathbb{P}}^{g-1})$, we may assume
${\operatorname{Aut}}({\mathbb{P}}^{g-1})$, we may assume ![]() $T_1=T_2$. Since Ti is a surface of minimal degree g − 2 containing the trigonal curve
$T_1=T_2$. Since Ti is a surface of minimal degree g − 2 containing the trigonal curve ![]() $C_i^\kappa$, we have
$C_i^\kappa$, we have ![]() $T_i\cong {\mathbb{F}}_e$ with
$T_i\cong {\mathbb{F}}_e$ with ![]() $e =g-2-2m(C_i)$. Therefore, we may deduce that isomorphism between two curves induces an automorphism of
$e =g-2-2m(C_i)$. Therefore, we may deduce that isomorphism between two curves induces an automorphism of ![]() ${\mathbb{F}}_e$. By remark 2.5, minimal degree surface scrolls in
${\mathbb{F}}_e$. By remark 2.5, minimal degree surface scrolls in ![]() ${\mathbb{P}}^5$ which are isomorphic as abstract variety are also projectively equivalent, hence we get the result.
${\mathbb{P}}^5$ which are isomorphic as abstract variety are also projectively equivalent, hence we get the result.
6. Curves of genus g = 17 and g = 18
In this section, we treat the two remaining cases g = 17 and g = 18. We first prove that there is no smooth curve of degree d = 15 and genus g = 17 in ![]() ${\mathbb{P}}^5$.
${\mathbb{P}}^5$.
Proposition 6.1. ![]() $\mathcal{H}_{15,17,5}=\emptyset$.
$\mathcal{H}_{15,17,5}=\emptyset$.
Proof. Since ![]() $\pi_1(15,5)=16 \lt g=17$,
$\pi_1(15,5)=16 \lt g=17$, ![]() $X\subset S\subset{\mathbb{P}}^5$ with
$X\subset S\subset{\mathbb{P}}^5$ with ![]() $\deg S=4$ by [Reference Harris19, th. 3.15] and S is a smooth rational normal scroll by remark 2.2 (c). Assume
$\deg S=4$ by [Reference Harris19, th. 3.15] and S is a smooth rational normal scroll by remark 2.2 (c). Assume ![]() $X\in|aH+bL|$. However, there is no pair of integers (a, b) satisfying the degree and genus formula (2) for
$X\in|aH+bL|$. However, there is no pair of integers (a, b) satisfying the degree and genus formula (2) for ![]() $(d,p_a(X))=(15,17)$.
$(d,p_a(X))=(15,17)$.
6.1. Irreducibility of  $\mathcal{H}_{15,18,5}$ and the moduli map
$\mathcal{H}_{15,18,5}$ and the moduli map  $\mu: \mathcal{H}_{15,18,5}\rightarrow {\mathcal{M}}_{18}$
$\mu: \mathcal{H}_{15,18,5}\rightarrow {\mathcal{M}}_{18}$
Proposition 6.2. ![]() $\mathcal{H}_{15,18,5}$ is irreducible,
$\mathcal{H}_{15,18,5}$ is irreducible, ![]() $\dim \mathcal{H}_{15,18,5}=68$ and every smooth
$\dim \mathcal{H}_{15,18,5}=68$ and every smooth ![]() $X\in\mathcal{H}_{15,18,5}$ is 4-gonal with a unique
$X\in\mathcal{H}_{15,18,5}$ is 4-gonal with a unique ![]() $g^1_4$.
$g^1_4$.
Proof. The irreducibility follows directly from [Reference Harris19, corollary 3.16, p. 100]. Since X is an extremal curve, ![]() $X\subset S\subset{\mathbb{P}}^5$ where S is a smooth rational normal scroll by remark 2.2 (c). By solving (2) for
$X\subset S\subset{\mathbb{P}}^5$ where S is a smooth rational normal scroll by remark 2.2 (c). By solving (2) for ![]() $p_a(X)=18$, we have
$p_a(X)=18$, we have ![]() $X\in |4H-L|$. By (3) and (4), we have
$X\in |4H-L|$. By (3) and (4), we have
X has a ![]() $g^1_4$ cut out by the ruling of the scroll which is unique by the Castelnuvo–Severi inequality.
$g^1_4$ cut out by the ruling of the scroll which is unique by the Castelnuvo–Severi inequality.
Since ![]() $\deg (X) \gt 2\deg(S)$, the theorem of Bezout gives
$\deg (X) \gt 2\deg(S)$, the theorem of Bezout gives ![]() $|{\mathcal{I}}_X(2)|=|{\mathcal{I}}_S(2)|$. Since S is cut out by quadrics, S is the base locus of
$|{\mathcal{I}}_X(2)|=|{\mathcal{I}}_S(2)|$. Since S is cut out by quadrics, S is the base locus of ![]() $|{\mathcal{I}}_X(2)|$ and therefore
$|{\mathcal{I}}_X(2)|$ and therefore ![]() $X\in\mathcal{H}_{15,18,5}$ is contained in a unique minimal degree surface; cf. [Reference Arbarello, Cornalba, Griffiths and Harris4, p. 120]. There are two non-isomorphic rational normal scrolls in
$X\in\mathcal{H}_{15,18,5}$ is contained in a unique minimal degree surface; cf. [Reference Arbarello, Cornalba, Griffiths and Harris4, p. 120]. There are two non-isomorphic rational normal scrolls in ![]() ${\mathbb{P}}^5$, which are the images of
${\mathbb{P}}^5$, which are the images of ![]() ${\mathbb{F}}_0$ and
${\mathbb{F}}_0$ and ![]() ${\mathbb{F}}_2$ under the morphism induced by appropriate very ample linear systems. Let Λ0 (Λ2 resp.) denotes the locus of smooth curves in
${\mathbb{F}}_2$ under the morphism induced by appropriate very ample linear systems. Let Λ0 (Λ2 resp.) denotes the locus of smooth curves in ![]() $\mathcal{H}_{15,18,5}$ contained in
$\mathcal{H}_{15,18,5}$ contained in ![]() ${\mathbb{F}}_0$ (
${\mathbb{F}}_0$ (![]() ${\mathbb{F}}_2$ resp.). Since each
${\mathbb{F}}_2$ resp.). Since each ![]() $X\in \mathcal{H}_{15,18,5}$ is contained in a unique minimal degree surface,
$X\in \mathcal{H}_{15,18,5}$ is contained in a unique minimal degree surface, ![]() $\Lambda _2\cap \Lambda _0=\emptyset$. However, we want to prove something stronger: we want to prove that no element of Λ0 is isomorphic to an element of Λ2. We will use the following lemma which asserts that the first scrollar invariant of the unique
$\Lambda _2\cap \Lambda _0=\emptyset$. However, we want to prove something stronger: we want to prove that no element of Λ0 is isomorphic to an element of Λ2. We will use the following lemma which asserts that the first scrollar invariant of the unique ![]() $g^1_4$ on
$g^1_4$ on ![]() $X\in \mathcal{H}_{15,18,5}$ detects the integer
$X\in \mathcal{H}_{15,18,5}$ detects the integer ![]() $e\in \{0,2\}$ such that
$e\in \{0,2\}$ such that ![]() $X\in \Lambda_e$.
$X\in \Lambda_e$.
Lemma 6.3. Take ![]() $e\in \{0,2\}$ and
$e\in \{0,2\}$ and ![]() $X\in \Lambda _e$. Let R be the only degree 4 line bundle on X such that
$X\in \Lambda _e$. Let R be the only degree 4 line bundle on X such that ![]() $h^0(X,R)=2$. Let c be the minimal integer such that
$h^0(X,R)=2$. Let c be the minimal integer such that ![]() $h^0(R^{\otimes c}) \ge c+2$, the first scrollar invariant of
$h^0(R^{\otimes c}) \ge c+2$, the first scrollar invariant of ![]() $|R|$. Then we have the following two cases for the integer c:
$|R|$. Then we have the following two cases for the integer c:
 \begin{equation*}
\begin{cases}
~~e=0, ~c=7, ~h^0(R^{\otimes7})=11\\
~e=2, ~c= 5, ~h^0(R^{\otimes 5})=7.
\end{cases}
\end{equation*}
\begin{equation*}
\begin{cases}
~~e=0, ~c=7, ~h^0(R^{\otimes7})=11\\
~e=2, ~c= 5, ~h^0(R^{\otimes 5})=7.
\end{cases}
\end{equation*}Proof. If e = 0 we have ![]() $X\in |{\mathcal{O}}_Q(4,7)|$ with
$X\in |{\mathcal{O}}_Q(4,7)|$ with ![]() $R ={\mathcal{O}}_X(0,1)$. Fix an integer
$R ={\mathcal{O}}_X(0,1)$. Fix an integer ![]() $t\ge 1$. From the cohomology sequence of the exact sequence
$t\ge 1$. From the cohomology sequence of the exact sequence
we have ![]() $h^0(R^{\otimes t}) = h^0(Q,{\mathcal{O}}_Q(0,t))+h^1(Q,{\mathcal{O}}_Q(-4,t-7))$ and hence
$h^0(R^{\otimes t}) = h^0(Q,{\mathcal{O}}_Q(0,t))+h^1(Q,{\mathcal{O}}_Q(-4,t-7))$ and hence ![]() $h^0(R^{\otimes7})=11$ and c = 7. For e = 2, we have
$h^0(R^{\otimes7})=11$ and c = 7. For e = 2, we have ![]() $X\in |4H-L|=|4h+11f|$ with
$X\in |4H-L|=|4h+11f|$ with ![]() $R ={\mathcal{O}}_X(f)$. We use the exact sequence
$R ={\mathcal{O}}_X(f)$. We use the exact sequence
to get ![]() $h^0(R^{\otimes 5})=7$ and c = 5. We omit routine computation.
$h^0(R^{\otimes 5})=7$ and c = 5. We omit routine computation.
The following is an immediate consequence of lemma 6.3.
Proposition 6.4. No smooth element of Λ2 is isomorphic to a smooth element of Λ0.
Proposition 6.5. Take ![]() $X\in \Lambda_0$. Then:
$X\in \Lambda_0$. Then:
(a) X is 4-gonal with a unique
 $g^1_4$, no base-point-free
$g^1_4$, no base-point-free  $g^1_c$ for
$g^1_c$ for  $5\le c\le 6$ and a unique
$5\le c\le 6$ and a unique  $g^1_7$.
$g^1_7$.(b)
 $\mu^{-1}(\mu(X)) =\mathrm{Aut}({\mathbb{P}}^5)X$.
$\mu^{-1}(\mu(X)) =\mathrm{Aut}({\mathbb{P}}^5)X$.(c)
 $\dim \mu(\mathcal{H}_{15,18,5}) = \dim \mu(\Lambda_0) =33$.
$\dim \mu(\mathcal{H}_{15,18,5}) = \dim \mu(\Lambda_0) =33$.
Proof. (a) follows from proposition 2.3. For (b), we fix any  $\tilde{X}\in \mathcal{H}_{15,18,5}$ isomorphic to X. Lemma 6.3 gives
$\tilde{X}\in \mathcal{H}_{15,18,5}$ isomorphic to X. Lemma 6.3 gives ![]() $\tilde{X}\in \Lambda_0$. Let
$\tilde{X}\in \Lambda_0$. Let ![]() $\tilde{S}$ (resp. S) be the minimal degree surface containing
$\tilde{S}$ (resp. S) be the minimal degree surface containing ![]() $\tilde{X}$ (resp. X). Thus, there is
$\tilde{X}$ (resp. X). Thus, there is ![]() $u\in {\operatorname{Aut}}({\mathbb{P}}^5)$ such that
$u\in {\operatorname{Aut}}({\mathbb{P}}^5)$ such that ![]() $u(\tilde{S}) = S$; cf. remark 2.5. Call
$u(\tilde{S}) = S$; cf. remark 2.5. Call ![]() ${\operatorname{Aut}}^0(S)\cong {\operatorname{Aut}}({\mathbb{P}}^1)\times{\operatorname{Aut}}({\mathbb{P}}^1)\subset{\operatorname{Aut}}(S)$ the connected component of
${\operatorname{Aut}}^0(S)\cong {\operatorname{Aut}}({\mathbb{P}}^1)\times{\operatorname{Aut}}({\mathbb{P}}^1)\subset{\operatorname{Aut}}(S)$ the connected component of ![]() ${\operatorname{Aut}}(S)$ containing the identity. By corollary 2.4, there is
${\operatorname{Aut}}(S)$ containing the identity. By corollary 2.4, there is ![]() $v\in {\operatorname{Aut}}^0(S)$ such that
$v\in {\operatorname{Aut}}^0(S)$ such that ![]() $v(u(\tilde{X})) =X$. Remark 2.5 provides the existence of
$v(u(\tilde{X})) =X$. Remark 2.5 provides the existence of ![]() $w\in {\operatorname{Aut}}({\mathbb{P}}^5)$ such that
$w\in {\operatorname{Aut}}({\mathbb{P}}^5)$ such that ![]() $w(S) =S$ and
$w(S) =S$ and ![]() $w_{|S} =v$. Thus
$w_{|S} =v$. Thus ![]() $w\circ u\in{\operatorname{Aut}}({\mathbb{P}}^5)$ satisfies
$w\circ u\in{\operatorname{Aut}}({\mathbb{P}}^5)$ satisfies ![]() $w\circ u (\tilde{S})=w(S)=S$ and hence
$w\circ u (\tilde{S})=w(S)=S$ and hence
(c) follows from
 \begin{align*} \dim \mu(\mathcal{H}_{15,18,5}) &= \dim \mu(\Lambda_0)=\dim\mathcal{H}_{15,18,5}-\dim\mu^{-1}(\mu(X))\\ &=\dim\mathcal{H}_{15,18,5}-\dim{\operatorname{Aut}}({\mathbb{P}}^5)=68-35=33.
\end{align*}
\begin{align*} \dim \mu(\mathcal{H}_{15,18,5}) &= \dim \mu(\Lambda_0)=\dim\mathcal{H}_{15,18,5}-\dim\mu^{-1}(\mu(X))\\ &=\dim\mathcal{H}_{15,18,5}-\dim{\operatorname{Aut}}({\mathbb{P}}^5)=68-35=33.
\end{align*}6.2. An epilogue, a remark on the larger-than-expected components
Throughout this article, we dealt with several Hilbert schemes with larger-than-expected components. Regarding the existence (or non-existence) of such components in general, the following conjecture is stated in [Reference Harris21, p. 142]:
Conjecture: (i) If ![]() $\mathcal{H}$ is any component of the Hilbert scheme
$\mathcal{H}$ is any component of the Hilbert scheme ![]() $\mathcal{H}_{d,g,r}$ such that the image of the rational map
$\mathcal{H}_{d,g,r}$ such that the image of the rational map ![]() $\mathcal{H}\longrightarrow \mathcal{M}_g$ has codimension g − 4 or less, then
$\mathcal{H}\longrightarrow \mathcal{M}_g$ has codimension g − 4 or less, then
(ii) Right after that, it is also remarked in [Reference Harris21, p. 143] that ‘to be honest, the available evidence suggests that the existence of a number ![]() $\beta(g)$ tending linearly to
$\beta(g)$ tending linearly to ![]() $\infty$ with g, such that any such component
$\infty$ with g, such that any such component ![]() $\mathcal{H}$ whose image in
$\mathcal{H}$ whose image in ![]() $\mathcal{M}_g$ has codimension
$\mathcal{M}_g$ has codimension ![]() $\beta\le\beta(g)$ has the expected dimension; we use the function g − 4 just for simplicity’.
$\beta\le\beta(g)$ has the expected dimension; we use the function g − 4 just for simplicity’.
Our results discussed in this article suggest that the function ![]() $\beta(g)=g-4$ may need to be replaced with smaller
$\beta(g)=g-4$ may need to be replaced with smaller ![]() $\beta(g)$.
$\beta(g)$.
Remark 6.6. (i) For ![]() $(d,g,r)=(15,15,5)$,
$(d,g,r)=(15,15,5)$,  $\mathcal{H}_{d,g,r}=\mathcal{H}^\mathcal{L}_{d,g,r}$ is irreducible and
$\mathcal{H}_{d,g,r}=\mathcal{H}^\mathcal{L}_{d,g,r}$ is irreducible and ![]() $\dim\mathcal{H}_{d,g,r}=64 \gt \mathcal{X}(d,g,r)=62$ by theorem 4.1. By theorem 4.1,
$\dim\mathcal{H}_{d,g,r}=64 \gt \mathcal{X}(d,g,r)=62$ by theorem 4.1. By theorem 4.1, ![]() ${\operatorname{codim}} \mu(\mathcal{H}_{d,g,r})=3\cdot g-3-(\dim\mathcal{H}_{d,g,r}-\dim{\operatorname{Aut}}({\mathbb{P}}^r))=13 \gt g-4$ and hence the family
${\operatorname{codim}} \mu(\mathcal{H}_{d,g,r})=3\cdot g-3-(\dim\mathcal{H}_{d,g,r}-\dim{\operatorname{Aut}}({\mathbb{P}}^r))=13 \gt g-4$ and hence the family ![]() $\mathcal{H}_{d,g,r}$ is special with big codimension in
$\mathcal{H}_{d,g,r}$ is special with big codimension in ![]() $\mathcal{M}_g$. Also, this does not give an evidence to disprove the conjecture.
$\mathcal{M}_g$. Also, this does not give an evidence to disprove the conjecture.
(ii) For ![]() $(d,g,r)=(15,16,5)$, the three components
$(d,g,r)=(15,16,5)$, the three components ![]() $\Gamma_i$ (
$\Gamma_i$ (![]() $i=1,2,3$) of
$i=1,2,3$) of  $\mathcal{H}_{d,g,r}=\mathcal{H}^\mathcal{L}_{d,g,r}$ have dimension larger than
$\mathcal{H}_{d,g,r}=\mathcal{H}^\mathcal{L}_{d,g,r}$ have dimension larger than ![]() $\mathcal{X}(d,g,r)=60$ by theorem 5.1. By proposition 5.18,
$\mathcal{X}(d,g,r)=60$ by theorem 5.1. By proposition 5.18, ![]() ${\operatorname{codim}}\mu(\Gamma_1)=12=g-4$, hence providing an evidence to the contrary to the conjecture if
${\operatorname{codim}}\mu(\Gamma_1)=12=g-4$, hence providing an evidence to the contrary to the conjecture if ![]() $\beta(g)=g-4$.
$\beta(g)=g-4$.
(iii) For ![]() $(d,g,r)=(15,13,5)$,
$(d,g,r)=(15,13,5)$, ![]() $\mathcal{H}_{d,g,r}$ is reducible with two components, one with the expected dimension and the other one with more than expected dimension whose image under the moduli map µ has codimension
$\mathcal{H}_{d,g,r}$ is reducible with two components, one with the expected dimension and the other one with more than expected dimension whose image under the moduli map µ has codimension  $g-4={\operatorname{codim}}\;\mathcal{M}^1_{g,3}=3g-3-(2g+1)$; proposition 3.2. Hence the literal statement of the above conjecture turns out to be untrue if one puts
$g-4={\operatorname{codim}}\;\mathcal{M}^1_{g,3}=3g-3-(2g+1)$; proposition 3.2. Hence the literal statement of the above conjecture turns out to be untrue if one puts ![]() $\beta(g)=g-4$. However, elements of this component are not linearly normal. There are other examples of this kind suggesting that
$\beta(g)=g-4$. However, elements of this component are not linearly normal. There are other examples of this kind suggesting that ![]() $\beta(g)=g-4$ is rather too large to ensure the validity of the above conjecture. By [Reference Cho, Keem and Park11, proposition 3.5], there exists a component of the Hilbert scheme with
$\beta(g)=g-4$ is rather too large to ensure the validity of the above conjecture. By [Reference Cho, Keem and Park11, proposition 3.5], there exists a component of the Hilbert scheme with ![]() $(d,g,r)=(2g-2-2k,g,r)$—subject to several crude and technical numerical conditions such as
$(d,g,r)=(2g-2-2k,g,r)$—subject to several crude and technical numerical conditions such as  $2\le \frac{g-4}{k-1},\frac{2g+2-2k}{3}-1 \lt r\le
g-2-2k,g \gt (k-1)^2$—dominating
$2\le \frac{g-4}{k-1},\frac{2g+2-2k}{3}-1 \lt r\le
g-2-2k,g \gt (k-1)^2$—dominating  $\mathcal{M}^1_{g,k}$, whereas
$\mathcal{M}^1_{g,k}$, whereas  ${\operatorname{codim}}\mathcal{M}^1_{g,k}=g+2-2k\le \beta(g)=g-4$. Again, curves in this component are not linearly normal.
${\operatorname{codim}}\mathcal{M}^1_{g,k}=g+2-2k\le \beta(g)=g-4$. Again, curves in this component are not linearly normal.
(iv) If one focus on components consisting of linearly normal curves, ![]() $\beta(g)=g-5$ would be a choice suggested by the example in (ii). The authors do not know of any example of a component with dimension greater-than-expected such that the image under the moduli map µ has codimension at most g − 5.
$\beta(g)=g-5$ would be a choice suggested by the example in (ii). The authors do not know of any example of a component with dimension greater-than-expected such that the image under the moduli map µ has codimension at most g − 5.
Acknowledgements
The authors are grateful to the referee for valuable comments and useful suggestions towards an overall improvement of the readability and clarity of this article.
Funding
The first named author is a member of GNSAGA of INdAM (Italy). The second named author was supported in part by the National Research Foundation of South Korea (2022R1I1A1A01055306).