1. Introduction
Archimedes (c. 287–c. 212 BC) was an exceptionally accomplished person in today’s achievements in science and engineering. Considering he lived more than 2000 years ago, his work is remarkable. Netz & Noel (Reference Netz and Noel2007) suggested that “the safest general characterisation of the European scientific tradition is that it consists of a series of footnotes to Archimedes (p. 27).” Archimedes contributed to a range of topics from the foundation of basic science to the engineering design of large machines in practice. He worked on basic geometry and mathematics and developed research methods; he discovered physics laws and reapplied them in his basic science research and his professional engineering design practice.
But why would design researchers study history? Studies of ancient or past systems designs through a design perspective could serve multiple purposes. The first purpose is a contribution to history: understanding how past systems were constructed and used through their contemporary reconstruction (Papadogiannis, Tsakoumaki & Chondros Reference Papadogiannis, Tsakoumaki and Chondros2010; Yan & Lin Reference Yan and Lin2011). Unfortunately, such a contribution is insufficient for design researchers. The second purpose is a contribution to contemporary design by attempting to develop past systems and using their insight as an inspiration for addressing contemporary design challenges. The development of TRIZ (Altshuller Reference Altshuller1984) is an example of such a study, as well as biomimicry (Helfman Cohen & Reich Reference Helfman Cohen and Reich2016). Another example is the study of Archimedes’ work (e.g., screw) with analytical, simulation and optimization methods to gain insight into contemporary applications (Waters & Aggidis Reference Waters and Aggidis2015; Simmons & Lubitz Reference Simmons and Lubitz2021). The third purpose is a combination of the first two – bootstrapping: contemporary perspective brings new insight into the history and that new insight, in turn, teaches us about today’s practice. Examples of bootstrapping can be found in different disciplines (Reich et al. Reference Reich, Shai, Subrahmanian, Hatchuel and Le Masson2008) as well as between history and design (Petroski Reference Petroski1985, Reference Petroski2013). This article attempts to focus on the third purpose.
Very little has remained of Archimedes’ writings, but from what is available, plentiful can be learned. There have been countless studies of Archimedes that present well what he achieved in the different scientific and engineering disciplines (e.g., Heath Reference Heath2002; Gow Reference Gow2005; Netz & Noel Reference Netz and Noel2007; Chondros Reference Chondros2010; Paipetis & Ceccarelli Reference Paipetis and Ceccarelli2010; Ceccarelli Reference Ceccarelli2014; Rorres Reference Rorres2017). Nevertheless, we are not aware of studies attempting to understand the process by which Archimedes developed his engineered systems, while there are very few studies attempting to describe some underlying principles of his mathematics work (e.g., Netz Reference Netz1999). This study attempts to go beyond a specific case analysis and asks whether we could describe a set of principles that would apply to Archimedes’ engineering and scientific work and would allow us to explain some of his work. These principles, which we call Archimedes’ Code, might not have been stated explicitly by Archimedes, but their prevalence suggests that they were natural to his work. This is similar in spirit to Netz’ (Reference Netz1999) study of Greek mathematicians attempting to “bring[s] out the set of practices common to Greek practitioners, but argue[s] that these practices were generally ‘invisible’ to the practitioners (p. 2).”
In addition to describing Archimedes’ presumed code, we also illustrate how Archimedes’ work implicitly makes use of various concepts that underlie design theory and complex systems engineering; they include the lever and its fulcrum (base); variety and dialogue; the dialogue between parts and whole and the transition from known knowledge to unknown knowledge. In the discussion, we use broad interpretations of physical phenomena, such as a lever or equilibrium, treating them as abstract concepts beyond their physical manifestations. Risking some overgeneralization, we think that this exposes what might be a broader contribution of Archimedes to engineering and design, similar to the aforementioned comment by Netz regarding Archimedes’ contribution to science. Considering that Archimedes was an ingenious designer, it need not be a surprise if he allowed himself to change the identities of objects to suit his needs; similarly, we use some concepts such as the lever in a very abstract manner. Another example of using concepts metaphorically and abstractly is the organism and organ structure concepts in design (Ferreirinha, Grothe-Møller & Hansen Reference Ferreirinha, Grothe-Møller and Hansen1990; Andreasen Reference Andreasen2011; Andreasen, Hansen & Cash Reference Andreasen, Hansen and Cash2015).
We bring design and systems engineering perspectives into the analysis to discover that Archimedes could be viewed as a reflective (Schön Reference Schön1983) and reflexive (Reich Reference Reich2017) practitioner, as such practices seem to have permeated his work. We argue that not only Archimedes was a transdisciplinary thinker, but that his inquiry method, intertwining engineering design and science, might have afforded him to develop ideas that preceded his time. As such, Archimedes could inspire contemporary scientists and practitioners. If Archimedes’ practices afforded his remarkable achievements, perhaps we should adopt them more profoundly.
This study is structured as follows. Section 2 discusses this study’s research process; Section 3 presents the lever concept and its consequences in addressing several problems. Section 4 discusses Archimedes’ Code. Section 5 demonstrates the use of the code in Archimedes’ work, constituting some validation of the code. Sections 6 and 7 discuss the generation of new knowledge from existing knowledge and Section 8 concludes this study.
2. Research process
The description of the research project is a personal journey rather than a formal description of research questions and validation actions. This description records the complexities of such research in case other researchers wish to conduct similar studies. As far as the study of Archimedes is concerned, Netz & Noel (Reference Netz and Noel2007) used the same style in reporting on their study of Archimedes’ Palimpsest.
This research had three stages: (a) focused and limited; (b) expanded and naïve and (c) moderate and conscious. The first stage started when I received an invitation to present a talk at the symposium on “The Diverse Worlds of Archimedes,” held at the Holon Institute of Technology on 8 November 2021. The invitation was based on the recently published book I co-authored called “We are not Users” (Subrahmanian, Reich & Krishnan Reference Subrahmanian, Reich and Krishnan2020). The vision of the talk was to present the book’s ideas to the audience and the plan was to use Archimedes’ work as a platform to implement it. The study was focused and limited to a few of Archimedes’ famous works, primarily the lever. If I stayed within these research boundaries, it would have been successful, as was demonstrated by the talk at the symposium, because the task was rather simple and it could be matched by my ability to interpret classic well-known Archimedes works.
As I read more, I became fascinated with Archimedes’ work that I was unaware of previously. At some point, when I studied the calculation of the area between a parabola and a secant line (see Section 4.1), I began to see patterns and became captivated; I tried to find them in each one of Archimedes’ works that I already studied. The more I found, the more I wanted to read and test these ideas. At some point, I thought that the study could contribute to the history of Archimedes and also contribute to design science – this became the new expanded vision that was beyond the original limited vision. This is where the second stage of this research started. In a way, the problem of the area of the parabola became my lever to study Archimedes differently.
The second stage vision to contribute to the historical understanding of Archimedes must be matched by relevant expertise and knowledge of the culture of history-related journals, and the research practices they expect to observe. As I am not trained as a historian and am unfamiliar with the research process and culture necessary to present historical contributions, the desired vision was not matched by my available resources and practices. I was enriched by other scholars presenting at the aforementioned symposium with new perspectives but this was not sufficient. Despite the ideas that were written in the article, which are quite similar to those presented in this article, several history-related journals refused to review the article. That was a failure. Such failure could be explained using the PSI framework (Reich & Subrahmanian Reference Reich and Subrahmanian2020a). Had I used it to plan the research (Reich & Subrahmanian Reference Reich and Subrahmanian2022b), it could have been avoided. Being a reflexive practitioner, using PSI to plan this research would have been useful here (Reich Reference Reich2017).
The failure of this stage led to the third stage of this research with a vision to present a plausible interpretation of Archimedes’ approach to deriving insight into engineering and mathematics, with some implications to present design research practice. To make sure I did not miss any aspect of the research, I used the PSI matrix to model this stage. The aligned PSI matrix of this research is presented in Table 1.
Table 1. The PSI matrix of the study of Archimedes

The reflection or alignment (A) layer, which makes sure that the study vision is realised and that all the research activities are aligned, was not previously defined explicitly. It now included discussions with the journal editor and the reviewers (through their review) as well as making sure that I presented broad historical sources to support the research approach and the findings.
This research study needed to be contextualised in other historical studies, in particular, those of Archimedes. The problem is that most of the sources are secondary, as very little original material has remained of Archimedes’ work. Many of the secondary sources are written in Greek or Latin. Consequently, in studying Archimedes we get further away from the original material. Further, Netz & Noel (Reference Netz and Noel2007) described the difficulty in interpreting old Greek writings because their letters are not subdivided by spaces [“You must bear in mind that, until late in the Middle Ages, Greek was written without spaces between the words. (p. 35),” see Figure 1 as an example]. A reader has to put the spaces based on the context. Netz & Noel (Reference Netz and Noel2007) gave examples of wrong interpretations and Acerbi (Reference Acerbi2003) also noted corrupted readings by scholars. Section 6.2 also summarises some misinterpretations of Archimedes’ work. Netz and Noel summarised their study approach as follows:
This is how readings take place: you can make a reading only after you have formed some kind of guess as to the possible meanings of the text to be read. This, above all, was why Heiberg had not succeeded in reading the infinity passage in the Method or in reading the Stomachion. He had expected neither actual infinity nor combinatorics (Netz & Noel Reference Netz and Noel2007, p. 254).
While this research approach may seem antithetical to a classical engineering research approach that attempts to be objective without any preconceptions of the results in mind, it is in fact, similar to case-study methodology (Eisenhardt Reference Eisenhardt1989). The validation of this research is not by presenting objective evidence, but by presenting plausible internally-consistent interpretations. The broader the applicability of these interpretations the better, and if additional support can corroborate it, it is also supportive.

Figure 1. One page from Archimedes Palimpsest after imaging, showing the original text. Source: The Walters Museum, CC BY 3.0 (https://creativecommons.org/licenses/by/3.0), via Wikimedia Commons.
Let me detail more cell O-I of the matrix in Table 1, addressing the question of how should we study Archimedes. An interesting answer would be: in the ‘Archimedean’ way. One can sit in the bathtub waiting for inspiration but this is unlikely to emerge. Inspiration requires some base knowledge for it to transpire. In the language of C-K theory (Hatchuel & Weil Reference Hatchuel and Weil2009), one needs the knowledge to form new concepts. One might argue that generating new concepts needs an intersection of at least two bases of knowledge (Johansson Reference Johansson2006), which is reflected in the splitting condition underlying design (Hatchuel et al. Reference Hatchuel, Le Masson, Reich and Subrahmanian2018). Personally, the problem of finding the area between a parabola and a secant line became a lever (Figure 2) from which to continue studying Archimedes. It gave me initial insight into Archimedes’ approach to addressing challenges. I then continued by interpreting Archimedes’ heat ray invention (Figure 3) as a guide to study different perspectives of his work, including the block and pulley system, heat ray, the screw and his analysis of buoyancy. I did not follow the chronological development of Archimedes’ works or systems, although it could have provided further insight; also, there are multiple views about this order (Knorr Reference Knorr1978). I focused on the essence of the works and used them to drive the formulation and validation of Archimedes’ Code which I formulated. I then showed how the code allowed Archimedes to create new knowledge from existing knowledge – an act fundamental to design. It is interesting to note that the two principles I used to study Archimedes’ work – the lever and the heat ray – are those that comprise his code.

Figure 2. Archimedes’ lever. The picture is public domain, via Wikimedia Commons.
3. The lever
The fulcrum of this study is an analysis of Archimedes’ lever. It is one of Archimedes’ iconic contributions with numerous interesting observations. A classic lever is composed of two elements: a basis also referred to as a fulcrum and a rod placed on it. From Archimedes’ statement “Give me a place to stand on, and I will move the earth,” it is clear that the fulcrum of the lever is critical to the ability to execute this impossible activity of moving the earth. The fulcrum represents something we know and can rely on; it is solid. It may be something we have already created on which more can be built. As in science, existing knowledge is the basis for generating discoveries echoing the phrase: “sitting on the shoulders of giants (John of Salisbury, 1151; quoted in Korolak Reference Korolak2008).”
Moving earth requires also a stiff rod placed on the fulcrum. The rod figuratively acts as our extension, a device to reach our senses and capabilities beyond our physical manifestation. The rod, the lever and virtually every man-made product have the same objective to serve as our extensions and amplifiers, from the microscope that allows us to look into atoms, to the telescope that allows us to explore far and back in time; we leverage them to sense the world and influence it. The history of science is closely intertwined with the evolution of designing levers (technology) that enhance our perceptual and physical power. Considering the scientific activities at CERN, or the recent launch of the James Webb Space Telescope, such levers could cost billions of dollars.
The moving or lifting action is a kind of exchange, a dialogue, where the lifted and lifter are both influenced by each other through the lever as the mediator. The rod that supports such a dialogue acts as a medium for transferring information or energy. To illustrate, a door that opens when we press the handle includes a mechanical lever in the handle, and analogously, a website account that opens when we type the password also includes a lever. With this abstraction, a cause-and-effect or an input–output relationship, such as turning on the switch of a lamp to display light, can be perceived as a lever.Footnote 1 Construed this way, any system can be perceived as a collection of levers, mechanisms for the transformation of states, orchestrated to work together to get to the desired state. The functional description and decomposition of a system (Pahl & Beitz Reference Pahl and Beitz1988; e.g., Figures 5.6, p/67) reflects such a composition of levers. Similarly, other system representations used in practice reflect such a decomposition (Hubka & Eder Reference Hubka and Eder2012; Andreasen et al. Reference Andreasen, Hansen and Cash2015). Similar to the representation of diverse functions or system elements from different disciplines with an input–output relationship through a function or an object in a standard way, we contend that we can call this input–output relationship a lever. The use of multiple interacting levers to describe a system is fundamental to this study of Archimedes, as we see later.
The act of lifting, this dialogue, has one important condition. Moving the earth is very difficult because of its weight and inertia. Similarly in a conceptual way, ‘moving’ the earth to a more environmentally sustainable state seems almost impossible. Archimedes understood that to move the earth, one had to get out of it, to get a different perspective, to get ‘out of the box’. This echoes a phrase probably wrongly attributed to Einstein “We can’t solve problems by using the same kind of thinking we used when we created them.” Moving or changing an object requires an external perspective. If the object is an organisation, people or a person, this mandates the need for reflection (Argyris & Schön Reference Argyris and Schön1978; Schön Reference Schön1983; Senge Reference Senge1990). Archimedes understood this concept of a reflective practitioner (Schön Reference Schön1983) and the necessity of varying perspectives (Subrahmanian et al. Reference Subrahmanian, Reich and Krishnan2020), formal and informal (Subrahmanian et al. Reference Subrahmanian, Konda, Levy, Reich, Westerberg and Monarch1993). He made significant use of them in his inquiries where he created external models to think about and leverage them. One clear example is his mathematics work, employing text and lettered diagrams, where each provided a different perspective that cannot be inferred from the other (Netz Reference Netz1999).
There is another important detail related to the lever, which is its balance or alignment. Balance also exists in large structures such as bridges or in the examples of Archimedes’ work, for example, as shown in Figure 9 and his buoyancy law. Balance is a general and important concept for any system. Any system must be balanced or aligned to be sustainable over time (Reich & Subrahmanian Reference Reich and Subrahmanian2020a; Reich Reference Reich2022; Reich Reference Reich, Nevo, Reich, Levin and Mishori2023). Even the research stages described in Section 2 must have balanced PSI models that make sure that the vision is aligned with the research activities, the required challenge is matched with participants’ knowledge, and reflection makes sure that everything is aligned.
To illustrate the concept of balance further, consider that moving the earth was beyond Archimedes’s capabilities. The task and his power were not balanced. He required the lever to balance the task with the means. We can go a step further into Archimedes’ work and ask how did Archimedes realise his big inventions. There is little information about how Archimedes managed the construction of his machines or boats (Di Pasquale Reference Di Pasquale2010); clearly, these projects involved developing the infrastructure to construct them including a skilled workforce, workshops and working procedures. Designing these elements to align with the types of machines that he built is an example of a necessary balancing that must be considered to succeed (Reich & Subrahmanian Reference Reich and Subrahmanian2020a). A study of Archimedes’ actual engineering practice might be interesting but is beyond the scope of this research.
Another example of such balancing or alignment is Thomas Edison, a prolific inventor who developed the first research lab at Menlo Park and subsequently at West Orange to work on his inventions, aligning the work model with skilful people to address challenging problems (Carlson Reference Carlson1988). The work conducted on Archimedes’ Palimpsest to uncover its content is another example of matching tools and methods with the expertise of people to form a balanced system that could handle the challenge of studying and interpreting the Palimpsest.
Those interpretations of the lever and its associated information are again quite broad but they are viable. We can also envision that Archimedes was aware of all these ideas, even if implicitly. We can suggest this because the former analysis repeats itself in Archimedes’ work. The principles are woven into much of what he achieved. The next two sections illustrate how they appear in diverse perspectives of Archimedes’ work.
4. The emergence of Archimedes’ Code
4.1. Calculating the area enclosed by a parabola and a secant line
Archimedes dealt extensively with the understanding of bodies in the plane and space. In Archimedes’ Palimpsest (Netz & Noel Reference Netz and Noel2007), we find a treatment for the problem of finding the area enclosed by a parabola and a secant line AB, see Figure 4. The hypothesis is that this area is a third of the area of the triangle
![]() $ \Delta $
ABC. This problem was very important for Archimedes as it allowed him to calculate the volume of shapes similar to boats, and together with his buoyancy principle, design ships (Nowacki Reference Nowacki2002): A combination of two theoretical contributions into a single real system design.
$ \Delta $
ABC. This problem was very important for Archimedes as it allowed him to calculate the volume of shapes similar to boats, and together with his buoyancy principle, design ships (Nowacki Reference Nowacki2002): A combination of two theoretical contributions into a single real system design.

Figure 4. Calculating the area enclosed by a parabola and a secant line AB. Credit: CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=642215.
The following reconstruction of the way that Archimedes solved this problem matches that in (Netz & Noel Reference Netz and Noel2007; Assis & Magnaghi Reference Assis and Magnaghi2012) with the addition of his principles; it is as follows, see also Figure 5. First, using his heat ray principle, he decomposed the triangle into many infinitesimal areas represented by line segments with infinitesimal width such as HE that are parallel to the axis of symmetry of the parabola. We further construct a lever JB such that JD=DB and the lever basis is at D. For each of the line segments, HE, we obtain equilibrium via the lever principle by: (a) hanging HE on point G of the lever JB and (b) hanging a small part of it represented by the line segment EF at point J. After repeating this for all infinitesimal areas (i.e., line segments) and recomposing all the intermediate results, we end up with the triangle
![]() $ \Delta $
ABC hanging from its centre of gravity I and the parabola hanging perpendicular to the page at point J. Since JD is three times larger than DI, and the lever is in equilibrium, we obtain that the area of the parabola times JD equals the area of
$ \Delta $
ABC hanging from its centre of gravity I and the parabola hanging perpendicular to the page at point J. Since JD is three times larger than DI, and the lever is in equilibrium, we obtain that the area of the parabola times JD equals the area of
![]() $ \Delta $
ABC times JD/3; consequently, the theorem is proven.
$ \Delta $
ABC times JD/3; consequently, the theorem is proven.
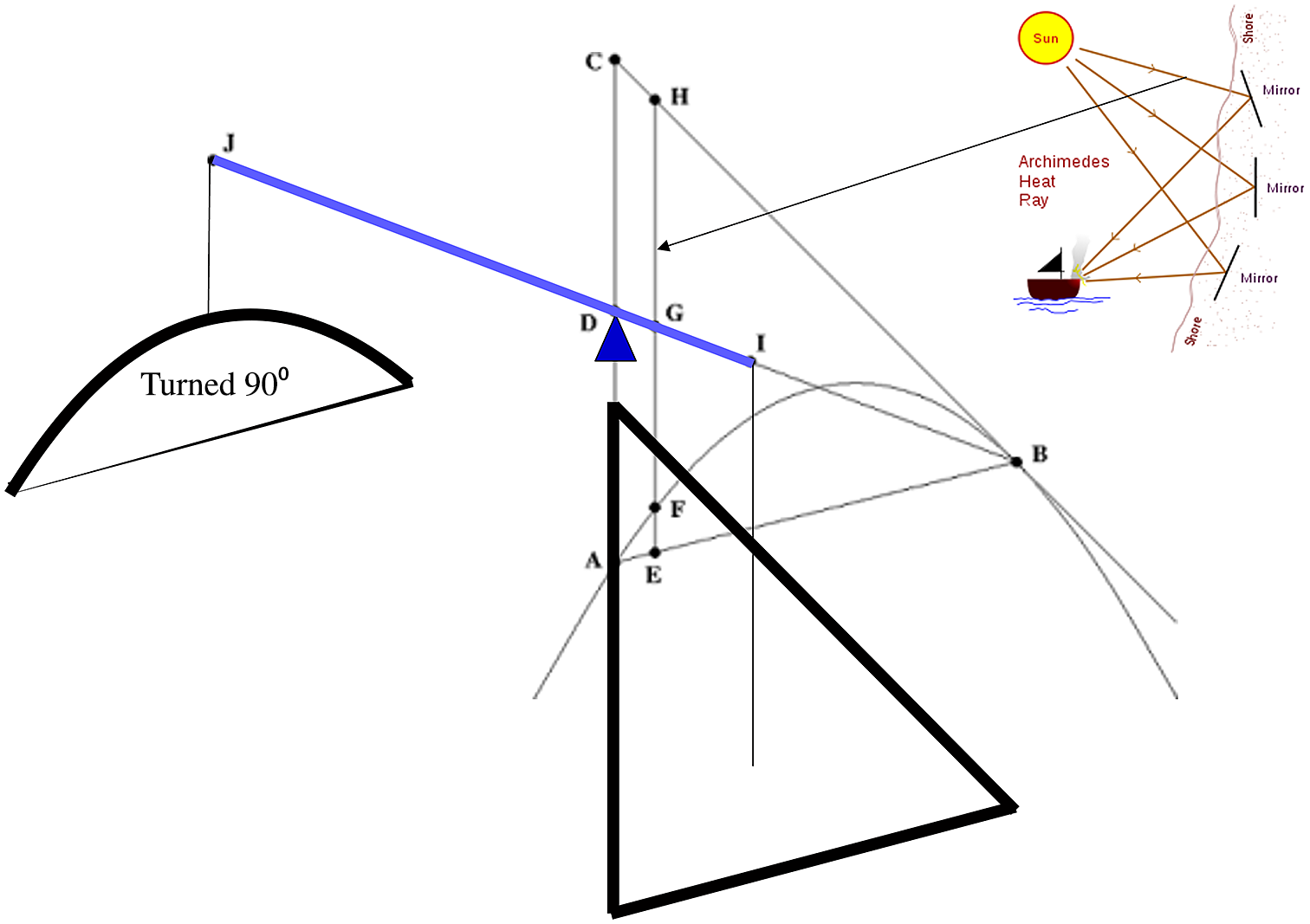
Figure 5. The solution process and the elements of Archimedes’ method. Collage of public domain pictures.
We see here perhaps the first example in the history of a reflexive practitioner (in addition to him being reflective). Being reflexive entails using one personally developed method in practice (Reich Reference Reich2017). Archimedes developed the law of the lever as a physical principle and used it now as a conceptual tool in a theoretical inquiry about basic geometry. This also demonstrates Archimedes’ flexibility in assigning object different identities: once a physical law and once a conceptual tool in basic geometry.
Archimedes called this method ‘the method of mechanical theorems’ and it appears in a letter to Eratosthenes. Archimedes’ solution can be considered the beginning of calculus when he used ‘infinitesimal’ rectangular shapes and combined them (Netz & Noel Reference Netz and Noel2007). In the process of proving the theorem, he designed a language (concepts), models of diverse geometric shapes located in different places in space and relationships between these models that sum up to a balanced whole.
Archimedes also used the same method to calculate volumes of bodies and also in other cases. Figure 6 shows on the right the objects and their geometric relationships, and on the left part, the objects are balanced on a lever following the application of Archimedes’ method. The result shows that the volume of the cylinder is twice the sum of the volumes of the other objects.
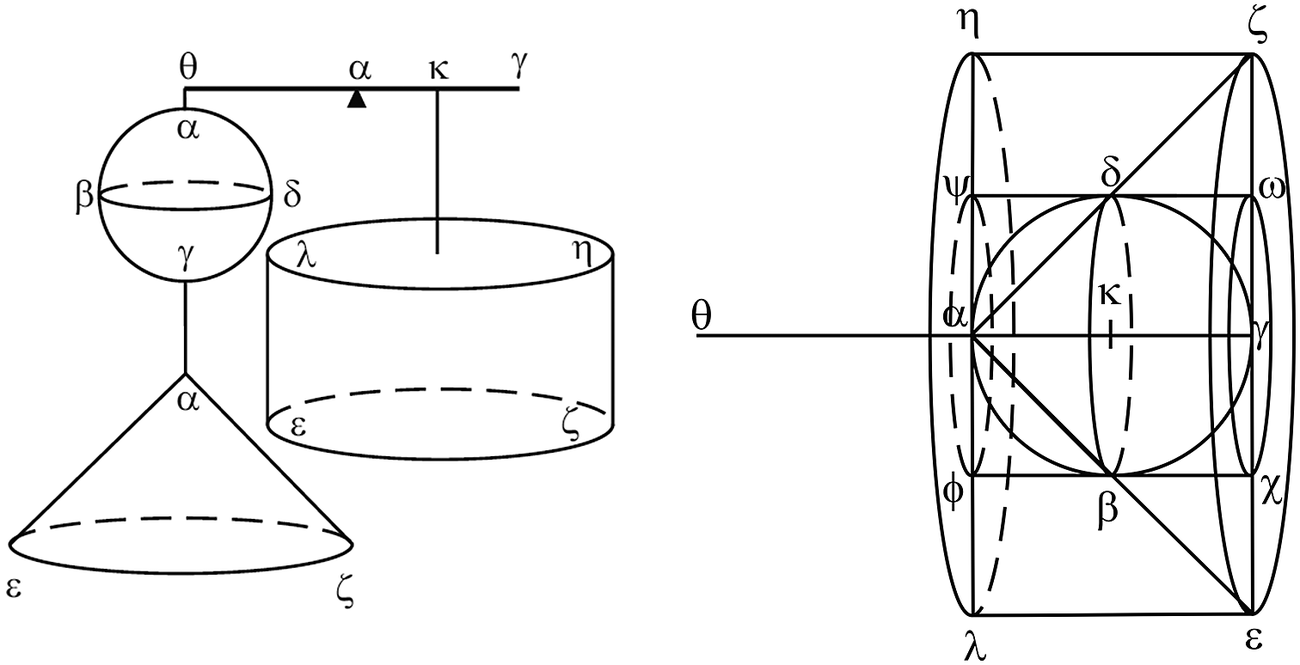
Figure 6. The volumes of a cylinder, cone and sphere. Reproduced from Assis & Magnaghi (Reference Assis and Magnaghi2012) by permission of the authors.
4.2. Archimedes’ Code
To find the area between the parabola and a secant line, Archimedes decomposed it into smaller problems (following the heat ray decomposition) of finding infinitesimal areas. He calculated these areas using his lever principle and then combined them on the lever to get the whole area. In the process, the subproblem elements were balanced and so is the final result after recomposing all the small areas. Equilibrium plays a critical role. We can generalise this process into a plausible process for addressing complex problems:
Archimedes’ Code: A complex problem can be addressed in the following way:
-
(i) Decompose the problem into simpler problems (i.e., following the heat ray principle).
-
(ii) For each simple problem, study it and apply principles in designing its solution (e.g., using the lever principle), or further, recursively decompose it into simpler problems.
-
(iii) Integrate the solutions into a balanced whole, potentially iterating with step 2 and moving up one level (e.g., the integration resembles the convergence of the different sun rays into a single location to burn it).
The hierarchical decomposition and the recursion mentioned in the code were not foreign to Greek mathematicians or Archimedes (Netz Reference Netz1999; Acerbi Reference Acerbi2003). They used them in their practice of mathematics, both related to expressions and diagrams. Netz (Reference Netz1999, p. 195) showed examples of tree structures of assertions in solving a problem. Hence we may assume that Archimedes used them also in his design practice, and in general, for addressing complex challenges. Archimedes’ Code is a framework for what we practice today when we design systems of any kind, such as a washing machine, a phone, a bridge or a car. The different complexities of these products are reflected in the amount of hierarchical decomposition necessary in steps 1 and 2 of the code; the difficulty to address step 2 for providing a technical solution to each subproblem and the difficulty to integrate the partial solutions into a whole in step 3. Archimedes’ Claw mentioned later (Figure 8), is a complex system that exhibits the code with recursive decomposition. The ability to decompose or represent a problem with multiple decompositions is manifested by Archimedes’ Stomachion discussed in Section 6.2.
As already mentioned, one could observe the application of recursion in Archimedes’ Code. The first sign that this concept was not foreign to Archimedes is that he used the law of the lever as a basic scientific method in calculating the area of the parabola, but there are more explicit examples. We will demonstrate such an example later (e.g., Section 5.1) and note that recursion appears in other works by Archimedes, including his definition of large numbers to solve the problem of counting soil particles on earth (Acerbi Reference Acerbi2003).
The ability to reuse concepts previously developed in different situations, for example, lever, or several similar mirrors, is predicated on the concept of flat space in design (Subrahmanian et al. Reference Subrahmanian, Reich, Konda, Dutoit, Cunningham, Patrick, Thomas and Westerberg1997; Reich et al. Reference Reich, Konda, Subrahmanian, Cunningham, Dutoit, Patrick, Thomas and Westerberg1999). A flat space is a conceptual space where all objects previously created are made available for observation and reused as objects in new models or systems; those systems are then put back onto the flat space. Figure 7 shows object A made out of three objects, which is then used as a component in a new system on the right. Object B in the flat space was used to build A and subsequently C. A flat space affords recursion. It also affords the reuse of parts as in Greek mathematics deduction practice (Netz Reference Netz1999). The hierarchical structure of object C in Figure 7 resembles the hierarchical structures that Netz (Reference Netz1999) presents. If Archimedes practised this in his mathematics, it may not be a surprise that we see traces of this in his engineering practice.

Figure 7. The flat space of objects.
To summarise the formulation of Archimedes’ Code, Netz & Noel (Reference Netz and Noel2007, p. 28) acknowledged that:
The two principles that the authors of modern science learned from Archimedes are:
-
(i) The mathematics of infinity.
-
(ii) The application of mathematical models to the physical world.
We claim that we can also learn from Archimedes the application of the strategies he used in mathematics to the physical world, and specifically to his design of engineering systems.
5. Archimedes’ Code applied in science and engineering
I now demonstrate the use of Archimedes’ Code to address additional challenges ranging from science to engineering design and at different scales. The appearance of the code in such diverse examples constitutes a validation of the code as a framework for addressing diverse problems.
5.1. Lifting systems
The block and pulley system implements Archimedes’ Code with recursion. On the left of Figure 8, we see two blocks and pulley systems. Each one has a basis and the top pulley acts as a lever. The system is devised such that some pulleys act in parallel and some sequentially to amplify the force afforded by the system; the composition of systems as parallel and serial ordering of components is a powerful strategy. In both, the lever principle is applied recursively to the hierarchical decomposition. The system on the right, Archimedes’ Claw, includes two large levers (the heat ray principle decomposed the problem into two subproblems, each solved by a large lever), each having a block and pulley system on their left side, constituting a complex lever (block and pulley system) inside a large lever. We see Archimedes’ Code applied here flexibly and recursively. We acknowledge that this picture is an artistic expression and not a display of an actual machine built by Archimedes; nevertheless, we assume that the ideas are based on ancient stories.

Figure 8. Lifting systems implementing Archimedes’ code recursively. Credits: left: Themightyquill, CC BY-SA 4.0, https://creativecommons.org/licenses/by-sa/4.0, via Wikimedia Commons; middle: Carhart, Henry; Chute, Horatio, Public domain, via Wikimedia Commons; right: reproduced from Lazos (Reference Lazos1995) by permission of the publisher.
5.2. Archimedes’ heat ray
The following example is the heat ray, see Figure 9. Undoubtedly, the multiplicity or decomposition and recomposition steps in Archimedes’ Code exist here in the multiplicity of mirrors and their focus on a single point, but surprisingly, also the lever appears here. Each mirror acts as a lever where a slight movement of the mirror causes a ray translation near the target. Here the lever is not a way to balance weight, but to amplify a small change in the angle of the mirror into a large movement of the ray path, as well as to amplify the heat transmitted in a single ray by combining several rays. Using the term lever for describing optical phenomena is not new, the term optical lever is quite old as a device that amplifies the measurement of small angles or dimensions (Jones Reference Jones1961). Consequently, the heat ray is a very clear example of a parallel composition of levers applied to the Sun’s rays.
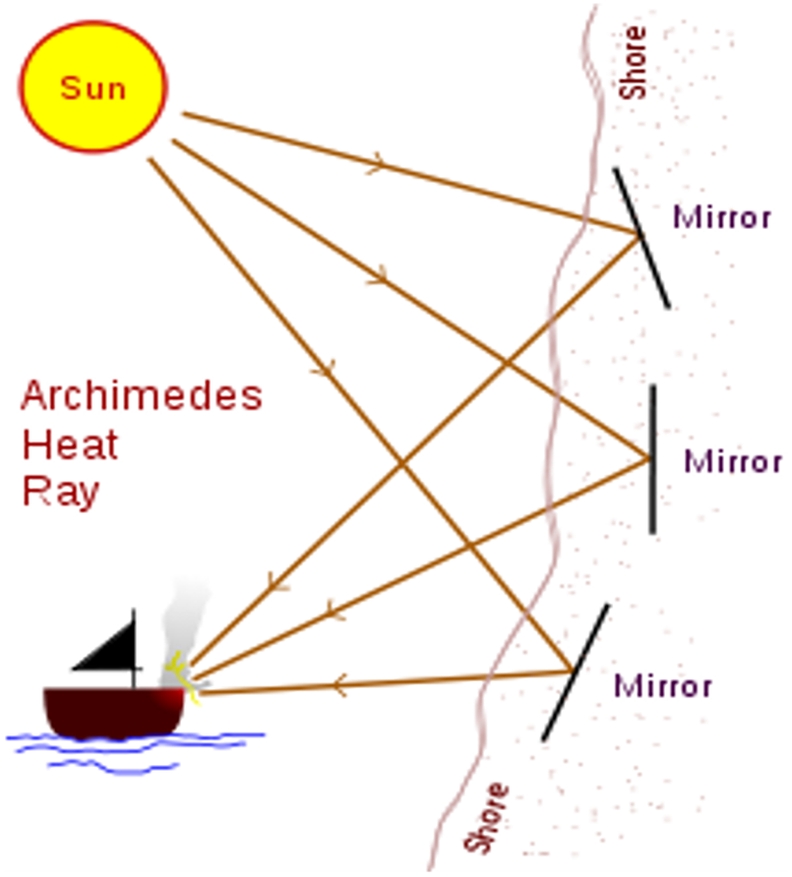
Figure 9. Archimedes’ heat ray. Credit: Finnrind (original); Pbroks13 (talk) (redraw), CC BY-SA 3.0, via Wikimedia Commons.
5.3. Archimedes’ screw
Archimedes’ screw is also built on the lever and heat ray principles, see Figure 10. The lever operation is embedded in the screw handle, the screw radius and the pitch (Ceccarelli Reference Ceccarelli2014, following Del Monte Reference Del Monte1577). The lever basis is the screw bearings. The multiplicity is implemented in the different helical surfaces connected sequentially into a long screw. The use of the code is as follows: to lift water to a certain height, decompose the problem to lift many small heights with a lever, and to recombine the solution such that the water is transferred from one to the next lever. This is an excellent example of a serial composition of helical levers.

Figure 10. Archimedes’ screw. The picture is public domain.
5.4. Buoyancy
The last example of Archimedes’ Code is that of buoyancy, see Figure 11. Here, too, one finds the principle of the lever. First, in the buoyancy of asymmetric bodies, or tilts of ships at sea, there is a moment generated by the gravity and buoyancy forces. The force increases with the tilt angle effectively acting as a lever. To study ship forms, Archimedes had to consider such infinitesimal thick shapes summed together in parallel in the longitudinal dimension with the multiplicity principle, effectively demonstrating the use of his code.

Figure 11. Floating objects as levers.
Floating objects in general act as levers around their centre of floatation. If they are pushed into the fluid, the opposite force is proportional to the push and other objects and fluid properties. Here also, extending to 3D objects requires using the multiplicity principle.
5.5. Summary
The four examples demonstrate that Archimedes’ Code permeates his scientific and engineering work; they validate the code. It is surprising to notice that the same principles work in such diverse cases and multiple levels of complexity. Conceptually, we see again the lever principle. Without the right models of knowledge, looking for such insight is moot. Let us dive more into understanding how Archimedes intentionally used his code to generate new knowledge.
6. Generating new from existing knowledge
When it comes to Archimedes, we will also find the lever and the heat ray – his code – when generating new knowledge. The process of generating new from existing knowledge has two stages.
-
(i) Producing and organising knowledge.
-
(ii) Leveraging existing knowledge to generate new knowledge.
We immediately observe that the first step includes the two stages, making it a recursive definition. This is not a surprise when studying Archimedes. It is part of the code definition. We will try to elaborate on these steps concerning Archimedes’ work, but the apparent recursion cannot be avoided.
Archimedes studied and interacted with the world around him constantly. He created models: sketched on the sand, ashes and the oil anointed on his body. Every place and time became an opportunity for exploration and learning. The models Archimedes drew became boundary objects (Subrahmanian et al. Reference Subrahmanian, Monarch, Konda, Granger, Milliken and Westerberg2003). To use them effectively to move the earth, he had to externalise them just as the basis of the lever has to be outside the earth to move it. Each boundary object became a lever for another object. The multiplicity of models created a variety of perspectives that could be contrasted and contested in a cognitive dialogue, leading to a web of knowledge. Patterns could emerge from the diversity of models, and recognising such patterns led to new insight – a eureka moment. This description of knowledge production and organisation uses Archimedes’ principles or his code, even if sometimes in an abstract manner. Consider now two examples in which Archimedes made explicit use of existing knowledge to generate the unknown through the use of his code.
6.1. Calculating the value of a π: method of exhaustion
Archimedes approached the problem of calculating π by approximations. As Bertrand Russell said (Auden & Kronenberger Reference Auden and Kronenberger1981), “All exact science is dominated by the idea of approximation,” but in Archimedes’ time, this was not practised. Figure 12 shows successive placements of polygons with a larger number of edges inside and outside of a circle. The decomposition into a multiplicity of subproblems exists. First, the problem is decomposed into an internal bounded polygon and an external bounding polygon and second, each polygon is subdivided into triangles to calculate its area. The lever here is less apparent but can be interpreted as the need to force the polygons to touch the circle from the inside and outside, causing them to rest in equilibrium on the touchpoints. By increasing the number of edges and calculating the areas of the inside and outside polygons, the value of π could be approximated with any accuracy. As an engineer and designer, Archimedes stopped at some temporary closure (Subrahmanian et al. Reference Subrahmanian, Monarch, Konda, Granger, Milliken and Westerberg2003; Subrahmanian et al. Reference Subrahmanian, Reich and Krishnan2020) with sufficient accuracy; with 96 edged, the value of π was bounded by
![]() . Archimedes effectively understood the concept of limit in calculus.
. Archimedes effectively understood the concept of limit in calculus.

Figure 12. Approximating the value of π. The picture is public domain.
Archimedes could have approached the calculation differently by placing a polygon inside and mounting a triangle on each edge and recursively continuing until desired. But such calculation leads to a more complicated calculation than the elegant bounded approximation. When he calculated the area of a parabola differently than what was presented above, he used this method and solved it by considering the sum of an infinite series of areas (Hahn Reference Hahn1998).
6.2. Stomachion: combinatorics
The last example is interesting as it exposes yet another facet of Archimedes’ ingenuity – the case of the Stomachion. The game has a square box containing 14 shapes, shown on the left of Figure 13. A single page written by Archimedes on the Stomachion was discovered by Heiberg only recently, in 1906, inside Archimedes Palimpsest (Netz & Noel Reference Netz and Noel2007). Initial study and further analyses did not reveal a clear objective that led Archimedes to study the Stomachion. As shown in Figures 14 and 15, scholars thought that the 14 shapes were meant to generate arbitrary interesting and creative shapes. Nevertheless, they were puzzled because according to them, this did not constitute an interesting challenge for Archimedes (Netz, Acerbi & Wilson Reference Netz, Acerbi and Wilson2004; Gow Reference Gow2005).

Figure 13. Two configurations of the Stomachion. The pictures are public domain.

Figure 14. A Stomachion elephant.

Figure 15. Figure construction outside the box. Credit: Meisenstrasse – Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=104322269.
A newer interpretation (Netz et al. Reference Netz, Acerbi and Wilson2004; Netz & Noel Reference Netz and Noel2007) suggests that Archimedes was interested in counting how many times a square can be formed from these 14 pieces; effectively studying combinatorics. It is, therefore, the first evidence of such work in history. Arriving at this interpretation required forming hypotheses from the written text, reading other available sources on the Stomachion, and understanding the historical context. The researchers reporting it wrote:
This is how readings take place: you can make a reading only after you have formed some kind of guess as to the possible meanings of the text to be read. This, above all, was why Heiberg had not succeeded in reading the infinity passage in the Method or in reading the Stomachion. He had expected neither actual infinity nor combinatorics (Netz & Noel Reference Netz and Noel2007, p. 254).
The story of finding the Palimpsest and interpreting it is an example of a complex challenge. It was read in different ways by different people, depending on the context and their expectations, and the team mobilised to decipher it and its available resources. This initial state was the lever from which they started. The readers had to integrate diverse sources and interact with the text to form an acceptable interpretation, out of several they tried; we can only appreciate these interpretations without knowing which is correct. Readings of his work resemble Archimedes’ work with external models: drawing, forming hypotheses and redrawing until insight emerges. Similarly, the interpretation of Archimedes’ work in this article follows the research plan presented in Section 2: studying Archimedes’ work, generating hypotheses about his work, refining the readings, and evolving the definition of Archimedes’ Code. The three stages of the research mentioned in Section 2 embed this evolution, as well as the review of this article which led to additional evolution. Is not this providing evidence that the study of different complex challenges goes through similar steps?
Finding different arrangements of the Stomachion pieces that fit into the square is a difficult task if we spread them out. It requires effort and concentration to succeed. Figure 13 depicts two possibilities to arrange the objects. It transpires that there are 17,152 possibilities according to a study in 2003 – a recent result for such an old game (Netz & Noel Reference Netz and Noel2007). By considering various symmetries, this number can be reduced to 536 options. It is much easier to use such considerations to generate new configurations than to spread all pieces and solve them. It is a case that one configuration acts as a lever for generating others by simple manipulations.
The Stomachion has continued to attract the imaginations of people. Further studies found all the configurations of pieces that fit into convex shapes (Rennhak Reference Rennhak2004) or attempted to create several shapes from the 14 pieces with some relations between their areas (e.g., 1:2:3) (Pitici Reference Pitici2008). The variety of surprising shapes that could be done with the Stomachion pieces is a testimony to its underlying richness. What then is the most interesting question related to the Stomachion and how does it represent Archimedes’ Code? The most interesting problem is designing the game itself: Dissecting the square in different ways into several (e.g., 14) pieces that give rise to interesting, as well as unanticipated shapes. Readers may find it interesting to take a square piece of paper and cut it, not perpendicular to the edges, into 14 pieces and try to assemble them into a different square shape. If it is difficult to perform with the original game, it is much more difficult to design the game. What would we call a successful game and can we tell that the present Stomachion is the optimal one? We do not have answers to these questions suggesting that designing the Stomachion is an example of an extremely difficult problem, which is quite surprising for a puzzle. Designing it followed careful studies of shapes and their relations (Netz et al. Reference Netz, Acerbi and Wilson2004) and potentially evolved following numerous attempts. We do not know whether Archimedes designed the Stomachion or not, but its design embeds the ideas of the newly formulated Archimedes’ Code.
7. Discussion on generating new knowledge
Rejecting the constraint of the Stomachion box, rejecting fixation, opens up many opportunities for generating endless new shapes; but they are easy to generate, almost unchallenging. We can go a step further, although this has not been practised yet. We suggest that if on each edge of the shape generated by the Stomachion pieces, or between two nodes on a figure, as the elephant in Figure 14, we draw a curved or even arbitrary line connecting the nodes and keeping it close to the edge as the relation between the polygon edges and the circle in Figure 12, we could enrich the shaped infinitely, as shown in Figure 16. The base geometry created by the Stomachion pieces could serve as a skeleton for the elaborated or decorated figure; it could be considered also as a lever for the new figure.

Figure 16. A Stomachion elephant with curved approximations.
In contrast to the out-of-the-box creation, generating new square shapes with the Stomachion pieces is a challenging task but it could be systematised algorithmically. Consequently, its generativity (Hatchuel et al. Reference Hatchuel, Le Masson, Reich and Weil2011) is rather low. In general, reducing constraints may ease creativity but still keep it challenging. Conversely, resolving constraints is an important objective in creativity-support methods such as TRIZ (Altshuller Reference Altshuller1984) and ASIT (Horowitz Reference Horowitz1999).
7.1. Design theory: knowledge generation
Interpreting the foregoing discussion in the language of C-K (Hatchuel & Weil Reference Hatchuel and Weil2009) suggests that the creative part of generating new shapes would be engaging in manipulating concepts in C, while the generation of new squares or other well-defined shapes (e.g., convex) would be considered perhaps as K orderings. For Archimedes, it was much more challenging to work on the K than on the C, although based on his inventions, he mastered the C. The best testament for this in the context of the Stomachion is asking the most interesting question: how could we design the shapes of the Stomachion in the first place, making it an interesting game? How do we make sure it is possible to generate even just one additional square shape? Designing the basic knowledge structure is a fascinating problem.
In the language of C-K, creating good structures of K endangers generativity (Hatchuel et al. Reference Hatchuel, Le Masson, Reich and Weil2011). Hence, to be able to design solutions to challenges, we need to construct our knowledge structures beforehand. Only in this way, do we have a good and stable basis and a lever to rely on. Within the 14 pieces of the Stomachion, lies the future capacity that can be obtained from the forms. It sets the framework for the future and that is why it is so important. Reviewing the C-K theory, this resonates with the challenge of developing future technologies to allow for developing new products without encountering gaps or missing knowledge in the future (Kokshagina et al. Reference Kokshagina, Gillier, Cogez, Le Masson and Weil2017).
The Stomachion teaches us that anything even as perfect as a square can be dissected, disassembled and reassembled in ways other than it was conceived. Similar ideas have been taught 100 years ago at the Bauhaus (Le Masson, Hatchuel & Weil Reference Le Masson, Hatchuel and Weil2016). Similarly, morphological thinking or charts (Zwicky Reference Zwicky1957) could be considered as a way to dissect a complex problem in different ways (e.g., functions, requirements and technologies) and to use available building blocks, new and inspirational inputs from nature, or other sources to address challenges. For example, a chart could have material, texture, smell and reflection parameters, and each parameter can have all the values available independent of its source. Such independence breaks objects’ identities, creating the ability to generate objects that no one has ever seen (Hatchuel et al. Reference Hatchuel, Le Masson, Reich and Subrahmanian2018). Consequently, one can map the Bauhaus teaching techniques to morphological thinking.
Archimedes demonstrated the expansion of knowledge not only within specific projects but across his work. When he developed the lever law, he abstracted it and made it generic knowledge to be used in science and practice. Similarly, his heat ray invention embeds the decomposition and recomposition strategy that became part of his code, again serving as a generic knowledge source. In using the methods he developed in his work, he demonstrated being a reflexive practitioner (Reich Reference Reich2017).
7.2. Patterns: pros and cons
The concept of a pattern is fundamental to human thinking. We learn patterns and similarly today, machine learning software learns patterns, so they could be identified quickly and efficiently in the future. The efficiency of processing patterns in real-time is critical (Eysenck & Keane Reference Eysenck and Keane2020); patterns can encode knowledge for sharing among people (Alexander Reference Alexander1977) and they are associated with superior human capabilities (Mattson Reference Mattson2014). But patterns are also fixating. As they emerge, they can attract attention. I, for example, can identify a Star of David or Swastika in places that others would not notice. In such situations, I may ignore other stimulations (Chabris & Simons Reference Chabris and Simons2010).
The Stomachion explains to us how we could be fixated by the constraint to operate in the square but also how to unfix us, allowing infinite options if we move out of the box. The Stomachion further informs us that if we dissect a square – a familiar object – into seemingly odd shapes in a particular manner, we can be enormously generative and otherwise get stuck in one shape. The way we chose to take an object and break it down, including the constraints between its constituents, the properties we use, and their common meanings, allow us to be generative.
The concept of flat space allows unlimited decomposition and recompositions to occur. If the space remains static then fixation will ensue. To be generative, the space of objects in the flat space will have to include patterns arising out of new perspectives and knowledge and their dissection in potentially unconventional ways. Depending on our objectives, we can design such patterns and objects – we can design the knowledge structures in the flat space so that we can design the context of the design problem. Considering these properties of the flat space, Archimedes’ design of the Stomachion, if indeed it was him, could be considered one of his significant theoretical accomplishments related to design.
7.3. Transdisciplinary theory and practice
By and large, previous analyses of Archimedes’ work focused on one invention or contribution at a time. There may be some that covered several topics related to a single subject, such as buoyancy, the law of the lever, the method of exhaustion, and the method of mechanical systems, since they are all related to ship design (Nowacki Reference Nowacki2002). But otherwise, the analyses were siloed. In contrast, Archimedes was a transdisciplinary scholar working on diverse topics, and only a transdisciplinary analysis, such as the one conducted in this article, can uncover the true richness of his work and ideas. Transdisciplinarity avoids disciplinary fixations leading to new opportunities.
Archimedes not only crossed disciplinary boundaries but also was a pragmatic scholar seamlessly combining theory and practice. While he advanced theory, a significant part of his theoretical work was driven by practice and his practical results were used as conceptual tools in his theoretical investigations. For example, much of his work on areas enclosed by curves, the volume of bodies and buoyancy, was driven by his interest in ship design (Nowacki Reference Nowacki2002; Di Pasquale Reference Di Pasquale2010). Archimedes also wanted to demonstrate the importance of practical knowledge. As Di Pasquale (Reference Di Pasquale2010) writes, quoting Plutarch, King Hieron II asked Archimedes to publicly demonstrate his mechanical knowledge. The opportunity came when it was time to launch the ship Syrakousia that Archimedes built for Hieron II, a ship that was the largest of his time. Archimedes sat and used a device potentially including a block and pulley system and an endless screw to move the ship himself.
Archimedes selected this simple device to counter Aristotle who considered every combination of the five basic machines (i.e., winch, pulley, lever, screw and wedge) to be limited for addressing complex challenges, such as moving a boat. Archimedes with his code knew better. It was the triumph of his practical knowledge over the theoretical abstract reasoning of Aristotle and he wanted to demonstrate this to the public. Perhaps this occasion was when he expressed his immortal statement: “Give me a place to stand on, and I will move the earth.”
8. Conclusion
A transdisciplinary study of Archimedes reveals a giant theoretician and practitioner that preceded his time. Reading ancient incomplete text is a process of forming hypotheses or patterns and using them to make sense. With such a view, every generation will appreciate Archimedes differently. Following recent advancements in design theory, we have a rich vocabulary to interpret Archimedes’ work that we did not have previously. This allows us to recognise Archimedes’ ingenuity more than before and arrive at what we called Archimedes’ Code. While Archimedes did not articulate explicitly a design theory or his code, we see the patterns emerging from his work.
Archimedes’ legacy goes beyond his specifically acknowledged inventions and scientific contributions to include now a specific plausible code that governed his work. This code is the basis for addressing complex problems. The fact that his powerful code demonstrates the principle of reflexive practice (Reich Reference Reich2017) suggests that we may want to adopt this principle also. Archimedes further demonstrated that science and practice should be seamlessly intertwined and that multidisciplinarity cannot be avoided and is extremely valuable, pointing design researchers to engage more in practically relevant problems (Reich Reference Reich2022).
This study by no means marks the definitive interpretation of Archimedes’ work. First, we did not analyse all of his work, and not from primary sources, but from different interpretations that were available. New writings may be discovered in the future enhancing or refuting our hypothesis about Archimedes’ Code. Second, new patterns of thoughts or ideas might emerge giving rise to new interpretations. Our analysis is only an approximate temporary closure.
Acknowledgments
This article started as a presentation at the symposium on ‘The Diverse Worlds of Archimedes,’ held at the Holon Institute of Technology on 8 November 2021. I thank Prof. Adir Pridor and Prof. David Raved for inviting me to give this lecture. Discussions with, and comments by, Eswaran Subrahmanian and Panos Papalambros improved this article. The anonymous reviewers also helped improve this article. The multiplicity of and dialogue between perspectives is a perpetual lever. I thank the copyright holders for the figures I used in this article. There was an attempt to identify the owners and ask for their permission, which was granted.
Financial support
This research received no specific grant from any funding agency, commercial or not-for-profit sectors.
Competing interest
The author has no competing interests to declare.





















