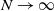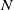1. Introduction
Over the last few years, there has been an increased level of activity on the study of collective behaviour phenomena from a multiscale modelling perspective. Classical examples in socio-economy, biology, and robotics are given by the interactions between self-propelled particles, such as animals and robots, see, e.g. [Reference Albi, Bellomo and Fermo1, Reference Bellomo and Soler6, Reference Cordier, Pareschi and Toscani13, Reference Degond, Liu, Motsch and Panferov14, Reference Estrada-Rodriguez and Gimperlein18, Reference Herty and Pareschi32]. Those particles interact according to a nonlinear model encoding various social rules for example attraction, repulsion, and alignment.
It is of great relevance for applications in the study of the impact of control inputs in such complex systems. Results in this direction allow the design of optimised actions such as collision-avoidance protocols for swarm robotics [Reference Choi, Kalise, Peszek and Peters10], pedestrian evacuation in crowd dynamics [Reference Albi, Bongini, Cristiani and Kalise2], the quantification of interventions in traffic management [Reference Tosin and Zanella37] or in opinion dynamics [Reference Albi, Herty and Pareschi4, Reference Garnier, Papanicolaou and Yang26]. From a mathematical point of view, a multiagent control problem is described by minimisation of an integral objective functional subject to a constraint that is the complex dynamic depicted by a system of ordinary differential equations (ODE).
The formulation of an interacting particle system at a microscopic level requires the study of large-scale systems of agents (or particles), and it requires a considerable effort both from a theoretical and numerical point of view. We may consider a different level of description, that is the derivation of mesoscopic or mean-field approximations of the original dynamic. Here, the density of the particles is obtained as the number of particles tends to infinity [Reference Cardaliaguet9, Reference Degond, Liu and Ringhofer15–Reference Duteil17, Reference Fornasier, Haskovec and Toscani21, Reference Ha and Liu30, Reference Ha and Tadmor31, Reference Herty and Ringhofer33–Reference Lasry and Lions35]. Of particular interest is therefore the design of controls in the mean-field control approaches [Reference Borzi and Grüne7, Reference Fornasier, Lisini, Orrieri and Savaré22–Reference Fornasier and Solombrino24].
In this paper, we focus on the turnpike phenomenon for mean-field optimal control problems. This topic has been studied recently for example in [Reference Cirant and Porretta11], and it concerns relations between the solutions of dynamic optimal control problems with objective functionals of tracking type and the corresponding static optimal control problems. The turnpike property states that the distance between the dynamic and the static optimal solution is small, in particular, for large time intervals. Hence, it allows to use this information about the structure of the dynamic optimal control to reduce the cost to obtain a numerical approximation by using the static optimal control that can be obtained more easily.
An early reference to the turnpike property is [Reference Samuelson36], and in [Reference Faulwasser, Grüne, Trelat and Zuazua20, Reference Zaslavski41, Reference Zaslavski42], overviews on discrete-time and continuous-time turnpike properties are given. The turnpike phenomenon for systems governed by ordinary differential equations has been studied also in detail in [Reference Geshkovski and Zuazua27, Reference Trélat and Zuazua39, Reference Zaslavski40]. Measure and integral turnpike properties have been studied in [Reference Trélat and Zhang38]. A turnpike analysis for systems that are governed by semilinear partial differential equations is presented in [Reference Grüne, Schaller and Schiela28], while the relation between the turnpike property and the receding-horizon method is investigated in [Reference Breiten and Pfeiffer8]. In [Reference Faulwasser, Flaßkamp, Ober-Blöbaum, Schaller and Worthmann19], manifold turnpikes are also studied. We can find in the literature a lot of studies for different variants of turnpike behaviour for both discrete and continuous-time optimisation problems governed by either finite or infinite dimensional systems, such as the exponential turnpike property (see e.g. [Reference Trélat and Zuazua39]) or the integral and measure turnpike properties, as in [Reference Trélat and Zhang38]. In this work, we consider the turnpike property with interior decay, which describes the situation that in the interior of the time interval, the distance between the dynamic optimal control/state pair and the corresponding static solution is often very small for sufficiently large time horizons. We are interested in particular on the question whether the turnpike property of a system persists in the limit of infinitely many ODEs and under which conditions such a turnpike property holds true on the mean-field level.
Next, we state the optimal control problem in detail. We consider the control of high-dimensional nonlinear dynamics accounting for the evolution of
$N$
agents at the microscopic level and, as described for example in [Reference Duteil17], the mean-field dynamics given by a non-local transport equation for the density of particles at position
$x \in \mathbb{R}^d$
and time
$t \in \mathbb{R}^+$
. The initial particle density
$\mu ^0(x)$
is given, and the control action is modelled by an additive term in the partial differential equation (PDE). More specifically, we consider a PDE of the type
\begin{equation} \partial _t \mu (t,\, x) + \partial _x \Bigl ( \left ( (P\ast \mu )(t,x) + u(t,x)\right ) \, \mu (t,\, x) \Bigr ) = 0, \qquad \mu (a, x) = \mu ^0(x), \end{equation}
where
$\ast$
denotes the convolution operator, the function
$P$
is given, and the real positive number
$a$
is the initial time. Dynamics of this type may also occur as non-local regularisations of balance laws, see, e.g., [Reference Bayen, Friedrich, Keimer, Pflug and Veeravalli5, Reference Coclite, De Nitti, Keimer and Pflug12].
We consider an optimal control problem for a finite large time horizon, subjected to system (1.1). The objective function that we want to minimise depends both on the control and the state
\begin{equation*} \textbf {J}_{( a,\, b)}(\mu, \,u)= \int _a^b f( \mu (t,\,x), \, u(t, x) ) \, dt, \end{equation*}
for a given real-valued function
$f$
\begin{equation} f(\mu, \,u) = \int _{\mathbb{R}^d} \left ( L(x) + \Psi (u(t,x)) \right ) \, d \mu (t,\, x), \end{equation}
and a time interval
$[a,b]$
with
$a\lt b$
real positive numbers. A particular example is given by
\begin{equation} \partial _t \mu (t,\, x) + \partial _x \Bigl ( \left ( (\mathcal{H}\ast \mu )(t,x) + u(t,x)\right ) \, \mu (t,\, x) \Bigr ) = 0, \end{equation}
where
$ (\mathcal{H}\ast \mu )(t,x) = \int _{\mathbb{R}^d} H(x-y)( y - x) \, d \mu (t, \, y)$
denotes a non-local integral operator and
$H$
a given continuous function. For this example, we assume that the integral objective function is the sum of a quadratic control cost and a tracking term. The tracking term is the mean-field limit of a microscopic term that aims all the particles to reach a constant consensus state
$\bar{\psi }$
. Hence, the size of the difference
\begin{equation*} \int _{\mathbb {R}^d} {\left \lVert x - \overline {\psi }\right \rVert }^2 \, d \mu (t, \, x) \end{equation*}
is minimised in a suitable norm, assuming that
$1 = \int _{\mathbb{R}^d} 1 \, d \mu (t, \, x)$
. For a parameter
$\gamma \geq 0$
, we consider
$f = \hat{f}$
\begin{equation} \hat{f}( \mu, \, u )= \int _{\mathbb{R}^d} \left ({\left \lVert x - \overline \psi \right \rVert }^2 + \gamma{\left \lVert u(t,x) \right \rVert }^2 \right ) \, d \mu (t,\, x) \,. \end{equation}
Note that this is a particular case included in the cost functional from [Reference Fornasier and Solombrino25]. Therein, the minimisation of a more general integral cost constrained by a PDE is considered. The analysis in [Reference Fornasier and Solombrino25] is applicable to our optimal control problem, in particular, the existence result for controls is provided in Theorem 4.7 but the turnpike property is not discussed.
The paper is organised as follows. In Section 2, the general dynamic optimal control problem is defined at microscopic level. Section 3 is devoted to the mean-field approximation of the microscopic dynamics and presents an existence result for the solution of the mesoscopic control problem. In Section 4, we show that the problem satisfies a strict dissipativity inequality both at the microscopic and mean-field level. In Section 5, we prove that a cheap control condition holds, we first discuss it for the case with a finite number of particles and then we extend it to the mean-field case. Finally, Section 6 uses the previous assumptions to prove the turnpike property with interior decay.
2. An optimal control problem for N particles
Let natural numbers
$d$
and
$N$
be given. Define the state space
\begin{equation*}X_N = ({\mathbb R}^d)^N.\end{equation*}
Let initial particle states
$\psi ^0\in X_N$
be given. For
$\psi _k(t) \in{\mathbb R}^d$
(
$k\in \{1,\ldots,N\}$
) as in [Reference Albi, Herty, Kalise and Segala3], we consider the system with the initial conditions
$\psi _k(a) = \psi ^0_k$
(
$k\in \{1,\ldots,N\}$
). Let a continuous function
\begin{equation*} P\;: \; {\mathbb R}^d \rightarrow {\mathbb R}, \quad \text {with} \ P(0)=0, \end{equation*}
be given that is bounded with respect to the maximum norm. For
$k\in \{1,\ldots,N\}$
the movement of the particles is governed by the ordinary differential equations
\begin{equation} \begin{split} \psi' _{\!\!k}(t) &= (P \ast \mu _N)(\psi _k(t)) + u_k(t) \\[5pt] &= \frac{1}{N} \sum _{i=1}^{N} P(\psi _i(t) - \psi _k(t)) + u_k(t), \quad \psi _k(a)= \psi ^0_k, \end{split} \end{equation}
where
$u_k(t) = u(t, \psi _k(t))$
and
\begin{equation*} \mu _N(t,x)= \frac {1}{N} \sum _{i=1}^{N} \delta (x-\psi _i(t)) \end{equation*}
is the empirical measure supported on the agents states. We search for a control
$u_k(t)$
that is a solution of the optimal control problem where the cost functional
\begin{align} \mathcal J_{(N,a,b)}(\psi, u) = \int _a^b f_N(\psi (t),u(t)) \, dt, \end{align}
is minimised, with
\begin{equation} \begin{split} f_N(\psi,u) &= \int _{\mathbb{R}^d} \left ( L(x) + \Psi (u(t,x)) \right ) \, d \mu _N(t,\, x) \\[5pt] &= \frac{1}{N} \sum _{k=1}^N \Bigl ( L(\psi _k(t)) + \Psi (u_k(t)) \Bigr ), \end{split} \end{equation}
where the optimisation horizon
$b-a$
expresses the time horizon along which we minimise the running cost. Thus, our objective is a function of the state and control variables. For
$k\in \{1,\ldots,N\}$
, we define the static variables
$\psi ^{(\sigma )}, \ u^{(\sigma )}$
, for the state and control respectively. Then with the initial data
$\psi _k(a) = \psi ^{(\sigma )}$
and the control
$u^{(\sigma )}_k = u^{(\sigma )} = 0$
, the system remains in the steady state
$ \psi _k(t) = \psi ^{(\sigma )}$
, for every
$k\in \{1,\ldots,N\}$
. The problem is similar to the problem that has been considered in [Reference Fornasier and Solombrino25].
For real positive numbers
$a, b$
, with
$b\gt a$
and an initial state
$\psi ^0\in X_N$
, we define the parametric optimisation problem
\begin{equation*}\mathcal Q(N, \, a,\, b, \, \psi ^0):\, \min _u \mathcal J_{(N,\, a,\, b)}(\psi, \,u) \end{equation*}
subject to (2.1), and
$\mathcal{V}(N, a,\,b,\,\psi ^0)$
the optimal value of
$\mathcal Q(N, \, a,\, b, \, \psi ^0)$
.
3. Existence of solutions in the mean-field limit
The original formulation of the interacting particle system (2.1) is at microscopic level through a system of ODEs, but the study of microscopic models for a large system of individuals implies a considerable effort especially in numerical simulations, as models on real data may take into account very large number of interacting individuals. To reduce this complexity, we can consider a more general level of description, that is the derivation of a mesoscopic approximation of the original dynamic. The basic idea is to analyse the density of particles, instead of focusing on the evolution of every single particle. Hence, we will consider continuous models in order to simulate the collective behaviour in case of analysing systems with a large number of agents
$N\gg 1$
. By passing to the mean-field limit
$N \rightarrow \infty$
of the ODE system (2.1), we obtain the PDE problem (1.1) which describes how the density of the particles
$\mu = \mu (t,x)$
changes in time.
In order to prove the existence of a mean-field limit for the dynamics (2.1) and the cost functional (2.2), we consider the functions with the following properties:
-
(P) The function
$P\;:\;\mathbb{R}^d \rightarrow \mathbb{R^d}$
, with
$P(0)=0$
, is a locally Lipschitz function such that
\begin{equation*} \Vert P(\psi ) \Vert \leq C_P \Vert \psi \Vert, \quad \text {for all } \psi \in \mathbb {R}^d. \end{equation*}
-
(L) The function
$L\;:\;\mathbb{R}^d \rightarrow [0, + \infty )$
is a continuous function with respect to the topology generated by the Euclidean distance on
$\mathbb{R}^d$
.(
$\Psi$
) -
ψ The function
$\Psi \;:\;\mathbb{R}^d \rightarrow [0, + \infty )$
, with
$\Psi (0)=0$
, is a non-negative convex function and there exist
$C_{\Psi } \geq 0$
and
$1\leq q \leq + \infty$
such thatfor all
\begin{equation*} \text {Lip} (\Psi, B(0,R)) \leq C_{\Psi } R^{q-1}, \end{equation*}
$R\gt 0$
.
Considering these three assumptions for the functions
$P,L,$
and
$\Psi$
, we can apply the existence Theorem 4.7 in [Reference Fornasier and Solombrino25]. In Theorem 3.1, we indicate with
$\mathcal{W}_1$
the Wasserstein distance between two probability measures
$\mu$
and
$\nu \in P_1(\mathbb{R}^d)$
as
\begin{equation*} \mathcal {W}_1(\mu,\nu ) \;:\!=\; \inf _{\gamma \in \Gamma (\mu,\nu )} \int _{\mathbb {R}^d\times \mathbb {R}^d} \Vert x-y \Vert \ d\gamma (x,y), \end{equation*}
where
$\Gamma (\mu,\nu )$
denotes the collection of all measures on
$\mathbb{R}^d\times \mathbb{R}^d$
with marginals
$\mu$
and
$\nu$
on the first and second factors respectively.
Theorem 3.1.
Let
$\mu ^0\in P_1(\mathbb{R}^d)$
be a given probability measure with compact support. We assume that the sequence
$(\mu _N^0)_{N\in \mathbb{N}}$
of empirical measures
$\mu _N^0(x) = \frac{1}{N} \sum _{i=1}^N \delta (x-\psi _i^0)$
is such that
$\lim _{N\rightarrow \infty } \mathcal{W}_1(\mu _N^0,\mu ^0) = 0$
. Let
\begin{equation*} \mu _N(t,x) = \frac {1}{N} \sum _{i=1}^N \delta (x-\psi _i(t)), \end{equation*}
be supported on the phase space trajectories
$\psi _i(t) \in \mathbb{R}^d$
, for
$i=1,\ldots,N$
, defining the solution of (2.1) in
$[a,b]$
with initial state
$\psi (a) = \psi ^0$
. Then, there exists a map
$\mu \in P_1(\mathbb{R}^d)$
such that
-
$\lim _{N\rightarrow \infty } \mathcal{W}_1(\mu _N(t),\mu (t)) = 0$
uniformly with respect to
$t\in [a,b]$
;
-
$\mu$
is a weak equi-compactly supported solution of (1.1);
-
regarding the cost functional (2.2), the following limit holds:
\begin{align*} \begin{split} \lim _{N\rightarrow \infty } \ & \int _a^b \int _{\mathbb{R}^d} \left ( L(x) + \Psi (u(t,x)) \right ) \, d \mu _N(t,\, x) \,dt \\[5pt] =& \int _a^b \int _{\mathbb{R}^d} \left ( L(x) + \Psi (u(t,x)) \right ) \, d \mu (t,\, x) \,dt. \end{split} \end{align*}
Theorem 3.1 holds for general
$P,L,\Psi$
functions that satisfy the hypothesis
$(P),(L),(\Psi )$
. We can observe these assumptions are satisfied for the example we took into account in the introduction 1, where
\begin{equation*} P (\psi ) \;:\!=\; H(\psi ) \psi, \qquad L(\psi ) \;:\!=\; \Vert \psi - \overline {\psi } \Vert ^2, \qquad \Psi (u) \;:\!=\; \gamma \Vert u \Vert ^2. \end{equation*}
We define the parametric mean-field optimisation problem
\begin{equation*}\textbf {Q}( a,\, b, \, \mu ^0):\, \min _{u} \textbf {J}_{( a,\, b)}(\mu, \,u) \end{equation*}
subject to (1.1). We recall the mean-field objective functional is
\begin{equation} \textbf{J}_{( a,\, b)}(\mu, \,u) = \int _a^b \int _{\mathbb{R}^d} \left ( L(x) + \Psi (u(t,x)) \right ) \, d \mu (t,\, x) \,dt. \end{equation}
We define the optimal value of the mean-field limit problem
$ \textbf{Q} (a,\, b, \, \mu ^0)$
as
${\textbf{V}}(a, \,b,\,\mu ^0)$
. The existence of solutions for
$ \textbf{Q} (a,\, b, \, \mu ^0)$
is guaranteed by Theorem 5.1 in [Reference Fornasier and Solombrino25].
4. The strict dissipativity inequality
In this section, we assume that the optimal control problem satisfies a strict dissipativity assumption. We start considering the
$N$
-particles problem, and then, we proceed with the mean-field limit formulation.
4.1 The strict dissipativity inequality for the microscopic problem
For any admissible pair
$(\psi (\!\cdot\!), u(\!\cdot\!))$
and for all
$\tau \in [a,\, b]$
, we assume that the following strict dissipativity inequality holds:
\begin{equation} \begin{split} \int _{a}^\tau & f_N( \psi (t),\, u(t) ) \, dt\\[5pt] &\geq \int _{a}^\tau \frac{1}{N} \left ( \| \psi (t) - \psi ^{(\sigma )}\|_N + \| u(t) - u^{(\sigma )} \|_N \right )^2 \, dt \end{split} \end{equation}
Here,
$\|z\|_N = \sqrt{ \sum _{k=1}^N \| z_k\|^2}$
,
$\left \lVert \cdot \right \rVert$
is the usual Euclidean norm, and
$f_N$
is the running cost in (2.3). Given an initial state
$\psi ^0$
, the problem
$\mathcal Q(N, \, a,\, b, \, \psi ^0)$
, i.e. the minimisation over
$u$
of the cost functional
$\mathcal J_{(N,a,b)}$
in (2.2), is then called a strictly dissipative problem in
$[a,b]$
at
$(\psi ^{(\sigma )},u^{(\sigma )})$
.
The strict dissipativity inequality (4.1) is a necessary condition for the turnpike property stated in Section 6, and it is one of the main ingredients for the proof of this property. We observe that the example presented in the Introduction 1, i.e. the minimisation of the functional (1.4) subject to the PDE (1.3), corresponds to a microscopic control problem with functional
\begin{equation*} f_N(\psi,u) = \frac {1}{N} \sum _{k=1}^N \left ( \| \psi _k(t) - \psi ^{(\sigma )}\|^2 + \gamma \, \| u(t) - u^{(\sigma )} \|^2 \right ), \end{equation*}
and static control
$u^{(\sigma )} =0$
. With some standard algebra manipulation, we can easily prove that the problem considered in this example is strictly dissipative.
4.2 The strict dissipativity inequality in the mean-field limit
We consider the following computation starting from (4.1)
\begin{equation} \begin{split} \int _{a}^\tau & f_N( \psi (t),\, u(t) ) \, dt\\[5pt] &\geq \int _{a}^\tau \frac{1}{N} \left ( \| \psi (t) - \psi ^{(\sigma )}\|_N + \| u(t) - u^{(\sigma )} \|_N \right )^2 \, dt\\[5pt] &\geq \int _{a}^\tau \frac{1}{N} \left ({ \sum _{k=1}^N \| \psi _k(t) - \psi ^{(\sigma )}\|^2} +{ \sum _{k=1}^N \| u_k(t) - u^{(\sigma )} \|^2} \right ) \, dt. \end{split} \end{equation}
Since all the quantities in (4.2) admit a mean-field limit, we can consider the problem for
$N\rightarrow \infty$
thanks to Theorem 3.1 and state a dissipativity inequality in
$[a,b]$
in terms of measures. We have for all
$\tau \in [a,\, b]$
\begin{equation} \begin{split} \int _a^\tau & f(\mu (t,x), \,u(t,x)) dt\\[5pt] &\geq \int _a^\tau \int _{\mathbb{R}^d} \left ( \| x - \psi ^{(\sigma )} \|^2 + \| u(t,x)- u^{(\sigma )} \|^2 \right ) \, d \mu (t,\, x) \,dt, \end{split} \end{equation}
where
$f$
is the functional in (1.2), and it is the mean-field limit of the microscopic running cost (2.3).
5. The cheap control condition
For our analysis, a cheap control condition is essential. It requires that the optimal values are bounded in terms of the distance between the initial state and the desired static state. We first discuss this assumption for the case with a finite number of particles and then extend it to the mean-field case.
5.1 The cheap control condition for the microscopic problem
In this section, we show that the optimisation problem
$\mathcal Q(N, \, a,\, b, \, \psi ^0)$
satisfies a cheap control condition in the following sense:
There exist a constant
$\mathcal C_0\gt 0$
such that for all initial times
$a$
, all initial states
$\psi ^0$
, and for all terminal times
$b\gt a$
, we have the inequality
\begin{equation} \mathcal{V} (N,\, a,\,b,\,\psi ^0) \leq \mathcal C_0 \, \frac{1}{N}\sum _{k=1}^N \|\psi ^0 - \psi ^{(\sigma )}\|. \end{equation}
Remark 1. The cheap control condition and the dissipativity inequality in (4.1) imply that
$\mathcal Q(N, \, a,\, b, \, \psi ^0)$
has the integral turnpike property, which means that for the corresponding optimal state/control
$(\psi, u)$
pair we have
\begin{equation} \int _a^b \left ( \| \psi (t) - \psi ^{(\sigma )}\|_N + \| u(t) - u^{(\sigma )} \|_N \right )^2 \, dt \leq{ \mathcal C_0} \sum _{k=1}^N \|\psi ^0 - \psi ^{(\sigma )}\|. \end{equation}
Since the right-hand side is independent of
$b-a$
, the inequality implies that the distance between the dynamic and the static optimal state and control is uniformly bounded with respect to the time horizon. This implies in particular that this distance must be small on the larger part of the time interval for sufficiently large time horizons.
In order to prove (5.1), we consider a stabilising feedback law that leads to exponential decay of
$ f_{N} (\psi (t), \, u(t))$
. Let a feedback parameter
$\beta \gt 0$
be given. We define the control
\begin{equation} u(t,\psi _k(t)) = \beta \left ( \psi ^{(\sigma )} - \psi _k(t) \right ) - \frac{1}{N} \sum _{l=1}^N P(\psi _l(t)- \psi _k(t)). \end{equation}
Then for the solution of the initial value problem with the initial states
$\psi ^0_k$
at the time
$a$
and the differential equations
\begin{equation*}\psi' _{\!\!k}(t) = \frac {1}{N} \sum _{l=1}^N P(\psi _l(t)- \psi _k(t)) + u(t,\psi _k(t))\end{equation*}
we have
\begin{equation*}\psi' _{\!\!k}(t) = \beta \left ( \psi ^{(\sigma )} - \psi _k(t) \right ). \end{equation*}
Lemma 5.1.
Consider the additional local assumption on bounded level sets of
$L$
:
\begin{equation} L(\psi ) \leq C_L \, \Vert \psi - \psi ^{(\sigma )}\Vert, \end{equation}
and let
\begin{equation*} \mathcal L_N(t) = \frac {1}{N} \|\psi _k(t) - \psi ^{(\sigma )} \|^2. \end{equation*}
Then,
$\mathcal L_N$
decays exponentially fast in time. Hence, we have inequality (5.1) with
$\mathcal C_0$
as defined in (5.6) below.
Proof. We have
\begin{eqnarray*} \partial _t \mathcal L_N(t) & = & \frac{2}{N} \langle \psi _k(t) - \psi ^{(\sigma )},\; \psi' _{\!\!k}(t) \rangle _{{\mathbb R}^d} \\[5pt] & = & \frac{2}{N} \langle \psi _k(t) - \psi ^{(\sigma )}, \; \beta \left ( \psi ^{(\sigma )} - \psi _k(t) \right ) \rangle _{{\mathbb R}^d} \\[5pt] & = & - \beta \, \frac{2}{N} \| \psi _k(t) - \psi ^{(\sigma )} \|^2 \\[5pt] & = & - 2 \, \beta \,\mathcal L_N(t). \end{eqnarray*}
Hence, we have
$\mathcal L_N(t) = \mathcal L_N(a) \,e^{-2\beta \, t}$
. Moreover, we even have
\begin{equation} \|\psi _k(t) - \psi ^{(\sigma )} \| = \|\psi _k(a) -\psi ^{(\sigma )} \| \,e^{-\beta \, t}. \end{equation}
We have the inequality
\begin{align*} \begin{split} \|u_k(t)\| &\leq \beta \left \| \psi ^{(\sigma )} - \psi _k(t) \right \| + \frac{C_P}{N} \sum _{l=1}^N \left (\|\psi _k(t) - \psi ^{(\sigma )} \| + \|\psi _l(t)- \psi ^{(\sigma )} \| \right )\\[5pt] &= (\beta + C_P) \left \| \psi ^{(\sigma )} - \psi _k(t) \right \| + \frac{C_P}{N} \sum _{l=1}^N \, \|\psi _l(t)- \psi ^{(\sigma )} \|, \end{split} \end{align*}
where we used the property
$(P)$
stated in Section 3. Hence we have
\begin{equation*} \|u_k(t)\| \leq e^{-\beta \, t}\, \left ( (\beta + C_P) \|\psi _k(a) - \psi ^{(\sigma )}\| + \frac {C_P}{N} \sum _{l=1}^N \|\psi _l(a)- \psi ^{(\sigma )} \| \right ). \end{equation*}
By property
$(\Psi )$
in Section 3, we know that
$\Psi (u)\leq C_\Psi \| u \|$
, therefore we can write
\begin{equation*} \Psi (u_k(t)) \leq e^{-\beta \, t}\,C_\Psi \, \left ( (\beta + C_P) \|\psi _k(a) - \psi ^{(\sigma )}\| + \frac {C_P}{N} \sum _{l=1}^N \|\psi _l(a)- \psi ^{(\sigma )} \| \right ). \end{equation*}
Adding the term
$L(\psi _k(t))$
on both sides, using (5.4) and (5.5), we have
\begin{align*} \begin{split} L(\psi _k&(t)) + \Psi (u_k(t)) \leq e^{-\beta \, t}\,C_L\, \|\psi _k(a) - \psi ^{(\sigma )}\| \, +\\[5pt] &+ e^{-\beta \, t}\,C_\Psi \, \left ( (\beta + C_P) \|\psi _k(a) - \psi ^{(\sigma )}\| + \frac{C_P}{N} \sum _{l=1}^N \|\psi _l(a)- \psi ^{(\sigma )} \| \right ). \end{split} \end{align*}
This yields
\begin{equation*} f_N(\psi (t),\, u(t)) \leq \Bigl ( C_L + \beta C_\Psi + 2 C_P C_\Psi \Bigr )e^{-\beta \, t} \frac {1}{N}\sum _{k=1}^N \|\psi _k(a) - \psi ^{(\sigma )}\|. \end{equation*}
Hence,
$f_N(\psi (t),\, u(t))$
decays exponentially fast with the rate
$\beta$
. For the optimal value, this implies
\begin{equation*} \mathcal V(N,\, a,\,b,\,\psi ^0) \leq \Bigl ( C_L + \beta C_\Psi + 2 C_P C_\Psi \Bigr ) \frac {1}{N \beta }\sum _{k=1}^N \|\psi _k(a) - \psi ^{(\sigma )}\|. \end{equation*}
Hence, (5.1) follows with
\begin{equation} \mathcal C_0= \frac{1}{ \beta } \Bigl ( C_L + \beta C_\Psi + 2 C_P C_\Psi \Bigr ). \end{equation}
5.2 The cheap control condition in the mean-field limit
Also for the cheap control condition, we can compute the limit inequality in terms of measures. Given
$\mathcal C_0\gt 0$
, for all initial times
$a\geq 0$
, terminal times
$b\gt a$
and initial states
$\mu (a,x)=\mu ^0(x)\in P_1(\mathbb{R}^d)$
, we have
\begin{equation} \textbf{{V}}(a,\,b,\,\mu ^0) \leq \mathcal{C}_0 \int _{\mathbb{R}^d} \|x - \psi ^{(\sigma )}\| \, d\mu ^0( x). \end{equation}
We recall that
$\textbf{V}$
is the optimal value of the mean-field optimisation problem. To prove the mean-field cheap control inequality, we follow the same idea of the microscopic case, namely we consider a stabilising feedback law that leads to exponential decay of the mean-field running cost. Combining (1.1) and (5.3), and letting
$N\rightarrow \infty$
we have
\begin{equation*} \partial _t \mu (t,x) + \partial _x \Bigl (\beta \left ( \psi ^{(\sigma )} - x \right ) \mu (t,x) \Bigr ) = 0. \end{equation*}
Lemma 5.2.
Consider the additional local assumption on bounded level sets of
$L$
in equation (5.4), then the cheap control condition holds also for the mean-field limit problem, that is (5.7) with
$\mathcal{C}_0$
the same constant (5.6) as in the microscopic case.
Proof. Considering the mean-field formulation of (5.3), we obtain
\begin{equation*} u(t,x) \mu (t,x)= \beta \left ( \psi ^{(\sigma )} - x \right ) \mu (t,x) - \mathcal {P}[\mu ](t,x) \mu (t,x). \end{equation*}
Thanks to property
$(P)$
in Section 3, this yields to
\begin{align*} \| u(t,x)\| \mu (t,x) & \leq \beta \, \| \psi ^{(\sigma )} - x \| \, \mu (t,x) + C_P \, \mu (t,x) \int _{\mathbb{R}^d} \left ( \| y - \psi ^{(\sigma )}\| + \| x- \psi ^{(\sigma )}\| \right ) \, d \mu (t, \, y) \\[5pt] & \leq (\beta + C_P) \, \| \psi ^{(\sigma )} - x \| \, \mu (t,x) + C_P \, \mu (t,x) \int _{\mathbb{R}^d} \| y - \psi ^{(\sigma )}\| \, d \mu (t, \, y). \end{align*}
We know that
$\Psi (u) \leq C_\Psi \|u\|$
(property
$(\Psi )$
, Section 3), hence we have
\begin{equation*} \Psi (u(t,x)) \mu (t,x) \end{equation*}
\begin{equation*} \leq C_\Psi (\beta + C_P) \, \| \psi ^{(\sigma )} - x \| \, \mu (t,x) + C_\Psi C_P \, \mu (t,x) \int _{\mathbb {R}^d} \| y - \psi ^{(\sigma )}\| \, d \mu (t, \, y). \end{equation*}
As in the proof of Lemma 5.1, we can add
$L(\psi _k(t))$
and integrate over in
$d\mu (t,x)$
on both sides. Then using (5.4) and (5.5), we obtain that the function
$f$
defined in equation (1.2) satisfies
\begin{align*} f(\mu (t,x), u(t,x)) \leq \Bigl (C_L + \beta C_\Psi + 2 C_P C_\Psi \Bigr )e^{-\beta \, t} \, \int _{\mathbb{R}^d} \| x- \psi ^{(\sigma )} \| \, d \mu (a,x). \end{align*}
For the optimal value, we obtain
\begin{equation*} {\textbf {V}}(a,\,b,\,\mu ^0) \leq \mathcal {C}_0\, \int _{\mathbb {R}^d} \| x- \psi ^{(\sigma )} \|\, d \mu (a,x). \end{equation*}
6. On the turnpike property with interior decay
In this section, we investigate whether the optimal control problems that we discuss satisfy a turnpike property with interior decay as discussed in [Reference Gugat29]. We start with the
$N$
-particle problem and then proceed with the mean-field limit problem.
6.1 The turnpike inequality for the microscopic problem
In this section, we present a turnpike property for the optimal control problem
$\mathcal Q(N, \, a,\, b, \, \psi ^0)$
that follows from the dissipativity inequality (4.1) and the cheap control condition (5.1). As the name indicates, this property focuses on the situation that the set where the distance between the optimal dynamic and the optimal static solution is small for large
$b$
is located in final part of the time interval
$[a, b]$
, that is an interval of the form
$[ b - (1 - \lambda )(b-a), b]$
with
$\lambda \in (0, 1)$
.
We define as
$\hat \psi (a,\, b, \, \psi ^0)(t)$
and
$\hat u(a, \, b,\, \psi ^0)(t)$
the optimal state and optimal control respectively at time
$t$
with initial state
$\psi (a) = \psi ^0 = \hat \psi (a,\, b, \, \psi ^0)(a)$
in the interval
$[a,b]$
. Let
$\lambda \in (0, \,1)$
be given. For
$b\gt 0$
consider the number
\begin{equation*} \mathcal A_\ast (b) \;:\!=\; {\frac {1}{N} \int \limits _{ {a + \lambda (b-a) }}^{ b} \left (\| \hat \psi (a, b,\, \psi ^0)(t) - \psi ^{(\sigma )} \|_N + \| \hat u(a, b,\, \psi ^0)(t) - u^{(\sigma )}\|_N \right )^2 \, dt. } \end{equation*}
Here, the static state given by
$ \psi ^{(\sigma )}$
with the constant control given by
$u^{(\sigma )}$
has the role of the turnpike. The number
$\mathcal A_\ast (b)$
measures the distance between the optimal state of
$\mathcal Q(N, \, a,\, b, \, \psi ^0)$
, and this turnpike on the time interval
$(a + \lambda (b-a), \, b)$
, where the first part of the time interval
$(a, b)$
is excluded.
The following theorem states that the optimal control problem with
$N$
agents has a turnpike property with interior decay:
Theorem 6.1.
The optimisation problem
$\mathcal Q(N, \, a,\, b, \, \psi ^0)$
has a turnpike property with interior decay in the sense that
\begin{equation*} \mathcal A_\ast (b) \leq \frac {\mathcal C_0^2}{ {\lambda \, (b-a) }} \frac {1}{N} \sum _{k=1}^N \|\psi ^0 - \psi ^{(\sigma )}\|. \end{equation*}
where
$\mathcal C_0$
is as in (5.6).
Proof. Due to (5.2), we have
\begin{equation*} \frac {1}{N} \int \limits _{a}^{ b} \left (\| \hat \psi (a, b,\, \psi ^0)(t) - \psi ^{(\sigma )} \|_N + \| \hat u(a, b,\, \psi ^0)(t) - u^{(\sigma )}\|_N \right )^2 \, dt \end{equation*}
\begin{equation*} \leq \frac {\mathcal C_0}{N} \sum _{k=1}^N \|\psi ^0 - \psi ^{(\sigma )}\|. \end{equation*}
Hence, there exists
$t_0 \in [a,\,{a + \lambda (b-a) }]$
such that
\begin{equation} \begin{split} \frac{1}{N} &\left (\| \hat \psi (a, b,\, \psi ^0)(t_0) - \psi ^{(\sigma )} \|_N + \| \hat u(a, b,\, \psi ^0)(t_0) - u^{(\sigma )}\|_N \right )^2 \\[5pt] &\leq \frac{1}{{\lambda (b - a)}} \frac{\mathcal C_0}{N} \sum _{k=1}^N \|\psi ^0 - \psi ^{(\sigma )}\|. \end{split} \end{equation}
The cheap control assumption implies that for the optimisation problem
$\mathcal Q(N, \, t_0, \, b, \, \hat \psi ^0)$
that starts at
$t_0$
with the initial state
$ \hat \psi ^0 = \hat \psi (a, b,\, \psi ^0)(t_0)$
we have
\begin{equation} \mathcal V(N,\, t_0,\,b,\, \hat \psi ^0) \leq \mathcal C_0 \, \frac{1}{N} \, \sum _{k=1}^N \| \hat \psi ^0(a, b,\, \psi ^0)(t_0) - \psi ^{(\sigma )}\|. \end{equation}
With (6.1), this implies
\begin{equation} \mathcal V(N,\, t_0,\,b,\, \hat \psi ^0) \leq \frac{\mathcal C_0^2}{{\lambda (b-a)}} \frac{1}{N} \sum _{k=1}^N \|\psi ^0 - \psi ^{(\sigma )}\|. \end{equation}
Due to (4.1) this yields
\begin{align*} \mathcal A_\ast (b) &\leq{\frac{1}{N} \int \limits _{ t_0 }^{ b} \left (\| \hat \psi (a, b,\, \psi ^0)(t) - \psi ^{(\sigma )} \|_N + \| \hat u(a, b,\, \psi ^0)(t) - u^{(\sigma )}\|_N \right )^2 \, dt }\\[5pt] &\leq \mathcal V(N,\, t_0,\,b,\, \hat \psi ^0) \\[5pt] &\leq \frac{\mathcal C_0^2}{{\lambda (b-a)}} \frac{1}{N} \sum _{k=1}^N \|\psi ^0 - \psi ^{(\sigma )}\|. \end{align*}
Hence, we have proved the theorem.
We have proved that on the interval
$[a + \lambda (b-a), \, b]$
, the contribution to the objective functional of this part of the time interval decays with
$\mathcal{O}{\left ( \tfrac{1}{\lambda (b - a)} \right )}$
.
6.1.1 Inductive refinement
Consider now the following statement
Theorem 6.2.
Let
$\alpha \in (0, \, 1)$
be given. The optimisation problem
$\mathcal Q(N, \, a,\, b, \, \psi ^0)$
has a turnpike property with interior decay in the sense that
\begin{equation*} \frac {1}{N} \int \limits _{ {a + ( 1 - \alpha ^2) (b-a) }}^{ b} \left (\| \hat \psi (a, b,\, \psi ^0)(t) - \psi ^{(\sigma )} \|_N + \| \hat u(a, b,\, \psi ^0)(t) - u^{(\sigma )}\|_N \right )^2 \, dt \end{equation*}
\begin{equation*} \leq \frac {\mathcal C_0^3}{ \alpha \, (1-\alpha )^2(b - a)^2} \frac {1}{N} \sum _{k=1}^N \|\psi ^0 - \psi ^{(\sigma )}\| \end{equation*}
where
$\mathcal C_0$
is as in (5.6).
Proof. We have shown that for
$\alpha \in (0, \, 1)$
in the intervals
\begin{equation*} [b - \alpha (b-a),\, b] = [ a + ( 1 - \alpha ) (b-a),\, b] \end{equation*}
the distance between the static and the dynamic solutions decays with the order
$\mathcal{O}\left ( \tfrac{1}{{(1-\alpha )( b-a)} } \right )$
.
We assume now that
$t_0\in [a, \,a + ( 1 - \alpha ) (b-a) ]$
has been chosen as in the previous section such that we have
\begin{equation} \begin{split} \frac{1}{N} &\left (\| \hat \psi (a, b,\, \psi ^0)(t_0) - \psi ^{(\sigma )} \|_N + \| \hat u(a, b,\, \psi ^0)(t_0) - u^{(\sigma )}\|_N \right )^2 \\[5pt] &\leq \frac{1}{ ( 1 - \alpha ) (b-a) } \frac{\mathcal C_0}{N} \sum _{k=1}^N \|\psi ^0 - \psi ^{(\sigma )}\|. \end{split} \end{equation}
Then as in the previous section using the dissipativity inequality (4.1) and the cheap control condition (5.1), we obtain
\begin{align*} \begin{split} \frac{1}{N} &\int \limits _{ t_0 }^{ b} \left (\| \hat \psi (a, b,\, \psi ^0)(t) - \psi ^{(\sigma )} \|_N + \| \hat u(a, b,\, \psi ^0)(t) - u^{(\sigma )}\|_N \right )^2 \, dt \\[5pt] & \leq \mathcal V(N,\, t_0,\,b,\, \hat \psi ^0) \\[5pt] &\leq \frac{\mathcal C_0^2}{ ( 1 - \alpha ) (b-a) } \frac{1}{N} \sum _{k=1}^N \|\psi ^0 - \psi ^{(\sigma )}\|. \end{split} \end{align*}
Similarly to (6.1), we find that due to (4.1) there exists
\begin{equation*} t_1 \in [a + (1 - \alpha )(b - a), \, a + (1 - \alpha ^2)(b - a) ] = [ b - \alpha (b-a),\, b - \alpha ^2(b-a)] \end{equation*}
such that
\begin{equation} \begin{split} \frac{1}{N} & \left (\| \hat \psi (a, b,\, \psi ^0)(t_1) - \psi ^{(\sigma )} \|_N + \| \hat u(a, b,\, \psi ^0)(t_1) - u^{(\sigma )}\|_N \right )^2 \\[5pt] &\leq \frac{1}{\alpha (1-\alpha ) (b-a)} \mathcal V(N,\, t_0,\,b,\, \hat \psi ^0) \\[5pt] & \leq \frac{1}{\alpha (1-\alpha ) (b-a)} \frac{\mathcal C_0^2}{ ( 1 - \alpha ) (b-a) } \frac{1}{N} \sum _{k=1}^N \|\psi ^0 - \psi ^{(\sigma )}\|.. \end{split} \end{equation}
Inequality (5.1) from the cheap control assumption implies that for the optimisation problem
$\mathcal Q(N, \, t_1, \, b, \, \hat \psi ^1)$
that starts at
$t_1$
with the initial state
$\hat \psi ^1 = \hat \psi (a, b,\, \psi ^0)(t_1)$
we have
\begin{equation} \mathcal V(N,\, t_1,\,b,\, \hat \psi ^1) \leq \mathcal C_0 \, \frac{1}{N} \sum _{k=1}^N \, \| \hat \psi ^1(a, b,\, \psi ^0)(t_1) - \psi ^{(\sigma )}\|. \end{equation}
With (6.5), this implies
\begin{equation} \mathcal V(N,\, t_1,\,b,\, \hat \psi ^1) \leq \frac{1}{\alpha (1-\alpha ) (b-a)} \frac{\mathcal C_0^3}{ ( 1 - \alpha ) (b-a) } \frac{1}{N} \sum _{k=1}^N \|\psi ^0 - \psi ^{(\sigma )}\|. \end{equation}
Due to the dissipativity inequality (4.1), this yields
\begin{align*} \begin{split} \frac{1}{N}& \int \limits _{ a + (1 - \alpha ^2)(b - a) }^{ b} \left (\| \hat \psi (a, b,\, \psi ^0)(t) - \psi ^{(\sigma )} \|_N + \| \hat u(a, b,\, \psi ^0)(t) - u^{(\sigma )}\|_N \right )^2 \, dt \\[5pt] &\leq \frac{1}{N} \int \limits _{ t_1 }^{ b} \left (\| \hat \psi (a, b,\, \psi ^0)(t) - \psi ^{(\sigma )} \|_N + \| \hat u(a, b,\, \psi ^0)(t) - u^{(\sigma )}\|_N \right )^2 \, ds \\[5pt] &\leq \mathcal V(N,\, t_1,\,b,\, \hat \psi ^1) \\[5pt] &\leq \frac{1}{\alpha (1-\alpha )^2 (b-a)^2}{\mathcal C_0^3} \frac{1}{N} \sum _{k=1}^N \|\psi ^0 - \psi ^{(\sigma )}\|. \end{split} \end{align*}
This ends the proof.
Hence on
$[ a + (1 - \alpha ^2)(b - a), b]$
, the contribution to the objective functional of this part of the time interval decays with
$\mathcal{O}\left ( \tfrac{1}{\alpha (1-\alpha )^2 (b-a)^2} \right )$
. Now we can proceed inductively to obtain a decay of the order
$\mathcal{O}\left ( 1/(b - a)^n \right )$
for
$n\in \{1,2,3,\, \ldots .\}$
with corresponding constants
$\mathcal C_n$
that grow with
$n$
. It is also possible to state Theorem 6.2 as an upper bound for an integral where the lower bound of the integration interval grows more slowly than linear, namely only with the order
$\sqrt{b-a}$
. For
$b\gt 1$
, define
\begin{equation*} \mathcal B_\ast (b) = \frac {1}{N} \int \limits _{ a + 2 \sqrt {b-a}- 1}^{ b} \left (\| \hat \psi (a, b,\, \psi ^0)(t) - \psi ^{(\sigma )} \|_N + \| \hat u(a, b,\, y_0)(t) - u^{(\sigma )}\|_N \right )^2 \, dt. \end{equation*}
Then, we have the following result.
Theorem 6.3.
For
$b\gt 1$
, the optimisation problem
$\mathcal Q(N, \, a,\, b, \, \psi ^0)$
has a turnpike property with interior decay in the sense that
\begin{equation*} \mathcal B_\ast (b) \leq \frac {1}{ \sqrt {b - a}(\sqrt {b - a} - 1) } \, { \mathcal C_0^3 } \, \frac {1}{N} \| \psi ^0 - \psi ^{(\sigma )}\|_N \end{equation*}
where
$\mathcal C_0$
is as in (5.6).
Proof. Set
$\alpha = 1 -\frac{1}{\sqrt{b-a}} \in (0, \, 1)$
. Then
$(1 - \alpha )^2 = \frac{1}{b - a}$
. Hence, we have
\begin{equation*}\alpha \, (1 - \alpha )^2\, (b -a)^2 = \sqrt {b - a}(\sqrt {b - a} - 1). \end{equation*}
Since
$1 - \alpha ^2 = \frac{ 2 \sqrt{b - a} - 1}{b - a}$
the assertion follows from Theorem 6.2.
Remark 2. Similarly as in [Reference Gugat29], we can sharpen this bound inductively.
6.2 The turnpike inequality in the mean-field limit
In this section, we state and prove the theorem for the turnpike property in term of measures, in order to do that, we use the mean-field version of the strict dissipativity (4.3) and cheap control (5.7) conditions.
Theorem 6.4.
Let
$\lambda \in (0, \,1)$
be given, and the interval
$[a,b]$
with
$b\gt 0$
. Consider the quantity
\begin{equation*} \textbf {A}_\ast (b) = \int _{a + \lambda (b-a)}^b \int _{\mathbb {R}^d} \left ( \| x - \psi ^{(\sigma )} \|^2 + \| \hat u_{(a, b,\mu ^0)}(t,x) - u^{(\sigma )}\|^2 \right )d \hat \mu _{(a, b,\mu ^0)}(t,x) \, dt, \end{equation*}
where we define as
$ \hat \mu _{(a, b,\mu ^0)}(t,x)$
and
$\hat u_{(a, b,\mu ^0)}(t,x)$
the density and control respectively at time
$t$
with initial condition
$\mu (a,x) = \mu ^0(x) = \hat \mu _{(a, b,\mu ^0)}(a,x)$
. Then, the optimisation problem
$\textbf{Q}(a,\, b, \, \mu ^0)$
has a turnpike property with interior decay in the sense that
\begin{equation*} \textbf {A}_\ast (b) \leq \frac {\mathcal C_0^2}{ \lambda (b-a)} \int _{\mathbb {R}^d} \| x- \psi ^{(\sigma )} \|\, d \mu (a,x). \end{equation*}
where
$\mathcal C_0$
is as in (5.6).
Proof. From the mean-field strict dissipativity (4.3) and cheap control (5.7) conditions, we know that the optimal density and control satisfy
\begin{equation} \begin{split} \int _a^b \int _{\mathbb{R}^d} & \left ( \| x - \psi ^{(\sigma )}\|^2 + \| u(t,x) - u^{(\sigma )} \|^2 \right ) d \mu (t,x) \, dt \\[5pt] &\leq{ \mathcal C_0} \int _{\mathbb{R}^d} \| x- \psi ^{(\sigma )} \|\, d \mu (a,x). \end{split} \end{equation}
Furthermore, we can write
\begin{align*} \begin{split} \int _a^b \int _{\mathbb{R}^d} & \left ( \| x - \psi ^{(\sigma )}\|^2 + \| \hat u_{(a, b,\mu ^0)}(t,x) - u^{(\sigma )} \|^2 \right ) d \hat \mu _{(a, b,\mu ^0)}(t,x) \, dt \\[5pt] &\leq{ \mathcal C_0} \int _{\mathbb{R}^d} \| x- \psi ^{(\sigma )} \|\, d \mu (a,x). \end{split} \end{align*}
Hence, there exists
$t_0 \in [a,\, a + \lambda (b- a) ]$
such that
\begin{equation} \begin{split} \int _{\mathbb{R}^d} & \left ( \| x - \psi ^{(\sigma )}\|^2 + \| \hat u_{(a, b,\mu ^0)}(t_0,x) - u^{(\sigma )} \|^2 \right ) d \hat \mu _{(a, b,\mu ^0)}(t_0,x) \, dt \\[5pt] &\leq \frac{ \mathcal C_0}{\lambda ( b -a) } \int _{\mathbb{R}^d} \| x- \psi ^{(\sigma )} \|\, d \mu (a,x). \end{split} \end{equation}
Thanks to the cheap control assumption (5.7), the optimisation problem
$\textbf{Q}(t_0, \, b, \, \hat \mu ^0)$
that starts at
$t_0$
with the initial density
$\hat \mu _{(a, b,\, \mu ^0)}(t_0,x)$
, satisfies
\begin{equation*} \textbf {V}(t_0,\,b,\, \hat \mu ^0) \leq { \mathcal C_0}\int _{\mathbb {R}^d} \| x- \psi ^{(\sigma )} \|\, d \hat \mu _{(a, b,\, \mu ^0)}(t_0,x). \end{equation*}
Together with (6.9), we obtain
\begin{equation*} \textbf {V}(t_0,\,b,\, \hat \mu ^0) \leq \frac { \mathcal C_0^2}{\lambda (b -a) } \int _{\mathbb {R}^d} \| x- \psi ^{(\sigma )} \|\, d \mu (a,x). \end{equation*}
Due to the dissipativity inequality (4.3), this yields
\begin{align*} \textbf{A}_\ast (b) &\leq \int _{t_0}^b \int _{\mathbb{R}^d} \left ( \| x - \psi ^{(\sigma )}\|^2 + \| \hat u_{(a, b,\mu ^0)}(t,x) - u^{(\sigma )} \|^2 \right ) d \hat \mu _{(a, b,\mu ^0)}(t,x) \, dt \\[5pt] &\leq \textbf{V}( t_0,\,b,\, \hat \mu ^0) \\[5pt] &\leq \frac{\mathcal C_0^2}{ \lambda (b-a)} \int _{\mathbb{R}^d} \| x- \psi ^{(\sigma )} \|\, d \mu (a,x), \end{align*}
that is the inequality stated in the theorem.
Remark 3. The bound we have in Theorem 6.4, on the distance between the optimal dynamic and the optimal static solution, can be inductively sharpened, using the same procedure of the microscopic case.
7. Conclusion
We have obtained a turnpike theorem for microscopic and mesoscopic optimal control problems that satisfy a strict dissipativity inequality. To prove the turnpike theorem, we have first shown that under appropriate assumptions the optimal control problems fulfil a cheap control condition. Providing suitable assumptions to guarantee the existence of solutions in the mean-field limit, we have proven the turnpike property both on the level of finitely many interacting particles and the mean-field limit. The turnpike property holds true without additional assumptions. Possible future work includes the numerical simulation and the extension, e.g. to the case that the microscopic model is governed by a second-order dynamics.
Financial Support
The authors thank the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) for the financial support through 320021702/GRK2326, 333849990/IRTG-2379, B04, B05 and B06 of 442047500/SFB1481, HE5386/18-1,19-2,22-1,23-1,25-1, ERS SFDdM035 and under Germany’s Excellence Strategy EXC-2023 Internet of Production 390621612 and under the Excellence Strategy of the Federal Government and the Länder. Support through the EU DATAHYKING is also acknowledged. This work was also funded by the DFG, TRR 154, Mathematical Modelling, Simulation and Optimization Using the Example of Gas Networks, project C03 and C05, Projektnr. 239904186.
Competing interests
The authors declare none.
Open access
