Article contents
Modulo ℓ distinction problems
Published online by Cambridge University Press: 30 September 2024
Abstract
Let 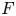 $F$ be a non-archimedean local field of characteristic different from 2 and residual characteristic
$F$ be a non-archimedean local field of characteristic different from 2 and residual characteristic 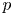 $p$. This paper concerns the
$p$. This paper concerns the 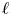 $\ell$-modular representations of a connected reductive group
$\ell$-modular representations of a connected reductive group 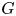 $G$ distinguished by a Galois involution, with
$G$ distinguished by a Galois involution, with 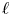 $\ell$ an odd prime different from
$\ell$ an odd prime different from 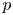 $p$. We start by proving a general theorem allowing to lift supercuspidal
$p$. We start by proving a general theorem allowing to lift supercuspidal 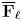 $\overline {\mathbf {F}}_{\ell }$-representations of
$\overline {\mathbf {F}}_{\ell }$-representations of 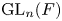 $\operatorname {GL}_n(F)$ distinguished by an arbitrary closed subgroup
$\operatorname {GL}_n(F)$ distinguished by an arbitrary closed subgroup 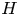 $H$ to a distinguished supercuspidal
$H$ to a distinguished supercuspidal 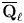 $\overline {\mathbf {Q}}_{\ell }$-representation. Given a quadratic field extension
$\overline {\mathbf {Q}}_{\ell }$-representation. Given a quadratic field extension 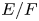 $E/F$ and an irreducible
$E/F$ and an irreducible 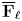 $\overline {\mathbf {F}}_{\ell }$-representation
$\overline {\mathbf {F}}_{\ell }$-representation 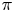 $\pi$ of
$\pi$ of 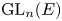 $\operatorname {GL}_n(E)$, we verify the Jacquet conjecture in the modular setting that if the Langlands parameter
$\operatorname {GL}_n(E)$, we verify the Jacquet conjecture in the modular setting that if the Langlands parameter 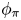 $\phi _\pi$ is irreducible and conjugate-selfdual, then
$\phi _\pi$ is irreducible and conjugate-selfdual, then 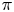 $\pi$ is either
$\pi$ is either 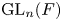 $\operatorname {GL}_n(F)$-distinguished or
$\operatorname {GL}_n(F)$-distinguished or 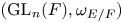 $(\operatorname {GL}_{n}(F),\omega _{E/F})$-distinguished (where
$(\operatorname {GL}_{n}(F),\omega _{E/F})$-distinguished (where 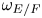 $\omega _{E/F}$ is the quadratic character of
$\omega _{E/F}$ is the quadratic character of 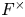 $F^\times$ associated to the quadratic field extension
$F^\times$ associated to the quadratic field extension 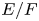 $E/F$ by the local class field theory), but not both, which extends one result of Sécherre to the case
$E/F$ by the local class field theory), but not both, which extends one result of Sécherre to the case 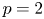 $p=2$. We give another application of our lifting theorem for supercuspidal representations distinguished by a unitary involution, extending one result of Zou to
$p=2$. We give another application of our lifting theorem for supercuspidal representations distinguished by a unitary involution, extending one result of Zou to 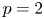 $p=2$. After that, we give a complete classification of the
$p=2$. After that, we give a complete classification of the 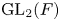 $\operatorname {GL}_2(F)$-distinguished representations of
$\operatorname {GL}_2(F)$-distinguished representations of 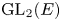 $\operatorname {GL}_2(E)$. Using this classification we discuss a modular version of the Prasad conjecture for
$\operatorname {GL}_2(E)$. Using this classification we discuss a modular version of the Prasad conjecture for 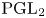 $\operatorname {PGL}_2$. We show that the ‘classical’ Prasad conjecture fails in the modular setting. We propose a solution using non-nilpotent Weil–Deligne representations. Finally, we apply the restriction method of Anandavardhanan and Prasad to classify the
$\operatorname {PGL}_2$. We show that the ‘classical’ Prasad conjecture fails in the modular setting. We propose a solution using non-nilpotent Weil–Deligne representations. Finally, we apply the restriction method of Anandavardhanan and Prasad to classify the 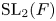 $\operatorname {SL}_2(F)$-distinguished modular representations of
$\operatorname {SL}_2(F)$-distinguished modular representations of 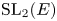 $\operatorname {SL}_2(E)$.
$\operatorname {SL}_2(E)$.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
References
- 2
- Cited by


