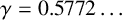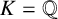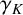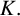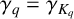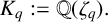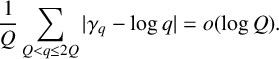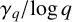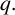1 Introduction
For a number field K, the Euler–Kronecker constant
$\gamma _K$
is given by
$$ \begin{align*} \gamma_K:=\lim_{s \to 1^+}\bigg(\frac{\zeta_K'(s)}{\zeta_K(s)} + \frac{1}{s-1}\bigg), \end{align*} $$
where
$\zeta _K(s)$
is the Dedekind zeta-function for
$K.$
The Euler–Mascheroni constant
$\gamma =0.5772\ldots \!$
is the
$K={\mathbb Q}$
case, where
$\zeta _{{\mathbb Q}}(s)=\zeta (s)$
is the Riemann zeta-function. We consider the constants
$\gamma _q=\gamma _{K_q}$
for cyclotomic fields
$K_q:={\mathbb Q}(\zeta _q)$
, where
$q\in {\mathbb Z}^{+}$
and
$\zeta _q$
is a primitive qth root of unity.
The recent interest in the distribution of the
$\gamma _q$
is inspired by work of Ihara [Reference Ihara and Ginzburg4, Reference Ihara and Rodier5]. He proposed, for every
$\varepsilon> 0$
, that there is a
$Q (\varepsilon )$
for which
$$ \begin{align*} (c_1-\varepsilon)\log q\le \gamma_q\le (c_2+\varepsilon)\log q \end{align*} $$
for every integer
$q \ge Q (\epsilon )$
, where
$0 < c_1 \le c_2 < 2$
are absolute constants. This conjecture was disproved by Ford et al. in [Reference Ford, Luca and Moree2] assuming a strong form of the Hardy–Littlewood k-tuple conjecture. However, assuming the Elliott–Halberstam conjecture (see [Reference Elliott and Halberstam1]), these same authors also proved that the conjecture holds for almost all primes
$q,$
with
$c_1 = c_2 = 1.$
We recall the Elliott–Halberstam Conjecture as formulated in terms of the Von Mangoldt function
$\Lambda (n),$
the Chebyshev function
$\psi (x)$
and Euler’s totient function
$\varphi (n).$
Elliott–Halberstam Conjecture (EH).
If we let
$$ \begin{align*}E(x;m,a):=\sum_{\substack{p\equiv a \pmod m\\ p\leq x\ {\mathrm{prime}}}} \Lambda(p) -\frac{\psi(x)}{\varphi(m)},\end{align*} $$
then for every
$\varepsilon>0$
and
$A>0$
, we have
$$ \begin{align*}\sum_{m\le x^{1-\varepsilon}}\max_{(a,m) = 1}\lvert{E(x;m,a)}\rvert\ll_{A,\varepsilon} \frac{x}{(\log x)^A}.\end{align*} $$
Assuming EH, Ford et al. proved (see [Reference Ford, Luca and Moree2, Theorem 6(i)]), for every
$\varepsilon> 0$
, that
$$ \begin{align*}1-\varepsilon < \frac{\gamma_q}{\log q} <1+\varepsilon \end{align*} $$
for almost all primes q (that is, the number of exceptional
$q \le x$
is
$o(\pi (x))$
as
$x\to \infty $
). Here we extend and refine this result to all integers
$q.$
Theorem 1.1. Under EH, for
$Q\rightarrow +\infty $
, we have
$$ \begin{align*} \frac{1}{Q}\sum_{Q<q\le 2Q} \lvert{\gamma_q - \log q}\rvert = o(\log Q), \end{align*} $$
where the sum is over integers q.
Remark 1.2. Theorem 1.1 shows that EH implies that the distribution of
$\gamma _q /\!\log q$
in
$[Q, 2Q]$
converges to the one point distribution supported on
$1$
.
To prove Theorem 1.1, we use the work of Fouvry [Reference Fouvry3] that allowed him to unconditionally prove that
$$ \begin{align*}\frac{1}{Q}\sum_{Q<q\le 2Q}\gamma_q=\log Q+O(\log\log Q).\end{align*} $$
Our conditional result is a point-wise refinement of Fouvry’s asymptotic formula under EH.
2 Proof of Theorem 1.1
For brevity, we shall assume that the reader is familiar with Fouvry’s paper [Reference Fouvry3]. The key formula is (see (3) of [Reference Fouvry3]) the following expression for
$\gamma _q$
in terms of logarithmic derivatives of Dirichlet L-functions:
$$ \begin{align} \gamma_q = \gamma + \sum_{1<q^*|q\ }\sum_{\chi^*\!\bmod q^*}\frac{L'(1,\chi^*)}{L(1,\chi^*)}. \end{align} $$
Here the inner sum runs over the primitive Dirichlet characters
$\chi ^*$
modulo
$q^*$
.
We follow the strategy and notation in [Reference Fouvry3], which makes use of the modified Chebyshev function
$$ \begin{align*} \psi(x;q,a):=\sum_{\substack{n\leq x\\ n\equiv a \pmod q}} \Lambda(n), \end{align*} $$
and the integral
$$ \begin{align*} \Phi_{\chi^*}(x):=\frac{1}{x-1}\int_{1}^x \bigg(\sum_{n\leq t}\frac{\Lambda(n)}{n}\chi^*(n)\bigg) \,dt. \end{align*} $$
However, we replace the sums
$\Gamma _i(Q)$
and
$\Gamma _{1,j}(Q)$
defined in [Reference Fouvry3] with the pointwise terms
$\gamma _i(q)$
and
$\gamma _{1,j}(q)$
. Following the approach in [Reference Fouvry3], which is based on (2.1), we have
$$ \begin{align*}\gamma_q = \gamma + A(q) + B(q) - \gamma_2(q) - \gamma_3(q) - (\gamma_{1,1}(q) + \gamma_{1,2}(q) + \gamma_{1,3}(q)),\end{align*} $$
where
$$ \begin{align*}A(q)&=\sum_{q^*|q} \,{\sum_{\chi^*\mod q^*}} \frac{L'}{L}(1,\chi^*)+\Phi_{\chi^*}(x), \\B(q)&=\sum_{\substack{\chi \bmod q\\ \chi\neq \chi_0}} \Phi_{\chi}(x)-\sum_{q^*|q}\,{\sum_{\chi^*\mod q^*}} \Phi_{\chi^*}(x), \\\gamma_2(q)&=\frac{1}{x-1}\int_1^x \frac{\varphi(q)\psi(t;q,1)-\psi(t)}{t} \,dt, \\\gamma_3(q)&=\frac{1}{x-1}\int_1^x \sum_{\substack{n\leq t\\(n,q) \neq 1}} \frac{\Lambda(n)}{n}\,dt, \\\gamma_{1,1}(q)&=\frac{1}{x-1}\int_1^x\int_1^{\min(q,t)}\bigg(\frac{\varphi(q)\psi(u;q,1)-\psi(u)}{u^2}\,du\bigg)\,dt, \\\gamma_{1,2}(q)&=\frac{1}{x-1}\int_1^x\int_{\min(q,t)}^{\min(x_1,t)}\bigg(\frac{\varphi(q)\psi(u;q,1)-\psi(u)}{u^2}\,du\bigg)\,dt, \\\gamma_{1,3}(q)&=\frac{1}{x-1}\int_1^x\int_{\min(x_1,t)}^t \bigg(\frac{\varphi(q)\psi(u;q,1)-\psi(u)}{u^2}\,du\bigg)\,dt. \end{align*} $$
To complete the proof, for
$\varepsilon>0$
, we let
$x := q^{100}$
and
$x_1 := q^{1 + \varepsilon }$
. Apart from
$\gamma _{1,1}(q),$
which gives the
$-\log q$
terms in Theorem 1.1, we shall show that these summands are all small.
Estimation of
$A(q)$
: By Proposition 1 and Remark (i) of [Reference Fouvry3],
$$ \begin{align*}\sum_{q=Q}^{2Q} \lvert{A(q)}\rvert =O(Q).\end{align*} $$
Estimation of
$B(q)$
: For
$B(q)$
, by (26) and Lemma 3 of [Reference Fouvry3], we simplify
$$ \begin{align*}B(q)&=-\frac{1}{x-1}\int_{1}^x \sum_{q^*|q}\ \sum_{\chi^*\,\mod q^*} \sum_{\substack{n \leq t\\(n,q)>1}} \frac{\Lambda(n)\chi^*(n)}{n} \,dt \\&= -\frac{1}{x-1}\int_{1}^x \sum_{q^*|q}\ \sum_{\chi^*\,\mod q^*}\ \sum_{\substack{p^v\leq t\\ p|q}} \frac{\log p\cdot\chi^*(p^v)}{p^v} \,dt \\&= -\frac{1}{x-1}\int_1^x \sum_{q^*|q}\ \sum_{\substack{p^v\leq t \\ p|q\\ p\nmid q^*}}\ \sum_{\substack{d|(p^v-1,q^*)}}\frac{\log p}{p^v} \cdot \varphi(d) \mu\bigg(\frac{q^*}{d}\bigg) \,dt \\&= -\frac{1}{x-1}\int_1^x \sum_{\substack{p^v\leq t\\ p|q}}\ \sum_{\substack{d|p^v-1}}\frac{\log p}{p^v}\cdot\varphi(d) \sum_{\substack{q^*|q\\d|q^*\\ p\nmid q^*}}\mu\bigg(\frac{q^*}{d}\bigg) \,dt. \end{align*} $$
We note that the innermost sum
$$ \begin{align*}\sum_{\substack{q^*|q\\ d|q^* \\ p\nmid q^*}}\mu\bigg(\frac{q^*}{d}\bigg)\end{align*} $$
is always
$0$
or
$1$
, so we conclude that
$B(q) \leq 0$
for any q. Proposition 2 of [Reference Fouvry3] gives
$$ \begin{align*}\sum_{q=Q}^{2Q}B(q)=O(Q),\end{align*} $$
and so we have
$$ \begin{align*}\sum_{q=Q}^{2Q}\lvert{B(q)}\rvert =O(Q).\end{align*} $$
Estimation of
$\gamma _2(q)$
: By Lemma 8 of [Reference Fouvry3], uniformly in Q with
$u\geq 1,$
we have
$$ \begin{align*}\sum_{q=Q}^{2Q} \psi(u;q,1) \ll u.\end{align*} $$
Therefore,
$$ \begin{align*}\sum_{q=Q}^{2Q} \lvert{\varphi(q)\psi(t;q,1)-\psi(t)}\rvert =O(Qt),\end{align*} $$
and so we conclude that
$$ \begin{align*}\sum_{q=Q}^{2Q} \lvert{\gamma_{2}(q)}\rvert = O(Q).\end{align*} $$
Estimation of
$\gamma _3(q)$
: By definition,
$\gamma _3$
is positive, so by (36) of [Reference Fouvry3],
$$ \begin{align*}\sum_{q=Q}^{2Q} \lvert{\gamma_{3}(q)}\rvert =O(Q).\end{align*} $$
Estimation of
$\gamma _{1,1}(q)$
: Since
$\psi (u;q,1)=0$
for
$u<q$
, we have
$$ \begin{align*} \gamma_{1,1}(q)=-\frac{1}{x-1}\int_1^x \bigg(\int_1^{\min(q,t)}\frac{\psi(u)}{u^2} \,du \bigg) \,dt. \end{align*} $$
Dividing both sides of (41) of [Reference Fouvry3] by Q,
$$ \begin{align*}\gamma_{1,1}(q)=-\log q + O(1).\end{align*} $$
Estimation of
$\gamma _{1,2}(q)$
: By the same proof as (42) of [Reference Fouvry3], we have
$$ \begin{align*} \sum_{q=Q}^{2Q} \lvert{\gamma_{1,2}(q)}\rvert \ll \varepsilon Q\log Q. \end{align*} $$
Summing the above estimates, we conclude unconditionally that
$$ \begin{align*} \frac{1}{Q}\sum_{q=Q}^{2Q} \lvert{\gamma_q-\log q}\rvert =\frac{1}{Q}\sum_{q=Q}^{2Q} \lvert{\gamma_{1,3}(q)}\rvert + O(\varepsilon \log Q). \end{align*} $$
Estimation of
$\gamma _{1,3}(q)$
: If we assume Conjecture EH holds, then we have (as in Lemma 7 of [Reference Fouvry3]) that
$$ \begin{align*} \sum_{\substack{q\le 2Q\\ (q,a)=1}}\varphi(q)\bigg\vert{\psi(x;q,a)-\frac{\psi(x)}{\varphi(q)}}\bigg\vert=O_A\big(Qx(\log x)^{-A+2}\big). \end{align*} $$
Therefore,
$$ \begin{align*} \frac{1}{Q} \sum_{q=Q}^{2Q}\lvert{\gamma_{1,3}(q)}\rvert=O_{\epsilon,A}(\log^{-A} Q). \end{align*} $$
By combining these estimates, we obtain the main result
$$ \begin{align*} \frac{1}{Q}\sum_{q=Q}^{2Q}\lvert{\gamma_q-\log q}\rvert=o(\log Q). \end{align*} $$
Acknowledgements
The authors thank Pieter Moree for helpful discussions regarding his work with Ford and Luca. We thank the referee for suggestions that improved the exposition in this paper.
Open access
