Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T00:09:13.303Z Has data issue: false hasContentIssue false
  • English
  • Français

Local cohomology modules of invariant rings

Published online by Cambridge University Press:  18 December 2015

TONY J. PUTHENPURAKAL
TONY J. PUTHENPURAKAL*
Affiliation:
Department of Mathematics, Indian Institute of Technology Bombay, Mumbai, India. e-mail: tputhen@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let K be a field and let R be a regular domain containing K. Let G be a finite subgroup of the group of automorphisms of R. We assume that |G| is invertible in K. Let RG be the ring of invariants of G. Let I be an ideal in RG. Fix i ⩾ 0. If RG is Gorenstein then:

  1. (i) injdimRGHiI(RG) ⩽ dim Supp HiI(RG);

  2. (ii) 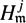$H^j_{\mathfrak{m}}$(HiI(RG)) is injective, where 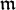$\mathfrak{m}$ is any maximal ideal of RG;

  3. (iii) μj(P, HiI(RG)) = μj(P′, HiIR(R)) where P′ is any prime in R lying above P.

We also prove that if P is a prime ideal in RG with RGP not Gorenstein then either the bass numbers μj(P, HiI(RG)) is zero for all j or there exists c such that μj(P, HiI(RG)) = 0 for j < c and μj(P, HiI(RG)) > 0 for all j ⩾ c.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 160 , Issue 2 , March 2016 , pp. 299 - 314
Copyright
Copyright © Cambridge Philosophical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Atiyah, M. F. and Macdonald, I. G.Introduction to Commutative Algebra (Addison-Wesley Publishing Co., Reading, Mass.-London-Don Mills, Ont. 1969).Google Scholar
[2]Bruns, W. and Herzog, J.Cohen–Macaulay rings (Cambridge University Press, 1993).Google Scholar
[3]Hartshorne, R.Affine duality and cofiniteness. Invent. Math. 9 (1969/1970), 145–164.CrossRefGoogle Scholar
[4]Huneke, C. and Sharp, R.Bass numbers of local cohomology modules. AMS Transactions. 339 (1993), 765–779.CrossRefGoogle Scholar
[5]Katzman, M.An example of an infinite set of associated primes of a local cohomology module. J. Algebra. 252 (2002), 161–166.CrossRefGoogle Scholar
[6]Lyubeznik, G.Finiteness properties of local cohomology modules (an application of D-modules to commutative algebra) Invent. Math. 113 (1993), 41–55.CrossRefGoogle Scholar
[7]Lyubeznik, G.F-modules: applications to local cohomology and D-modules in characteristic p>0. J. Reine Angew. Math. 491 (1997) 65–130.CrossRefGoogle Scholar
[8]Matsumura, H.Commutative Ring Theory (Cambridge University Press, 1989).Google Scholar
[9]Singh, A.p-torsion elements in local cohomology modules. Math. Res. Lett. 7 (2000), 165–176.CrossRefGoogle Scholar
[10]Singh, A. and Swanson, I.Associated primes of local cohomology modules and of Frobenius powers. Int. Math. Res. Not. 33 (2004), 1703–1733.CrossRefGoogle Scholar
[11]Traves, W.Differential operators on orbifolds. J. Symbolic Comput. 41 (2006), 1295–1308.CrossRefGoogle Scholar
[12]Watanabe, K.Certain invariant subrings are Gorenstein. I. Osaka J. Math. 11 (1974), 1–8.Google Scholar