Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-20T22:00:25.618Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Iwasawa theory of the Lubin–Tate moduli space

Part of: Algebraic groups Algebraic number theory: local and $p$-adic fields Locally compact groups and their algebras

Published online by Cambridge University Press:  26 February 2013

Jan Kohlhaase
Jan Kohlhaase*
Affiliation:
Mathematisches Institut, Westfälische Wilhelms-Universität Münster, Einsteinstraße 62, D-48149 Münster, Germany (email: kohlhaaj@math.uni-muenster.de)
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the affine formal algebra 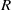$R$ of the Lubin–Tate deformation space as a module over two different rings. One is the completed group ring of the automorphism group 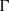$\Gamma $ of the formal module of the deformation problem, the other one is the spherical Hecke algebra of a general linear group. In the most basic case of height two and ground field 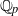$\mathbb {Q}_p$, our structure results include a flatness assertion for 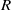$R$ over the spherical Hecke algebra and allow us to compute the continuous (co)homology of 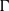$\Gamma $ with coefficients in 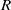$R$.

Keywords

moduli spacesformal groups$p$-adic representation theory

MSC classification

Secondary: 14L05: Formal groups, $p$-divisible groups 22D10: Unitary representations of locally compact groups 11S23: Integral representations
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 5 , May 2013 , pp. 793 - 839
Copyright
Copyright © 2013 The Author(s) 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[Beh12]Behrens, M., The homotopy groups of the $E(2)$-local sphere at $p \gt 3$, revisited, Adv. Math. 230 (2012), 458–492.Google Scholar
[Bor91]Borel, A., Linear algebraic groups, Graduate Texts in Mathematics, vol. 126, second edition (Springer, New York, 1991).Google Scholar
[Bos08]Bosch, S., Lectures on formal and rigid geometry, Preprint (2008), available atwww.math.uni-muenster.de/sfb/about/publ/heft378.pdf.Google Scholar
[Bou06]Bourbaki, N., Algèbre commutative (Springer, Berlin, 2006).CrossRefGoogle Scholar
[Bru66]Brumer, A., Pseudocompact algebras, profinite groups and class formations, J. Algebra 4 (1966), 442–470.CrossRefGoogle Scholar
[Cha96]Chai, C.-L., The group action on the closed fiber of the Lubin–Tate moduli space, Duke Math. J. 82 (1996), 725–754.Google Scholar
[deJ95]de Jong, J., Crystalline Dieudonné module theory via formal and rigid geometry, Publ. Inst. Hautes Études Sci. 82 (1995), 5–96.Google Scholar
[DH95]Devinatz, E. S. and Hopkins, M. J., The action of the Morava stabilizer group on the Lubin–Tate moduli space of lifts, Amer. J. Math. 117 (1995), 669–710.Google Scholar
[Dri74]Drinfeld, V. G., Elliptic modules, Math. USSR Sbornik 23 (1974), 561–592.CrossRefGoogle Scholar
[FGL08]Fargues, L., Genestier, A. and Lafforgue, V., L’isomorphisme entre les tours de Lubin–Tate et de Drinfeld, Progress in Mathematics, vol. 262 (Birkhäuser, Boston, MA, 2008).Google Scholar
[Gro11]Große-Klönne, E., On the universal module of -adic spherical Hecke algebras, Preprint (2011), available at http://www.math.hu-berlin.de/∼zyska/Grosse-Kloenne/Preprints.html.Google Scholar
[GH94]Gross, B. H. and Hopkins, M. J., Equivariant vector bundles on the Lubin–Tate moduli space, Contemp. Math. 158 (1994), 23–88.Google Scholar
[Gru79]Grünenfelder, L., On the homology of filtered and graded rings, J. Pure Appl. Algebra 14 (1979), 21–37.CrossRefGoogle Scholar
[Haz78]Hazewinkel, M., Formal groups and applications, Pure and Applied Mathematics, vol. 78 (Academic Press, New York, 1978).Google Scholar
[Hov93]Hovey, M., Bousfield localization functors and Hopkins’ chromatic splitting conjecture, in The Čech centennial (Boston, MA, 1993), Contemporary Mathematics, vol. 181 (American Mathematical Society, Providence, RI, 1993), 225–250.Google Scholar
[HvO96]Huishi, L. and van Oystaeyen, F., Zariskian filtrations, -Monographs in Mathematics, vol. 2 (Kluwer, 1996).Google Scholar
[Kna88]Knapp, A., Lie groups, lie algebras, and cohomology, Mathematical Notes, vol. 34 (Princeton, 1988).Google Scholar
[Koh12]Kohlhaase, J., Iwasawa modules arising from deformation spaces of -divisible formal group laws, Preprint (2012), available at http://www.math.uni-muenster.de/u/kohlhaaj/publ.html.Google Scholar
[Koh11]Kohlhaase, J., The cohomology of locally analytic representations, J. Reine Angew. Math. (Crelle) 651 (2011), 187–240.Google Scholar
[KS12]Kohlhaase, J. and Schraen, B., Homological vanishing theorems for locally analytic representations, Math. Ann. 353 (2012), 219–258.CrossRefGoogle Scholar
[Laz65]Lazard, M., Groupes analytiques -adiques, Publ. Inst. Hautes Études Sci. 26 (1965), 5–219.Google Scholar
[NSW00]Neukirch, J., Schmidt, A. and Wingberg, K., Cohomology of Number Fields, Grundlehren der Mathematischen Wissenschaften, vol. 323 (Springer, New York, 2000).Google Scholar
[OS10]Orlik, S. and Strauch, M., On Jordan–Hölder series of some locally analytic representations, Preprint (2010); arXiv:1001.0323.Google Scholar
[PR94]Platonov, V. and Rapinchuk, A., Algebraic groups and number theory, Pure and Applied Mathematics, vol. 139 (Academic Press, New York, 1994).Google Scholar
[RZ96]Rapoport, M. and Zink, Th., Period spaces for -divisible groups, Annals of Mathematics Studies, vol. 141 (Princeton University Press, Princeton, NJ, 1996).Google Scholar
[Sch11]Schneider, P., -adic Lie groups, Grundlehren der Mathematischen Wissenschaften, vol. 344 (Springer, 2011).Google Scholar
[ST02a]Schneider, P. and Teitelbaum, J., Locally analytic distributions and $p$-adic representation theory, with applications to $\mathrm {GL}_2$, J. Amer. Math. Soc. 15 (2002), 443–468.Google Scholar
[ST02b]Schneider, P. and Teitelbaum, J., Banach space representations and Iwasawa theory, Israel J. Math. 127 (2002), 359–380.Google Scholar
[SY95]Shimomura, K. and Yabe, A., The homotopy groups $\pi _*(L_2S^0)$, Topology 34 (1995), 261–289.Google Scholar
[Str08]Strauch, M., Deformation spaces of one-dimensional formal groups and their cohomology, Adv. Math. 217 (2008), 889–951.CrossRefGoogle Scholar
[Stu00]Stumbo, F., Minimal length coset representatives for quotients of parabolic subgroups in Coxeter groups, Boll. Unione Mat. Ital. 8 (2000), 699–715.Google Scholar
[Sym04]Symonds, P., The Tate–Farrell Cohomology of the Morava stabilizer group $S_{p-1}$ with coefficients in $E_{p-1}$, Contemp. Math. 346 (2004), 485–492.Google Scholar
[SW00]Symonds, P. and Weigel, T., Cohomology of $p$-adic analytic groups, in New horizons in pro- groups, Progress in Mathematics, vol. 184, eds du Sautoy, M., Segal, D. and Shalev, A. (Birkhäuser, 2000), 349–410.Google Scholar
[Wil98]Wilson, J. S., Profinite groups, London Mathematical Society Monographs, vol. 19 (Oxford, 1998).Google Scholar
[Yu95]Yu, J.-K., On the moduli of quasi-canonical liftings, Compositio Math. 96 (1995), 293–321.Google Scholar