Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-22T11:06:37.508Z Has data issue: false hasContentIssue false
  • English
  • Français

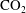Dissolution of a $\text{CO}_{2}$ spherical cap bubble adhered to a flat surface in air-saturated water

Published online by Cambridge University Press:  16 June 2015

Pablo Peñas-López ,
Miguel A. Parrales  and
Javier Rodríguez-Rodríguez
Pablo Peñas-López*
Affiliation:
Fluid Mechanics Group, Universidad Carlos III de Madrid, Avda. de la Universidad 30, 28911 Leganés (Madrid), Spain
Miguel A. Parrales
Affiliation:
Fluid Mechanics Group, Universidad Carlos III de Madrid, Avda. de la Universidad 30, 28911 Leganés (Madrid), Spain
Javier Rodríguez-Rodríguez
Affiliation:
Fluid Mechanics Group, Universidad Carlos III de Madrid, Avda. de la Universidad 30, 28911 Leganés (Madrid), Spain
*
†Email address for correspondence: papenasl@ing.uc3m.es
Get access Rights & Permissions [Opens in a new window]

Abstract

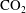Bubbles adhered to partially hydrophobic flat surfaces often attain a spherical cap shape with a contact angle much greater than zero. We address the fundamental problem of the diffusion-driven dissolution of a sessile spherical cap bubble (SCB) adhered to a flat smooth surface. In particular, we perform experiments on the dissolution of $\text{CO}_{2}$ bubbles (with initial radii 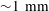${\sim}1~\text{mm}$) immersed in air-saturated water adhered to two substrates with different levels of hydrophobicity. It is found that the contact angle dynamics plays an important role in the bubble dissolution rate. A dissolution model for a multicomponent SCB in an isothermal and uniform pressure environment is then devised. The model is based on the quasi-stationary approximation. It includes the effect of the contact angle dynamics, whose behaviour is predicted by means of a simplified model based on the results obtained from adhesion hysteresis. The presence of an impermeable substrate hinders the overall rate of mass transfer. Two approaches are considered in its determination: (a) the inclusion of a diffusion boundary layer–plate interaction model and (b) a finite-difference solution. The model solutions are compared with the experimental results, yielding fairly good agreement.

JFM classification

Drops and Bubbles: Bubble dynamics Interfacial Flows (free surface): Contact lines
Type
Papers
Information
Journal of Fluid Mechanics , Volume 775 , 25 July 2015 , pp. 53 - 76
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arfken, G. 1970 Mathematical Methods for Scientists, 2nd edn, chap. 2, pp. 112–114. Academic.Google Scholar
Cussler, E. L. 1997 Diffusion, Mass Transfer in Fluid Systems, 2nd edn. Cambridge University Press.Google Scholar
Dietrich, E., Kooij, E. S., Zhang, X., Zandvliet, H. J. W. & Lohse, D. 2015 Stick–jump mode in surface droplet dissolution. Langmuir 31 (16), 4696–4703.CrossRefGoogle ScholarPubMed
Duda, J. L. & Vrentas, J. S. 1969 Mathematical analysis of bubble dissolution. AIChE J. 15 (3), 351–356.CrossRefGoogle Scholar
Duda, J. L. & Vrentas, J. S. 1971 Heat or mass transfer-controlled dissolution of an isolated sphere. Intl J. Heat Mass Transfer 14 (3), 395–407.Google Scholar
Enríquez, O. R., Sun, C., Lohse, D., Prosperetti, A. & van der Meer, D. 2014 The quasi-static growth of $\text{CO}_{2}$ bubbles. J. Fluid Mech. 741, R1.Google Scholar
Epstein, P. S. & Plesset, M. S. 1950 On the stability of gas bubbles in liquid–gas solutions. J. Chem. Phys. 18 (11), 1505–1509.Google Scholar
Eral, H. B., ’t Mannetje, D. J. C. M. & Oh, J. M. 2013 Contact angle hysteresis: a review of fundamentals and applications. Colloid Polym. Sci. 291 (2), 247–260.Google Scholar
Holocher, J., Peeters, F., Aeschbach-Hertig, W., Kinzelbach, W. & Kipfer, R. 2003 Kinetic model of gas bubble dissolution in groundwater and its implications for the dissolved gas composition. Environ. Sci. Technol. 37 (7), 1337–1343.Google Scholar
Hong, S.-J., Chang, F.-M., Chou, T.-H., Chan, S. H., Sheng, Y.-J. & Tsao, H.-K. 2011 Anomalous contact angle hysteresis of a captive bubble: advancing contact line pinning. Langmuir 27 (11), 6890–6896.Google Scholar
Kentish, S., Lee, J., Davidson, M. & Ashokkumar, M. 2006 The dissolution of a stationary spherical bubble beneath a flat plate. Chem. Engng Sci. 61 (23), 7697–7705.Google Scholar
Lee, W. T., McKechnie, J. S. & Devereux, M. G. 2011 Bubble nucleation in stout beers. Phys. Rev. E 83, 051609.Google Scholar
Liebermann, L. 1957 Air bubbles in water. J. Appl. Phys. 28 (2), 205–211.CrossRefGoogle Scholar
Lohse, D. & Zhang, X. 2015 Surface nanobubbles and nanodroplets. Rev. Mod. Phys. (in press).Google Scholar
Sander, R. 2014 Compilation of Henry’s law constants, version 3.99. Atmos. Chem. Phys. Discuss. 14 (21), 29615–30521.Google Scholar
Shim, S., Wan, J., Hilgenfeldt, S., Panchal, P. D. & Stone, H. A. 2014 Dissolution without disappearing: multicomponent gas exchange for $\text{CO}_{2}$ bubbles in a microfluidic channel. Lab on a Chip 14, 2428–2436.Google Scholar
Snoeijer, J. H. & Andreotti, B. 2013 Moving contact lines: scales, regimes, and dynamical transitions. Annu. Rev. Fluid Mech. 45 (1), 269–292.Google Scholar
Stauber, J. M., Wilson, S. K., Duffy, B. R. & Sefiane, K. 2014 On the lifetimes of evaporating droplets. J. Fluid Mech. 744, R2.Google Scholar
Subramanian, R. S. & Weinberg, M. C. 1981 Asymptotic expansions for the description of gas bubble dissolution and growth. AIChE J. 27 (5), 739–748.Google Scholar
Takemura, F., Liu, Q. & Yabe, A. 1996 Effect of density-induced natural convection on the absorption process of single bubbles under a plate. Chem. Engng Sci. 51 (20), 4551–4560.Google Scholar
Weijs, J. H. & Lohse, D. 2013 Why surface nanobubbles live for hours. Phys. Rev. Lett. 110, 054501.Google Scholar
Weinberg, M. C. & Subramanian, R. S. 1980 Dissolution of multicomponent bubbles. J. Am. Ceram. Soc. 63 (9–10), 527–531.Google Scholar
Wise, D. L. & Houghton, G. 1968 Effect of an impermeable wall on bubble collapse in diffusion coefficient measurements. Chem. Engng Sci. 23 (12), 1502–1503.Google Scholar
Yung, C.-N., De Witt, K. J., Brockwell, J. L., McQuillen, J. B. & Chai, A.-T. 1989 A numerical study of parameters affecting gas bubble dissolution. J. Colloid Interface Sci. 127 (2), 442–452.Google Scholar