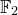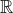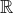Refine listing
Actions for selected content:
300 results in 14Hxx
Wall-crossing integral chow rings of
 ${\overline {\mathcal {M}}}_{1,n\leq 4}$
${\overline {\mathcal {M}}}_{1,n\leq 4}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 05 December 2025, e196
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Explicit formulas for the Grothendieck class of
 $\overline {\mathcal{M}}_{0,n}$
$\overline {\mathcal{M}}_{0,n}$
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Complete families of generic covers of elliptic curves
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On (2,2)-decomposable genus 4 Jacobians
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 12 September 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Rank of the Normal Functions of the Ceresa and Gross–Schoen Cycles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 08 September 2025, e141
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Universal-existential theories of fields
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 03 September 2025, pp. 1-30
-
- Article
- Export citation
Vanishing of Brauer groups of moduli stacks of stable curves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 July 2025, e115
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The space of solvable Pell–Abel equations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1483-1511
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Brauer groups of moduli of genus three curves, abelian threefolds and plane curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 19 September 2025, pp. 1664-1697
- Print publication:
- July 2025
-
- Article
- Export citation
Abelian varieties with no power isogenous to a Jacobian
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 30 October 2025, pp. 1404-1457
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Automorphism groups and signatures of smooth septic curves
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 13 May 2025, pp. 1-22
-
- Article
- Export citation
Orbifold Euler characteristics for compactified universal Jacobians over
 $\overline{\mathcal{M}}_{g,\,n}$
$\overline{\mathcal{M}}_{g,\,n}$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 13 May 2025, pp. 1-16
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maximal real varieties from moduli constructions
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear syzygies of curves in weighted projective space
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 15 August 2025, pp. 916-944
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Corrigendum: Conformal blocks for Galois covers of algebraic curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 15 August 2025, pp. 945-946
- Print publication:
- April 2025
-
- Article
-
- You have access
- HTML
- Export citation
Rationality and arithmetic of the moduli of abelian varieties
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MUKAI’S PROGRAM FOR NONPRIMITIVE CURVES ON K3 SURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 17 March 2025, pp. 1053-1091
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bi-algebraic geometry of strata of differentials in genus zero
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 30 June 2025, pp. 503-535
- Print publication:
- March 2025
-
- Article
- Export citation
Theory of heat equations for sigma functions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 28 February 2025, pp. 365-422
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LINEAR SYSTEMS OF GEOMETRICALLY IRREDUCIBLE PLANE CUBICS OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 27 February 2025, pp. 303-311
- Print publication:
- October 2025
-
- Article
- Export citation