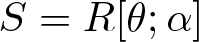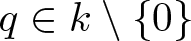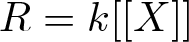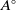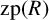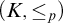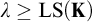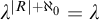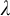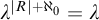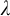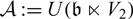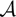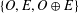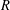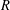Refine listing
Actions for selected content:
39 results in 16Pxx
Property
 $(\diamond)$ for Ore extensions of small Krull dimension
$(\diamond)$ for Ore extensions of small Krull dimension
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 21 May 2025, pp. 1-19
-
- Article
- Export citation
The Quantitative Kurosh Problem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 13 February 2025, e42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Noetherianity of twisted Zhu’s algebras and bimodules
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 675-704
-
- Article
- Export citation
Finite domination and Novikov homology over strongly $\mathbb {Z}^2$
 -graded rings
-graded rings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 28 July 2023, pp. 1786-1818
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A characterisation of atomicity
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 459-465
- Print publication:
- September 2023
-
- Article
- Export citation
The finite dual of commutative-by-finite Hopf algebras
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 21 March 2022, pp. 62-89
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE PROBABILITY OF ZERO MULTIPLICATION IN FINITE RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 83-88
- Print publication:
- August 2022
-
- Article
- Export citation
SOME STABLE NON-ELEMENTARY CLASSES OF MODULES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 13 September 2021, pp. 93-117
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE METRIC DIMENSION OF THE ANNIHILATING-IDEAL GRAPH OF A FINITE COMMUTATIVE RING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 27 April 2021, pp. 362-368
- Print publication:
- June 2021
-
- Article
- Export citation
GRADED TWISTED CALABI–YAU ALGEBRAS ARE GENERALIZED ARTIN–SCHELTER REGULAR
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 245 / March 2022
- Published online by Cambridge University Press:
- 02 February 2021, pp. 100-153
- Print publication:
- March 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERALISED QUANTUM DETERMINANTAL RINGS ARE MAXIMAL ORDERS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 04 August 2020, pp. 515-525
- Print publication:
- September 2021
-
- Article
- Export citation
THE PRIME IDEALS AND SIMPLE MODULES OF THE UNIVERSAL ENVELOPING ALGEBRA U(𝔟⋉V2)
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue S1 / December 2020
- Published online by Cambridge University Press:
- 29 July 2019, pp. S77-S98
- Print publication:
- December 2020
-
- Article
- Export citation
SIMPLICITY AND CHAIN CONDITIONS FOR ULTRAGRAPH LEAVITT PATH ALGEBRAS VIA PARTIAL SKEW GROUP RING THEORY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 299-319
- Print publication:
- December 2020
-
- Article
- Export citation
On Annelidan, Distributive, and Bézout Rings
- Part of
- Boolean algebras (Boolean rings)
- Distributive lattices
- Conditions on elements
- Local rings and generalizations
- Modules, bimodules and ideals
- Rings and algebras arising under various constructions
- Radicals and radical properties of rings
- Chain conditions, growth conditions, and other forms of finiteness
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 03 May 2019, pp. 1082-1110
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
FINITE UNITARY RINGS IN WHICH ALL SYLOW SUBGROUPS OF THE GROUP OF UNITS ARE CYCLIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 13 February 2019, pp. 403-412
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
A Morita Cancellation Problem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 708-731
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Factorizations in Bounded Hereditary Noetherian Prime Rings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 19 November 2018, pp. 395-442
-
- Article
- Export citation
CHAIN CONDITIONS ON ÉTALE GROUPOID ALGEBRAS WITH APPLICATIONS TO LEAVITT PATH ALGEBRAS AND INVERSE SEMIGROUP ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 403-411
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
On a Class of Automaton Algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 May 2016, pp. 31-38
-
- Article
- Export citation
A LOCALISABLE CLASS OF PRIMITIVE IDEALS OF UNIFORM NILPOTENT IWASAWA ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 1-15
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation