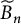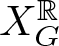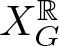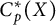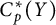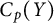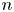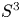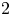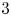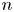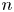Refine listing
Actions for selected content:
77 results in 57Nxx
Thin Gordian unlinks
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 19 November 2025, pp. 1-15
-
- Article
- Export citation
EXISTENCE AND DEFORMABILITY OF TOPOLOGICAL MORSE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 30 October 2025, pp. 1-7
-
- Article
- Export citation
Characterization of some convex curves on the 3-sphere
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 06 October 2025, pp. 1-21
-
- Article
- Export citation
Mapping class groups of h-cobordant manifolds
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 08 August 2025, e132
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BALANCING STRUCTURE AND DYNAMICS: DYNAMICAL NETWORKS AND EMBEDDING AS A MODELLING PARADIGM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 04 July 2025, pp. 570-571
- Print publication:
- December 2025
-
- Article
-
- You have access
- HTML
- Export citation
 $\mathbb {Z}$-disks in
$\mathbb {Z}$-disks in  ${\mathbb {C}} P^2$
${\mathbb {C}} P^2$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 27 August 2025, pp. 1357-1403
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ASYMPTOTIC DIMENSION AND GEOMETRIC DECOMPOSITIONS IN DIMENSIONS 3 AND 4
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 21 April 2025, pp. 176-201
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
STATED SKEIN MODULES OF 3-MANIFOLDS AND TQFT
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 19 March 2025, pp. 663-703
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rigidity of flat holonomies
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1048-1077
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Homotopy classification of 4-manifolds with finite abelian 2-generator fundamental groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 2 / September 2024
- Published online by Cambridge University Press:
- 08 November 2024, pp. 263-283
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Simplicial volume of manifolds with amenable fundamental group at infinity
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 22 April 2024, pp. 563-570
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear actions of $\mathbb {Z}/p\times \mathbb {Z}/p$
 on $S^{2n-1}\times S^{2n-1}$
on $S^{2n-1}\times S^{2n-1}$
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1699-1712
- Print publication:
- December 2024
-
- Article
- Export citation
Twisted Blanchfield pairings and twisted signatures III: Applications
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 15 April 2024, pp. 501-540
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Corrigendum: A certain structure of Artin groups and the isomorphism conjecture
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 23 February 2024, pp. 729-730
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
Stratification of the transverse momentum map
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 12 February 2024, pp. 518-585
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cohomology of a real toric variety and shellability of posets arising from a graph
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 03 November 2023, pp. 1044-1084
-
- Article
- Export citation
Linear equivalence of scattered metric spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 29 May 2023, pp. 1354-1367
- Print publication:
- December 2023
-
- Article
- Export citation
The rational homotopy type of homotopy fibrations over connected sums
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 03 April 2023, pp. 133-142
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Embedding spheres in knot traces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 20 October 2021, pp. 2242-2279
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Primary decomposition in the smooth concordance group of topologically slice knots
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 13 August 2021, e57
-
- Article
-
- You have access
- Open access
- HTML
- Export citation