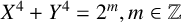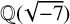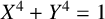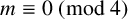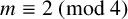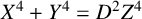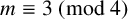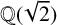Refine listing
Actions for selected content:
364 results in 11Rxx
NOTES ON GENERALISED INTEGRAL POLYNOMIAL PELL EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 09 December 2025, pp. 1-13
-
- Article
- Export citation
NONCOMMUTATIVE IWASAWA THEORY OF ABELIAN VARIETIES OVER GLOBAL FUNCTION FIELDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 01 December 2025, pp. 1-35
-
- Article
- Export citation
GENERALISED MAZUR’S GROWTH NUMBER CONJECTURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 28 November 2025, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Totally positive elements with m partitions exist in almost all real quadratic fields
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 21 November 2025, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE DESCENT CONJECTURE FOR RATIONAL POINTS AND ZERO-CYCLES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 19 November 2025, pp. 1-49
-
- Article
- Export citation
An asymptotic formula for Tate–Shafarevich groups of CM elliptic curves at supersingular primes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 13 November 2025, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NON-DIOPHANTINE SETS IN RINGS OF FUNCTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 12 November 2025, pp. 1-14
-
- Article
- Export citation
A classification of
 $\mathbb {Q}$-linear maps from
$\mathbb {Q}$-linear maps from  $\overline {\mathbb {Q}}^\times /\overline {\mathbb {Q}}^\times _{\mathrm {tors}}$ to
$\overline {\mathbb {Q}}^\times /\overline {\mathbb {Q}}^\times _{\mathrm {tors}}$ to  $\mathbb {R}$
$\mathbb {R}$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 21 October 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN EFFECTIVE VERSION OF THE PRIMITIVE ELEMENT THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 13 October 2025, pp. 1-8
-
- Article
- Export citation
Rigid meromorphic cocycles for orthogonal groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 30 September 2025, e160
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Improvements on dimension growth results and effective Hilbert’s irreducibility theorem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 September 2025, e153
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The average size of 3-torsion in class groups of 2-extensions
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 15 September 2025, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear relations of four conjugates of an algebraic number
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 04 September 2025, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integer solutions of the generalized polynomial Pell equations and their finiteness: The quadratic case
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 27 August 2025, pp. 1-12
-
- Article
- Export citation
THE FERMAT QUARTIC X4 + Y4 = 2m IN QUADRATIC NUMBER FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 15 August 2025, pp. 1-10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting cyclic extensions with local conditions and applications to L-values in the critical strip
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 08 August 2025, pp. 1-39
-
- Article
- Export citation
Ergodicity and algebraicity of the fast and slow triangle maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 46 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 08 August 2025, pp. 93-127
- Print publication:
- January 2026
-
- Article
- Export citation
RIGID INNER FORMS OVER GLOBAL FUNCTION FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 21 July 2025, pp. 2181-2256
- Print publication:
- November 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Fitting ideals of anticyclotomic Selmer groups of elliptic curves with good ordinary reduction
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 14 July 2025, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Elliptic curves and spin
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 11 July 2025, pp. 519-539
- Print publication:
- November 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation





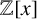

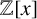
















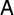
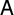
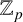
















 .
.