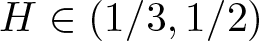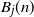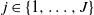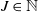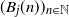1012 results in 60Fxx
Sample path moderate deviations for non-stationary power-law shot noise processes
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 28 March 2025, pp. 1-27
-
- Article
- Export citation
A central limit theorem for jump diffusion processes in the presence of round-off errors
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 25 March 2025, pp. 1-39
-
- Article
- Export citation
Graph connectivity with fixed endpoints in the random-connection model
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences , First View
- Published online by Cambridge University Press:
- 21 February 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Probabilistic voting models with varying speeds of Correlation decay
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 17 February 2025, pp. 35-64
- Print publication:
- March 2025
-
- Article
- Export citation
Edge Statistics for Lozenge Tilings of Polygons, II: Airy Line Ensemble
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 12 February 2025, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Interacting urns on directed networks with node-dependent sampling and reinforcement
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 03 February 2025, pp. 1-25
-
- Article
- Export citation
Large deviation principle for slow-fast rough differential equations via controlled rough paths
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 January 2025, pp. 1-31
-
- Article
- Export citation
QUENCHED CENTRAL LIMIT THEOREM FOR DVORETZKY COVERING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 28 January 2025, pp. 368-378
- Print publication:
- April 2025
-
- Article
- Export citation
The elephant random walk in the triangular array setting
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 16 January 2025, pp. 1-13
-
- Article
- Export citation
Measure comparison problems for dilations of convex bodies
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 270-285
- Print publication:
- March 2025
-
- Article
- Export citation
On affine multicolor urns grown under multiple drawing
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 24 December 2024, pp. 1-24
-
- Article
-
- You have access
- HTML
- Export citation
Moderate deviations of many-server queues via idempotent processes
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 20 December 2024, pp. 1-35
-
- Article
-
- You have access
- HTML
- Export citation
Central Limit Theorem for tensor products of free variables
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 December 2024, pp. 1-33
-
- Article
-
- You have access
- HTML
- Export citation
On the asymptotic normality of persistent Betti numbers
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 03 December 2024, pp. 1-32
-
- Article
-
- You have access
- HTML
- Export citation
Gaussian fluctuations for the two-urn model
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 02 December 2024, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Gaussian approximation and moderate deviations of Poisson shot noises with application to compound generalized Hawkes processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 305-345
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Precise large deviations of the net loss process in a non-standard two-dimensional risk model
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 39 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 15 November 2024, pp. 44-63
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Approximation of subgraph counts in the uniform attachment model
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 10 October 2024, pp. 90-114
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stationary measures and the continuous-state branching process conditioned on extinction
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 07 October 2024, pp. 1-27
-
- Article
-
- You have access
- HTML
- Export citation
On the rate of convergence for an α-stable central limit theorem under sublinear expectation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 October 2024, pp. 209-233
- Print publication:
- March 2025
-
- Article
-
- You have access
- HTML
- Export citation