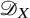 $\mathscr {D}_{X}$-modules
$\mathscr {D}_{X}$-modules
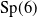 $\mathrm{Sp}(6)$
$\mathrm{Sp}(6)$
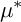 $\mu ^*$-ZARISKI PAIRS OF SURFACE SINGULARITIES
$\mu ^*$-ZARISKI PAIRS OF SURFACE SINGULARITIES
Email your librarian or administrator to recommend adding this to your organisation's collection.