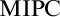1 Introduction
The one-variable fragment of any standard first-order logic—intermediate, substructural, many-valued, modal, or otherwise—consists of consequences in the logic constructed using one distinguished variable x, unary relation symbols, propositional connectives, and the quantifiers
![]() $(\forall {x})$
and
$(\forall {x})$
and
![]() $(\exists {x})$
. Such a fragment may be conveniently reformulated as a propositional modal logic by replacing occurrences of an atom
$(\exists {x})$
. Such a fragment may be conveniently reformulated as a propositional modal logic by replacing occurrences of an atom
![]() $P(x)$
with a propositional variable p, and occurrences of
$P(x)$
with a propositional variable p, and occurrences of
![]() $(\forall {x})$
and
$(\forall {x})$
and
![]() $(\exists {x})$
with
$(\exists {x})$
with
![]() $\Box $
and
$\Box $
and
![]() $\Diamond $
, respectively. Typically, this modal logic is algebraizable—that is, it enjoys soundness and completeness with respect to some suitable class of algebraic structures—and hence, unlike the full first-order logic, can be studied using the tools of universal algebra.
$\Diamond $
, respectively. Typically, this modal logic is algebraizable—that is, it enjoys soundness and completeness with respect to some suitable class of algebraic structures—and hence, unlike the full first-order logic, can be studied using the tools of universal algebra.
Any standard semantics for a first-order logic, where quantifiers range over domains of models, yields a relational semantics for the one-variable fragment. On the other hand, a Hilbert-style axiomatization does not (at least directly) yield an axiomatization for the fragment, since a derivation of a one-variable formula may involve additional variables. Axiomatizations are well known for the modal counterparts
![]() $\mathrm {S5}$
[Reference Halmos16] and
$\mathrm {S5}$
[Reference Halmos16] and
![]() $\mathrm {MIPC}$
[Reference Bull4, Reference Monteiro and Varsavsky22] of the one-variable fragments of first-order classical logic and first-order intuitionistic logic, respectively, and similar results have been obtained for the modal counterparts of one-variable fragments of other first-order intermediate logics [Reference Bezhanishvili1, Reference Bezhanishvili and Harding2, Reference Caicedo, Metcalfe, Rodríguez and Rogger5–Reference Caicedo and Rodríguez7, Reference Ono and Suzuki24, Reference Suzuki27, Reference Suzuki28] and many-valued logics [Reference Castaño, Cimadamore, Varela and Rueda8, Reference Di Nola and Grigolia12, Reference Metcalfe, Tuyt, Olivetti, Negri, Sandu and Verbrugge21, Reference Rutledge26]. However, a general approach to the problem of axiomatizing one-variable fragments of first-order logics has been lacking.Footnote
1
$\mathrm {MIPC}$
[Reference Bull4, Reference Monteiro and Varsavsky22] of the one-variable fragments of first-order classical logic and first-order intuitionistic logic, respectively, and similar results have been obtained for the modal counterparts of one-variable fragments of other first-order intermediate logics [Reference Bezhanishvili1, Reference Bezhanishvili and Harding2, Reference Caicedo, Metcalfe, Rodríguez and Rogger5–Reference Caicedo and Rodríguez7, Reference Ono and Suzuki24, Reference Suzuki27, Reference Suzuki28] and many-valued logics [Reference Castaño, Cimadamore, Varela and Rueda8, Reference Di Nola and Grigolia12, Reference Metcalfe, Tuyt, Olivetti, Negri, Sandu and Verbrugge21, Reference Rutledge26]. However, a general approach to the problem of axiomatizing one-variable fragments of first-order logics has been lacking.Footnote
1
In this paper, we address this problem for a broad family of semantically defined first-order logics. In Section 2, we introduce (one-variable) first-order logics via models defined over classes of
![]() $\mathcal {L}$
-lattices: structures for an algebraic signature
$\mathcal {L}$
-lattices: structures for an algebraic signature
![]() $\mathcal {L}$
with a lattice reduct. In particular, first-order intermediate logics and first-order substructural logics can be defined over classes of Heyting algebras and
$\mathcal {L}$
with a lattice reduct. In particular, first-order intermediate logics and first-order substructural logics can be defined over classes of Heyting algebras and
![]() $\mathsf {FL_e}$
-algebras, respectively. For the sake of generality (e.g., when
$\mathsf {FL_e}$
-algebras, respectively. For the sake of generality (e.g., when
![]() $\mathcal {L}$
-lattices are just lattices), consequence is defined for equations between two first-order formulas; however, this often (e.g., for any intermediate or substructural logic) corresponds to the usual notion of consequence between formulas.
$\mathcal {L}$
-lattices are just lattices), consequence is defined for equations between two first-order formulas; however, this often (e.g., for any intermediate or substructural logic) corresponds to the usual notion of consequence between formulas.
In Section 3, we introduce potential axiomatizations for consequence in the modal counterparts of the one-variable fragments of these semantically defined logics. We define an m-
![]() $\mathcal {L}$
-lattice to be an
$\mathcal {L}$
-lattice to be an
![]() $\mathcal {L}$
-lattice expanded with modalities
$\mathcal {L}$
-lattice expanded with modalities
![]() $\Box $
and
$\Box $
and
![]() $\Diamond $
satisfying certain equations familiar from modal logic, and given any class
$\Diamond $
satisfying certain equations familiar from modal logic, and given any class
![]() $\mathsf {K}$
of
$\mathsf {K}$
of
![]() $\mathcal {L}$
-lattices, let
$\mathcal {L}$
-lattices, let
![]() $\mathsf {mK}$
denote the class of m-
$\mathsf {mK}$
denote the class of m-
![]() $\mathcal {L}$
-lattices with an
$\mathcal {L}$
-lattices with an
![]() $\mathcal {L}$
-lattice reduct in
$\mathcal {L}$
-lattice reduct in
![]() $\mathsf {K}$
. For example, if
$\mathsf {K}$
. For example, if
![]() $\mathsf {K}$
is a variety of Heyting algebras, then
$\mathsf {K}$
is a variety of Heyting algebras, then
![]() $\mathsf {mK}$
is a variety of monadic Heyting algebras in the sense of [Reference Monteiro and Varsavsky22]. We then show that m-
$\mathsf {mK}$
is a variety of monadic Heyting algebras in the sense of [Reference Monteiro and Varsavsky22]. We then show that m-
![]() $\mathcal {L}$
-lattices are in one-to-one correspondence with
$\mathcal {L}$
-lattices are in one-to-one correspondence with
![]() $\mathcal {L}$
-lattices equipped with a subalgebra satisfying a relative completeness condition, generalizing previous results in the literature (see, e.g., [Reference Bezhanishvili1, Reference Tuyt29]). We also show that if
$\mathcal {L}$
-lattices equipped with a subalgebra satisfying a relative completeness condition, generalizing previous results in the literature (see, e.g., [Reference Bezhanishvili1, Reference Tuyt29]). We also show that if
![]() $\mathsf {K}$
is any class of
$\mathsf {K}$
is any class of
![]() $\mathcal {L}$
-lattices closed under taking subalgebras and direct powers (in particular, any variety), then consequence in the one-variable fragment of the first-order logic defined over
$\mathcal {L}$
-lattices closed under taking subalgebras and direct powers (in particular, any variety), then consequence in the one-variable fragment of the first-order logic defined over
![]() $\mathsf {K}$
corresponds to consequence in the functional members of
$\mathsf {K}$
corresponds to consequence in the functional members of
![]() $\mathsf {mK}$
: m-
$\mathsf {mK}$
: m-
![]() $\mathcal {L}$
-lattices consisting of functions from a set W to an
$\mathcal {L}$
-lattices consisting of functions from a set W to an
![]() $\mathcal {L}$
-lattice
$\mathcal {L}$
-lattice
![]() $\mathbf {A}\in \mathsf {K}$
.
$\mathbf {A}\in \mathsf {K}$
.
In Section 4, we close the circle, obtaining an axiomatization of consequence in the one-variable fragment of any first-order logic defined over a variety
![]() $\mathsf {V}$
of
$\mathsf {V}$
of
![]() $\mathcal {L}$
-lattices that has the superamalgamation property: an algebraic property that is equivalent in some settings to the logical Craig interpolation property. We show that every member of
$\mathcal {L}$
-lattices that has the superamalgamation property: an algebraic property that is equivalent in some settings to the logical Craig interpolation property. We show that every member of
![]() $\mathsf {mV}$
is functional—generalizing a representation theorem of Bezhanishvili and Harding for monadic Heyting algebras [Reference Bezhanishvili and Harding2]—and hence that the defining equations for
$\mathsf {mV}$
is functional—generalizing a representation theorem of Bezhanishvili and Harding for monadic Heyting algebras [Reference Bezhanishvili and Harding2]—and hence that the defining equations for
![]() $\mathsf {mV}$
provide the desired axiomatization. In particular, we axiomatize the one-variable fragments of a broad range of first-order logics, including the seven consistent first-order intermediate logics that have Craig interpolation, first-order extensions of substructural logics such as
$\mathsf {mV}$
provide the desired axiomatization. In particular, we axiomatize the one-variable fragments of a broad range of first-order logics, including the seven consistent first-order intermediate logics that have Craig interpolation, first-order extensions of substructural logics such as
![]() $\mathsf {FL_e}$
,
$\mathsf {FL_e}$
,
![]() $\mathsf {FL_{ew}}$
, and
$\mathsf {FL_{ew}}$
, and
![]() $\mathsf {FL_{ec}}$
, a first-order lattice logic, and a first-order version of the modal logic
$\mathsf {FL_{ec}}$
, a first-order lattice logic, and a first-order version of the modal logic
![]() $\mathrm {K}$
.
$\mathrm {K}$
.
In Section 5, we present an alternative proof-theoretic strategy for establishing completeness of an axiomatization for the one-variable fragment of a first-order logic, the key idea being to show that additional variables can be eliminated from derivations of one-variable formulas in a suitable sequent calculus. As a concrete example, we obtain a new completeness proof for the one-variable fragment of the first-order version of the substructural logic
![]() $\mathrm {FL_e}$
by establishing an interpolation property for derivations in a cut-free sequent calculus. We then explain how the proof generalizes to a family of first-order substructural logics, including
$\mathrm {FL_e}$
by establishing an interpolation property for derivations in a cut-free sequent calculus. We then explain how the proof generalizes to a family of first-order substructural logics, including
![]() $\mathrm {FL_{ew}}$
,
$\mathrm {FL_{ew}}$
,
![]() $\mathrm {FL_{ec}}$
, and
$\mathrm {FL_{ec}}$
, and
![]() $\mathrm {FL_{ewc}}$
(intuitionistic logic). Finally, in Section 6, we discuss the limitations of the methods described in the paper and potential extensions to broader families of first-order logics.
$\mathrm {FL_{ewc}}$
(intuitionistic logic). Finally, in Section 6, we discuss the limitations of the methods described in the paper and potential extensions to broader families of first-order logics.
2 A family of first-order logics
Let
![]() $\mathcal {L}$
be any algebraic signature, and let
$\mathcal {L}$
be any algebraic signature, and let
![]() $\mathcal {L}_n$
denote the set of operation symbols of
$\mathcal {L}_n$
denote the set of operation symbols of
![]() $\mathcal {L}$
of arity
$\mathcal {L}$
of arity
![]() $n\in \mathbb {N}$
. We will assume throughout this paper that
$n\in \mathbb {N}$
. We will assume throughout this paper that
![]() $\mathcal {L}_2$
contains distinct symbols
$\mathcal {L}_2$
contains distinct symbols ![]() and
and ![]() , referring to such a signature as lattice-oriented.
, referring to such a signature as lattice-oriented.
We call an algebraic structure ![]() an
an
![]() $\mathcal {L}$
-lattice if
$\mathcal {L}$
-lattice if
![]() $\star ^{\mathbf {A}}$
is an n-ary operation on A for each
$\star ^{\mathbf {A}}$
is an n-ary operation on A for each
![]() $\star \in \mathcal {L}_n$
(
$\star \in \mathcal {L}_n$
(
![]() $n\in \mathbb {N}$
), and
$n\in \mathbb {N}$
), and ![]() is a lattice with respect to the induced order
is a lattice with respect to the induced order ![]() . As usual, superscripts will be omitted when these are clear from the context.
. As usual, superscripts will be omitted when these are clear from the context.
Example 2.1. Let
![]() $\mathcal {L}_s$
be the lattice-oriented signature with binary operation symbols
$\mathcal {L}_s$
be the lattice-oriented signature with binary operation symbols ![]() ,
, ![]() ,
,
![]() $\cdot $
, and
$\cdot $
, and
![]() $\to $
, and constant symbols
$\to $
, and constant symbols
![]() $\mathrm {f}$
and
$\mathrm {f}$
and
![]() $\mathrm {e}$
. An
$\mathrm {e}$
. An
![]() $\mathsf {FL_e}$
-algebra—also referred to as a commutative pointed residuated lattice—is an
$\mathsf {FL_e}$
-algebra—also referred to as a commutative pointed residuated lattice—is an
![]() $\mathcal {L}_s$
-lattice
$\mathcal {L}_s$
-lattice ![]() such that
such that ![]() is a commutative monoid and
is a commutative monoid and
![]() $\to $
is the residuum of
$\to $
is the residuum of
![]() $\cdot $
, that is,
$\cdot $
, that is, ![]() , for all
, for all
![]() $a,b,c\in ~A$
. The class of
$a,b,c\in ~A$
. The class of
![]() $\mathsf {FL_e}$
-algebras forms a variety
$\mathsf {FL_e}$
-algebras forms a variety
![]() $\mathsf {FL_e}$
that provides algebraic semantics for the full Lambek calculus with exchange
$\mathsf {FL_e}$
that provides algebraic semantics for the full Lambek calculus with exchange
![]() $\mathrm {FL_e}$
—also known as multiplicative additive intuitionistic linear logic without additive constants (see, e.g., [Reference Galatos, Jipsen, Kowalski and Ono13, Reference Metcalfe, Paoli and Tsinakis20]). Algebraic semantics for other well-known substructural logics are provided by various subvarieties of
$\mathrm {FL_e}$
—also known as multiplicative additive intuitionistic linear logic without additive constants (see, e.g., [Reference Galatos, Jipsen, Kowalski and Ono13, Reference Metcalfe, Paoli and Tsinakis20]). Algebraic semantics for other well-known substructural logics are provided by various subvarieties of
![]() $\mathsf {FL_e}$
; e.g.
$\mathsf {FL_e}$
; e.g.
-
• the full Lambek calculus with exchange and weakening
 $\mathrm {FL_{ew}}$
, and full Lambek calculus with exchange and contraction
$\mathrm {FL_{ew}}$
, and full Lambek calculus with exchange and contraction
 $\mathrm {FL_{ec}}$
, correspond to the varieties
$\mathrm {FL_{ec}}$
, correspond to the varieties
 $\mathsf {FL_{ew}}$
and
$\mathsf {FL_{ew}}$
and
 $\mathsf {FL_{ec}}$
of
$\mathsf {FL_{ec}}$
of
 $\mathsf {FL_e}$
-algebras satisfying the equations
$\mathsf {FL_e}$
-algebras satisfying the equations  , and
, and  , respectively;
, respectively; -
• intuitionistic logic
 $\mathrm {IL}$
corresponds to the variety
$\mathrm {IL}$
corresponds to the variety
 $\mathsf {HA}$
of Heyting algebras, term-equivalent to
$\mathsf {HA}$
of Heyting algebras, term-equivalent to
 $\mathsf {FL_{ewc}}=\mathsf {FL_{ew}}\cap \mathsf {FL_{ec}}$
(just identify
$\mathsf {FL_{ewc}}=\mathsf {FL_{ew}}\cap \mathsf {FL_{ec}}$
(just identify
 $\cdot $
and
$\cdot $
and  );
); -
• classical logic
 $\mathrm {CL}$
and Gödel logic
$\mathrm {CL}$
and Gödel logic
 $\mathrm {G}$
correspond to the varieties
$\mathrm {G}$
correspond to the varieties
 $\mathsf {BA}$
of Boolean algebras, and
$\mathsf {BA}$
of Boolean algebras, and
 $\mathsf {GA}$
of Gödel algebras, axiomatized relative to
$\mathsf {GA}$
of Gödel algebras, axiomatized relative to
 $\mathsf {HA}$
by the equations
$\mathsf {HA}$
by the equations
 $(x\to \mathrm {f})\to \mathrm {f}\approx x$
and
$(x\to \mathrm {f})\to \mathrm {f}\approx x$
and  , respectively;
, respectively; -
• Łukasiewicz logic
 corresponds to the variety
corresponds to the variety
 $\mathsf {MV}$
of MV-algebras, term-equivalent to the variety of
$\mathsf {MV}$
of MV-algebras, term-equivalent to the variety of
 $\mathsf {FL_{ew}}$
-algebras satisfying the equation
$\mathsf {FL_{ew}}$
-algebras satisfying the equation  .
.
Full first-order logics can be defined over an arbitrary predicate language with formulas built using propositional connectives from the algebraic signature
![]() $\mathcal {L}$
(see, e.g., [Reference Cintula and Noguera11, Section 7.1]). However, it suffices here to restrict our attention to the one-variable setting and a fixed (generic) predicate language. Let
$\mathcal {L}$
(see, e.g., [Reference Cintula and Noguera11, Section 7.1]). However, it suffices here to restrict our attention to the one-variable setting and a fixed (generic) predicate language. Let
![]() $\mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
denote the set of one-variable
$\mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
denote the set of one-variable
![]() $\mathcal {L}$
-formulas
$\mathcal {L}$
-formulas
![]() $\varphi ,\psi ,\chi ,\dots $
built inductively using a countably infinite set of unary predicates
$\varphi ,\psi ,\chi ,\dots $
built inductively using a countably infinite set of unary predicates
![]() $\{P_i\}_{i\in \mathbb {N}}$
, a distinguished variable x, connectives in
$\{P_i\}_{i\in \mathbb {N}}$
, a distinguished variable x, connectives in
![]() $\mathcal {L}$
, and quantifiers
$\mathcal {L}$
, and quantifiers
![]() $\forall ,\exists $
. We call an ordered pair of one-variable
$\forall ,\exists $
. We call an ordered pair of one-variable
![]() $\mathcal {L}$
-formulas
$\mathcal {L}$
-formulas
![]() $\varphi ,\psi \in \mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
, written
$\varphi ,\psi \in \mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
, written
![]() $\varphi \approx \psi $
, an
$\varphi \approx \psi $
, an
![]() $\mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
-equation, and write
$\mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
-equation, and write ![]() as an abbreviation for
as an abbreviation for ![]() .Footnote
2
.Footnote
2
Now let
![]() $\mathbf {A}$
be any
$\mathbf {A}$
be any
![]() $\mathcal {L}$
-lattice, let S be a non-empty set, and let
$\mathcal {L}$
-lattice, let S be a non-empty set, and let
![]() $\mathcal {I}(P_i)$
be a map from S to A for each
$\mathcal {I}(P_i)$
be a map from S to A for each
![]() $i\in \mathbb {N}$
, writing
$i\in \mathbb {N}$
, writing
![]() $u\mapsto f(u)$
to denote a map assigning to each
$u\mapsto f(u)$
to denote a map assigning to each
![]() $u\in S$
some
$u\in S$
some
![]() $f(u)\in A$
. We call the ordered pair
$f(u)\in A$
. We call the ordered pair ![]() an
an
![]() $\mathbf {A}$
-structure if the following inductively defined partial map
$\mathbf {A}$
-structure if the following inductively defined partial map ![]() is total:
is total:

If
![]() $\mathbf {A}$
is complete—that is,
$\mathbf {A}$
is complete—that is,
![]() $\bigwedge X$
and
$\bigwedge X$
and
![]() $\bigvee X$
exist in A, for all
$\bigvee X$
exist in A, for all
![]() $X \subseteq A$
—then
$X \subseteq A$
—then ![]() is always an
is always an
![]() $\mathbf {A}$
-structure; otherwise, whether or not the partial map
$\mathbf {A}$
-structure; otherwise, whether or not the partial map ![]() is total depends on
is total depends on
![]() $\mathcal {I}$
. E.g., for
$\mathcal {I}$
. E.g., for ![]() and
and
![]() $S=\mathbb {N}$
, if
$S=\mathbb {N}$
, if ![]() , for all
, for all
![]() $n\in \mathbb {N}$
, then
$n\in \mathbb {N}$
, then ![]() is undefined, but if
is undefined, but if ![]() for all
for all
![]() $i\in \mathbb {N}$
and
$i\in \mathbb {N}$
and
![]() $n\in S$
, for some fixed
$n\in S$
, for some fixed
![]() $K\in \mathbb {N}$
, then
$K\in \mathbb {N}$
, then
![]() ${\mathfrak {{S}}}$
is an
${\mathfrak {{S}}}$
is an
![]() $\mathbf {A}$
-structure.
$\mathbf {A}$
-structure.
We say that an
![]() $\mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
-equation
$\mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
-equation
![]() $\varphi \approx \psi $
is valid in an
$\varphi \approx \psi $
is valid in an
![]() $\mathbf {A}$
-structure
$\mathbf {A}$
-structure
![]() ${\mathfrak {{S}}}$
, and write
${\mathfrak {{S}}}$
, and write
![]() ${\mathfrak {{S}}}\models \varphi \approx \psi $
, if
${\mathfrak {{S}}}\models \varphi \approx \psi $
, if ![]() . More generally, consider any class of
. More generally, consider any class of
![]() $\mathcal {L}$
-lattices
$\mathcal {L}$
-lattices
![]() $\mathsf {K}$
. We say that an
$\mathsf {K}$
. We say that an
![]() $\mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
-equation
$\mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
-equation
![]() $\varphi \approx \psi $
is a (sentential) semantical consequence of a set of
$\varphi \approx \psi $
is a (sentential) semantical consequence of a set of
![]() $\mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
-equations T in
$\mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
-equations T in
![]() $\mathsf {K}$
, and write
$\mathsf {K}$
, and write
![]() $T\vDash ^{\forall }_{\mathsf {K}}\varphi \approx \psi $
, if for any
$T\vDash ^{\forall }_{\mathsf {K}}\varphi \approx \psi $
, if for any
![]() $\mathbf {A}\in \mathsf {K}$
and
$\mathbf {A}\in \mathsf {K}$
and
![]() $\mathbf {A}$
-structure
$\mathbf {A}$
-structure
![]() ${\mathfrak {{S}}}$
,
${\mathfrak {{S}}}$
,
In certain cases, we can restrict our attention to the complete members of
![]() $\mathsf {K}$
. Let us say that
$\mathsf {K}$
. Let us say that
![]() $\mathsf {K}$
admits regular completions if, for any
$\mathsf {K}$
admits regular completions if, for any
![]() $\mathbf {A}\in \mathsf {K}$
, there exists an
$\mathbf {A}\in \mathsf {K}$
, there exists an
![]() $\mathcal {L}$
-lattice embedding h of
$\mathcal {L}$
-lattice embedding h of
![]() $\mathbf {A}$
into a complete member
$\mathbf {A}$
into a complete member
![]() $\mathbf {B}$
of
$\mathbf {B}$
of
![]() $\mathsf {K}$
that preserves all existing meets and joins, noting that for any
$\mathsf {K}$
that preserves all existing meets and joins, noting that for any
![]() $\mathbf {A}$
-structure
$\mathbf {A}$
-structure ![]() , the
, the
![]() $\mathbf {B}$
-structure
$\mathbf {B}$
-structure ![]() , with
, with ![]() for each
for each
![]() $i\in I$
, satisfies
$i\in I$
, satisfies ![]() for all
for all
![]() $\varphi \in \mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
. Clearly, semantical consequence in such a class
$\varphi \in \mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
. Clearly, semantical consequence in such a class
![]() $\mathsf {K}$
coincides with semantical consequence in the class of complete members of
$\mathsf {K}$
coincides with semantical consequence in the class of complete members of
![]() $\mathsf {K}$
.
$\mathsf {K}$
.
Example 2.2. A sufficient, but by no means necessary, condition for a class of
![]() $\mathcal {L}$
-lattices to admit regular completions is closure under MacNeille completions (see, e.g., [Reference Harding17]). This is the case in particular for
$\mathcal {L}$
-lattices to admit regular completions is closure under MacNeille completions (see, e.g., [Reference Harding17]). This is the case in particular for
![]() $\mathsf {BA}$
and
$\mathsf {BA}$
and
![]() $\mathsf {HA}$
; indeed, they are the only non-trivial varieties of Heyting algebras that have this property [Reference Bezhanishvili and Harding3]. A broad family of varieties of
$\mathsf {HA}$
; indeed, they are the only non-trivial varieties of Heyting algebras that have this property [Reference Bezhanishvili and Harding3]. A broad family of varieties of
![]() $\mathsf {FL_e}$
-algebras—including
$\mathsf {FL_e}$
-algebras—including
![]() $\mathsf {FL_e}$
,
$\mathsf {FL_e}$
,
![]() $\mathsf {FL_{ew}}$
, and
$\mathsf {FL_{ew}}$
, and
![]() $\mathsf {FL_{ec}}$
—are also closed under MacNeille completions, and for a still broader family—including
$\mathsf {FL_{ec}}$
—are also closed under MacNeille completions, and for a still broader family—including
![]() $\mathsf {GA}$
—this is true for the class of their subdirectly irreducible members [Reference Ciabattoni, Galatos and Terui9]. Note, however, that in some cases—e.g.,
$\mathsf {GA}$
—this is true for the class of their subdirectly irreducible members [Reference Ciabattoni, Galatos and Terui9]. Note, however, that in some cases—e.g.,
![]() $\mathsf {MV}$
[Reference Gehrke and Priestley14]—neither the variety nor the class of its subdirectly irreducible members admits regular completions.
$\mathsf {MV}$
[Reference Gehrke and Priestley14]—neither the variety nor the class of its subdirectly irreducible members admits regular completions.
Let
![]() $\mathrm {Fm}_{\Box }(\mathcal {L})$
denote the set of propositional formulas
$\mathrm {Fm}_{\Box }(\mathcal {L})$
denote the set of propositional formulas
![]() $\alpha ,\beta ,\dots $
built inductively using a countably infinite set of propositional variables
$\alpha ,\beta ,\dots $
built inductively using a countably infinite set of propositional variables
![]() $\{p_i\}_{i\in \mathbb {N}}$
, connectives in
$\{p_i\}_{i\in \mathbb {N}}$
, connectives in
![]() $\mathcal {L}$
, and unary connectives
$\mathcal {L}$
, and unary connectives
![]() $\Box $
and
$\Box $
and
![]() $\Diamond $
, and call an ordered pair of propositional formulas
$\Diamond $
, and call an ordered pair of propositional formulas
![]() $\alpha ,\beta \in \mathrm {Fm}_{\Box }(\mathcal {L})$
, written
$\alpha ,\beta \in \mathrm {Fm}_{\Box }(\mathcal {L})$
, written
![]() $\alpha \approx \beta $
, an
$\alpha \approx \beta $
, an
![]() $\mathrm { Fm}_{\Box }(\mathcal {L})$
-equation. The (standard) translation functions
$\mathrm { Fm}_{\Box }(\mathcal {L})$
-equation. The (standard) translation functions
![]() $({-})^\ast $
and
$({-})^\ast $
and
![]() $({-})^\circ $
between
$({-})^\circ $
between
![]() $\mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
and
$\mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
and
![]() $\mathrm {Fm}_{\Box }(\mathcal {L})$
are defined inductively by
$\mathrm {Fm}_{\Box }(\mathcal {L})$
are defined inductively by
 $$ \begin{align*} (P_i(x))^\ast &= p_i & p_i^\circ &= P_i(x) & i\in\mathbb{N},\\ (\star(\varphi_1,\dots,\varphi_n))^\ast &= \star(\varphi^\ast_1,\dots,\varphi^\ast_n) & (\star(\alpha_1,\dots,\alpha_n))^\circ &= \star(\alpha^\circ_1,\dots,\alpha^\circ_n) & \star\in\mathcal{L}_n,\\ ((\forall{x}) \varphi)^\ast &=\Box \varphi^\ast & (\Box\alpha)^\circ &= (\forall{x}) \alpha^\circ, \\ ((\exists{x}) \varphi)^\ast &=\Diamond \varphi^\ast & (\Diamond\alpha)^\circ &= (\exists{x}) \alpha^\circ, \end{align*} $$
$$ \begin{align*} (P_i(x))^\ast &= p_i & p_i^\circ &= P_i(x) & i\in\mathbb{N},\\ (\star(\varphi_1,\dots,\varphi_n))^\ast &= \star(\varphi^\ast_1,\dots,\varphi^\ast_n) & (\star(\alpha_1,\dots,\alpha_n))^\circ &= \star(\alpha^\circ_1,\dots,\alpha^\circ_n) & \star\in\mathcal{L}_n,\\ ((\forall{x}) \varphi)^\ast &=\Box \varphi^\ast & (\Box\alpha)^\circ &= (\forall{x}) \alpha^\circ, \\ ((\exists{x}) \varphi)^\ast &=\Diamond \varphi^\ast & (\Diamond\alpha)^\circ &= (\exists{x}) \alpha^\circ, \end{align*} $$
and lift in the obvious way to (sets of)
![]() $\mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
-equations and
$\mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
-equations and
![]() $\mathrm {Fm}_{\Box }(\mathcal {L})$
-equations.
$\mathrm {Fm}_{\Box }(\mathcal {L})$
-equations.
Clearly,
![]() $(\varphi ^\ast )^\circ = \varphi $
for any
$(\varphi ^\ast )^\circ = \varphi $
for any
![]() $\varphi \in \mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
and
$\varphi \in \mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
and
![]() $(\alpha ^\circ )^\ast = \alpha $
for any
$(\alpha ^\circ )^\ast = \alpha $
for any
![]() $\alpha \in \mathrm {Fm}_{\Box }(\mathcal {L})$
, and we may therefore switch between first-order and modal notations as convenient. To axiomatize consequence in the one-variable first-order logic based on a class of
$\alpha \in \mathrm {Fm}_{\Box }(\mathcal {L})$
, and we may therefore switch between first-order and modal notations as convenient. To axiomatize consequence in the one-variable first-order logic based on a class of
![]() $\mathcal {L}$
-lattices
$\mathcal {L}$
-lattices
![]() $\mathsf {K}$
, it therefore suffices to find a (natural) axiomatization of a class
$\mathsf {K}$
, it therefore suffices to find a (natural) axiomatization of a class
![]() $\mathsf {C}$
of algebras in the signature of
$\mathsf {C}$
of algebras in the signature of
![]() $\mathcal {L}$
expanded with
$\mathcal {L}$
expanded with
![]() $\Box ,\Diamond $
such that
$\Box ,\Diamond $
such that
![]() $\vDash ^{\forall }_{\mathsf {K}}$
corresponds to equational consequence in
$\vDash ^{\forall }_{\mathsf {K}}$
corresponds to equational consequence in
![]() $\mathsf {C}$
. More precisely, let us call a homomorphism from the formula algebra with universe
$\mathsf {C}$
. More precisely, let us call a homomorphism from the formula algebra with universe
![]() $\mathrm {Fm}_{\Box }(\mathcal {L})$
to some
$\mathrm {Fm}_{\Box }(\mathcal {L})$
to some
![]() $\mathbf {A}\in \mathsf {C}$
an
$\mathbf {A}\in \mathsf {C}$
an
![]() $\mathbf {A}$
-evaluation, and define for any set
$\mathbf {A}$
-evaluation, and define for any set
![]() $\mathrm {\Sigma }\cup \{\alpha \approx \beta \}$
of
$\mathrm {\Sigma }\cup \{\alpha \approx \beta \}$
of
![]() $\mathrm {Fm}_{\Box }(\mathcal {L})$
-equations,
$\mathrm {Fm}_{\Box }(\mathcal {L})$
-equations,

Our goal in this paper is to provide a (natural) axiomatization of a variety
![]() $\mathsf {V}$
such that for any set of
$\mathsf {V}$
such that for any set of
![]() $\mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
-equations
$\mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
-equations
![]() $T\cup \{\varphi \approx \psi \}$
,
$T\cup \{\varphi \approx \psi \}$
,
Example 2.3. If
![]() $\mathsf {K}$
is
$\mathsf {K}$
is
![]() $\mathsf {BA}$
, then
$\mathsf {BA}$
, then
![]() $\vDash ^{\forall }_{\mathsf {K}}$
is consequence in the one-variable fragment of first-order classical logic, corresponding to
$\vDash ^{\forall }_{\mathsf {K}}$
is consequence in the one-variable fragment of first-order classical logic, corresponding to
![]() $\mathrm {S5}$
, and
$\mathrm {S5}$
, and
![]() $\mathsf {V}$
is the variety of monadic Boolean algebras defined in [Reference Halmos16]. If
$\mathsf {V}$
is the variety of monadic Boolean algebras defined in [Reference Halmos16]. If
![]() $\mathsf {K}$
is
$\mathsf {K}$
is
![]() $\mathsf {HA}$
, then
$\mathsf {HA}$
, then
![]() $\vDash ^{\forall }_{\mathsf {K}}$
is consequence in the one-variable fragment of first-order intuitionistic logic, corresponding to
$\vDash ^{\forall }_{\mathsf {K}}$
is consequence in the one-variable fragment of first-order intuitionistic logic, corresponding to
![]() $\mathrm {MIPC}$
, and
$\mathrm {MIPC}$
, and
![]() $\mathsf {V}$
is the variety of monadic Heyting algebras defined in [Reference Monteiro and Varsavsky22]. Analogous results have been obtained for first-order intermediate logics in [Reference Bezhanishvili1, Reference Bezhanishvili and Harding2, Reference Caicedo, Metcalfe, Rodríguez and Rogger5–Reference Caicedo and Rodríguez7, Reference Ono and Suzuki24, Reference Suzuki27, Reference Suzuki28]. In particular, if
$\mathsf {V}$
is the variety of monadic Heyting algebras defined in [Reference Monteiro and Varsavsky22]. Analogous results have been obtained for first-order intermediate logics in [Reference Bezhanishvili1, Reference Bezhanishvili and Harding2, Reference Caicedo, Metcalfe, Rodríguez and Rogger5–Reference Caicedo and Rodríguez7, Reference Ono and Suzuki24, Reference Suzuki27, Reference Suzuki28]. In particular, if
![]() $\mathsf {K}$
is
$\mathsf {K}$
is
![]() $\mathsf {GA}$
, then
$\mathsf {GA}$
, then
![]() $\vDash ^{\forall }_{\mathsf {K}}$
is consequence in the one-variable fragment of the first-order logic of linear frames, and
$\vDash ^{\forall }_{\mathsf {K}}$
is consequence in the one-variable fragment of the first-order logic of linear frames, and
![]() $\mathsf {V}$
is the variety of monadic Heyting algebras satisfying the prelinearity axiom
$\mathsf {V}$
is the variety of monadic Heyting algebras satisfying the prelinearity axiom ![]() [Reference Caicedo, Metcalfe, Rodríguez and Tuyt6]. However, if
[Reference Caicedo, Metcalfe, Rodríguez and Tuyt6]. However, if
![]() $\mathsf {K}$
is the class of totally ordered members of
$\mathsf {K}$
is the class of totally ordered members of
![]() $\mathsf {GA}$
, then
$\mathsf {GA}$
, then
![]() $\vDash ^{\forall }_{\mathsf {K}}$
is consequence in the one-variable fragment of first-order Gödel logic, the first-order logic of linear frames with a constant domain, and
$\vDash ^{\forall }_{\mathsf {K}}$
is consequence in the one-variable fragment of first-order Gödel logic, the first-order logic of linear frames with a constant domain, and
![]() $\mathsf {V}$
is the variety of monadic Gödel algebras, i.e., monadic Heyting algebras satisfying the prelinearity axiom and the constant domain axiom
$\mathsf {V}$
is the variety of monadic Gödel algebras, i.e., monadic Heyting algebras satisfying the prelinearity axiom and the constant domain axiom ![]() [Reference Caicedo and Rodríguez7]. Similarly, if
[Reference Caicedo and Rodríguez7]. Similarly, if
![]() $\mathsf {K}$
is the class of totally ordered MV-algebras, then
$\mathsf {K}$
is the class of totally ordered MV-algebras, then
![]() $\vDash ^{\forall }_{\mathsf {K}}$
is consequence in the one-variable fragment of first-order Łukasiewicz logic, and
$\vDash ^{\forall }_{\mathsf {K}}$
is consequence in the one-variable fragment of first-order Łukasiewicz logic, and
![]() $\mathsf {V}$
is the variety of monadic MV-algebras [Reference Rutledge26].
$\mathsf {V}$
is the variety of monadic MV-algebras [Reference Rutledge26].
3 An algebraic approach
As our basic modal structures, let us define an m-lattice to be any algebraic structure ![]() with lattice reduct
with lattice reduct ![]() that satisfies the following equations:
that satisfies the following equations:

Let ![]() stand for
stand for ![]() . It is easily shown that every m-lattice also satisfies the following equations and quasi-equations:
. It is easily shown that every m-lattice also satisfies the following equations and quasi-equations:

Now let
![]() $\mathcal {L}$
be any fixed lattice-oriented signature. We define an m-
$\mathcal {L}$
be any fixed lattice-oriented signature. We define an m-
![]() $\mathcal {L}$
-lattice to be any algebraic structure
$\mathcal {L}$
-lattice to be any algebraic structure ![]() such that
such that
![]() $\mathbf {A}$
is an
$\mathbf {A}$
is an
![]() $\mathcal {L}$
-lattice,
$\mathcal {L}$
-lattice, ![]() is an m-lattice, and the following equation is satisfied for each
is an m-lattice, and the following equation is satisfied for each
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $\star \in \mathcal {L}_n$
:
$\star \in \mathcal {L}_n$
:
Using (
![]() $\star _\Box $
),
$\star _\Box $
),
![]() $\mathrm {(L3_\Box )}$
, and (L3
$\mathrm {(L3_\Box )}$
, and (L3
![]() $_\Diamond $
), it follows that
$_\Diamond $
), it follows that ![]() also satisfies for each
also satisfies for each
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $\star \in \mathcal {L}_n$
, the equation
$\star \in \mathcal {L}_n$
, the equation
Given a class
![]() $\mathsf {K}$
of
$\mathsf {K}$
of
![]() $\mathcal {L}$
-lattices, let
$\mathcal {L}$
-lattices, let
![]() $\mathsf {mK}$
denote the class of m-
$\mathsf {mK}$
denote the class of m-
![]() $\mathcal {L}$
-lattices with an
$\mathcal {L}$
-lattices with an
![]() $\mathcal {L}$
-lattice reduct in
$\mathcal {L}$
-lattice reduct in
![]() $\mathsf {K}$
. Note that if
$\mathsf {K}$
. Note that if
![]() $\mathsf {K}$
is a variety, then so is
$\mathsf {K}$
is a variety, then so is
![]() $\mathsf {mK}$
.
$\mathsf {mK}$
.
Example 3.1. It is straightforward to show that the notion of an m-
![]() $\mathcal {L}_s$
-lattice encompasses other algebraic structures considered in the literature. In particular,
$\mathcal {L}_s$
-lattice encompasses other algebraic structures considered in the literature. In particular,
![]() $\mathsf {mHA}$
and
$\mathsf {mHA}$
and
![]() $\mathsf {mBA}$
are the varieties of monadic Heyting algebras [Reference Monteiro and Varsavsky22] and monadic Boolean algebras [Reference Halmos16], respectively. Moreover, if
$\mathsf {mBA}$
are the varieties of monadic Heyting algebras [Reference Monteiro and Varsavsky22] and monadic Boolean algebras [Reference Halmos16], respectively. Moreover, if
![]() $\mathbf {A}$
is an
$\mathbf {A}$
is an
![]() $\mathsf {FL_e}$
-algebra, then every m-
$\mathsf {FL_e}$
-algebra, then every m-
![]() $\mathcal {L}_s$
-lattice
$\mathcal {L}_s$
-lattice ![]() satisfies the equations
satisfies the equations
and
![]() $\mathsf {mFL_e}$
is therefore the variety of monadic
$\mathsf {mFL_e}$
is therefore the variety of monadic
![]() $\mathsf {FL_e}$
-algebras introduced in [Reference Tuyt29]. Let us just check (L6
$\mathsf {FL_e}$
-algebras introduced in [Reference Tuyt29]. Let us just check (L6
![]() $_\Box $
), the proof for (L6
$_\Box $
), the proof for (L6
![]() $_\Diamond $
) being very similar. Consider any
$_\Diamond $
) being very similar. Consider any
![]() $a,b\in A$
. Since
$a,b\in A$
. Since ![]() , by (L1
, by (L1
![]() $_\Diamond $
), also
$_\Diamond $
), also ![]() . Hence, using (L3
. Hence, using (L3
![]() $_\Box $
), (
$_\Box $
), (
![]() $\to _\Box $
), and (L5
$\to _\Box $
), and (L5
![]() $_\Box $
),
$_\Box $
),
Conversely, since ![]() , by (L1
, by (L1
![]() $_\Box $
), it follows by residuation that
$_\Box $
), it follows by residuation that ![]() and hence, using (L5
and hence, using (L5
![]() $_\Diamond $
), (L3
$_\Diamond $
), (L3
![]() $_\Diamond $
), and (
$_\Diamond $
), and (
![]() $\to _\Diamond $
),
$\to _\Diamond $
),
By residuation again, ![]() .
.
Example 3.2. The variety
![]() $\mathsf {mGA}$
corresponds to the one-variable fragment of Corsi’s first-order logic of linear frames [Reference Caicedo, Metcalfe, Rodríguez and Tuyt6], whereas the variety of monadic Gödel algebras—axiomatized relative to
$\mathsf {mGA}$
corresponds to the one-variable fragment of Corsi’s first-order logic of linear frames [Reference Caicedo, Metcalfe, Rodríguez and Tuyt6], whereas the variety of monadic Gödel algebras—axiomatized relative to
![]() $\mathsf {mGA}$
by the constant domain axiom—corresponds to the one-variable fragment of first-order Gödel logic, the first-order logic of linear frames with a constant domain [Reference Caicedo and Rodríguez7]. Note, however, that the variety axiomatized relative to
$\mathsf {mGA}$
by the constant domain axiom—corresponds to the one-variable fragment of first-order Gödel logic, the first-order logic of linear frames with a constant domain [Reference Caicedo and Rodríguez7]. Note, however, that the variety axiomatized relative to
![]() $\mathsf {mMV}$
by the constant domain axiom does not satisfy
$\mathsf {mMV}$
by the constant domain axiom does not satisfy
![]() $\Diamond x \cdot \Diamond x \approx \Diamond (x \cdot x)$
and therefore properly contains the variety of monadic MV-algebras studied in [Reference Castaño, Cimadamore, Varela and Rueda8, Reference Di Nola and Grigolia12, Reference Rutledge26]. Consider, for example, the MV-algebra
$\Diamond x \cdot \Diamond x \approx \Diamond (x \cdot x)$
and therefore properly contains the variety of monadic MV-algebras studied in [Reference Castaño, Cimadamore, Varela and Rueda8, Reference Di Nola and Grigolia12, Reference Rutledge26]. Consider, for example, the MV-algebra ![]() (in the language of
(in the language of
![]() $\mathsf {FL_e}$
-algebras) with the usual order, where
$\mathsf {FL_e}$
-algebras) with the usual order, where
![]() $a\cdot b:=\max (0,a+b-1)$
and
$a\cdot b:=\max (0,a+b-1)$
and
![]() $a\to b:=\min (1,1-a+b)$
. Let
$a\to b:=\min (1,1-a+b)$
. Let
![]() $\Box 0 = \Box \frac 12= \Diamond 0 = 0$
and
$\Box 0 = \Box \frac 12= \Diamond 0 = 0$
and
![]() $\Box 1=\Diamond \frac 12=\Diamond 1 =1$
. Then
$\Box 1=\Diamond \frac 12=\Diamond 1 =1$
. Then ![]() satisfies the constant domain axiom, but
satisfies the constant domain axiom, but
![]() $\Diamond \frac 12\cdot \Diamond \frac 12= 1\cdot 1=1\neq 0=\Diamond 0=\Diamond (\frac 12\cdot \frac 12)$
.
$\Diamond \frac 12\cdot \Diamond \frac 12= 1\cdot 1=1\neq 0=\Diamond 0=\Diamond (\frac 12\cdot \frac 12)$
.
We now provide a useful description of m-
![]() $\mathcal {L}$
-lattices that generalizes results in the literature for varieties such as monadic Heyting algebras [Reference Bezhanishvili1] and monadic
$\mathcal {L}$
-lattices that generalizes results in the literature for varieties such as monadic Heyting algebras [Reference Bezhanishvili1] and monadic
![]() $\mathsf {FL_e}$
-algebras [Reference Tuyt29].
$\mathsf {FL_e}$
-algebras [Reference Tuyt29].
Lemma 3.3. Let ![]() be any m-
be any m-
![]() $\mathcal {L}$
-lattice. Then
$\mathcal {L}$
-lattice. Then ![]() forms a subalgebra
forms a subalgebra
![]() $\Box \mathbf {A}$
of
$\Box \mathbf {A}$
of
![]() $\mathbf {A}$
, where
$\mathbf {A}$
, where ![]() and,
and,
Proof The fact that
![]() $\Box A$
forms a subalgebra of
$\Box A$
forms a subalgebra of
![]() $\mathbf {A}$
follows directly using (
$\mathbf {A}$
follows directly using (
![]() $\star _\Box $
) for each operation symbol
$\star _\Box $
) for each operation symbol
![]() $\star $
of
$\star $
of
![]() $\mathcal {L}$
, and
$\mathcal {L}$
, and
![]() $\Box A =\Diamond A$
follows from (L3
$\Box A =\Diamond A$
follows from (L3
![]() $_\Box $
) and (L3
$_\Box $
) and (L3
![]() $_\Diamond $
). Now consider any
$_\Diamond $
). Now consider any
![]() $a\in A$
. If
$a\in A$
. If
![]() $b\in \Box A$
satisfies
$b\in \Box A$
satisfies ![]() , then
, then ![]() , by (L4
, by (L4
![]() $_\Box $
) and (L5
$_\Box $
) and (L5
![]() $_\Box $
). But
$_\Box $
). But ![]() , by (L1
, by (L1
![]() $_\Box $
), so
$_\Box $
), so ![]() . Analogous reasoning establishes that
. Analogous reasoning establishes that ![]() .
.
Let us call a sublattice
![]() $\mathbf {L}_0$
of a lattice
$\mathbf {L}_0$
of a lattice
![]() $\mathbf {L}$
relatively complete if for any
$\mathbf {L}$
relatively complete if for any
![]() $a\in L$
, the set
$a\in L$
, the set ![]() contains a maximum and the set
contains a maximum and the set ![]() contains a minimum. Equivalently,
contains a minimum. Equivalently,
![]() $\mathbf {L}_0$
is relatively complete if the inclusion map
$\mathbf {L}_0$
is relatively complete if the inclusion map
![]() $f_0$
from
$f_0$
from ![]() to
to ![]() has left and right adjoints, that is, if there exist order-preserving maps
has left and right adjoints, that is, if there exist order-preserving maps
![]() $\Box \colon L\to L_0$
and
$\Box \colon L\to L_0$
and
![]() $\Diamond \colon L\to L_0$
such that for all
$\Diamond \colon L\to L_0$
such that for all
![]() $a\in L$
and
$a\in L$
and
![]() $b\in L_0$
,
$b\in L_0$
,
Let us also say that a subalgebra
![]() $\mathbf {A}_0$
of an
$\mathbf {A}_0$
of an
![]() $\mathcal {L}$
-lattice
$\mathcal {L}$
-lattice
![]() $\mathbf {A}$
is relatively complete if this property holds with respect to their lattice reducts. In particular, by Lemma 3.3, the subalgebra
$\mathbf {A}$
is relatively complete if this property holds with respect to their lattice reducts. In particular, by Lemma 3.3, the subalgebra
![]() $\Box \mathbf {A}$
of
$\Box \mathbf {A}$
of
![]() $\mathbf {A}$
is relatively complete for any m-
$\mathbf {A}$
is relatively complete for any m-
![]() $\mathcal {L}$
-lattice
$\mathcal {L}$
-lattice ![]() . The following result establishes a converse.
. The following result establishes a converse.
Lemma 3.4. Let
![]() $\mathbf {A}_0$
be a relatively complete subalgebra of an
$\mathbf {A}_0$
be a relatively complete subalgebra of an
![]() $\mathcal {L}$
-lattice
$\mathcal {L}$
-lattice
![]() $\mathbf {A}$
, and define
$\mathbf {A}$
, and define ![]() and
and ![]() for each
for each
![]() $a\in A$
. Then
$a\in A$
. Then ![]() is an m-
is an m-
![]() $\mathcal {L}$
-lattice and
$\mathcal {L}$
-lattice and
![]() $\Box _0 A =\Diamond _0 A = A_0$
.
$\Box _0 A =\Diamond _0 A = A_0$
.
Proof It is straightforward to check that ![]() is an m-lattice; for example, it satisfies (L2
is an m-lattice; for example, it satisfies (L2
![]() $_\Box $
), since for any
$_\Box $
), since for any
![]() $a_1,a_2\in A$
,
$a_1,a_2\in A$
,

Since
![]() $\mathbf {A}_0$
is a subalgebra of
$\mathbf {A}_0$
is a subalgebra of
![]() $\mathbf {A}$
, clearly
$\mathbf {A}$
, clearly ![]() also satisfies (
also satisfies (
![]() $\star _\Box $
). Hence
$\star _\Box $
). Hence ![]() is an m-
is an m-
![]() $\mathcal {L}$
-lattice and
$\mathcal {L}$
-lattice and
![]() $\Box _0 A =\Diamond _0 A = A_0$
.
$\Box _0 A =\Diamond _0 A = A_0$
.
Combining Lemmas 3.3 and 3.4 yields the following representation theorem for m-
![]() $\mathcal {L}$
-lattices.
$\mathcal {L}$
-lattices.
Theorem 3.5. Let
![]() $\mathsf {K}$
be any class of
$\mathsf {K}$
be any class of
![]() $\mathcal {L}$
-lattices. Then there exists a one-to-one correspondence between the members of
$\mathcal {L}$
-lattices. Then there exists a one-to-one correspondence between the members of
![]() $\mathsf {mK}$
and ordered pairs
$\mathsf {mK}$
and ordered pairs ![]() such that
such that
![]() $\mathbf {A}\in \mathsf {K}$
and
$\mathbf {A}\in \mathsf {K}$
and
![]() $\mathbf {A}_0$
is a relatively complete subalgebra of
$\mathbf {A}_0$
is a relatively complete subalgebra of
![]() $\mathbf {A}$
, implemented by the maps
$\mathbf {A}$
, implemented by the maps ![]() and
and ![]() .
.
Next, given any
![]() $\mathcal {L}$
-lattice
$\mathcal {L}$
-lattice
![]() $\mathbf {A}$
and set W, let
$\mathbf {A}$
and set W, let
![]() $\mathbf {A}^W$
be the
$\mathbf {A}^W$
be the
![]() $\mathcal {L}$
-lattice with universe
$\mathcal {L}$
-lattice with universe
![]() $A^W$
, where the operations are defined pointwise.
$A^W$
, where the operations are defined pointwise.
Proposition 3.6. Let
![]() $\mathbf {A}$
be an
$\mathbf {A}$
be an
![]() $\mathcal {L}$
-lattice, W a set, and
$\mathcal {L}$
-lattice, W a set, and
![]() $\mathbf {B}$
a subalgebra of
$\mathbf {B}$
a subalgebra of
![]() $\mathbf {A}^W$
such that for each
$\mathbf {A}^W$
such that for each
![]() $f\in B$
, the elements
$f\in B$
, the elements
![]() $\bigwedge _{v\in W}f(v)$
and
$\bigwedge _{v\in W}f(v)$
and
![]() $\bigvee _{v\in W}f(v)$
exist in
$\bigvee _{v\in W}f(v)$
exist in
![]() $\mathbf {A}$
and the following constant functions belong to B:
$\mathbf {A}$
and the following constant functions belong to B:
 $$ \begin{align*} \Box f\colon W\to A;\:u\mapsto\bigwedge_{v\in W} f(v) \quad\text{and}\quad\Diamond f\colon W\to A;\:u\mapsto\bigvee_{v\in W}f(v). \end{align*} $$
$$ \begin{align*} \Box f\colon W\to A;\:u\mapsto\bigwedge_{v\in W} f(v) \quad\text{and}\quad\Diamond f\colon W\to A;\:u\mapsto\bigvee_{v\in W}f(v). \end{align*} $$
Then ![]() is an m-
is an m-
![]() $\mathcal {L}$
-lattice, and if
$\mathcal {L}$
-lattice, and if
![]() $\mathbf {A}$
belongs to a class
$\mathbf {A}$
belongs to a class
![]() $\mathsf {K}$
of
$\mathsf {K}$
of
![]() $\mathcal {L}$
-lattices closed under taking subalgebras and direct powers,
$\mathcal {L}$
-lattices closed under taking subalgebras and direct powers, ![]() .
.
Proof It is straightforward to check that ![]() satisfies
satisfies
![]() $\mathrm {(L1_\Box )}$
,
$\mathrm {(L1_\Box )}$
,
![]() $\mathrm {(L2_\Box )}$
,
$\mathrm {(L2_\Box )}$
,
![]() $\mathrm {(L1_\Diamond )}$
, and
$\mathrm {(L1_\Diamond )}$
, and
![]() $\mathrm {(L2_\Diamond )}$
. To confirm that
$\mathrm {(L2_\Diamond )}$
. To confirm that ![]() is an m-
is an m-
![]() $\mathcal {L}$
-lattice—and therefore, if
$\mathcal {L}$
-lattice—and therefore, if
![]() $\mathbf {A}$
belongs to a class
$\mathbf {A}$
belongs to a class
![]() $\mathsf {K}$
of
$\mathsf {K}$
of
![]() $\mathcal {L}$
-lattices closed under taking subalgebras and direct powers, a member of
$\mathcal {L}$
-lattices closed under taking subalgebras and direct powers, a member of
![]() $\mathsf {mK}$
—observe that
$\mathsf {mK}$
—observe that
![]() $\Box f$
and
$\Box f$
and
![]() $\Diamond f$
are, by definition, constant functions for any
$\Diamond f$
are, by definition, constant functions for any
![]() $f\in B$
. Hence
$f\in B$
. Hence ![]() clearly also satisfies
clearly also satisfies
![]() $\mathrm {(L3_\Box )}$
and
$\mathrm {(L3_\Box )}$
and
![]() $\mathrm { (L3_\Diamond )}$
. Moreover, for any
$\mathrm { (L3_\Diamond )}$
. Moreover, for any
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $\star \in \mathcal {L}_n$
, and
$\star \in \mathcal {L}_n$
, and
![]() $f_1,\dots ,f_n\in B$
, the function
$f_1,\dots ,f_n\in B$
, the function
![]() $\star (\Box f_1,\dots ,\Box f_n)$
is constant and therefore equal to
$\star (\Box f_1,\dots ,\Box f_n)$
is constant and therefore equal to
![]() $\Box (\star (\Box f_1,\dots ,\Box f_n))$
, so
$\Box (\star (\Box f_1,\dots ,\Box f_n))$
, so ![]() satisfies (
satisfies (
![]() $\star _\Box $
).
$\star _\Box $
).
Let us call an m-
![]() $\mathcal {L}$
-lattice
$\mathcal {L}$
-lattice ![]() -functional if it is constructed as described in Proposition 3.6 for some
-functional if it is constructed as described in Proposition 3.6 for some
![]() $\mathcal {L}$
-lattice
$\mathcal {L}$
-lattice
![]() $\mathbf {A}$
and set W. Given any class of
$\mathbf {A}$
and set W. Given any class of
![]() $\mathcal {L}$
-lattices
$\mathcal {L}$
-lattices
![]() $\mathsf {K}$
, we call an m-
$\mathsf {K}$
, we call an m-
![]() $\mathcal {L}$
-lattice
$\mathcal {L}$
-lattice
![]() $\mathsf {K}$
-functional if it is isomorphic to an
$\mathsf {K}$
-functional if it is isomorphic to an ![]() -functional m-
-functional m-
![]() $\mathcal {L}$
-lattice for some
$\mathcal {L}$
-lattice for some
![]() $\mathbf {A}\in \mathsf {K}$
and set W, omitting the prefix
$\mathbf {A}\in \mathsf {K}$
and set W, omitting the prefix
![]() $\mathsf {K}$
- if the class is clear from the context.
$\mathsf {K}$
- if the class is clear from the context.
The following result identifies the semantics of one-variable first-order logics with evaluations into functional m-
![]() $\mathcal {L}$
-lattices.
$\mathcal {L}$
-lattices.
Proposition 3.7. Let
![]() $\mathbf {A}$
be any
$\mathbf {A}$
be any
![]() $\mathcal {L}$
-lattice.
$\mathcal {L}$
-lattice.
-
(a) Let
 be any
be any
 $\mathbf {A}$
-structure. Then
$\mathbf {A}$
-structure. Then  forms an
forms an  -functional m-
-functional m-
 $\mathcal {L}$
-lattice
$\mathcal {L}$
-lattice
 $\mathbf {B}$
and the
$\mathbf {B}$
and the
 $\mathbf {B}$
-evaluation
$\mathbf {B}$
-evaluation
 $g^{\mathfrak {{S}}}$
, defined by setting
$g^{\mathfrak {{S}}}$
, defined by setting  for each
for each
 $i\in \mathbb {N}$
, satisfies for all
$i\in \mathbb {N}$
, satisfies for all
 $\varphi ,\psi \in \mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
,
$\varphi ,\psi \in \mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
, 
-
(b) Let
 $\mathbf {B}$
be any
$\mathbf {B}$
be any  -functional m-
-functional m-
 $\mathcal {L}$
-lattice for some set W, and let g be any
$\mathcal {L}$
-lattice for some set W, and let g be any
 $\mathbf {B}$
-evaluation. Then
$\mathbf {B}$
-evaluation. Then  , where
, where  for each
for each
 $i\in \mathbb {N}$
, is an
$i\in \mathbb {N}$
, is an
 $\mathbf {A}$
-structure satisfying for all
$\mathbf {A}$
-structure satisfying for all
 $\varphi ,\psi \in \mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
,
$\varphi ,\psi \in \mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
, 
Proof (a) To show that
![]() $\mathbf {B}$
is
$\mathbf {B}$
is ![]() -functional, it suffices to observe that for any
-functional, it suffices to observe that for any ![]() , since
, since
![]() ${\mathfrak {{S}}}$
is an
${\mathfrak {{S}}}$
is an
![]() $\mathbf {A}$
-structure, the elements
$\mathbf {A}$
-structure, the elements ![]() and
and ![]() exist in
exist in
![]() $\mathbf {A}$
and correspond to the constant functions
$\mathbf {A}$
and correspond to the constant functions ![]() and
and ![]() , respectively. The fact that
, respectively. The fact that ![]() for all
for all
![]() $\varphi \in \mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
, follows by an easy induction on the definition of
$\varphi \in \mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
, follows by an easy induction on the definition of
![]() $\varphi $
, from which it follows also that
$\varphi $
, from which it follows also that
![]() ${\mathfrak {{S}}}\models \varphi \approx \psi \iff g^{\mathfrak {{S}}}(\varphi ^\ast )=g^{\mathfrak {{S}}}(\psi ^\ast )$
, for all
${\mathfrak {{S}}}\models \varphi \approx \psi \iff g^{\mathfrak {{S}}}(\varphi ^\ast )=g^{\mathfrak {{S}}}(\psi ^\ast )$
, for all
![]() $\varphi ,\psi \in \mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
.
$\varphi ,\psi \in \mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
.
(b) Since
![]() $\mathbf {B}$
is
$\mathbf {B}$
is ![]() -functional, the elements
-functional, the elements
![]() $\bigwedge _{v\in W}f(v)$
and
$\bigwedge _{v\in W}f(v)$
and
![]() $\bigvee _{v\in W}f(v)$
exist in
$\bigvee _{v\in W}f(v)$
exist in
![]() $\mathbf {A}$
for every
$\mathbf {A}$
for every
![]() $f\in B$
. We prove that
$f\in B$
. We prove that ![]() , by induction on the definition of
, by induction on the definition of
![]() $\varphi $
, from which it follows immediately that
$\varphi $
, from which it follows immediately that ![]() is an
is an
![]() $\mathbf {A}$
-structure and
$\mathbf {A}$
-structure and
![]() ${\mathfrak {{W}}}\models \varphi \approx \psi \iff g(\varphi ^\ast )=g(\psi ^\ast )$
, for all
${\mathfrak {{W}}}\models \varphi \approx \psi \iff g(\varphi ^\ast )=g(\psi ^\ast )$
, for all
![]() $\varphi ,\psi \in \mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
. In particular, for the case where
$\varphi ,\psi \in \mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
. In particular, for the case where
![]() $\varphi =(\forall {x})\psi $
, using the induction hypothesis for the second line,
$\varphi =(\forall {x})\psi $
, using the induction hypothesis for the second line,

The case where
![]() $\varphi =(\exists {x})\psi $
is very similar.
$\varphi =(\exists {x})\psi $
is very similar.
Let
![]() $\mathsf {K}$
be any class of
$\mathsf {K}$
be any class of
![]() $\mathcal {L}$
-lattices and denote by
$\mathcal {L}$
-lattices and denote by
![]() $\mathsf {fK}$
the class of all
$\mathsf {fK}$
the class of all
![]() $\mathsf {K}$
-functional m-
$\mathsf {K}$
-functional m-
![]() $\mathcal {L}$
-lattices. Then, as a direct consequence of Proposition 3.7, for any set of
$\mathcal {L}$
-lattices. Then, as a direct consequence of Proposition 3.7, for any set of
![]() $\mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
-equations
$\mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
-equations
![]() $T\cup \{\varphi \approx \psi \}$
,
$T\cup \{\varphi \approx \psi \}$
,
If
![]() $\mathsf {K}$
is closed under taking subalgebras and direct powers, then
$\mathsf {K}$
is closed under taking subalgebras and direct powers, then
![]() $\mathsf {fK}\subseteq \mathsf {mK}$
, by Proposition 3.6, and we obtain the following relationship between consequence in the first-order logic defined over
$\mathsf {fK}\subseteq \mathsf {mK}$
, by Proposition 3.6, and we obtain the following relationship between consequence in the first-order logic defined over
![]() $\mathsf {K}$
and consequence in the variety
$\mathsf {K}$
and consequence in the variety
![]() $\mathsf {mK}$
.
$\mathsf {mK}$
.
Corollary 3.8. Let
![]() $\mathsf {K}$
be a class of
$\mathsf {K}$
be a class of
![]() $\mathcal {L}$
-lattices closed under taking subalgebras and direct powers. Then for any set of
$\mathcal {L}$
-lattices closed under taking subalgebras and direct powers. Then for any set of
![]() $\mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
-equations
$\mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
-equations
![]() $T\cup \{\varphi \approx \psi \}$
,
$T\cup \{\varphi \approx \psi \}$
,
Moreover, if every member of
![]() $\mathsf {mK}$
is
$\mathsf {mK}$
is
![]() $\mathsf {K}$
-functional (i.e.,
$\mathsf {K}$
-functional (i.e.,
![]() $\mathsf {fK}=\mathsf {mK}$
), then
$\mathsf {fK}=\mathsf {mK}$
), then
Let us remark that a stricter notion of a functional algebra for a class
![]() $\mathsf {K}$
of
$\mathsf {K}$
of
![]() $\mathcal {L}$
-lattices is considered in [Reference Bezhanishvili and Harding2, Reference Cintula, Metcalfe, Tokuda, Fernandéz-Duque, Palmigiano and Pinchinat10] that coincides in our setting with the notion of being
$\mathcal {L}$
-lattices is considered in [Reference Bezhanishvili and Harding2, Reference Cintula, Metcalfe, Tokuda, Fernandéz-Duque, Palmigiano and Pinchinat10] that coincides in our setting with the notion of being
![]() $\mathsf {K}^c$
-functional, where
$\mathsf {K}^c$
-functional, where
![]() $\mathsf {K}^c$
is the class of complete members of
$\mathsf {K}^c$
is the class of complete members of
![]() $\mathsf {K}$
. That is, an m-
$\mathsf {K}$
. That is, an m-
![]() $\mathcal {L}$
-lattice
$\mathcal {L}$
-lattice ![]() is
is
![]() $\mathsf {K}^c$
-functional if it is isomorphic to a subalgebra of
$\mathsf {K}^c$
-functional if it is isomorphic to a subalgebra of ![]() for some complete
for some complete
![]() $\mathcal {L}$
-lattice
$\mathcal {L}$
-lattice
![]() $\mathbf {A}\in \mathsf {K}$
and set W, where
$\mathbf {A}\in \mathsf {K}$
and set W, where
![]() $\Box $
and
$\Box $
and
![]() $\Diamond $
are defined as described in Proposition 3.6.
$\Diamond $
are defined as described in Proposition 3.6.
4 A functional representation theorem
Adapting the proof of a similar result for Heyting Algebras [Reference Bezhanishvili and Harding2, Theorem 3.6], we prove in this section that if a variety
![]() $\mathsf {V}$
of
$\mathsf {V}$
of
![]() $\mathcal {L}$
-lattices has the superamalgamation property, then every member of
$\mathcal {L}$
-lattices has the superamalgamation property, then every member of
![]() $\mathsf {mV}$
is
$\mathsf {mV}$
is
![]() $\mathsf {V}$
-functional, and hence, by Corollary 3.8, consequence in the one-variable first-order logic defined over
$\mathsf {V}$
-functional, and hence, by Corollary 3.8, consequence in the one-variable first-order logic defined over
![]() $\mathsf {V}$
corresponds to consequence in
$\mathsf {V}$
corresponds to consequence in
![]() $\mathsf {mV}$
.
$\mathsf {mV}$
.
We first recall the necessary algebraic notions. Let
![]() $\mathsf {K}$
be a class of
$\mathsf {K}$
be a class of
![]() $\mathcal {L}$
-lattices. A V-formation in
$\mathcal {L}$
-lattices. A V-formation in
![]() $\mathsf {K}$
is a
$\mathsf {K}$
is a
![]() $5$
-tuple
$5$
-tuple ![]() consisting of
consisting of
![]() $\mathbf {A},\mathbf {B}_1,\mathbf {B}_2\in \mathsf {K}$
and embeddings
$\mathbf {A},\mathbf {B}_1,\mathbf {B}_2\in \mathsf {K}$
and embeddings
![]() $f_1\colon \mathbf {A}\to \mathbf {B}_1$
,
$f_1\colon \mathbf {A}\to \mathbf {B}_1$
,
![]() $f_2\colon \mathbf {A}\to \mathbf {B}_2$
. An amalgam in
$f_2\colon \mathbf {A}\to \mathbf {B}_2$
. An amalgam in
![]() $\mathsf {K}$
of a V-formation
$\mathsf {K}$
of a V-formation ![]() in
in
![]() $\mathsf {K}$
is a triple
$\mathsf {K}$
is a triple ![]() consisting of
consisting of
![]() $\mathbf {C}\in \mathsf {K}$
and embeddings
$\mathbf {C}\in \mathsf {K}$
and embeddings
![]() $g_1\colon \mathbf {B}_1\to \mathbf {C}$
,
$g_1\colon \mathbf {B}_1\to \mathbf {C}$
,
![]() $g_2\colon \mathbf {B}_2\to \mathbf {C}$
such that
$g_2\colon \mathbf {B}_2\to \mathbf {C}$
such that
![]() $g_1\circ f_1 = g_2\circ f_2$
; it is called a superamalgam if also for any
$g_1\circ f_1 = g_2\circ f_2$
; it is called a superamalgam if also for any
![]() $b_1\in B_1$
,
$b_1\in B_1$
,
![]() $b_2\in B_2$
and distinct
$b_2\in B_2$
and distinct
![]() $i,j\in \{1,2\}$
,
$i,j\in \{1,2\}$
,
The class
![]() $\mathsf {K}$
is said to have the superamalgamation property if every V-formation in
$\mathsf {K}$
is said to have the superamalgamation property if every V-formation in
![]() $\mathsf {K}$
has a superamalgam in
$\mathsf {K}$
has a superamalgam in
![]() $\mathsf {K}$
.
$\mathsf {K}$
.
Theorem 4.1. Let
![]() $\mathsf {K}$
be a class of
$\mathsf {K}$
be a class of
![]() $\mathcal {L}$
-lattices that is closed under taking direct limits and subalgebras, and has the superamalgamation property. Then every member of
$\mathcal {L}$
-lattices that is closed under taking direct limits and subalgebras, and has the superamalgamation property. Then every member of
![]() $\mathsf {mK}$
is functional.
$\mathsf {mK}$
is functional.
Proof Consider any ![]() . Then
. Then
![]() $\mathbf {A}\in \mathsf {K}$
and, since
$\mathbf {A}\in \mathsf {K}$
and, since
![]() $\mathsf {K}$
is closed under taking subalgebras, also
$\mathsf {K}$
is closed under taking subalgebras, also
![]() $\Box \mathbf {A}\in \mathsf {K}$
. We let
$\Box \mathbf {A}\in \mathsf {K}$
. We let
![]() $W:=\mathbb {N}^{>0}$
and define inductively a sequence of
$W:=\mathbb {N}^{>0}$
and define inductively a sequence of
![]() $\mathcal {L}$
-lattices
$\mathcal {L}$
-lattices ![]() in
in
![]() $\mathsf {K}$
and sequences of
$\mathsf {K}$
and sequences of
![]() $\mathcal {L}$
-lattice embeddings
$\mathcal {L}$
-lattice embeddings ![]() ,
, ![]() ,
, ![]() .
.
Let ![]() and let
and let
![]() $f_0\colon \Box \mathbf {A}\to \mathbf {A}$
be the inclusion map. For each
$f_0\colon \Box \mathbf {A}\to \mathbf {A}$
be the inclusion map. For each
![]() $i\in W$
, there exists inductively, by assumption, a superamalgam
$i\in W$
, there exists inductively, by assumption, a superamalgam ![]() of the V-formation
of the V-formation ![]() , and we define also
, and we define also ![]() .
.
Now let
![]() $\mathbf {L}$
be the direct limit of the system
$\mathbf {L}$
be the direct limit of the system ![]() with an associated sequence of
with an associated sequence of
![]() $\mathcal {L}$
-lattice embeddings
$\mathcal {L}$
-lattice embeddings ![]() . Since
. Since
![]() $\mathsf {K}$
is closed under taking direct limits,
$\mathsf {K}$
is closed under taking direct limits,
![]() $\mathbf {L}$
belongs to
$\mathbf {L}$
belongs to
![]() $\mathsf {K}$
. The first two superamalgamation steps of this construction are depicted in the following diagram:
$\mathsf {K}$
. The first two superamalgamation steps of this construction are depicted in the following diagram:

Since the operations of
![]() $\mathbf {L}^W$
are defined pointwise,
$\mathbf {L}^W$
are defined pointwise, ![]() is the universe of a subalgebra
is the universe of a subalgebra
![]() $\mathbf {B}$
of
$\mathbf {B}$
of
![]() $\mathbf {L}^W$
. We can also show that for each
$\mathbf {L}^W$
. We can also show that for each
![]() $a\in A$
, the elements
$a\in A$
, the elements
 $$ \begin{align*} \bigwedge_{j\in W}l_j\circ g_j(a)\quad\text{and}\quad\bigvee_{j\in W}l_j\circ g_j(a) \end{align*} $$
$$ \begin{align*} \bigwedge_{j\in W}l_j\circ g_j(a)\quad\text{and}\quad\bigvee_{j\in W}l_j\circ g_j(a) \end{align*} $$
exist in L and hence that ![]() , with
, with
![]() $\Box $
and
$\Box $
and
![]() $\Diamond $
defined in Proposition 3.6, is an
$\Diamond $
defined in Proposition 3.6, is an ![]() -functional m-
-functional m-
![]() $\mathcal {L}$
-lattice. Let
$\mathcal {L}$
-lattice. Let
![]() $a\in A$
and fix some
$a\in A$
and fix some
![]() $i\in W$
. It suffices to show that
$i\in W$
. It suffices to show that
![]() $l_i\circ g_i(\Box a)$
and
$l_i\circ g_i(\Box a)$
and
![]() $l_i\circ g_i(\Diamond a)$
are the greatest lower bound and the least upper bound, respectively, of
$l_i\circ g_i(\Diamond a)$
are the greatest lower bound and the least upper bound, respectively, of ![]() . Observe first that for any
. Observe first that for any
![]() $k\in W$
,
$k\in W$
,
where the first and last equations follow from the definition of
![]() $f_k$
and the second follows from the fact that
$f_k$
and the second follows from the fact that
![]() $\mathbf {L}$
is a direct limit. Hence for each
$\mathbf {L}$
is a direct limit. Hence for each
![]() $j\in W$
,
$j\in W$
,
So
![]() $l_i\circ g_i(\Box a)$
is a lower bound of S. Now suppose that
$l_i\circ g_i(\Box a)$
is a lower bound of S. Now suppose that
![]() $c\in L$
is another lower bound of S. Since
$c\in L$
is another lower bound of S. Since
![]() $\mathbf {L}$
is a direct limit, there exist
$\mathbf {L}$
is a direct limit, there exist
![]() $k\in W$
and
$k\in W$
and
![]() $d\in A_k$
such that
$d\in A_k$
such that
Since
![]() $l_{k+1}$
is an embedding,
$l_{k+1}$
is an embedding, ![]() . Hence, since
. Hence, since ![]() is a superamalgam of
is a superamalgam of ![]() , there exists
, there exists
![]() $b\in \Box A$
such that
$b\in \Box A$
such that
But
![]() $s_{k+1}$
and
$s_{k+1}$
and
![]() $g_{k+1}$
are embeddings and
$g_{k+1}$
are embeddings and
![]() $f_0$
is the inclusion map, so
$f_0$
is the inclusion map, so ![]() and
and ![]() . The latter inequality together with
. The latter inequality together with
![]() $b\in \Box A$
, yields
$b\in \Box A$
, yields ![]() . Hence also
. Hence also ![]() , and, using the first inequality,
, and, using the first inequality,
So
![]() $\bigwedge _{j\in W} l_j\circ g_j(a)=l_i\circ g_i(\Box a)$
exists in L and the constant function
$\bigwedge _{j\in W} l_j\circ g_j(a)=l_i\circ g_i(\Box a)$
exists in L and the constant function ![]() belongs to B. Also, symmetrically,
belongs to B. Also, symmetrically,
![]() $\bigvee _{j\in W}l_j\circ g_j(a)=l_i\circ g_i(\Diamond a)$
exists in L and the constant function
$\bigvee _{j\in W}l_j\circ g_j(a)=l_i\circ g_i(\Diamond a)$
exists in L and the constant function ![]() belongs to B.
belongs to B.
To show that ![]() is functional, it remains to prove that the following map is an isomorphism:
is functional, it remains to prove that the following map is an isomorphism:
Since the operations of
![]() $\mathbf {L}^W$
are defined pointwise and
$\mathbf {L}^W$
are defined pointwise and
![]() $l_i$
and
$l_i$
and
![]() $g_i$
are
$g_i$
are
![]() $\mathcal {L}$
-lattice embeddings for each
$\mathcal {L}$
-lattice embeddings for each
![]() $i\in W$
, also f is an
$i\in W$
, also f is an
![]() $\mathcal {L}$
-lattice embedding. Clearly, it is onto, by the definition of B. Moreover, recalling that
$\mathcal {L}$
-lattice embedding. Clearly, it is onto, by the definition of B. Moreover, recalling that
![]() $l_i\circ g_i(\Box a)=\bigwedge _{j\in W} l_i\circ g_i(a)$
for each
$l_i\circ g_i(\Box a)=\bigwedge _{j\in W} l_i\circ g_i(a)$
for each
![]() $a\in A$
, it follows that
$a\in A$
, it follows that

and, similarly,
![]() $f(\Diamond a)=\Diamond f(a)$
.
$f(\Diamond a)=\Diamond f(a)$
.
Combining Theorem 4.1 with Corollary 3.8 yields the following result.
Corollary 4.2. If
![]() $\mathsf {V}$
is a variety of
$\mathsf {V}$
is a variety of
![]() $\mathcal {L}$
-lattices that has the superamalgamation property, then for any set
$\mathcal {L}$
-lattices that has the superamalgamation property, then for any set
![]() $T\cup \{\varphi \approx \psi \}$
of
$T\cup \{\varphi \approx \psi \}$
of
![]() $\mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
-equations,
$\mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
-equations,
Example 4.3. The variety of lattices has the superamalgamation property [Reference Grätzer15]. Hence, by Theorem 4.1, every m-lattice is functional, and consequence in the one-variable first-order lattice logic corresponds to consequence in m-lattices.
Example 4.4.
![]() $\mathsf {FL_e}$
,
$\mathsf {FL_e}$
,
![]() $\mathsf {FL_{ew}}$
, and
$\mathsf {FL_{ew}}$
, and
![]() $\mathsf {FL_{ec}}$
, and many other varieties of
$\mathsf {FL_{ec}}$
, and many other varieties of
![]() $\mathsf {FL_e}$
-algebras have the superamalgamation property, which is equivalent in this setting to the Craig interpolation property for the associated substructural logic (see, e.g., [Reference Galatos, Jipsen, Kowalski and Ono13]). Hence, for any such variety
$\mathsf {FL_e}$
-algebras have the superamalgamation property, which is equivalent in this setting to the Craig interpolation property for the associated substructural logic (see, e.g., [Reference Galatos, Jipsen, Kowalski and Ono13]). Hence, for any such variety
![]() $\mathsf {V}$
—notably, for
$\mathsf {V}$
—notably, for
![]() $\mathsf {V}\in \{\mathsf {FL_e},\mathsf {FL_{ew}},\mathsf {FL_{ec}}\}$
—every member of
$\mathsf {V}\in \{\mathsf {FL_e},\mathsf {FL_{ew}},\mathsf {FL_{ec}}\}$
—every member of
![]() $\mathsf {mV}$
is functional, and consequence in the one-variable first-order substructural logic defined over
$\mathsf {mV}$
is functional, and consequence in the one-variable first-order substructural logic defined over
![]() $\mathsf {V}$
corresponds to consequence in
$\mathsf {V}$
corresponds to consequence in
![]() $\mathsf {mV}$
.
$\mathsf {mV}$
.
Example 4.5. A normal modal logic has the Craig interpolation property if and only if the associated variety of modal algebras—Boolean algebras with an operator—has the superamalgamation property [Reference Maksimova19]. Moreover, there exist infinitely many such logics [Reference Rautenberg25], including well-known cases such as
![]() $\mathrm {K}$
,
$\mathrm {K}$
,
![]() $\mathrm {KT}$
,
$\mathrm {KT}$
,
![]() $\mathrm {K4}$
, and
$\mathrm {K4}$
, and
![]() $\mathrm {S4}$
. Hence our results yield axiomatizations for the one-variable fragments of infinitely many first-order logics defined over varieties of modal algebras.
$\mathrm {S4}$
. Hence our results yield axiomatizations for the one-variable fragments of infinitely many first-order logics defined over varieties of modal algebras.
Suppose finally that
![]() $\mathsf {K}$
is a class of
$\mathsf {K}$
is a class of
![]() $\mathcal {L}$
-lattices that is not only closed under taking direct limits and subalgebras and has the superamalgamation property, but also admits regular completions. In this case, we can adapt the proof of Theorem 4.1 to show that every member of
$\mathcal {L}$
-lattices that is not only closed under taking direct limits and subalgebras and has the superamalgamation property, but also admits regular completions. In this case, we can adapt the proof of Theorem 4.1 to show that every member of
![]() $\mathsf {K}$
is
$\mathsf {K}$
is
![]() $\mathsf {K}^c$
-functional, which—as noted at the end of Section 3—corresponds to the stricter notion of a functional algebra considered in [Reference Bezhanishvili and Harding2, Reference Cintula, Metcalfe, Tokuda, Fernandéz-Duque, Palmigiano and Pinchinat10]. Just observe that, given some
$\mathsf {K}^c$
-functional, which—as noted at the end of Section 3—corresponds to the stricter notion of a functional algebra considered in [Reference Bezhanishvili and Harding2, Reference Cintula, Metcalfe, Tokuda, Fernandéz-Duque, Palmigiano and Pinchinat10]. Just observe that, given some ![]() , the direct limit
, the direct limit
![]() $\mathbf {L}\in \mathsf {K}$
constructed in the proof embeds into some
$\mathbf {L}\in \mathsf {K}$
constructed in the proof embeds into some
![]() $\boldsymbol{\bar{\mathbf{L}}}\in \mathsf {K}^c$
and hence, reasoning as before,
$\boldsymbol{\bar{\mathbf{L}}}\in \mathsf {K}^c$
and hence, reasoning as before, ![]() is isomorphic to a subalgebra of
is isomorphic to a subalgebra of ![]() .
.
5 A proof-theoretic strategy
In this section, we describe an alternative proof-theoretic strategy for establishing completeness of axiomatizations for one-variable fragments of first-order logics. The key step is to prove that a derivation of a one-variable formula in a sequent calculus for the first-order logic can be transformed into a derivation that uses just one variable. To illustrate, we consider the first-order version of the full Lambek calculus with exchange
![]() $\mathrm {FL_e}$
, then extend the method to a broader family of first-order substructural logics.
$\mathrm {FL_e}$
, then extend the method to a broader family of first-order substructural logics.
The crucial feature of the first-order version of
![]() $\mathrm {FL_e}$
needed for our approach is the fact that it can be presented as a cut-free sequent calculus with the standard rules for quantifiers. Any derivation of a one-variable formula
$\mathrm {FL_e}$
needed for our approach is the fact that it can be presented as a cut-free sequent calculus with the standard rules for quantifiers. Any derivation of a one-variable formula
![]() $\varphi $
in this calculus will therefore consist of sequents containing only subformulas of
$\varphi $
in this calculus will therefore consist of sequents containing only subformulas of
![]() $\varphi $
with some free occurrences of the variable x replaced by other variables. In particular, the derivation will not introduce any new occurrences of quantifiers or bound variables, but may introduce free variables not occurring in
$\varphi $
with some free occurrences of the variable x replaced by other variables. In particular, the derivation will not introduce any new occurrences of quantifiers or bound variables, but may introduce free variables not occurring in
![]() $\varphi $
via the rules for the universal quantifier on the right and the existential quantifier on the left. Hence, to reason about derivations of one-variable formulas, we may consider a fragment of the sequent calculus restricted to formulas that contain only unary predicates and one bound variable, but may contain further free variables.
$\varphi $
via the rules for the universal quantifier on the right and the existential quantifier on the left. Hence, to reason about derivations of one-variable formulas, we may consider a fragment of the sequent calculus restricted to formulas that contain only unary predicates and one bound variable, but may contain further free variables.
More formally, let
![]() $\mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
be the set of first-order formulas built inductively using unary predicates
$\mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
be the set of first-order formulas built inductively using unary predicates
![]() $\{P_i\}_{i\in \mathbb {N}}$
, variables
$\{P_i\}_{i\in \mathbb {N}}$
, variables
![]() $\{x\}\cup \{x_i\}_{i\in \mathbb {N}}$
, connectives in
$\{x\}\cup \{x_i\}_{i\in \mathbb {N}}$
, connectives in
![]() $\mathcal {L}_s$
, and quantifiers
$\mathcal {L}_s$
, and quantifiers
![]() $(\forall {x})$
and
$(\forall {x})$
and
![]() $(\exists {x})$
. Clearly,
$(\exists {x})$
. Clearly,
![]() $\mathrm {Fm}_{\forall }^{1}(\mathcal {L}_s)\subseteq \mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
. We write
$\mathrm {Fm}_{\forall }^{1}(\mathcal {L}_s)\subseteq \mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
. We write
![]() $\varphi (\bar {w})$
to denote that the free variables of
$\varphi (\bar {w})$
to denote that the free variables of
![]() $\varphi \in \mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
belong to a set
$\varphi \in \mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
belong to a set
![]() $\bar {w}$
, and indicate by
$\bar {w}$
, and indicate by
![]() $\varphi (\bar {w},y)$
that y is not among the variables in
$\varphi (\bar {w},y)$
that y is not among the variables in
![]() $\bar {w}$
.
$\bar {w}$
.
For the purposes of this paper, we define a sequent to be an ordered pair of finite multisets of formulas
![]() $\mathrm {\Gamma },\mathrm {\Delta }$
in
$\mathrm {\Gamma },\mathrm {\Delta }$
in
![]() $\mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
, denoted by
$\mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
, denoted by
![]() $\mathrm {\Gamma }{{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }$
, such that
$\mathrm {\Gamma }{{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }$
, such that
![]() $\mathrm {\Delta }$
contains at most one
$\mathrm {\Delta }$
contains at most one
![]() $\mathcal {L}_s$
-formula.Footnote
3
As usual, we denote the multiset sum of two finite multisets of formulas
$\mathcal {L}_s$
-formula.Footnote
3
As usual, we denote the multiset sum of two finite multisets of formulas
![]() $\mathrm {\Gamma }_1$
and
$\mathrm {\Gamma }_1$
and
![]() $\mathrm {\Gamma }_2$
by
$\mathrm {\Gamma }_2$
by
![]() $\mathrm {\Gamma }_1,\mathrm {\Gamma }_2$
, and the empty multiset by an empty space. We also define, for
$\mathrm {\Gamma }_1,\mathrm {\Gamma }_2$
, and the empty multiset by an empty space. We also define, for
![]() $n\in \mathbb {N}^{>0}$
and
$n\in \mathbb {N}^{>0}$
and
![]() $\varphi _1,\dots ,\varphi _n,\psi \in \mathrm { Fm}_{\forall }^{1+}(\mathcal {L}_s)$
,
$\varphi _1,\dots ,\varphi _n,\psi \in \mathrm { Fm}_{\forall }^{1+}(\mathcal {L}_s)$
,
We write
![]() $\mathrm {\Gamma }(\bar {w})$
to denote that the free variables occurring in a finite multiset of formulas
$\mathrm {\Gamma }(\bar {w})$
to denote that the free variables occurring in a finite multiset of formulas
![]() $\mathrm {\Gamma }$
belong to a set
$\mathrm {\Gamma }$
belong to a set
![]() $\bar {w}$
.
$\bar {w}$
.
The sequent calculus
![]() ${\mathrm {\forall 1FL_e}}$
is displayed in Figure 1, where the quantifier rules are subject to the following side-conditions:
${\mathrm {\forall 1FL_e}}$
is displayed in Figure 1, where the quantifier rules are subject to the following side-conditions:
-
(i) If the conclusion of an application of
 $({\forall \,{\Rightarrow }})$
or
$({\forall \,{\Rightarrow }})$
or
 $({\Rightarrow }\, \exists )$
contains at least one free occurrence of a variable, then the variable u occurring in its premise also occurs freely in its conclusion.
$({\Rightarrow }\, \exists )$
contains at least one free occurrence of a variable, then the variable u occurring in its premise also occurs freely in its conclusion. -
(ii) The variable y occurring in the premise of an application of
 $({\Rightarrow }\, \forall )$
or
$({\Rightarrow }\, \forall )$
or
 $(\exists \, {\Rightarrow })$
does not occur freely in its conclusion.
$(\exists \, {\Rightarrow })$
does not occur freely in its conclusion.
If there exists a derivation d of a sequent
![]() $\mathrm {\Gamma }{{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }$
in a sequent calculus
$\mathrm {\Gamma }{{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }$
in a sequent calculus
![]() $\mathrm {S}$
, we write
$\mathrm {S}$
, we write
![]() $d\vdash _{_{\mathrm {S}}}\mathrm {\Gamma }{{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }$
or simply
$d\vdash _{_{\mathrm {S}}}\mathrm {\Gamma }{{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }$
or simply
![]() $\vdash _{_{\mathrm {S}}}\mathrm {\Gamma }{{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }$
.
$\vdash _{_{\mathrm {S}}}\mathrm {\Gamma }{{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }$
.

Figure 1 The sequent calculus
![]() ${\mathrm {\forall 1FL_e}}$
.
${\mathrm {\forall 1FL_e}}$
.
The following relationship between derivability of sequents in
![]() ${\mathrm {\forall 1FL_e}}$
and (first-order) validity of equations in
${\mathrm {\forall 1FL_e}}$
and (first-order) validity of equations in
![]() $\mathsf {FL_e}$
is a direct consequence of the completeness of a cut-free sequent calculus for the first-order version of
$\mathsf {FL_e}$
is a direct consequence of the completeness of a cut-free sequent calculus for the first-order version of
![]() $\mathrm {FL_e}$
.
$\mathrm {FL_e}$
.
Proposition 5.1 (cf. [Reference Komori18, Reference Ono and Komori23]).
For any sequent
![]() $\mathrm {\Gamma }{{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }$
containing formulas from
$\mathrm {\Gamma }{{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }$
containing formulas from
![]() $\mathrm {Fm}_{\forall }^{1}(\mathcal {L}_s)$
,
$\mathrm {Fm}_{\forall }^{1}(\mathcal {L}_s)$
,
We now establish an interpolation property for the calculus
![]() ${\mathrm {\forall 1FL_e}}$
. For any derivation d of a sequent in
${\mathrm {\forall 1FL_e}}$
. For any derivation d of a sequent in
![]() ${\mathrm {\forall 1FL_e}}$
, let
${\mathrm {\forall 1FL_e}}$
, let
![]() ${\mathrm {md}}(d)$
denote the maximum number of applications of the rules
${\mathrm {md}}(d)$
denote the maximum number of applications of the rules
![]() $({\Rightarrow }\,\forall )$
and
$({\Rightarrow }\,\forall )$
and
![]() $(\exists \,{\Rightarrow })$
that occur on a branch of d. Note that the assumption in the following lemma that no variable in
$(\exists \,{\Rightarrow })$
that occur on a branch of d. Note that the assumption in the following lemma that no variable in
![]() $\bar {w}\cup \{y,z\}$
lies in the scope of a quantifier is required for the proof to ensure that any formula
$\bar {w}\cup \{y,z\}$
lies in the scope of a quantifier is required for the proof to ensure that any formula
![]() $(\forall {x})\varphi (x)$
or
$(\forall {x})\varphi (x)$
or
![]() $(\exists {x})\varphi (x)$
occurring in d contains no free variables; however, in order to deal with the cases of
$(\exists {x})\varphi (x)$
occurring in d contains no free variables; however, in order to deal with the cases of
![]() $({\Rightarrow }\,\forall )$
and
$({\Rightarrow }\,\forall )$
and
![]() $(\exists \,{\Rightarrow })$
, the formula
$(\exists \,{\Rightarrow })$
, the formula
![]() $\chi (\bar {w})\in \mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
is not required to satisfy this condition.
$\chi (\bar {w})\in \mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
is not required to satisfy this condition.
Lemma 5.2. Let
![]() $\mathrm {\Gamma }(\bar {w},y),\Pi (\bar {w},z){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }(\bar {w},z)$
be any sequent such that
$\mathrm {\Gamma }(\bar {w},y),\Pi (\bar {w},z){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }(\bar {w},z)$
be any sequent such that
![]() $y\neq z$
,
$y\neq z$
,
![]() $x\not \in \bar {w}\cup \{y,z\}$
, and no variable in
$x\not \in \bar {w}\cup \{y,z\}$
, and no variable in
![]() $\bar {w}\cup \{y,z\}$
lies in the scope of a quantifier. If
$\bar {w}\cup \{y,z\}$
lies in the scope of a quantifier. If
![]() $d\vdash _{_{\mathrm {\forall 1FL_e}}}\mathrm {\Gamma }(\bar {w},y),\Pi (\bar {w},z){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }(\bar {w},z)$
, then there exist
$d\vdash _{_{\mathrm {\forall 1FL_e}}}\mathrm {\Gamma }(\bar {w},y),\Pi (\bar {w},z){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }(\bar {w},z)$
, then there exist
![]() ${\chi (\bar {w})\in \mathrm { Fm}_{\forall }^{1+}(\mathcal {L}_s)}$
and derivations
${\chi (\bar {w})\in \mathrm { Fm}_{\forall }^{1+}(\mathcal {L}_s)}$
and derivations
![]() $d_1,d_2$
in
$d_1,d_2$
in
![]() ${\mathrm {\forall 1FL_e}}$
such that
${\mathrm {\forall 1FL_e}}$
such that ![]() and
and
Proof By a straightforward inspection of the rules of
![]() ${\mathrm {\forall 1FL_e}}$
, no variable in
${\mathrm {\forall 1FL_e}}$
, no variable in
![]() $\bar {w}\cup \{y,z\}$
can lie in the scope of a quantifier in a sequent occurring in a derivation in
$\bar {w}\cup \{y,z\}$
can lie in the scope of a quantifier in a sequent occurring in a derivation in
![]() ${\mathrm {\forall 1FL_e}}$
of
${\mathrm {\forall 1FL_e}}$
of
![]() $\mathrm {\Gamma }(\bar {w},y),\Pi (\bar {w},z){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }(\bar {w},z)$
. We prove the claim by induction on the height of d, considering in turn the last rule applied in the derivation.
$\mathrm {\Gamma }(\bar {w},y),\Pi (\bar {w},z){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }(\bar {w},z)$
. We prove the claim by induction on the height of d, considering in turn the last rule applied in the derivation.
Observe first that if y does not occur in
![]() $\mathrm {\Gamma }$
, we can define
$\mathrm {\Gamma }$
, we can define
![]() $\chi (\bar {w}):=\prod \mathrm {\Gamma }$
, and obtain a derivation
$\chi (\bar {w}):=\prod \mathrm {\Gamma }$
, and obtain a derivation
![]() $d_1$
of
$d_1$
of
![]() $\mathrm {\Gamma }(\bar {w},y){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\chi (\bar {w})$
, ending with repeated applications of
$\mathrm {\Gamma }(\bar {w},y){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\chi (\bar {w})$
, ending with repeated applications of
![]() $({\Rightarrow }\,\cdot )$
,
$({\Rightarrow }\,\cdot )$
,
![]() $({\Rightarrow }\,\mathrm {e})$
, and
$({\Rightarrow }\,\mathrm {e})$
, and ![]() , and a derivation
, and a derivation
![]() $d_2$
of
$d_2$
of
![]() $\Pi (\bar {w},z),\chi (\bar {w}){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }(\bar {w},z)$
that extends d with repeated applications of
$\Pi (\bar {w},z),\chi (\bar {w}){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }(\bar {w},z)$
that extends d with repeated applications of
![]() $(\cdot \,{\Rightarrow })$
and
$(\cdot \,{\Rightarrow })$
and
![]() $(\mathrm {e}\,{\Rightarrow })$
, such that
$(\mathrm {e}\,{\Rightarrow })$
, such that
![]() ${\mathrm {md}}(d_1)=0$
and
${\mathrm {md}}(d_1)=0$
and
![]() ${\mathrm {md}}(d_2)={\mathrm {md}}(d)$
. Similarly, if z does not occur in
${\mathrm {md}}(d_2)={\mathrm {md}}(d)$
. Similarly, if z does not occur in
![]() $\Pi ,\mathrm {\Delta }$
, we can define
$\Pi ,\mathrm {\Delta }$
, we can define
![]() $\chi (\bar {w}):=\prod \Pi \to \sum \mathrm {\Delta }$
, and obtain a derivation
$\chi (\bar {w}):=\prod \Pi \to \sum \mathrm {\Delta }$
, and obtain a derivation
![]() $d_1$
of
$d_1$
of
![]() $\mathrm {\Gamma }(\bar {w},y){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\chi (\bar {w})$
that extends d with repeated applications of
$\mathrm {\Gamma }(\bar {w},y){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\chi (\bar {w})$
that extends d with repeated applications of
![]() $(\cdot \,{\Rightarrow })$
,
$(\cdot \,{\Rightarrow })$
,
![]() $(\mathrm {e}\,{\Rightarrow })$
, and
$(\mathrm {e}\,{\Rightarrow })$
, and
![]() $({\Rightarrow }\,\mathrm {f})$
, followed by an application of
$({\Rightarrow }\,\mathrm {f})$
, followed by an application of
![]() $({\Rightarrow }\to )$
, and a derivation
$({\Rightarrow }\to )$
, and a derivation
![]() $d_2$
of
$d_2$
of
![]() $\Pi (\bar {w},z),\chi (\bar {w}){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }(\bar {w},z)$
ending with repeated applications of
$\Pi (\bar {w},z),\chi (\bar {w}){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }(\bar {w},z)$
ending with repeated applications of ![]() ,
,
![]() $({\Rightarrow }\,\cdot )$
,
$({\Rightarrow }\,\cdot )$
,
![]() $({\Rightarrow }\,\mathrm {e})$
, and
$({\Rightarrow }\,\mathrm {e})$
, and
![]() $(\mathrm {f}\,{\Rightarrow })$
, followed by an application of
$(\mathrm {f}\,{\Rightarrow })$
, followed by an application of
![]() $(\to {\Rightarrow })$
, such that
$(\to {\Rightarrow })$
, such that
![]() ${\mathrm {md}}(d_1)={\mathrm {md}}(d)$
and
${\mathrm {md}}(d_1)={\mathrm {md}}(d)$
and
![]() ${\mathrm {md}}(d_2)=0$
.
${\mathrm {md}}(d_2)=0$
.
For the base cases where d ends with ![]() ,
,
![]() $({\Rightarrow }\,\mathrm {e})$
, or
$({\Rightarrow }\,\mathrm {e})$
, or
![]() $(\mathrm {f}\,{\Rightarrow })$
, either y does not occur in
$(\mathrm {f}\,{\Rightarrow })$
, either y does not occur in
![]() $\mathrm {\Gamma }$
or z does not occur in
$\mathrm {\Gamma }$
or z does not occur in
![]() $\Pi ,\mathrm {\Delta }$
. For the remainder of the proof, let us assume that y occurs in
$\Pi ,\mathrm {\Delta }$
. For the remainder of the proof, let us assume that y occurs in
![]() $\mathrm {\Gamma }$
and z occurs in
$\mathrm {\Gamma }$
and z occurs in
![]() $\Pi ,\mathrm {\Delta }$
. The cases where d ends with an operational rule for one of the propositional connectives are all straightforward, so let us just consider
$\Pi ,\mathrm {\Delta }$
. The cases where d ends with an operational rule for one of the propositional connectives are all straightforward, so let us just consider
![]() $(\to {\Rightarrow })$
as an example.
$(\to {\Rightarrow })$
as an example.
Suppose for the first subcase that
![]() $\mathrm {\Gamma }(\bar {w},y)$
is
$\mathrm {\Gamma }(\bar {w},y)$
is
![]() $\mathrm {\Gamma }_1(\bar {w},y),\mathrm {\Gamma }_2(\bar {w},y),\varphi (\bar {w},y)\to \psi (\bar {w},y)$
and
$\mathrm {\Gamma }_1(\bar {w},y),\mathrm {\Gamma }_2(\bar {w},y),\varphi (\bar {w},y)\to \psi (\bar {w},y)$
and
![]() $\Pi (\bar {w},z)$
is
$\Pi (\bar {w},z)$
is
![]() $\Pi _1(\bar {w},z),\Pi _2(\bar {w},z)$
, and
$\Pi _1(\bar {w},z),\Pi _2(\bar {w},z)$
, and
 $$ \begin{align*} d^{\prime}_1&\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}_1(\bar{w},y),\Pi_1(\bar{w},z){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\varphi(\bar{w},y),\\ d^{\prime}_2&\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}_2(\bar{w},y),\psi(\bar{w},y),\Pi_2(\bar{w},z){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z), \end{align*} $$
$$ \begin{align*} d^{\prime}_1&\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}_1(\bar{w},y),\Pi_1(\bar{w},z){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\varphi(\bar{w},y),\\ d^{\prime}_2&\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}_2(\bar{w},y),\psi(\bar{w},y),\Pi_2(\bar{w},z){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z), \end{align*} $$
where ![]() . Two applications of the induction hypothesis produce
. Two applications of the induction hypothesis produce
![]() $\chi _1(\bar {w}),\chi _2(\bar {w})\in \mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
and derivations
$\chi _1(\bar {w}),\chi _2(\bar {w})\in \mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
and derivations
![]() $d^{\prime }_{11},d^{\prime }_{12},d^{\prime }_{21},d^{\prime }_{22}$
such that
$d^{\prime }_{11},d^{\prime }_{12},d^{\prime }_{21},d^{\prime }_{22}$
such that ![]() ,
, ![]() , and
, and
 $$ \begin{align*} d^{\prime}_{11}\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}_1(\bar{w},y),\chi_1(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\varphi(\bar{w},y), & \quad d^{\prime}_{12}\vdash_{_{\mathrm{\forall1FL_e}}}\Pi_1(\bar{w},z){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi_1(\bar{w}),\\ d^{\prime}_{21}\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}_2(\bar{w},y),\psi(\bar{w},y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi_2(\bar{w}), & \quad d^{\prime}_{22}\vdash_{_{\mathrm{\forall1FL_e}}}\Pi_2(\bar{w},z),\chi_2(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z). \end{align*} $$
$$ \begin{align*} d^{\prime}_{11}\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}_1(\bar{w},y),\chi_1(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\varphi(\bar{w},y), & \quad d^{\prime}_{12}\vdash_{_{\mathrm{\forall1FL_e}}}\Pi_1(\bar{w},z){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi_1(\bar{w}),\\ d^{\prime}_{21}\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}_2(\bar{w},y),\psi(\bar{w},y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi_2(\bar{w}), & \quad d^{\prime}_{22}\vdash_{_{\mathrm{\forall1FL_e}}}\Pi_2(\bar{w},z),\chi_2(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z). \end{align*} $$
Let
![]() $\chi (\bar {w}):=\chi _1(\bar {w})\to \chi _2(\bar {w})$
. Then
$\chi (\bar {w}):=\chi _1(\bar {w})\to \chi _2(\bar {w})$
. Then
![]() $d^{\prime }_{11}$
and
$d^{\prime }_{11}$
and
![]() $d^{\prime }_{21}$
, together with applications of
$d^{\prime }_{21}$
, together with applications of
![]() $(\to {\Rightarrow })$
and
$(\to {\Rightarrow })$
and
![]() $({\Rightarrow }\to )$
, and
$({\Rightarrow }\to )$
, and
![]() $d^{\prime }_{12}$
and
$d^{\prime }_{12}$
and
![]() $d^{\prime }_{22}$
, together with an application of
$d^{\prime }_{22}$
, together with an application of
![]() $(\to {\Rightarrow })$
, yield derivations
$(\to {\Rightarrow })$
, yield derivations
![]() $d_1$
and
$d_1$
and
![]() $d_2$
, respectively, such that
$d_2$
, respectively, such that ![]() and
and
 $$ \begin{align*} & d_{1}\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}_1(\bar{w},y),\mathrm{\Gamma}_2(\bar{w},y),\varphi(\bar{w},y)\to\psi(\bar{w},y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi(\bar{w}),\\ & d_{2}\vdash_{_{\mathrm{\forall1FL_e}}}\Pi_1(\bar{w},z),\Pi_2(\bar{w},z),\chi(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z). \end{align*} $$
$$ \begin{align*} & d_{1}\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}_1(\bar{w},y),\mathrm{\Gamma}_2(\bar{w},y),\varphi(\bar{w},y)\to\psi(\bar{w},y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi(\bar{w}),\\ & d_{2}\vdash_{_{\mathrm{\forall1FL_e}}}\Pi_1(\bar{w},z),\Pi_2(\bar{w},z),\chi(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z). \end{align*} $$
For the second subcase, suppose that
![]() $\mathrm {\Gamma }(\bar {w},y)$
is
$\mathrm {\Gamma }(\bar {w},y)$
is
![]() $\mathrm {\Gamma }_1(\bar {w},y),\mathrm {\Gamma }_2(\bar {w},y)$
and
$\mathrm {\Gamma }_1(\bar {w},y),\mathrm {\Gamma }_2(\bar {w},y)$
and
![]() $\Pi (\bar {w},z)$
is
$\Pi (\bar {w},z)$
is
![]() $\Pi _1(\bar {w},z),\Pi _2(\bar {w},z),\varphi (\bar {w},z)\to \psi (\bar {w},z)$
, and
$\Pi _1(\bar {w},z),\Pi _2(\bar {w},z),\varphi (\bar {w},z)\to \psi (\bar {w},z)$
, and
 $$ \begin{align*} d^{\prime}_1&\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}_1(\bar{w},y),\Pi_1(\bar{w},z){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\varphi(\bar{w},z),\\ d^{\prime}_2&\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}_2(\bar{w},y),\Pi_2(\bar{w},z),\psi(\bar{w},z){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z), \end{align*} $$
$$ \begin{align*} d^{\prime}_1&\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}_1(\bar{w},y),\Pi_1(\bar{w},z){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\varphi(\bar{w},z),\\ d^{\prime}_2&\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}_2(\bar{w},y),\Pi_2(\bar{w},z),\psi(\bar{w},z){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z), \end{align*} $$
where ![]() . Two applications of the induction hypothesis produce
. Two applications of the induction hypothesis produce
![]() $\chi _1(\bar {w}),\chi _2(\bar {w})\in \mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
and derivations
$\chi _1(\bar {w}),\chi _2(\bar {w})\in \mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
and derivations
![]() $d^{\prime }_{11},d^{\prime }_{12},d^{\prime }_{21},d^{\prime }_{22}$
such that
$d^{\prime }_{11},d^{\prime }_{12},d^{\prime }_{21},d^{\prime }_{22}$
such that ![]() ,
, ![]() , and
, and
 $$ \begin{align*} d^{\prime}_{11}\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}_1(\bar{w},y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi_1(\bar{w}), & \quad d^{\prime}_{12}\vdash_{_{\mathrm{\forall1FL_e}}}\Pi_1(\bar{w},z),\chi_1(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\varphi(\bar{w},z),\\ d^{\prime}_{21}\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}_2(\bar{w},y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi_2(\bar{w}), & \quad d^{\prime}_{22}\vdash_{_{\mathrm{\forall1FL_e}}}\Pi_2(\bar{w},z),\psi(\bar{w},z),\chi_2(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z). \end{align*} $$
$$ \begin{align*} d^{\prime}_{11}\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}_1(\bar{w},y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi_1(\bar{w}), & \quad d^{\prime}_{12}\vdash_{_{\mathrm{\forall1FL_e}}}\Pi_1(\bar{w},z),\chi_1(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\varphi(\bar{w},z),\\ d^{\prime}_{21}\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}_2(\bar{w},y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi_2(\bar{w}), & \quad d^{\prime}_{22}\vdash_{_{\mathrm{\forall1FL_e}}}\Pi_2(\bar{w},z),\psi(\bar{w},z),\chi_2(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z). \end{align*} $$
Let
![]() $\chi (\bar {w}):=\chi _1(\bar {w})\cdot \chi _2(\bar {w})$
. Then
$\chi (\bar {w}):=\chi _1(\bar {w})\cdot \chi _2(\bar {w})$
. Then
![]() $d^{\prime }_{11}$
and
$d^{\prime }_{11}$
and
![]() $d^{\prime }_{21}$
, together with an application of
$d^{\prime }_{21}$
, together with an application of
![]() $({\Rightarrow }\,\cdot )$
, and
$({\Rightarrow }\,\cdot )$
, and
![]() $d^{\prime }_{12}$
and
$d^{\prime }_{12}$
and
![]() $d^{\prime }_{22}$
, together with applications of
$d^{\prime }_{22}$
, together with applications of
![]() $(\to {\Rightarrow })$
and
$(\to {\Rightarrow })$
and
![]() $(\cdot \,{\Rightarrow })$
, yield derivations
$(\cdot \,{\Rightarrow })$
, yield derivations
![]() $d_1$
and
$d_1$
and
![]() $d_2$
, respectively, such that
$d_2$
, respectively, such that ![]() and
and
 $$ \begin{align*} & d_{1}\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}_1(\bar{w},y),\mathrm{\Gamma}_2(\bar{w},y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi(\bar{w}),\\ & d_{2}\vdash_{_{\mathrm{\forall1FL_e}}}\Pi_1(\bar{w},z),\Pi_2(\bar{w},z),\varphi(\bar{w},z)\to\psi(\bar{w},z),\chi(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z). \end{align*} $$
$$ \begin{align*} & d_{1}\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}_1(\bar{w},y),\mathrm{\Gamma}_2(\bar{w},y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi(\bar{w}),\\ & d_{2}\vdash_{_{\mathrm{\forall1FL_e}}}\Pi_1(\bar{w},z),\Pi_2(\bar{w},z),\varphi(\bar{w},z)\to\psi(\bar{w},z),\chi(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z). \end{align*} $$
Next, we consider all the cases where d ends with an application of one of the quantifier rules.
-
•
 $({\forall \,{\Rightarrow }})$
: Suppose first that
$({\forall \,{\Rightarrow }})$
: Suppose first that
 $\mathrm {\Gamma }(\bar {w},y)$
is
$\mathrm {\Gamma }(\bar {w},y)$
is
 $\mathrm {\Gamma }'(\bar {w},y),(\forall {x})\varphi (x)$
and where
$\mathrm {\Gamma }'(\bar {w},y),(\forall {x})\varphi (x)$
and where $$ \begin{align*} d'\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}'(\bar{w},y),\varphi(u),\Pi(\bar{w},z){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z), \end{align*} $$
$$ \begin{align*} d'\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}'(\bar{w},y),\varphi(u),\Pi(\bar{w},z){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z), \end{align*} $$
 ${\mathrm {md}}(d')={\mathrm {md}}(d)$
and, using the assumption that no other variable lies in the scope of a quantifier, x is the only variable occurring in
${\mathrm {md}}(d')={\mathrm {md}}(d)$
and, using the assumption that no other variable lies in the scope of a quantifier, x is the only variable occurring in
 $\varphi $
. Since y occurs in
$\varphi $
. Since y occurs in
 $\mathrm {\Gamma }$
and z occurs in
$\mathrm {\Gamma }$
and z occurs in
 $\Pi ,\mathrm {\Delta }$
, it follows from side-condition (i) for
$\Pi ,\mathrm {\Delta }$
, it follows from side-condition (i) for
 $({\forall \,{\Rightarrow }})$
that
$({\forall \,{\Rightarrow }})$
that
 $u\in \bar {w}\cup \{y,z\}$
. For the first subcase, suppose that
$u\in \bar {w}\cup \{y,z\}$
. For the first subcase, suppose that
 $u\in \bar {w}\cup \{y\}$
. An application of the induction hypothesis produces
$u\in \bar {w}\cup \{y\}$
. An application of the induction hypothesis produces
 $\chi (\bar {w})\in \mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
and derivations
$\chi (\bar {w})\in \mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
and derivations
 $d_1',d_2$
such that
$d_1',d_2$
such that  and
If u occurs in
and
If u occurs in $$ \begin{align*} d_1'\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}'(\bar{w},y),\varphi(u){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi(\bar{w}),\quad d_2\vdash_{_{\mathrm{\forall1FL_e}}}\Pi(\bar{w},z),\chi(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z). \end{align*} $$
$$ \begin{align*} d_1'\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}'(\bar{w},y),\varphi(u){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi(\bar{w}),\quad d_2\vdash_{_{\mathrm{\forall1FL_e}}}\Pi(\bar{w},z),\chi(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z). \end{align*} $$
 $\mathrm {\Gamma }'(\bar {w},y),\chi (\bar {w})$
, then extending
$\mathrm {\Gamma }'(\bar {w},y),\chi (\bar {w})$
, then extending
 $d_1'$
with an application of
$d_1'$
with an application of
 $({\forall \,{\Rightarrow }})$
yields a derivation
$({\forall \,{\Rightarrow }})$
yields a derivation
 $d_1$
such that
$d_1$
such that  and Otherwise, by substituting u uniformly with y in
and Otherwise, by substituting u uniformly with y in $$ \begin{align*} d_1\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}'(\bar{w},y),(\forall{x})\varphi(x){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi(\bar{w}). \end{align*} $$
$$ \begin{align*} d_1\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}'(\bar{w},y),(\forall{x})\varphi(x){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi(\bar{w}). \end{align*} $$
 $d_1'$
, we obtain a derivation of
$d_1'$
, we obtain a derivation of
 $\mathrm {\Gamma }'(\bar {w},y),\varphi (y){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\chi (\bar {w})$
and obtain
$\mathrm {\Gamma }'(\bar {w},y),\varphi (y){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\chi (\bar {w})$
and obtain
 $d_1$
as described previously.
$d_1$
as described previously.
For the second subcase, consider
 $u=z$
. An application of the induction hypothesis produces
$u=z$
. An application of the induction hypothesis produces
 $\chi '(\bar {w})\in \mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
and derivations
$\chi '(\bar {w})\in \mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
and derivations
 $d_1',d_2'$
such that
$d_1',d_2'$
such that  and
Let
and
Let $$ \begin{align*} d_1'\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}'(\bar{w},y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi'(\bar{w}), \quad d_2'\vdash_{_{\mathrm{\forall1FL_e}}}\varphi(z),\Pi(\bar{w},z),\chi'(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z). \end{align*} $$
$$ \begin{align*} d_1'\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}'(\bar{w},y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi'(\bar{w}), \quad d_2'\vdash_{_{\mathrm{\forall1FL_e}}}\varphi(z),\Pi(\bar{w},z),\chi'(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z). \end{align*} $$
 . Combining an instance
. Combining an instance
 $(\forall {x})\varphi (x)\vphantom {A}\Rightarrow {\vphantom {A}}(\forall {x})\varphi (x)$
of
$(\forall {x})\varphi (x)\vphantom {A}\Rightarrow {\vphantom {A}}(\forall {x})\varphi (x)$
of  with
with
 $d_1'$
and an application of
$d_1'$
and an application of
 $({\Rightarrow }\,\cdot )$
yields a derivation
$({\Rightarrow }\,\cdot )$
yields a derivation
 $d_1$
such that
$d_1$
such that  and Also,
and Also, $$ \begin{align*} d_1\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}'(\bar{w},y),(\forall{x})\varphi(x){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi(\bar{w}). \end{align*} $$
$$ \begin{align*} d_1\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}'(\bar{w},y),(\forall{x})\varphi(x){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi(\bar{w}). \end{align*} $$
 $d_2'$
extended with applications of
$d_2'$
extended with applications of
 $({\forall \,{\Rightarrow }})$
and
$({\forall \,{\Rightarrow }})$
and
 $(\cdot \,{\Rightarrow })$
yields a derivation
$(\cdot \,{\Rightarrow })$
yields a derivation
 $d_2$
such that
$d_2$
such that  and Suppose next that
and Suppose next that $$ \begin{align*} d_2\vdash_{_{\mathrm{\forall1FL_e}}}\Pi(\bar{w},z),\chi(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z). \end{align*} $$
$$ \begin{align*} d_2\vdash_{_{\mathrm{\forall1FL_e}}}\Pi(\bar{w},z),\chi(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z). \end{align*} $$
 $\Pi (\bar {w},z)$
is
$\Pi (\bar {w},z)$
is
 $\Pi '(\bar {w},z),(\forall {x})\varphi (x)$
and where
$\Pi '(\bar {w},z),(\forall {x})\varphi (x)$
and where $$ \begin{align*} d'\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}(\bar{w},y),\Pi'(\bar{w},z),\varphi(u){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z), \end{align*} $$
$$ \begin{align*} d'\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}(\bar{w},y),\Pi'(\bar{w},z),\varphi(u){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z), \end{align*} $$
 ${\mathrm {md}}(d')={\mathrm {md}}(d)$
and x is the only variable occurring in
${\mathrm {md}}(d')={\mathrm {md}}(d)$
and x is the only variable occurring in
 $\varphi $
. Since y occurs in
$\varphi $
. Since y occurs in
 $\mathrm {\Gamma }$
and z occurs in
$\mathrm {\Gamma }$
and z occurs in
 $\Pi ,\mathrm {\Delta }$
, it follows from side-condition (i) for
$\Pi ,\mathrm {\Delta }$
, it follows from side-condition (i) for
 $({\forall \,{\Rightarrow }})$
that
$({\forall \,{\Rightarrow }})$
that
 $u\in \bar {w}\cup \{y,z\}$
. The case of
$u\in \bar {w}\cup \{y,z\}$
. The case of
 $u\in \bar {w}\cup \{z\}$
is very similar to the first subcase above, so consider
$u\in \bar {w}\cup \{z\}$
is very similar to the first subcase above, so consider
 $u=y$
. An application of the induction hypothesis produces
$u=y$
. An application of the induction hypothesis produces
 $\chi '(\bar {w})\in \mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
and derivations
$\chi '(\bar {w})\in \mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
and derivations
 $d_1',d_2'$
such that
$d_1',d_2'$
such that  and
Let
and
Let $$ \begin{align*} d_1'\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}(\bar{w},y),\varphi(y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi'(\bar{w}),\quad d_2'\vdash_{_{\mathrm{\forall1FL_e}}}\Pi'(\bar{w},z),\chi'(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z). \end{align*} $$
$$ \begin{align*} d_1'\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}(\bar{w},y),\varphi(y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi'(\bar{w}),\quad d_2'\vdash_{_{\mathrm{\forall1FL_e}}}\Pi'(\bar{w},z),\chi'(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z). \end{align*} $$
 . Extending
. Extending
 $d_1'$
with applications of
$d_1'$
with applications of
 $({\forall \,{\Rightarrow }})$
and
$({\forall \,{\Rightarrow }})$
and
 $({\Rightarrow }\to )$
yields a derivation
$({\Rightarrow }\to )$
yields a derivation
 $d_1$
such that
$d_1$
such that  and Also,
and Also, $$ \begin{align*} d_1\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}(\bar{w},y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi(\bar{w}). \end{align*} $$
$$ \begin{align*} d_1\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}(\bar{w},y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi(\bar{w}). \end{align*} $$
 $d_2'$
and an instance
$d_2'$
and an instance
 $(\forall {x})\varphi (x){{\vphantom {A}\Rightarrow {\vphantom {A}}}}(\forall {x})\varphi (x)$
of
$(\forall {x})\varphi (x){{\vphantom {A}\Rightarrow {\vphantom {A}}}}(\forall {x})\varphi (x)$
of  combined with an application of
combined with an application of
 $(\to {\Rightarrow })$
yield a derivation
$(\to {\Rightarrow })$
yield a derivation
 $d_2$
such that
$d_2$
such that  and
and  $$ \begin{align*} d_2\vdash_{_{\mathrm{\forall1FL_e}}}\Pi'(\bar{w},z),(\forall{x})\varphi(x),\chi(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z). \end{align*} $$
$$ \begin{align*} d_2\vdash_{_{\mathrm{\forall1FL_e}}}\Pi'(\bar{w},z),(\forall{x})\varphi(x),\chi(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z). \end{align*} $$
-
•
 $({\Rightarrow }\,\forall )$
: Suppose that
$({\Rightarrow }\,\forall )$
: Suppose that
 $\mathrm {\Delta }(\bar {w},z)$
is
$\mathrm {\Delta }(\bar {w},z)$
is
 $(\forall {x})\varphi (x)$
and for some variable u that does not occur freely in
$(\forall {x})\varphi (x)$
and for some variable u that does not occur freely in
 $\mathrm {\Gamma }(\bar {w},y),\Pi (\bar {w},z){{\vphantom {A}\Rightarrow {\vphantom {A}}}}(\forall {x})\varphi (x)$
, where
$\mathrm {\Gamma }(\bar {w},y),\Pi (\bar {w},z){{\vphantom {A}\Rightarrow {\vphantom {A}}}}(\forall {x})\varphi (x)$
, where $$ \begin{align*} d'\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}(\bar{w},y),\Pi(\bar{w},z){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\varphi(u), \end{align*} $$
$$ \begin{align*} d'\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}(\bar{w},y),\Pi(\bar{w},z){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\varphi(u), \end{align*} $$
 ${\mathrm {md}}(d')={\mathrm {md}}(d)-1$
and x is the only variable occurring in
${\mathrm {md}}(d')={\mathrm {md}}(d)-1$
and x is the only variable occurring in
 $\varphi $
. An application of the induction hypothesis produces
$\varphi $
. An application of the induction hypothesis produces
 $\chi '(\bar {w},u)\in \mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
and derivations
$\chi '(\bar {w},u)\in \mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
and derivations
 $d^{\prime }_{1},d^{\prime }_{2}$
such that
$d^{\prime }_{1},d^{\prime }_{2}$
such that  and Let
and Let $$ \begin{align*} d_1'\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}(\bar{w},y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi'(\bar{w},u),\quad d^{\prime}_2\vdash_{_{\mathrm{\forall1FL_e}}}\Pi(\bar{w},z),\chi'(\bar{w},u){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\varphi(u). \end{align*} $$
$$ \begin{align*} d_1'\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}(\bar{w},y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi'(\bar{w},u),\quad d^{\prime}_2\vdash_{_{\mathrm{\forall1FL_e}}}\Pi(\bar{w},z),\chi'(\bar{w},u){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\varphi(u). \end{align*} $$
 . Extending
. Extending
 $d_1'$
with an application of
$d_1'$
with an application of
 $({\Rightarrow }\,\forall )$
yields a derivation
$({\Rightarrow }\,\forall )$
yields a derivation
 $d_1$
such that
$d_1$
such that  and Also, extending
and Also, extending $$ \begin{align*} d_1\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}(\bar{w},y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi(\bar{w}). \end{align*} $$
$$ \begin{align*} d_1\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}(\bar{w},y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi(\bar{w}). \end{align*} $$
 $d_2'$
with applications of
$d_2'$
with applications of
 $({\forall \,{\Rightarrow }})$
and
$({\forall \,{\Rightarrow }})$
and
 $({\Rightarrow }\,\forall )$
yield a derivation
$({\Rightarrow }\,\forall )$
yield a derivation
 $d_2$
such that
$d_2$
such that  and
and  $$ \begin{align*} d_2\vdash_{_{\mathrm{\forall1FL_e}}}\Pi(\bar{w},z),\chi(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}(\forall{x})\varphi(x). \end{align*} $$
$$ \begin{align*} d_2\vdash_{_{\mathrm{\forall1FL_e}}}\Pi(\bar{w},z),\chi(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}(\forall{x})\varphi(x). \end{align*} $$
-
•
 $({\Rightarrow }\,\exists )$
: Suppose that
$({\Rightarrow }\,\exists )$
: Suppose that
 $\mathrm {\Delta }(\bar {w},z)$
is
$\mathrm {\Delta }(\bar {w},z)$
is
 $(\exists {x})\varphi (x)$
and where
$(\exists {x})\varphi (x)$
and where $$ \begin{align*} d'\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}(\bar{w},y),\Pi(\bar{w},z){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\varphi(u), \end{align*} $$
$$ \begin{align*} d'\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}(\bar{w},y),\Pi(\bar{w},z){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\varphi(u), \end{align*} $$
 ${\mathrm {md}}(d')={\mathrm {md}}(d)$
and x is the only variable occurring in
${\mathrm {md}}(d')={\mathrm {md}}(d)$
and x is the only variable occurring in
 $\varphi $
. Since y occurs in
$\varphi $
. Since y occurs in
 $\mathrm {\Gamma }$
and z occurs in
$\mathrm {\Gamma }$
and z occurs in
 $\Pi ,\mathrm {\Delta }$
, it follows from side-condition (i) for
$\Pi ,\mathrm {\Delta }$
, it follows from side-condition (i) for
 $({\Rightarrow }\,\exists )$
that
$({\Rightarrow }\,\exists )$
that
 $u\in \bar {w}\cup \{y,z\}$
. For the first subcase, suppose that
$u\in \bar {w}\cup \{y,z\}$
. For the first subcase, suppose that
 $u\in \bar {w}\cup \{z\}$
. An application of the induction hypothesis produces
$u\in \bar {w}\cup \{z\}$
. An application of the induction hypothesis produces
 $\chi (\bar {w})\in \mathrm { Fm}_{\forall }^{1+}(\mathcal {L}_s)$
and derivations
$\chi (\bar {w})\in \mathrm { Fm}_{\forall }^{1+}(\mathcal {L}_s)$
and derivations
 $d_1,d_2'$
such that
$d_1,d_2'$
such that  and If u occurs in
and If u occurs in $$ \begin{align*} d_1\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}(\bar{w},y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi(\bar{w}),\quad d_2'\vdash_{_{\mathrm{\forall1FL_e}}}\Pi(\bar{w},z),\chi(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\varphi(u). \end{align*} $$
$$ \begin{align*} d_1\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}(\bar{w},y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi(\bar{w}),\quad d_2'\vdash_{_{\mathrm{\forall1FL_e}}}\Pi(\bar{w},z),\chi(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\varphi(u). \end{align*} $$
 $\Pi (\bar {w},z),\chi (\bar {w})$
, then extending
$\Pi (\bar {w},z),\chi (\bar {w})$
, then extending
 $d_2'$
with an application of
$d_2'$
with an application of
 $({\Rightarrow }\,\exists )$
yields a derivation
$({\Rightarrow }\,\exists )$
yields a derivation
 $d_2$
such that
$d_2$
such that  and Otherwise, by substituting u uniformly with z in
and Otherwise, by substituting u uniformly with z in $$ \begin{align*} d_2\vdash_{_{\mathrm{\forall1FL_e}}}\Pi(\bar{w},z),\chi(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}(\exists{x})\varphi(x). \end{align*} $$
$$ \begin{align*} d_2\vdash_{_{\mathrm{\forall1FL_e}}}\Pi(\bar{w},z),\chi(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}(\exists{x})\varphi(x). \end{align*} $$
 $d_2'$
, we obtain a derivation of
$d_2'$
, we obtain a derivation of
 $\Pi (\bar {w},z),\chi (\bar {w}){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\varphi (z)$
and obtain
$\Pi (\bar {w},z),\chi (\bar {w}){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\varphi (z)$
and obtain
 $d_2$
as described previously.
$d_2$
as described previously.
For the second subcase, consider
 $u=y$
. An application of the induction hypothesis produces
$u=y$
. An application of the induction hypothesis produces
 $\chi '(\bar {w})\in \mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
and derivations
$\chi '(\bar {w})\in \mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
and derivations
 $d_1',d_2'$
such that
$d_1',d_2'$
such that  and Let
and Let $$ \begin{align*} d_1'\vdash_{_{\mathrm{\forall1FL_e}}}\Pi(\bar{w},z){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi'(\bar{w}),\quad d_2'\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}(\bar{w},y),\chi'(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\varphi(y). \end{align*} $$
$$ \begin{align*} d_1'\vdash_{_{\mathrm{\forall1FL_e}}}\Pi(\bar{w},z){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi'(\bar{w}),\quad d_2'\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}(\bar{w},y),\chi'(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\varphi(y). \end{align*} $$
 . Combining
. Combining
 $d_2'$
with applications of
$d_2'$
with applications of
 $({\Rightarrow }\,\exists )$
and
$({\Rightarrow }\,\exists )$
and
 $({\Rightarrow }\to )$
yields a derivation
$({\Rightarrow }\to )$
yields a derivation
 $d_1$
such that
$d_1$
such that  and Also, combining the instance
and Also, combining the instance $$ \begin{align*} d_1\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}(\bar{w},y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi(\bar{w}). \end{align*} $$
$$ \begin{align*} d_1\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}(\bar{w},y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi(\bar{w}). \end{align*} $$
 $(\exists {x})\varphi (x){{\vphantom {A}\Rightarrow {\vphantom {A}}}}(\exists {x})\varphi (x)$
of
$(\exists {x})\varphi (x){{\vphantom {A}\Rightarrow {\vphantom {A}}}}(\exists {x})\varphi (x)$
of  and
and
 $d_1'$
with
$d_1'$
with
 $(\to {\Rightarrow })$
yields a derivation
$(\to {\Rightarrow })$
yields a derivation
 $d_2$
such that
$d_2$
such that  and
and  $$ \begin{align*} d_2\vdash_{_{\mathrm{\forall1FL_e}}}\Pi(\bar{w},z),\chi(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}(\exists{x})\varphi(x). \end{align*} $$
$$ \begin{align*} d_2\vdash_{_{\mathrm{\forall1FL_e}}}\Pi(\bar{w},z),\chi(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}(\exists{x})\varphi(x). \end{align*} $$
-
•
 $(\exists \,{\Rightarrow })$
: Suppose first that
$(\exists \,{\Rightarrow })$
: Suppose first that
 $\mathrm {\Gamma }(\bar {w},y)$
is
$\mathrm {\Gamma }(\bar {w},y)$
is
 $\mathrm {\Gamma }'(\bar {w},y),(\exists {x})\varphi (x)$
and for some variable u that does not occur freely in
$\mathrm {\Gamma }'(\bar {w},y),(\exists {x})\varphi (x)$
and for some variable u that does not occur freely in
 $\mathrm {\Gamma }(\bar {w},y),\Pi (\bar {w},z){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }(\bar {w},z)$
, where
$\mathrm {\Gamma }(\bar {w},y),\Pi (\bar {w},z){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }(\bar {w},z)$
, where $$ \begin{align*} d'\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}'(\bar{w},y),\varphi(u),\Pi(\bar{w},z){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z), \end{align*} $$
$$ \begin{align*} d'\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}'(\bar{w},y),\varphi(u),\Pi(\bar{w},z){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z), \end{align*} $$
 ${\mathrm {md}}(d')={\mathrm {md}}(d)-1$
and x is the only variable occurring in
${\mathrm {md}}(d')={\mathrm {md}}(d)-1$
and x is the only variable occurring in
 $\varphi $
. An application of the induction hypothesis produces
$\varphi $
. An application of the induction hypothesis produces
 $\chi '(\bar {w},u)\in \mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
and derivations
$\chi '(\bar {w},u)\in \mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
and derivations
 $d_1',d_2'$
such that
$d_1',d_2'$
such that  and
Let
and
Let $$ \begin{align*} d_1'\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}'(\bar{w},y),\varphi(u){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi'(\bar{w},u),\quad \!d_2'\vdash_{_{\mathrm{\forall1FL_e}}}\Pi(\bar{w},z),\chi'(\bar{w},u){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z). \end{align*} $$
$$ \begin{align*} d_1'\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}'(\bar{w},y),\varphi(u){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi'(\bar{w},u),\quad \!d_2'\vdash_{_{\mathrm{\forall1FL_e}}}\Pi(\bar{w},z),\chi'(\bar{w},u){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z). \end{align*} $$
 . Combining
. Combining
 $d^{\prime }_1$
with applications of
$d^{\prime }_1$
with applications of
 $({\Rightarrow }\,\exists )$
and
$({\Rightarrow }\,\exists )$
and
 $(\exists \,{\Rightarrow })$
yields a derivation
$(\exists \,{\Rightarrow })$
yields a derivation
 $d_1$
such that
$d_1$
such that  and Also, extending
and Also, extending $$ \begin{align*} d_1\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}'(\bar{w},y),(\exists{x})\varphi(x){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi(\bar{w}). \end{align*} $$
$$ \begin{align*} d_1\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}'(\bar{w},y),(\exists{x})\varphi(x){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi(\bar{w}). \end{align*} $$
 $d_2'$
with an application of
$d_2'$
with an application of
 $(\exists \,{\Rightarrow })$
yields a derivation
$(\exists \,{\Rightarrow })$
yields a derivation
 $d_2$
such that
$d_2$
such that  and Now suppose that
and Now suppose that $$ \begin{align*} d_2\vdash_{_{\mathrm{\forall1FL_e}}}\Pi(\bar{w},z),\chi(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z). \end{align*} $$
$$ \begin{align*} d_2\vdash_{_{\mathrm{\forall1FL_e}}}\Pi(\bar{w},z),\chi(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z). \end{align*} $$
 $\Pi (\bar {w},z)$
is
$\Pi (\bar {w},z)$
is
 $\Pi '(\bar {w},z),(\exists {x})\varphi (x)$
and for some variable u that does not occur freely in
$\Pi '(\bar {w},z),(\exists {x})\varphi (x)$
and for some variable u that does not occur freely in
 $\mathrm {\Gamma }(\bar {w},y),\Pi (\bar {w},z){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }(\bar {w},z)$
, where
$\mathrm {\Gamma }(\bar {w},y),\Pi (\bar {w},z){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }(\bar {w},z)$
, where $$ \begin{align*} d'\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}(\bar{w},y),\Pi'(\bar{w},z),\varphi(u){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z), \end{align*} $$
$$ \begin{align*} d'\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}(\bar{w},y),\Pi'(\bar{w},z),\varphi(u){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z), \end{align*} $$
 ${\mathrm {md}}(d')={\mathrm {md}}(d)-1$
and x is the only variable occurring in
${\mathrm {md}}(d')={\mathrm {md}}(d)-1$
and x is the only variable occurring in
 $\varphi $
. An application of the induction hypothesis produces
$\varphi $
. An application of the induction hypothesis produces
 $\chi '(\bar {w},u)\in \mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
and derivations
$\chi '(\bar {w},u)\in \mathrm {Fm}_{\forall }^{1+}(\mathcal {L}_s)$
and derivations
 $d_1',d_2'$
such that
$d_1',d_2'$
such that  and
Let
and
Let $$ \begin{align*} d_1'\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}(\bar{w},y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi'(\bar{w},u),\quad d_2'\vdash_{_{\mathrm{\forall1FL_e}}}\Pi'(\bar{w},z),\varphi(u),\chi'(\bar{w},u){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z). \end{align*} $$
$$ \begin{align*} d_1'\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}(\bar{w},y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi'(\bar{w},u),\quad d_2'\vdash_{_{\mathrm{\forall1FL_e}}}\Pi'(\bar{w},z),\varphi(u),\chi'(\bar{w},u){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z). \end{align*} $$
 . The derivation
. The derivation
 $d_1'$
together with an application of
$d_1'$
together with an application of
 $({\Rightarrow }\,\forall )$
yields a derivation
$({\Rightarrow }\,\forall )$
yields a derivation
 $d_1$
such that
$d_1$
such that  and Also,
and Also, $$ \begin{align*} d_1\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}(\bar{w},y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi(\bar{w}). \end{align*} $$
$$ \begin{align*} d_1\vdash_{_{\mathrm{\forall1FL_e}}}\mathrm{\Gamma}(\bar{w},y){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\chi(\bar{w}). \end{align*} $$
 $d_2'$
together with applications of
$d_2'$
together with applications of
 $({\forall \,{\Rightarrow }})$
and
$({\forall \,{\Rightarrow }})$
and
 $(\exists \,{\Rightarrow })$
yields a derivation
$(\exists \,{\Rightarrow })$
yields a derivation
 $d_2$
such that
$d_2$
such that  and
and  $$ \begin{align*}d_2\vdash_{_{\mathrm{\forall1FL_e}}}\Pi(\bar{w},y),(\exists{x})\varphi(x),\chi(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z).\\[-42pt]\end{align*} $$
$$ \begin{align*}d_2\vdash_{_{\mathrm{\forall1FL_e}}}\Pi(\bar{w},y),(\exists{x})\varphi(x),\chi(\bar{w}){{\vphantom{A}\Rightarrow{\vphantom{A}}}}\mathrm{\Delta}(\bar{w},z).\\[-42pt]\end{align*} $$
Using this lemma we can now reprove, by proof-theoretic means, the special case of Corollary 4.2 for the variety
![]() $\mathsf {FL_e}$
.
$\mathsf {FL_e}$
.
Theorem 5.3. For any set
![]() $T\cup \{\varphi \approx \psi \}$
of
$T\cup \{\varphi \approx \psi \}$
of
![]() $\mathrm {Fm}_{\forall }^{1}(\mathcal {L}_s)$
-equations,
$\mathrm {Fm}_{\forall }^{1}(\mathcal {L}_s)$
-equations,
Proof The right-to-left direction follows directly from Corollary 3.8. For the converse, note first that due to compactness and the local deduction theorem for
![]() $\vDash ^{\forall }_{\mathsf {V}}$
(see [Reference Cintula and Noguera11, Sections 4.6 and 4.8]), we can restrict to the case where
$\vDash ^{\forall }_{\mathsf {V}}$
(see [Reference Cintula and Noguera11, Sections 4.6 and 4.8]), we can restrict to the case where
![]() $T = \emptyset $
. Hence, by Proposition 5.1, it suffices to prove that for any sequent
$T = \emptyset $
. Hence, by Proposition 5.1, it suffices to prove that for any sequent
![]() $\mathrm {\Gamma }{{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }$
consisting only of formulas from
$\mathrm {\Gamma }{{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }$
consisting only of formulas from
![]() $\mathrm {Fm}_{\forall }^{1}(\mathcal {L}_s)$
,
$\mathrm {Fm}_{\forall }^{1}(\mathcal {L}_s)$
,
We proceed by induction on the lexicographically ordered pair ![]() , where
, where
![]() ${\mathrm {ht}}(d)$
is the height of the derivation d. The base cases are clear and the cases for the last application of a rule in d except
${\mathrm {ht}}(d)$
is the height of the derivation d. The base cases are clear and the cases for the last application of a rule in d except
![]() $({\Rightarrow }\,\forall )$
and
$({\Rightarrow }\,\forall )$
and
![]() $(\exists \,{\Rightarrow })$
all follow by applying the induction hypothesis and the equations defining
$(\exists \,{\Rightarrow })$
all follow by applying the induction hypothesis and the equations defining
![]() $\mathsf {mFL_e}$
. Just note that for each such application, the premises contain only formulas from
$\mathsf {mFL_e}$
. Just note that for each such application, the premises contain only formulas from
![]() $\mathrm {Fm}_{\forall }^{1}(\mathcal {L}_s)$
with at least one fewer symbol. In particular, for
$\mathrm {Fm}_{\forall }^{1}(\mathcal {L}_s)$
with at least one fewer symbol. In particular, for
![]() $({\forall \,{\Rightarrow }})$
and
$({\forall \,{\Rightarrow }})$
and
![]() $({\Rightarrow }\,\exists )$
, it can be assumed that the variable u occurring in the premise is x and the result follows using (L1
$({\Rightarrow }\,\exists )$
, it can be assumed that the variable u occurring in the premise is x and the result follows using (L1
![]() $_\Box $
) or (L1
$_\Box $
) or (L1
![]() $_\Diamond $
).
$_\Diamond $
).
Suppose now that the last rule applied in d is
![]() $({\Rightarrow }\,\forall )$
, where
$({\Rightarrow }\,\forall )$
, where
![]() $\mathrm {\Delta }$
is
$\mathrm {\Delta }$
is
![]() $(\forall {x})\psi (x)$
and x may occur freely in
$(\forall {x})\psi (x)$
and x may occur freely in
![]() $\mathrm {\Gamma }$
. Then
$\mathrm {\Gamma }$
. Then
![]() $d'\vdash _{_{\mathrm {\forall 1FL_e}}}\mathrm {\Gamma }{{\vphantom {A}\Rightarrow {\vphantom {A}}}}\psi (z)$
with
$d'\vdash _{_{\mathrm {\forall 1FL_e}}}\mathrm {\Gamma }{{\vphantom {A}\Rightarrow {\vphantom {A}}}}\psi (z)$
with
![]() ${\mathrm {md}}(d')={\mathrm {md}}(d)-1$
, where z is a variable distinct from x. We write
${\mathrm {md}}(d')={\mathrm {md}}(d)-1$
, where z is a variable distinct from x. We write
![]() $\mathrm {\Gamma }(y)$
and
$\mathrm {\Gamma }(y)$
and
![]() $d'(y)$
to denote
$d'(y)$
to denote
![]() $\mathrm {\Gamma }$
and
$\mathrm {\Gamma }$
and
![]() $d'$
with all free occurrences of x replaced by y. Clearly,
$d'$
with all free occurrences of x replaced by y. Clearly,
![]() $d'(y)\vdash _{_{\mathrm {\forall 1FL_e}}}\mathrm {\Gamma }(y){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\psi (z)$
with
$d'(y)\vdash _{_{\mathrm {\forall 1FL_e}}}\mathrm {\Gamma }(y){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\psi (z)$
with
![]() ${\mathrm {md}}(d'(y))={\mathrm {md}}(d')$
. Note also that no occurrence of y or z lies in the scope of a quantifier in
${\mathrm {md}}(d'(y))={\mathrm {md}}(d')$
. Note also that no occurrence of y or z lies in the scope of a quantifier in
![]() $\mathrm {\Gamma }(y){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\psi (z)$
. Hence, by Lemma 5.2, there exist a sentence
$\mathrm {\Gamma }(y){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\psi (z)$
. Hence, by Lemma 5.2, there exist a sentence
![]() $\chi $
and derivations
$\chi $
and derivations
![]() $d_1,d_2$
such that
$d_1,d_2$
such that ![]() and
and
Since
![]() $\chi $
is a sentence and x does not occur freely in
$\chi $
is a sentence and x does not occur freely in
![]() $\mathrm {\Gamma }(y)$
or
$\mathrm {\Gamma }(y)$
or
![]() $\psi (z)$
, we can assume that
$\psi (z)$
, we can assume that
![]() $d_1$
and
$d_1$
and
![]() $d_2$
do not contain any free occurrences of x, and, by substituting all occurrences of y in
$d_2$
do not contain any free occurrences of x, and, by substituting all occurrences of y in
![]() $d_1$
, and z in
$d_1$
, and z in
![]() $d_2$
, with x, obtain derivations
$d_2$
, with x, obtain derivations
![]() $d^{\prime }_1$
of
$d^{\prime }_1$
of
![]() $\mathrm {\Gamma }{{\vphantom {A}\Rightarrow {\vphantom {A}}}}\chi $
and
$\mathrm {\Gamma }{{\vphantom {A}\Rightarrow {\vphantom {A}}}}\chi $
and
![]() $d^{\prime }_2$
of
$d^{\prime }_2$
of
![]() $\chi {{\vphantom {A}\Rightarrow {\vphantom {A}}}}\psi (x)$
with
$\chi {{\vphantom {A}\Rightarrow {\vphantom {A}}}}\psi (x)$
with
![]() ${\mathrm {md}}(d^{\prime }_1)={\mathrm {md}}(d_1)$
and
${\mathrm {md}}(d^{\prime }_1)={\mathrm {md}}(d_1)$
and
![]() ${\mathrm {md}}(d^{\prime }_2)={\mathrm {md}}(d_2)$
. Hence, by the induction hypothesis twice,
${\mathrm {md}}(d^{\prime }_2)={\mathrm {md}}(d_2)$
. Hence, by the induction hypothesis twice, ![]() and
and ![]() . Since
. Since
![]() $((\forall {x})\chi )^\ast =\Box \chi ^\ast $
and
$((\forall {x})\chi )^\ast =\Box \chi ^\ast $
and
![]() $\chi $
is a sentence,
$\chi $
is a sentence,
![]() $\vDash _{\mathsf {mFL_e}}\chi ^\ast \approx ((\forall {x})\chi )^\ast $
, and hence the equations defining
$\vDash _{\mathsf {mFL_e}}\chi ^\ast \approx ((\forall {x})\chi )^\ast $
, and hence the equations defining
![]() $\mathsf {mFL_e}$
yield also
$\mathsf {mFL_e}$
yield also ![]() . So
. So ![]() .
.
Suppose finally that the last rule applied in d is
![]() $(\exists \,{\Rightarrow })$
, where
$(\exists \,{\Rightarrow })$
, where
![]() $\mathrm {\Gamma }$
is
$\mathrm {\Gamma }$
is
![]() $\mathrm {\Gamma }',(\exists {x})\psi (x)$
and x may occur freely in
$\mathrm {\Gamma }',(\exists {x})\psi (x)$
and x may occur freely in
![]() $\mathrm {\Gamma }'$
and
$\mathrm {\Gamma }'$
and
![]() $\mathrm {\Delta }$
. Then
$\mathrm {\Delta }$
. Then
![]() $d'\vdash _{_{\mathrm {\forall 1FL_e}}}\mathrm {\Gamma }',\psi (y){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }$
with
$d'\vdash _{_{\mathrm {\forall 1FL_e}}}\mathrm {\Gamma }',\psi (y){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }$
with
![]() ${\mathrm {md}}(d')={\mathrm {md}}(d)-1$
, where y is a variable distinct from x. We write
${\mathrm {md}}(d')={\mathrm {md}}(d)-1$
, where y is a variable distinct from x. We write
![]() $\mathrm {\Gamma }'(z)$
,
$\mathrm {\Gamma }'(z)$
,
![]() $\mathrm {\Delta }(z)$
, and
$\mathrm {\Delta }(z)$
, and
![]() $d'(z)$
to denote
$d'(z)$
to denote
![]() $\mathrm {\Gamma }'$
,
$\mathrm {\Gamma }'$
,
![]() $\mathrm {\Delta }$
, and
$\mathrm {\Delta }$
, and
![]() $d'$
with all free occurrences of x replaced by z. Clearly,
$d'$
with all free occurrences of x replaced by z. Clearly,
![]() $d'(z)\vdash _{_{\mathrm {\forall 1FL_e}}}\mathrm {\Gamma }'(z),\psi (y){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }(z)$
with
$d'(z)\vdash _{_{\mathrm {\forall 1FL_e}}}\mathrm {\Gamma }'(z),\psi (y){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }(z)$
with
![]() ${\mathrm {md}}(d'(z))={\mathrm {md}}(d')$
. By Lemma 5.2, there exist a sentence
${\mathrm {md}}(d'(z))={\mathrm {md}}(d')$
. By Lemma 5.2, there exist a sentence
![]() $\chi $
and derivations
$\chi $
and derivations
![]() $d_1,d_2$
such that
$d_1,d_2$
such that ![]() and
and
Since
![]() $\chi $
is a sentence and x does not occur freely in
$\chi $
is a sentence and x does not occur freely in
![]() $\psi (y)$
,
$\psi (y)$
,
![]() $\mathrm {\Gamma }'(z)$
, or
$\mathrm {\Gamma }'(z)$
, or
![]() $\mathrm {\Delta }(z)$
, we can assume that
$\mathrm {\Delta }(z)$
, we can assume that
![]() $d_1$
and
$d_1$
and
![]() $d_2$
do not contain any free occurrences of x, and, by substituting all occurrences of y in
$d_2$
do not contain any free occurrences of x, and, by substituting all occurrences of y in
![]() $d_1$
, and z in
$d_1$
, and z in
![]() $d_2$
, with x, obtain derivations
$d_2$
, with x, obtain derivations
![]() $d^{\prime }_1$
of
$d^{\prime }_1$
of
![]() $\psi (x){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\chi $
and
$\psi (x){{\vphantom {A}\Rightarrow {\vphantom {A}}}}\chi $
and
![]() $d^{\prime }_2$
of
$d^{\prime }_2$
of
![]() $\mathrm {\Gamma }',\chi {{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }$
with
$\mathrm {\Gamma }',\chi {{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }$
with
![]() ${\mathrm {md}}(d^{\prime }_1)={\mathrm {md}}(d_1)$
and
${\mathrm {md}}(d^{\prime }_1)={\mathrm {md}}(d_1)$
and
![]() ${\mathrm {md}}(d^{\prime }_2)={\mathrm {md}}(d_2)$
. Hence, by the induction hypothesis,
${\mathrm {md}}(d^{\prime }_2)={\mathrm {md}}(d_2)$
. Hence, by the induction hypothesis, ![]() and
and ![]() . Since
. Since
![]() $((\exists {x})\chi )^\ast =\Diamond \chi ^\ast $
and
$((\exists {x})\chi )^\ast =\Diamond \chi ^\ast $
and
![]() $\chi $
is a sentence,
$\chi $
is a sentence,
![]() $\vDash _{\mathsf {mFL_e}}\chi ^\ast \approx ((\exists {x})\chi )^\ast $
, and hence the equations defining
$\vDash _{\mathsf {mFL_e}}\chi ^\ast \approx ((\exists {x})\chi )^\ast $
, and hence the equations defining
![]() $\mathsf {mFL_e}$
yield also
$\mathsf {mFL_e}$
yield also ![]() . So
. So ![]() .
.
The proof-theoretic strategy described above extends easily to varieties of
![]() $\mathsf {FL_e}$
-algebras axiomatized relative to
$\mathsf {FL_e}$
-algebras axiomatized relative to
![]() $\mathsf {FL_e}$
by equations of a certain simple form. Given a variable x, let
$\mathsf {FL_e}$
by equations of a certain simple form. Given a variable x, let
![]() $x^0:=\mathrm {e}$
and
$x^0:=\mathrm {e}$
and
![]() $x^{k+1}:=x\cdot x^k$
, for each
$x^{k+1}:=x\cdot x^k$
, for each
![]() $k\in \mathbb {N}$
, and given a multiset
$k\in \mathbb {N}$
, and given a multiset
![]() $\Pi $
and
$\Pi $
and
![]() $k\in \mathbb {N}$
, let
$k\in \mathbb {N}$
, let
![]() $\Pi ^k$
denote the multiset union of k copies of
$\Pi ^k$
denote the multiset union of k copies of
![]() $\Pi $
. Now let S be the set of equations
$\Pi $
. Now let S be the set of equations ![]() , and define sequent rules
, and define sequent rules

Given any
![]() $S'\subseteq S$
, denote by
$S'\subseteq S$
, denote by
![]() $\mathsf {FL_e}+S'$
the variety of
$\mathsf {FL_e}+S'$
the variety of
![]() $\mathsf {FL_e}$
-algebras axiomatized relative to
$\mathsf {FL_e}$
-algebras axiomatized relative to
![]() $\mathsf {FL_e}$
by the equations in
$\mathsf {FL_e}$
by the equations in
![]() $S'$
, and by
$S'$
, and by
![]() ${\mathrm {\forall 1FL_e}}+r(S')$
the sequent calculus
${\mathrm {\forall 1FL_e}}+r(S')$
the sequent calculus
![]() ${\mathrm {\forall 1FL_e}}$
extended with the rules
${\mathrm {\forall 1FL_e}}$
extended with the rules
![]() $r(\varepsilon )$
for each equation
$r(\varepsilon )$
for each equation
![]() $\varepsilon $
in
$\varepsilon $
in
![]() $S'$
. Then for any sequent
$S'$
. Then for any sequent
![]() $\mathrm {\Gamma }{{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }$
containing formulas from
$\mathrm {\Gamma }{{\vphantom {A}\Rightarrow {\vphantom {A}}}}\mathrm {\Delta }$
containing formulas from
![]() $\mathrm {Fm}_{\forall }^{1}$
(see, e.g., [Reference Komori18, Reference Ono and Komori23]),
$\mathrm {Fm}_{\forall }^{1}$
(see, e.g., [Reference Komori18, Reference Ono and Komori23]),
Moreover, the additional cases required to adapt the proof of Lemma 5.2 to
![]() ${\mathrm {\forall 1FL_e}}+r(S')$
are straightforward, since each application of a rule
${\mathrm {\forall 1FL_e}}+r(S')$
are straightforward, since each application of a rule
![]() $r(\varepsilon )$
for
$r(\varepsilon )$
for
![]() $\varepsilon \in S'$
has just one premise. Hence, following the proof of Theorem 5.3 yields the following more general result.
$\varepsilon \in S'$
has just one premise. Hence, following the proof of Theorem 5.3 yields the following more general result.
Theorem 5.4. For any
![]() $S'\subseteq S$
and set
$S'\subseteq S$
and set
![]() $T\cup \{\varphi \approx \psi \}$
of
$T\cup \{\varphi \approx \psi \}$
of
![]() $\mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
-equations,
$\mathrm {Fm}_{\forall }^{1}(\mathcal {L})$
-equations,
In particular, we obtain alternative proof-theoretic proofs of completeness for the axiomatizations of the one-variable fragments of the first-order extensions of
![]() $\mathrm {FL_{ew}}$
,
$\mathrm {FL_{ew}}$
,
![]() $\mathrm {FL_{ec}}$
, and
$\mathrm {FL_{ec}}$
, and
![]() $\mathrm {FL_{ewc}}$
(intuitionistic logic).
$\mathrm {FL_{ewc}}$
(intuitionistic logic).
6 Concluding remarks
Let us conclude this paper by mentioning some interesting directions for further research. The most general challenge for a class
![]() $\mathsf {K}$
of
$\mathsf {K}$
of
![]() $\mathcal {L}$
-lattices may be stated as follows: provide a (natural) axiomatization of the equational consequence relation
$\mathcal {L}$
-lattices may be stated as follows: provide a (natural) axiomatization of the equational consequence relation
![]() $\vDash ^{\forall }_{\mathsf {K}}$
, or, equivalently, in algebraic terms, provide a (natural) axiomatization of the generalized quasivariety generated by the class of all
$\vDash ^{\forall }_{\mathsf {K}}$
, or, equivalently, in algebraic terms, provide a (natural) axiomatization of the generalized quasivariety generated by the class of all ![]() -functional m-
-functional m-
![]() $\mathcal {L}$
-lattices where
$\mathcal {L}$
-lattices where
![]() $\mathbf {A}\in \mathsf {K}$
and W is any set. In this paper, we have shown that when
$\mathbf {A}\in \mathsf {K}$
and W is any set. In this paper, we have shown that when
![]() $\mathsf {K}$
is a variety of
$\mathsf {K}$
is a variety of
![]() $\mathcal {L}$
-lattices that has the superamalgamation property, the required generalized quasivariety is the variety
$\mathcal {L}$
-lattices that has the superamalgamation property, the required generalized quasivariety is the variety
![]() $\mathsf {mK}$
of m-
$\mathsf {mK}$
of m-
![]() $\mathcal {L}$
-lattices (Corollary 4.2), axiomatized relative to
$\mathcal {L}$
-lattices (Corollary 4.2), axiomatized relative to
![]() $\mathsf {K}$
by a set of axioms familiar from modal logic. However, if
$\mathsf {K}$
by a set of axioms familiar from modal logic. However, if
![]() $\mathsf {K}$
lacks the superamalgamation property or is not a variety, further axioms may be required.
$\mathsf {K}$
lacks the superamalgamation property or is not a variety, further axioms may be required.
One potential generalization is to consider varieties of
![]() $\mathcal {L}$
-lattices that have the weaker super generalized amalgamation property, which corresponds for substructural logics (even those without exchange) to the Craig interpolation property [Reference Galatos, Jipsen, Kowalski and Ono13]. In particular, such a result would yield an axiomatization for the one-variable fragment of the first-order version of the full Lambek Calculus
$\mathcal {L}$
-lattices that have the weaker super generalized amalgamation property, which corresponds for substructural logics (even those without exchange) to the Craig interpolation property [Reference Galatos, Jipsen, Kowalski and Ono13]. In particular, such a result would yield an axiomatization for the one-variable fragment of the first-order version of the full Lambek Calculus
![]() $\mathrm {FL}$
, although we conjecture that completeness would hold only for valid equations and not consequences. Alternatively, such a generalization might be established proof-theoretically for first-order versions of substructural logics like
$\mathrm {FL}$
, although we conjecture that completeness would hold only for valid equations and not consequences. Alternatively, such a generalization might be established proof-theoretically for first-order versions of substructural logics like
![]() $\mathrm {FL}$
that have a cut-free sequent calculus, by lifting the proof-theoretic strategy presented in Section 5 to sequents based on sequences of formulas.
$\mathrm {FL}$
that have a cut-free sequent calculus, by lifting the proof-theoretic strategy presented in Section 5 to sequents based on sequences of formulas.
A further interesting line of inquiry concerns the case where
![]() $\mathsf {K}$
consists of the totally ordered members of a variety of
$\mathsf {K}$
consists of the totally ordered members of a variety of
![]() $\mathcal {L}$
-lattices, and hence forms a positive universal class. First, let
$\mathcal {L}$
-lattices, and hence forms a positive universal class. First, let
![]() $\mathsf {V}$
be any variety of semilinear
$\mathsf {V}$
be any variety of semilinear
![]() $\mathrm {FL_e}$
-algebras:
$\mathrm {FL_e}$
-algebras:
![]() $\mathcal {L}_s$
-lattices that are isomorphic to a subdirect product of totally ordered
$\mathcal {L}_s$
-lattices that are isomorphic to a subdirect product of totally ordered
![]() $\mathrm {FL_e}$
-algebras. It is not hard to show that in this case,
$\mathrm {FL_e}$
-algebras. It is not hard to show that in this case,
![]() $\vDash ^{\forall }_{\mathsf {V}}(\exists {x})\varphi \cdot (\exists {x})\varphi \approx (\exists {x})(\varphi \cdot \varphi )$
. However, if
$\vDash ^{\forall }_{\mathsf {V}}(\exists {x})\varphi \cdot (\exists {x})\varphi \approx (\exists {x})(\varphi \cdot \varphi )$
. However, if ![]() (e.g., if
(e.g., if
![]() $\mathsf {V}$
is
$\mathsf {V}$
is
![]() $\mathsf {MV}$
or the variety of all semilinear
$\mathsf {MV}$
or the variety of all semilinear
![]() $\mathrm {FL_e}$
-algebras), then
$\mathrm {FL_e}$
-algebras), then
![]() $\not \vDash _{\mathsf {mV}}\Diamond x\cdot \Diamond x \approx \Diamond (x\cdot x)$
, as proved in Example 3.2, so
$\not \vDash _{\mathsf {mV}}\Diamond x\cdot \Diamond x \approx \Diamond (x\cdot x)$
, as proved in Example 3.2, so
![]() $\mathsf {mV}$
does not correspond to the one-variable fragment of the first-order logic based on
$\mathsf {mV}$
does not correspond to the one-variable fragment of the first-order logic based on
![]() $\mathsf {V}$
.
$\mathsf {V}$
.
Now let
![]() $\mathsf {V_{to}}$
be the class of totally ordered members of
$\mathsf {V_{to}}$
be the class of totally ordered members of
![]() $\mathsf {V}$
. Then not only
$\mathsf {V}$
. Then not only
![]() $\vDash ^{\forall }_{\mathsf {V_{to}}}(\exists {x})\varphi \cdot (\exists {x})\varphi \approx (\exists {x})(\varphi \cdot \varphi )$
, but also
$\vDash ^{\forall }_{\mathsf {V_{to}}}(\exists {x})\varphi \cdot (\exists {x})\varphi \approx (\exists {x})(\varphi \cdot \varphi )$
, but also ![]() , where x does not occur in
, where x does not occur in
![]() $\psi $
. Although a general approach to obtaining axiomatizations of the one-variable fragments of the first-order logics based on
$\psi $
. Although a general approach to obtaining axiomatizations of the one-variable fragments of the first-order logics based on
![]() $\mathsf {V}$
and
$\mathsf {V}$
and
![]() $\mathsf {V_{to}}$
is lacking, success for specific cases indicate a possible way forward. Most notably, the one-variable fragment of first-order Łukasiewicz logic can be defined over the class
$\mathsf {V_{to}}$
is lacking, success for specific cases indicate a possible way forward. Most notably, the one-variable fragment of first-order Łukasiewicz logic can be defined over the class
![]() $\mathsf {MV_{to}}$
of totally ordered MV-algebras and corresponds to the variety of monadic MV-algebras, defined relative to
$\mathsf {MV_{to}}$
of totally ordered MV-algebras and corresponds to the variety of monadic MV-algebras, defined relative to
![]() $\mathsf {mMV}$
by
$\mathsf {mMV}$
by
![]() $\Diamond x\cdot \Diamond x \approx \Diamond (x\cdot x)$
and
$\Diamond x\cdot \Diamond x \approx \Diamond (x\cdot x)$
and ![]() [Reference Rutledge26]. Interestingly, a proof of this latter result is given in [Reference Castaño, Cimadamore, Varela and Rueda8] using the fact that
[Reference Rutledge26]. Interestingly, a proof of this latter result is given in [Reference Castaño, Cimadamore, Varela and Rueda8] using the fact that
![]() $\mathsf {MV_{to}}$
has the amalgamation property (see also [Reference Metcalfe, Tuyt, Olivetti, Negri, Sandu and Verbrugge21, Reference Tuyt29] for related results), suggesting that the approach developed in this paper might be adapted to one-variable fragments of first-order logics based on classes of totally ordered algebras that have the amalgamation property.
$\mathsf {MV_{to}}$
has the amalgamation property (see also [Reference Metcalfe, Tuyt, Olivetti, Negri, Sandu and Verbrugge21, Reference Tuyt29] for related results), suggesting that the approach developed in this paper might be adapted to one-variable fragments of first-order logics based on classes of totally ordered algebras that have the amalgamation property.
Acknowledgements
The authors would like to thank the anonymous referee for their careful reading of the paper and valuable comments.
Funding
The first author was supported by RVO 67985807 and Czech Science Foundation grant GA22-01137S, and the second two authors by Swiss National Science Foundation grant 200021_215157. This project has also received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie Grant Agreement No. 101007627.