Article contents
NEW GENERALISATIONS OF VAN HAMME’S (G.2) SUPERCONGRUENCE
Published online by Cambridge University Press: 18 May 2022
Abstract
Swisher [‘On the supercongruence conjectures of van Hamme’, Res. Math. Sci. 2 (2015), Article no. 18] and He [‘Supercongruences on truncated hypergeometric series’, Results Math. 72 (2017), 303–317] independently proved that Van Hamme’s (G.2) supercongruence holds modulo
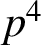 $p^4$
for any prime
$p^4$
for any prime
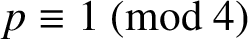 $p\equiv 1\pmod {4}$
. Swisher also obtained an extension of Van Hamme’s (G.2) supercongruence for
$p\equiv 1\pmod {4}$
. Swisher also obtained an extension of Van Hamme’s (G.2) supercongruence for
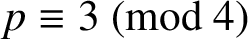 $p\equiv 3 \pmod 4$
and
$p\equiv 3 \pmod 4$
and
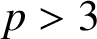 $p>3$
. In this note, we give new one-parameter generalisations of Van Hamme’s (G.2) supercongruence modulo
$p>3$
. In this note, we give new one-parameter generalisations of Van Hamme’s (G.2) supercongruence modulo
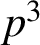 $p^3$
for any odd prime p. Our proof uses the method of ‘creative microscoping’ introduced by Guo and Zudilin [‘A q-microscope for supercongruences’, Adv. Math. 346 (2019), 329–358].
$p^3$
for any odd prime p. Our proof uses the method of ‘creative microscoping’ introduced by Guo and Zudilin [‘A q-microscope for supercongruences’, Adv. Math. 346 (2019), 329–358].
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
References
- 2
- Cited by



