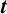 $\boldsymbol {t}$
$\boldsymbol {t}$
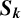 $\boldsymbol {S_k}$
-MEASURE OF TOTALLY POSITIVE ALGEBRAIC INTEGERS
$\boldsymbol {S_k}$
-MEASURE OF TOTALLY POSITIVE ALGEBRAIC INTEGERS
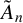 $\tilde {A}_n$
OVER FINITE FIELDS
$\tilde {A}_n$
OVER FINITE FIELDS
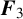 $\boldsymbol F_3$
$\boldsymbol F_3$
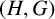 $(H, G)$
-COINCIDENCES SET IN REPRESENTATION SPHERES
$(H, G)$
-COINCIDENCES SET IN REPRESENTATION SPHERES
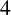 $4$
-MANIFOLDS
$4$
-MANIFOLDS
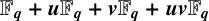 $\boldsymbol {\mathbb {F}_q+u\mathbb {F}_q+v\mathbb {F}_q+uv\mathbb {F}_q}$
$\boldsymbol {\mathbb {F}_q+u\mathbb {F}_q+v\mathbb {F}_q+uv\mathbb {F}_q}$