No CrossRef data available.
Article contents
ESTIMATING THE SIZE OF THE 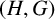 $(H, G)$-COINCIDENCES SET IN REPRESENTATION SPHERES
$(H, G)$-COINCIDENCES SET IN REPRESENTATION SPHERES
Published online by Cambridge University Press: 17 October 2022
Abstract
Let W be a real vector space and let V be an orthogonal representation of a group G such that
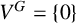 $V^{G} = \{0\}$
(for the set of fixed points of G). Let
$V^{G} = \{0\}$
(for the set of fixed points of G). Let
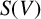 $S(V)$
be the sphere of V and suppose that
$S(V)$
be the sphere of V and suppose that
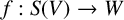 $f: S(V) \to W$
is a continuous map. We estimate the size of the
$f: S(V) \to W$
is a continuous map. We estimate the size of the
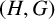 $(H, G)$
-coincidences set if G is a cyclic group of prime power order
$(H, G)$
-coincidences set if G is a cyclic group of prime power order
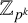 $\mathbb {Z}_{p^k}$
or a p-torus
$\mathbb {Z}_{p^k}$
or a p-torus
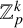 $\mathbb {Z}_p^k$
.
$\mathbb {Z}_p^k$
.
MSC classification
Primary:
55M20: Fixed points and coincidences
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
References
Blagojević, P. V. M., Frick, F. and Ziegler, G., ‘Counterexamples to the Topological Tverberg Conjecture and other applications of the constraint method’, J. Eur. Math. Soc. (JEMS) 21 (2019), 2107–2116.CrossRefGoogle Scholar
Błaszczyk, Z., Marzantowicz, W. and Singh, M., ‘Equivariant maps between representation spheres’, Bull. Belg. Math. Soc. Simon Stevin 24(4) (2017), 621–630.10.36045/bbms/1515035011CrossRefGoogle Scholar
Błaszczyk, Z., Marzantowicz, W. and Singh, M., ‘General Bourgin–Yang theorems’, Topology Appl. 249 (2018), 112–126.10.1016/j.topol.2018.09.010CrossRefGoogle Scholar
Bredon, G. E., Introduction to Compact Transformation Groups, Pure and Applied Mathematics, 46 (Academic Press, New York, 1972).Google Scholar
de Mattos, D., dos Santos, E. L. and Souza, T. O., ‘
 $\left(H,G\right)$
-coincidence theorems for manifolds and a topological Tverberg type theorem for any natural number
$\left(H,G\right)$
-coincidence theorems for manifolds and a topological Tverberg type theorem for any natural number
 $r$
’, Bull. Belg. Math. Soc. Simon Stevin 24 (2017), 567–579.10.36045/bbms/1515035007CrossRefGoogle Scholar
$r$
’, Bull. Belg. Math. Soc. Simon Stevin 24 (2017), 567–579.10.36045/bbms/1515035007CrossRefGoogle Scholar
Gonçalves, D. L., Jaworowski, J and Pergher, P. L. Q., ‘Measuring the size of the coincidence set’, Topology Appl. 125 (2002), 465–470.CrossRefGoogle Scholar
Gonçalves, D. L., Jaworowski, J., Pergher, P. L. Q. and Volovikov, A. Y., ‘Coincidences for maps of spaces with finite group actions’, Topology Appl. 145(1–3) (2004), 61–68.CrossRefGoogle Scholar
Marzantowicz, W., de Mattos, D. and dos Santos, E. L., ‘Bourgin–Yang version of the Borsuk–Ulam theorem for
 ${\mathbb{Z}}_{p^k}$
-equivariant maps’, Algebr. Geom. Topol. 12 (2012), 2245–2258.CrossRefGoogle Scholar
${\mathbb{Z}}_{p^k}$
-equivariant maps’, Algebr. Geom. Topol. 12 (2012), 2245–2258.CrossRefGoogle Scholar
Marzantowicz, W., de Mattos, D. and dos Santos, E. L., ‘Bourgin–Yang version of the Borsuk–Ulam theorem for
 $p$
-toral groups’, J. Fixed Point Theory Appl. 19 (2017), 1427–1437.CrossRefGoogle Scholar
$p$
-toral groups’, J. Fixed Point Theory Appl. 19 (2017), 1427–1437.CrossRefGoogle Scholar
Serre, J.-P., Linear Representations of Finite Groups, Graduate Texts in Mathematics, 42 (Springer, New York, 1977).CrossRefGoogle Scholar



