Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-19T10:55:32.303Z Has data issue: false hasContentIssue false
  • English
  • Français

An Elementary Proof of the Prime-Number Theorem for Arithmetic Progressions

Published online by Cambridge University Press:  20 November 2018

Atle Selberg
Atle Selberg*
Affiliation:
The Institute for Advanced Study and Syracuse University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we shall give an elementary proof of the theorem

(1.1)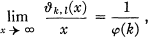

where φ(k) denotes Euler's function, and

(1.2)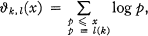

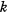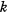where p denotes the prime, and and are integers with (,) = 1, positive.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 2 , 1950 , pp. 66 - 78
Copyright
Copyright © Canadian Mathematical Society 1950

References

1 “An Elementary Proof of the Prime-number Theorem,” Ann. of Math., vol. 50 (1949), 305–313.Google Scholar

2 “An Elementary Proof of Dirichlet's Theorem about Primes in an Arithmetic Progression,” Ann. of Math., vol. 50 (1949), 297–304.Google Scholar

3 We write instead of where no misunderstanding can occur.Google Scholar

4 Instead of (2.8) we might use the somewhat sharper inequality

which can be proved in a similar way.

5 See for instance Dirichlet-Dedekind: Vorlesungen iiber Zahlentheorie (the beginning of §135)

6 For example, by showing that the number of terms with .

7 For example, by noting that a “period-parallelogram“ may always be chosen so that neither of its sides is greater than a diagonal.

8 Or, otherwise expressed, that the lattice may be built up of “period-parallelograms“ with both sides .

9 By residues, we understand here residues belonging to the reduced residue system.

10 By values we mean here residues mod .

11 For there is then a y in the interval with .

12 For there is then a y in the interval with .